新型直圆导角复合型多轴柔性铰链的柔度计算及其性能分析

刘庆玲 罗 萍 于常娟

廊坊师范学院数学与信息科学学院，廊坊，065000

摘要：设计出一种新型多轴柔性铰链——直圆导角复合型多轴柔性铰链，以卡氏第二定理为理论基础，推导了柔度计算式。利用所得结果进行实例计算，并进行有限元分析，通过结果对比验证了计算式的正确性。定义了铰链的厚长比λ，分析了柔度相对误差与λ之间的关系。利用所得柔度计算式，分析了铰链结构参数对其柔度的影响。通过与直圆型多轴柔性铰链的对比，得出直圆导角复合型多轴柔性铰链的转动能力与对载荷的敏感性均优于前者的结论。

关键词：复合型多轴柔性铰链；直圆导角；柔度；有限元；厚长比

0 引言

柔性铰链是构成柔性机构的最基本柔性结构，是影响柔性机构整体性能的关键［1⁃2］。柔度是柔性铰链最重要的性能参数，柔度矩阵能够反映出不同方向上铰链所承受载荷与对应变形之间的解析映射关系［3⁃5］。依据柔性铰链的结构特点以及传递运动和能量的方向，柔性铰链可分为单轴、双轴与多轴柔性铰链。双轴、多轴柔性铰链具有多个转动自由度，可用于三维空间的运动。根据铰链切口轮廓曲线形状的不同，柔性铰链可分为柱形、圆弧形（直圆形）、导角形、椭圆形等不同类型，分别满足不同运动范围及运动精度的要求［6⁃8］。文献［9⁃11］针对圆弧型、直圆型、椭圆型多轴柔性铰链的柔度进行了研究，得出了柔度计算式。

为了综合利用不同类型多轴柔性铰链的优势，本文提出一种直圆导角复合型多轴柔性铰链，利用卡氏第二定理，导出其柔度计算式，同时采用有限元法对其进行验证分析，并对复合型多轴柔性铰链的性能进行研究。

1 直圆导角复合型多轴柔性铰链的柔度计算

直圆导角复合型多轴柔性铰链是由半个直圆型多轴柔性铰链、半个导角型多轴柔性铰链组合而成的，其结构如图1所示。图1中，R为直圆半径，r为导角半径，l为铰链的长度，t为铰链截面最小直径，固定端距离为x的任意截面的横截面直径为t（x）。

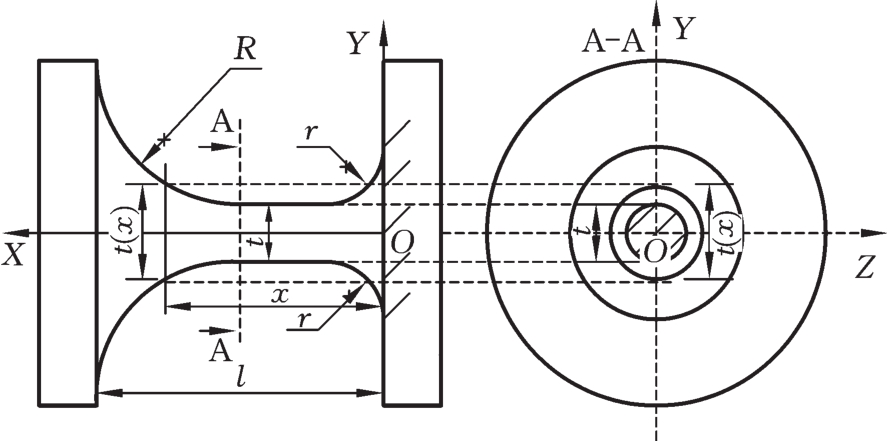
图1 直圆导角复合型多轴柔性铰链结构示意图
Fig.1 Sketch of right circular-corner filleted hybrid multiple-axis flexure hinge

设复合型多轴柔性铰链右端固定，左端为自由端，考虑一般情况，自由端承受力F1x、F1y、F1z和力矩 M1x、M1y、M1z的共同作用，如图 2 所示。铰链的变形是由力和力矩共同产生的，以铰链固定端为坐标原点，建立图2所示坐标系，图中，1表示铰链自由端，2表示铰链的中心。基于卡氏第二定理对多轴柔性铰链的变形进行分析，用铰链自由端1处的变形表征其柔度。

图2 多轴柔性铰链受力分析示意图
Fig.2 Sketch of flexure hinge load

依据多轴柔性铰链的运动特性，由卡式第二定理可得柔性铰链在自由端处的变形与载荷的关系：

式中，u1x、u1y、u1z分别为自由端处沿X、Y、Z轴的位移；θ1x、θ1y、θ1z分别为自由端处绕X、Y、Z轴的转角；C为多轴柔性铰链的柔度矩阵。

依 据 矩 阵 互 等 定 理 ，有 C1,y⁃Mz=C1,θz⁃Fy，C1,z⁃My=C1,θy⁃Fz。

对式（1）中各位移矢量应用卡式第二定理，有

式中，U为多轴柔性铰链的变形能，包括轴向拉伸变形能、弯曲变形能（包括对Z轴、Y轴的弯曲变形能）及扭转变形能。

根据多轴柔性铰链空间多自由度的运动特性及其承受的载荷，由材料力学可得多轴柔性铰链的变形能U：

式中，Uax为X方向的拉伸变形能；Uby、Ubz为相对Y轴、Z轴的弯曲变形能；Ut为扭转变形能；E为材料的弹性模量；G为材料的剪切模量；A（x）为铰链上任意位置处的横截面积；Iy（x）、Iz（x）为铰链上任意位置处相对于Y、Z轴的截面惯性矩；J（x）为铰链上任意位置处的截面极惯性矩。

依据图2中多轴柔性铰链的承载特点，式（4）中的各力与力矩分别为

依据多轴柔性铰链横截面的对称性（图1）可得 Iy（x）=Iz（x）=I（x），故 有 C1,y⁃Fy=C1,z⁃Fz，C1,θy⁃My=C1,θz⁃Mz，C1,y⁃Mz=C1,z⁃My。

图1中，直圆导角复合型多轴柔性铰链上距固定端距离为x的任意截面的横截面直径为t（x），该处的横截面积、截面惯性矩、极惯性矩分别为

将式（5）、式（6）代入式（4），再代入式（3），将所得变形能代入式（2），则由式（1）可得各柔度项。设定积分计算式如下：

可得直圆导角复合型多轴柔性铰链各柔度项计算式：

由图1可得直圆导角复合型多轴柔性铰链上任意位置处横截面的直径t(x)：

将式（8）代入式（7）进行积分，即可得各柔度项计算式。为了简化计算，采用分段积分法，各部分的积分变量选取如下：直圆部分选取直圆圆弧的圆心角为积分变量，设为θ1，则有t1（θ1）=t+2R（1-cosθ1），积分区间为［0，π/2］；导角部分以导角圆弧的圆心角为积分变量，设为θ2，则有t2（θ2）=t+2r（1-cosθ2），积分区间为［-π/2，0］；直梁部分以x为积分变量，积分区间为［r，l/2］；设t/（2R）+1=c1，t/（2r）+1=c2［12］。

采用新的积分变量进行积分，简化了积分计算过程。求得直圆导角复合型多轴柔性铰链的各柔度：

2 柔度实例计算及有限元验证

2.1 实例计算

直圆导角复合型多轴柔性铰链结构如图1所示，材料为铍青铜，弹性模量E=126 GPa，泊松比µ=0.35。给定几何参数如下：铰链长度l=20 mm，直圆半径R=10 mm，导角半径r=5 mm，改变最小截面直径t的值，使其分别取1，2，3，4，5，6，7，8 mm，采用式（9）计算各柔度项，计算结果列于表1。

表1 柔度计算结果与有限元分析结果
Tab.1 Results of compliance computation and finite element

t(mm)1 2 3 4 5 6 7 8解析解有限元解解析解有限元解解析解有限元解解析解有限元解解析解有限元解解析解有限元解解析解有限元解解析解有限元解C1,x⁃Fx(m/N)1.323 4×10-71.378 9×10-74.042 1×10-84.195 7×10-82.020 4×10-82.123 4×10-81.232 6×10-81.293 0×10-88.382 9×10-98.894 2×10-96.106 6×10-96.363 1×10-94.665 4×10-94.995 7×10-93.689 0×10-93.925 1×10-9C1,y⁃Fy(m/N)7.706 2×10⁃58.114 6×10-55.615 0×10-66.047 3×10-61.231 8×10-61.343 9×10-64.226 2×10-74.793 3×10-71.849 4×10-72.216 4×10-79.430 5×10-811.709 9×10-85.341 6×10-86.958 9×10-83.266 3×10-84.616 8×10-8C1,y⁃Mz(N⁃1)9.427 5×10⁃39.880 1×10-36.733 7×10-47.144 4×10-41.453 6×10-41.564 8×10-44.917 7×10-55.360 9×10-52.125 3×10-52.499 5×10-51.071 7×10-51.293 9×10-50.600 9×10-50.761 1×10-50.364 1×10-50.477 8×10-5C1,θx⁃Mx(rad/(N ·m))1.663 5 1.745 1 0.118 2 0.125 8 2.543 3×10-22.713 7×10-28.581 4×10-39.302 2×10-33.700 5×10-34.225 9×10-31.862 5×10-32.179 1×10-31.042 5×10-31.230 1×10-30.630 6×10-30.763 0×10-3C1,θz⁃Mz(rad/(N ·m))1.232 2 1.279 0 8.756 7×10-29.151 7×10-21.883 9×10-21.983 1×10-26.356 6×10-36.858 8×10-32.741 1×10-33.155 0×10-31.379 6×10-31.647 2×10-30.772 2×10-30.953 5×10-30.467 1×10-30.590 1×10-3

2.2 有限元分析

采用有限元法对文中的柔度计算式进行验证，ANSYS环境中选取Solid186单元类型，按照实例中给定的直圆导角复合型多轴柔性铰链的几何参数建立对应的有限元模型，划分网格，施加约束，t=2 mm对应的有限元模型如图3所示。在铰链末端施加单位载荷F1x=F1y=F1z=1 N，M1x=M1y=M1z=1N·m，其自由端的变形为柔度，变形结果列于表1。

图3 直圆导角复合型多轴柔性铰链有限元模型（R=10 mm，r=5 mm，t=2 mm）
Fig.3 Finite element model of right circular-corner filleted hybrid multiple-axis flexure hinge（R=10 mm，r=5 mm，t=2 mm）

2.3 结果分析

利用表1数据分析柔度计算结果相对于有限元仿真结果的相对误差。定义铰链的厚长比λ=t/l（铰链长度l=2R）。

由表1中的数据可以看出，柔度项C1,x⁃Fx的误差随着厚长比λ的变化基本在7%以内；其余柔度项的误差随着厚长比的增加呈明显增大趋势，柔度项C1,y⁃Fy最为显著。厚长比λ≤0.2时，所有柔度项的误差在12%以内；厚长比λ＞0.2时，除C1,x⁃Fx之外的各柔度项误差明显增大，最大误差接近30%。

上述柔度项的计算未考虑剪切的影响，然而随着铰链厚长比的增大，剪切对Y向线变形的影响最为显著，影响程度与铰链厚长比成正比，这是造成误差增大的主要原因（考虑剪切影响的厚长比另文阐述）。由表1中数据可以看出，文中的柔度计算式所得结果与有限元结果具有一致的变化趋势，在一定参数范围内，验证了文中所得柔度计算式的正确性，同时也表明，在某些参数范围内，剪切的影响不能忽略。

3 直圆导角复合型多轴柔性铰链的性能分析

由直圆导角复合型多轴柔性铰链的柔度计算式可知，各柔度项取决于铰链的材料及其结构参数。所有柔度项均与材料的弹性模量E或剪切模量G成反比，与直圆半径R成正比。铰链的导角半径r、最小截面直径t对各柔度项的影响具体分析如下。

3.1 铰链导角半径r对柔度的影响

选取一组具有不同导角半径的直圆导角复合型多轴柔性铰链，材料同前，直圆半径R=10 mm，最小截面直径t=2 mm，导角半径r分别为2 mm、4 mm、6 mm、8 mm、10 mm。采用式（9）计算铰链各柔度项，结果列于表2。

表2 不同导角半径直的计算柔度
Tab.2 Compliance computation under the different filleted radius

C1,x⁃Fx r C1,y⁃Fy C1,y⁃Mz C1,θx⁃Mx C1,θz⁃Mz（mm）2 4 6 8 1 0（10-8m/N）4.303 4 4.152 7 3.917 3 3.637 2 3.328 8（10-6m/N）6.609 4 5.648 3 5.540 2 5.206 8 4.525 9（10-4N-1）7.217 6 6.967 8 6.422 4 5.560 1 4.368 7（rad/（N·m））0.151 0 0.129 5 0.106 7 0.083 0 0.059 0（rad/（N·m））0.111 8 0.096 0 0.079 0 0.061 5 0.043 7

由表2数据可得，随着导角半径r的增大，复合型多轴柔性铰链的柔度减小。导角半径r=2 mm的铰链的转动能力和对轴向载荷的敏感程度近似为导角半径r=10 mm的铰链的2.6倍和1.4倍。当r=10 mm时，直圆导角复合型多轴柔性铰链变为直圆型多轴柔性铰链，可明显看出，直圆导角复合型多轴柔性铰链的柔度优于直圆型多轴柔性铰链，能够获得更大的运动范围。

3.2 最小截面直径t对柔度的影响

由表1数据可明显看出，t=1 mm对应的各柔度远远大于t=2 mm对应的各柔度，随着t的增大，各柔度明显减小。柔度对参数t的变化最为敏感，故铰链最小截面直径是影响铰链性能最重要的结构参数。

4 结论

（1）设计出一种新型多轴柔性铰链——直圆导角复合型多轴柔性铰链，依据卡式第二定理，建立直圆导角复合型多轴柔性铰链的柔度矩阵。采用分段积分法，分别选择直圆圆弧、导角圆弧所对应的圆心角为积分变量，简化了计算过程，得出直圆导角复合型多轴柔性铰链的柔度计算式。

（2）选择一组具有不同最小截面直径的直圆导角复合型多轴柔性铰链，采用文中得出的柔度计算式进行实例计算，同时对其进行有限元分析，在一定参数范围内验证了柔度计算式的正确性。

（3）定义铰链的厚长比λ，分析了各柔度项的相对误差与厚长比λ之间的关系，厚长比λ≤0.2时，所有柔度项的误差在12%以内；厚长比λ＞0.2时，除C1,x⁃Fx之外的各柔度项误差明显增大，最大误差接近30%。剪切影响是造成柔度计算误差增大的主要原因，一定参数范围内，不能忽略剪切的影响。

（4）利用所得的柔度计算式，通过实例计算，分析了直圆导角复合型多轴柔性铰链的导角半径r与最小截面直径t对各柔度项的影响；同时指出直圆导角复合型多轴柔性铰链的柔度以及对轴向载荷的敏感性均优于直圆型多轴柔性铰链。

参考文献：

［1］ PAROS J M，WEISBORO L.How to Design Flex⁃ure Hinges［J］.Machine Design，1965，37（27）：151⁃157

［2］ 刘庆玲,翁海珊,邱丽芳.微位移机构中变截面柔性铰链等效刚度的求解方法研究［J］.中国机械工程，2010，21（8）：917⁃919 LIU Qingling，WENG Haishan，QIU Lifang.Study on the Equivalent Stiffness of a Flexure Hinge and Its Application in Micro⁃displacement Compliant Mechanism ［J］.China MechanicalEngineering，2010，21（8）：917⁃919

［3］ 卢倩,黄卫清,王寅,等.深切口椭圆柔性铰链优化设计［J］.光学精密工程，2015，23（1）：206⁃215.LU Qian，HUANG Weiqing，WANG Yin，et al.Op⁃timization Design of Deep⁃notch Elliptical Flexure Hinges［J］.Optics and Precision Engineering，2015，23（1）：206⁃215.

［4］ 李玉和,李庆祥,陈璐云,等.单轴柔性铰链设计方法的研究［J］.清华大学学报（自然科学版），2002，42（2）：172⁃174.LI Yuhe，LI Qingxiang，CHEN Luyun，et al.Study on Design Method of One⁃axis Flexure Hinge［J］.J.Tsinghua Univ.（Sci.&Technol.），2002，42（2）：172⁃174.

［5］ 赵磊,巩岩,华洋洋.直梁圆角形柔性铰链的柔度矩阵分析［J］.中国机械工程，2013，24（18）：2462⁃2468.ZHAO Lei，GONG Yan，HUA Yangyang.Rotation Analysis of Corner⁃filled Flexure Hinge［J］.China Mechanical Engineering，2013,24（18）：2462⁃2468.

［6］ LOBONTIU N.Compliant Mechanisms：Design of the Flexure Hinges［M］.New Work：CRC Press LLC，2003.

［7］ 曹锋,焦宗夏.双轴椭圆柔性铰链的设计计算［J］.工程力学，2007，24（4）：178⁃182.CAO Feng，JIAO Zongxia.Design of Double⁃axis Elliptical Flexure Hinge［J］.Engineering Mechanics，2007,24（4）：178⁃182.

［8］ 李宗轩,张雷,姚劲松,等.Cartwheel型双轴柔性铰链设计［J］.光学精密工程,2013,21（9）：2317⁃2325.LI Zongxuan，ZHANG Lei，YAO Jingsong，et al.De⁃sign of Cartwheel Bi⁃axial Flexural Hinge［J］.Op⁃tics and Precision Engineering，2013，21（9）：2317⁃2325.

［9］ 姚建涛,李立建,杨维,等.直圆柔性球铰柔度矩阵的解析计算［J］.光学精密工程，2014，22（7）：1857⁃1863.YAO Jiantao，LI Lijian，YANG Wei，et al.Analyti⁃cal Calculation of Compliance Matrix for Right⁃cir⁃cular Flexure Spherical Hinge［J］.Optics and Preci⁃sion Engineering，2014，22（7）：1857⁃1863.

［10］ 杨春辉,刘平安.圆弧型柔性球铰柔度设计计算［J］.工程设计学报，2014,21（4）：389⁃392.YANG Chunhui，LIU Pingan.Design and Calcula⁃tion of Compliance of Arc Flexure Spherical Hinge［J］.Chinese Journal of Engineering Design，2014,21（4）：389⁃392.

［11］ 陈应舒,朱淳逸.椭圆弧型柔性球铰的柔度矩阵计算与分析［J］.机械设计与研究,2015,31（5）：51⁃54.CHEN Yingshu，ZHU Chunyi.Calculationand Analysis of Flexibility Matrix of Elliptic Arc Flex⁃ure Spherical Hinge［J］.Machine Design and Re⁃search，2015，31（5）：51⁃54.

［12］ 刘庆玲,翁海珊,邱丽芳.新型单边直圆椭圆混合柔性铰链的柔度计算及其性能分析［J］.工程力学，2010，27（10）：52⁃56.LIU Qingling，WENG Haishan，QIU Lifang.Com⁃pliances Calculation and Behavior Analysis of the Half Right Circular Elliptical Hybrid Flexure Hinge［J］.Engineering Mechanics，2010,27（10）：52⁃56.*

Compliance Calculation and Behavior Analysis of a Novel Right Circular Corner-filled Hybrid Multiple-axis Flexure Hinge

LIU Qingling LUO Ping YU Changjuan
Department of Mathematics and Information Science，Langfang Normal University，Langfang，Hebei，065000

Abstract：A novel multiple⁃axis flexure hinge—right circular corner⁃filleted hybrid multiple⁃axis flexure hinge was presented.Based on Castigliano’s second theorem，compliance formulas were formulat⁃ed.Compliance calculations and finite element simulation were performed simultaneously for a sets of ex⁃amples.By contrast to the results，correctness of the compliance formulas were verified.The ratio λnamed as thickness⁃length ratio was defined，and the relation between the compliance errors and λwere analyzed.By means of the compliance formulas，the effects of the structural parameters on the compliance were an⁃alyzed.Compared with the right⁃circlar multiple⁃axis flexure hinges，compliance and sensitivity to the load of the novel hybrid multiple⁃axis flexure hinge are better than those of the right⁃circlar multiple⁃axis flexure hinge.

Key words：hybrid multiple⁃axis flexure hinge；right circular corner⁃filleted；compliance；finite ele⁃ment；thickness⁃length ratio

基金项目：河北省教育厅重点课题（ZD2015108）；河北省教育厅青年基金资助项目（QN2016132）；廊坊师范学院博士基金资助项目（LSLB201708）

收稿日期：2017－12－29

DOI：10.3969/j.issn.1004⁃132X.2018.20.013 开放科学(资源服务)标识码(OSID)：

中图分类号：TH122

(编辑 张 洋)

作者简介：刘庆玲，女，1971年生，教授。研究方向为柔性机构的性能分析与测试。发表论文30余篇。E⁃mail：249885316@qq.com。