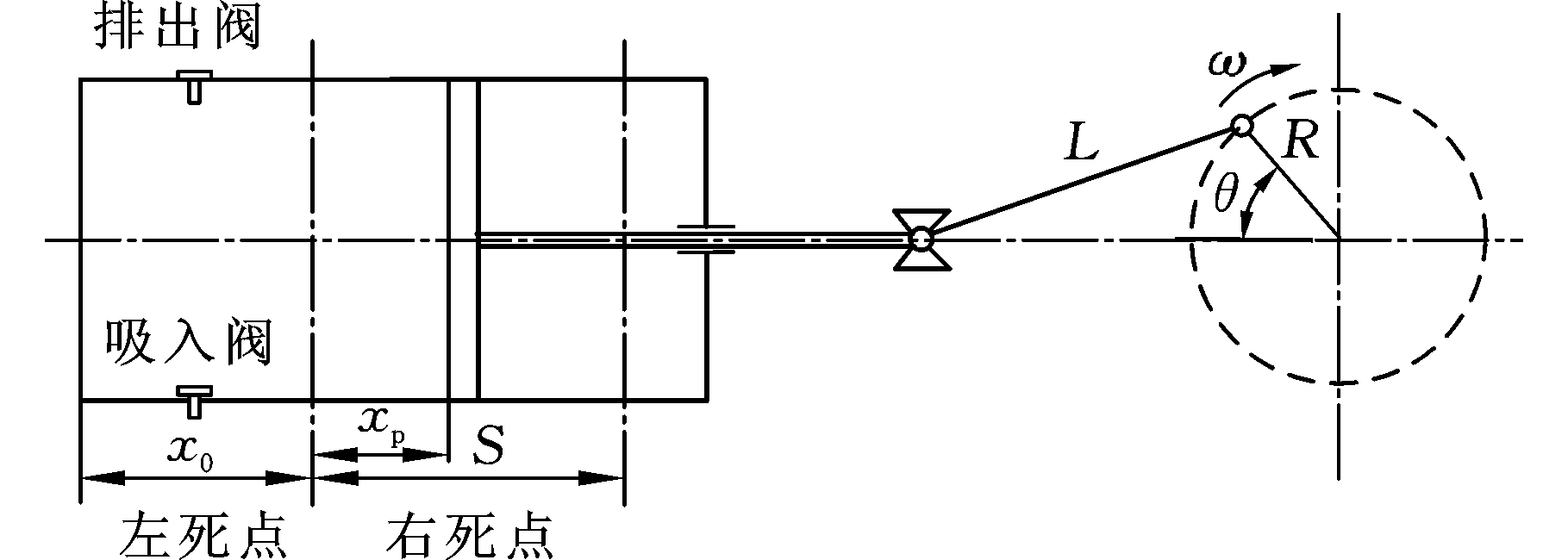
图1 往复泵的工作原理
Fig.1 Working principle of reciprocating pump
往复泵是一种通用的水力机械设备,在国民经济的各个领域得到了广泛应用。泵阀是往复泵的重要部件,往复泵泵阀主要采用自动锥形阀结构。弹簧是自动锥形阀的重要组成部分,目前自动锥形阀所应用的弹簧为定刚度系数弹簧。对于定刚度系数弹簧的自动锥形阀,国内外学者对其阀盘运动规律、阀盘结构参数设计进行了系统研究。文献[1]综合考虑泵阀动态特性、魏氏效应对连续流条件的影响,建立了阀盘运动规律的二阶常微分方程。针对阿道尔夫阀盘运动微分方程在阀盘开启瞬时存在奇点的问题,文献[2-4]考虑流体可压缩性对泵筒内流体连续流的影响,建立了适应范围更广的阀盘运动规律的数学模型。对定刚度系数弹簧自动锥形阀阀盘运动规律的仿真结果表明[5]:增大弹簧刚度有利于减小泵阀滞后关闭角,提高泵的容积效率;增大弹簧刚度也有利于降低阀盘落座速度,减轻阀盘对阀座的冲击,提高阀盘与阀座的疲劳寿命。但笔者仿真结果表明,增大弹簧刚度会减小阀盘升程,即减小了阀隙过流面积,增大了阀隙水力损失,因此,单纯增大或减小弹簧刚度并不能系统改善往复泵的动力性能。为此,笔者设计了变刚度系数弹簧的自动锥形阀,在最大阀盘升程一定条件下,仿真分析变刚度系数弹簧自动锥形阀的动力性能,探索提高自动锥形阀动力性能的有效途径。
为便于研究,作如下简化和假设:①忽略液体在液缸内流动时的沿程阻力损失;②忽略连杆、活塞以及液缸等元件的弹性变形;③假设液缸内的液体密度与压力与液缸内的位置无关。以吸入阀为例,建立泵阀运动规律的数学模型。往复泵的工作原理见图1,自动锥形阀结构见图2。

图1 往复泵的工作原理
Fig.1 Working principle of reciprocating pump
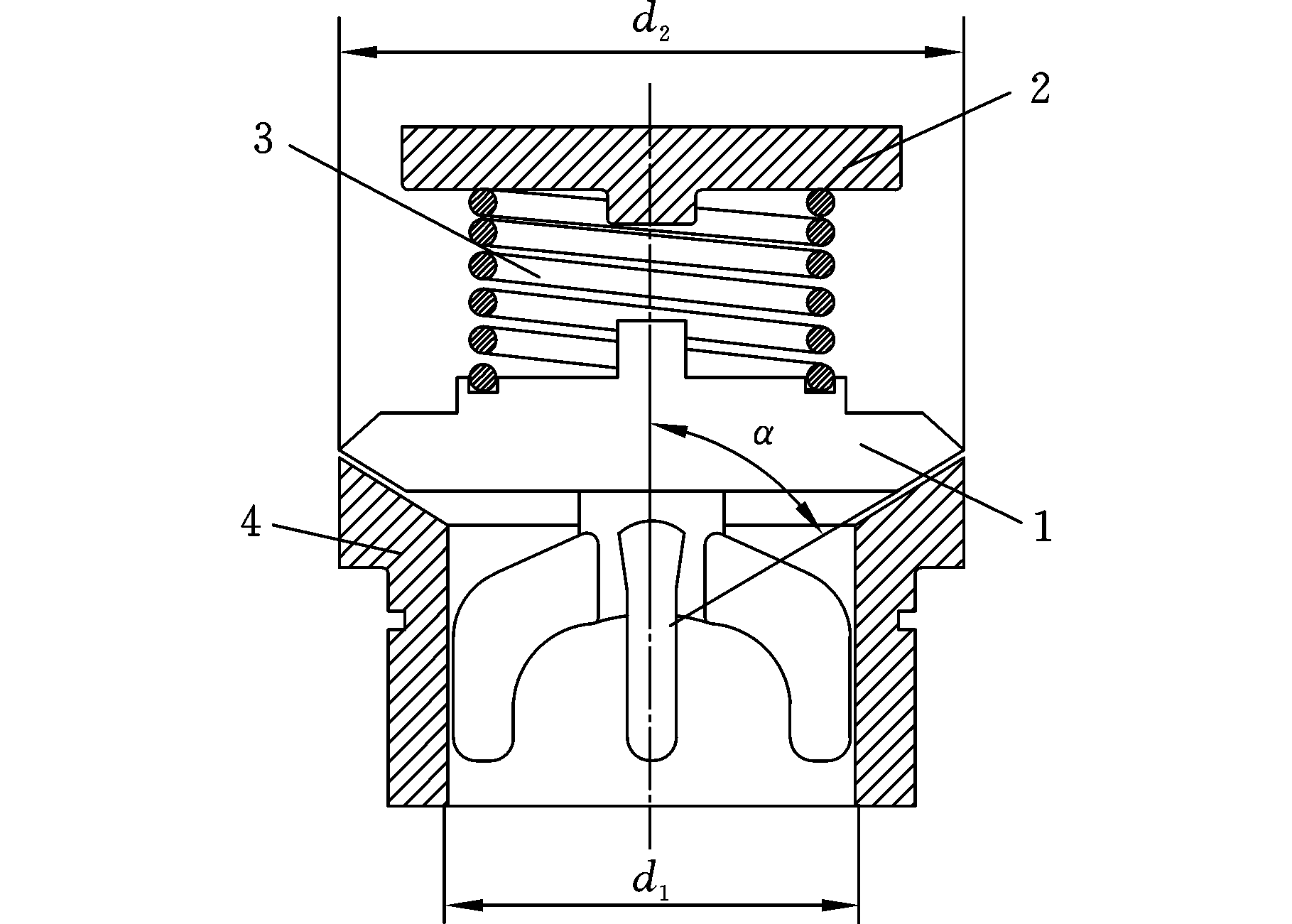
图2 自动锥形阀结构
Fig.2 Structure of automatic poppet valve
对于定刚度系数弹簧的自动锥形阀,弹簧刚度既影响阀盘的运动规律,也影响阀隙的水力特性[6]。增大弹簧刚度,有利于减小阀盘滞后关闭角、降低阀盘落座速度[7-9],但增大弹簧刚度也减小了阀盘升程以及阀隙过流面积、增加了阀隙水力损失。受非线性弹簧广泛实际应用的启示,若弹簧刚度随阀盘升程变化而变化,并同时兼顾阀盘滞后关闭角、落座速度、最大升程等泵阀性能指标,优化弹簧刚度与升程的函数关系,则可以改善泵阀的综合性能。基于上述思想,假设弹簧刚度k与升程h的函数关系为
k=f(h)
(1)
式中,k为弹簧刚度,N/m;h为阀盘升程,m。
往复泵在吸液过程中,活塞由左死点向右运动,泵缸内压力开始减小,缸内压力减小到一定程度后,吸入阀开启,此时阀盘分别受到以下力的作用[10-12]:阀盘下部与上部液体压差作用下产生的举升力、阀盘自身重力、弹簧弹力、液体对阀盘的水力阻力以及阀盘导向爪与阀座之间的摩擦力(摩擦力的作用方向与阀盘的运动速度方向相反),由牛顿第二定律得到阀盘的运动微分方程:
(2)
式中,ms为阀盘质量,kg;p为液缸内液体压力,Pa;ps为吸入管内吸入阀口处的液体压力,Pa;fs为阀盘面积,m2;g为重力加速度,m/s2;h0为弹簧预压量,m;λ1为阻力系数;Rm为阀座对阀盘导向爪的摩擦力,N。
弹簧预压量h0与弹簧预压力F0之间的关系为
F0=f(h0)h0
(3)
式(2)中,液体对阀盘的水力阻力、阀座对阀盘导向爪的摩擦力一般较小,忽略这两项力的影响,吸入阀运动微分方程简化为
(4)
根据单位时间内泵缸内流体质量的增量dM1应等于经过泵阀阀隙流入泵缸的流体质量dM2,即可建立流体连续性方程:
dM1=dM2
(5)
dM1=[Fp(xp+x0)-Vs]dρ-ρdVs+Fpρdxp
(6)
式中,Fp为液缸内圆面积,m2;ρ为t时刻液缸内液体的密度,kg/m3;Vs为t时刻阀盘、阀隙与阀座所形成的空间体积,m3;xp为t时刻活塞的位移,m;x0为余隙长度,m。
液缸内的液体密度与压力之间的函数关系为
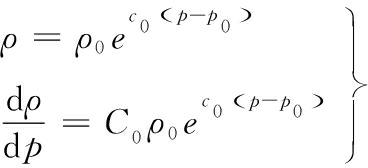
(7)
式中,ρ0为液缸内液体在标准下的密度,kg/m3;C0为液体的压缩系数;p0为标准压力,Pa。
活塞运动位移xp与速度vp分别为
xp=R[1-cosωt+0.5λ(sinωt)2]
(8)
vp=Rω[sinωt+0.5λsin(2ωt)]
(9)
式中,ω为曲柄转动的角速度,rad/s;λ为连杆半径与长度之比,λ=R/L;R为连杆半径,m;L为连杆长度,m。
单位时间内经过阀隙流入液缸的液体质量
(10)
式中,μ为流量系数;εs为系数,εs=±1;ρxs为经过阀隙流动液体的密度,kg/m3;fxs为阀隙的过流面积,m2。
当ps-p≥0时,εs=1,ρxs=ρs(ρs为液体在吸入压力ps条件下的密度);ps-p<0时,εs=-1,ρxs=ρ。
阀隙的过流面积
fxs=πd2hsinα
(11)
式中,d2为阀盘直径,m;α为阀锥角,rad。
综上推导,有
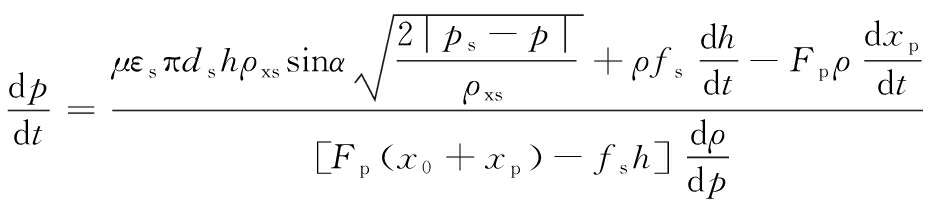
(12)
由于滞后角的存在,活塞运动到左死点时,排出阀并未关闭,阀盘还存在一定的滞后高度,当排出阀关闭时,活塞由左死点向右走过的距离为xod,曲柄转过的对应角度为ψod(排出阀的滞后关闭角)。随着柱塞的继续运动,泵缸内的压强开始逐渐减小。当阀盘的上下压差Δp产生的举升力足以克服阀盘的重力与弹簧力时,吸入阀开启,由此可推导出泵阀的开启压差与开启压力分别为
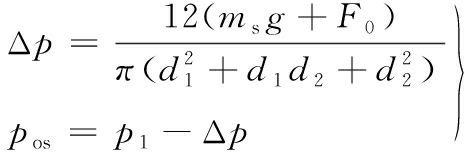
(13)
式中,d1为阀座孔内径,m;d2为阀盘直径,m。
根据泵缸内液体质量守恒,可求得吸入阀打开瞬时的活塞位移:
(14)
式中,ρd为液体在排出压力pd下的密度;ρos为液体在排出压力pos下的密度。
根据活塞位移,可求得吸入阀打开时刻tos满足
(15)
吸入阀运动的初始条件为
(16)
根据上文建立的吸入阀运动微分方程、泵阀连续流方程以及初始条件,可以建立描述吸入阀运动规律的数学模型,写成以下一阶常微分方程组如下:
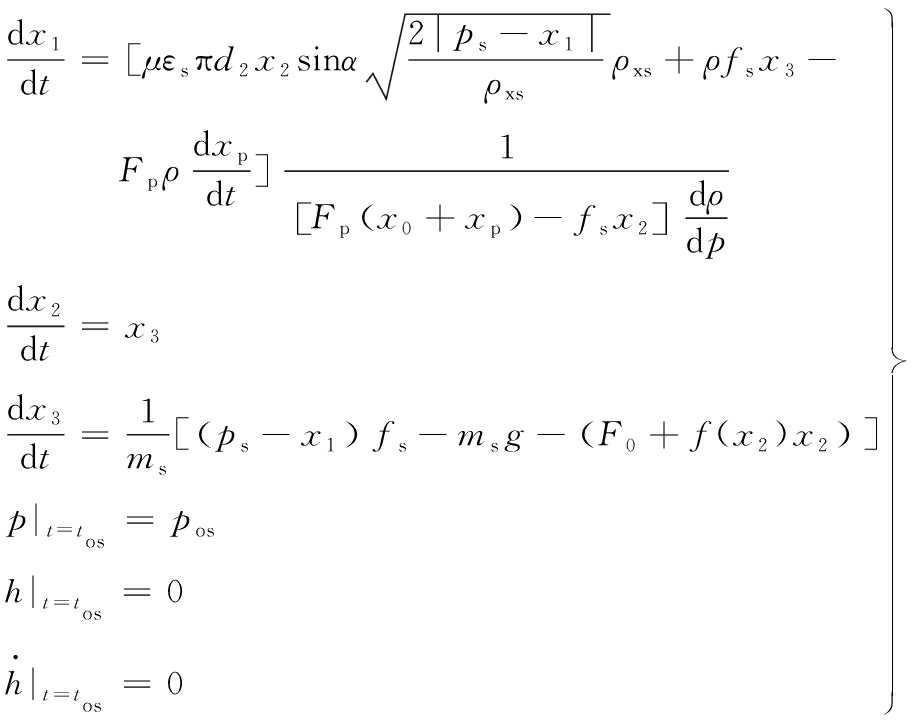
(17)
式中,x1为液缸内液体压力;x2为泵阀升程;x3为阀盘的运动速度。
根据上文建立的泵阀运动微分方程,采用龙格-库塔法建立描述泵阀运动规律的仿真模型,并编制了描述泵阀运动规律的仿真程序。为了验证仿真模型的仿真精度,对油田3NB-1300型钻井往复泵进行了动态仿真与实测结果对比,该泵的仿真试验参数如下:冲程0.254 m,液缸直径0.170 m,钻井液密度1100 kg/m3,阀盘质量4.0 kg,弹簧刚度系数7500 N/m,阀弹簧预紧力230 N。定弹簧刚度条件下,对不同频率下的阀盘最大升程进行了仿真计算,仿真结果与实测结果[2]见表1。由表1可见,泵阀最大升程的仿真误差小于±10%。
表1 泵阀最大升程仿真结果与实测结果对比
Tab.1 Maximum lift simulation results compared with measured results
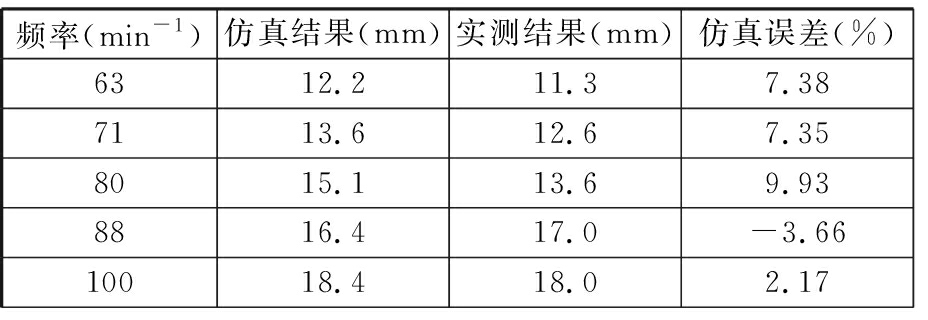
频率(min-1)仿真结果(mm)实测结果(mm)仿真误差(%)6312.211.37.387113.612.67.358015.113.69.938816.417.0-3.6610018.418.02.17
弹簧刚度与阀盘升程的函数关系会影响阀盘的运动规律。为验证变刚度弹簧可以改善往复泵动力性能的设计思想,本文假设弹簧刚度与阀盘升程的关系为线性函数,即
k=ah+b
(18)
式中,a、b为常数。
式(18)中,系数a、b的不同组合既影响不同升程时弹簧的瞬时刚度,也影响弹簧刚度与升程曲线的变化趋势。当a<0时,弹簧刚度随升程的变化规律为减函数模式;当a>0时,弹簧刚度随升程的变化规律为增函数模式。为使仿真结果具有可比性,在阀盘最大升程一定的条件下,仿真分析了系数a、b组合对阀盘落座速度与滞后高度的影响。定弹簧刚度,系数a、b不同组合时变弹簧刚度的阀盘最大升程,阀盘落座速度与阀盘滞后高度见表2。变弹簧刚度(a=-8×105 N/m2,b=2.89×104 N/m)、定弹簧刚度时阀盘升程曲线、液缸内压力趋向与阀盘速度曲线分别见图3~图5。
表2 不同弹簧刚度类型动态仿真结果
Tab.2 Dynamic simulation results of different spring stiffness types

弹簧类型a(N/m2)b(N/m)最大升程(mm)落座速度滞后高度 仿真结果(mm/s)下降率(%)仿真结果 (mm)下降率(%)定刚度弹簧01000015.8132.600.89390变刚度弹簧90 0006 30015.8133.80.900.905 31.2812 0005 50015.8134.01.060.909 31.7215 0001 00015.8134.81.650.912 92.13-300 00018 50015.8128.1-3.390.857 2-4.11-500 00023 00015.8125.9-5.050.837 7-6.29-800 00028 90015.8122.7-7.470.811 4-9.23
注:下降率指变弹簧刚度时相对于定弹簧高度时的下降率。

图3 不同弹簧刚度类型升程对比曲线
Fig.3 Lift contrast curves of different spring stiffness type
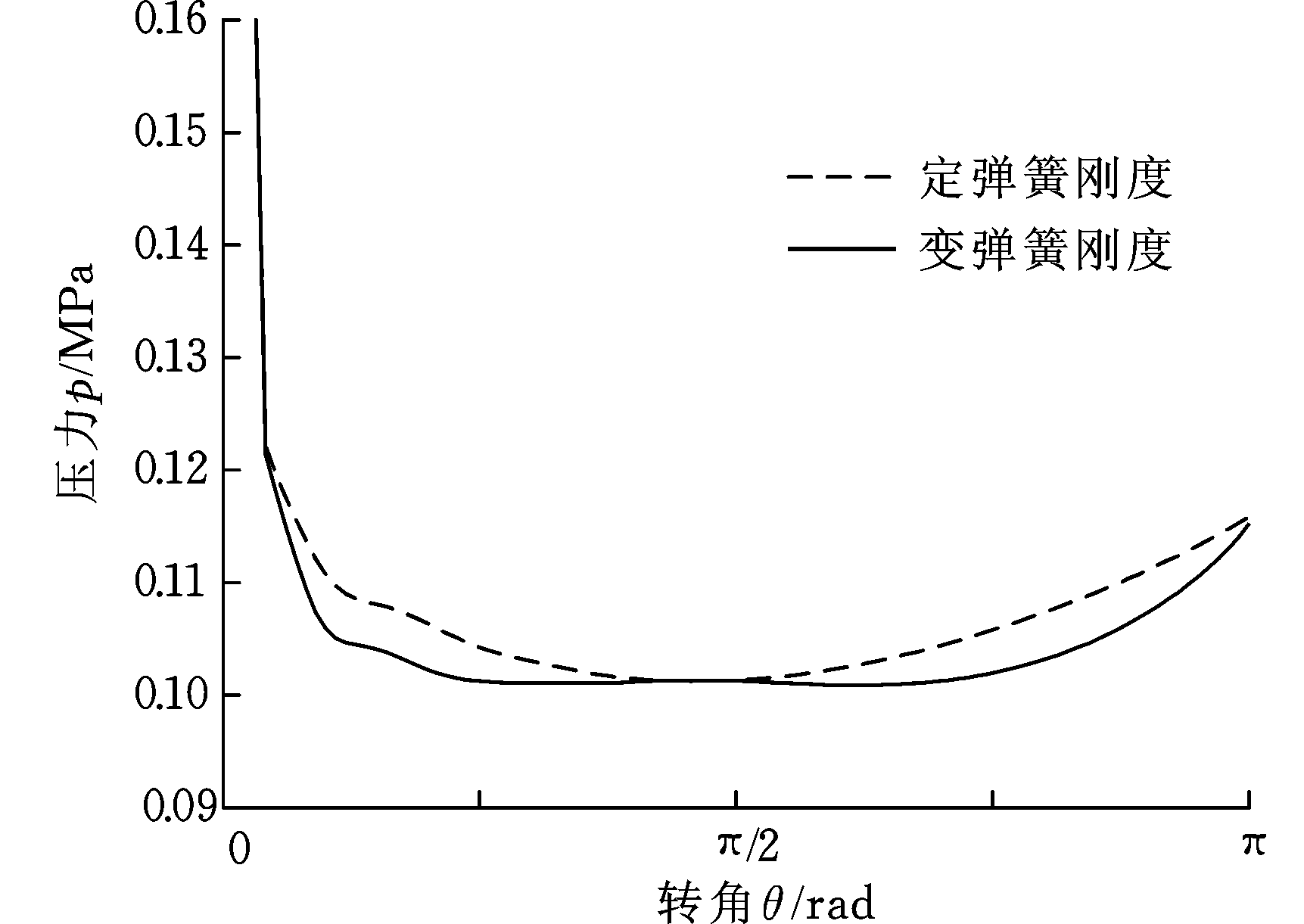
图4 不同弹簧刚度类型压力对比曲线
Fig.4 Pressure contrast curves of different spring stiffness type
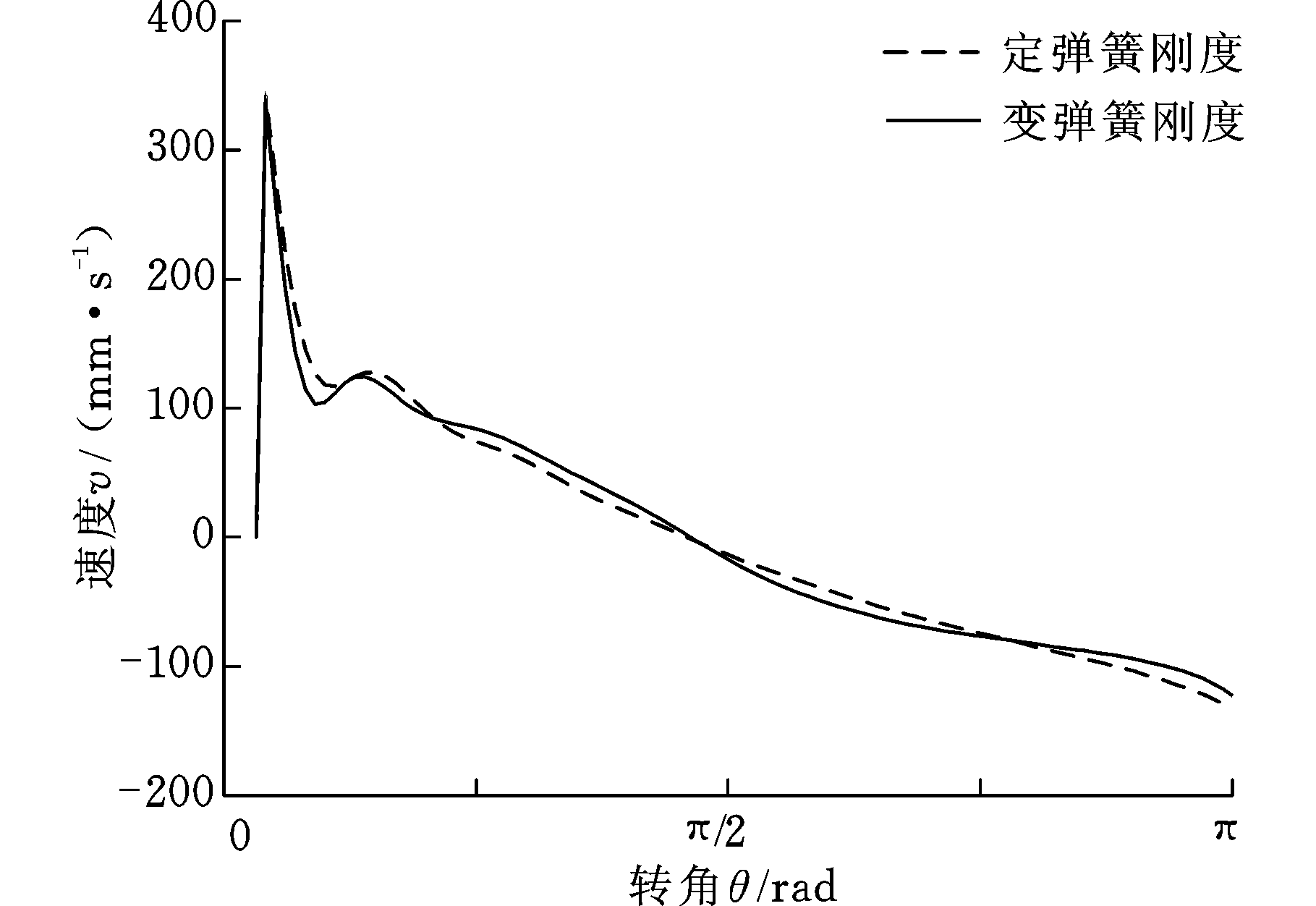
图5 不同弹簧刚度类型阀盘速度对比曲线
Fig.5 Velocity contrast curves of different spring stiffness type
对比表2中仿真结果可得以下结论:
(1)弹簧刚度随升程的变化规律对阀盘的运动特性具有显著影响。在阀盘最大升程一定的条件下,与定刚度弹簧的阀盘落座速度、阀盘滞后高度比较:减函数变刚度弹簧的阀盘落座速度最多减小7.47%、滞后高度最多减小9.23%;增函数变刚度弹簧的阀盘落座速度与滞后高度均有所增大。显然,应用减函数模式的变刚度弹簧有利于改善泵阀的动力性能。
(2)当采用减函数模式的变刚度弹簧代替定刚度弹簧时,阀盘动力性能参数的改善程度取决于系数a、b,优化系数a、b可以进一步改善变刚度弹簧泵阀的动力性能。
(1)仿真结果表明:弹簧刚度与升程的函数关系显著影响阀盘的动力特性;当假设弹簧刚度是阀盘升程的线性函数时,减函数模式的变刚度弹簧有利于改善泵阀的动力性能。
(2)初步仿真算例表明:在阀盘最大升程一定的条件下,与定刚度弹簧的阀盘落座速度、阀盘滞后高度比较,减函数变刚度弹簧的阀盘落座速度最多减小7.47%、滞后高度最多减小9.23%,有利于提高泵的容积效率以及阀盘与阀座的疲劳寿命。
(3)对于变刚度弹簧往复泵锥阀,阀盘的动力特性参数是弹簧刚度函数的泛函,有关弹簧刚度函数的优化问题有待深入研究;对于变刚度弹簧的弹簧设计、弹簧与泵阀组件的安装方式有待深入研究。
[1] Adolph U.Vorausberechnung der Funktion und der Schlaggrenge Selbsttätiger Flach Sitzventile von Kolbenpumpen bei Reiner Flüssigkeitsstromung[M]. Dresden: Dissertation T. U.,1967.
[2] 董世民,王春华,阎乐好. 往复泵自动锥形阀运动规律的新模型与仿真[J]. 流体机械,2001,29(6):19-22.
DONG Shingmin,WANG Chunhua,YAN Lehao. A New Model and Simulation of Self-acting Conical Valve of Reciprocating Pumps[J]. Fluid Machinery,2001,29(6):19-22.
[3] 戴相富,周和平,庞东晓,等. 自动锥形阀运动规律数学模型及仿真[J].石油机械,2003,31(8):6-8.
DAI Xiangfu,ZHOU Heping,PANG Dongxiao,et al. Mathematical Model and Computerized Simulation of Motion Law of Automatic Conical Valve Motion[J]. China Petroleum Machinery,2003,31(8):6-8.
[4] 孟英峰,梁红,张仲良.往复泵泵阀运动规律的建模与仿真[J]. 石油机械,1995,23(5):16-20.
MENG Yinfeng,LIANG Hong,ZHANG Zhongliang. Mathematic Model and Simulation Program for Valve Motion on Reciprocating Pumps [J]. China Petroleum Machinery,1995,23(5):16-20.
[5] 雷中清. 2000型车载压裂泵液力端工作机理的研究[D]. 成都:西南石油大学,2012.
LEI Zhongqing. Study on Working Mechanism on Fluid End of 2000 Vehicle-mounted Fracturing Pump[D]. Chengdu:Southwest Petroleum University,2012.
[6] QIAN Jinyuan,GAO Zhixin,WANG Jiankai,et al. Experimental and Numerical Analysis of Spring Stiffness on Flow and Valve Core Movement in Pilot Control Globe Valve[J]. Mechanical Systems and Signal Processing,2017,42(27):17192-17201.
[7] 闫国军,赵军明,董泳. 往复泵阀运动规律的研究[J]. 中国机械工程,2004,15(18):1617-1619.
YAN Guojun,ZHAO Junming,DONG Yong. Study on Kinematics of Reciprocating Pump Valve[J]. China Mechanical Engineering,2004,15(18):1617-1619.
[8] 杨国安,乔舰,宋征,等.钻井泵阀寿命分析[J].振动与冲击,2010;29(1):58-61.
YANG Guoan,QIAO Jian,SONG Zheng,et al. Service Life Analysis for Drilling Pump Valve[J]. Journal of Vibration and Shock,2010,29(1):58-61.
[9] 张生昌,王炤东,邓鸿英,等. 气液单向阀弹簧刚度对开启特性的仿真分析[J]. 液压气动与密封,2014,14(2):19-21.
ZHANG Shengchang,WANG Zhaodong,DENG Hongying,et al. Simulation on Effect of Gas-liquid Check Value Spring Stiffness to Opening Characteristic[J]. Hydraulics Pneumatics&Seals,2014,14(2):19-21.
[10] 肖厚韬,祝爽.往复泵泵阀弹簧受力分析[J].机械管理开发,2016;153(1):57-60.
XIAO Houtao,ZHU Shuang. Analysis on Action Force of the Pump Spring of the Reciprocating Pump[J]. Mechanical Management and Develop,2016,153(1):57-60.
[11] JUN Fengpei,CHAO He,LYU Miaorong,et al. The Valve Motion Characteristics of a Reciprocating Pump[J]. Mechanical Systems and Signal Processing,2016,s66/67:657-664.
[12] 杨国安,黄聪,冯德音. 基于MATLAB的钻井泵阀运动特性分析[J]. 石油矿场机械,2008,37(4):37-41.
YANG Guoan,HUANG Cong,FEI Deiyin. Motion Characteristic Analysis of Drilling Pump Valve Based on MATLAB[J].Oil Field Equipment,2008,37(4):37-41.