0 引言
天线是卫星通信的核心部件,根据反射面类型的不同,可分为固面天线、可充气天线、网状反射面天线。为了适应航天发射与运载的需要,天线均为可展结构。网状反射面可展天线具有收纳率高、质量小、口径大等优点,是目前星载天线较为理想的结构形式[1]。
为了确保天线在轨顺利展开,降低故障率,需对其进行大量的地面展开试验,从而发现其设计、制造缺陷,为天线的在轨安全可靠展开提供设计依据和技术保障。地面展开试验中,如何利用微重力生成机构与装置,模拟空间的微重力环境(重力补偿)是目前研究的热点[2]。
重力补偿的基本思想和原理为:创造全场失重环境或在工作空间对物体的全部工作位置与姿态施加外力而平衡重力,从而实现零/微重力模拟。目前微重力模拟的方法主要有:自由下落法、抛物线飞行法、中性浮力法、气浮法和悬吊法。针对展开过程缓慢、运动复杂的大型空间可展结构,一般采用悬吊法对其进行重力补偿[3]。
SATO等[4]设计了空间机械手的微重力悬吊系统,并由实验证明该系统能达到0.01g重力环境的卸载效果。WHITE等[5]设计了一种主动悬吊方案,并通过运用混合控制和模糊控制算法消除了配重惯性、系统摩擦对卸载精度的影响。MEGURO等[6-7]基于地面展开困难指数对在轨实际展开与地面试验之间的差异进行了评估,通过对ETS-Ⅷ卫星所载天线进行实验分析,比较了展开困难指数与天线展开精度的关系,指出对于大型可展天线,地面展开试验还不足以评估其在轨展开可靠性。TSUNODA等[8-9]针对构架式可展天线提出了一种磁悬浮卸载方案,并进行了地面实验,结果表明,在收缩杆处悬吊能达到较好的卸载效果。
齐乃明等[10]针对做复杂运动的空间结构,设计了机-电-气组合的地面微重力模拟实验系统,并采用等效滑模控制策略补偿了各种不确定因素的影响。刘巍等[11]对斜面悬吊法和垂直悬吊法进行了综述,并就其实际应用效果进行了分析与比较。刘振等[12]针对摇臂转向架式星球车提出了由单根索与摇臂配重组成的微重力模拟方法,并对其进行了验证分析。姚燕生等[13]建立了悬挂式重力补偿系统的动力学模型,给出该模型的最优控制参数,并通过试凑法验证了优化模型的正确性。
目前常采用悬吊法中的吊丝配重法,对环形天线进行重力补偿,但此种方法采用了桁架展开牵引吊丝从动的方案,运动中存在吊丝非铅锤效应,使得重力卸载不充分并对桁架产生附加横向力,影响地面试验数据精度。针对吊丝配重法的不足,本文提出了一种基于吊丝主动水平定位和运动的重力补偿方案。
1 环形天线及传统重力补偿方式
1.1 环形天线
如图1所示,环形天线由前索网、金属反射网、周边桁架、调节索、后索网5个部分组成。其中,前后索网由柔性索连接而成,通过内部预应力与调节索张力的作用来逼近抛物面;金属反射网由金属丝编织而成,附着在前索网上,用于完成电磁波反射任务;周边桁架由多个桁架单元组成,用于支撑前后索网及反射面,并实现天线的展开与收拢。
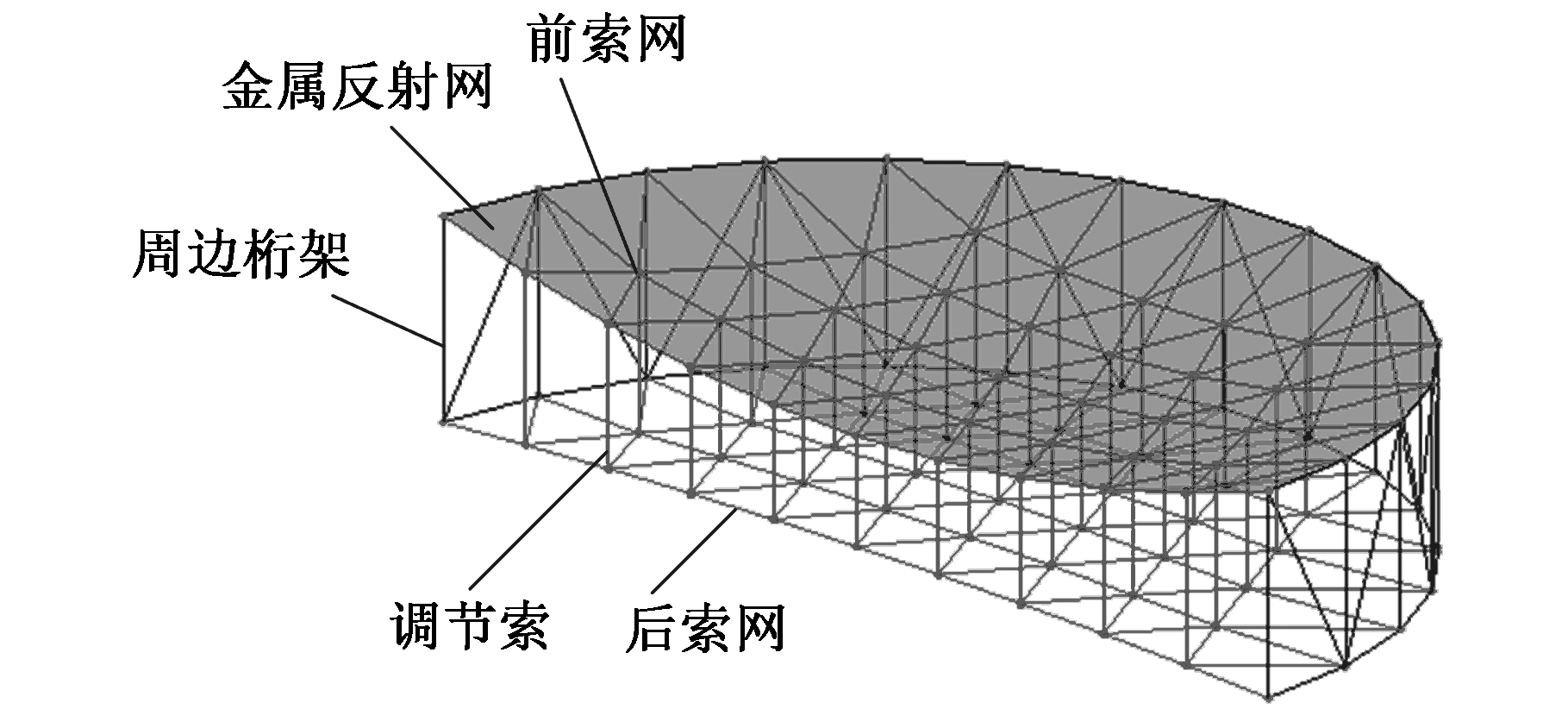
图1 环形天线组成
Fig.1 Structure of perimeter truss deployable reflector
如图2所示,每个桁架单元由同步铰链、横杆、T形铰链、竖杆、斜杆等组成。其展开过程如下:展开拉索依次通过每个桁架单元的T形铰链和斜杆,在展开拉索电机作用下收拢,进而带动斜杆收缩,使单元展开,并在同步铰链的作用下,每个桁架单元将同时由收拢态逐渐展开,直至整个周边桁架展开到位。
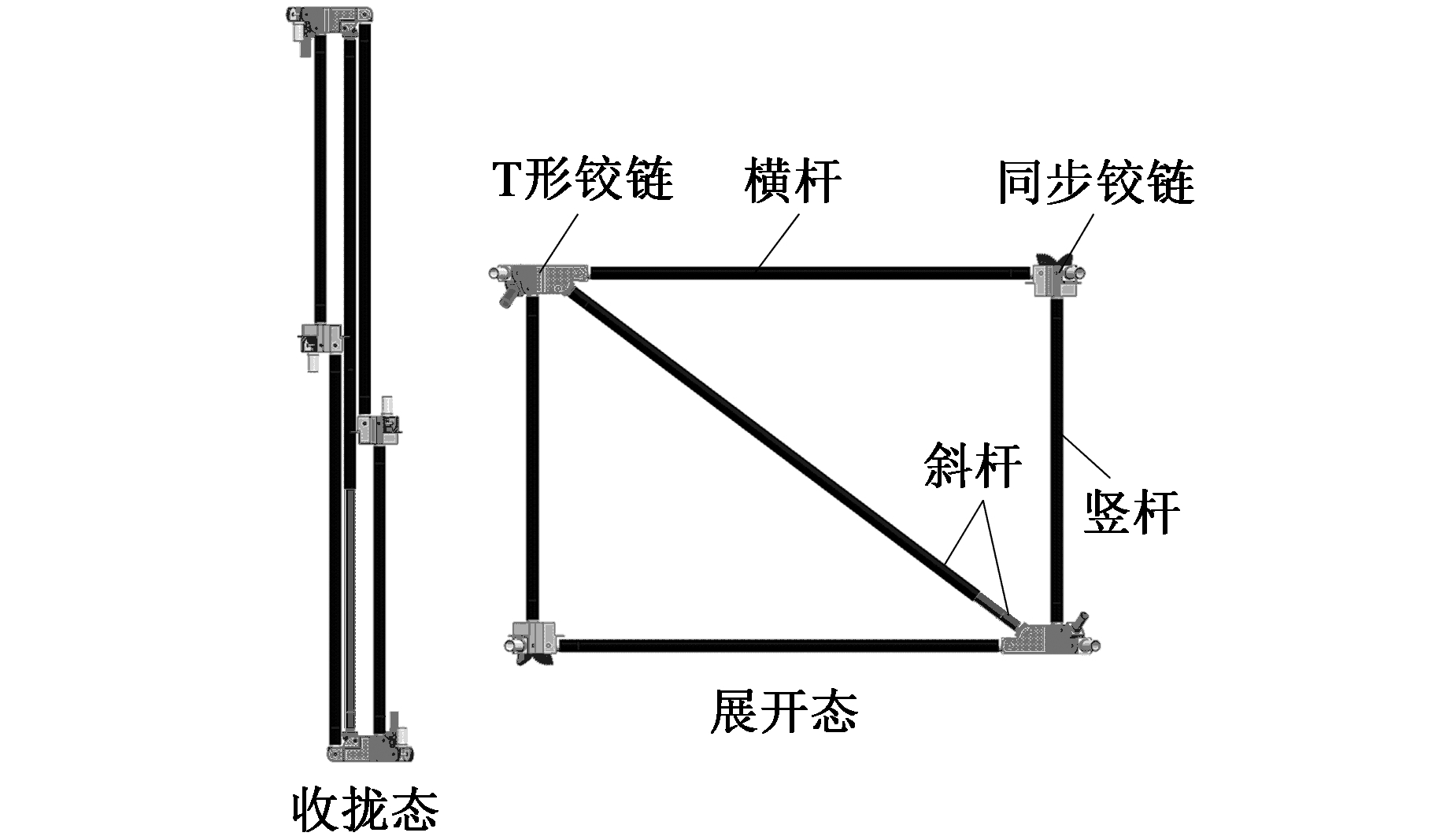
图2 桁架单元结构
Fig.2 Structure of parallelogram part
1.2 传统吊丝配重法
环形天线展开过程十分缓慢,其展开过程可以近似为静态过程,又考虑到其结构的对称性,故考虑采用吊丝配重法来进行重力补偿。如图3所示,吊丝配重法具体装置主要由滑轮车、高精导轨、配重和定滑轮组成。吊丝通过定滑轮与滑轮车后分别连接配重和天线悬吊点,通过滑轮车在导轨上的水平运动来实现吊丝的定位。在天线展开的牵引下,吊丝带动滑轮车沿导轨追从悬吊点水平运动,使吊丝保持近似铅锤;由配重为吊丝提供悬吊力抵消重力,实现天线的重力补偿。

图3 吊丝配重法
Fig.3 Hanging wire counterweight method
吊丝配重法利用天线展开牵引吊丝运动,这种从动的定位方式使吊丝在运动过程中存在非铅锤效应。如图4所示,当吊丝产生非铅锤效应时,其偏角为α时,吊丝中悬吊力将变为F2,并且会产生横向分力F1,而吊丝张力F等于重力G,故悬吊力F2小于G,即悬吊点铅锤力不足,且受到了吊丝附加横向力F1的作用,导致天线展开过程受外力影响。

图4 吊丝非铅锤效应
Fig.4 Non plumb-bob effect of sling
2 展开运动学分析
2.1 展开运动分析
如图5所示,选取天线固定杆铰链节点O1建立总体坐标系,g1、g2、g3为总体坐标系基矢量。g1沿固定端T形铰链角平分面指向天线中心O;g2垂直于固定端T形铰链角平分面向里;g3沿固定端竖杆向上。设桁架单元个数为2n,横杆与竖杆的长分别为l和h,并且编号为i的横杆与基矢量g2和g3的夹角分别为θi和φ,其中i=1,2,…,2n,Oi为T形铰链节点,Pi为同步铰链节点。

图5 基矢量设定
Fig.5 Setting of base vector
由于竖杆两端铰链水平面位移相同,故对T形铰链节点位移进行求解。其中,节点O2的矢径
O2=(lsinφsinθ1)g1+(lsinφcosθ1)g2+
(lcosφ+h)g3
(1)
同理可得节点O3的矢径:
O3=O2+(lsinφsinθ2)g1+(lsinφcosθ2)g2+
(lcosφ+h)g3
(2)
依此类推,可得节点Oi的矢径:
Oi=Oi-1+(lsinφsinθi-1)g1+
(lsinφcosθi-1)g2+(lcosφ+h)g3
(3)
由式(3)可知,各个铰链节点在天线展开过程中的位置都可以用广义坐标φ来描述。由式(3)可得节点Oi在水平面的位移si为
si=lsinφ[(sinθ1+sinθ2+…+sinθi-1)2+
(cosθ1+cosθ2+…+cosθi-1)2]1/2
(4)
由于θi-1为各铰链左侧单元横杆与基矢量g2的夹角,故当桁架结构已知时,θi-1为确定值;lsinφ表示展开过程中横杆在水平面的投影长度,结合式(4)可知,各节点在水平面的运动均为直线运动,并且位移互成比例。由桁架结构可知,前索网面与后索网面各铰链节点在基矢量g1和g2的位移分量相等;又考虑到卸载装置对天线展开运动的避让因素,故选取前索网面各铰链节点为悬吊点。令
ri=[(sinθ1+sinθ2+…+sinθi-1)2+
(cosθ1+cosθ2+cosθi-1)2]1/2
(5)
由式(5)可知铰链节点水平面的位移比为![]() 设最远端T形铰链水平面位移为sn+1,则有
设最远端T形铰链水平面位移为sn+1,则有
sn+1=rn+1lsinφ
(6)
结合式(6)和各铰链节点传动比![]() 可以求得各铰链节点位移。以上分析表明前索网面各铰链节点水平面位移可以由广义坐标φ来表示;又由文献[14-15]可知,展开拉索驱动电机控制参数也可以由广义坐标φ来表示,故可以通过控制展开拉索驱动电机和吊丝定位电机的驱动参数,来实现吊丝与悬吊点的同步运动。
可以求得各铰链节点位移。以上分析表明前索网面各铰链节点水平面位移可以由广义坐标φ来表示;又由文献[14-15]可知,展开拉索驱动电机控制参数也可以由广义坐标φ来表示,故可以通过控制展开拉索驱动电机和吊丝定位电机的驱动参数,来实现吊丝与悬吊点的同步运动。
2.2 展开过程的重力与重心分析
如图6所示,对展开态环形天线进行静力分析。首先对模型进行简化:将铰链质量附加给竖杆,粗细斜杆等效为一根斜杆。简化后横杆、斜杆、竖杆质量分别为m1、m2、m3。选取与转接臂固连的竖杆1下端点为原点,x轴沿杆1下端点指向杆n+1下端点,z轴沿杆1向上,y轴由右手定则确定。设转接臂对天线提供的外力与外力矩为:Fx、Fy、Fz、Mx、My、Mz,由环形天线结构的对称性及其整体受力分析可知,Fx、Fy、Mx、Mz均为零。
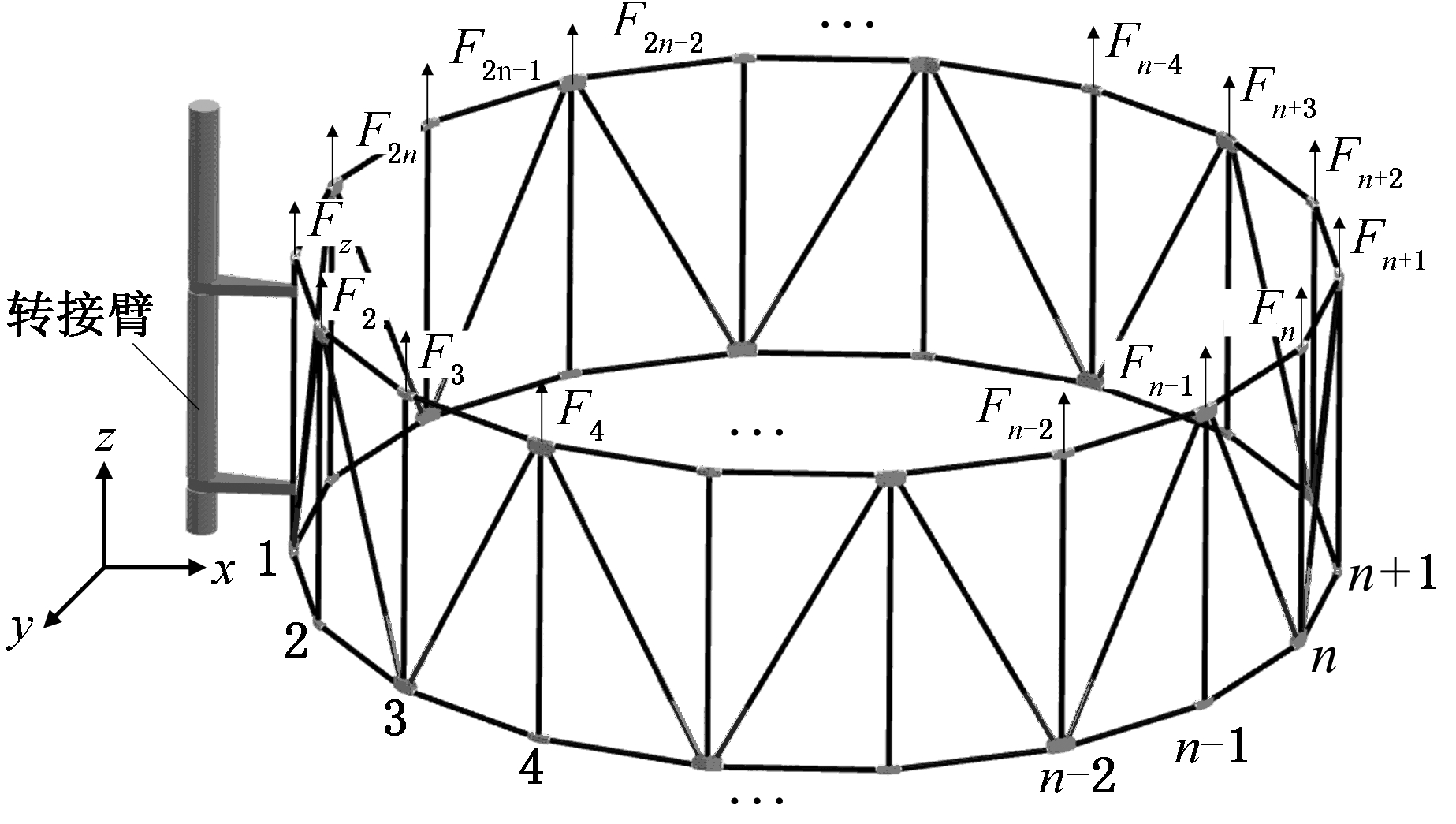
图6 铰链节点悬吊受力示意图
Fig.6 Diagram of the force hanged at hinge
由平衡条件可得
Fz+F2+F3+…+F2n=2n(2m1+m2+m3)g
(7)
在环形天线展开过程中横杆、斜杆z方向位移均为l/2,偶数编号竖杆z方向位移为l。结合式(7),由能量守恒可得
F2+F4+…+F2n=n(2m1+m2+m3)g
(8)
由式(7)、式(8)可得
(F2-Fn+2)-(F3-Fn+3)+…+(F2n-Fn)=
Fz-Fn+1
(9)
结合式(9),由天线中心点力矩为零可得
My=0 Fz=Fn+1
故在进行悬吊卸载时,环形天线转接臂处仅受到铅锤方向的作用力,即天线前索网面各铰链节点均由铅垂向上的外力抵消重力,实现其微重力模拟。由天线结构对称性可知,在进行悬吊卸载时,天线各悬吊点所受悬吊力相等,均为(2m1+m2+m3)g。
3 吊丝主动定位重力补偿方案设计
为了避免吊丝非铅锤效应的产生,本文提出了一种基于吊丝主动定位的重力补偿方案。主要通过吊丝定位电机驱动不同悬吊点对应的支路传动系统,实现吊丝与天线悬吊点的同步运动。以六单元环形天线为例,对该方案进行说明。
3.1 结构设计
如图7a所示,卸载系统主要由吊丝随动机构Ⅰ及吊丝驱动机构Ⅱ两大部分组成。
如图7b所示,吊丝随动机构Ⅰ主要由定滑轮4、支路基座5、丝杠6、导轨7、丝杠螺母8、动滑轮连接件9和动滑轮10等组成。支路基座上安装有丝杠、导轨和定滑轮,由丝杠螺母、动滑轮连接件和动滑轮组成滑轮车,在丝杠螺母的带动下滑轮车沿导轨直线运动;结合图7a可知,吊丝通过动滑轮与定滑轮后分别与配重和悬吊点连接,故采用丝杠螺母机构来控制动滑轮位置以实现吊丝的定位。
如图7c所示,吊丝驱动机构Ⅱ主要由支路齿轮11、总路第一齿轮12、正弦机构13、换向锥齿轮14、联轴器15、吊丝定位电机16、总路基座17和总路第二齿轮18等组成。其中电机与联轴器相连,通过换向锥齿轮后与正弦机构相连,正弦机构的推杆设有轮齿与总路第一齿轮啮合,进而带动总路第二齿轮转动。总路第二齿轮与最远端铰链节点对应的支路齿轮啮合;相邻支路齿轮间相互啮合,并且其传动比等于对应铰链节点水平面位移比;通过支路换向锥齿轮换向后,由滚珠丝杠进行传动,进而使滑轮车直线运动。
3.2 控制方案
由2.1节可知,随动系统滑轮车水平位移和天线横杆展角φ(t)存在正弦关系,故本文方案通过控制吊丝定位电机使之输出转角φ(t),再由正弦机构提取其正弦分量,并通过齿轮齿条机构将之转化为转动,最后经过传动系统使滑轮车和悬吊节点水平面位移相等(图8),具体原理如下。
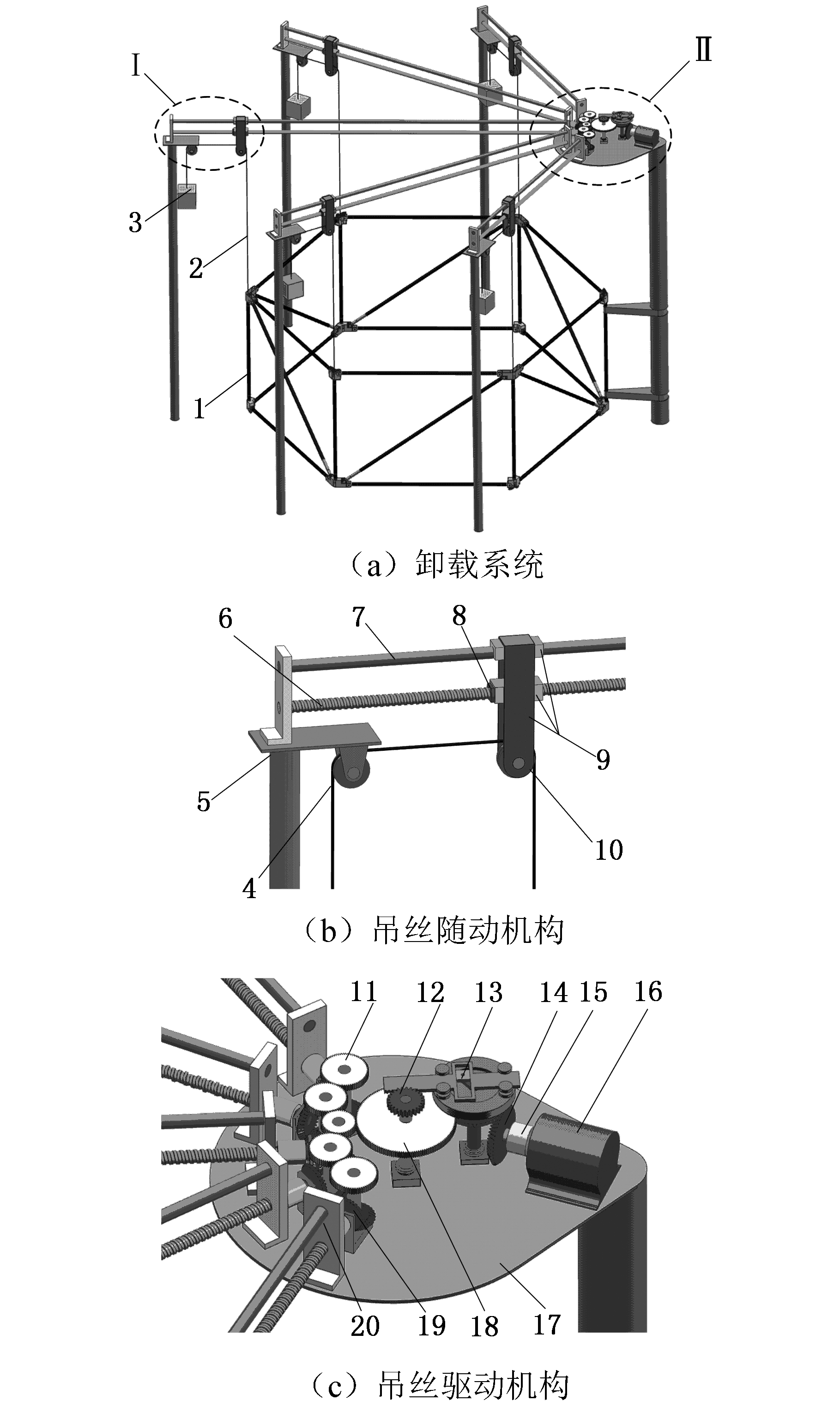
1.环形天线 2.吊丝 3.配重 4.定滑轮 5.支路基座 6.丝杠 7.导轨 8.丝杠螺母 9.动滑轮连接件 10.动滑轮11.支路齿轮 12.总路第一齿轮 13.正弦机构 14.换向锥齿轮 15.联轴器 16.吊丝定位电机 17.总路基座 18. 总路第二齿轮 19.支路换向锥齿轮 20.支路联轴器
图7 重力补偿方案示意图
Fig.7 Gravity compensation scheme
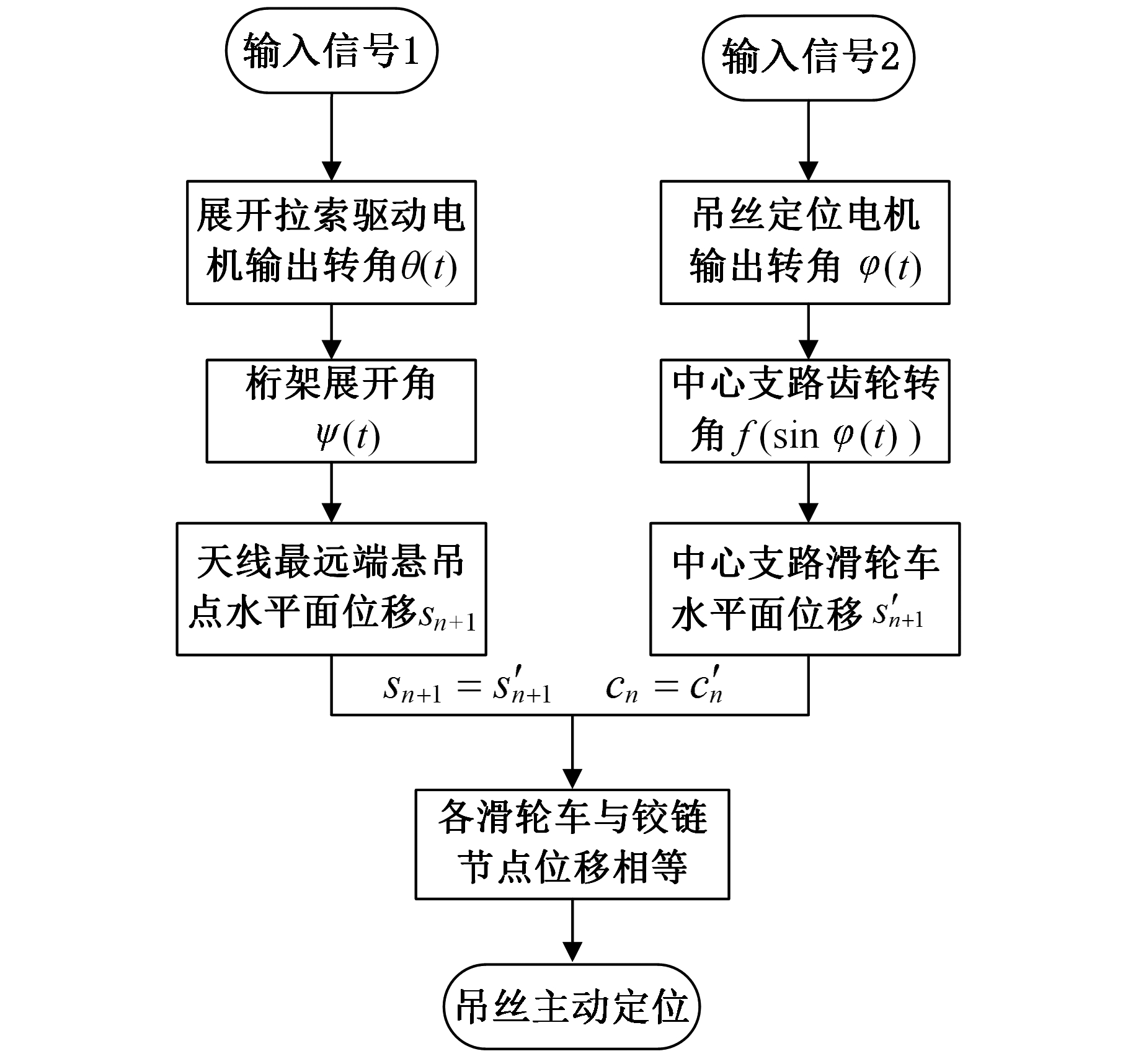
图8 吊丝主动定位控制方法
Fig.8 Control of active positioning slings
设随动系统换向锥齿轮传动比为1,正弦机构摇杆臂长为r1,总路第一齿轮半径为r2,总路第二齿轮半径为r3,中心支路齿轮半径为r4,丝杠螺距为e,各支路齿轮传动比为ci,则总路第一齿轮转角
(10)
由传动关系可得中心支路齿轮转角
(11)
结合式(11)和丝杠螺距e可得中心支路滑轮车位移
(12)
由于![]() 结合式(6)、式(12)可知,若各支路滑轮车与对应悬吊节点水平位移相同,则中心支路滑轮车与铰链位移相同(即
结合式(6)、式(12)可知,若各支路滑轮车与对应悬吊节点水平位移相同,则中心支路滑轮车与铰链位移相同(即![]() 有
有
(13)
由式(13)可知,通过调整各齿轮半径、丝杠螺距等参数,可使滑轮车和铰链节点的位移相等。
综上所述,本文方案通过对随动系统滑轮车施加主动控制,消除了原有吊丝配重法的原理误差,实现了随动系统滑轮车对悬吊节点的实时跟随,避免了非铅锤效应的产生。
4 算例分析
利用ADAMS软件,建立了口径为2 m、高度为0.7 m的六单元环形天线缩比模型,在与固定杆相连的横杆处施加驱动,使之按展开角φ=πt/600展开。在悬吊点与滑轮车之间施加相互作用力,使其大小等于悬吊力,方向随两者运动变化,以此来模拟吊丝,分析非铅锤效应对重力卸载的影响。
以固定端右侧横杆处输出转矩为指标,对比分析重力环境、失重环境和在重力环境下施加补偿(本文方案)这3种重力环境对其输出转矩的影响。

图9 不同重力环境对比
Fig.9 Comparison of different gravity environment
如图9所示,当天线在重力环境下展开时,需要克服天线自身重力做功,所以其固定端右侧横杆输出转矩较大。失重环境下,由于模型中未考虑摩擦等因素的影响,所以固定端右侧横杆输出转矩为零。在重力环境下对天线进行悬吊卸载后,天线展开过程中固定端横杆输出转矩与失重环境下近似相等,故在地面展开试验中,有必要对天线进行重力补偿。
如2.1节所述,选取前索网面P3节点对应的滑轮车和铰链节点在x、y方向位移进行分析。由于本文所设计的重力补偿方案不存在原理误差,故其在仿真中滑轮车和铰链节点的位移相同,因此本文仅对吊丝配重法进行仿真分析,其具体结果如下。
由图10、图11可知,吊丝配重法中滑轮车与悬吊点在x、y方向的位移不能达到完全同步,其误差达到厘米级,故其运动过程中发生了吊丝非铅锤效应。由于吊丝配重法中吊丝偏斜问题无法避免,故实际中经常采用增大吊丝长度来减小吊丝偏斜的影响[3]。

图10 x方向位移
Fig.10 Displacement of x-axis

图11 y方向位移
Fig.11 Displacement of y-axis
由于吊丝配重法存在原理缺陷,故吊丝在运动过程中会发生偏斜,使得吊丝悬吊力不足,影响卸载精度。而本文所提出的吊丝主动定位与运动的重力补偿方案,在吊丝定位电机与展开拉索驱动电机的耦合控制下,消除了该原理误差,能够有效地保证吊丝位置的准确性,避免吊丝的非铅锤效应,提高环形天线重力补偿的精度。
5 结论
(1)通过对环形天线展开过程进行运动学分析,发现其前索网面各铰链节点在水平面内直线运动且位移对应成比例,其水平面位移与桁架展开角存在确定的函数关系。
(2)根据前索网面各铰链节点水平面位移间的关系,本文提出了一种基于吊丝主动水平定位和运动的重力补偿方案。通过吊丝定位电机与展开拉索驱动电机的耦合控制,实现了吊丝定位与运动的主动控制。
(3)经仿真验证,本文设计的吊丝主动水平定位和运动的重力补偿方案有效避免了传统吊丝配重法中吊丝非铅锤效应的产生,提高了重力补偿的准确性。
[1] 周志成,董富祥.空间大型天线多体动力学分析[M].北京:中国宇航出版社,2015:200-208.
ZHOU Zhicheng,DONG Fuxiang.Multi-body Dynamics Analysis for Large Space Antennas[M].Beijing:China Astronautic Publishing House,2015:200-208.
[2] 韦娟芳.卫星天线展开过程的零重力环境模拟设备[J].空间电子技术,2006,3(2):29-32.
WEI Juanfang.Zero-gravity Environment Simulation of the Deployment Process of the Satellite Antenna[J].Space Electronic Technology,2006,3(2):29-32.
[3] 徐文福,梁斌,李成,等.空间机器人微重力模拟实验系统研究综述[J].机器人,2009,31(1):88-96.
XU Wenfu,LIANG Bin,LI Cheng,et al.A Review on Simulated Micro-gravity Experiment Systems of Space Robot[J].Robot,2009,31(1):88-96.
[4] SATO Y,EJIRI A,IIDA Y,et al.Micro-G Emulation System Using Constant-tension Suspension for a Space Manipulator[C]// IEEE International Conference on Robotics and Automation. California,1991,3:1893-1900.
[5] WHITE G C,XU Y.An Active Vertical-direction Gravity Compensation System[J].IEEE Transactions on Instrumentation and Measurement,1994,43(6):786-792.
[6] MEGURO A,ISHIKAWA H,TSUJIHATA A.Study on Ground Verification for Large Deployable Modular Structures[J].Journal of Spacecraft and Rockets,2006,43(4):780-787.
[7] MEGURO A,SHINTATE K,USUI M,et al.In-orbit Deployment Characteristics of Large Deployable Antenna Reflector Onboard Engineering Test Satellite Ⅷ[J].Acta Astronautica,2009,65(9/10):1306-1316.
[8] TSUNODA H,HARIU K,KAWAKAMI Y,et al.Deployment Test Methods for a Large Deployable Mesh Reflector[J].Journal of Spacecraft and Rockets,1997,34(6):811-816.
[9] TSUNODA H,HARIU K,KAWAKAMI Y,et al.Structural Design and Deployment Test Methods for a Large Deployable Mesh Reflector[C]//38th Structures, Structural Dynamics, and Materials Conference. Kissimmee, FL, USA,1997:2963-2971.
[10] 齐乃明,张文辉,高九州,等.三维空间微重力地面模拟试验系统设计[J].机械工程学报,2011,47(9):16-20.
QI Naiming,ZHANG Wenhui,GAO Jiuzhou,et al.Design of Ground Simulation Test System for Three-dimensional Spatial Microgravity Environment[J].Journal of Mechanical Engineering,2011,47(9):16-20.
[11] 刘巍,张磊,赵维.载人低重力模拟技术现状与研究进展[J].航天医学与医学工程,2012,25(6):463-468.
LIU Wei,ZHANG Lei,ZHAO Wei.Current Situation and Research Progress of Low Gravity Simulation[J].Space Medicine & Medical Engineering,2012,25(6):463-468.
[12] 刘振,高海波,邓宗全,等.摇臂转向架式星球车单索重力补偿[J].机械工程学报,2013,49(7):113-124.
LIU Zhen,GAO Haibo,DENG Zongquan,et al.Gravity Compensation for Rocker-bogie Rovers Through Single String Tension[J].Journal of Mechanical Engineering,2013,49(7):113-124.
[13] 姚燕生,梅涛,刘明,等.悬挂式重力补偿系统精密跟踪方法[J].哈尔滨工业大学学报,2009,41(11):205-208.
YAO Yansheng,MEI Tao,LIU Ming,et al.Precision Tracking Method in Suspension System for Gravity Compensation[J].Journal of Harbin Institute of Technology,2009,41(11):205-208.
[14] 李团结,张琰,李涛.周边桁架可展天线展开过程动力学分析及控制[J].航空学报,2009,30(3):444-449.
LI Tuanjie,ZHANG Yan,LI Tao.Deployment Dynamic Analysis and Control of Hoop Truss Deployable Antenna[J].Acta Aeronautica et Astronautica Sinica,2009,30(3):444-449.
[15] 齐朝晖,常进官,王刚.周边桁架式可展开天线展开分析与控制[J].宇航学报,2014,35(1):61-68.
QI Zhaohui,CHANG Jinguan,WANG Gang.Analysis and Control of Deployment Process for Hoop Truss Deployable Antenna[J].Journal of Astronautics,2014,35(1):61-68.
