0 引言
机车轴承是铁路机车行走部的关键部件，在重载工况下工作，振动信号噪声大， 其损伤特征提取难[1]。王晓冬等[2]针对机车轴承信号特征，构造自适应多小波，以峭度最大为目标函数，采用基于遗传算法的多小波谱峭度来确定最佳频带，有效地提取了轴承信号的特征分量。LEI等[3]提出了基于小波包变换的谱峭度方法，以小波包分量的峭度最大为指标，从多层小波包分量中寻找最佳小波包分量，以此分离出了机车包含轴承损伤特征的有效分量。ZHAO等[4]提出了基于集成经验模态分解的最佳模式分量的包络阶次跟踪分析方法，在轴承转速不恒定时，采用该方法可以扑捉轴承故障的特征。LI等[5]提出了一种基于相关分析的独立变分模态分解方法，以提取有效分量用于包络分析，发现了机车轴承的微弱故障和混合故障。上述这些方法中，小波变换方法对频带的划分无法做到自适应，经验模态分解方法缺乏完备的理论基础，因此，采用高效的信号处理方法是提取轴承故障特征的关键。经验小波变换(empirical wavelet transform, EWT)[6]结合了小波分析的完备理论性和经验模式分解的自适应性，通过信号的频谱局部极大值的频率自适应划分其分析频带，并基于划分的子频带构造一系列合适的正交小波滤波器组对信号进行分解。然而，信噪比较低的工程信号的噪声频谱较宽，频谱上噪声分量的谱峰会影响信号的峰值分布，干扰子频带划分的合理性，使EWT提取特征的有效性受到影响。为了克服EWT基于频谱局部极大值划分频带方法的不足，针对机车轴承的故障特征提取，笔者提出一种采用信号时频峭度谱局部极小值划分频带的方法，在时频变换的基础上求取信号的时频峭度谱，由其峭度谱局部极小值对应的频率来确定子频带的边界，构造正交小波滤波器组对信号进行EWT。仿真实验和工程应用表明，改进后的EWT能够克服噪声的干扰，有效地提取轴承的损伤故障特征。
1 基于时频峭度谱的经验小波变换
1.1 经验小波变换(EWT)
经验小波变换是经验模态分解原理与小波框架理论相结合的一种信号分析方法[6]，即把任意的一个时域信号看成是一组调频调幅信号分量的组合，应用小波框架理论，基于信号的频域分布特征构造一系列小波滤波器组，以此提取不同频带的调频调幅分量。经验小波变换原理如下：
(1)对信号进行傅里叶变换，求取其频谱。设信号f(t)的傅里叶变换为
(1)
把信号f(t)的频谱记为
(2)根据信号的频谱特征，分割频带。在频谱f(ω)上寻找M个局部极大值，并按降序排列，然后将它们对应的频率按升序排列后记为ωm(m=1，2，…，M)。将分析频带[0, π]划分成N(N≤M)个子频带。设以ωn为中心的调幅调频分量所在的子频带为[Ωn-1, Ωn][7]，其中，Ωn-1=(ωn-1+ωn)/2， n=2,3,…,N。令Ω0=0，ΩN=π，这样可把信号的分析频带 [0, π]划分成N个连续的、互不交叠的子频带。
(3)构造小波滤波器组。对于子频带[Ωn-1, Ωn]，尺度函数
和小波函数
分别为[6]
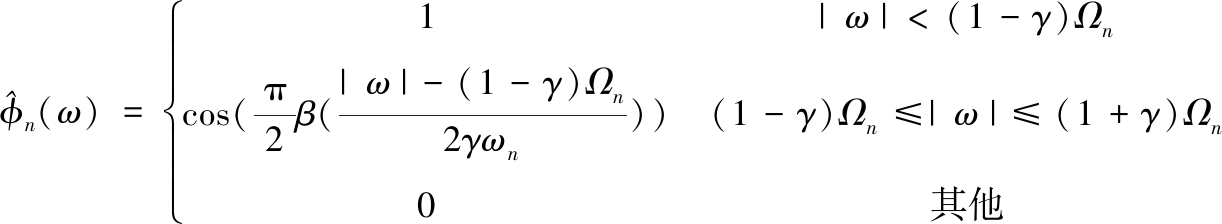
(2)
(3)
对于信号f(t)，在N个子频带上，利用式(2)、式(3)可以设计出1个低通滤波器(尺度函数)和N-1个带通滤波器(小波函数)组成的自适应小波滤波器组。
(4)信号分解。根据小波变换方法来定义经验小波变换
在子频带[Ωn-1, Ωn]的经验小波变换的细节系数为[8]
(4)
逼近系数为
(5)
其中，F-1[•]表示Fourier逆变换；
(•)、
(•)分别表示
•
(•)的共轭。小波分解得到的低频分量f0(t)和高频分量fk(t)分别为[6]
*φ1(t)
(6)
*φk(t)
(7)
其中，*表示函数的卷积运算。
经验小波变换是完全重构的，重构表达式为[9]
*
*φn(t)=
(8)
设试验信号为
y(t)=sin(240πt)+sin(80πt)+cos(20πt)
(9)
图1为信号时域波形和频谱，采样频率为2 000 Hz，数据长度为1 024，图1b中的短虚线为采用上述方法得到的频带划分边界线。加入白噪声的信号y(t)的时域波形如图1c所示，信噪比为-1.5 dB，图1d为其频带分割图，可以看到，噪声分量产生的谱峰(局部极大值)影响了频带分割的有效性，信号y(t)的3个分量的峰值并没有处在分割子频带的中心位置。当信号被噪声污染时，噪声信号分量的无效局部峰值会影响经验小波变换的频带划分的合理性[9]，使得EWT分解得到的信号分量的有效性降低。
1.2 基于时频峭度谱的经验小波变换改进算法
(a)无噪声时的波形图
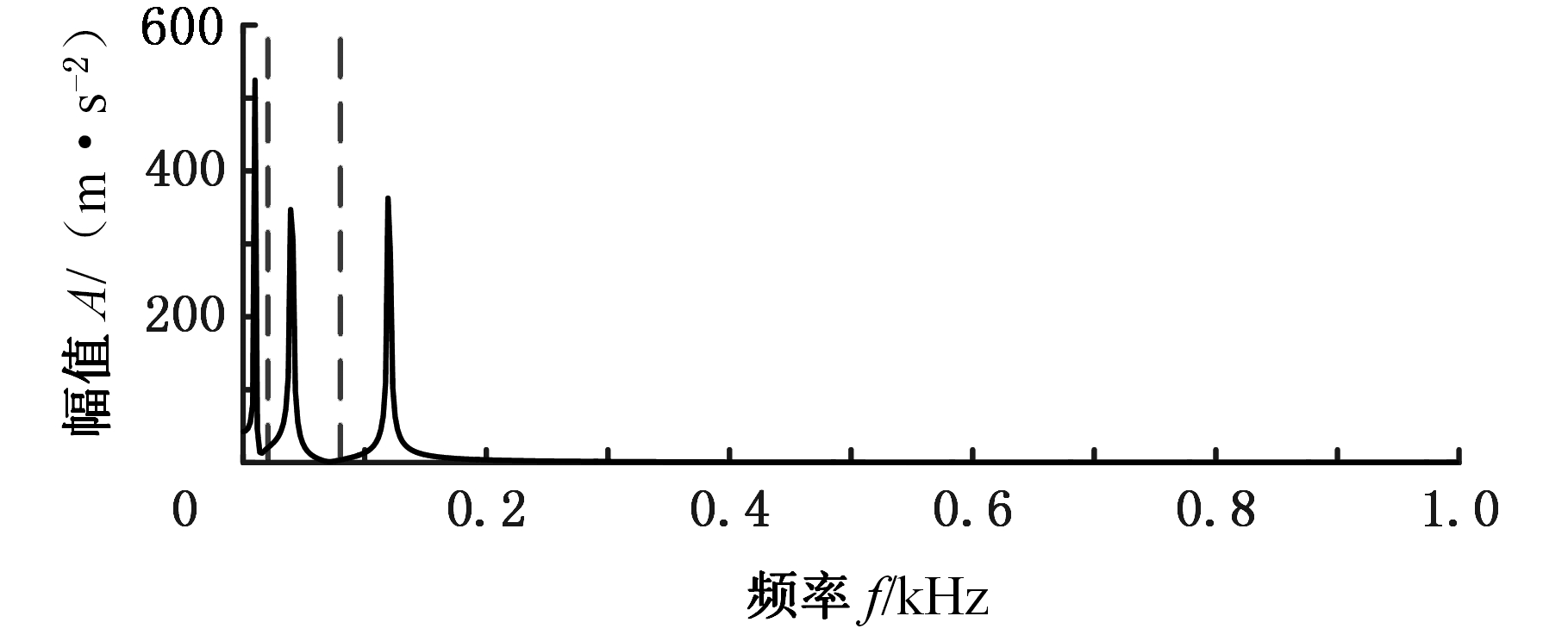
(b)无噪声时的频谱分割图
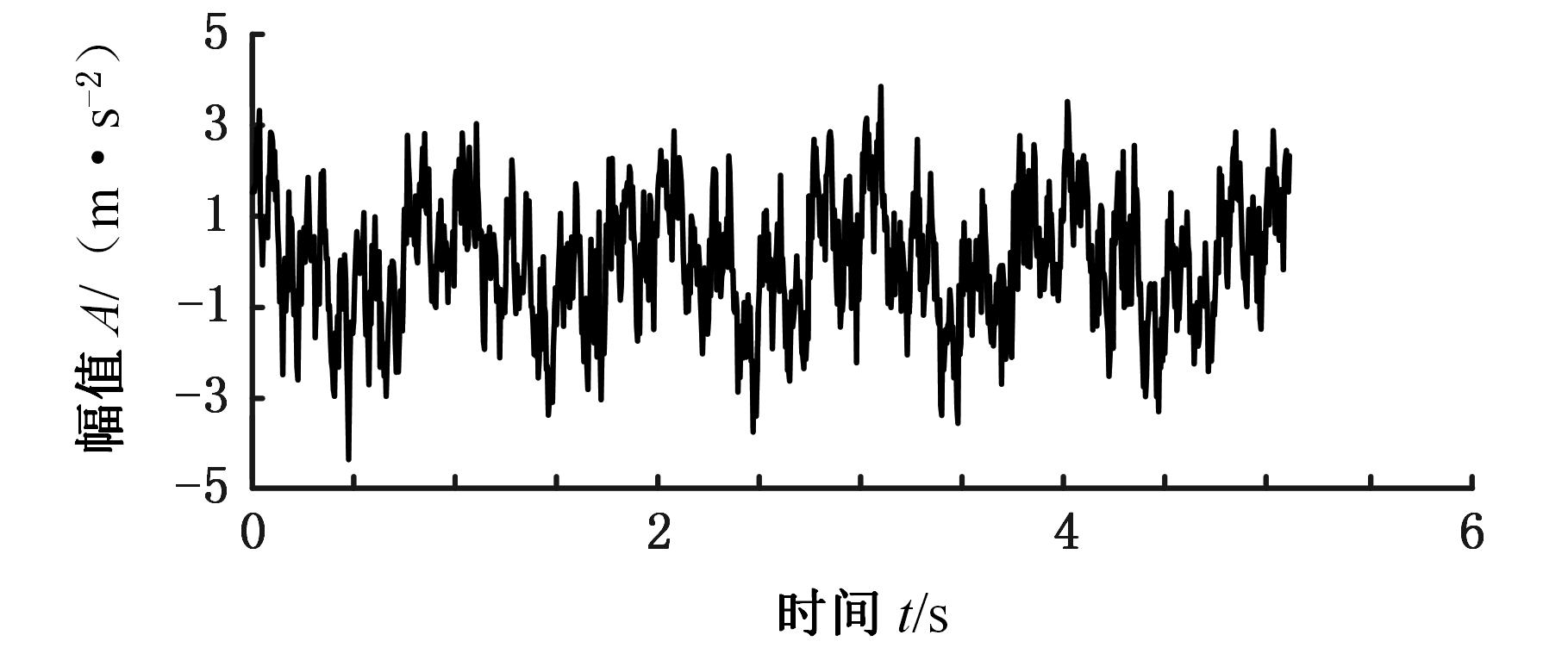
(c)有噪声时的波形图
(d)有噪声时的频谱分割图
图1 信号的波形和频谱分割
Fig.1 Waveform and spectral segmentation of a signal
为了克服信号噪声分量的谱峰对频带划分的影响，本文用一种信号时频峭度谱代替信号的频谱，通过峭度峰值对应的频率来确定子频带的边界，以此为基础构造小波滤波器组，提取信号中的幅值调制分量。改进的经验小波变换原理如下。
(1)对信号进行时频变换。时域信号f(t)的傅里叶变换为
的时频变换即频率切片小波变换为[10]
(10)
其中，κ为常数，用于调节时频分辨率，
为频率切片函数p(t)的傅里叶变换，这里选取高斯小波函数作为频率切片函数；
为
的共轭函数。由于ω=2πf，当κ为常数时，变换结果W(t, ω, κ)可写为W′(t, f)。设采样频率为fs，信号长度为N，W′(t, f)为信号f(t)在时频空间[0,tN-1,0,fs/2]的时频变换。在时频子空间[t1, t2, f1, f2]上的信号分量为[11]
(11)
(2)以时频分解结果为基础，求信号的时频峭度谱。在信号f(t)的时频空间上，定义频带宽度为ΔW，步长为fp，此处的频带宽度ΔW和步长fp均取为3倍的特征频率，则在时频子空间[0, tN-1, (k-1)fp, (k-1)fp+ΔW]上的重构信号分量为
(12)
k=1，2，…，kf
式中，kf为fs/(2fp)的整数部分。
则yk(t)的峭度为
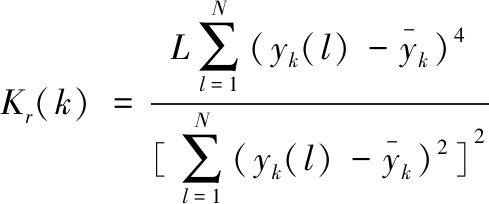
(13)
式中，
为yk(t)的均值。
信号f(t)在频带[0, fs/2]的峭度为KR=(Kr(1)，Kr(2)，…，Kr(kf))。令时频子空间[0, tN-1, (k-1)fp, (k-1)fp+ΔW]的中心频率为
则各个时频子空间中心频率的所组成的向量Fc=(fc(1)，fc(2)，…，fc(kf)),从而得到信号f(t)的一种时频峭度曲线。
(3)找出信号时频峭度谱最大值相邻的局部极小值及其对应的频率，确定子频带边界。在时频峭度谱上找出L-1个局部极小值对应的频率{ωm|m=1，2，…，L-1}和最大值对应的频率fmax。从这L-1个局部极小值中找出与最大值相邻的2个局部极小值。 2个相邻的局部极小值之间必定存在一个局部最大峰值，该峰值对应的频率为调频调制分量的中心频率，本文就只划分了3个频带，因此有子频带分界点Ω0、Ω1、Ω2、Ω3，其中，Ω0=0，Ω3=π，可把信号的分析频带[0，π]划分成3个连续的、互不交叠子频带。
(4)在子频带为[Ωn-1，Ωn](n=1,2,3)上按照式(2)、式(3)构造滤波器组，再由式(4)、式(5)求出小波系数和逼近系数，最终由式(6)、式(7)求出信号的各个子频带的分解分量。
2 仿真实验
设轴承损伤的冲击响应分量s(t)=exp(-2πf2t)sin(2πf1t)，其中，固有频率f1=2 000 Hz，f2=70 Hz；损伤冲击重复频率为120 Hz，叠加白噪声的试验信号如图2所示，加噪后信号的信噪比为-11.76 dB，采样频率为12 000 Hz，数据长度为4 096。
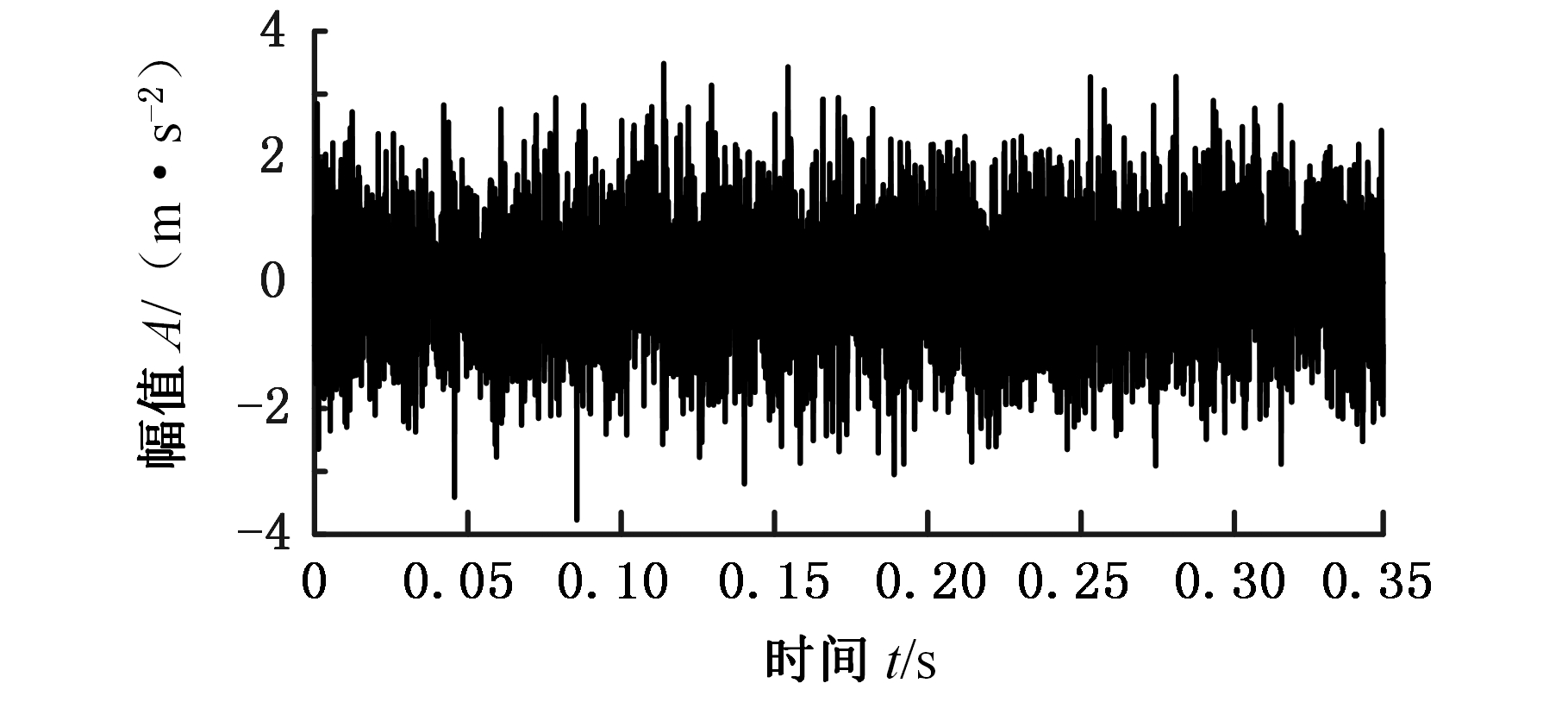
图2 试验信号
Fig.2 Test signal
图3为试验信号的频谱和包络谱。由图3a可以隐约观察到试验信号以2 000 Hz为中心频率的共振频带。图3b的包络谱上显示出120 Hz冲击频率及其倍频所对应的峰值。
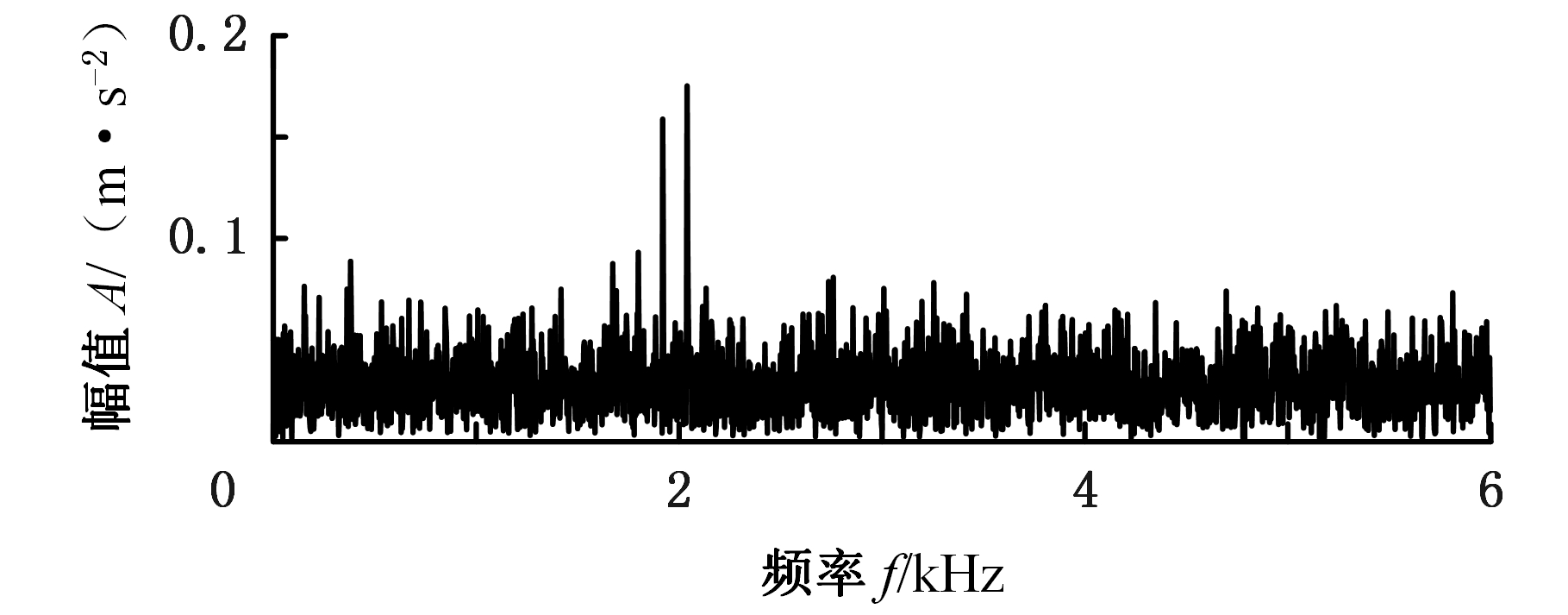
(a)信号频谱
(b)信号包络谱
图3 试验信号的频谱和包络谱
Fig.3 Spectrum and envelope spectrum of the test signal
为了简化说明，试验仅使用频谱中的前3个较大峰值进行子频带边界运算。图4所示为采用传统方法的边界划分结果，可以看到中心频率2 000 Hz及其边频带被划分到2个相邻子频带，因此，EWT分解后，图5中的子频带Ⅱ和子频带Ⅲ的信号分量都会含有重复性冲击响应分量，两个频带分量的包络谱都包含120 Hz及其倍频的谱峰。显然，噪声分量对频谱的影响改变了频谱的局部最大值分布，使子频带边界的计算产生了偏差，出现了不合理的频带分割。
图6所示为采用改进方法的边界划分结果，可以看到，以中心频率为2 000 Hz及其边频带被划在子频带Ⅱ中。
图7为峭度最大峰值所在的子频带Ⅱ的分量包络谱，3个显著的峰值对应的频率分别为重复冲击频率及其2倍频、3倍频。
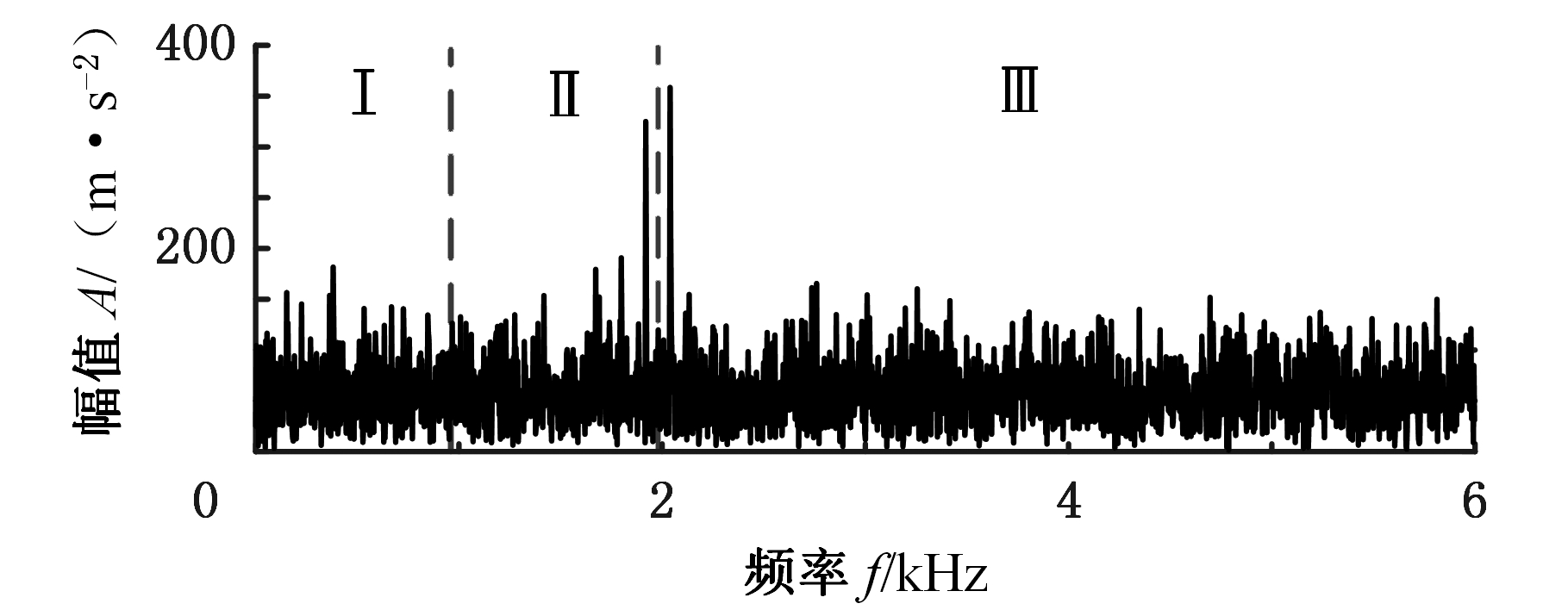
图4 EWT频谱分割(试验信号)
Fig.4 EWT spectrum segmentation(test signal)
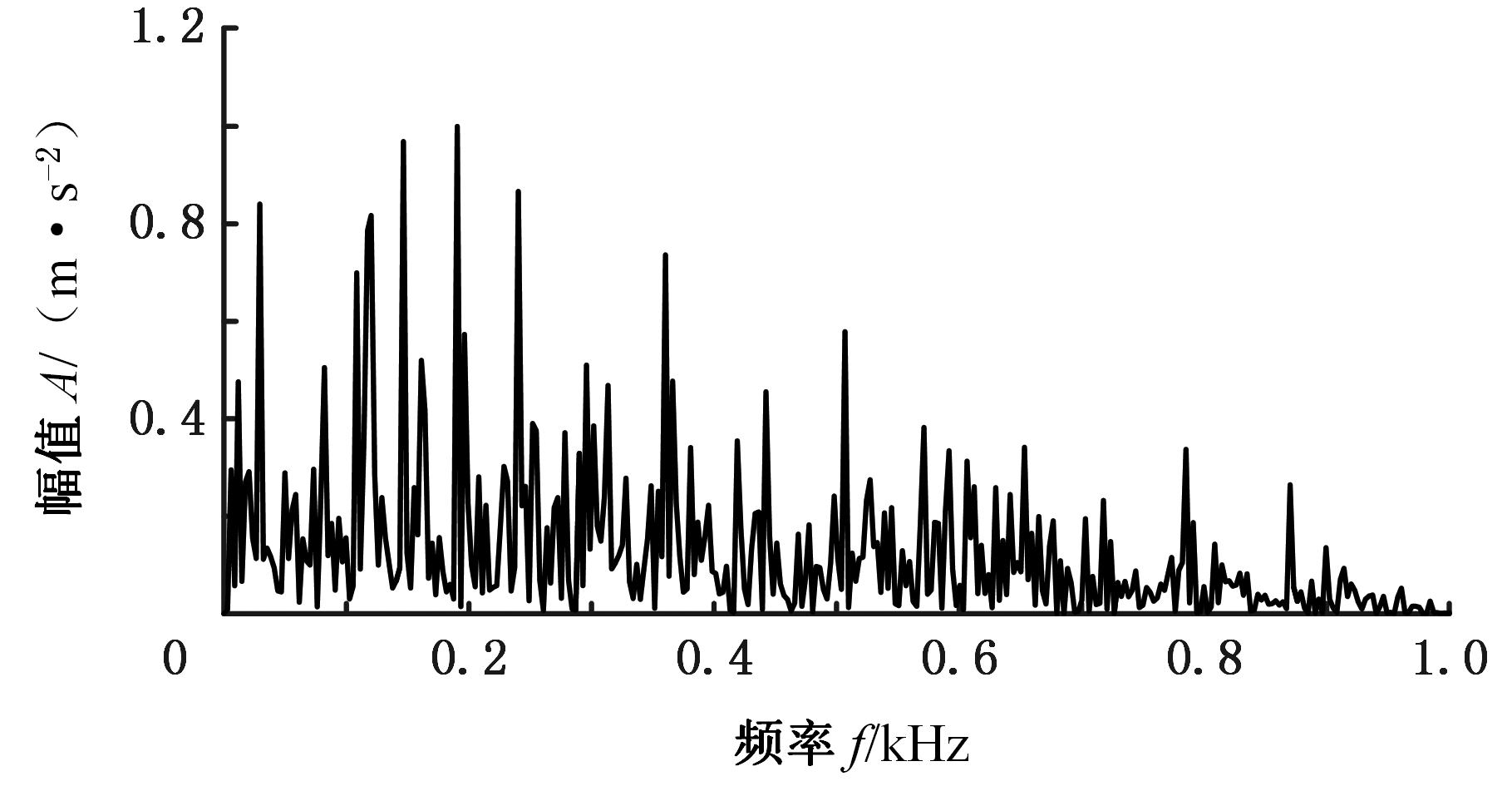
(a)子频带Ⅱ的分量包络谱
(b)子频带Ⅲ的分量包络谱
图5 EWT分量的包络谱(试验信号)
Fig.5 Envelope spectrum of EWT component(test signal)
(a)时频峭度谱的划分
(b)对应的频谱划分
图6 改进的EWT频谱分割(试验信号)
Fig.6 Improved EWT spectrum segmentation(test signal)
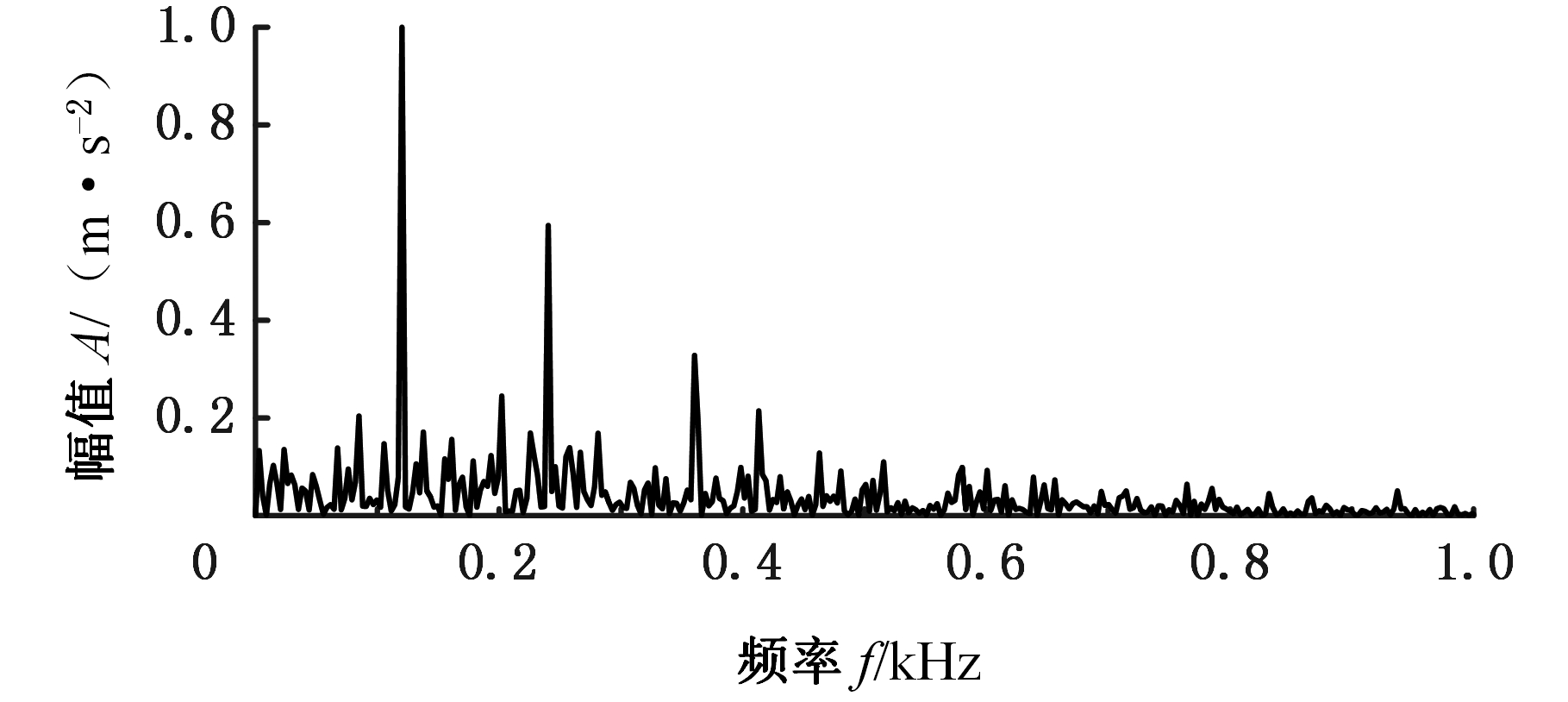
图7 改进的EWT子频带Ⅱ的分量包络谱(试验信号)
Fig.7 Envelope spectrum of improved EWT subbandⅡ
(test signal)
3 工程应用
东风43418型机车行走部的轴承型号为52732QT，滚子直径为34 mm，轴承内径为160 mm，外径为290 mm，滚子个数为17。实验数据来自于机车轴承试验台，实验模拟了不同转速和载荷条件下轴承的工作状态，采用加速度传感器采集轴承轴瓦的振动信号，采样频率为12.8 kHz。分别采用传统EWT算法和改进EWT算法分析轴承的振动信号，信号长度为8 192。
图8为一组无损伤轴承的振动信号，实验载荷为2 002 kg，转速为378 r/min(6.3 Hz)，此时，内圈、外圈和滚动体的损伤特征频率分别为61.64 Hz、45.46 Hz 和40.74 Hz。
图8 无损伤时振动信号
Fig.8 Vibration signal without damage
由图9可以看出，子频带Ⅱ和子频带Ⅲ的幅值较大，因此分别对该子频带的分量进行包络谱分析。
图10所示为子频带Ⅱ和子频带Ⅲ的分量包络谱，这两个频带的分量包络谱在6.25 Hz、20.31 Hz处有较大的峰值，它们分别对应转频及其3倍频，但由于噪声的干扰，还存在其他干扰峰值，转频并不明显。
图11所示为采用改进EWT算法时，该信号以时频峭度谱划的分子频带边界，可以看出，子频带Ⅲ的峭度峰值最大，对该子频带的分量进行包络谱分析。
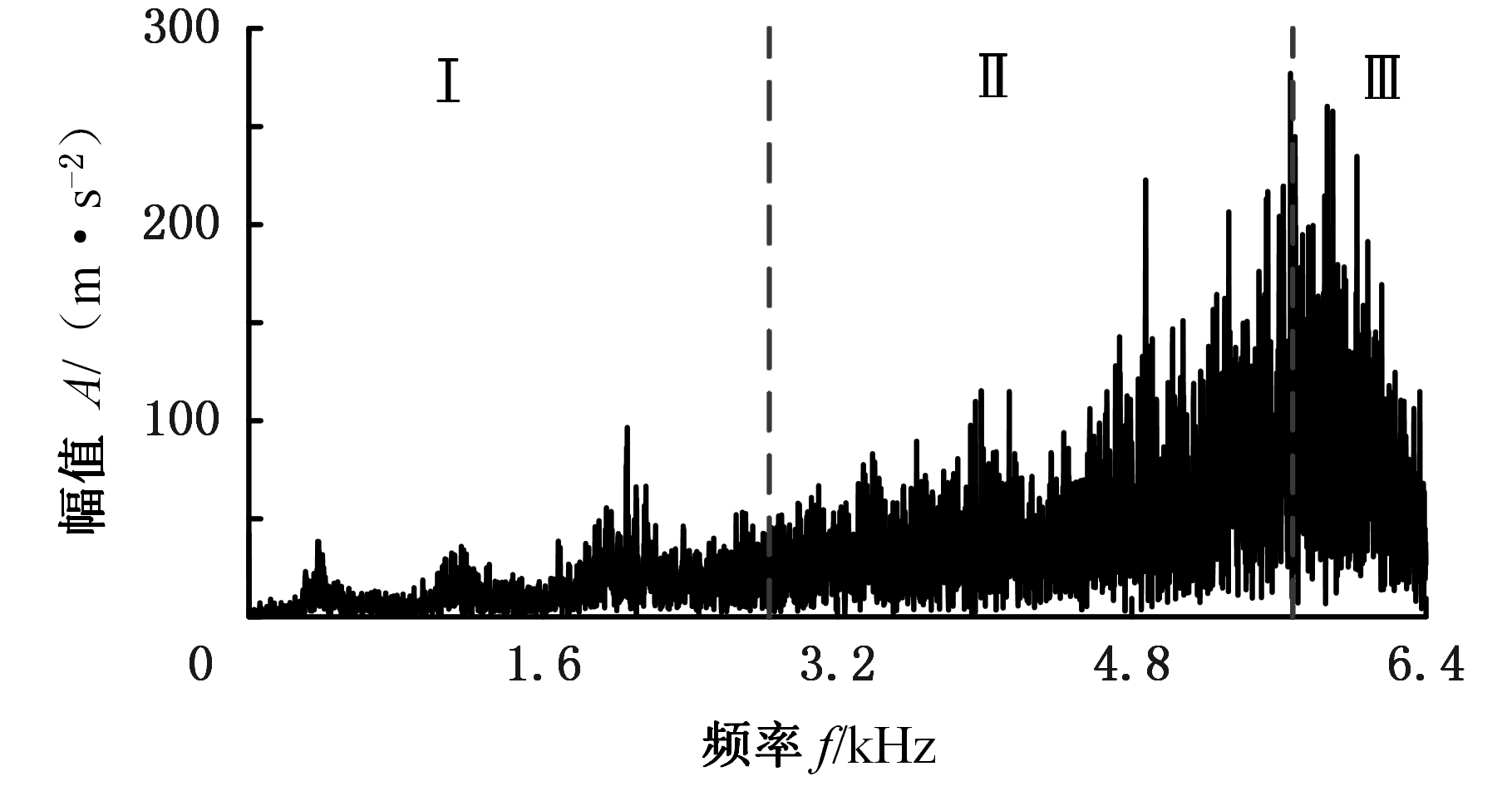
图9 EWT频谱边界划分(无损伤)
Fig.9 Boundary division of EWT spectrum(no damage)
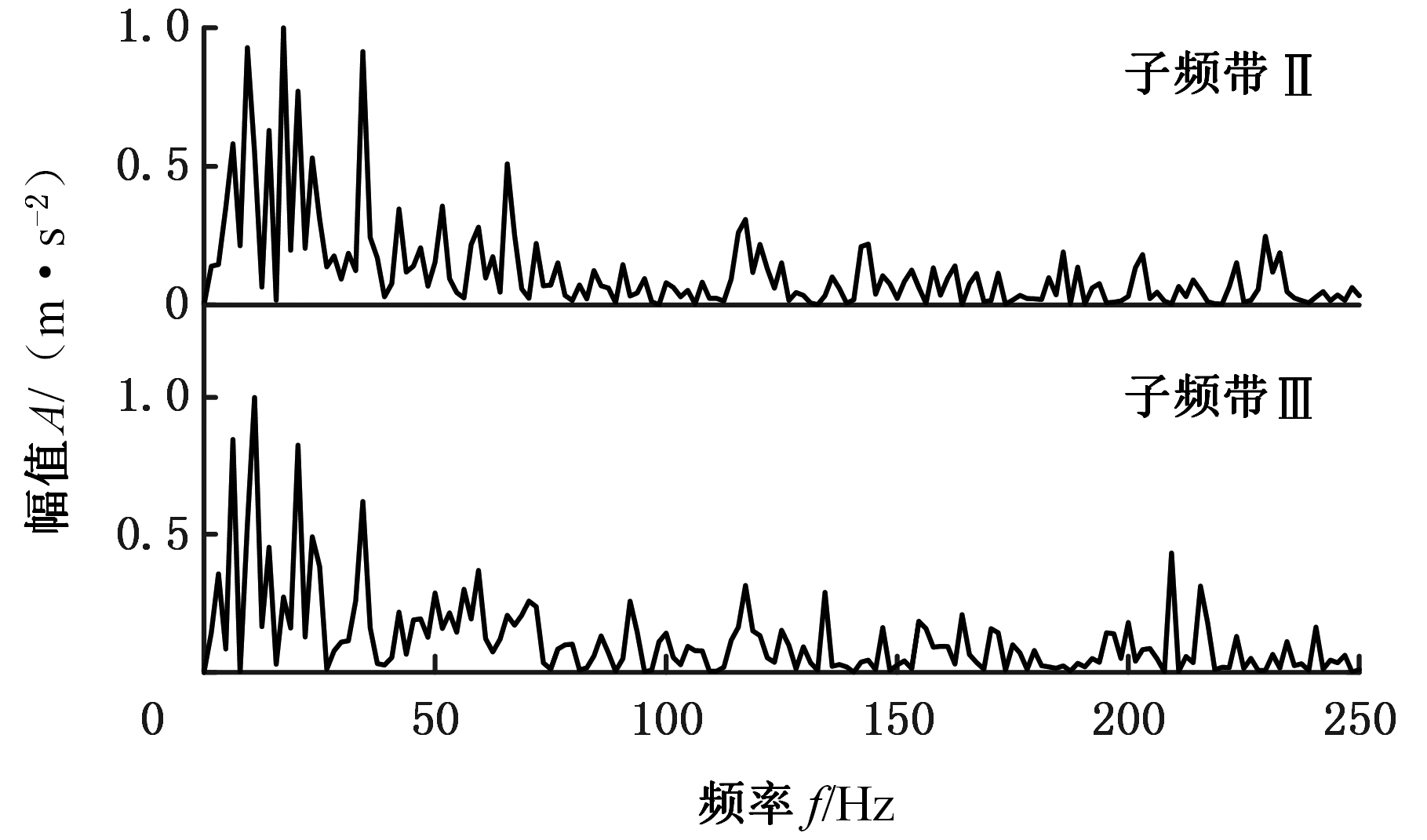
图10 EWT分量的包络谱(无损伤)
Fig.10 Envelope spectrum of EWT component(no damage)
图11 时频峭度谱的边界划分(无损伤)
Fig.11 Boundary division of time-frequency kurtosis spectrum(no damage)
图12中，包络谱在6.25 Hz、20.31 Hz处有较大的峰值，它们分别对应转频及其3倍频，20.31 Hz是基频的3倍频，没有发现其他的损伤特征频率。
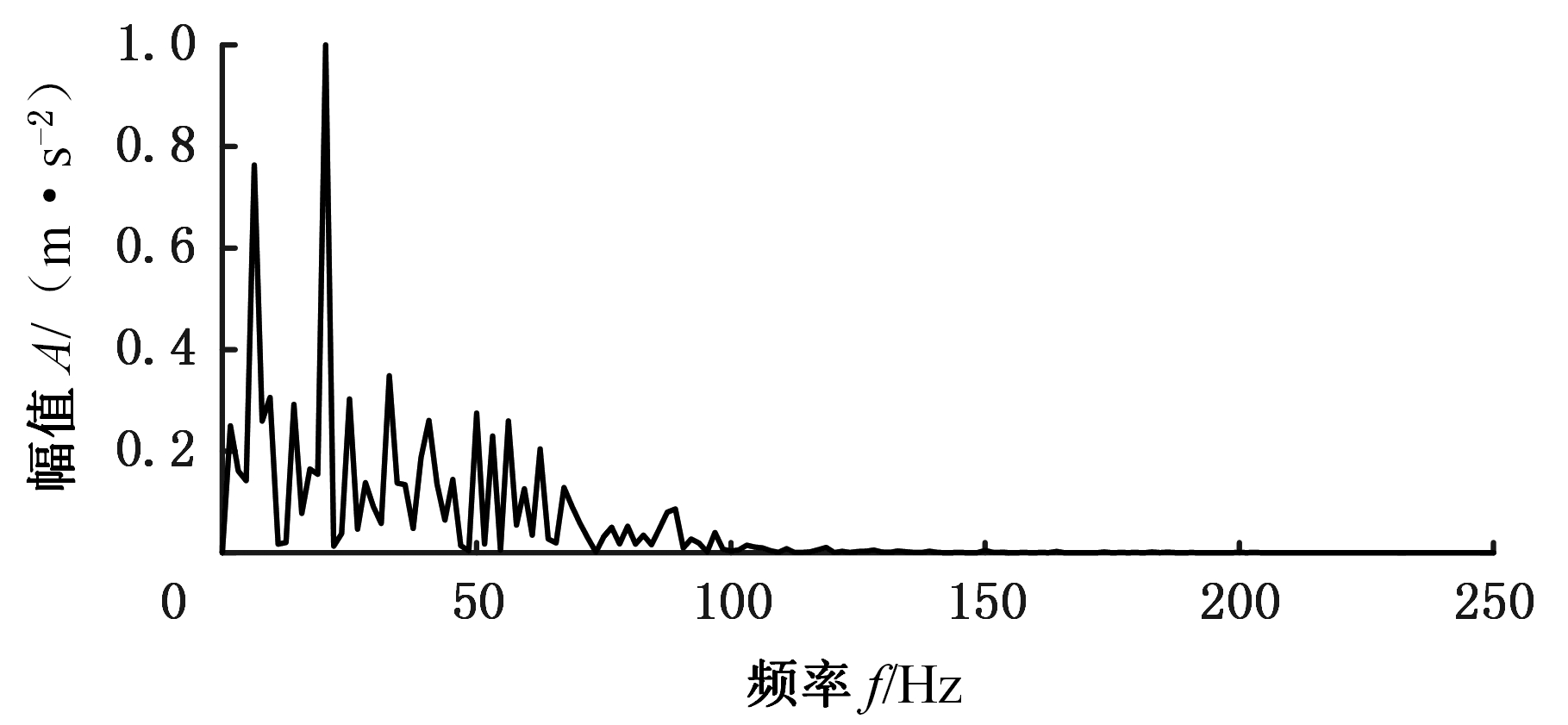
图12 改进的EWT子频带Ⅲ的分量包络谱(无损伤)
Fig.12 Envelope spectrum of improved EWT subbandⅢ(no damage)
图13为外圈存在损伤的轴承振动信号，此时，载荷为1 992 kg，转速为611 r/min(10.18 Hz)，计算可知其内圈、外圈和滚动体的损伤特征频率分别为99.64 Hz、73.48 Hz和65.85 Hz。
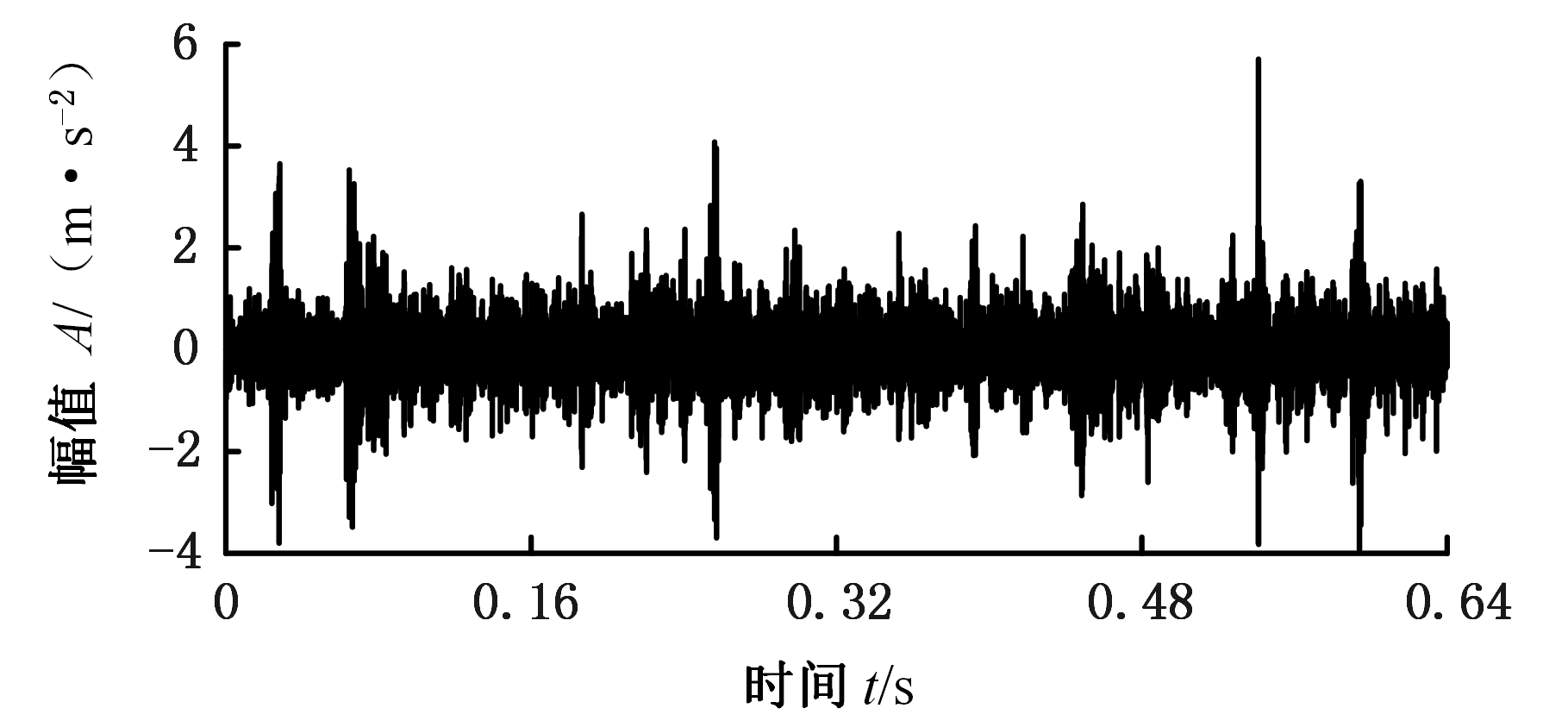
图13 外圈损伤的轴承振动信号
Fig.13 Bearing vibration signal of outer ring damage
图14所示为采用传统EWT算法的边界划分结果，可以看出子频带Ⅱ的幅值较大，因此对该子频带的分量进行包络谱分析。
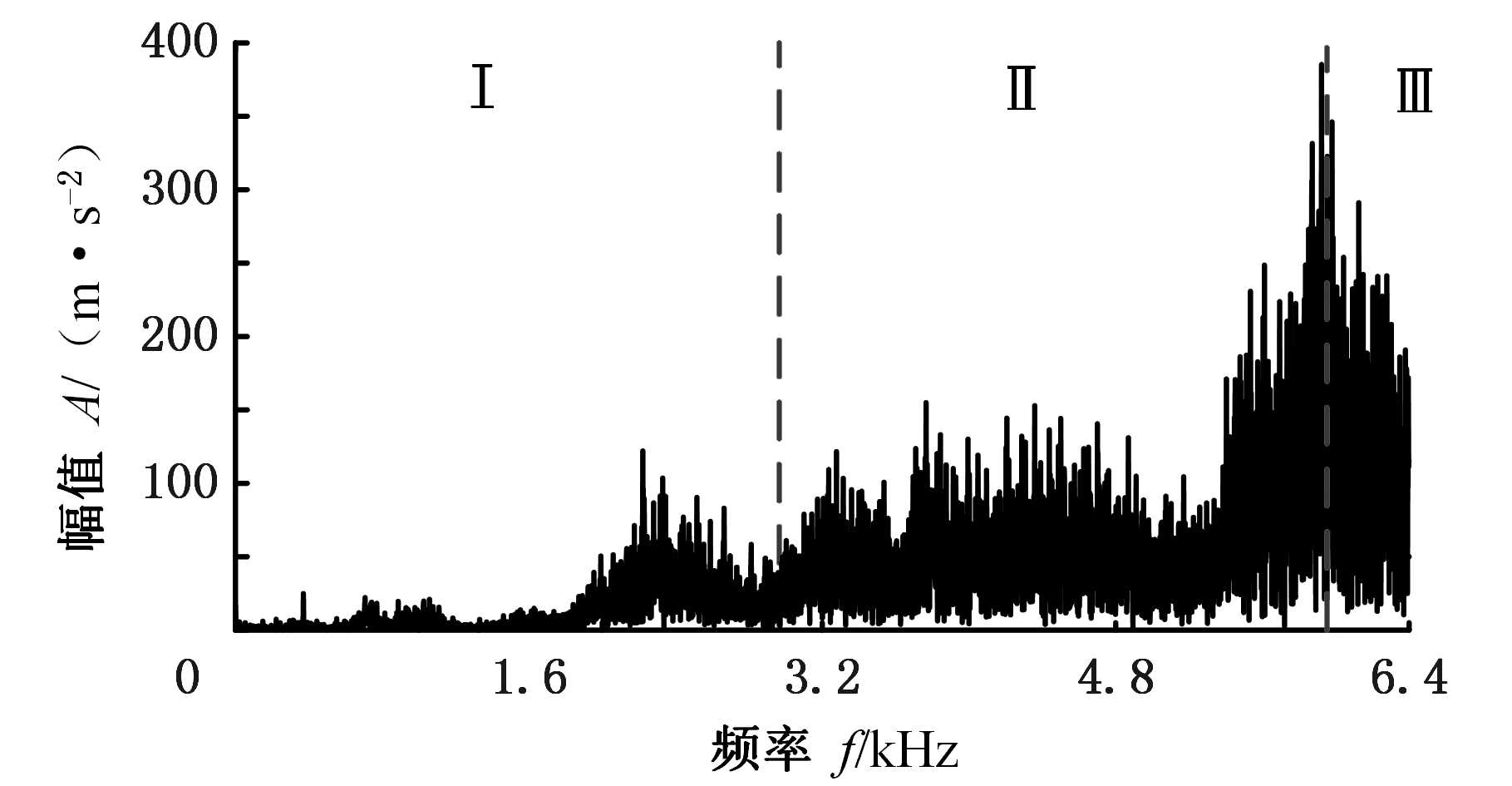
图14 EWT频谱边界划分(外圈)
Fig.14 Boundary division of EWT spectrum(outer ring)
图15中，该频带的分量包络谱在53.13 Hz、73.44 Hz、79.69 Hz处有较大的峰值，但由于噪声的干扰，还存在其他峰值，使得故障判断结果存在较大误差。图16所示为采用改进EWT算法时，该信号基于时频峭度谱划的分子频带边界。
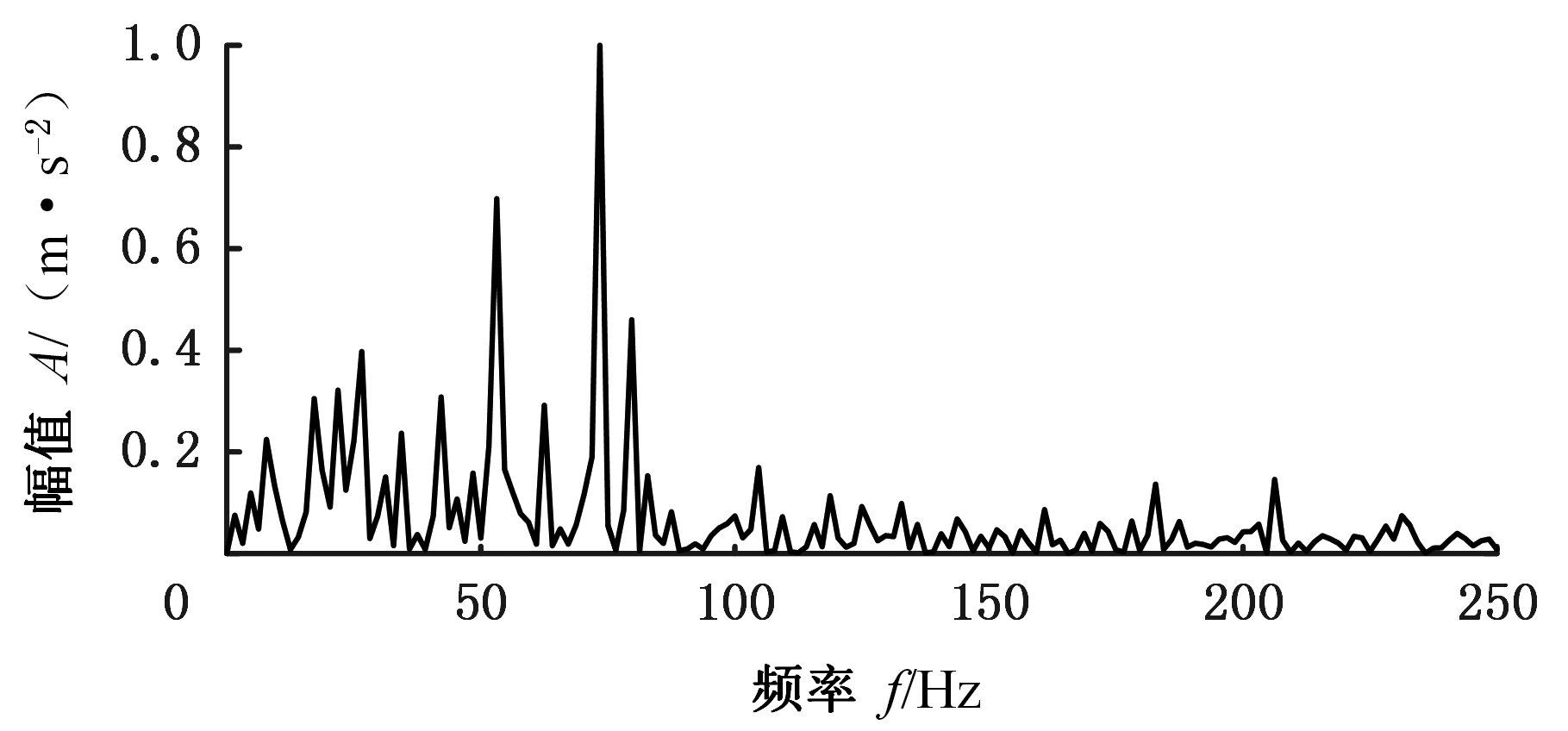
图15 EWT子频带Ⅱ的分量包络谱(外圈)
Fig.15 Envelope spectrum of EWT subbandⅡ(outer ring)
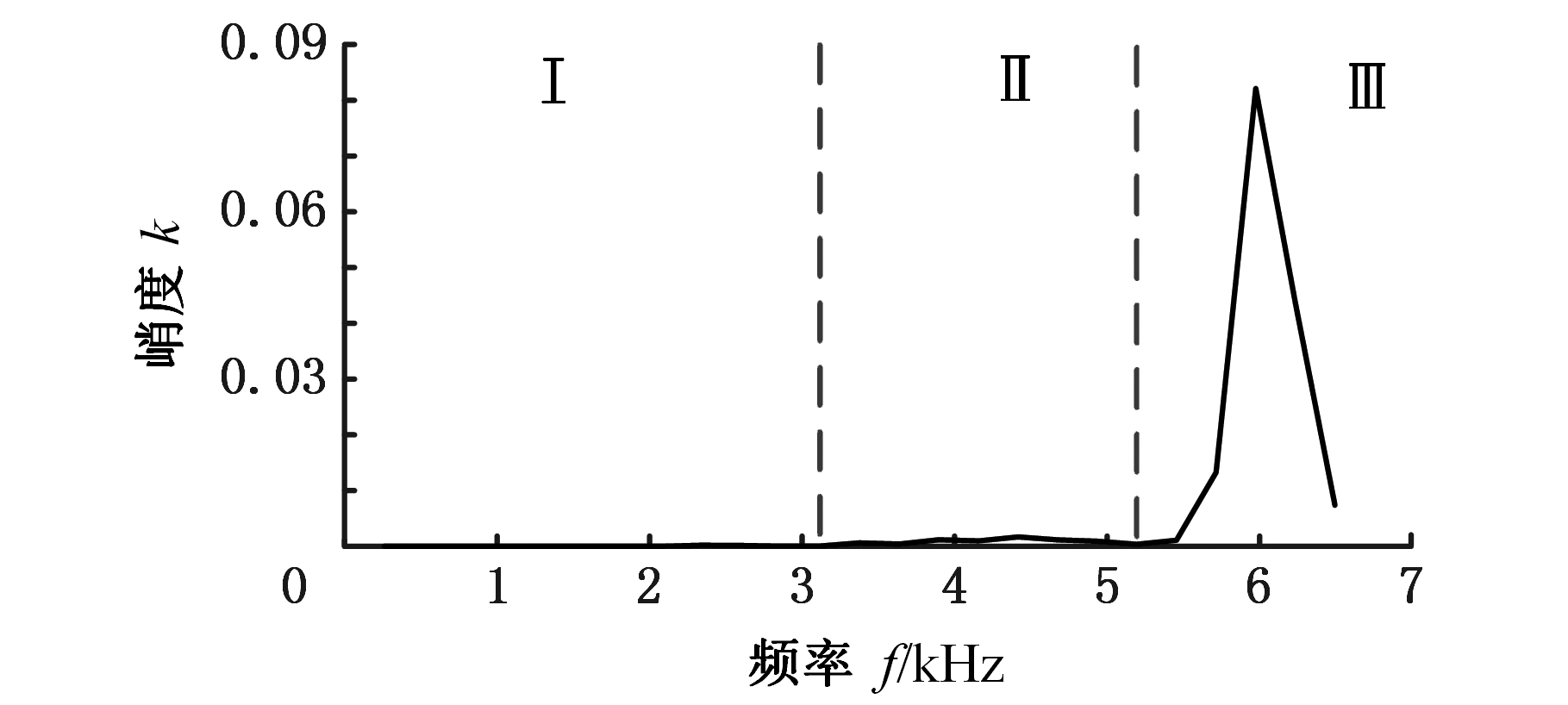
图16 时频峭度谱的边界划分(外圈)
Fig.16 Boundary division of time-frequency 6kurtosis spectrum(outer ring)
图17是最大峭度所在的子频带Ⅲ的分量的包络谱，可以观察到包络谱上2个较大峰值对应的频率分别26.56 Hz、73.44 Hz，它们分别为外圈损伤的特征频率及其1/3倍频。
图17 子频带Ⅲ分量的包络谱(外圈)
Fig.17 Envelope spectrum of subbandⅢ(outer ring)
图18所示为滚动体损伤的振动信号，此时，载荷为2 001 kg，转速为531 r/min(8.85 Hz)，计算可知，其内圈、外圈和滚动体的损伤特征频率分别为86.59 Hz、63.86 Hz和57.23 Hz。
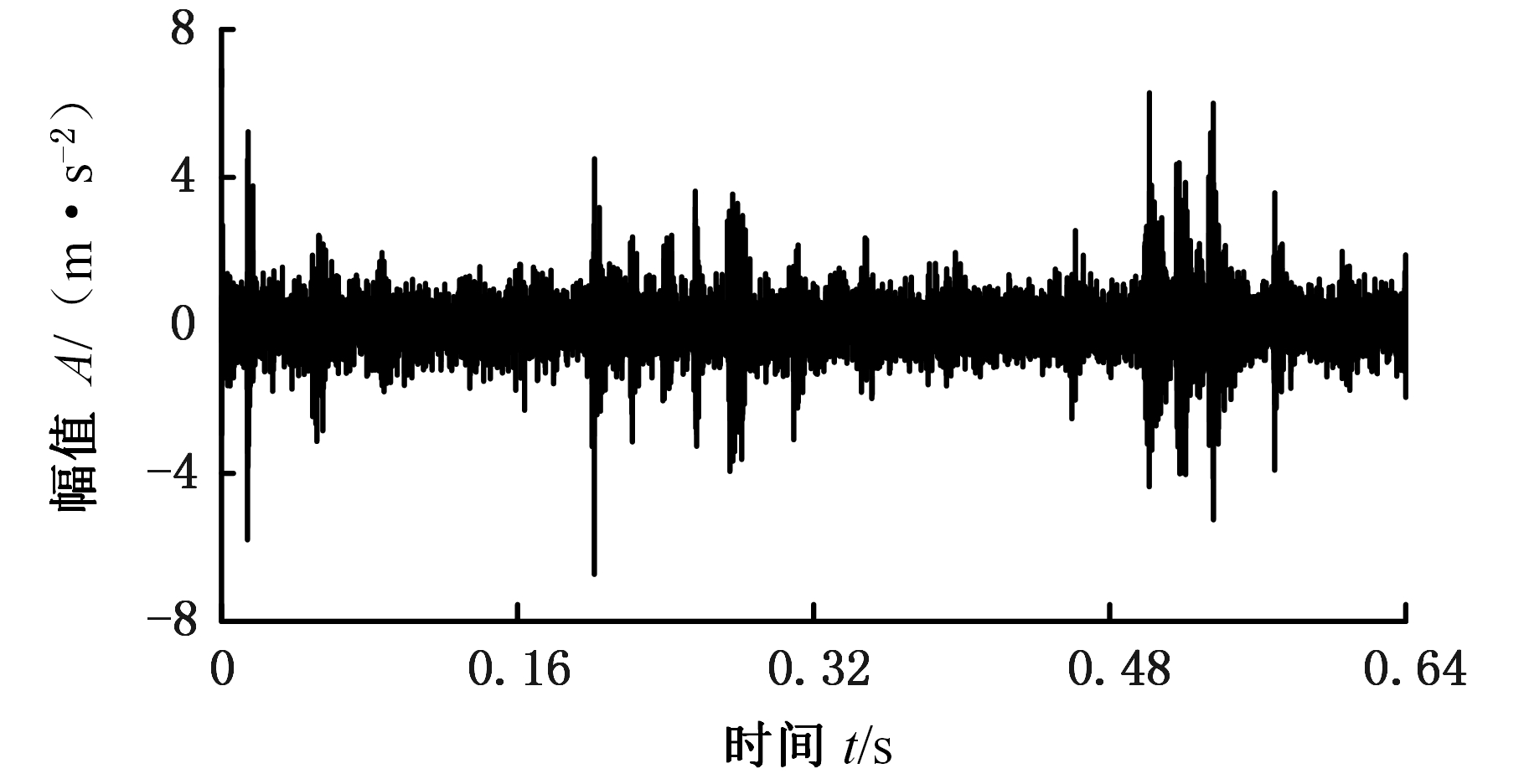
图18 滚动体损伤的振动信号
Fig.18 Vibration signal of rolling element damage
图19所示为采用传统EWT算法的边界划分结果，可以看出子频带Ⅱ的幅值较大，因此对该子频带的分量进行包络谱分析，如图20所示。该频带的分量包络谱在26.56 Hz、46.88 Hz、57.81 Hz处有较大的峰值，但由于噪声的干扰，滚子损伤特征频率并不明显，且还存在其他干扰峰值。
图19 EWT频谱边界划分(滚动体)
Fig.19 Boundary division of EWT spectrum(rolling element)
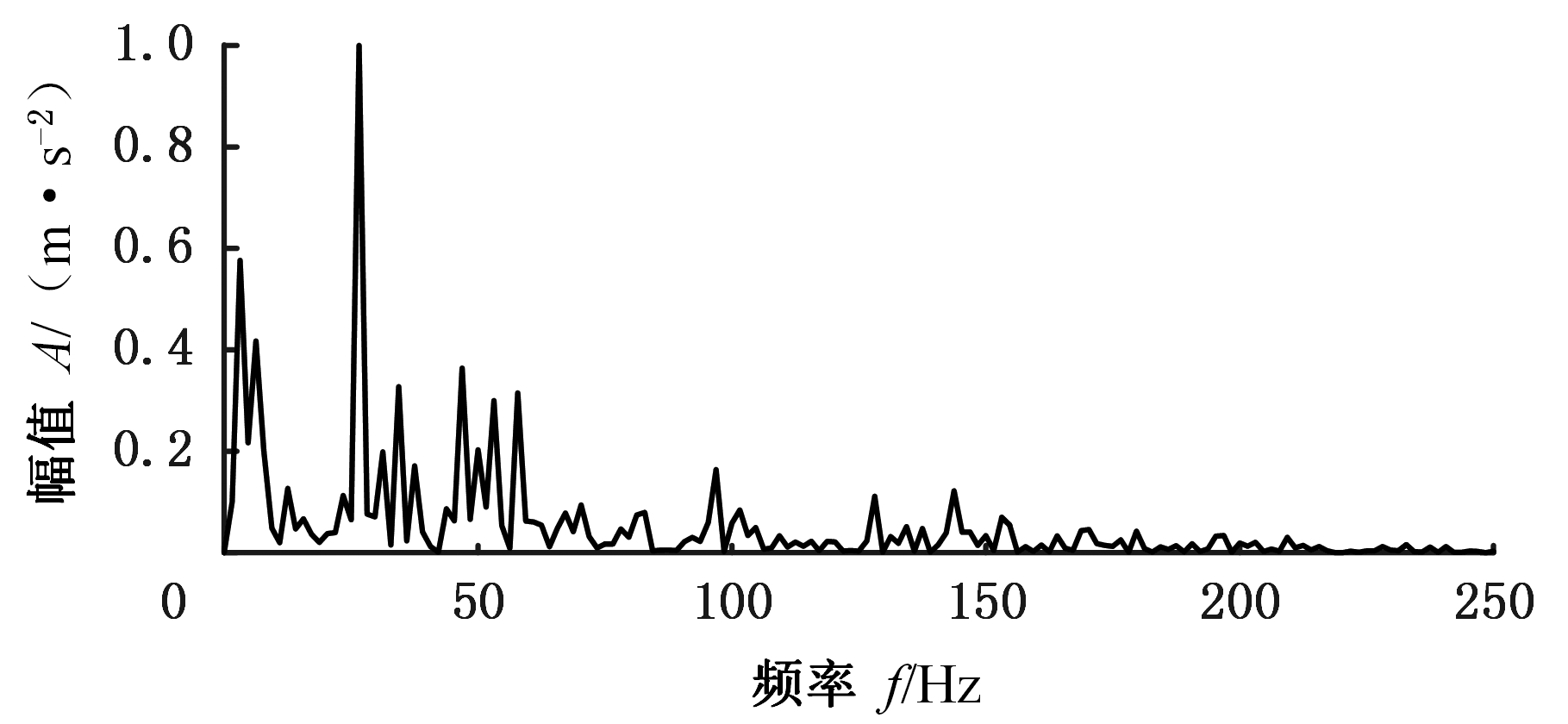
图20 EWT子频带Ⅱ的分量包络谱(滚动体)
Fig.20 Envelope spectrum of EWT subbandⅡ(rolling element)
改进EWT算法分析时，仅以较大的3个峰值为主进行子频带划分，如图21所示。
图21 时频峭度谱的边界划分(滚动体)
Fig.21 Boundary division of time-frequency kurtosis spectrum (rolling element)
同样，对最大峰值所在的子频带Ⅱ的分量做包络谱分析(见图22)，57.81 Hz处有显著的峰值，该频率正是滚子损伤的特征频率，另外，另一个峰值对应的频率为26.56 Hz，它是转频的3倍频。
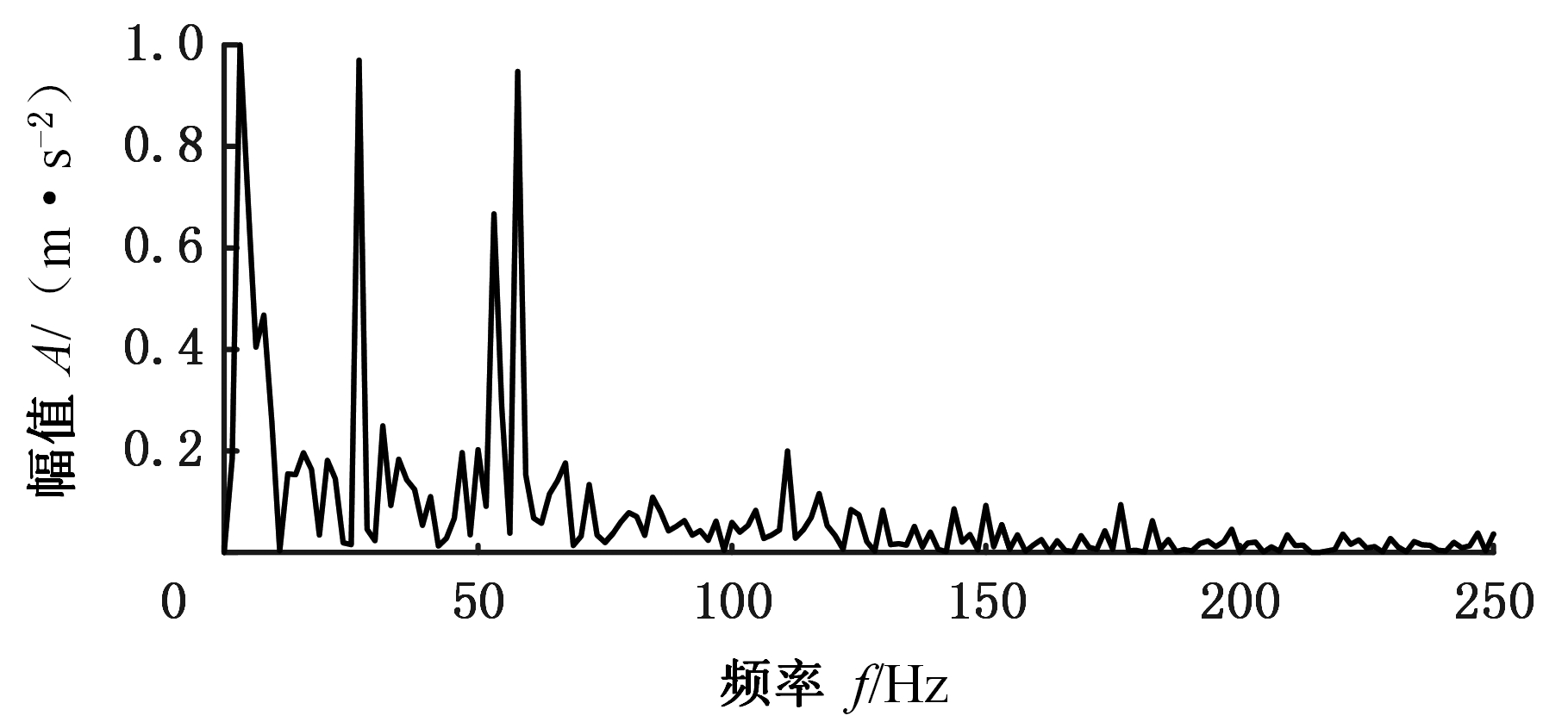
图22 子频带Ⅱ的分量包络谱(滚动体)
Fig.22 Envelope spectrum of subbandⅡ(rolling element)
4 结论
在信号时频分解的基础上，通过时频区间分量重构的方法来构建时频峭度谱，该时频峭度谱能够反映信号冲击特性的频域分布特征；采用时频峭度谱代替频谱确定子频带的边界，克服了噪声分量对子频带边界划分的影响，获得了合理的子频带划分；以此为基础构造的正交滤波器组能够有效地分离出信号的特征分量；时频峭度谱的峰值可用于检测轴承振动信号子频带中的最佳共振频带，该最佳共振频带可作为选用EWT的分解分量提取损伤特征频率的依据。改进EWT方法有效地提取了重载工况下机车轴承的损伤特征。
[1] 何正嘉. 机械故障诊断理论及应用[M].北京:高等教育出版社, 2010.
HE Zhengjia. Theory and Application of Mechanical Fault Diagnosis [M]. Beijing: Higher Education Press, 2010.
[2] 王晓冬，何正嘉，訾艳阳. 滚动轴承故障诊断的多小波谱峭度方法[J]. 西安交通大学学报，2010,44(3):77-81.
WANG Xiaodong, HE Zhengjia, ZI Yanyang. Multi-wavelet Spectral Kurtosis Method for Fault Diagnosis of Rolling Bearings[J]. Journal of Xi’an Jiaotong University, 2010, 44(3): 77-81.
[3] LEI Yaguo, LIN Jing, HE Zhengjia,et al. Application of an Improved Kurtogram Method for Fault Diagnosis of Rolling Element Bearings[J]. Mechanical Systems and Signal Processing, 2011, 25(5):1738-1749.
[4] ZHAO Ming, LIN Jing, XU Xiaoqiang, et al. Multi-fault Detection of Rolling Element Bearings under Harsh Working Condition Using IMF-based Adaptive Envelope Order Analysis[J].Sensors,2014, 14(11)：20320-20346.
[5] LI Zipeng, CHEN Jinglong, ZI Yanyang, et al. Independence-oriented VMD to Identify Fault Feature for Wheel Set Bearing Fault Diagnosis of High Speed Locomotive[J]. Mechanical Systems and Signal Processing, 2017, 85(15):512-529.
[6] GILLES J. Empirical Wavelet Transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010.
[7] SINGH O, SUNKARIA R K. ECG Signals Denoising via Empirical Wavelet Transform[J]. Australasian Physical and Engineering Sciences in Medicine, 2017, 40(1):219-229.
[8] 王友仁，陈伟，孙灿飞，等.基于能量聚集度经验小波变换的齿轮箱早期微弱故障诊断[J].中国机械工程,2017,28(12):1484-1490.
WANG Youren, CHEN Wei, SUN Canfei, et al. Early Weak Fault Diagnosis of Gearboxes Based on Energy Aggregation and EWT[J].China Mechanical Engineering, 2017,28(12):1484-1490.
[9] WANG Dong, ZHAO Yang, YI Cai, et al. Sparsity Guided Empirical Wavelet Transform for Fault Diagnosis of Rolling Element Bearings[J]. Mechanical Systems and Signal Processing, 2018, 101:292-308.
[10] YAN Zhonghong，MIYAMOTO A，JIANG Zhongwei，et al. An Overall Theoretical Description of Frequency Slice Wavelet Transform[J]. Mechanical Systems and Signal Processing，2010，24(2)：491-507.
[11] 段晨东，高鹏，徐先锋，等. 一种基于时频峭度谱的滚动轴承损伤诊断方法[J]. 机械工程学报，2015，51(11)：78-83.
DUAN Chendong, GAO Peng, XU Xianfeng,et al. A Diagnosis Method of Rolling Bearing Damage Based on Time-frequency Kurtosis Spectrum[J]. Journal of Mechanical Engineering, 2015, 51(11): 78-83.
