0 引言
共因故障是指由于空间、环境、设计以及人为等方面的共同原因所造成的多个部件同时发生故障的现象,是一种广泛存在于工程系统中且在系统设计、制造、安装、运行的任何阶段都会发生的相依故障事件[1-3]。在共因故障中,受共同原因影响的部件集合称为共因部件组。
共因故障增大了系统各单元的故障概率,降低了采用冗余配置提高系统可靠性的效果。随着单部件级可靠性的大幅度提升和冗余技术的应用,这种由多部件相关故障引起的系统可靠性退化甚至安全隐患问题日益加剧,促使了大量系统分析人员和学者相继投入到共因故障影响下的系统可靠性研究中。李春洋等[4]提出了一种考虑共因故障的多态系统可靠性优化模型,为复杂系统的可靠性冗余配置优化问题提供了较完整的解决方案。针对大部分包含共因故障的系统可靠性分析模型缺乏考虑共因故障动态特征问题,王家序等[5]基于动态故障树对包含不完全共因故障的系统可靠性进行了建模分析。
上述研究侧重于解决共因故障的表征、发生概率求解以及相关性解析等问题,有关共因故障的严重性测度问题还有待进一步研究。作为产品全寿命周期中的关键测度指标,故障严重性是指某一故障模式对系统功能、用户人身安全以及周围环境等方面的影响程度,是识别产品各种缺陷与薄弱环节的基础。在故障模式、影响及其危害性分析(failure mode effect and criticality analysis,FMECA)过程中,故障严重度还可以用于确定故障风险优先序数(risk priority number, RPN)和故障危害性分析(criticality analysis, CA)。文献[6]从消除故障所需付出的努力程度视角定义了故障严重度,使其能够更真实、定量地反映系统及其组成单元的故障严重性。文献[7]将武器装备的故障严重度划分为4个类别,旨在定性地区别武器装备的各个故障模式。文献[8]以等级表的形式对指挥、控制、通信、计算机、情报、监视和侦察系统的故障严重性进行了测度,然而该方法只是定量地表征故障严重度,难以确切表征不同严重度故障之间的区别。文献[9]针对上述测度方法的缺陷,提出了一种故障严重度非线性转换函数,解决了不同故障在严重度方面的各类运算问题。文献[10]针对文献[9]中的指数型故障严重等级非线性转换函数无法反映故障之间的关联性问题,提出了一种基于Copula函数的3阶转换方程。
上述故障严重性测度方法与技术仅针对系统组成单元(或子系统)的单一故障,对系统中的共因故障难以为继。无法回避的是,在共因故障的影响下,在系统组成单元单一故障所造成的危害性后果基础上,势必还会出现由单元故障间的关联性所导致的额外严重性危害。如果继续按照以往的方法对系统组成单元故障进行严重性测度,则会低估单元故障的严重性,从而导致后续的故障消除资源配置结果出现偏差,影响系统运行效率。由此,在共因故障存在的条件下,探索新的故障严重性测度模型与方法势在必行。
本文基于合作博弈思想构建考虑共因故障影响的系统组成单元故障严重性Shapley值测度模型。在模型构建过程中,系统组成单元被看作是合作博弈中的参与主体,共因部件组则是博弈过程中形成的联盟。首先,在已有故障严重等级测度的基础上,构建最优非线性转换函数;其次根据共因故障特征提出其联合严重性测度方法;最后在确定共因部件组数量和种类的基础上求解单元故障修正严重度,即系统组成单元对各个共因故障联合严重度的期望贡献度。
1 故障严重性测度
1.1 单一故障严重性测度
根据文献[8],系统组成单元(或子系统)单一故障的严重程度可分为表1所示的10个等级。
表1 故障严重度排序等级
Tab.1 Ordinal scale of fault severity
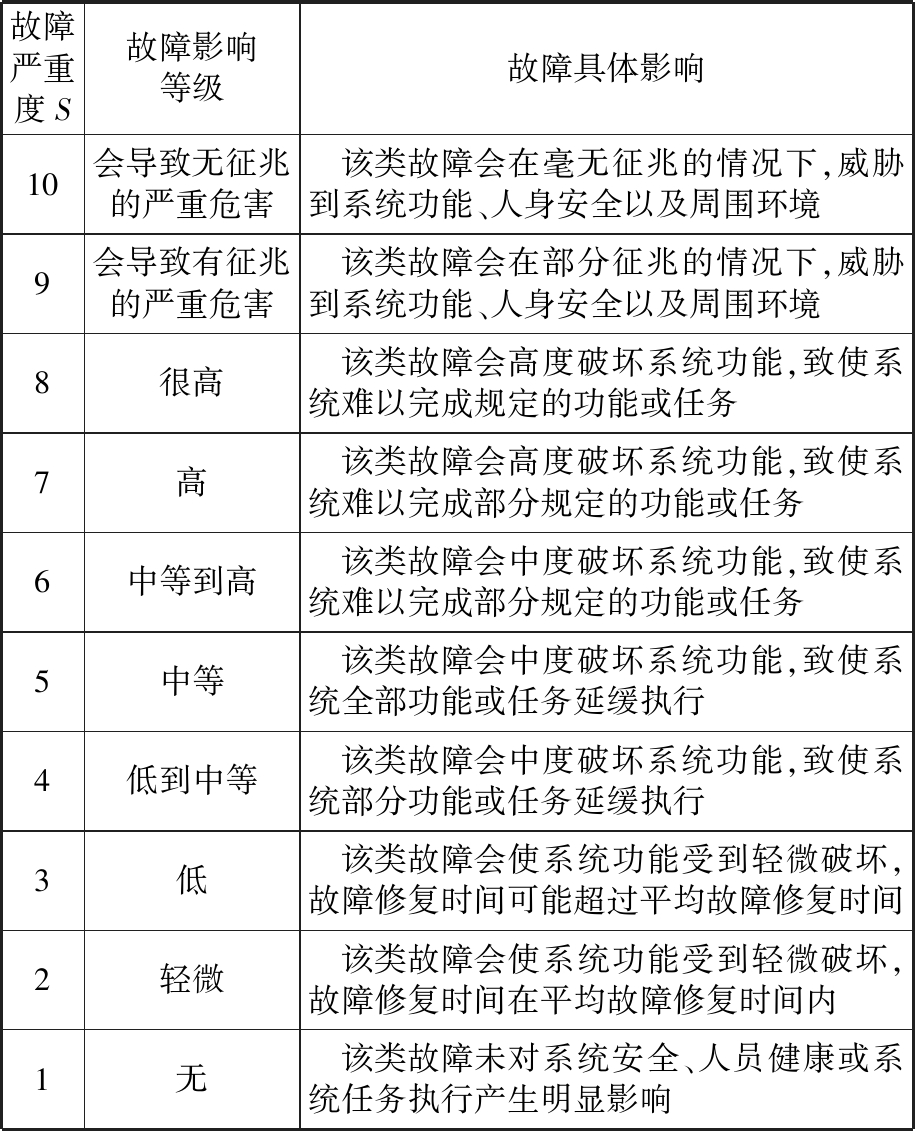
故障严重度S故障影响等级故障具体影响10会导致无征兆的严重危害 该类故障会在毫无征兆的情况下,威胁到系统功能、人身安全以及周围环境9会导致有征兆的严重危害 该类故障会在部分征兆的情况下,威胁到系统功能、人身安全以及周围环境8很高 该类故障会高度破坏系统功能,致使系统难以完成规定的功能或任务7高 该类故障会高度破坏系统功能,致使系统难以完成部分规定的功能或任务6中等到高 该类故障会中度破坏系统功能,致使系统难以完成部分规定的功能或任务5中等 该类故障会中度破坏系统功能,致使系统全部功能或任务延缓执行4低到中等 该类故障会中度破坏系统功能,致使系统部分功能或任务延缓执行3低 该类故障会使系统功能受到轻微破坏,故障修复时间可能超过平均故障修复时间2轻微 该类故障会使系统功能受到轻微破坏,故障修复时间在平均故障修复时间内1无 该类故障未对系统安全、人员健康或系统任务执行产生明显影响
表1中的这类故障严重等级虽然能够为系统分析人员提供一些有价值的故障严重性信息,但其测度结果带有一定的主观色彩,且有时难以反映系统及其组成单元的真实情况。首先这些等级是在故障影响等级与故障严重度线性相关的假设下制定的;其次这些等级之间的乘除运算是缺乏意义的,如不能简单地认为导致无征兆严重危害的故障严重度是导致中等危害的故障模式严重度的两倍。因为相对于轻微故障,严重故障对系统、人员以及周围环境造成的破坏性更大,故人们为了消除这种故障所带来的不良后果所需的资源更多,即故障影响等级越高,相邻影响等级故障之间的严重度差别越大,但如图1所示,在两者线性相关的假设下,ΔS45=ΔS78,这显然是不符合工程系统实际的。
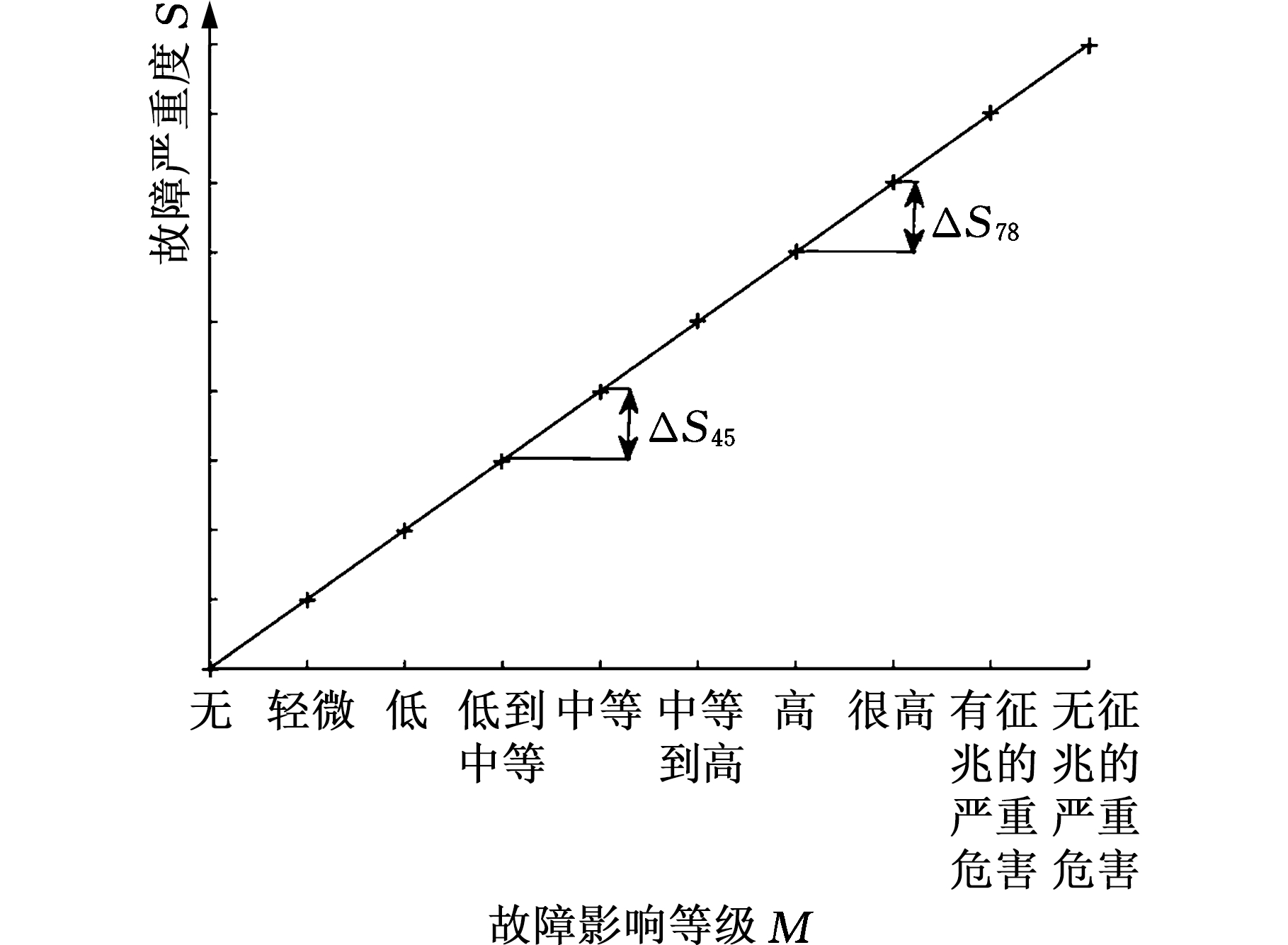
图1 线性假设下故障影响等级与严重度之间的变化关系示意图
Fig.1 Relationship between the impact ranking andfault severity under the linear hypothesis
为了使故障严重性测度更加符合工程实际,本文对原有故障严重等级进行非线性转换,如图2所示,S′表示修正后的故障严重度;![]() 表示随着故障影响等级的增大,相邻影响等级故障之间的严重度差别逐渐增大。
表示随着故障影响等级的增大,相邻影响等级故障之间的严重度差别逐渐增大。
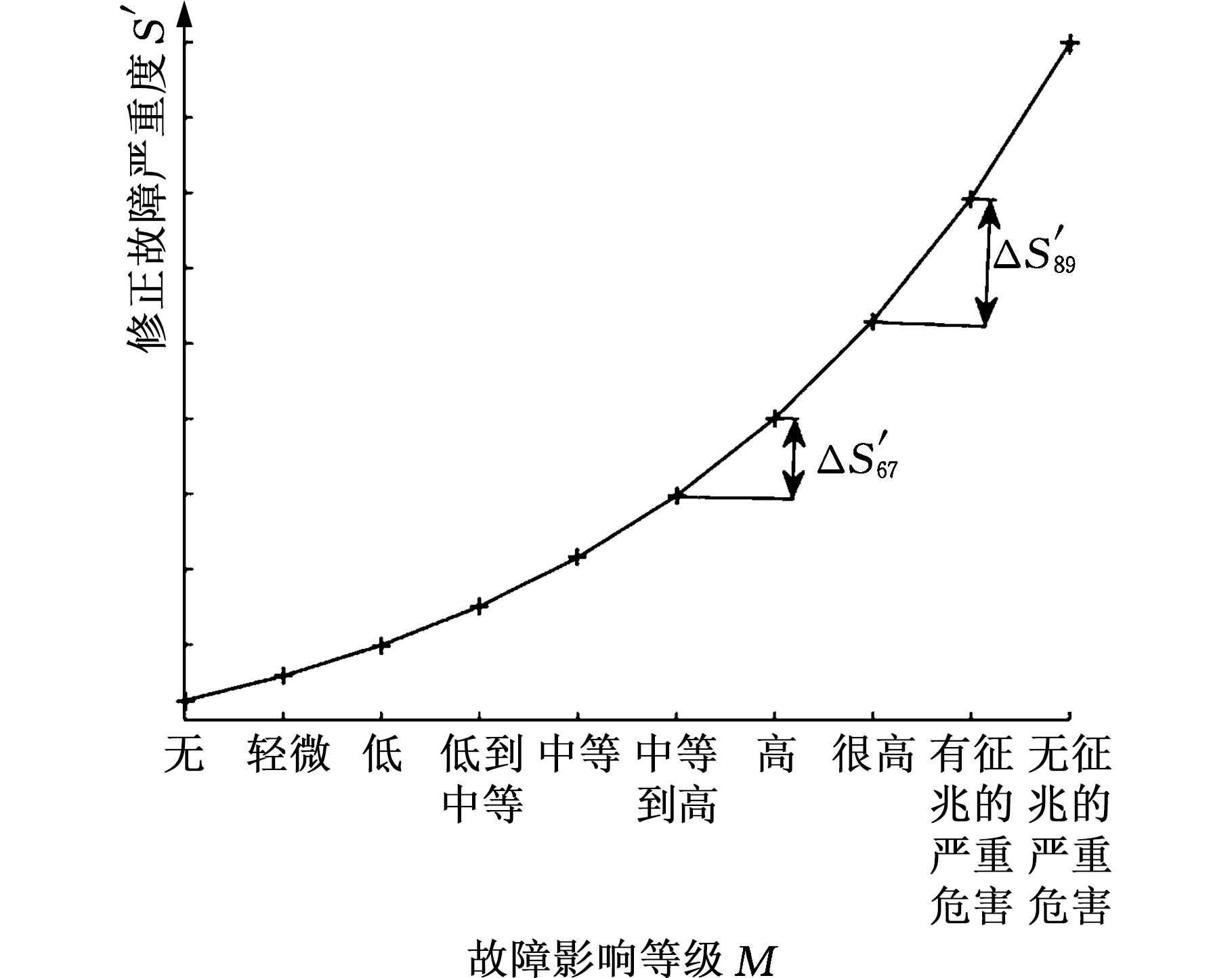
图2 故障严重度等级非线性转换示意图
Fig.2 Nonlinear transformation of fault severity ranking
故障严重等级非线性变换函数应满足以下要求:①![]() ②
②![]() ③
③![]() 即该函数是故障影响等级的单调递增函数且增长速度随着故障严重等级的增加而增加。目前该函数的具体形式主要包括含有变换系数的指数函数(S′=exp(αS),α为变换系数)以及基于Copula函数的3阶转换方程:
即该函数是故障影响等级的单调递增函数且增长速度随着故障严重等级的增加而增加。目前该函数的具体形式主要包括含有变换系数的指数函数(S′=exp(αS),α为变换系数)以及基于Copula函数的3阶转换方程:
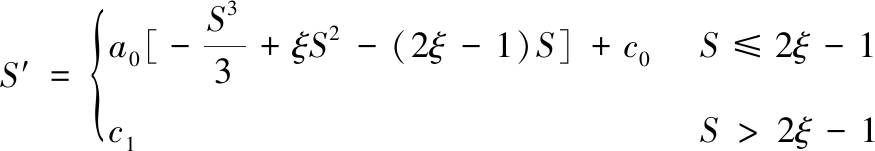
(1)
式中,ξ为故障严重度集中水平;a0、c0、c1均为待定参数;n为单元个数。
根据文献[9-10]中关于两种非线性转换函数的参数赋值与求解方法,求得不同非线性转换方法下的故障严重等级变换值,如表2所示。
表2 不同方法求得的故障严重等级非线性变换值
Tab.2 Different nonlinear transformationsof fault severity scale
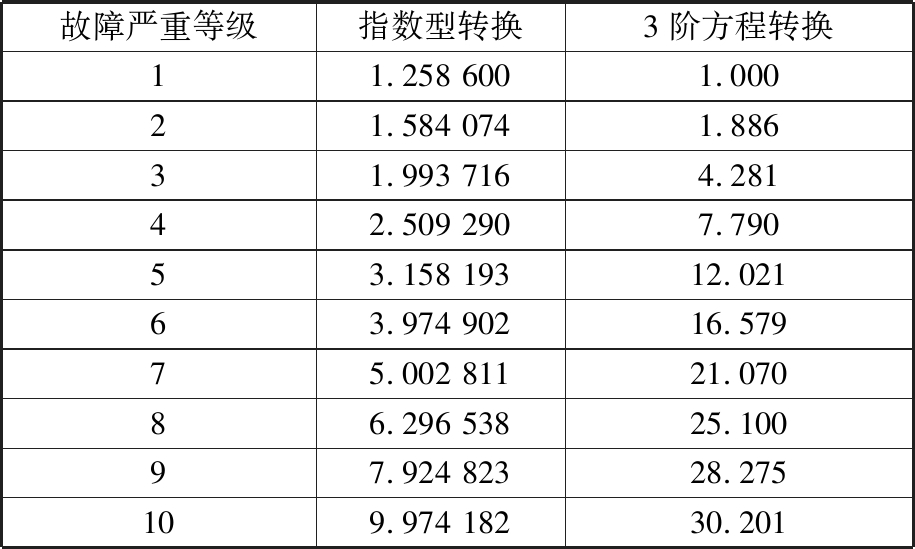
故障严重等级指数型转换3阶方程转换11.258 6001.00021.584 0741.88631.993 7164.28142.509 2907.79053.158 19312.02163.974 90216.57975.002 81121.07086.296 53825.10097.924 82328.275109.974 18230.201
根据故障严重等级非线性转换原则,故障影响等级越高,相邻影响等级故障严重度之间的差别越大。为了评判各个方法对故障严重等级的转换效果,求得经由不同非线性函数转换得到的故障严重度在各个影响等级的相对变化率(图3):
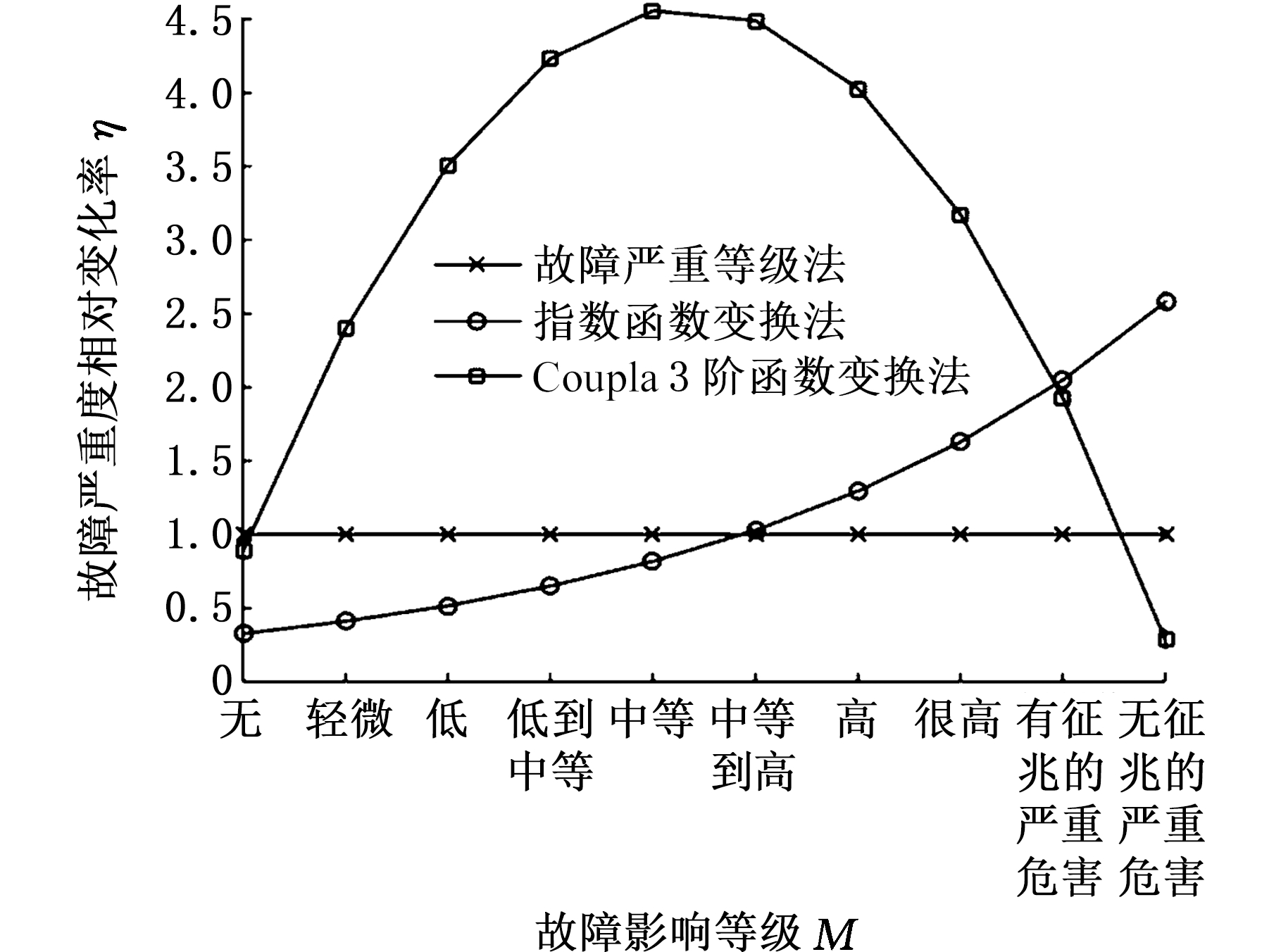
图3 不同非线性函数对故障严重等级的转换效果
Fig.3 Different nonlinear transformations offault severity ranking
由图3可知,直接运用原始故障等级难以反映不同影响等级故障严重度之间的差别;基于Copula函数的3阶方程由于其相对变化率的波动性变化,造成其只有部分区间(即峰值左侧区域)适用于描述系统及其组成单元故障的真实情况;经由指数型变换的故障严重度变化率一直呈增长趋势,但其在反映两个故障严重等级相对变化方面具有一定的局限性,因为所求得的相对变化率![]() 只与函数本身参数值有关,与故障特性无关。
只与函数本身参数值有关,与故障特性无关。
为了使故障严重等级非线性变换函数更贴近单元不同影响等级故障所导致的后果差异性,本文针对以上两种非线性转换函数的不足,提出了一种二次型变换函数,旨在保证转换后故障严重度函数单调增长的同时反映故障本身的特性变化。构建步骤如下:
首先,令故障严重度变换函数的增长速率为![]() (γ为变换速率);然后,得到非线性转换后的故障严重度函数
(γ为变换速率);然后,得到非线性转换后的故障严重度函数![]() 最后令
最后令![]() 求得待定系数γ和b,其中E1、E2分别表示非线性变换后的上下限值,可根据实际要求人为确定。
求得待定系数γ和b,其中E1、E2分别表示非线性变换后的上下限值,可根据实际要求人为确定。
1.2 共因故障联合严重性测度
当共因故障发生时人们不仅要逐个修复每个单元的单一故障,还需要额外增加资源以消除由于故障之间的关联性所带来的额外危害性,因此可将共因故障的联合严重度定义如下。
定义1 对于任一共因部件组C,其所有单元同时发生故障时所造成影响的严重程度为
(2)
式中,S′(C)为非线性转换后的共因故障联合严重度;m为由于同一故障原因而同时发生故障的单元数量,即共因部件组C内含有的单元数量;![]() 为共因部件组C内单元j单独发生故障时的严重等级非线性转换函数;
为共因部件组C内单元j单独发生故障时的严重等级非线性转换函数;![]() 为由于共因部件组内单元故障之间的关联性所造成额外影响程度。
为由于共因部件组内单元故障之间的关联性所造成额外影响程度。
值得注意的是,随着同时发生故障的单元数量增加,km值也将逐渐增大,这是因为共因部件组所包含的单元数量越多,故障之间的关联性越大,由此而造成的故障消除资源投入量越多。
2 考虑共因故障影响的单元故障严重性Shapley值测度模型
系统中不同的组成单元有可能从属于不同的共因部件组,而且同一组成单元也有可能从属于多个不同的共因部件组。为了合理测度共因故障影响下的系统组成单元故障严重性,需要确定单元在不同共因部件组所发挥的作用大小,即该单元故障对不同共因故障联合严重度的期望贡献度。
根据合作博弈思想,若有n个参与主体,则集合N={1,2,…,n}的任一子集C(C⊆N)称为合作博弈的一个联盟,包括空集联盟以及所有参与人的总联盟。联盟特征函数v(C)表示联盟内参与主体共同协作时获得的总效用。通常在合作博弈中隐含有以下两个假设:①参与主体清楚地知道组成每个联盟所能产生的总效用值;②参与主体需要完全参与到一个特定联盟中。
当共因故障诱因被触发时,系统中至少有两个组成单元(或子系统)发生故障,此时可以认为同时发生故障的单元在共同故障原因促发下产生了某种程度上的合作关系,因此,本文借用合作博弈思想,将共因故障发生时出现故障的单元看作是合作博弈中的参与主体。联盟即共因部件组,由在不同原因影响下同时发生故障的单元(或子系统)构成。相应的特征函数v(C)表示共因部件组C内参与单元同时发生的故障对系统、人员以及周围环境所造成后果的严重程度。分配向量则是将共因故障严重度分配至共因部件组内单元所得到的向量。
根据合作博弈效用分配原则以及解的性质等,可将合作博弈分配解分为核心、Shapley值、谈判集以及内核与核仁等[11]。其中,Shapley值方法[12]不仅计算过程简便且最终结果具有稳定性(解存在且唯一)、公平性等,因此本节运用Shapley值求解单元故障严重性。
根据Shapley值的构建思想,需要首先确定共因部件组的形成概率,然后计算系统组成单元对各个不同共因部件组故障联合严重度的边际贡献,最后求解单元对系统故障危害性的期望贡献度。
本节将单元对共因部件组的参与方法定义为其在不同共因部件组中的排列组合形式。由于各个单元对不同共因部件组的参与情况是随机的,对于包含n个组成单元的系统,根据单元加入各个共因部件组的先后顺序和共因部件组内的单元总体数量可确定共有n!种不同的参与方法。为确定某一包含单元i的共因部件组Ci的形成概率,现将系统全集I拆分成三部分进行考虑:参与单元i、单元i参与之前的共因部件组Ci即{Ci\i}以及全集的剩余部分{I\Ci}。
如果参与单元i和已形成联盟{Ci\i}的单元合作组成联盟,则系统的剩余单元会形成联盟{I\Ci}。共因部件组Ci内所包含单元的数量可表示为|Ci|且|Ci|≤n,联盟{I\Ci}的参与单元数量为n-|Ci|。由于联盟Ci在单元i未参与之前共有(n-|Ci|)!种组合方法,联盟{I\Ci}的n-|Ci|个参与单元有(n-|Ci|)!种组成方法,且每种组合都是等概率出现的,因此任一包含单元i的联盟形成概率为![]()
单元i对共因部件组Ci故障严重度的边际贡献可表示为
ψCi=S′(Ci)-S′(Ci\i)
(3)
式中,S′(Ci)为共因部件组Ci内单元同时发生故障的联合严重度;S′(Ci\i)为从共因部件组Ci中去除单元i后的单元同时发生故障的联合严重度;k|Ci|为共因部件组Ci对联合故障严重度的影响系数。
因此,在共因故障影响下,对于任一包含n个单元的系统,某一组成单元i对系统故障危害性的期望贡献度,即故障修正严重度为
(4)
式中,P为共因部件组的形成概率。
3 案例研究
在工程实际中,数控机床各组成单元(或子系统)的故障并不是独立存在的,存在某些原因导致多个单元(或子系统)同时发生故障的现象[10]。主轴作为数控机床的核心子系统,在数控机床的设计、制造以及运行过程中,都起着至关重要的作用。
某型号数控机床主轴系统的功能结构如图4所示,该主轴系统的组成单元包括启动组件、支撑组件、润滑组件、密封组件、测量组件以及制动组件等。在系统运行过程中,系统分析人员要在共因故障存在的条件下测度各个组成单元的故障严重性,以提前发现系统中的各种缺陷和薄弱环节,并尽早采取有效的改进和补偿措施。
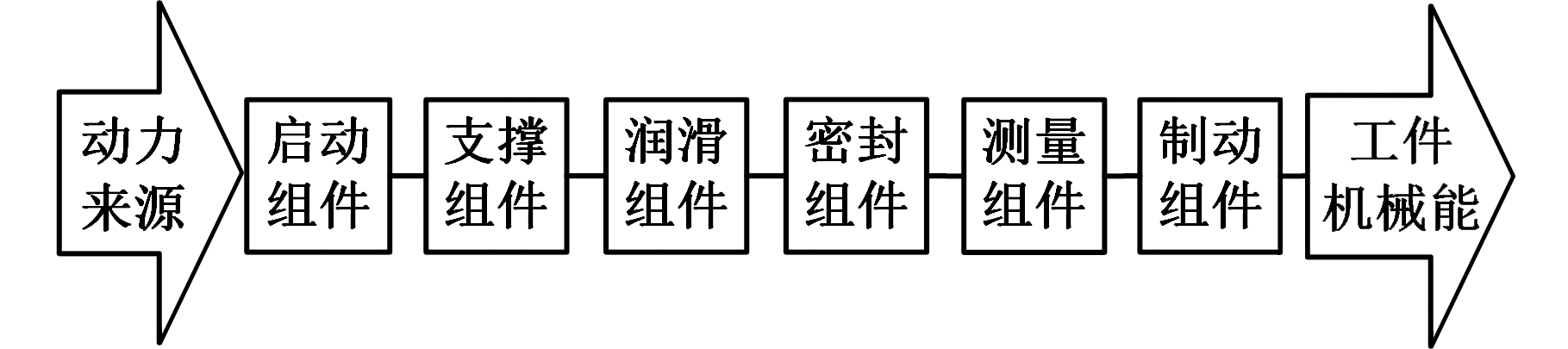
图4 某数控机床主轴系统功能结构图
Fig.4 Functional configuration diagram of spindlesystem of a CNC
在系统运行初期,系统分析人员还没有意识到共因故障的存在,只能根据各个单元的单一故障特征,按照原有工程手册中的评定原则对系统组成单元的故障严重度定级,结果见表3。
表3 单元单一故障严重等级
Tab.3 Single fault severity ranking of each component

单元名称启动组件支撑组件润滑组件密封组件校准组件制动组件故障严重等级565478
随着系统的运行,工作人员对系统的认知也逐渐加深,并且意识到了共因故障的存在及其带来的危害性。为了重新测度系统各个组成单元的故障严重性,首先要选择合适的故障严重等级非线性转换函数。在已有指数型变换函数以及Copula 3阶方程的基础上,重新构建了二次型变换函数并令Ε1=1,Ε2=25,求得ξ=5.83,γ=0.235,b=-4.48。
计算共因故障联合严重度时,将k值设定为k1=0,k2=0.1,k3=0.2,k4=0.3,k5=0.4,k6=0.5。根据式(4)可求得不同非线性变换下考虑共因故障影响的各个单元故障严重性Shapley值测度表达式:

(5)
i=1,2,3,4,5,6
代入数据得到最终的故障严重性测度值,如表4所示。
表4 共因故障影响下某数控机床主轴系统组成单元故障严重性Shapley测度值
Tab.4 Shapley-based fault severity for componentsof spindle system in a CNC with consideration ofcommon cause fault
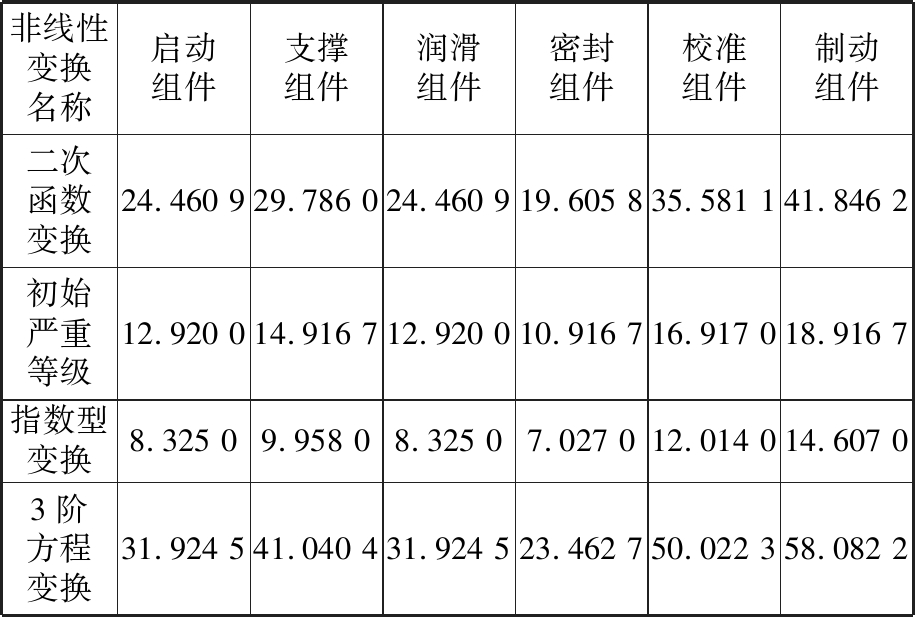
非线性变换名称启动组件支撑组件润滑组件密封组件校准组件制动组件二次函数变换24.460 929.786 024.460 919.605 835.581 141.846 2初始严重等级12.920 014.916 712.920 010.916 716.917 018.916 7指数型变换8.325 09.958 08.325 07.027 012.014 014.607 03阶方程变换31.924 541.040 431.924 523.462 750.022 358.082 2
为了分析共因故障对系统组成单元故障严重性测度的影响,现求得不同转换方法下单元故障严重度在考虑共因故障前后的相对变化率(即![]() 其中φi表示单元i故障严重性Shapley测度值),如图5所示。
其中φi表示单元i故障严重性Shapley测度值),如图5所示。
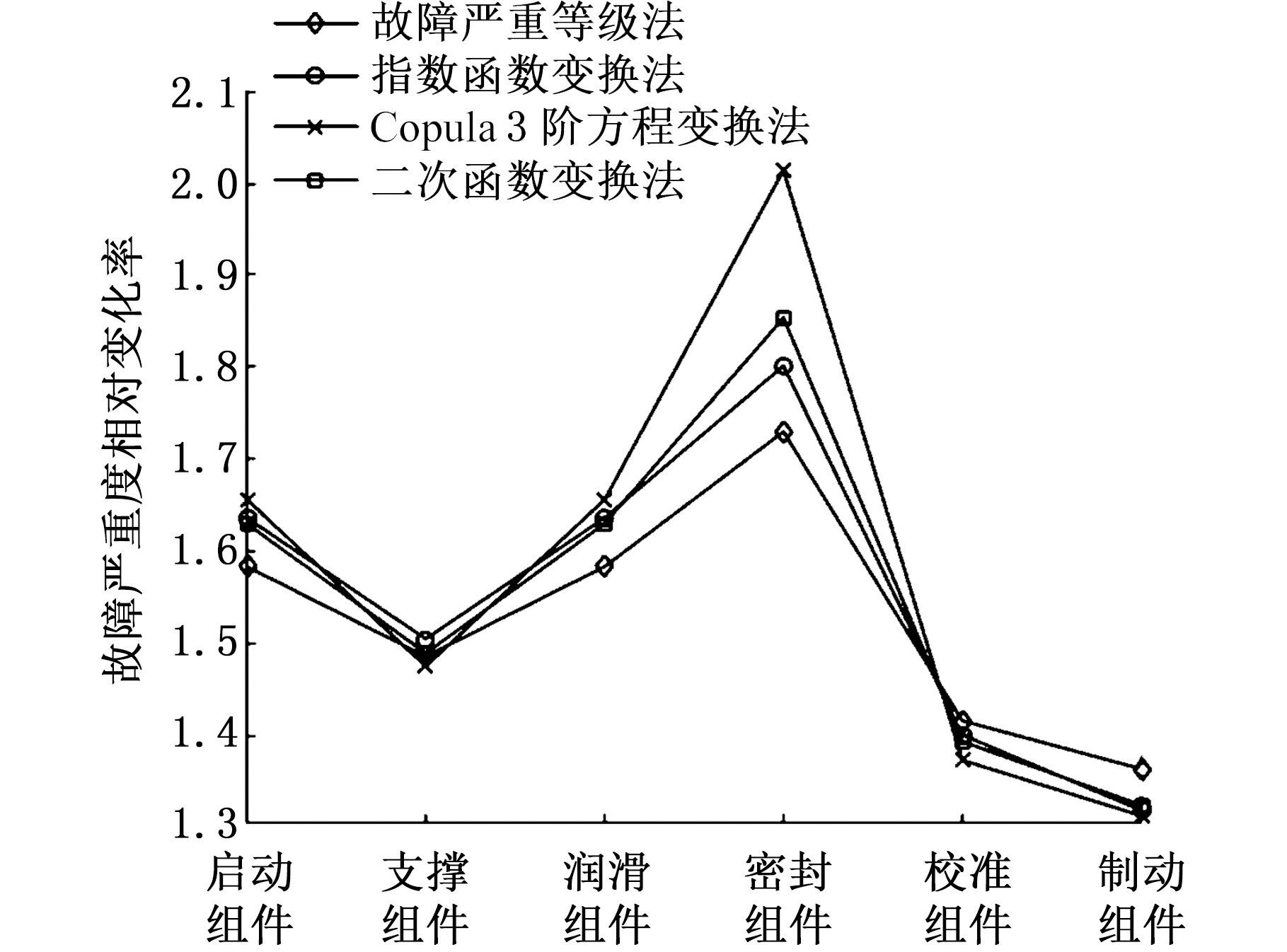
图5 共因故障对于某数控机床主轴系统组成单元故障严重度的影响示意图
Fig.5 The influence of common cause failure on thefault severity of the spindle components in a CNC
由图5可知,不同转换方法下的单元故障严重度相对变化趋势大体相似,但3阶方程的变化幅度最大,主要原因在于其函数变化率的抛物形波动。对于系统组成单元,不同的转换方法都显示密封组件的变化最大,而制动组件的变化最小,这是因为密封组件对共因故障的期望贡献值较大,即与其他组件相比,密封组件与其他单元的关联性较强;而制动组件相对独立,与其他组件的相关性较弱。由此,系统单元故障严重性Shapley测度值从侧面剖析了共因故障的内部机理,解构了共因部件组内的单元特征。
4 结论
(1)在单一故障严重等级非线性转换的基础上,提出了共因故障联合严重性测度方法。在对传统故障严重等级进行非线性转换的基础上,结合单元故障间的相关性影响,定义了共因故障的联合严重性及其测度方法。
(2)构建了一种考虑共因故障的单元故障严重性Shapley值测度模型。基于合作博弈思想,根据Shapley值算法步骤,求解出了系统组成单元对各个共因故障联合严重度的期望贡献。
(3)通过某型号机床主轴系统的故障严重度分析实例,介绍了所提方法在共因故障存在条件下合理测度单元故障严重性的应用可行性,为进一步识别系统缺陷与薄弱环节提供了决策支持。
[1] MISRA K B. Handbook of Per-formability Engineering[M]. London: Springer Science & Business Media, 2008.
[2] O’CONNOR A, MOSLEH A. A General Cause Based Methodology for Analysis of Common Cause and Dependent Failures in System Risk and Reliability Assessments [J]. Reliability Engineering & System Safety, 2016, 145:341-350.
[3] KAN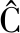 EV D,
EV D, 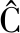 EPIN M. A New Method for Explicit Modelling of Single Failure Event within Different Common Cause Failure Groups [J]. Reliability Engineering & System Safety, 2012, 103(3):84-93.
EPIN M. A New Method for Explicit Modelling of Single Failure Event within Different Common Cause Failure Groups [J]. Reliability Engineering & System Safety, 2012, 103(3):84-93.
[4] 李春洋, 陈循, 易晓山. 考虑共因失效的多态系统可靠性优化[J]. 中国机械工程, 2010,21(2):155-159.
LI Chunyang, CHEN Xun, YI Xiaoshan. Reliability Optimization of Multi-state System in Presence of Common Cause Failures [J]. China Mechanical Engineering, 2010,21(2):155-159.
[5] 王家序, 周青华, 肖科,等. 不完全共因失效系统动态故障树模型分析方法[J]. 系统工程与电子技术, 2012, 34(5):1062-1067.
WANG Jiaxu, ZHOU Qinghua, XIAO Ke, et al. Dynamic Fault Tree Model Analysis of Systems Subjected to Incomplete Common-cause Failure [J]. Journal of Systems Engineering and Electronics, 2012, 34(5):1062-1067.
[6] YADAV O P, ZHUANG X. A Practical Reliability Allocation Method Considering Modified Criticality Factors [J]. Reliability Engineering & System Safety, 2014, 129:57-65.
[7] 曾声奎. 系统可靠性设计分析教程[M]. 北京:北京航空航天大学出版社, 2004.
ZENG Shengkui. Tutorial of System Reliability Design Analysis [M]. Beijing: Beihang University Press, 2004.
[8] Department of the Army. TM 5-689-4. Failure Modes, Effects and Criticality Analysis (FMECA) for Command, Control, Communications, Computer, Intelligence, Surveillance, and Reconnaissance (C4ISR) Facilities[EB/OL]. [2017-11-01].https://www.wbdg.org/FFC/ARMYCOE/COETM/tm_5_698_4.pdf.
[9] KIM K O, YANG Y, ZUO M J. A New Reliability Allocation Weight for Reducing the Occurrence of Severe Failure Effects [J]. Reliability Engineering & System Safety, 2013, 117: 81-88.
[10] 杨周, 朱云鹏, 张义民,等. 基于Copula函数的数控车床可靠性综合分配方法[J]. 兵工学报, 2016, 37(1):131-140.
YANG Zhou, ZHU Yunpeng, ZHANG Yimin. A Comprehensive Reliability Allocation Method for Numerical-controlled Lathes Based on Copula Function[J]. Acta Armamentarii, 2016, 37(1):131-140.
[11] 李天文. 面向多Agent系统的博弈联盟形成与分配问题研究[D]. 昆明:云南大学, 2013.
LI Tianwen. Research on the Formation and Allocation of Game Coalition for Multi Agent System [D]. Kunming: Yunnan University, 2013.
[12] SHAPLEY L S. A Value for n-person Games [J]. Contributions to the Theory of Games, 1953, 28(2): 307-317.
