0 引言
在实际钻井工况中,顶驱下部悬挂着几千米长的钻杆,钻杆内部流动着高压泥浆,与此同时,顶驱还要承受扭矩、拉力等多种载荷作用,其受力状态极其复杂。顶驱的旋转以及承受的载荷主要通过中心管来传递,而中心管与下部钻杆的连接则通过螺纹来实现,螺纹连接的可靠性直接决定了钻井效率的高低[1]。据统计,64%的油套管失效事故都发生在螺纹处,国内则高达86%[2-3],随着我国石油钻采工业的迅猛发展,这一比例可能将继续上升。螺纹接头是油套管连接最薄弱的环节,提高油套管螺纹的连接性能是保证钻井工作顺利进行的前提[4],为了解决日益突出的螺纹过早失效问题(粘扣、断裂等),近年来国内外学者对钻杆螺纹和套管螺纹进行了大量研究。兰洪波等[5]通过设计新型双台肩钻杆接头,利用有限元软件分析了各种载荷工况下的接头强度;袁光杰等[6]通过对偏梯形套管螺纹进行研究,分析了管螺纹在摩擦因素和锥度下的应力分布;BAHAI[7]利用二维参数化模型,分析在轴向力和弯矩作用下钻杆接头的应力集中因子;CHEN等[8]利用钻具接头二维轴对称模型进行了有限元分析,发现应力主要集中在第一圈螺纹牙根部以及距离公扣最远端螺纹牙处;SHAHANI等[9]通过三维二维有限元模型对比,研究不同载荷作用下钻杆接头的接触应力分布;BRENNAN等[10]对锥螺纹钻杆接头进行了应力强度分析。上述文献均采用二维轴对称模型,通过数值计算方法对螺纹连接强度、力学特性以及失效破坏等进行研究,得出了较为正确的结论。上述分析方法尚未经过实验验证,采用二维轴对称模型时未考虑螺旋升角对应力分布的具体影响,这在很大程度上降低了有限元分析的可靠性。
本文基于弹塑性理论、von Mises屈服准则以及中心管材料本构模型实验研究结果,建立扭矩作用下螺纹接头三维和二维数值仿真模型,对比二维、三维的仿真结果并建立过盈量(过盈量是指螺纹接头台肩处沿轴线方向的形变量)与扭矩之间的关系曲线,证明二维分析方法适用于螺纹接头分析。深入研究了接头力学性能,分析其失效原因并进行参数优化,定量分析了在紧扣扭矩作用下的力学行为,评价螺纹参数对应力大小的影响,综合考虑载荷作用下螺纹连接强度和生产成本并挑选出最优值。
1 顶驱中心管螺纹力学模型
1.1 紧扣扭矩下的螺纹接头受力特征
中心管接头通过螺纹啮合实现公扣和母扣的相互连接,三维模型较二维轴对称模型的区别在于螺纹牙带有一定的螺旋升角,在公扣端面施加紧扣扭矩,啮合过程中会由于台肩面和螺纹牙啮合面的挤压作用而产生相互作用力,受力特征见图1。

注: 代表垂直纸面向里的作用力;
代表垂直纸面向里的作用力; 代表垂直纸面向外的作用力;△代表固定边界。
代表垂直纸面向外的作用力;△代表固定边界。
图1 紧扣扭矩作用下的螺纹接头受力特征
Fig.1 Force analysis of threaded joint subjected to tightening torque
截取公扣螺纹牙体上一段微元,其上存在着垂直于接触面的正应力σ和沿着接触面的剪应力τ,它们在单位啮合长度上的合应力为P,将合应力分解为沿水平方向的应力Px和竖直方向的应力Py。假设第i牙螺纹的啮合长度为si,则第i牙螺纹承担的力和力矩分别为[11]
Fi=![]() Pyds
Pyds
(1)
Ti=![]() Pxlds
Pxlds
(2)
式中,l为啮合面所对应的半径。
则所有螺纹牙上承担的合力和合力矩为
(3)
(4)
由平衡方程可知,螺纹牙产生的合力和合力矩与台肩处产生的力和力矩相等,即
(5)
在扭矩作用下,公扣相对于母扣沿螺旋升角方向运动,实现接头的上扣。
二维模型通过在台肩施加过盈量来模拟上扣。为了准确表征紧扣扭矩与螺纹过盈量的关系,在螺纹拧紧过程中,既要考虑弹性阶段位移量变化,也要考虑塑性阶段的位移变化,螺纹接头台肩处位移量与螺纹转角和螺距之间的关系如下[12]:
(6)
式中,θ为螺纹转角,(°);p为螺距,mm;s为螺纹的位移量,mm。
(1) 弹性阶段预紧力与转角之间的关系。螺纹台肩面之间接触为体弹性接触,通过台肩面面积和转角可以得出台肩面材料变化的体积,再根据材料的体积弹性模量K、刚度C,可以得出预紧力的方程式:
(7)
式中,E为弹性模量;μn为泊松比;L为内螺纹接头长度,mm;D1为台肩面接触面环面大径,mm;D2为台肩面接触面环面小径,mm。
(2) 屈服阶段预紧力与转角之间的关系。材料屈服之后的塑性变形阶段,可以根据双线性强化力学模型表示预紧力与转角之间的关系,方程表示为
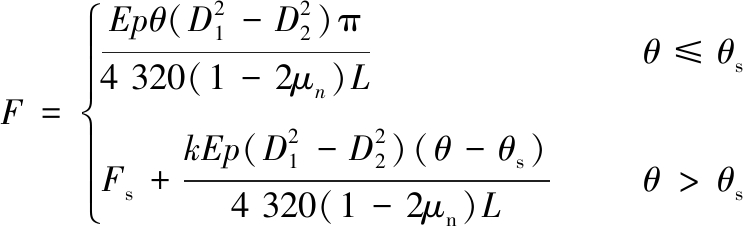
(8)
式中,θs为弹性段与屈服段分界点时的螺纹转角,(°);Fs为弹性段与屈服段分界点时的螺纹预紧力,N;k为屈服段简化后的调整系数。
螺纹转角和扭矩的最终关系式如下:

(9)
式中,T为紧扣扭矩;ρ′为非矩形螺纹摩擦角;μt为台肩面摩擦因数;![]() 为中径;ψ为螺纹升角;Ts为临界扭矩;ρ″为锥螺纹摩擦角。
为中径;ψ为螺纹升角;Ts为临界扭矩;ρ″为锥螺纹摩擦角。
1.2 顶驱中心管接头模型网格划分
基于分块网格划分方法对二维模型和三维模型进行网格划分,其有限元网格划分情况见图2。螺纹和台肩部分采用精细网格,以保证计算精度;其他区域采用相对稀疏的网格,以控制计算效率。公扣端面施加外载荷,母扣端面施加固定约束。

(a)二维轴对称有限元模型

(b)三维有限元模型
图2 螺纹接头有限元模型
Fig.2 Finite element model of thread joint
1.3 中心管材料本构模型试验研究
中心管螺纹接头所用材料为SAE4137H合金钢,系各向同性弹塑性材料,对接头材料进行拉伸试验,20 ℃环境温度下获得3种试样的基本参数和试验数据,见表1。由图3应力应变曲线可以得出:材料弹性模量为210 GPa,屈服强度为860 MPa,抗拉强度为975 MPa,泊松比为0.29,考虑到含40%~60%(质量分数)锌粉末的螺纹脂的影响,配合面间(包括螺纹之间和台肩面之间)的摩擦因数取0.08[13]。在有限元分析中定义塑性数据须采用真实应力应变关系,其关系曲线见图4。
1.4 有限元数值仿真模型验证
为了确保数值仿真结果的可靠性,本文通过钻具接头胀扣实验,利用拆装架液压系统对螺纹接头施加紧扣扭矩(图5左),对比研究不同紧扣扭矩下接头外缘的膨胀变化规律。实验以API标准NC31型特殊扣为研究对象,建立与图5右相同规格的连接螺纹力学模型。为了保证实验结果的可靠性,改变接头螺纹锥度和外径,分别测得3组不同结构接头胀扣数据。通过有限元仿真,获得了实验结果与模拟结果的对比图,见图6。图6表明,实验结果与有限元仿真结果变化趋势相同,结果虽存在一定差异,但最大误差不超过30%,这些误差是由建模、网格划分、有限元分析以及实验过程中产生的误差所造成的,在可接受的范围内。总体上两者结果吻合较好,验证了三维模型建模的准确性以及仿真结果的可靠性,表明所建立的模型以及分析方法能满足钻具接头力学性能研究的需要。
表1 3种试样拉伸试验数据
Tab.1 Tensile test data of three samples

试样直径(mm)面积(mm2)原始标距(mm)引伸计标距(mm)延伸率(%)断面收缩率最大力(kN)抗拉强度(MPa)屈服力(kN)屈服极限(MPa)弹性模量(GPa)屈强比①10.0479.169505013.465.4777.1597567.55860220.620.88②10.0278.854505013.367.1076.3897067.14855205.610.88③10.0679.487505013.568.2378.2198277.63880214.040.89
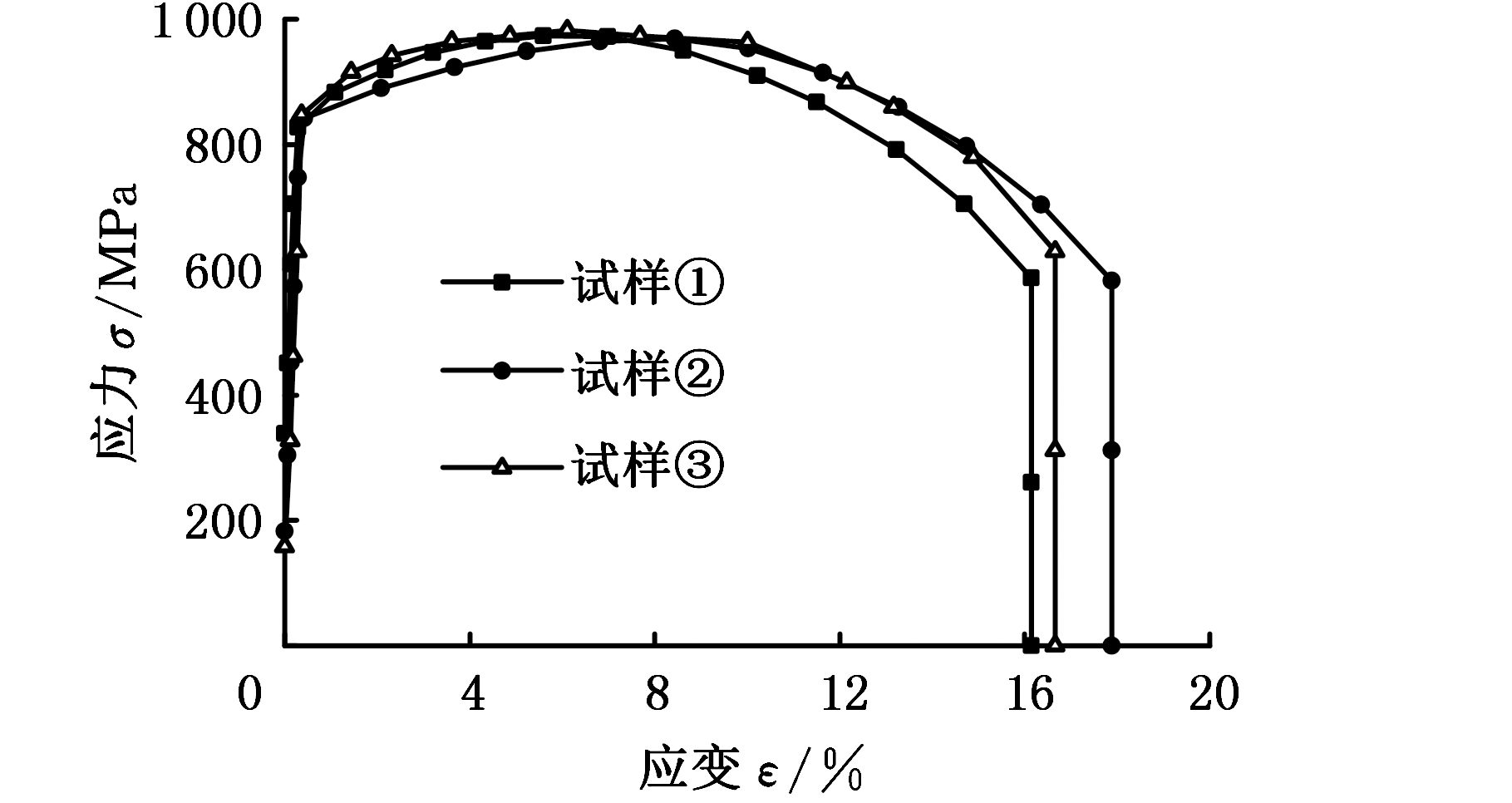
图3 应力应变曲线
Fig.3 Stress-strain curve

图4 真实应力应变曲线
Fig.4 True stress-strain curve

图5 钻具拆装架与螺纹接头
Fig.5 Drilling tool makeup and breakout stand and the threaded connection
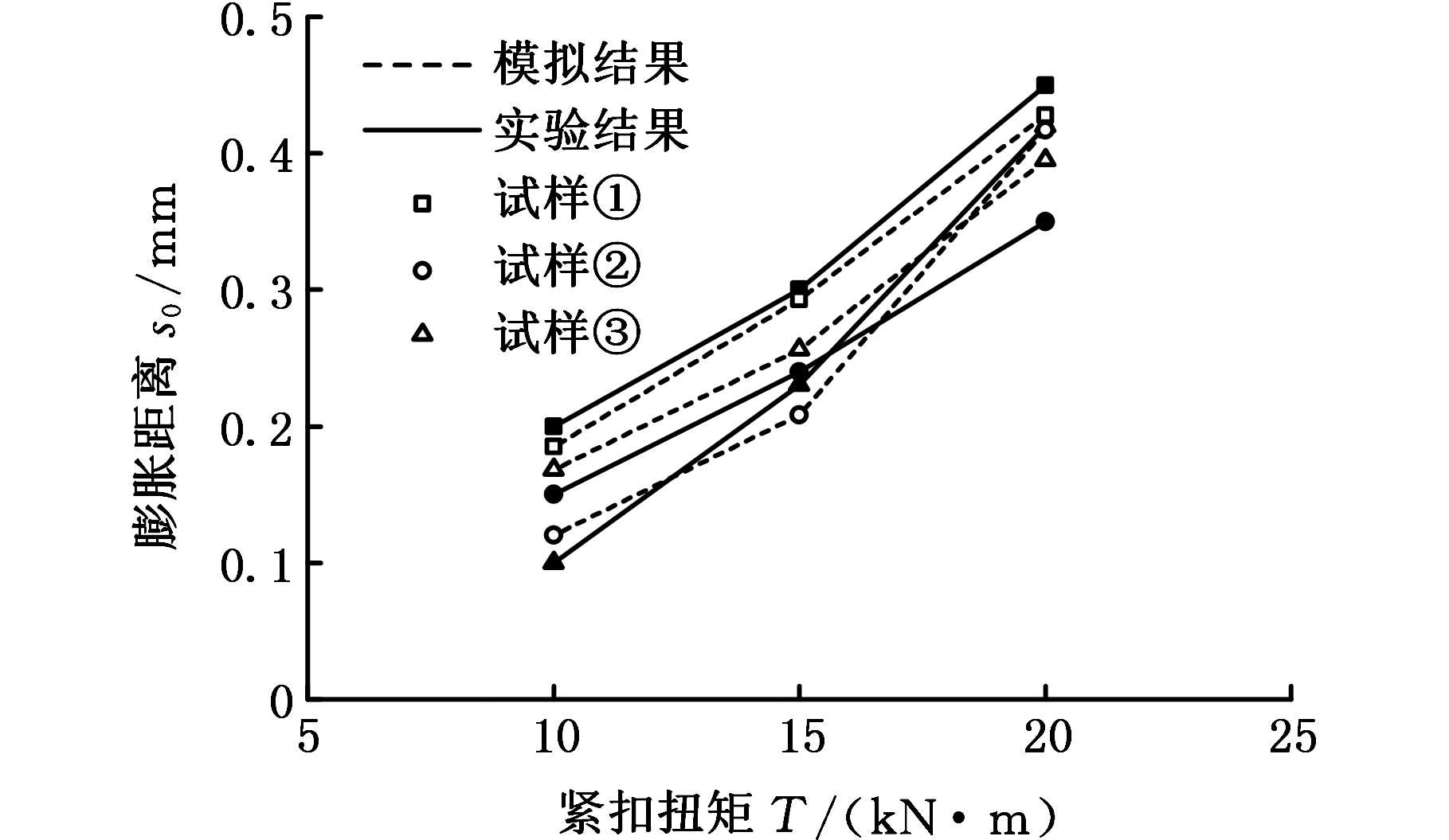
图6 实验结果与有限元结果对比
Fig.6 Comparison of experimental results and finite element results
2 螺纹接头力学行为模拟及连接性能分析
2.1 二维、三维有限元结果对比分析
利用有限元软件模拟螺纹接头的紧扣过程,分析在不同紧扣扭矩作用下的螺纹受力情况。为了避免数值振荡[13],采用图7所示光滑的加载曲线对三维有限元模型进行加载,加载时间设置为1 s。
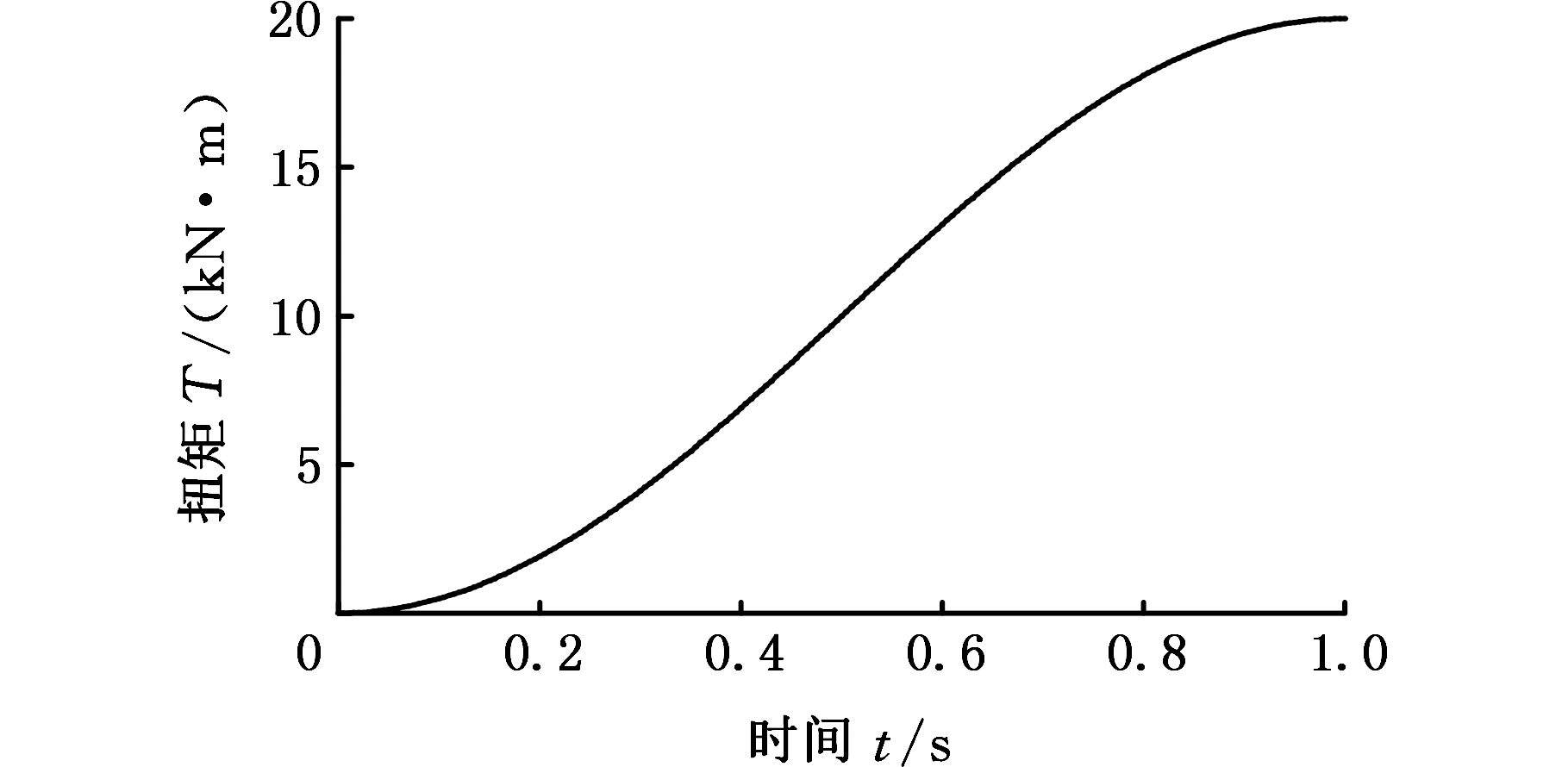
图7 扭矩加载曲线
Fig.7 Torque loading curve
图8、图9所示分别为5 kN·m和10 kN·m紧扣扭矩作用下螺纹接头等效应力和接触压力分布情况。可以看出,应力主要集中在公扣台肩应力释放槽、母扣镗孔处以及公扣前几圈螺纹牙处,且螺纹牙应力分布很不均匀,前几圈螺纹牙承受的载荷明显高于后几圈螺纹牙,这是由外载荷作用下公扣、母扣变形极不协调的受力特点所决定的。紧扣作用下,螺纹接头台肩处的接触压力也很大,分别是100 MPa和200 MPa,且最大接触压力分布在应力释放槽附近,虽未达到材料的屈服极限,但是当外载荷急剧变化时,台肩容易被挤毁,导致主密封失效。虽然螺纹牙等效应力以及啮合面的接触压力不大,但是由于其分布不均匀,对牙体本身有较大的损伤,尤其是靠近台肩面的前几圈螺纹牙。

(a)T=5 kN·m
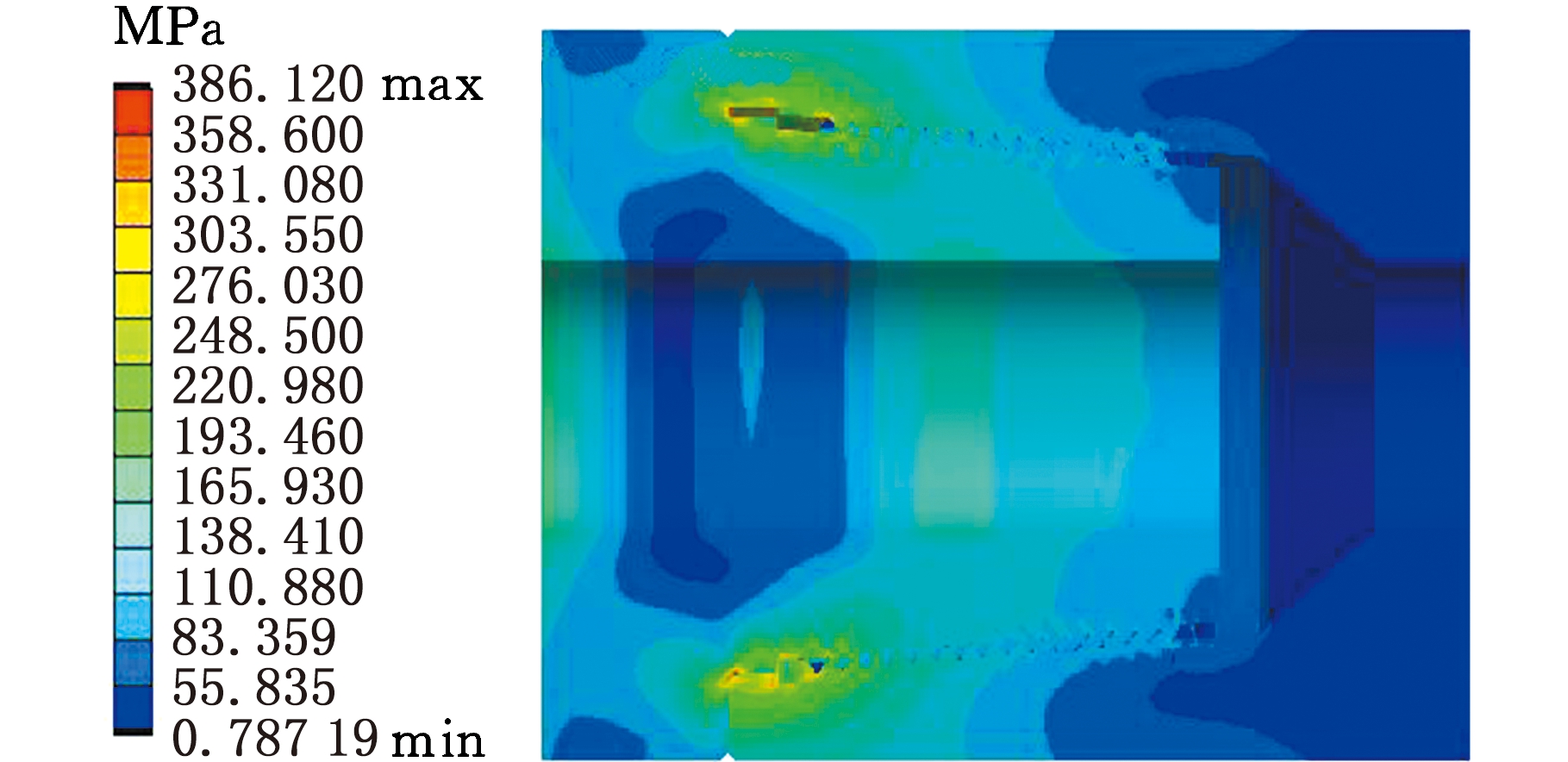
(b)T=10 kN·m
图8 不同紧扣扭矩下螺纹接头应力分布(三维)
Fig.8 Stress distribution of threaded joints under different tightening torque(3D)

(a)T=5 kN·m
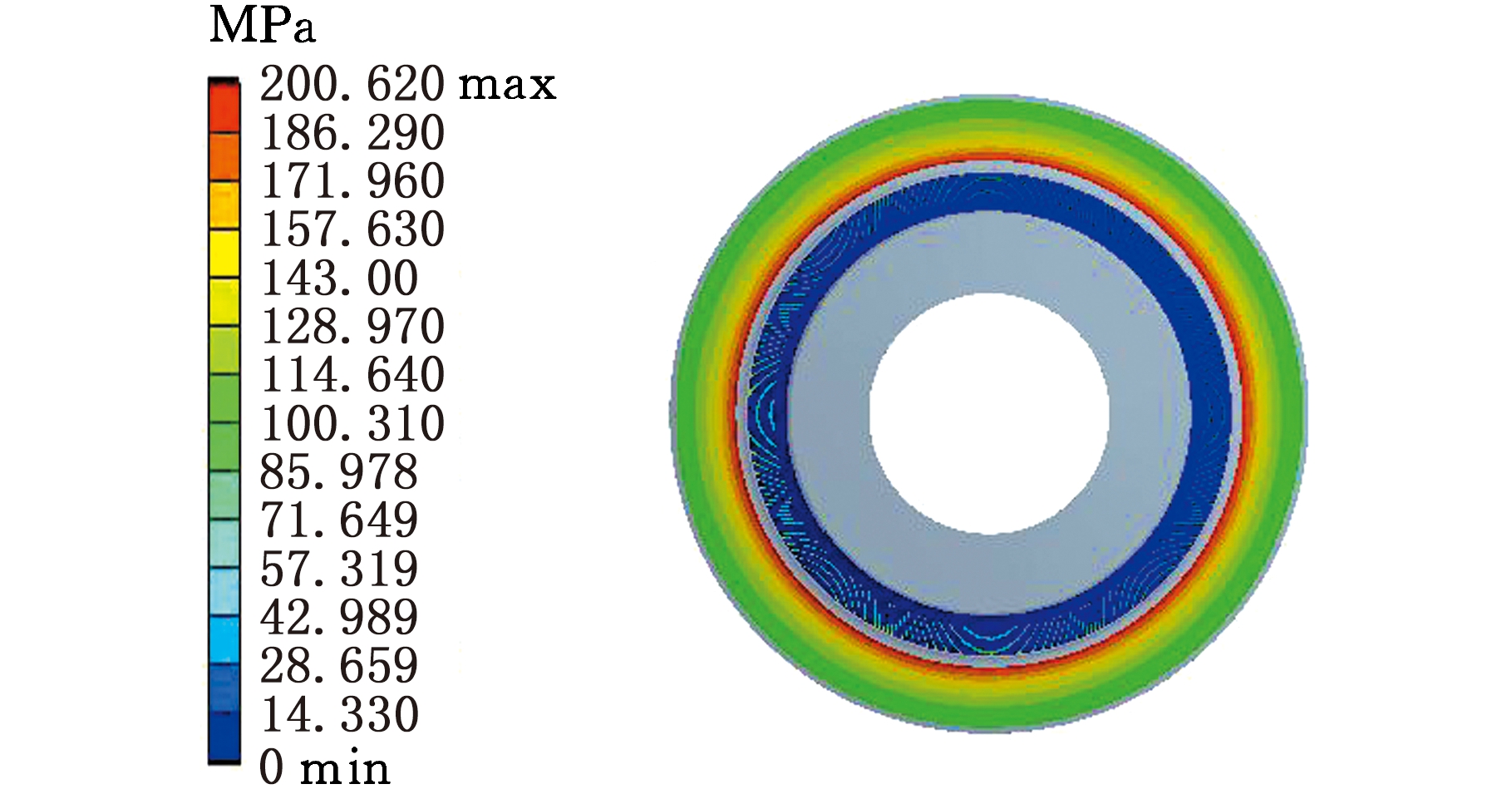
(b)T=10 kN·m
图9 不同紧扣扭矩下螺纹接头接触压力分布(三维)
Fig.9 Contact pressure distribution of threaded joints under different tightening torque(3D)
通过扭矩转角之间的关系可以推导出三维模型扭矩与过盈量的关系,有限元分析中公扣沿轴向的进给距离正是二维轴对称有限元模型台肩处的过盈量,表2为部分扭矩对应的过盈量。图10所示为紧扣作用下二维轴对称有限元模型的应力分布情况,最大应力出现在第一圈螺纹牙根处,螺纹接头的整体应力分布与三维模型的分析结果基本吻合,第一圈螺纹牙根处峰值应力不超过15%,且前几圈螺纹牙、母扣镗孔处以及应力释放槽处均存在应力集中,两端螺纹牙受力不均匀明显,同三维模型有相同的应力分布,符合连接螺纹的应力变化规律。
表2 过盈量与扭矩的关系
Tab.2 Relationship between the amount ofinterference and torque

扭矩(kN·m)过盈量(mm)扭矩(kN·m)过盈量(mm)扭矩(kN·m)过盈量(mm)00150.122 9300.244 150.042 1200.160 4350.300 2100.082 5250.201 1400.415 1
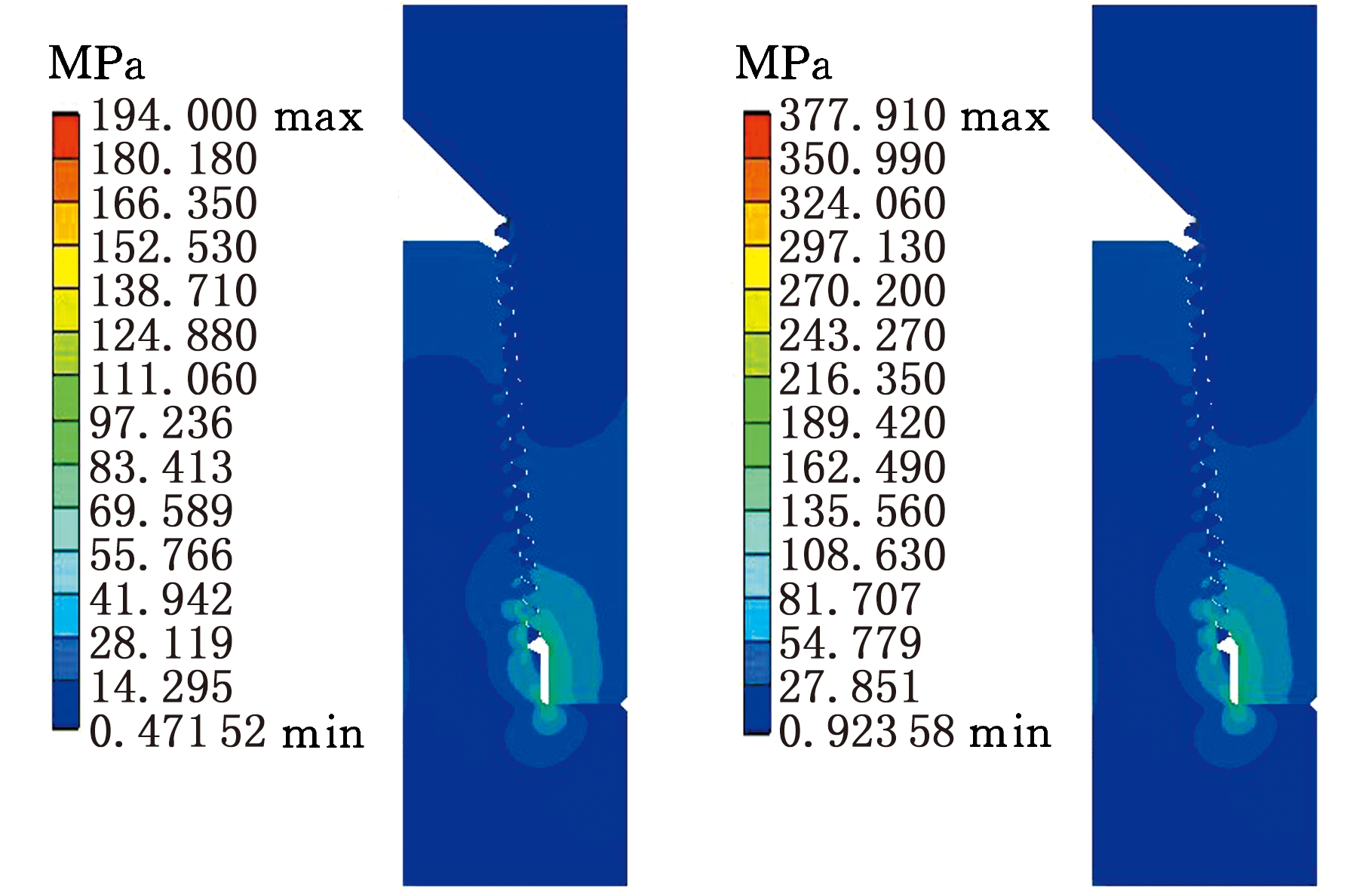
(a)T=5 kN·m (b)T=10 kN·m
图10 不同紧扣扭矩下螺纹接头应力分布(二维)
Fig.10 Stress distribution of threaded joints under different tightening torque(2D)
图11为不同紧扣扭矩下二维、三维模型的最大应力对比图,可以看出,随着扭矩增大,两者最大应力变化趋势基本相同,30 kN·m前最大应力呈现线性增大的趋势,随着扭矩继续增大,应力增速逐渐减缓,在40 kN·m时已经达到材料的拉伸极限,符合材料拉伸试验得出的弹塑性关系。二维模型与三维模型峰值应力最大偏差不超过15%,表明两者在有限元分析结果上具有很好的相似性。

图11 紧扣扭矩作用下的二维模型和三维模型最大应力对比
Fig.11 Max stress comparison between 2D and 3D models under tightening torque
图12所示为25 kN·m时二维模型与三维模型公扣和母扣螺纹牙应力对比,可以看出,三维模型和轴对称模型的螺纹牙应力变化趋势基本相同,呈L形分布,前4圈螺纹牙应力变化幅值最大,第5颗到第16颗螺纹牙应力分布较均匀,且公扣上螺纹牙应力均高于母扣,公扣第1圈螺纹牙应力较母扣均高出60%,表明公扣出现应力集中和丝扣破坏的风险更大。母扣壁厚通常较公扣大,由于尺寸效应,公扣更容易出现粘扣、断裂等现象。从上述分析可以得出,相同紧扣扭矩时,螺纹接头的三维模型最大应力略高于二维模型,螺纹牙应力变化趋势基本相同,两者之间由于螺旋升角产生的误差较小,可以忽略不计。三维模型虽然能更好模拟接头的上扣特性,但是考虑到计算成本和收敛性,以下分析均采用二维轴对称模型。

图12 25 kN·m时二维、三维模型公扣和母扣螺纹牙应力对比
Fig.12 Max stress comparison of the threads of pin and box over 2D and 3D models under 25 kN·m make-up torque
2.2 中心管螺纹连接性能分析
图13、图14分别为不同紧扣扭矩下各螺纹牙最大等效应力与最大接触压力的变化趋势图。随着紧扣扭矩增大,螺纹牙根部最大等效应力及啮合面接触压力均呈现增大的趋势,靠近台肩面的前4颗螺纹牙等效应力和接触压力都比较大,且变化幅度最大,说明前4圈螺纹牙本体变形量较大,牙体承受的载荷大。中间段螺纹牙,尤其是第5颗到第14颗螺纹牙间应力分布比较均匀,随着紧扣扭矩增大,螺纹牙应力基本呈现线性增大的趋势,而中间段及末端的螺纹牙接触压力则逐渐减小直至稳定状态,变化趋势不显著,总体上螺纹牙应力以及接触压力分布开始变得不均匀。与此同时,由于中心管螺纹采用真实应力-应变关系曲线定义材料的弹塑性变化,当紧扣扭矩超过35 kN·m时,螺纹牙应力增长速度便急剧降低,此时已超过材料的屈服极限860 MPa,继续增大紧扣扭矩,螺纹牙根部容易出现局部塑性变形,对螺纹的承载性能和连接性能是不利的,同时过高的紧扣扭矩容易致使接触压力不断增大,最终导致螺纹啮合面产生粘扣。

图13 不同紧扣扭矩下螺纹牙最大等效应力对比
Fig.13 Max stress comparison of the threaded teeth under tightening torque
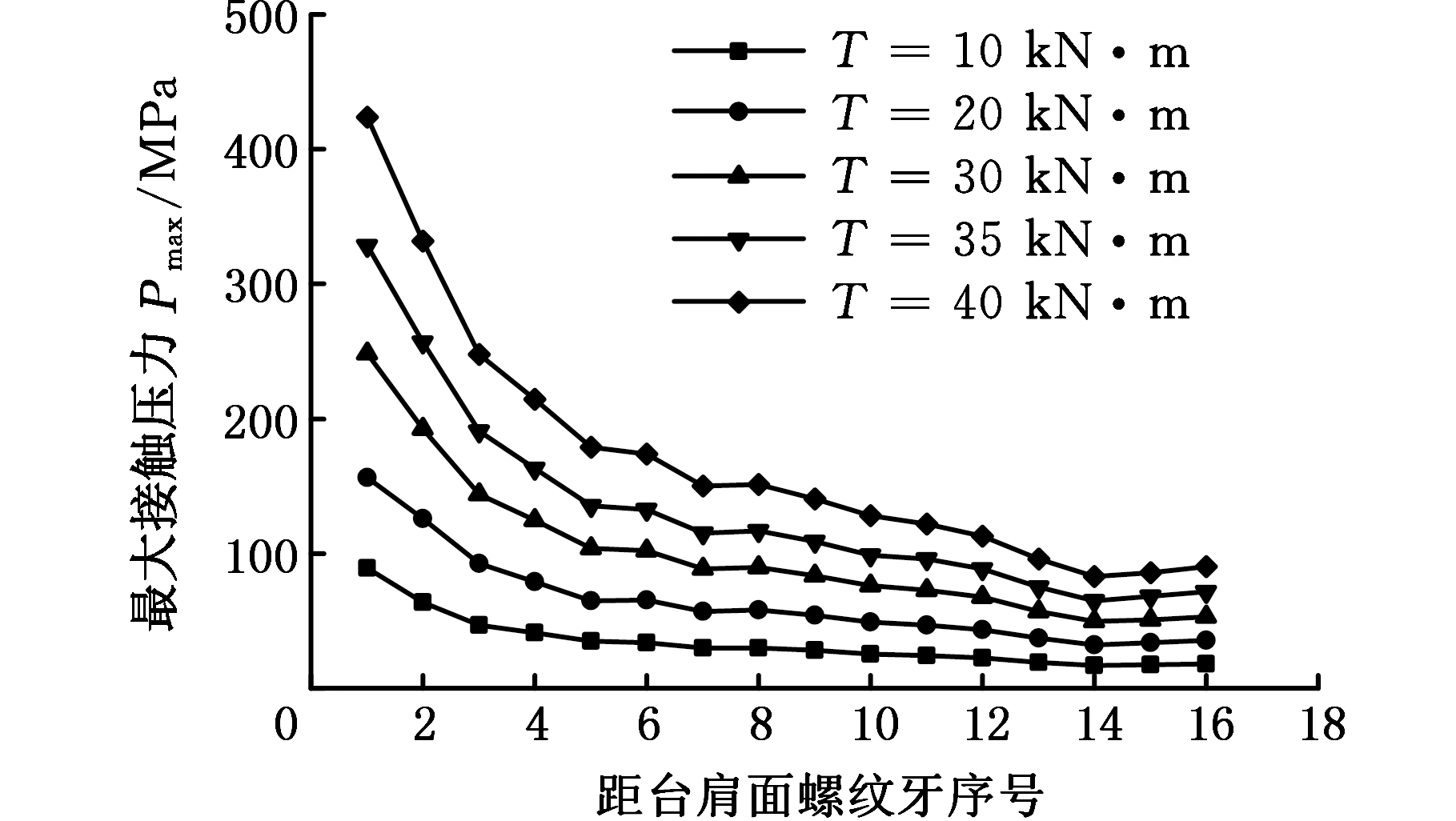
图14 不同紧扣扭矩下螺纹牙最大接触压力对比
Fig.14 Max contact pressure comparison of the threaded teeth under tightening torque
图15、图16所示为紧扣扭矩作用下,对顶驱中心管螺纹接头施加不同轴向拉力FL时螺纹牙最大等效应力以及接触压力变化情况。通过施加轴向拉力模拟顶驱下部悬挂的几千米钻柱,随着钻井深度不断增大,中心管螺纹承受的轴向拉力也在不断增大。可以看出,接头在施加一定紧扣扭矩后,螺纹牙应力呈现先减小后增大的趋势,且轴向拉力越大,末端螺纹牙应力和接触压力上升趋势越显著。图13、图14表明,在材料弹性阶段,每增大10 kN·m紧扣扭矩,螺纹牙最大等效应力大约增大200 MPa,接触压力增大约100 MPa;而每增大500 kN轴向拉力,螺纹牙最大等效应力以及接触压力增幅却很小,且第1颗螺纹牙根处应力和啮合面的压力变化不大,第2颗到第16颗螺纹牙间应力与接触压力呈现平行增大的趋势,表明相比于轴向载荷,连接螺纹对紧扣作用更加敏感。虽然第1颗螺纹牙应力与接触压力变化幅度极小,但仍处于所有螺纹牙中受载最大的区域,实际钻井工作中,冲击载荷与波动载荷会持续作用在螺纹接头上,往往更容易增加螺纹牙出现粘扣和断裂的风险。

图15 不同拉力下螺纹牙最大等效应力对比
Fig.15 Max stress comparison of the threaded teeth under tensile force
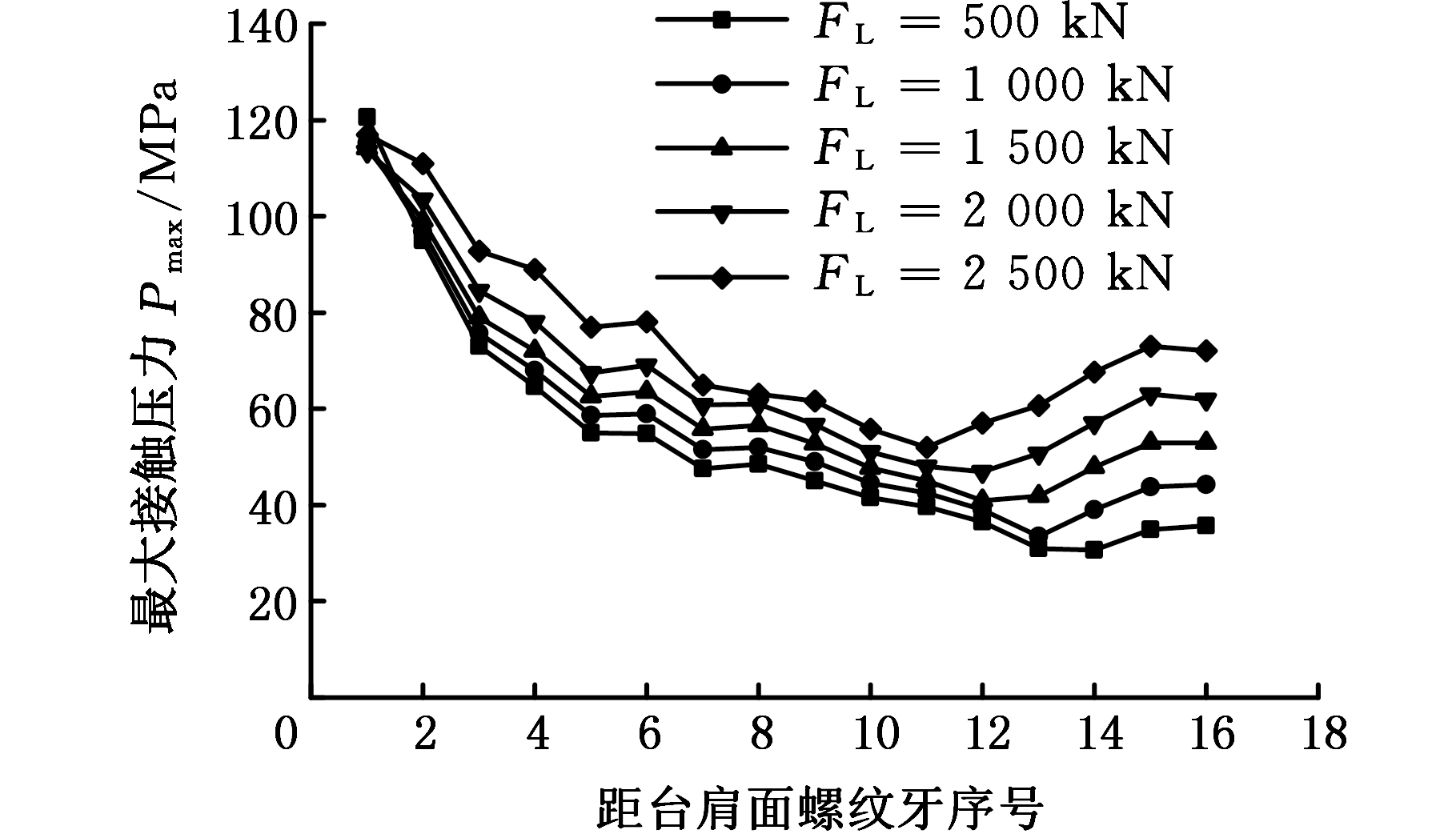
图16 不同拉力下螺纹牙最大接触压力对比
Fig.16 Max contact pressure comparison of the threaded teeth under tensile force
3 螺纹接头参数敏感性分析
螺纹接头受上扣扭矩、内/外压、轴向拉力等复杂外载荷作用时,各螺纹牙的受力很不均匀,前几圈螺纹牙容易应力集中,导致接头过早失效。从有限元分析结果来看,紧扣扭矩对螺纹安全性影响较大,一般情况下,在材料弹性阶段,每增大5 kN·m紧扣扭矩,螺纹最大等效应力大约增大100 MPa,扭矩为40 kN·m时已经接近材料的抗拉极限,相比于轴力以及内外压力,连接螺纹对扭矩更加敏感,且扭矩更容易对螺纹造成破坏。图17为某油田钻井现场顶驱中心管螺纹失效图,从接头断口形貌可以判断出,裂纹是从光滑断面处开始萌生的,而裂纹的萌生位置正是螺纹牙起始处。为了改善API 6-5/8细牙扣螺纹接头在牙根处的受力,减小应力集中现象,施加25 kN·m紧扣扭矩,对连接螺纹锥度、螺距及有效螺纹长度等参量进行敏感性分析,以此提高连接强度和抗粘扣性能。

图17 顶驱中心管螺纹接头失效图
Fig.17 Failure graph of threaded joint of drive center pipe
3.1 锥度对连接性能的影响
中心管接头连接螺纹常用的锥度为1∶6[14],为了比较不同锥度下连接螺纹最大Mises应力和接触压力值,选取1∶6、1∶8、1∶10、1∶12四种锥度进行对比分析,在紧扣扭矩作用下,所得结果见图18。锥度变化对第1圈螺纹牙承受的应力和接触压力影响最大,对中间段和末端螺纹牙的影响较小。在锥度为1∶6时应力和接触压力最大,若继续增加紧扣扭矩,第1圈螺纹牙很可能粘扣失效;连接锥度为1∶8时接触压力和等效应力最小,分别为374.5 kN和429.5 MPa,远低于材料的屈服极限。在实际生产中,螺纹接头承受的的外载荷更加复杂,适当选取锥度大的接头,能减少过扭情况下螺纹产生的环向应力,避免发生纵向开裂[15]。

图18 不同锥度下连接螺纹各螺纹牙最大Mises应力、最大接触压力曲线图
Fig.18 Plot of max stress and contact pressure of screw threads in different taper angles
3.2 螺纹有效长度对连接性能的影响
螺纹有效长度的增大对连接强度并没有产生太大影响(图19),在前几圈关键螺纹牙处的最大Mises应力值变化幅度并不大,有效螺纹长度在130~135 mm之间时最大应力变化幅度最小。螺纹长度变大时,有效啮合螺纹牙数会增多,啮合长度增加有助于降低钻井液泄漏的可能性,但是提高了生产成本,因此在螺纹长度选择时,不宜选取过长的螺纹接头。

图19 连接螺纹有效螺纹长度变化时各螺纹牙最大应力和最大接触压力曲线图
Fig.19 Plot of max stress and contact pressure of screw threads’ variation of effective thread length
3.3 螺距对连接性能的影响
随着螺距增大,螺纹牙最大等效应力和接触压力先增大后减小(图20)。当螺距p=8 mm时,螺纹最大Mises应力为806 MPa,开始接近SAE4137H合金钢的屈服极限;当螺距p=14 mm时,第1圈螺纹牙处的最大应力仅为449.8 MPa,远小于材料的屈服极限。螺距变化对中间及末端螺纹牙的连接强度影响较小,接触压力和最大Mises应力分布较均匀,粘扣风险较前几牙低。螺距也并非越大越好,螺距为12 mm和14 mm时的最大应力幅值变化不大,继续增大螺距并不会有效减小牙根处的应力,反而会浪费材料增大制造成本,由于螺距增大,螺纹牙的有效啮合长度会减小,产生应力腐蚀的风险将会升高。
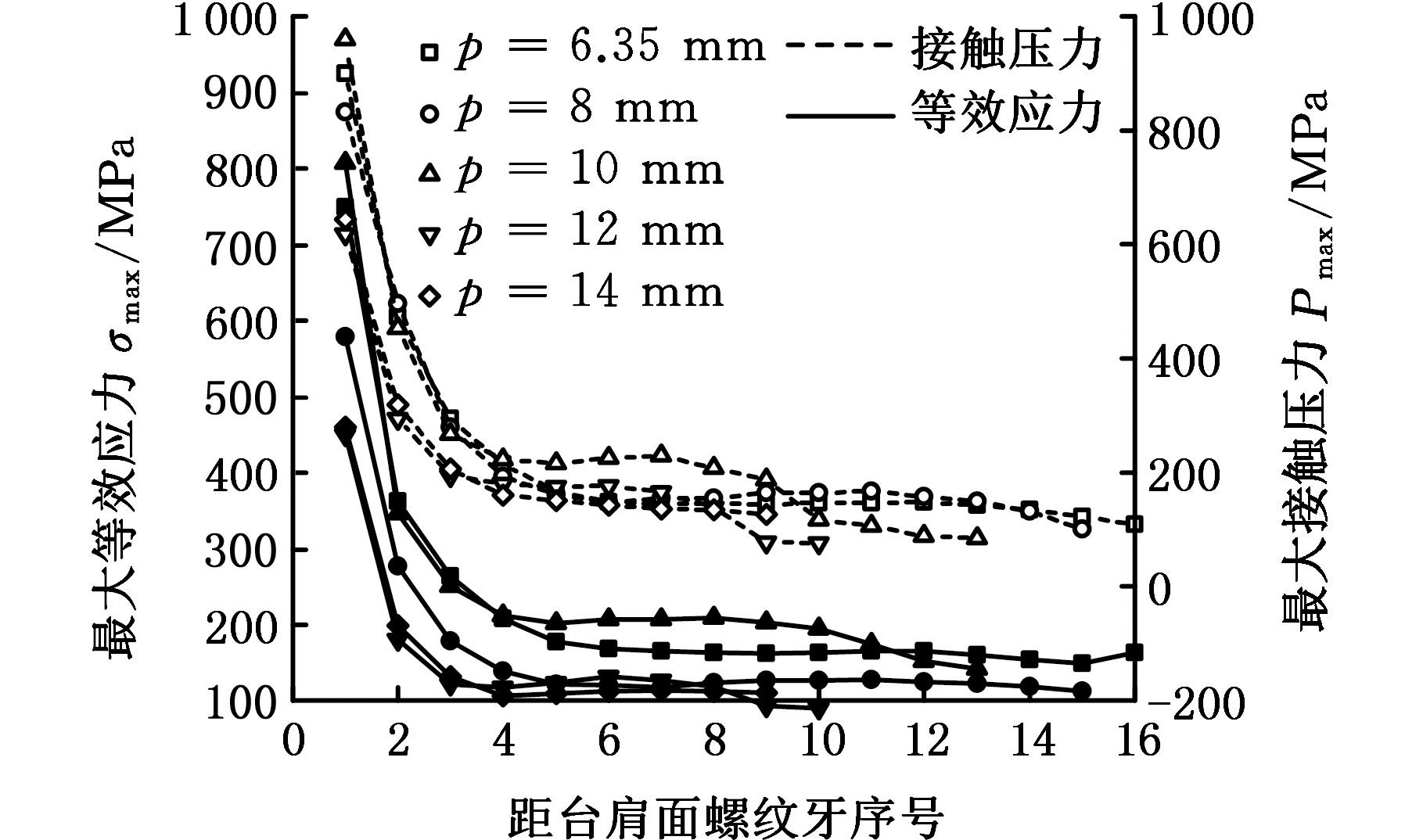
图20 螺距变化时各螺纹牙最大应力和最大接触压力曲线图
Fig.20 Plot of max stress and contact pressure of threads’ variation of pitch
4 结论
(1)综合考虑顶驱螺纹接头连接强度、密封性能以及生产成本,在保证连接螺纹各项指标性能满足规定的范围内,尽量选取较小锥度、较大螺距和较大的有效螺纹长度的接头。对于API标准的6-5/8连接螺纹接头,在不改变螺纹牙型的情况下,推荐使用以下螺纹参数:锥度为1∶8;螺距为12 mm;有效螺纹长度为130 mm。
(2)螺纹紧扣的目的是防止松扣,对于大斜度大位移井,由于本身井筒摩阻扭矩较大,导致井口处极限扭矩和扭矩波动也较大(现场实践表明,60°井斜大位移井,6 000 m井可达到30~40 kN·m井口扭矩),在这种情况下,为防止松扣可采用非常规设计改善螺纹连接强度,以提高紧扣扭矩。对于直井,尤其是容易产生安全问题的深直井,井口扭矩并不大,尤其要注意合理施加紧扣扭矩。
[1] 李鹏,牟新明,高明,等. 顶驱中心管强度有限元分析[J]. 石油矿场机械,2009(9):59-62.
LI Peng, MOU Xinming, GAO Ming, et al. Finite Element Analysis in Center Pipe of Top Drive[J]. Oil Field Equipment,2009(9):59-62.
[2] SCHWIND B. Mobil Qualifies Three Tubing/Casing Connection Product Lines[J]. Petroleum Engineer International, 1998,71:59-62.
[3] 袁光杰,姚振强. 油套管螺纹连接抗粘扣技术的研究现状及展望[J]. 钢铁,2003,38(11):66-69.
YUAN Guangjie, YAO Zhenqiang. Recent Situation and Future of Anti-galling Technique for API Round Thread [J]. Iron and Steel, 2003, 38(11): 66-69.
[4] 陈守俊,李强,张毅,等. 圆锥管连接螺纹牙变形及应力分布研究[J]. 中国机械工程,2010,21(17):2044-2049.
CHEN Shoujun, LI Qiang, ZHANG Yi, et al. Research on Deformation and Stress Distribution on Thread Teeth at Conic Thread Connections[J]. China Mechanical Engineering, 2010,21 (17):2044-2049.
[5] 兰洪波,高德利,张国辉. φ149.3mm钻杆高强度接头数值分析[J]. 天然气工业,2008(9):67-68.
LAN Hongbo, GAO Deli, ZHANG Guohui. Numerical Analysis of 5-7/8″High-strength Drill Pipe Joint[J]. Natural Gas Industry, 2008(9):67-68.
[6] 袁光杰, 林元华, 姚振强, 等. API偏梯形套管螺纹连接的接触应力场研究[J].钢铁,2004,39(9):66-69.
YUAN Guangjie, LIN Yuanhua, YAO Zhenqiang, et al. Research on Contact Stress Field of API ButTress Casing Thread Connection[J]. Iron and Steel, 2004, 39(9): 66-69.
[7] BAHAI H. A Parametric Model for Axial and Bending Stress Concentration Factors in API Drill String Threaded Connectors[J]. International Journal of Pressure Vessels and Piping,2001, 78(7):495-505.
[8] CHEN S J, LI Q, YI Z, et al. Finite Element Analysis of Tooth Load Distribution on P-110S Conic Threaded Connections[J]. International Journal of Pressure Vessels and Piping,2011, 88(2):88-93.
[9] SHAHANI A R, SHARIFI S M H. Contact Stress Analysis and Calculation of Stress Concentration Factors at the Tool Joint of a Drill Pipe[J]. Mater. Des., 2009, 30:3615-3621.
[10] BRENNAN F B, DOVER W D. Stress Intensity Factors for Threaded Connections[J]. Engrg. Fracture Mech., 1995, 134:545-567.
[11] 狄勤丰,陈锋,王文昌,等.双台肩钻杆接头三维力学分析[J].石油学报,2012,33(5):871-877.
DI Qinfeng, CHEN Feng, WANG Wenchang, et al. Three-dimentional Mechanical Analysis of the Double-shouldered Tool Joint[J]. Acta Petrolei Sinica, 2012,33(5):871-877.
[12] 赵楠. 螺杆钻具螺纹承载能力评价方法研究[D]. 成都:西南石油大学,2013.
ZHAO Nan. Research on Evaluation Method of Thread Bearing Capacity of the Screw Drill[D]. Chengdu: Southwest Petroleum University, 2013.
[13] 狄勤丰,陈锋,李宁,等.超深井钻具接头极限工作扭矩图版及其应用[J]. 石油学报,2016,37(4):516-522.
DI Qinfeng, CHEN Feng, LI Ning, et al. Determination of Operating Load Limits for Rotary Shouldered Connections with Three-dimensional Finite Element Analysis[J]. Acta Petrolei Sinica, 2016,37(4):516-522.
[14] API RP7A1-1992. Recommended Practice for Testing for Thread Compound for Rotary Shouldered Connections[S]. Washington D C: American Petroleum Institute Production Department, 1992.
[15] 王勇,高连新,袁鹏斌.双台肩钻杆内螺纹接头纵向开裂原因分析[J].机床与液压,2015(22):183-186.
WANG Yong, GAO Lianxin, YUAN Pengbin. Cause Analysis of Vertical Fracture of the Rifled Connection of Double-shouldered Drill Pipe[J]. Machine Tool & Hydraulics, 2015(22):183-186.
