0 引言!
高扬程全平衡卷扬式垂直升船机只采用钢丝绳作为其承船厢的弹性支座,承船厢属于狭长型矩形盛水容器,且由于扬程较高,导致其承船厢的惯性较大,支承刚度偏低,进而造成全平衡卷扬式垂直升船机的整体动态特性较差[1],由此对升船机运动稳定性进行研究显得非常必要和紧迫。高扬程全平衡卷扬式垂直升船机系统是由多个子结构相互耦合形成的机电液复杂系统,在承船厢提升和下降的运行过程中,厢内液体晃荡又会对结构产生影响,这都使得承船厢与主提升机悬吊系统的整体动力学特性较为复杂[2-5]。
杨淳等[6]按照1∶25的比例尺建立了承船厢物理模型,通过测量悬吊钢丝绳拉力、厢内水体波高和承船厢运行速度等,得出随着承船厢纵倾趋势增大,厢内水体波动更明显,两吊点处钢丝绳受力分布不均匀趋势也会增强的规律。朱世洪等[7]通过对比例模型进行理论分析和试验,得到了承船厢在漏水事故下的稳定运行条件,结果表明在平衡重总重不变的情况下,增大转矩平衡重的质量对升船机的安全运行有利。石端伟等[8]采用刚性子结构法建立了三峡大坝全平衡卷扬式垂直升船机的动力学模型,运用Wilson-θ法求解系统的瞬态响应,仿真计算结果与原型实测中的各参数基本一致,证明三峡大坝升船机设计方案是安全可靠的。李海涛等[9]给出了包括船厢中水体的流体动力学方程在内的耦合系统控制方程,通过该控制方程可以计算地震作用下承船厢内水体的响应、承船厢的晃动和水中船的运动状态。
在升船机稳定性方面,陈锦珍等[10]考虑漏水工况,根据静力平衡的原理推导出船厢失稳条件的判别式。程耿东等[11-12]研究了包括承船厢、提升钢丝绳、重力平衡重、承船厢中的水和船舶在内的全平衡卷扬式垂直升船机系统的自振特性和稳定性,得出了影响系统自振特性的关键因素,计算出保持系统稳定性的临界吊点位置。上述研究均未考虑主提升机系统中同步轴的影响。石端伟等[13]分析了承船厢与水体系统在刚性竖直振动下的稳定性,根据流体力学势流理论建立了一组8变量的非线性微分方程组,采用龙格库塔法对水体系统进行了数值仿真。廖乐康等[14-15]考虑同步轴的影响,建立了全平衡卷扬式垂直升船机的动力学模型,推导了计算临界吊点中心距的计算公式,但是该研究没有考虑重力平衡重的影响。以上研究均没有对全平衡卷扬式垂直升船机在高扬程(H≥120m)下的稳定性进行探讨。
本文建立了一个包括承船厢、提升钢丝绳、重力平衡重、承船厢中的水体、同步轴、卷筒和滑轮在内的全平衡卷扬式垂直升船机系统的动力学模型,运用笛卡儿法则推导了系统失稳的临界吊点中心距的计算公式;研究了扬程的变化对系统稳定性的影响程度;对全平衡卷扬式垂直升船机进行系统动力学仿真求解得出系统的主要位移响应,根据位移响应的收敛程度判定系统的稳定性;通过将仿真计算结果与本文公式对比,进一步验证公式的正确性。
1 动力学模型的建立
全平衡卷扬式垂直升船机的承船厢处于悬吊状态时的示意图见图1。承船厢中的水体自由表面以角位移θ做自由表面晃动,承船厢以角位移α做纵倾运动,h为承船厢厢内水体深度,β为深度y处单位厚度薄膜的旋转角速度。

图1 承船厢的纵倾运动示意图
Fig.1 Diagram for longitudinal motion of ship chamber
当承船厢以初始角加速度α··做纵倾运动时,承船厢中的水体自由表面被激发以角加速度θ··做晃动振动,在承船厢底部与端部产生液动压力而形成倾覆力矩。由于承船厢的纵向长度一般都远大于承船厢的高度和宽度,故可忽略承船厢侧壁受到的来自水体的倾覆力矩,仅计算水动压力沿承船厢底部分布不均形成的倾覆力矩。在分析时将承船厢内水体水域尺寸近似等同为承船厢尺寸。在某一水深y处,有一单位厚度薄膜(图1中阴影部分),在不可压缩的条件下,流体速度在x方向的分量应满足:
由文献[15]知,θ与β 应满足

其中,I、J是与容器几何形状有关的积分,即
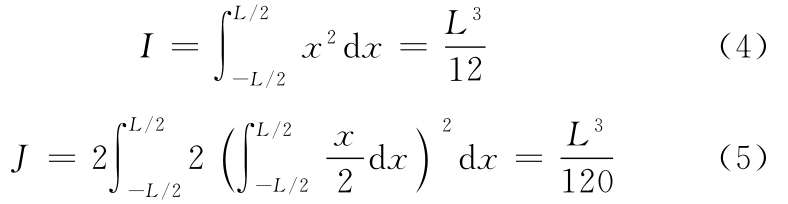
其中,L为承船厢内水域纵向长度。又由文献[16]知:
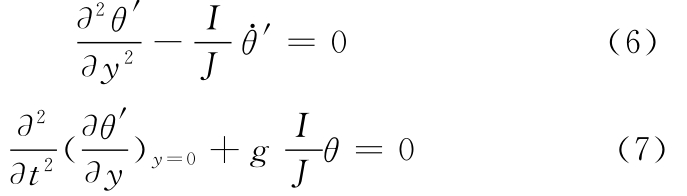
式中,g为重力加速度。
联立式(2)、式(3)、式(6)和式(7),可得
设p为承船厢中水体自由表面晃动产生的压力,当y=0时,p=0。由伯努利方程、式(1)~式(3)可得
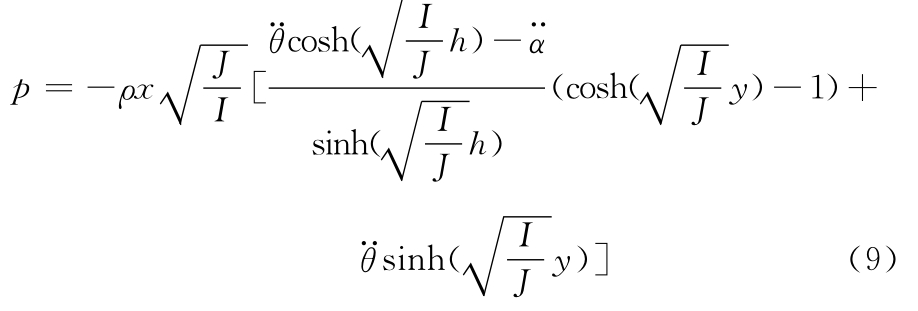
式中,p为水的密度。
其中,h 为设计水深。当y=-h 时,由于 h/L1,所 以 1 - cosh
h/L1,所 以 1 - cosh  h/L)≈-5 h2/L2,sinh( 槡1 0 h/L)≈
h/L)≈-5 h2/L2,sinh( 槡1 0 h/L)≈ /L,可求得水体对承船厢的水动压力:
/L,可求得水体对承船厢的水动压力:
由水动压力引起的倾覆力矩

式中,B为承船厢内水域横向宽度。
此外,由承船厢自身的倾斜以及水体自由面晃动而造成的水深不均所引起的倾覆力矩

因此,承船厢的总倾覆力矩由动水压力和静水压力两部分组成:
主提升机悬吊与承船厢系统如图2所示,系统所处工况为承船厢提升之前,且夹紧装置、安全制动器和工作制动器均已松开,此时将承船厢视为受动、静水压作用的刚性梁。图2中,φ1、φ2分别为两吊点处卷筒、滑轮组在同步轴上的转动角位移,y1为承船厢在竖直方向上的位移,y2、y3为重力平衡重在竖直方向上的位移,则该系统的总动能、总势能分别为

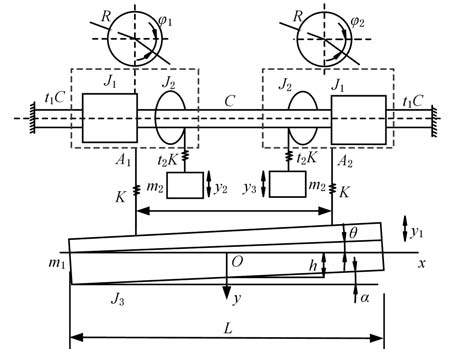
图2 全平衡卷扬式垂直升船机系统
Fig.2 Fully balanced hoist vertical shiplift

式中,t1为电动机传动轴刚度与同步轴刚度之比,一般取t1=2;t2为重力平衡重提升钢丝绳刚度与承船厢提升钢丝绳之比,一般取t2=4;a为临界吊点中心距;R为卷筒半径;J1为卷筒转动惯量;J2为滑轮转动惯量;J3为承船厢与水体绕质心的转动惯量;m1为承船厢水体质量;m2为重力平衡重质量;C为同步轴刚度;K 为钢丝绳刚度;γ1为卷扬机扭转振动的阻尼系数;γ2为承船厢纵倾运动的阻尼系数。
由拉格朗日第二类方程[17],有

式中,γ3为承船厢做竖直运动的阻尼系数。
式(20)中,F为动水压力与静水压力对承船厢底造成的水动载荷,有

将式(10)代入式(23)中,得F=0。令
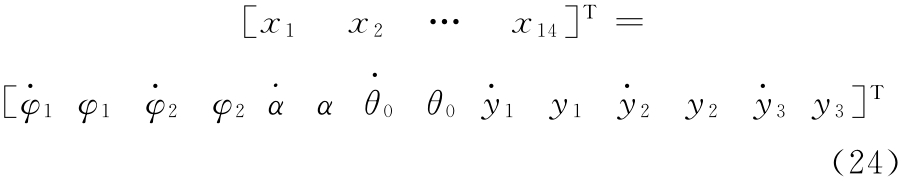
则系统的动力学方程可整理成

式(27)~式(30)中,Ci(i=1,2,…,19)的表达式分别为


2 临界吊点中心距计算公式
式(25)中矩阵A的特征方程为
其中,系数bi(i=0,1,…,14)可由式(25)~式(30)求出。
对于形如式(40)的一元n次实系数代数方程,设系数序列T为
由笛卡儿法则,式(41)中依次相邻的两个数bk,bk+1(k=0,1,…,13)符号相反,则称两数之间有一次变号。设系数序列T变号次数为q,若有q=0,则式(40)无正根。根据运动稳定性理论,可判定系统是稳定的。由式(25)和式(40)可知,b0=1>0。因此,有
当主提升机悬吊与承船厢系统处于纵倾稳定的工况下时,临界吊点中心距a必须满足式(42)。以构皮滩大坝水电站二级垂直升船机为算例,计算参数见表1。
表1 构皮滩大坝水电站二级垂直升船机计算参数
Tab.1 Parameters of the second step of GouPitan shiplift
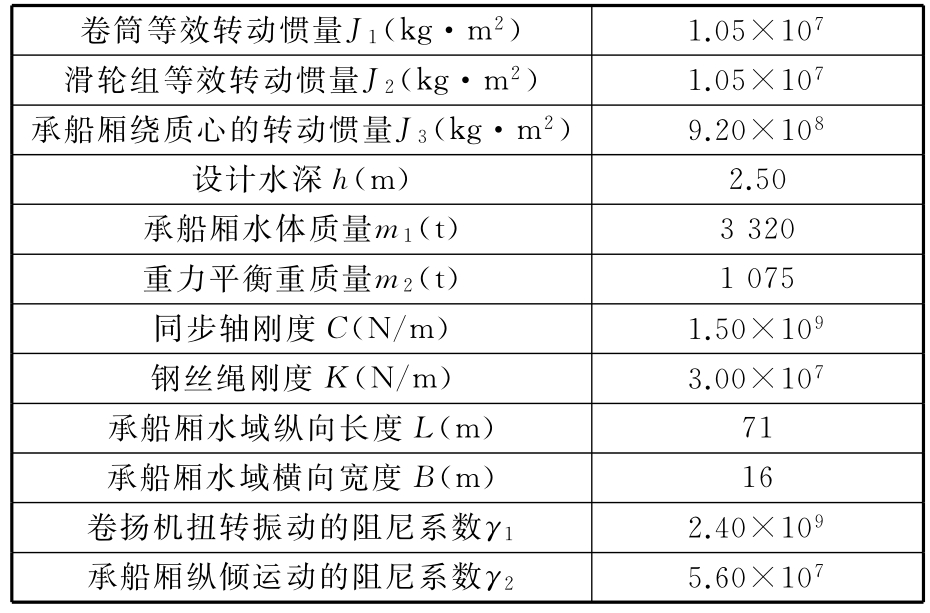
卷筒等效转动惯量J1(kg·m2) 1.05×107滑轮组等效转动惯量J2(kg·m2) 1.05×107承船厢绕质心的转动惯量J3(kg·m2) 9.20×108设计水深h(m) 2.50承船厢水体质量m1(t) 3 320重力平衡重质量m2(t) 1 075同步轴刚度C(N/m) 1.50×109钢丝绳刚度K(N/m) 3.00×107承船厢水域纵向长度L(m) 71承船厢水域横向宽度B(m) 16卷扬机扭转振动的阻尼系数γ1 2.40×109承船厢纵倾运动的阻尼系数γ2 5.60×107
将表1中的参数代入式(42)计算出bi(i=1,2,…,14),可以找出若干个存在零点的以临界吊点中心距a为自变量的系数bi的表达式,从而可求解出与之相对应的零点ai。考虑稳定性最差的情况,即取max bi()和与之相对应的系数bi的表达式,将max ai()视为此时的临界吊点中心距,根据此系数bi的表达式推导出临界吊点中心距计算公式。
经过计算可知,只有系数b13和b14的表达式存在零点。当a∈0,30m[]时,系数bi的表达式(i=12,13,14)的函数曲线形态如图3所示。b13和b14对应的零点分别为a13=12.99m,a14=17.24 m。较大的零点a14=17.24m即为此升船机的临界吊点中心距,对应的是系数b14的表达式,联立式(31)~(39),将b14进行变换,可得临界吊点中心距a的计算公式如下:


图3 bi(i=12,13,14)的函数曲线形态
Fig.3 Function curve shape for bi(i=12,13,14)
3 扬程对稳定性的影响
承船厢钢丝绳刚度
式中,n为提升钢丝绳的总根数,取n=48;E为钢丝绳的弹性模量,取E=4.91×1010 N/m2;d 为钢丝绳横截面直径。
卷筒的尺寸会随着钢丝绳横截面积的变化而变化,对于垂直升船机,有
式中,D为卷筒直径。
联立式(43)~式(45),可得临界吊点中心距a关于提升扬程H 和钢丝绳的横截面直径d变化的函数:
目前全世界提升扬程最大的垂直升船机为三峡大坝升船机,提升扬程H=113m。为了保证系统在高扬程(H≥120m)下具有足够的稳定性安全裕度,必须使函数f(H,d)在一定的约束条件下最小化。当升船机系统的提升扬程增大时,相应的钢丝绳横截面积也应增大。以水口大坝升船机为算例,约束条件定为
采用拉格朗日乘子法对式(46)在满足约束条件式(47)时进行最小值寻优,则当H=120m,d=80mm 时,amin=26.7m。可见提升扬程越小,钢丝绳横截面积越大,越有利于增强系统的稳定性。
提升扬程对临界吊点中心距和钢丝绳横截面直径的影响如图4所示。可以看出,当钢丝绳横截面直径不变时,临界吊点中心距随着提升扬程的增大而增大;当提升扬程不变时,临界吊点中心距随着钢丝绳横截面直径的减小而增大。这是因为提升扬程与横截面直径都直接影响钢丝绳的刚度,当提升扬程越高、钢丝绳横截面直径越小时,钢丝绳刚度就越小,过小的刚度导致钢丝绳的弹性过大,即承船厢与主提升机悬吊系统之间的支承弹性增强,导致承船厢抗倾覆的能力减弱,从而增强了系统的不稳定性,使得临界吊点中心距增大。

图4 扬程对临界吊点中心距和钢丝绳横截面直径的影响
Fig.4 Influence of lifting height on the critical distance of lifting points and sectional diameter of the wire rope
4 系统动力学仿真
以构皮滩大坝二级垂直升船机为算例,运用四阶变步长龙格库塔法,对主提升机悬吊与承船厢系统进行动力学仿真,计算各自由度位移响应曲线。各角位移初始条件如下:φ10=0°,φ20=0°,α0=0.24°,θ0=0.2°。仿真计算时间为500s。当a为17.17m 和17.18m 时,系统角位移φ1、φ2、α、θ响应曲线如图5所示。当a=17.17m时,各角位移曲线都处于发散状态;当a=17.18m时,系统的角位移曲线均逐渐收敛于零值,主提升机悬吊与承船厢系统处于稳定状态。因此,a=17.18m为主提升机悬吊与承船厢系统的临界吊点中心距。

图5 a=17.17m和17.18m时系统的角位移响应
Fig.5 Angle displacement responses when a=17.17mand 17.18m
当a=17.18m时,承船厢纵倾角位移α在一段时间后达到最大响应值,这是因为相对于其他角位移,初始承船厢纵倾角位移α0取值较大,承船厢在纵倾过程中受到的倾覆力矩较大。水体自由面晃动角位移θ对阻尼影响较敏感,故达到稳定状态(即位移响应衰减到零)的时间最短。由于承船厢在初始纵倾时一端吊点钢丝绳伸长,另一端吊点钢丝绳缩短,两吊点钢丝绳为了恢复到初始没有发生弹性变形的状态,使得两吊点处卷筒和滑轮组旋转角位移φ1和φ2曲线的方向相反。同理,当a=17.17m时,承船厢纵倾角位移α曲线最先开始发散,角位移φ1和φ2曲线发散趋势相反,水体自由面晃动角位移θ曲线发散速度最慢。
将由式(43)计算得到的临界吊点中心距分别与系统动力学仿真得到的临界吊点中心距进行对比,得到计算误差为9.02%,在工程误差允许范围之内,验证了理论计算公式的正确性。
5 结论
(1)推导了计算临界吊点中心距的计算公式,该公式能指导全平衡卷扬式垂直升船机系统中吊点中心距、提升钢丝绳刚度、卷扬机卷筒半径、同步轴刚度的设计,判断高扬程全平衡卷扬式垂直升船机系统的稳定性。由该公式可看出,重力平衡重的质量、卷筒和滑轮的转动惯量与临界吊点中心距无关。
(2)扬程越高,升船机系统的稳定性越差。对于高扬程(H≥120m)全平衡卷扬式垂直升船机的设计,应注意增大钢丝绳的横截面直径,以保证钢丝绳具有足够的刚度,从而使得系统在一定的吊点中心距下能够保持稳定。
(3)从动力学仿真的位移响应求解结果中可以看出,承船厢纵倾角的动态响应最明显,且达到稳定状态的时间也最长,因此,在升船机实际运行过程中,为了防止出现过大的初始倾斜角度,应使夹持锁定装置保持较高的工作可靠度。
[1] SHI Duanwei,PENG Hui,ZHAO Tiezhu,et al.Finite Element and Experimental Analysis of Pinion Bracket-assembly of Three Gorges Project Ship Lift[J].Journal of Central South University,2015,22:1307-1309.
[2] BROUET H.The Ship Lift at Strépy-Thieu,Canal du Centre,Belgium[J].Proceedings of the Institution of Civil Engineers-Transport,1997,123:178-185.
[3] MICHAEL B.For 75Years Ship Lift of Rothensee[J].BAUTECHNIK,2014,90(5):380-387.
[4] BAI W,LIU X,KOH C G.Numerical Study of Violent LNG Sloshing Induced by Realistic Ship Motions Using Level Set Method[J].Ocean Engineering,2015,97:100-113.
[5] LIAO Chanyi, WU Yichuang, CHANG Chingyuan,et al.Theoretical Analysis Based on Fundamental Functions of Thin Plate and Experimental Measurement for Vibration Characteristics of a Plate Coupled with Liquid[J].Journal of Sound and Vibration,2017,394:545-574.
[6] 杨淳,曾祥.三峡升船机承船厢整体动态特性研究[J].长江科学院院报,1992,9(2):12-20.YANG Chun,ZENG Xiang.A Study on Integral Dynamic Characteristics of Chamber of Ship Lift of the Three Gorges Project[J].Journal of Yangtze River Scientific Research Institute,1992,9(2):12-20.
[7] 朱世洪,周赤,刘敦煌.三峡升船机船厢失水事故动态特性研究 [J].长江科学院院报,2002,19(3):7-9.ZHU Shihong,ZHOU Chi,LIU Dunhuang.Study on Dynamic Properties of Ship Lift during Waterlosing from Ship Chamber of Three Gorges Project[J].Journal of Yangtze River Scientific Research Institute,2002,19(3):7-9.
[8] 石端伟,鲍务均,肖晓晖.三峡钢丝绳卷扬全平衡式垂直升船机机电耦合系统动力学仿真[J].华中师范大学学报(自然科学版),2002(2):169-172.SHI Duanwei,BAO Wujun,XIAO Xiaohui.Dynamic Simulation of Mechanical Electric Coupled System of The Three Gorges Wire Rope Hoist Full Balanced Vertical Ship Lift[J].Journal of Central Normal University(Natural Sciences),2002(2):169-172.
[9] 李海涛,程耿东,阮诗伦.升船机系统在地震作用下的响应[J].大连理工大学学报,2005,45(4):473-479.LI Haitao,CHENG Gengdong,RUAN Shilun.Seismic Response of Ship Lift System[J].Journal of Dalian University of Technology,2005,45(4):473-479.
[10] 陈锦珍,马光耀.垂直全平衡升船机承船厢的稳定性分析[J].水利水运科学研究,1996(4):301-308.CHEN Jinzhen,MA Guangyao.Chamber Stability of Hoisting Fully Balancing Type Vertical Ship Lift[J].Hydro-Science and Engineering,1996(4):301-308.
[11] 程耿东,李海涛,阮诗伦.重力全平衡提升式升船机的自振特性和稳定性分析[J].机械强度,2005,27(3):276-281.CHENG Gengdong,LI Haitao,RUAN Shilun.Free Vibration Characteristics and Stability Analysis of Ship Lift System[J].Journal of Mechanical Strength,2005,27(3):276-281.
[12] 阮诗伦,程耿东.三峡升船机船-水-厢耦合系统的非线性有限元时域计算[J].计算力学学报,2003,20(3):290-294.RUAN Shilun,CHENG Gengdong.Calculation of-Ship-water-chamber Coupled System in the Ship Lift with Finite Element Method in Time Domain[J].Chinese Journal of Computational Mechanics,2003,20(3):290-294.
[13] 石端伟,宋政,廖乐康.升船机承船厢水体参激振动的耦合分析[J].武汉大学学报(工学版),2003,36(1):77-80.SHI Duanwei,SONG Zheng,LIAO Lekang.Coupling Analysis of Ship-chamber of Ship Lift and Parametric Vibration of Water[J].Engineering Journal of Wuhan University,2003,36(1):77-80.
[14] 廖乐康,张圣坤.承船厢二维非线性晃动的分析[J].船舶力学,2006,10(2):47-55.LIAO Lekang,ZHANG Shengkun.Analysis on 2-D Nonlinear Slosh of Ship-chamber[J].Journal of Ship Mechanics,2006,10(2):47-55.
[15] LIAO Lekang.Safety Analysis and Design of Full Balanced Hoist Vertical Ship Lifts[J].Structural Engineering and Mechanics,2014,49(3):311-327.
[16] 居荣初,曾心传.弹性结构与液体的耦联振动理论[M].北京:地震出版社,1983:117-118.QU Rongchu,ZENG Xinchuan.Vibration Theory of Elastic and Liquid Coupled Structure[M].Beijing:Seismological Press,1983:117-118.
[17] 石端伟,吴庆鸣,曾令刚.GP6500型管片安装机虚拟样机设计与研究[J].中国机械工程,2006,17(13):1341-1345.SHI Duanwei,WU Qingming,ZENG Linggang.Design and Research on Virtual Prototype of GP6500Segment Erector[J].China Mechanical Engineering,2006,17(13):1341-1345.
