0 引言
随着工业机器人的发展，人们对RV减速器的传动精度和使用寿命提出了越来越高的要求，摆线轮作为RV减速器的关键部件，开展其齿廓修形技术的研究很有必要。CHMURAWA等[1]通过分析摆线轮齿廓修形与摆线轮载荷之间的关系，得到了修形后具有良好性能的摆线轮，但对具体修形方法涉及较少。库特略夫采[2]通过分析摆线针轮传动理论，提出了一套适用于标准齿廓的摆线轮齿形受力分析理论，却忽略了修形后的摆线轮齿廓的变化对受力的影响。LEHMANN等[3]分析了摆线轮成形机理、误差分布规律以及径向修形引起的间隙和法向修形引起的间隙之间的关系。由于核心技术保密等因素，目前可检索到的国外相关的研究报道极少[4]。国内方面,王秋成[5]建立了包括等距、移距和转角三种修形方式的摆线轮齿形的通用参数方程，并提出了一种符合工程实际的摆线针轮啮合受力的分析方法。严勇等[6]对齿轮啮合过程进行分析，提出分段复合修正的思想，在齿根和齿顶处采用圆弧修正，在主要传力段进行转角修正和微量鼓形修正。此外，关天民等[7]提出了“反弓”齿廓的概念，通过“正等距+负移距”组合修形方式对摆线轮进行修形，并且给出了优化设计方法。该齿廓与传统组合修形方式获得的齿廓相比，可以有效减小最大接触力，提高齿面承载能力。陈振宇[8]提出了基于成形磨削的摆线轮齿廓的分段修形方法，王新春[9]在其基础上分析了齿轮啮合时的润滑问题，确定了摆线针轮润滑的最小油膜厚度，从而给出了摆线轮齿根处非工作段的三次拟合样条曲线。
本文提出一种基于接触应力均化的摆线轮齿廓修形方法，该方法以压力角较小的齿廓工作段为修形区间，综合考虑齿侧间隙(简称“侧隙”)和传动精度，以各齿齿面接触应力方差最小的转角修形齿廓为目标齿廓，采用“负等距+正移距”组合修形方式逼近目标齿廓，在保证传动精度的前提下可以均化齿面接触应力，有效提高RV减速器的使用寿命。
1 摆线轮齿廓常用修形方法对比分析
1.1 摆线轮齿廓基本修形方式
根据摆线轮成形机理，目前最基本的摆线轮齿廓修形方式有等距修形、移距修形和转角修形三种，包含以上三种修形参数的摆线轮齿廓方程为[10]：
(1)
式中，xc、yc分别为齿廓点的横坐标和纵坐标；θ为针轮相对于转臂的转角；rp为针轮中心距；rrp为针轮半径；Zp为针轮齿数；Zc为摆线轮齿数；
为修形后的短幅系数；A为偏心距；Δθ、Δrp、Δrrp分别为转角、移距、等距修形量。
本文以RV-80E样机为研究对象，样机参数如表1所示。
表1 RV-80E样机基本参数
Tab.1 RV-80E prototype basic parameters
摆线轮齿数针轮齿数针轮半径(mm)针轮中心距(mm)偏心距(mm)39404801.75
取相同的等距和移距以及适当的转角分别对齿廓进行修形，代入式(1)中，得到的齿廓与标准齿廓对比如图1所示。
图1 修形后的齿廓
Fig.1 Modification profile
由图1可知，三种基本修形方式具有如下特点：①在修形量相同情况下, 等距修形和移距修形能在齿顶和齿根处形成相同的间隙，而在其他位置，等距修形的法向间隙大于移距修形的法向间隙。②转角修形齿廓在齿根与齿顶处没有间隙，从齿顶到齿根，径向间隙先增大后减小，因此选择合适的转角修形量，能够保证齿根与齿顶处无间隙啮合，而在齿廓工作段留有适当的间隙,以有效补偿制造误差和安装误差，同时为润滑留下足够的空间。
1.2 齿面受力分析
图2为摆线轮初始间隙示意图，当最先接触点所受力为Fb时，产生的对应形变为δb，所传递的力矩为Tc，其余各个位置的受力记为Fi，变形记为δi，初始间隙记为Δφi，有[11]
(2)
图2 初始间隙示意图
Fig.2 Initial gap diagram
由于最先接触点并非恰好为
点，因此在不考虑非线性因素的条件下，可以得到各啮合处的变形位移δi与最先接触点的变形位移δb的关系：
(3)
式中，θT为初始啮合时针轮转过的角度;θi为第i号齿啮合时针轮相对于转臂的转角。
修形后的摆线轮在传递转矩时，由于摆线轮与针轮之间存在接触变形，在啮合点或者待啮合点法线方向会产生相应的变形δi。
经过修形后的摆线轮，如果不考虑弹性变形的补偿作用，摆线轮与针轮之间存在大小不同的初始间隙，初始间隙表达式为[11]
(4)
只有变形量δi的值大于该位置初始间隙ΔQi的各齿才参与啮合。以图3为例，只有2～10号齿之间的变形量大于初始间隙，因此只有2～10号针齿参与了啮合。
图3 初始间隙和变形量分布曲线
Fig.3 The distribution curve of initial gap and deformation
由力矩平衡关系可知Fb与δb的关系：
(5)
式中，Li 为摆线轮传动力臂。
由于RV减速器中的针齿都有一半插入针齿座上，因此针齿销的弯曲变形很小，可以忽略不计，则总的变形量近似为接触变形，总的变形量与接触力的关系可表示为
(6)
(7)
式中，E为弹性模量；μ为泊松比；b为摆线轮宽度；|ρ|为最先接触点处的曲率半径ρ的绝对值。
修形后的摆线轮曲率半径可由下式计算：
(8)
接触应力可由赫兹公式得到：
(9)
其中，|Fi|为各齿之间的啮合接触力Fi的模；Ee为当量弹性模数；ρei为当量曲率半径，有
(10)
式中， ρi为摆线轮在某啮合点处的曲率半径。
将得到的各齿之间的接触力代入到赫兹公式中，可以得到摆线轮与针轮啮合时各齿之间的接触应力分布情况。
1.3 两种基本组合修形方式比较
采用单一修形方式修形往往无法满足RV减速器高精度的要求。在实际加工过程中，一般采用“正等距+负移距”和“负等距+正移距”两种组合修形方式来对摆线轮进行修形。在修形量相同情况下，移距修形相较于等距修形所形成的回转角较小。根据修形量选取公式[12]：
(11)
(12)
给定相同径向间隙Δ=0.02 mm，可以计算得到两种组合修形方式下对应的回转角，如表2所示。
表2 修形量和回转角
Tab.2 Reshaping amount and angle of rotation
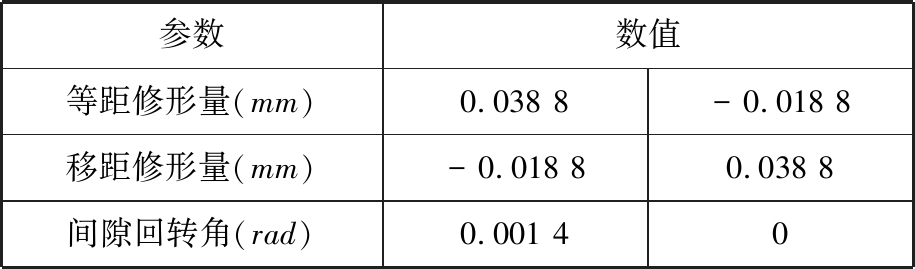
参数数值等距修形量(mm)0.038 8-0.018 8移距修形量(mm)-0.018 80.038 8间隙回转角(rad)0.001 40
由表2可知，通过“负等距+正移距”修形后的摆线轮齿廓相较于通过“正等距+负移距”修形后的摆线轮齿廓，在与标准摆线轮配合传动时，抵消间隙所需要转过的角度(间隙回转角)较小。
根据表2所给的参数，可以作出经过“负等距+正移距”和“正等距+负移距”组合修形方式修形后的齿廓与原齿廓的对比图(图4)。
图4 两种组合修形方式齿廓对比
Fig.4 Tooth profile comparison chart of two combinations of shaping methods
由图4可知，通过“负等距+正移距”组合修形方式形成的摆线轮齿廓相较于通过“正等距+负移距”组合修形方式形成的摆线轮齿廓更接近于标准齿廓。
以表2中的修形量为例，施加相同载荷，对两种组合修形方式修形后的摆线针轮接触应力进行比较，结果如图5所示。
图5 接触应力对比图
Fig.5 Compare figure of contact stress
由图5可知，经过“正等距+负移距”组合修形的摆线轮相较于经过“负等距+正移距”组合修形的摆线轮，在施加相同载荷时，参与啮合的齿数更多，并且各齿受力较小，较均衡，而后者参与啮合的齿数较少，各齿之间受力变化较大。
综上，在保证径向间隙相同的情况下，通过“负等距+正移距”组合修形的摆线轮相较于通过“正等距+负移距”组合修形的摆线轮，在传动时，虽然同时啮合的齿数较少，各齿受力较集中，但是引起的间隙回转角较小，能有效提高RV减速器的传动精度。因此目前主要采用“负等距+正移距”的组合修形方式。
2 接触应力均化的摆线轮修形方法
由于通过转角修形形成的齿廓与标准针轮啮合时，齿根与齿顶处无间隙，在齿廓工作段留有适当的间隙，同时啮合齿轮具有传动平稳性好、同时啮合齿数多、整体刚度大等优点，因此在采用“负等距+正移距”组合修形方式时，以合适的转角修形齿廓为优化目标，在给定径向间隙的条件下使得经过组合修形的齿廓逼近转角修形的齿廓。基于接触应力均化的修形流程如图6所示。
图6 基于齿面接触应力均化流程图
Fig.6 The flow chart of cycloidal wheel based on contact stress equalizatio
2.1 最佳组合修形逼近算法
由式(1)可知，给定初始的转角修形量Δθz，可得到优化目标转角修形齿廓的参数方程点集，记为(xzi，yzi)，同理，根据“负等距+正移距”的修形方式，给定初始等距修形量Δrrp和移距修形量Δrp，可以得到待优化的组合修形齿廓参数方程点集，记为(xci，yci)，如图7所示。
图7 修形量优化示意图
Fig.7 Modification quantity optimization schematic
将摆线轮的主要工作齿廓在x轴方向的投影平均分成k份，转角修形齿廓曲线与组合修形齿廓曲线并不重合，所以在横坐标相同时，纵坐标不一定重合，即令xci=xzi时，yci-yzi≠0，将工作齿廓区间的k个点所对应纵坐标的差值的绝对值求和，再取其平均值，作为评判组合修形齿廓接近转角齿廓的参数。所求平均值越小，两者之间接近程度越高，因此目标函数可以定义为
(13)
定义变量为
采用“负等距+正移距”组合修形方式，初始条件为：m1≤0，m2≥0，m1+m2=Δ。根据以上求解过程，利用MATLAB对修形量进行优化求解。
2.2 确定最优修形区间
在摆线轮与针轮啮合传动过程中，压力角越小，传动效率越高，同时曲柄轴轴承所承受的力越小。
图8所示为压力角在一个啮合周期内变化规律。只有在xj点处压力角取最小值，而啮合时是一个区间，因而要保证该区间内压力角平均值最小，在压力角最小点附近取边界点xb和点xe，保证xe-xb=θw，其中θw为区间的范围，可根据摆线针轮传动时期望共同啮合齿数Nw求得，即
(14)
图8 优化区间示意图
Fig.8 Optimization interval diagram
根据压力角的解析式
a=arctan(dyc/dxc)-arctan(yc/xc)
(15)
可以求得最小压力角处对应的横坐标值xj。在0和xj点之间给定一个初始值xb0，并以它为起点，xb0+θw为终点，设置步长i，计算该区间各点对应压力角和的平均值。遍历0～xj区间，将所得平均值最小的对应起点xb作为摆线轮工作齿廓的起点，则点xe=xb+θw为摆线轮工作齿廓的终点。
2.3 径向间隙和侧隙的确定
摆线轮径向间隙主要影响非工作齿廓的形状；工作段侧隙则要考虑多个因素综合选取，因为它会直接影响RV减速器传动精度、整机刚度以及平稳性等整机性能。
假设弥补摆线轮因加工误差所需的啮合侧隙为cw，弥补因齿轮热变形所需的啮合侧隙为ch，润滑的最小侧隙为cr，假设RV减速器背隙所允许的最大值为rb。由力臂的计算公式可知，在力臂最大处，为满足上述初始条件所需要的最小的转角为
(16)
假定加工误差、热变形、油膜最小厚度很小且为常数，那么Δθz也是一个常量，但是以该转角修形齿廓作为拟合修形目标齿廓时，齿廓受力方式并非是最好的。实际上，Δθz在较小范围内变化时，组合修形拟合得到的等距与移距修形量变化并不明显，回差也变化较小，回转角也只是有微小的变化，并且可以通过后续的转角修形进行弥补。
在初始间隙、优化区间都相同时，以转角修形量分别为Δθz0=0.000 5 rad，Δθz1=0.000 55 rad，Δθz2=0.000 6 rad为例，得到对应的拟合等距和移距修形量如表3所示。
表3 修形量优化求解结果
Tab.3 Theresult of shape modification optimization solution
修形量Δθz0(rad)Δθz1(rad)Δθz2(rad)Δrrp(mm)0.047 60.062 40.077 2Δrp(mm)-0.027 6-0.042 4-0.057 2
进一步将上述得到的拟合等距和移距修形量代入到摆线针轮受力求解方程中，得到摆线轮与针轮的接触应力变化曲线，如图9所示。
图9 接触应力对比图
Fig.9 Compare figure of contact stress
由图9可知，在载荷相同条件下，选择不同的转角修形齿廓作为拟合修形的目标齿廓，优化修形后的摆线轮与标准针轮传动时，同时啮合的齿数以及各齿之间的接触应力分布都有明显的差异，因此需要在转角合理范围内找到一个最佳的Δθz值作为最佳的拟合转角修形量。
假定θz为最佳的转角修形量，代入最优修形区间求解和最优组合逼近算法中，可以得到摆线轮工作齿廓的起点和终点以及最优的拟合等距修形量
和移距修形量
该修形量对应的最小回转角为
λ′=θT
(17)
根据式(16)可知,经组合修形方式得到的摆线轮需的转角修形量为
θz=θT-Δθz
(18)
将上述得到的最优拟合等距修形量和移距修形量
代入到式(1)中，即可得到拟合修行后的摆线轮齿廓方程。
2.4 最佳拟合转角修形量的求解
由于传动时是多个齿同时啮合的，而所有啮合齿的接触应力方差相较于应力平均值变化更加明显，所以采用方差衡量修形的效果。
根据材料的热变形、润滑要求以及整机的背隙等要求，初步选择目标齿廓转角修形的范围为θb～θe。在该区间内任取θi，首先，将θi代入最优区间的确定算法求解出工作齿廓的起点和终点横坐标xb和xe；然后，将xb和xe代入最优组合修形逼近算法中求解出最优拟合等距修形量和移距修形量
最后，将最优拟合等距修形量和移距修形量以及修形区间代入齿面应力求解方程中，即可得到对应转角下的齿面应力，并求出此时同时啮合各齿的接触应力方差。遍历θb～θe区间，选取同时啮合各齿接触应力分布方差最小所对应的转角修形量作为最佳拟合转角修形量。
以θb=0.000 5 rad，θe=0.000 8 rad，初始间隙Δ=0.02 mm为例，将区间划分成n=40等份依次进行搜索，可得到各拟合转角修形量下各组啮合齿的接触应力方差分布如图10所示。
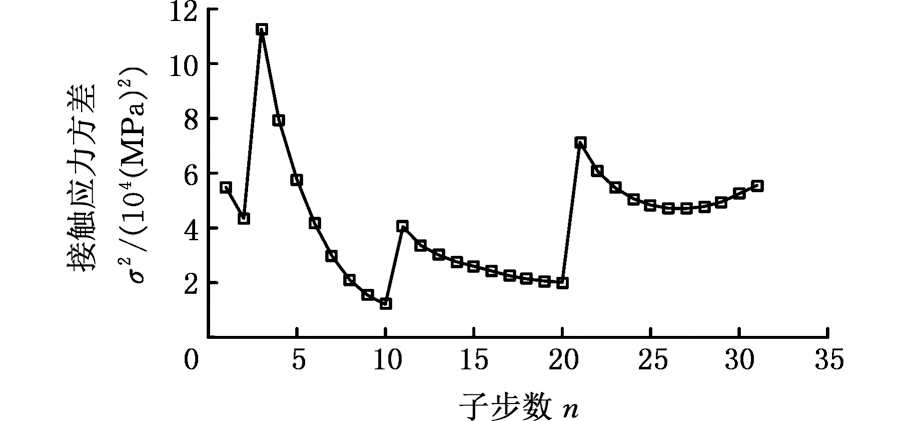
图10 接触应力方差图
Fig.10 Contact stress variance diagram
由接触应力方差图可知，选择不同转角作为修形的目标齿廓，优化后的齿面接触应力是有明显差异的。
3 仿真分析与试验对比
3.1 仿真分析
本文以RV-80E样机为研究对象，对基于接触应力均化的修形方法的理论正确性以及优越性进行验证。各初始条件如表4所示。
表4 求解初始条件
Tab.4 Solving initial conditions
参数数值径向间隙Δ(mm)0.02共同啮合齿数Nw10拟合转角修形量起点θb(rad)0.000 4拟合转角修形量终点θe(rad)0.000 8拟合点数k500子步数n40允许的最小侧隙Δθ0(rad)0.000 5
将表4中的初始条件代入到最佳拟合转角修形量的求解中，得到的各主要参数如表5所示。
表5 主要参数计算结果
Tab.5 The calculation result of main parameter
参数数值齿廓工作段起点xb(rad) 1.710 4齿廓工作段终点xe(rad)3.281 2最优的等距修形量Δr′rp(mm)0.059 4最优的移距修形量Δr′p(mm)-0.039 4对应的最优转角修形量Δθz(rad)0.000 58
同时，根据最佳转角修形量的求解过程，可以得到每个子步对应转角修形量下，摆线针轮传动时同时啮合的齿数以及各齿之间的最大接触应力分布情况，其中摆线针轮传动受力情况与拟合转角修形量之间的关系如图11所示。
图11 啮合齿接触应力分布与拟合转角修形量的关系
Fig.11 Relationship between the contact stress distribution of the meshing teeth and the amount of deformation of the fitted corner
由图11可知，随着转角修形量的增大，经组合修形优化后的摆线轮，在与针轮啮合时，同时啮合的齿数随之增多；在转角修形量不变时，各齿之间的最大接触应力先逐渐增大，达到峰值后，逐渐减小。
为了更直观地比较不同转角修形量对应的齿面应力分布情况，在拟合转角范围内，选取求得的最佳拟合转角修形量前后各一段区间，得到一系列转角修形所对应的接触应力分布图，选取接触应力变化较为明显的对应转角修形量，画出对应拟合转角修形量下的摆线针轮齿面接触应力分布如图12所示。
图12 对应拟合转角下的接触应力分布图
Fig.12 Contact stress distribution figure corresponding to the fitted corner
由图12可知，转角修形量与最佳转角修形量相差越小时，各齿之间接触应力越均衡，转角修形量与最佳转角修形量相差越大，各齿之间的接触应力变化也越大；此外，随着转角修形量的增大，同时啮合的齿数也呈增加趋势。
由于“负等距+正移距”组合修形方式理论上可以满足摆线针轮传动回转角为“0”的条件，因此取Δθz=0，根据表3中的最佳等距和最佳移距修形量，利用最佳拟合转角修形量的求解方法，可以求得此时最佳拟合转角为
θT=5.699 0×10-4 rad
根据式(18)可以得到所需的转角θz为
θz=θT=5.699 0×10-4 rad
图13 齿廓对比图
Fig.13 Tooth profile comparison figure
图14 接触应力对比图
Fig.14 Compare figure of contact stress
将表5中的最优等距和最优移距修形量
代入式(1)中，可以得到基于接触应力均化的摆线轮齿廓。为了进一步与目前主要使用的“负等距+正移距”组合修形方式对比，在保证相同间隙的条件下，取最优负等距与最优正移距修形量代入式(1)中和应力求解方程中，可以作出分别经过两种修形方式后的摆线轮齿廓对比图(图13)和接触应力对比图(图14)。由图13、图14可知，采用基于接触应力均化的修形方式，在保证传动精度的同时，也可以有效改善齿面受力状况。
3.2 试验对比分析
在仿真分析的基础上，采用基于接触应力均化修形方式(参数如表5所示)和传统修形方式(参数如表6所示)修形出摆线轮，然后组装成RV减速器整机进行样机试验。
表6 传统修形方式的参数
Tab.6 Traditional modification method parameters
参数数值齿廓工作段起点xb(rad) 1.710 4齿廓工作段终点xe(rad)3.281 2等距修形量Δr′rp(mm)-0.020 0移距修形量Δr′p(mm)0.030 0
传动误差是RV减速器综合性能的重要指标，本文选用ZRT-Ⅱ型工业机器人减速器试验台(图15)测量样机的传动误差，输入端与输出端均安装有高精度角度传感器，可以实时精确测量输出端与输入端角度变化。
图15 ZRT-Ⅱ型工业机器人减速器试验台
Fig.15 ZRT-Ⅱ industrial robot reducer test bench
传动误差计算公式为
Δθe=(θin-θout)/i0
式中，θin为输入端角度；θout为输出端角度；i0为传动比，样机传动比为121。
在额定转速下，分别测量样机的传动误差，并绘制传动误差与输出角度之间的曲线图，见图16和图17。
图16 传统修形方法的传动误差曲线
Fig.16 Transmission error curve of traditional shaping method
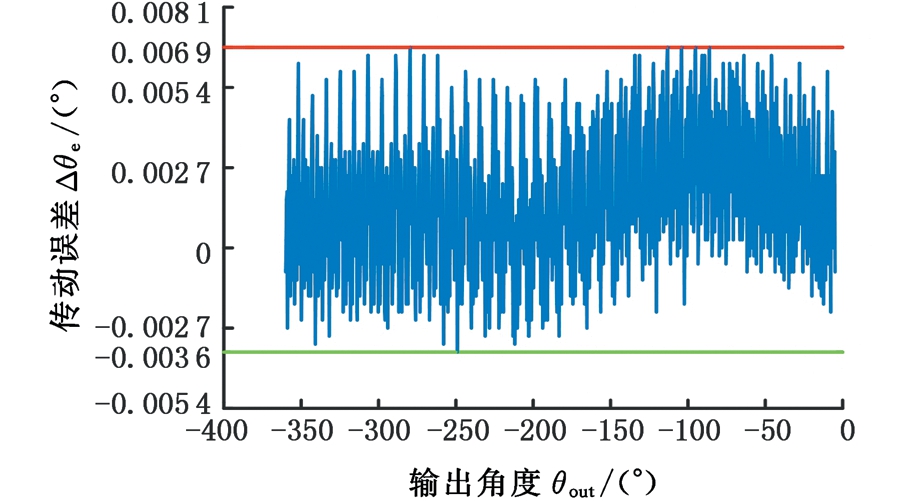
图17 接触应力均化方法的传动误差曲线
Fig.17 Transmission error curve of contact stress equalization method
由传动误差曲线可知，采用传统修形方法的摆线轮传动误差介于-0.004 4°～0.007 2° ，采用接触应力均化修形方法的摆线轮传动误差介于-0.003 6°～0.006 9°。相较于传统修形方式，采用基于接触应力均化的修形方式，能够有效减小传动误差的最大值和最小值，降低RV减速器传动误差的波动范围，有效提高传动的稳定性。
为进一步验证基于接触应力均化修形方法的优越性，将组装好的样机安装在ZRT-IS型垂直寿命试验台上进行试验，试验台如图18所示。
图18 ZRT-IS型垂直寿命试验台
Fig.18 ZRT-IS horizontal life test bench
试验条件设置为：额定转速下以1.2倍额定负载运转。观察RV减速器运行1 000 h 、2 000 h、3 000 h摆线齿廓磨损情况，结果如表7所示。两种修形方式的摆线轮在运行2 000 h、3 000 h的齿廓磨损对比见图19。
由表7和图19可知，采用传统修形方式，齿面磨损严重并且比较集中；采用基于接触应力均化的摆线轮修形方式，能够有效均化齿面受力，极大地改善齿面受力状况，延长摆线轮的有效使用寿命。
表7 齿廓磨损对比
Tab.7 Tooth profile wear comparison
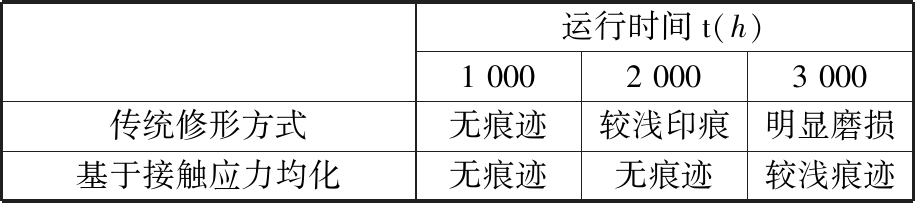
运行时间t(h)1 0002 0003 000传统修形方式无痕迹较浅印痕明显磨损基于接触应力均化无痕迹无痕迹较浅痕迹
(a)基于接触应力均化运行(t=2 000 h) (b)传统修形方式运行(t=2 000 h)
(c)基于接触应力均化运行(t=3 000 h) (d)传统修形方式运行(t=3 000 h)
图19 齿廓磨损对比图
Fig.19 Figure wear tooth profile comparison
4 结论
(1)采用“负等距+正移距”的组合修形方式，以同时啮合各齿之间接触应力分布方差最小为优化目标修形，修形后的啮合齿面接触应力分布均匀，受力状况明显改善。
(2)给出了基于齿面接触应力均化的计算方法，包括最佳转角修形量的求解和对应等距和移距修形量的求解。该算法简单实用。
(3)通过RV-80E仿真以及试验对比分析，验证了该方法的正确性和可行性。相较于传统修形方法，基于齿面接触应力均化的修形方法，可使啮合齿数增加，齿面接触应力明显减小，延长摆线轮的有效使用寿命，降低传动误差。
[1] CHMURAWA M, LOKIEC A. Distribution of Loads in Cycloidal Planetary Gear Cycloid including Modification of Equidistant[C]//Proceedings of the 16th European ADAMS User Conference. Berchtesgaden, 2001: 14-15.
[2] 库特略夫采 В Н. 齿轮减速器的结构与计算[M]. 江耕华，顾永寿，泽. 上海：上海科学技术出版社, 1982.
KUTLOVSCHE B Н. Structure and Calculation of Gear Reducer [M]. JIANG Genghua, GU Yongshou, Trans. Shanghai： Shanghai Science and Technology Press, 1982.
[3] LEHMANN M. Die Berechnung der Kräfteim Trochoiden-Getriebe[J]. Antriebstechnik, 1979, 18(2): 613-616.
[4] 关天民. FA型摆线针轮行星传动齿形优化方法与相关理论的研究[D]. 大连：大连交通大学, 2005.
GUAN Tianmin. Research on Optimization Method and Related Theory of FA Type Cycloid Pinwheel Planetary Transmission[D]. Dalian： Dalian Jiaotong University, 2005.
[5] 王秋成. 摆线轮齿形修整的优化[J]. 浙江工业大学学报, 1989(1):7-16.
WANG Qiucheng. Optimization of Tooth Profile Trimming of Cycloid[J]. Journal of Zhejiang University of Technology, 1989(1): 7-16.
[6] 严勇, 汤子琳. 摆线齿轮最佳复合修正齿形的研究[J]. 重庆大学学报(自然科学版), 1993, 16(5):137-140.
YAN Yong, TANG Zilin. Research on the Best Composite Modified Tooth Profile of Cycloidal Gear[J]. Journal of Chongqing University(Natural Science Edition), 1993, 16(5): 137-140.
[7] 关天民, 张东生. 摆线针轮行星传动中反弓齿廓研究及其优化设计[J]. 机械工程学报, 2005, 41(1):151-156.
GUAN Tianmin, ZHANG Dongsheng. Research and Optimization Design of Anti-bow Profile in Cycloid Pinwheel Planetary Transmission[J]. Journal of Mechanical Engineering, 2005, 41(1):151-156.
[8] 陈振宇. RV减速器的误差建模与摆线齿廓修形[D]. 天津：天津大学, 2014.
CHEN Zhenyu. Error Modeling and Cycloid Profile Reconstruction of RV Reducer [D]. Tianjin： Tianjin University, 2014.
[9] 王新春. 摆线轮齿廓修形及RV减速器设计[D]. 哈尔滨：哈尔滨工业大学, 2017.
WANG Xinchun. Cycloidal Profile Modification and RV Reducer Design [D]. Harbin： Harbin Institute of Technology, 2017.
[10] 洪淳赫. 关于修正摆线轮啮合初始间隙分布规律的探讨[J]. 机械传动, 1991(1):31-34.
HONG Chunhe. Discussion on Correcting the Distribution Law of Initial Clearance of Cycloidal Engagement[J]. Mechanical Transmission, 1991(1): 31-34.
[11] 李力行. 摆线针轮行星传动的齿形修正及受力分析[J]. 大连交通大学学报, 1984, 22(4):32-43.
LI Lixing. Tooth Shape Correction and Force Analysis of Cycloidal Pinion Planetary Transmission[J]. Journal of Dalian Jiaotong University, 1984, 22(4): 32-43.
[12] GUAN T. Optimum Profile Modification on Cycloid Disks in the Cycloid Gearing Mechanism with Small Teeth Difference[J]. China Mechanical Engineering, 2002, 13(10):805-811.
