0 引言
贝叶斯网络(Bayesian network,BN)作为不确定性知识表达和推理中的重要理论模型,已在数据挖掘和故障诊断等领域得到广泛应用[1]。目前故障诊断研究大部分采用批量式算法,该算法对已有数据进行一次性学习得到网络结构,新数据到来时抛弃已有结构,将新旧数据整合到一起,在一个更大的数据集下重新学习,需要较大的存储空间和计算时间,造成了资源浪费,考虑到实际应用中很多数据不断产生,批量式算法已不能满足要求。而增量式算法依次处理数据样本,能够将变化环境中的新采样纳入模式中,且更新在先前基础上完成,是一种以新数据的出现为顺序来更新学习结果的学习方式[2]。
许多学者对批量式算法在故障诊断方面的应用进行了研究。刘彬等[3]提出了一种基于BN的改进结构算法并建立了具有较高诊断准确率的回转窑故障诊断模型,但该模型没有考虑新数据产生时模型结构和参数的变化情况,不具有灵活性;ZHU等[4]提出了一种基于BN的电力系统故障诊断方法,该方法建立了基于简化BN的三元模型,用于输电系统故障区段的估计,新数据到来时需对所有数据进行重新学习,不能适应外界环境变化,说明批量式算法已经不能满足实际应用需求。近年来,部分学者对增量式算法进行了研究。田凤占等[5]将EM(expectation maximization)算法和遗传算法引入增量学习过程,定义新变异算子且扩展传统交叉算子,提出了一种包含隐变量的增量学习算法,提高了学习精度,但该算法在存储空间方面不占优势;ALCOBE[6]提出了一种将批量爬山(hill-climbing,HC)算法转换为增量形式的启发式方法,在一定程度上节省了时间和存储空间;王飞等[7]提出了一种基于遗传算法的增量学习方法,需在时效性和准确率之间折中选择;ZHU等[8]建立了一种基于BN和增量学习的农作物疾病动态诊断的数学模型,但该模型实时性较差;YASIN等[9]对MMHC算法进行改进,得到了一种增量贝叶斯结构学习算法,但该算法不能满足应用需求。考虑到实际应用,随着新数据的增加会出现两种情况:①新旧数据来自同一分布,只需更新参数;②新旧数据来自不同分布,参数偏离稳定,数据与结构表现出不适应,当这种不适应达到一定程度时,则需更新结构。由此增量学习方法可分为两类:一类是结构不变,只进行参数调整;另一类是先更新结构,后更新参数。
针对上述现状,本文将专家知识与数据学习相结合得到原结构和原参数,构造WTUN (whether to update network)函数用于判断新数据集到达时原结构是否改变,若是,则定义Affect函数用于衡量数据对结构中各节点的平均影响程度,利用爬山算子对影响较大节点的马尔可夫毯结构进行修正得到候选结构,利用改进的评分函数选择评分最大的结构作为最优结构,无论结构是否改变均利用EM算法更新参数,得到一种贝叶斯增量学习算法(incremental learning algorithm, ILA)。将该算法应用到篦冷机工艺参数建模中,利用模型分析参数间的影响,对原模型进行增量维护,最后对二次风温进行故障诊断,找出导致故障发生的原因并采取措施,可提升热回收效率从而达到节约能源的目的。
1 ILA算法
1.1 ILA算法的构建
数据学习要求获得大量数据样本,且所得结构不准确,专家知识学习主观性较强,易产生较大误差,将两种方法相结合会相对准确且能提高效率[10],本文结合数据学习与专家知识获得原贝叶斯结构G?,利用最大似然估计(maximum likelihood estimation,MLE)算法学习得到原参数θ?ijk?。
在实际应用中,新数据连续产生,每隔Δt?时间采集一次新数据,将进行批量式学习的数据作为初始旧数据集D?o,可表示为D?o=f?(D?p,t?0);Δt?1时间内产生的数据作为新数据集D?n,而Δt?2时间内新数据到达时将其作为新数据集D?n,Δt?1时间内的数据则作为旧数据,依此类推,学习过程中只保留当前的D?o和D?n,过程如下:
(1)
其中,t?0为初始时间,k?=1,2,…,m?,m?为新数据集的个数。BIC函数如下:
(2)
其中,P?(D?/G?)表示似然概率,即给定结构情况下关于数据的后验概率;q?i?是变量X?i?父节点取值组合的数目;r?i?是变量X?i?取值的数目;N?ijk?是X?i?取k?值、X?i?的父节点取j?值时的样本数目,也称为充分统计因子。由式(2)可以判断数据与结构的拟合程度,其实质是对每个样本在结构中有相互影响关系的变量条件概率的求和[11],依据其思想,构建WTUN函数:
WTUN?(D?|G?)=
(3)
依据马尔可夫毯原则[12]对式(3)进行化简。在BN中节点x?i?的马尔可夫毯结构包括它的父节点、子节点及子节点的父节点,当节点x?i?的马尔可夫毯给定时,在该网络中x?i?与其他变量条件独立,因此,网络中的条件概率可化简为
P?(x?i?|x?1,x?2,…,x?i?-1,x?i?+1,…,x?n?)=
P?(x?i?|MB?(x?i?))
(4)
依据乘法公式,可将式(4)变换为
P?(x?i?|MB?(x?i?))=P?(x?i?,MB?(x?i?))/P?(MB?(x?i?))
(5)
由于式(5)中P?(MB?(x?i?))不包含x?i?,即无论x?i?取何值,P?(MB?(x?i?))的取值相同,视为常量,根据随机变量形式链式规则,将式(5)化简为
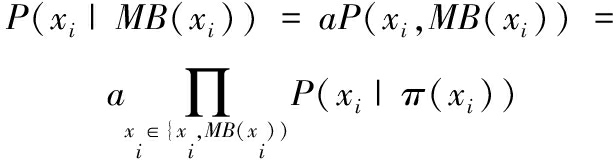
(6)
根据马尔可夫毯原则将式(6)中的![]() 分成3部分,由于其他节点的条件概率项与节点x?i?无关,可视为常量,故式(6)可化简为
分成3部分,由于其他节点的条件概率项与节点x?i?无关,可视为常量,故式(6)可化简为
P?(x?i?|MB?(x?i?))=bP?(x?i?|π?(x?i?))·
(7)
式中,P?(x?i?|π?(x?i?))为x?i?的条件概率;![]() 为x?i?子节点的条件概率。
为x?i?子节点的条件概率。
将式(7)代入式(6),再代入式(4)可得
(8)
式中,π?(x?i?)为节点x?i?的父节点;x?j?为贝叶斯结构中节点x?i?的子节点;π?(x?j?)为节点x?i?的子节点的父节点。
由式(8)可看出,WTUN函数是对结构中有相互影响关系变量的条件概率的求和,与BIC函数计算结果相比,只是某些概率项的系数有所增大,故可用于判断数据与原结构的拟合程度。对于给定的D?o、D?n,以及正数阈值β?∈[0,1],若
(9)
则需更新结构,否则只更新参数。
若式(9)不成立,即原结构不需要调整,只需对BN进行参数学习,根据EM算法思想[13],将原参数变为先验参数,将以下结果作为新的参数:
(10)
式中,![]() 为先验参数;
为先验参数;![]() 为增量数据的充分统计因子。
为增量数据的充分统计因子。
若式(9)成立,则需要进行结构调整,在新的结构上更新参数。构造Affect函数,计算当前数据对各节点的平均影响程度,给定阈值δ?,存储并记录Affect值大于阈值δ?的节点集S?,通过爬山算子S?中各节点的马尔可夫范围进行修正,得到候选结构集G?q,利用改进评分函数对G?q进行评分,选取评分最高的结构作为最优结构G?good,并利用式(10)更新参数,完成BN的增量维护。
已知P?(D?n|G?)可以体现新数据与原结构的拟合程度,新数据对G?的所有影响由P?(D?n|G?)的变化相对于参数θ?ijk?的变化组成[14],则当前数据对原结构中各节点的平均影响表示为
(11)
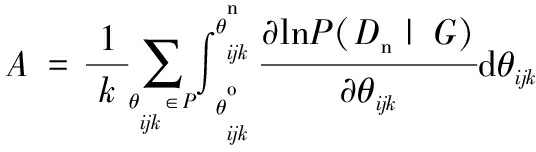
式中,A?为新数据对原结构每个节点的平均影响;B?为原数据对原结构每个节点的平均影响。
对A?进行化简,有
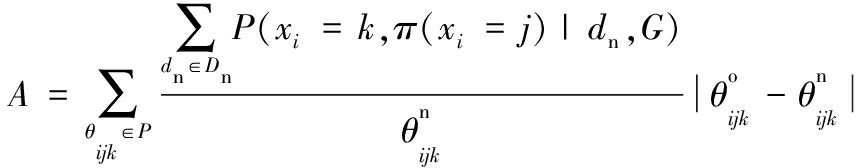
(12)
其中,d?n为新数据集样本个数;P?为结构对应的条件概率集,又已知
则式(12)可化简为

(13)
同理可得B?,则Affect函数表达式为

(14)
θ?ijk?=P?(X?i?=k?|π?(X?i?=j?))
式中,![]() 为原数据集的充分统计因子;k?为该节点条件概率表中概率的个数;α?为新数据集所占比率。
为原数据集的充分统计因子;k?为该节点条件概率表中概率的个数;α?为新数据集所占比率。
利用式(14)计算每个节点的Affect值,给定阈值δ?,存储并记录Affect值大于阈值δ?的节点集S?,利用增加弧、反转弧、删除弧三种操作集合op?={op?(1),op?(2),…,op?(k?)}修正S?中每个节点的马尔可夫毯结构,得到候选结构集:
G?q?=op?(j?)(MB?(S?i?))
(15)
式中,op?(j?)为3种操作之一;MB?(S?i?)为节点集S?中某个节点的马尔可夫毯结构。
对G?q中的结构进行评分:

(16)
式中,N?n、N?o分别为新旧数据的数量;λ?为调整新旧数据学习速度及趋势的因素,如果新数据与原结构不匹配,则λ?增大,否则λ?减小;g?为结构集G?q中的个体;pen?(g)为结构g?的惩罚函数,防止数据与结构的过度拟合。
选取G?q中评分最大的结构作为最优增量结构G?good,即
(17)
得到G?good后,利用式(10)更新参数,完成BN的增量学习过程。
1.2 ILA算法实现
ILA算法的流程图见图1。对ILA算法分步进行简要描述,算法步骤如下:

图1 ILA算法流程图
Fig.1 The flow chart of ILA algorithm
(1)输入初始数据集、批量式算法与专家知识结合获得原贝叶斯结构G?,利用MLE算法学习得到原参数;
(2)检测到新数据,利用WTUN函数判断G?是否改变,若是则转步骤(3),否则利用EM算法更新参数,转步骤(6);
(3)利用Affect函数找到数据对节点影响大的节点集S?,并得到每个节点的马尔可夫毯结构的集合G?p;
(4)在原结构中利用op?(j?)对步骤(3)得到的G?p中的结构进行修改,得到候选结构集G?q;
(5)使用Score函数对步骤(4)中的每个候选结构进行评分,以评分最大的结构作为增量结构G?good,利用EM算法更新参数;
(6)输出增量学习后的结构和参数。
2 ILA算法的仿真实验
2.1 WTUN函数有效性验证
有新数据的WTUN函数值越大,说明贝叶斯网络对新数据的拟合程度越好,随着新数据的增加,与新旧结构的WTUN值在不断变化,若与新结构的相适性越来越好,则可将WTUN函数用于判断数据与结构拟合程度的可行性。
利用经典Asia、Car及Alarm网络进行仿真验证,以Asia网络为例,其标准网络如图2所示。利用Netica软件的smulate cases功能生成8000组数据作为原数据集D?o,修改概率分布表,在不产生环路的条件下,删除和增加一定数量的边后得到的网络如图3所示,用同样的方法再产生8000组数据作为新数据集D?n,部分数据结果见表1。

图2 原Asia网络
Fig.2 The original Asia network
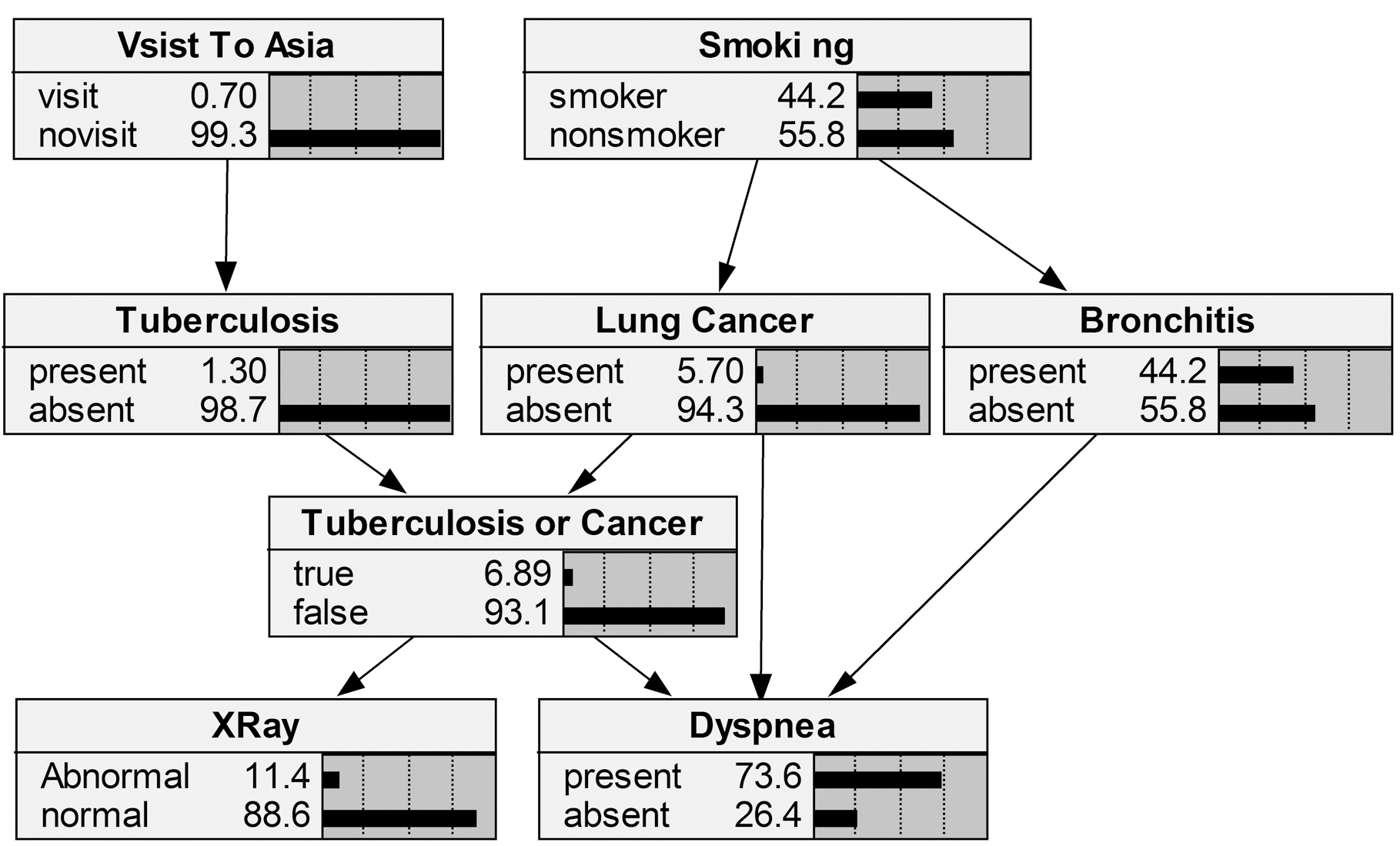
图3 新Asia网络
Fig.3 The new Asia network
表1 Asia网络部分数据举例
Tab.1 Some data samples in Asia

IDnumTuberculosisXRayTbOrCaCancerDyspneaBronchitisVisitAsiaSmoking1absentnormalfalseabsentabsentabsentno_visitnon_smoker2absentabnormalfalsepresentpresentpresentno_visitsmoker3presentabnormaltrueabsentpresentabsentno_visitsmoker4absentabnormaltruepresentpresentabsentno_visitsmoker5absentnormalfalseabsentabsentabsentvisitnon_smoker………………………
对图2所示的网络,分别加入0~100%的新数据,随着新数据的增加,分别计算含不同比例新数据下的WTUN?(D?n|G?)及WTUN?(D?n|G?n),对Car、Alarm与Asia进行相同操作,WTUN值的变化情况分别如图4和图5所示。

图4 WTUN值随原结构变化情况
Fig.4 The WTUN value varies with the original structure

图5 WTUN值随新结构变化情况
Fig.5 The WTUN value varies with the new structure
由图4可知,随新数据的增加,与原结构的WTUN值越来越小,即数据与原结构的适应性越来越差。由图5可知,与新结构的WTUN值越来越大,即数据与新结构的拟合程度越来越好,而且变化比较平稳,从而验证了WTUN函数的有效性。
2.2 Affect函数正确性验证
利用Asia网络验证Affect函数的正确性。同样利用图2所示网络作为原网络,生成2 000组原数据,利用图3所示网络作为新网络,生成8 000组新数据,即考虑10 000组数据中含20%原数据和80%新数据的情况,说明α?的值为0.8。利用式(14)计算数据对原网络各个节点的Affect值,并给定阈值δ?为1,以节点Bronchitis为例说明式(14)的具体计算过程,该节点的原参数与新参数的学习结果分别见表2和表3。
当Bronchitis=present,Smoking=smoker时,节点Bronchitis的Affect值为
表2 节点Bronchitis的原条件概率
Tab.2 The original conditional probability ofnode Bronchitis

Smoking=smokerSmoking=nonsmokerBronchitis=present0.60.4Bronchitis=absent0.30.7
表3 节点Bronchitis的新条件概率
Tab.3 The new conditional probability of node Bronchitis

Smoking=smokerSmoking=nonsmokerBronchitis=present0.57240.4276Bronchitis=absent0.33870.6613
其中,497和156分别为D?o与D?n中满足Bronchitis=present、Smoking=smoker的样本数量。同理可计算另外3种情况下的数值,这4个值求和的结果即节点Bronchitis的Affect值。因此,可得到每个节点的Affect值,结果见表4。
表4 Asia网络中数据对各节点的影响情况
Tab.4 The influence of data on each node in Asia network

节点及简称Affect值与阈值相比是否要修改与原结构对比是否判断正确Visit To Asia(v)1.862是否Smoking(S)39.467是是Tuberculosis(T)2.474是是Lung Cancer(L)2.5888是是Bronchitis(B)12.396是是Tuberculosis or Bronchitis(O)0.032否否XRay(X)0.24否是Dyspnea(D)185.7682是是
由表4结果可知,Affect函数判断数据对结构影响度的准确率为75%。为了排除数据的偶然性,在上述条件下进行20次试验取平均值,最终得到准确率为72.5%,由此可以验证Affect函数的正确性。
2.3 增量学习算法有效性仿真证明
在Affect函数正确性验证实验中,由表4可知,当加入8 000组新数据时,根据Affect值大小判断需要修正的节点分别为D?、S?、B?、v?、L?、T?,对这些节点马尔可夫毯结构用爬山算子进行修改,利用Score函数进行评分,得到评分最大的最优网络结构,如图6所示。

图6 ILA算法得到的最优结构
Fig.6 Optimal structure obtained by incremental algorithm
考虑评分比值、Log-less比值、时间比值3个指标,将ILA算法分别与批量爬山、增量爬山(incremental hill-climbing,IHC)算法[6]进行学习结果质量以及时间消耗两方面的仿真对比分析。通过Nursery网络,Alarm网络生成的数据集对算法进行仿真,对每组数据集独立运行算法 20 次,运行结果见表5和表6。评分比值、Log-less比值、时间比值定义分别为
(18)
(19)
(20)
其中,*代表与ILA对比的算法,Log-less值的计算公式为![]() 代表数据集,P?B(d?)代表学习到贝叶斯网络的预测概率,D?test为采样的数据集。
代表数据集,P?B(d?)代表学习到贝叶斯网络的预测概率,D?test为采样的数据集。
表5 ILA与HC算法学习质量与时间消耗对比
Tab.5 Comparison of the quality of learning results andtime consumption between ILA and HC algorithm

数据集评分比值Log-less比值时间比值Nursery网络20 0000.9891.0010.281 710 0000.9911.0000.605 25 0000.9841.0030.785 7Alarm网络20 0000.9931.0020.547 210 0000.9881.0000.769 05 0000.9911.0010.863 2
表6 ILA与IHC算法学习质量与时间消耗对比
Tab.6 Comparison of the quality of learning results andtime consumption between ILA and IHC algorithm
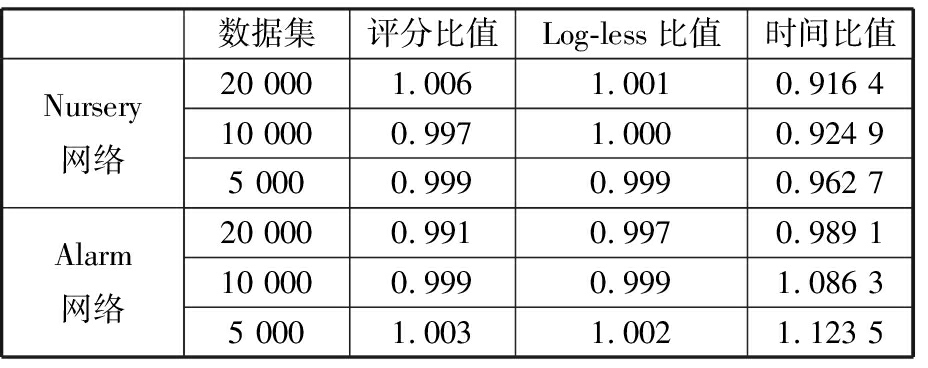
数据集评分比值Log-less比值时间比值Nursery网络20 0001.0061.0010.916 410 0000.9971.0000.924 95 0000.9990.9990.962 7Alarm网络20 0000.9910.9970.989 110 0000.9990.9991.086 35 0001.0031.0021.123 5
由表5和表6可看出ILA算法与批量HC算法及增量IHC算法的评分比值和Log-less比值很接近,说明本文所提算法与HC算法、IHC算法学习到的结构质量相当。时间比值与1相差越大,则ILA算法的时间越占优势,表5表明本文所提算法相比批量式算法明显减少了时间消耗,且数据量越大,本文算法的时间消耗越有优势。表6表明ILA算法与IHC算法的时间消耗相当,个别情况稍逊于IHC算法。
根据Alarm网络生成的训练数据,分别读入k?为500、1 000个事例进行一次增量学习,分别比较ILA算法与HC算法、增量遗传算法(incremental genetic algorithm,IGA)[7]的存储量,如图7所示。

图7 三种算法的存储量对比
Fig.7 The comparison of the storage capacity ofthree algorithms
由图7可以看出,批量HC算法的存储量随事例数的增大呈线性增长,这是因为批量HC算法每次要将新旧数据合在一起重新学习,IGA 需要的存储量先上升达到一个顶峰后下降的过程,虽然后期存储量趋于常数,但前期存储量较大,而本文所提算法通过Affect函数判断出新数据对原结构哪些节点影响大,只对这些节点进行了局部修改,极其有效地提高了效率,减少了存储空间,存储开销优于HC与IGA算法。综上所述,ILA算法是有效的。
3 篦冷机工艺参数建模及故障诊断
篦冷机是新型干法水泥生产线的关键设备,担负着出窑熟料的冷却、输送和热回收任务[15],其工作状态直接影响到水泥厂的效益及水泥用户的利益,但其工艺参数较多且影响错综复杂,且故障具有很大不确定性,人工排查方式效率很低。由于BN强大的推理能力及方便的决策机制,故将ILA算法应用到篦冷机熟料换热系统,对诊断模型进行维护。首先根据篦冷机原理确定BN的变量,其次结合专家知识与数据学习建立篦冷机原始模型,然后利用ILA算法的增量机制更新初始模型,最后利用变量消元算法进行故障诊断。
3.1 变量选取与工艺参数建模
篦冷机结构如图8所示,根据其工艺原理选取变量,其范围与状态分类的对应关系见表7。利用MATLAB对这8个参数的数据进行离散化处理,然后通过专家知识与SHC算法[16]结合的方法建立原始模型,利用EM算法对所建立的结构和原数据进行参数学习,得到原始模型,如图9所示。

图8 篦冷机结构示意图
Fig.8 Schematic diagram of grate cooler
表7 变量范围与变量状态分类的对应关系
Tab.7 Range of variables and correspondence ofvariable state classification
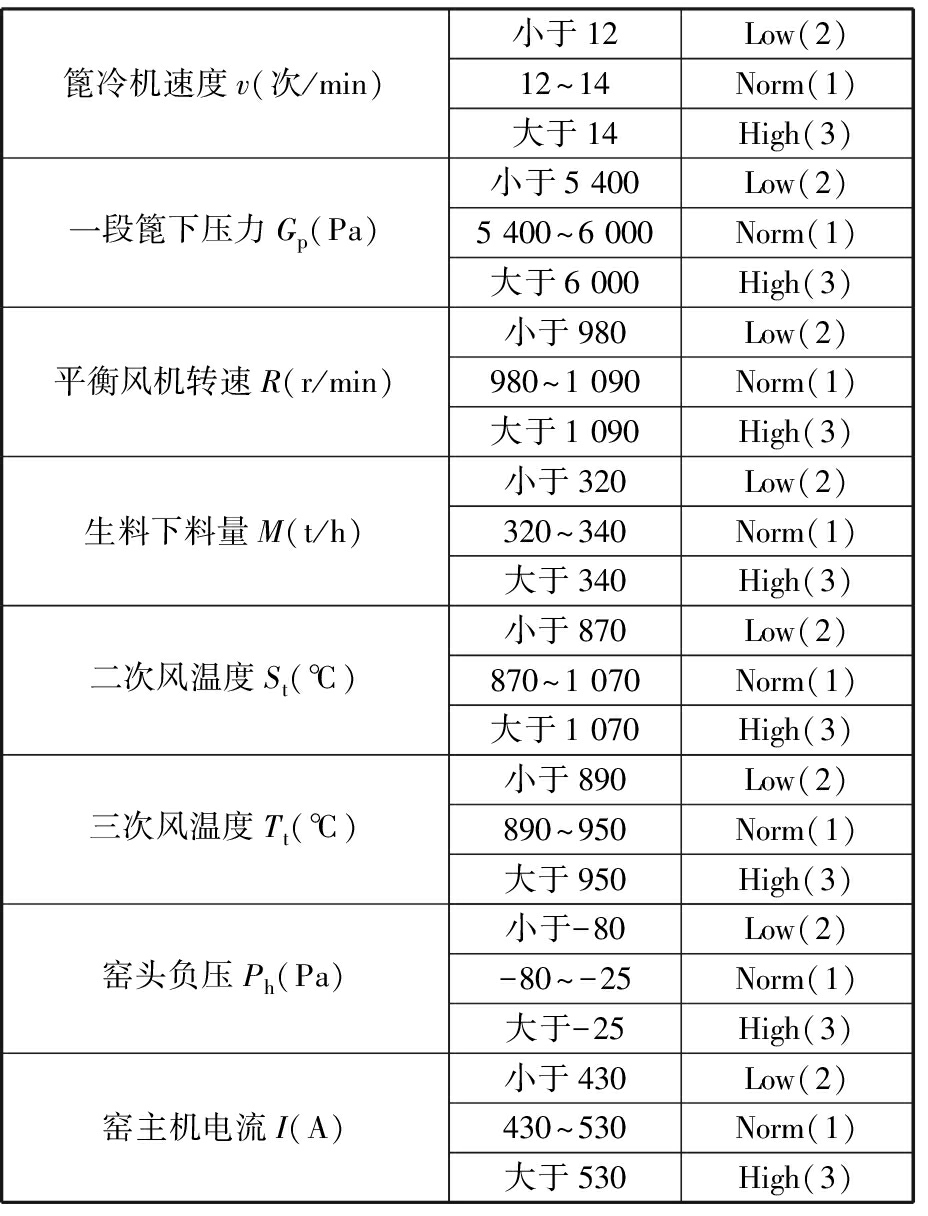
篦冷机速度v(次/min)小于12Low(2)12~14Norm(1)大于14High(3)一段篦下压力Gp(Pa)小于5 400Low(2)5 400~6 000Norm(1)大于6 000High(3)平衡风机转速R(r/min)小于980Low(2)980~1 090Norm(1)大于1 090High(3)生料下料量M(t/h)小于320Low(2)320~340Norm(1)大于340High(3)二次风温度St(℃)小于870Low(2)870~1 070Norm(1)大于1 070High(3)三次风温度Tt(℃)小于890Low(2)890~950Norm(1)大于950High(3)窑头负压Ph(Pa)小于-80Low(2)-80~-25Norm(1)大于-25High(3)窑主机电流I(A)小于430Low(2)430~530Norm(1)大于530High(3)

图9 篦冷机原始模型
Fig.9 Original model of grate cooler
3.2 基于ILA算法的诊断模型更新
在原始模型的基础上,检测到新数据时,利用ILA算法,加入1 000组新数据和加入10 000组新数据时的学习结果分别如图10、图11所示,实现了诊断模型的更新。
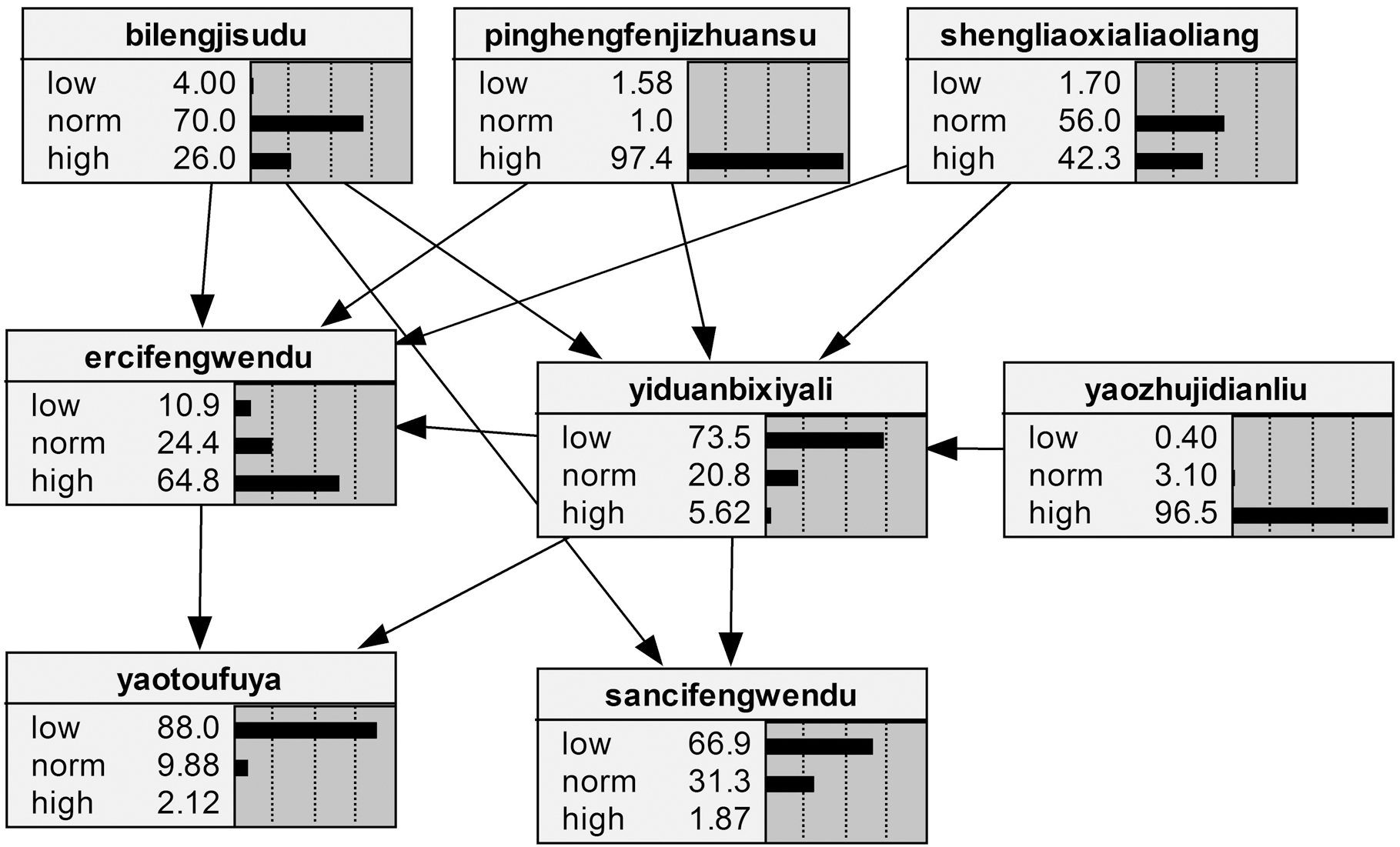
图10 加入1 000组新数据时增量学习结果
Fig.10 Incremental learning results when adding1 000 new sets of data

图11 加入10 000组新数据时增量学习结果
Fig.11 Incremental learning results when adding10 000 new sets of data
由图10和图11可以看出,1 000组新数据不足以引起结构的改变,只是参数进行了更新,而加入10 000组新数据则引起了结构的变化,同时参数也发生改变。根据初始模型,利用ILA、IHC算法进行增量学习,利用SHC算法进行批量学习得到的诊断模型如图12~图14所示。由图12~图14可知:利用SHC得到的诊断模型偏差较大,如忽略了喂料量对二次风温的影响,错误添加了二室风温对二室篦下压力的影响。
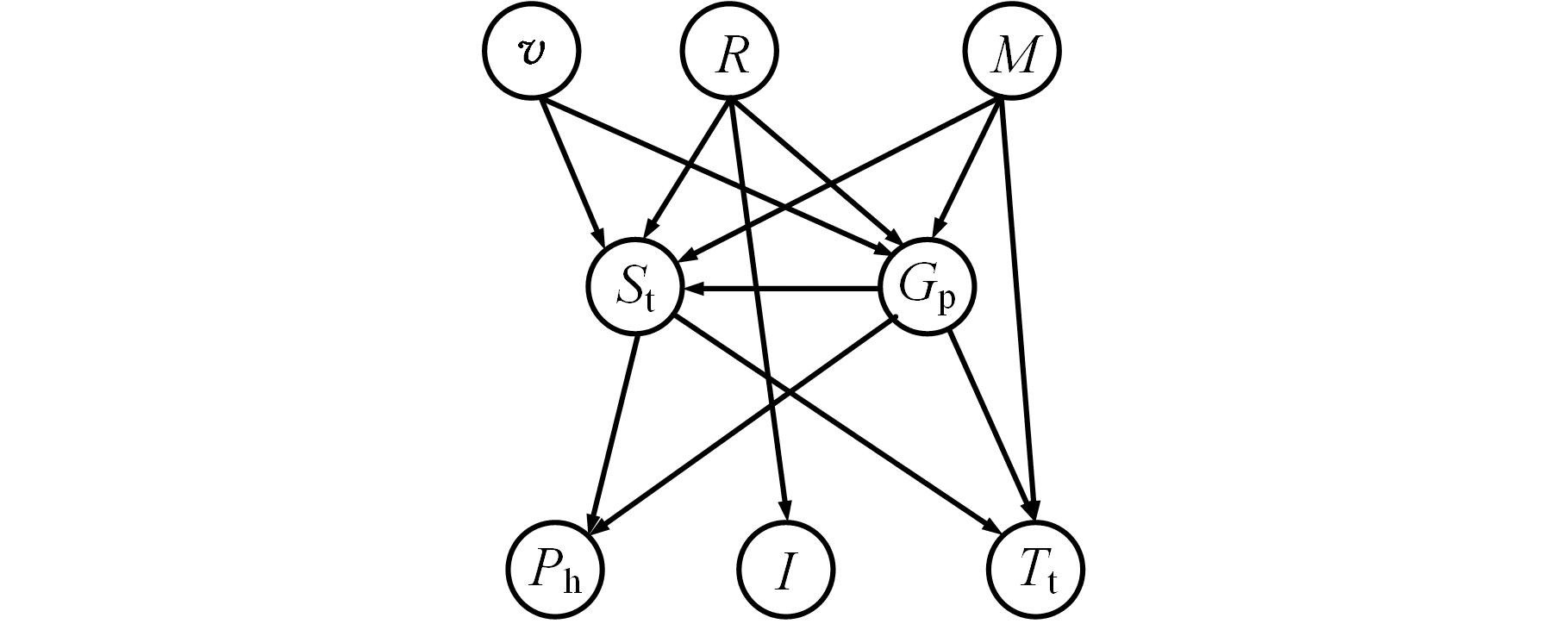
图12 利用ILA算法得到的诊断模型
Fig.12 Diagnosis model based on ILA algorithm

图13 利用IHC算法得到的诊断模型
Fig.13 Diagnosis model based on IHC algorithm
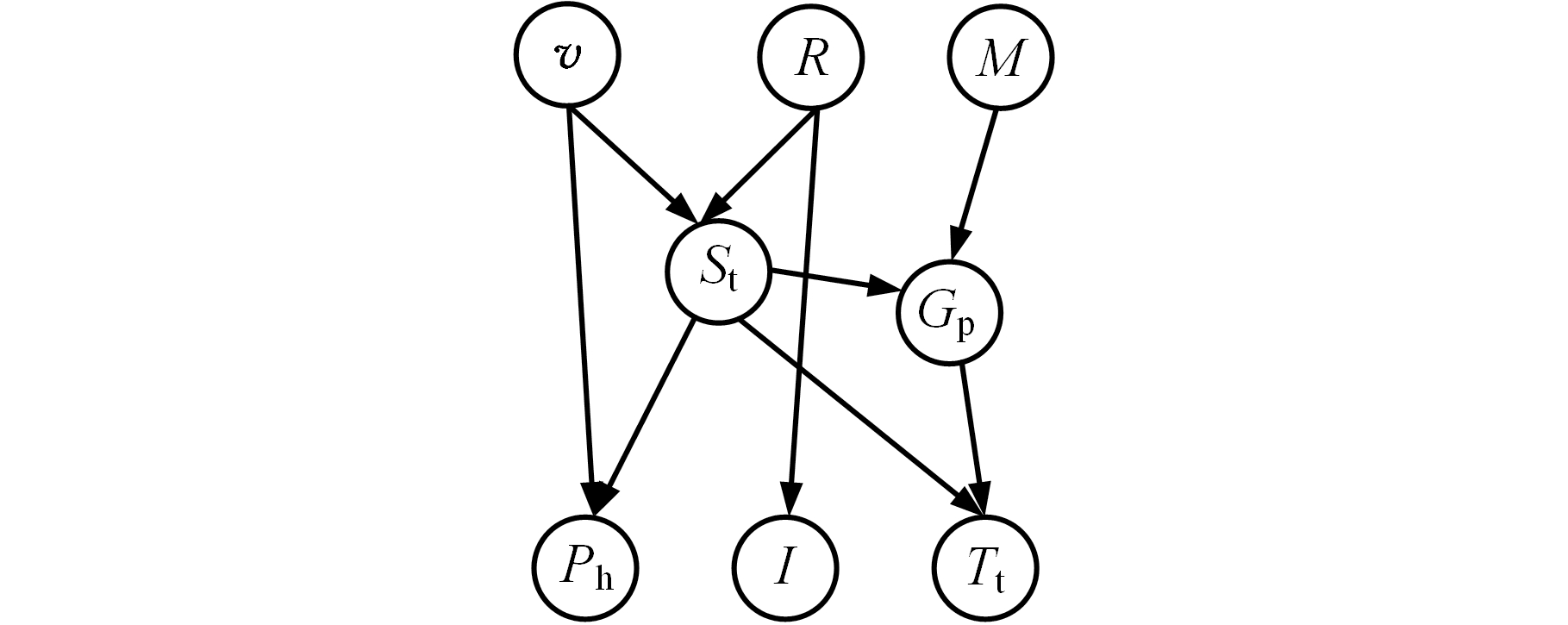
图14 利用SHC算法得到的诊断模型
Fig.14 Diagnosis model based on SHC algorithm
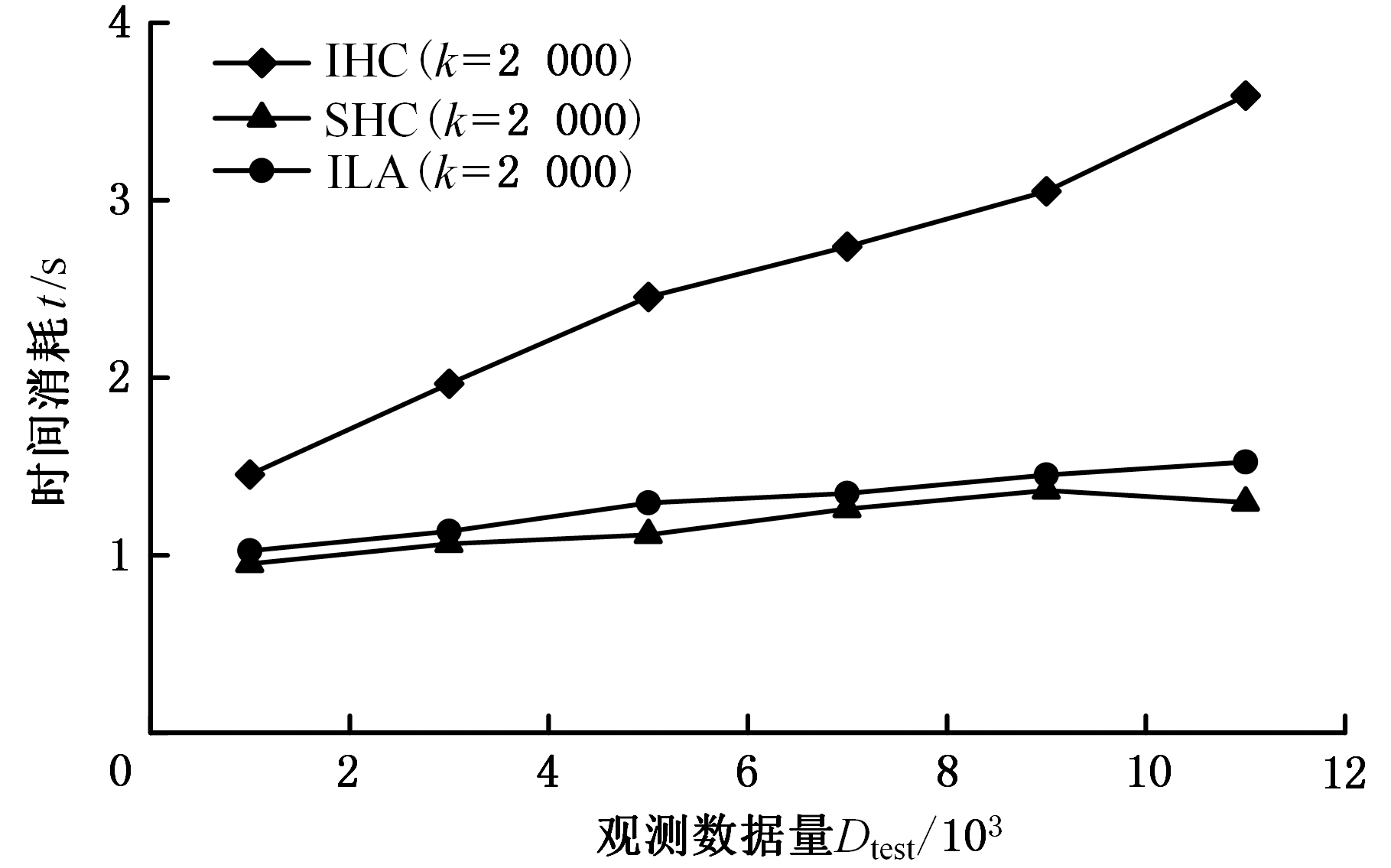
图15 三种算法得到篦冷机结构的时间消耗
Fig.15 Comparison of the three algorithms for the timeconsumption of the structure of the grate cooler
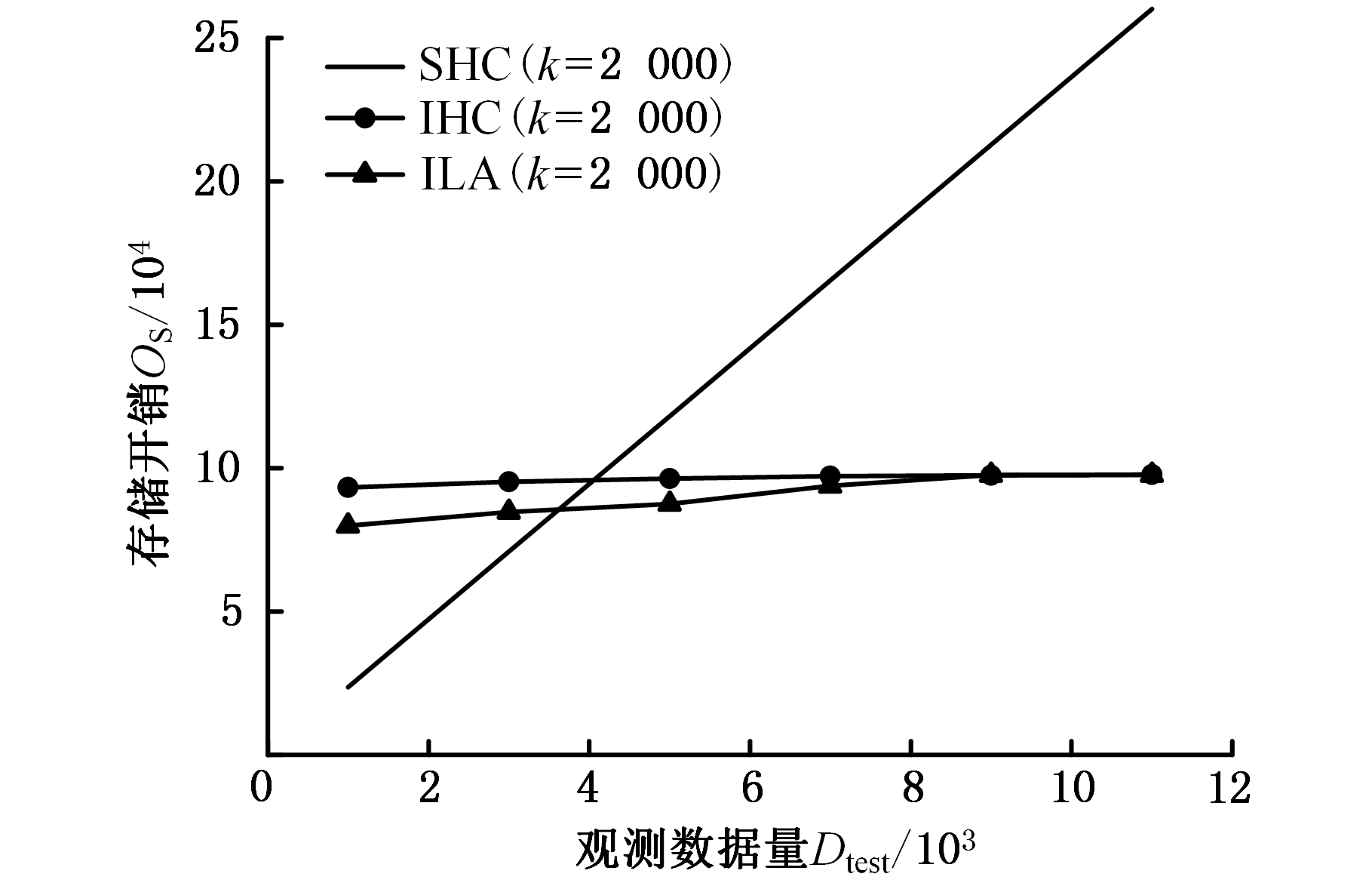
图16 三种算法得到篦冷机结构的存储量
Fig.16 Comparison of the three algorithms for thestoragecapacity of the structure of the grate cooler
3种算法得到的模型的运行时间以及存储开销对比如图15、图16所示。由图15、图16可知,在篦冷机熟料换热系统中,随着数据量的增大,批量式SHC算法的运行时间越来越长,存储量呈线性增长,而增量ILA算法时间消耗增加不明显,稍逊于增量IHC算法,虽然开始存储量稍逊于IHC算法,但当观测数据量达到8 000左右时,与IHC算法相当,基本可以满足要求。
3.3 熟料二次风温故障诊断
二次风温是篦冷机的重要参数,由篦下高压冷却风机与高温熟料进行热交换得到,二次风在窑头负压作用下,进入回转窑供窑内燃烧,二次风温偏低会使热回收效率变差,造成燃料煤的大量浪费,同时产生大量废气污染环境,提高二次风温可、节省燃煤,达到节约能源的目的。如监测到二次风温忽然偏低,由图12可知导致二次风温忽然偏低的原因为V?、R?、M?及G?p,以10 000组数据为例,利用变量消元法计算后验概率:
α?(0.0648 0.1174 0.8178)
α?(0.3524 0.2191 0.4285)
![]() =
=
α?0.2416 0.6545 0.1039
![]() =
=
α?0.3248 0.2159 0.4393
通过比较后验概率α?可知,二次风温忽然降低是由篦速偏高导致的,应及时减小篦速,最大程度上减少燃煤的浪费与氮氧化物等污染废气的排放。从数据集中筛选出满足二次风温偏小征兆的数据1 000、3 000、5 000、8 000组进行测试性诊断实验,记录每一组数据对应的诊断结果,部分验证结果见表8。
表8 ILA算法的部分验证结果
Tab.8 Partial verification results of ILA algorithm

序号二次风温篦速诊断结果1St=2R=3正确2St=2R=3正确3St=2R=1错误4St=2R=3正确
由诊断结果可得到各算法在每一组测试集的正确诊断故障数:
H?=D?ture/D?test
(21)
其中,H?为正确诊断率;D?ture为诊断正确的数据数;D?test为测试集大小。最终得到3种算法对比结果,如图17所示。由图17可知:在每组测试数据中,利用ILA对二次风温进行故障诊断的准确率要高于SHC算法以及IHC算法,能够基本满足实际生产中二次风温故障诊断的需求。

图17 三种算法诊断准确率对比
Fig.17 Comparison of diagnostic accuracy of three algorithms
4 结论
仿真实验结果表明,ILA算法能有效完成网络更新,一定程度上节省了时间和存储空间,在真实数据环境下建立的篦冷机诊断模型具有较高的诊断准确率,避免了由于二次风温故障诊断不及时导致的浪费资源、污染环境等问题,为篦冷机换热系统故障诊断提供了新的思路。
[1] 杨昌昊,竺长安,胡小建. 基于贝叶斯网的复杂系统故障诊断方法[J].中国机械工程,2009, 20(22):2726-2732.
YANG Changhao,ZHU Chang’an,HU Xiaojian.Methods on Complex System Fault Diagnosis Based on Bayesian Network[J].China Mechanical Engineering,2009, 20(22): 2726-2732.
[2] SAMET S, MIN A, GRANGER E, et al. Incremental Learning of Privacy-preserving Bayesian Networks [J].Appl. Soft Comput., 2013, 13(8): 3657-3667.
[3] 刘彬, 刘永记, 刘浩然, 等. 基于贝叶斯改进结构算法的回转窑故障诊断模型研究[J].中国机械工程, 2017, 28(18): 2143-2151.
LIU Bin, LIU Yongji, LIU Haoran, et al.Research on Fault Diagnosis Model of Rotary Kiln Based on Improved Bayesian Structure Algorithm[J].China Mechanical Engineering, 2017, 28(18): 2143-2151.
[4] ZHU Y, LIMIN H, LU J. Bayesian Networks-based Approach for Power Systems Fault Diagnosis[J]. IEEE Transactions on Power Delivery, 2006, 21(2): 634-639.
[5] 田凤占, 黄丽, 于剑, 等. 包含隐变量的贝叶斯网络增量学习方法[J]. 电子学报, 2005, 33(11): 1925-1928.
TIAN Fengzhan, HUANG Li, YU Jian, et al. Incremental Learning Method for Bayesian Networks with Hidden Variables[J]. Journal of Electronics, 2005, 33(11): 1925-1928.
[6] ALCOBE J R. An Incremental Algorithm for Tree-shaped Bayesian Network Learning[C]// Eureopean Conference on Artificial Intelligence.Lyon, 2002:350-354.
[7] 王飞, 刘大有, 王淞昕. 基于遗传算法的Bayesian网结构增量学习的研究[J]. 计算机研究与发展, 2005, 42(9): 1461-1466.
WANG Fei, LIU Dayou, WANG Songxin.Research on Incremental Learning of Bayesian Nets Based on Genetic Algorithm[J].Computer Research and Development, 2005, 42(9): 1461-1466.
[8] ZHU Y, LIU D, CHEN G, et al. Mathematical Modeling for Active and Dynamic Diagnosis of Crop Diseases Based on Bayesian Networks and Incremental Learning [J]. Mathematical & Computer Modelling, 2013, 58(3/4): 514-523.
[9] YASIN A, LERAY P. Incremental Bayesian Network Structure Learning in High Dimensional Domains[C]// International Conference on Modeling, Simulation and Applied Optimization. Hammamet, 2013:1-6.
[10] 慕春棣, 戴剑彬, 叶俊. 用于数据挖掘的贝叶斯网络[J].软件学报, 2000, 11(5): 660-666.
MU Chunli, DAI Jianbin, YE Jun.Bayesian Networks for Data Mining[J].Journal of Software, 2000, 11(5): 660-666.
[11] LI S H, ZHANG J, SUN B L, et al. An Incremental Structure Learning Approach for Bayesian Network[C]// Control and Decision Conference.Changsha, 2014:4817-4822.
[12] MADDEN M G. Evaluation of the Performance of the Markov Blanket Bayesian Classifier Algorithm[R]. Galway: National University of Ireland, 2002.
[13] 王宝帅, 杜兰, 和华,等. 基于复高斯模型的样本缺失窄带雷达信号重构算法[J]. 电子与信息学报, 2015, 37(5): 1065-1070.
WANG Baoshuai, DU Lan, HE Hua, et al.Reconstruction Algorithm of Narrowband Radar Signals with Missing Samples Based on Complex Gauss Model [J]. Journal of Electronics and Information, 2015, 37(5): 1065-1070.
[14] YUE K, FANG Q, WANG X, et al. A Parallel and Incremental Approach for Data-intensive Learning of Bayesian Networks[J]. IEEE Transactions on Cybernetics, 2015, 45(12): 2890-2904.
[15] 王美琪, 刘彬, 闻岩,等. 篦冷机内水泥熟料温度的软测量[J].机械工程学报, 2016, 52(6): 159-165.
WANG Meiqi, LIU Bin, WEN Yan, et al. Soft Measurement of Cement Clinker Temperature in Grate Cooler[J]. Journal of Mechanical Engineering, 2016, 52(6): 159-165.
[16] 刘浩然, 吕晓贺, 李轩,等. 基于Bayesian改进算法的回转窑故障诊断模型研究[J].仪器仪表学报, 2015, 36(7): 1554-1561.
LIU Haoran, LYU Xiaohe, LI Xuan, et al. An effective Inference Algorithm for Fault Diagnosis[J].Control and Decision, 2015, 30(11): 2033-2040.
