0 引言
天线作为宇航探测、导航定位、气象分析等领域中数据信息交互的重要设备,应用范围十分广泛[1]。并联机构因其结构紧凑、比刚度大、承载能力强、运动惯性小、不存在累积误差等特点[2]在天线领域有其独特应用[3]。
文献[4]采用Stewart并联机构作为大型射电望远镜支撑架,分析了该机构的指向精度。文献[5]将Stewart并联机构应用于上海65 m射电望远镜天线副反射面调整系统。世界上最大的单口径射电望远镜——500 m口径球面射电望远镜(FAST)[6],其馈源舱也是通过Stewart并联平台驱动。文献[7]研究了影响Stewart并联机构用于天线座架的主要因素,并设计了相关构型。
从工作运动需求方面考虑,天线多为俯仰及方位运动,即要求在0°~360°方位、0°~90°俯仰范围内连续可调,两转动并联机构即可实现,两转一移三自由度并联机构则更为合适。而相较于Stewart六自由度并联机构,少自由度并联机构自由度少于6,分支及构件数目减少,结构更为简单、制造成本更低,易于保证高可靠性。文献[8]采用3-RPS(R为转动副,P为移动副,S为球面副)并联机构作为天线支撑机构。文献[9]提出了3-RSR并联机构用作卫星天线支撑的方案。目前,并联机构在天线领域已有应用,但多见于地面基站,机构定平台与基座固连,而考虑基座运动的并联车载天线机构研究尚不充分[10]。车载天线在其运行过程中,固定于车体的天线基座随车辆行驶而运动,同时随地面路况的变化而振动,振动频率变化[11]会对天线运动精度及其动态特性产生影响,这种影响对高精度、高速度、高可靠性的天线而言是不容忽视的[12-13]。
动力学模型是进行动力学设计与特性分析的基础。文献[14]采用凯恩方法建立了5UPS/PRPU并联机床动力学模型。文献[15]利用拉格朗日方程建立了二自由度球面并联机构动力学模型。文献[16]借助虚功原理对Stewart并联机构进行了动力学分析。文献[17]研究了基于面向对象的机械产品动态设计建模方法。文献[18-19]利用动态优化设计方法设计研究了振动筛,并求解得到系统的固有频率、响应和主振型。文献[20]利用子结构位移法分析了Delta机械手的动态性能。
本文针对车载天线应用环境,以3-RSR型并联车载天线机构为研究对象,建立基体运动下机构动力学模型,以固有频率为目标进行优化,并考虑风雪载荷进行动力学仿真分析。
1 3-RSR并联天线机构动力学建模
1.1 天线机构基本组成与初始参数
图1中天线面为1.8 m口径,采用铝合金;3-RSR并联机构由动平台、定平台和3条结构完全相同的RSR支链组成,为钢材质;与定平台相连的转动副为驱动副。

图1 3-RSR并联天线三维模型
Fig.1 3-RSR parallel antenna three-dimensional model
考虑运动一致、受力均匀,3-RSR并联机构整体结构对称,机构上下连杆长度相等,设为L;定平台、动平台铰链点外接圆半径相等,设为R,3个铰链点呈120°均布;机构初始高度设为H。为实现天线俯仰90°、方位360°转动的工作要求,进行机构运动学分析,通过位置反解,设计确定3-RSR并联天线机构初始参数如表1所示。
表1 3-RSR并联天线机构初始参数
Tab.1 Initial parameters of 3-RSR parallelantenna mechanism

上/下连杆长度L(mm)420上/下连杆直径d(mm)30定/动平台铰链点外接圆半径R(mm)150动平台初始高度H(mm)630输入转动副转动范围βi(°)80~210
1.2 天线机构坐标系建立与几何描述
3-RSR并联天线机构简图见图2,以P?i?i?=1,2,3表示与定平台相连的转动副,G?i?(i?=1,2,3)表示球副,Q?i?i?=1,2,3表示与动平台相连的转动副。以定平台质心O?为原点建立定坐标系Oxyz?,其中,x?轴指向铰链点P?1,z?轴垂直于定平台,方向向上;以动平台质心C?为原点建立动坐标系Cuvw?,其中,u?轴指向铰链点Q?1,w?轴垂直于动平台,方向向上。M?点为OC?与G?1G?2G?3平面的交点。建立大地坐标系Gstk?,初始时原点G?与机构定坐标系原点O?重合,s?轴与x?轴重合,k?轴与z?轴重合。

图2 3-RSR并联天线机构简图
Fig.2 Schematic diagram of 3-RSR antenna structure
因3-RSR并联机构结构对称,故矢量OC始终垂直于各支链中间球副所构成的平面G?1G?2G?3,即有
OC⊥MGi?
(1)
根据式(1)几何关系,有
OM(M-Gi?)T=0
(2)
机构各分支链中球副G?i?点坐标可以表示为
Gi?=((R?+L?cosβ?i?)cosθ?i?, (R?+L?cosβ?i?)sinθ?i?,?L?sinβ?i?)T
其中,R?为定平台铰链点P?i?外接圆半径(即质心O?到转动副P?i?的距离);L?为机构下连杆长度;β?i?i?=1,2,3为各分支输入转动角度;θ?i?为OP?i?与定坐标系x?轴夹角。
将M?点、G?i?点坐标代入求解方程,即可得到动平台中心点C?在定坐标系下的显式表达X?C?、Y?C?、Z?C?。
在机构运动过程中,动平台平面Q?1Q?2Q?3与定平台平面P?1P?2P?3始终关于3个分支链中间球副所形成的平面G?1G?2G?3对称,已知G?1、G?2、G?3在定坐标系下的坐标表达,可得G?1G?2G?3平面的法向矢量为
kG?=G1G2×G2G3
(3)
机构定平台转动副Pi?坐标可表示为
Pi?=(L?cosθ?i?,?L?sinθ?i?, 0)T
取3-RSR并联机构某单支链,其几何关系如图3所示。由对称关系可知,Pi?Qi?垂直于G?1G?2G?3平面,Pi?Qi?与kG?方向相同。由P?i?、G?i?、Q?i?三点之间的几何关系,在已知P?i?点坐标和kG?的前提下,易得Q?i?点在定坐标系下的坐标表达。

图3 3-RSR并联机构单支链几何关系
Fig.3 Geometric relationship of single branched chain of3-RSR parallel mechanism
1.3 基体运动下天线机构动力学模型
当天线机构基体跟随运载车辆运动,同时机构自身进行跟踪目标的运动时,其动平台中心点C?相对于大地坐标系的运动为上述两个独立运动的叠加。根据坐标矢量叠加法则,可得此时机构动平台中心点C?在大地坐标系下的坐标表示为
CD=CC+CG
(4)
式中,CC为仅考虑机构自身进行跟踪目标的运动时C?点在大地坐标系下的坐标;CG为仅考虑基体跟随运载车辆运动时C?点在大地坐标系下的坐标。
将CD对时间求导,可得基体运动情况下动平台质心相对于大地坐标系的线速度vD。由合成定理,基体运动情况下动平台质心在定坐标系下的角速度为
ωD=ωC+ωG
(5)
式中,ωC为仅考虑机构自身进行跟踪目标的运动时动平台中心在大地坐标系下的角速度;ωG为仅考虑基体跟随运载车辆运动时动平台中心在大地坐标系下的角速度。
根据机构动平台在大地坐标系下的线速度和角速度,可求得在基体运动情况下机构的动能为
(6)
式中,m?为机构动平台质量;ID为动平台相对于动坐标系的惯性张量。
机构的势能为
U?D=mgZ?CD
(7)
式中,Z?CD为动平台中心在大地坐标系下的k?坐标值。
由主动力为非保守力时的拉格朗日方程可得
(8)
K?D=T?D-U?D
式中,K?D为拉格朗日函数;τDi?为第i?支链的广义力或力矩。
经整理可得机构在基体运动情况下的动力学方程为
(9)
式中,J为机构雅可比矩阵;MD(β?)为机构惯性项;![]() 为哥氏力系数项;GD(β?)为机构重力项。
为哥氏力系数项;GD(β?)为机构重力项。
2 3-RSR并联天线机构动力学优化
天线结构固有频率因其影响天线的伺服带宽,故而是系统动态性能及稳定评估的重要参考。以提高3-RSR并联天线机构固有频率为主要目标,选取定/动平台铰链点所在外接圆半径R?、分支链杆长L?、机构动平台初始高度H作为机构优化的设计变量,开展动力学优化。优化目标函数可以描述为
(10)
式中,ω?为天线机构固有频率;f?of为优化目标函数;g?i?表示优化问题的约束条件函数。
3-RSR并联机构存在运动学奇异位形,即动平台从初始位形(上、下平台平行)运动到最高位置,上、下连杆轴线共线时,机构处于奇异位形。为了规避机构奇异位形,机构动平台初始高度H与机构支链连杆长度L?之间需满足条件
g?1=H?-2L?<0
(11)
为满足天线俯仰90°、方位360°转动的工作空间要求,设计变量的取值范围还需满足如下几何尺寸约束(单位mm):
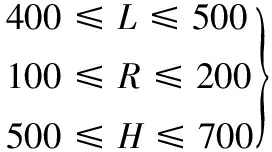
(12)
选择遗传算法对天线机构结构参数予以优化,优化过程中各基本参数及有关设定见表2。
依据优化目标函数、约束条件以及遗传算法优化过程所设的各个参数,利用MATLAB工具软件编制程序,运行所得适应度函数优化迭代的变化如图4所示。
表2 遗传算法参数设置
Tab.2 Parameter settings of genetic algorithm
种群规模适应度计算选择算法交叉概率变异概率20排序法随机遍历抽样0.70.002

图4 适应度函数优化迭代收敛过程图
Fig.4 Diagram of fitness function optimization iterativeconvergence process
在迭代过程中,当运行至51代时,计算结果收敛,相应机构参数为L?=453.5 mm,R?=197.9 mm,H?=500.3 mm,此时机构固有频率为26.30 Hz。
由图5可知,优化后3-RSR并联机构各个方向上的固有频率均有所提高。其中优化前机构固有频率最小值为18.02 Hz,优化后固有频率最小值为26.30 Hz,提高了45.9%。

图5 3-RSR并联天线机构的固有频率
Fig.5 Inherent frequency values of 3-RSRantenna mechanism
图6为天线俯仰90°过程中优化前后3-RSR并联机构雅可比矩阵条件数λ?变化曲线,优化前机构雅可比矩阵条件数λ?最小为1.26,而优化后λ?为1.03,机构各向同性有所提高。

图6 3-RSR机构雅可比矩阵条件数
Fig.6 Condition number of Jacobian matrix of3-RSR mechanism
球副的转角范围是影响天线机构工作空间的重要因素之一。优化前后3-RSR并联机构球副转角φ?如图7所示,在俯仰90°极限位姿下,优化前各支链球副转角φ?最大达到106°,优化后机构球副的最大转角φ?减小至88°,降低了球副设计的难度。

(a)优化前
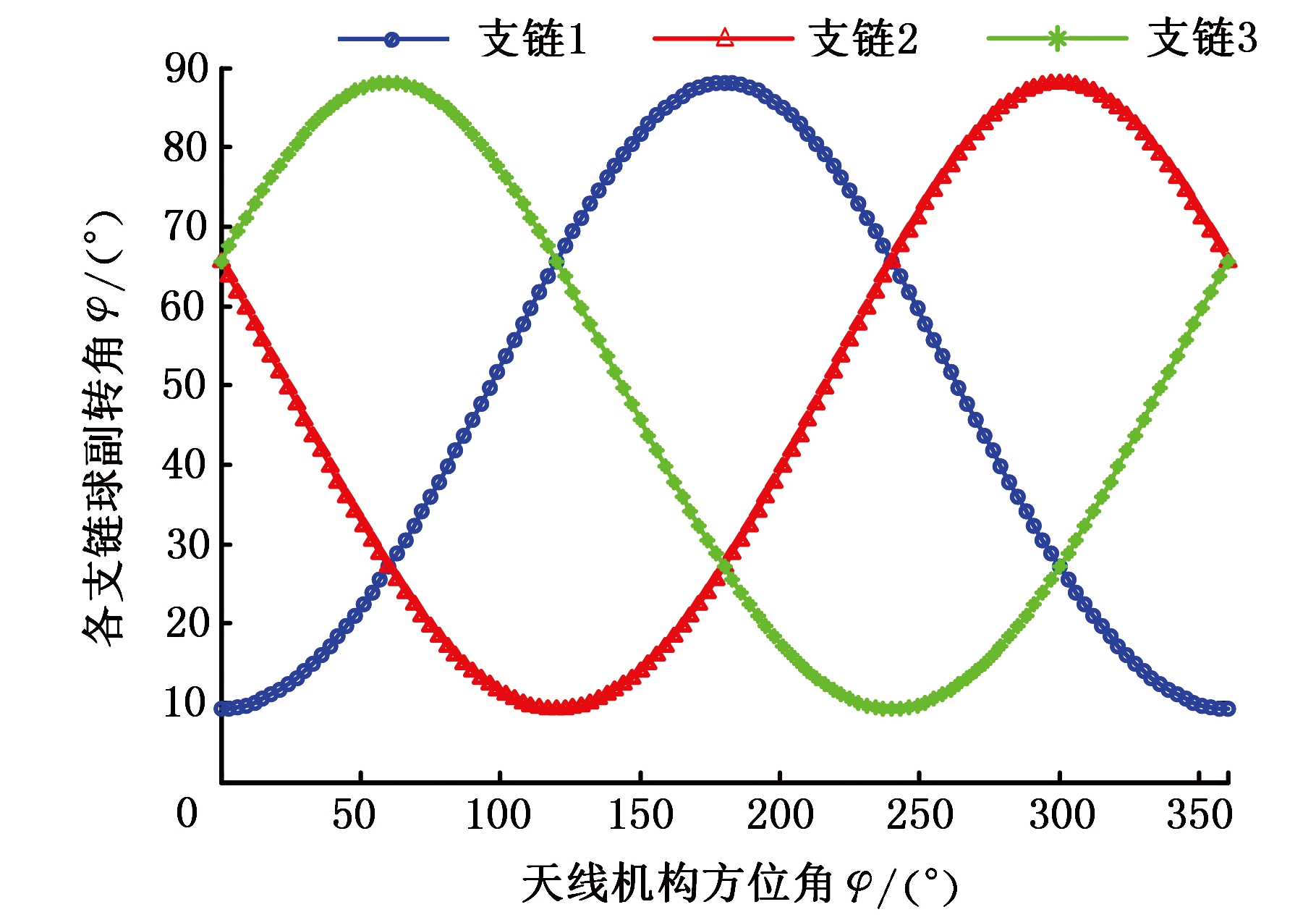
(b)优化后
图7 天线俯仰90°时各支链球副转角
Fig.7 Rotation angle of each branch ball with theantenna pitched at 90°
此外,车载天线受限于运载车辆空间,因此机构运动包络空间也是设计考量的因素之一。车载天线主要有两种状态,分别为正常工作状态和天线收藏状态。天线机构正常运行时,动平台在初始位姿高度下进行俯仰、方位运动,以实现跟踪目标和接收信号的功能,此时机构运动包络空间为一球体,如图8a所示。天线机构在收藏状态时,天线在初始位姿高度下沿定平台法线方向竖直向下运动,因此收藏状态下天线系统的运动包络空间包含在工作状态运动包络空间之内,如图8b所示。

(a)工作状态

(b)收藏状态
图8 3-RSR机构运动包络空间
Fig.8 Motion enveloping space of 3-RSR mechanism
由前所述,天线机构的运动包络空间为机构在工作状态下形成的球面所包围的体积,其中球心位于机构中心轴线上的1/2初始位姿高度处,故3-RSR并联天线机构的运动包络空间表达式为
(13)
式中,d?a为天线口径;h?a为天线面到动平台的垂直距离。
据此计算,优化前3-RSR并联天线机构运动包络空间体积为5.59 m3,而优化后为5.09 m3,减小了8.9%。
综上可见,优化后3-RSR并联天线机构在保证固有频率提高的前提下,机构各向同性、球副转角要求、运动包络空间均有改善,综合性能更优。
3 3-RSR并联天线机构动力学仿真
车载天线放置于车体之上并跟随车辆运动,且多在户外作业,环境复杂,其中风载荷、积雪载荷和车体随机激励均对天线机构指向精度存在较大影响。
3.1 天线机构工况模型的构建
天线受到的风载荷包括风阻力和风力矩两部分[21],其中,风阻力计算式为
F?f=C?fqA?
(14)
式中,C?f为风力系数,由风洞试验给出,天线在不同姿态下风力系数最大为1.47;q?为动压,![]() 为风速;ρ?为空气密度,气温为20 ℃时ρ?=1.205 kg/m3;A?为天线抛物面在垂直于风向上的投影面积。
为风速;ρ?为空气密度,气温为20 ℃时ρ?=1.205 kg/m3;A?为天线抛物面在垂直于风向上的投影面积。
当天线为俯仰90°工作状态时,风侧吹天线受力面积最大,A?取天线抛物面口面积。
天线所受风力矩计算式为
M?f=C?mqAD?
(15)
式中,C?m为风力矩系数,参考风洞试验,天线在不同姿态下风力矩系数最大取0.15;D?为天线与转轴垂直方向的尺寸。
所受积雪载荷按照天线口径计算,天线抛物面曲线方程为
y?=2.15x?2-3.74x?-0.174
(16)
则天线抛物面内积雪的体积
(17)
进而天线抛物面内由积雪产生的重力为
G?x?=ρ?x?gV?x?
(18)
式中,ρ?x?为湿雪密度。
车体随机激励模型的建立首先需分析影响车体运行的主要因素。路面不平度是引起汽车在运行时产生振动的一个主要激励源,当由路面不平度激起的振动达到一定程度时,车辆行驶的平顺性以及承载系统的可靠性将大大降低。除此之外,还需要考虑车速的影响,不同的车速也会使车辆产生不同的激励。路面激励的时域模型[22]为
(19)
式中,n?00为下截止空间频率,n?00=0.011 m-1;u?为车辆行驶速度;n?0为参考空间频率,n?0=0.1 m-1;G?q?(n?0)为路面不平度系数;W?(t?)为均值为0的高斯白噪声。
由式(19)在MATLAB/Simulink中搭建随机路面仿真模型,如图9所示,分别取不同等级路面对应的设计车速,生成相应的路面随机模型。在仿真模型中只需输入不同等级路面的路面不平度系数和对应的车辆运行速度,即可得到对应情况下的路面随机激励。

图9 随机路面生成模型
Fig.9 Random pavement model
以B级路面为例,其路面不平度系数G?q?(n?0)为64×10-6m3。通过随机路面生成模型,分别生成车速为60 km/h和80 km/h时的车体随机激励曲线,如图10所示。可见,随着车速的提高,路面随机激励的幅值h?不断增大,仿真结果与车辆在道路上的实际行驶情况相符。

(a)u?=60 km/h

(b)u?=80 km/h
图10 不同车速下的路面激励-时间曲线
Fig.10 Pavement excitation-time curve at different speed
3.2 天线机构驱动力矩仿真分析
对应不同的环境条件,天线有保精度运行和可驱动运行两种工作状态。天线机构主要在保精度运行状态下工作,本文即针对天线保精度运行要求分析机构所需驱动力矩。
选择两条轨迹进行仿真,轨迹1为天线抛物面做0°~90°俯仰运动,天线轴线指向支链1;轨迹2为天线抛物面做0°~90°俯仰运动,天线轴线指向支链2与支链3中间。
在保精度运行状态下,天线需要在风力不大于13.8 m/s(6级风)时实现在0°~90°之间任意姿态的俯仰运动。此处选用6级风载荷产生的风力、风力矩进行分析,并选择车辆以80 km/h的车速运行在B级路面上时车体振动产生的路面随机激励。
风向分为风沿x?轴吹向天线抛物面和风始终垂直吹向天线抛物面两种情况。其中,风始终沿x?轴吹向天线抛物面时,3-RSR并联机构在两条规划运动轨迹下各分支驱动力矩M?变化曲线见图11。风始终垂直吹向天线抛物面时,3-RSR并联机构在两条运动轨迹下各分支驱动力矩M?变化曲线见图12。由图11、图12可知,受车体随机激励的影响,机构驱动力矩也呈现较大的随机性,相比于风始终沿x?轴吹向天线抛物面的情况,天线机构在风始终垂直吹向天线面的情况下,支链驱动力矩更大。

(a)运动轨迹1

(b)运动轨迹2
图11 风沿x轴吹向天线抛物面的3-RSR机构驱动力矩
Fig.11 Driving moment of 3-RSR mechanism withwind blowing to antenna paraboloid alongxaxis
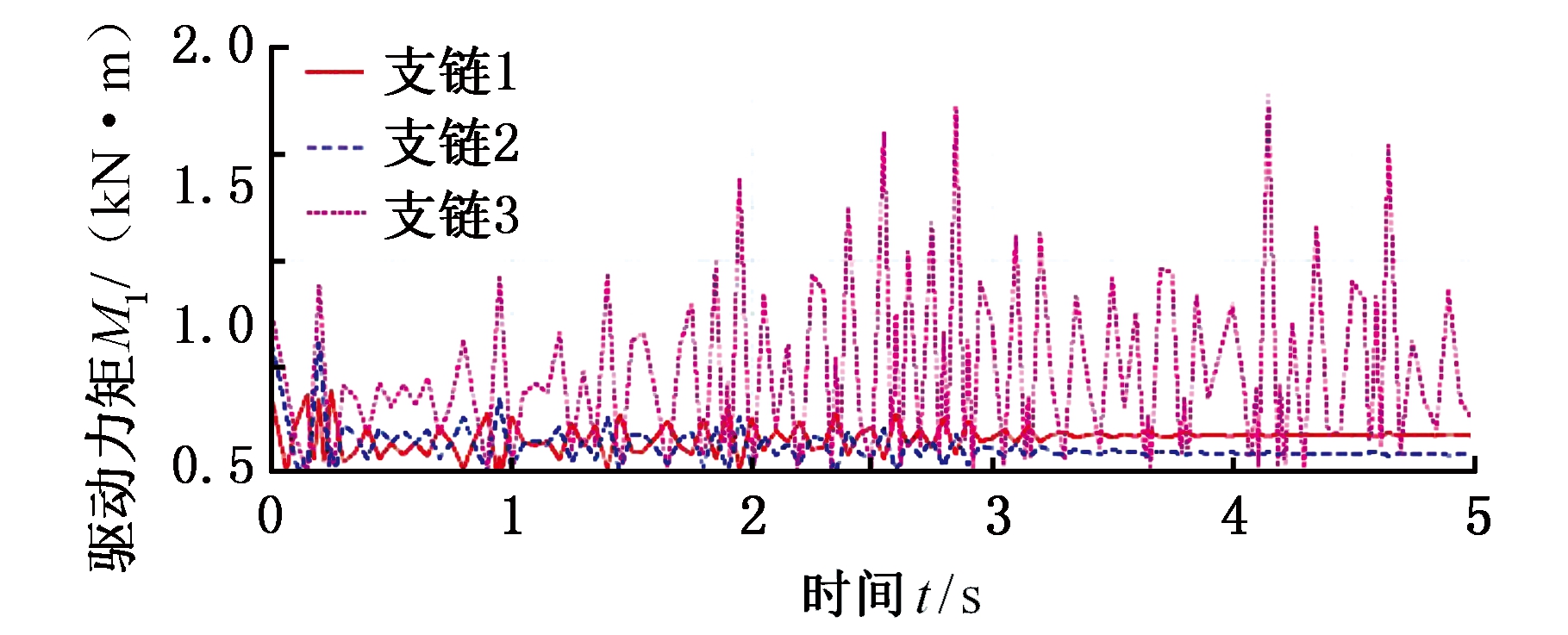
(a)运动轨迹1

(b)运动轨迹2
图12 风垂直吹向天线抛物面的3-RSR机构驱动力矩
Fig.12 Driving moment of 3-RSR mechanism withwind blowing vertically to antenna paraboloid
4 结论
(1)考虑基体运动,利用拉格朗日方程法建立了3-RSR型并联式车载天线机构动力学模型,以固有频率最大化为目标,以机构规避奇异和边界几何尺寸为约束条件,通过遗传算法进行动力学优化,获得了综合性能较优的机构参数。
(2)考虑风雪载荷与车体随机激励建立了天线工况模型,针对所规划运动轨迹完成仿真分析,绘制出天线机构驱动力矩变化曲线,为并联式天线样机研制提供了参考。
[1] 约翰·克劳斯, 罗纳德·马赫夫克. 天线[M]. 3版. 北京: 电子工业出版社, 2011: 1-9.
KRAUS J D,MARHEFKA R J. Antennas:For All Applications[M]. 3rd ed. Beijing: Electronic Industry Press, 2011:1-9.
[2] 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社,2006: 100-114.
HUANG Zhen, ZHAO Yongsheng, ZHAO Tieshi. Advanced Spatial Mechanism[M].Beijing: Higher Education Press,2006: 100-114.
[3] ARTEMENKO Y N, SIL’VESTROV E, KORENOVSKII V, et al. Method for the Synthesize of Parallel-structure Mechanisms for Orientating a Space Telescope Antenna[J]. Journal of Machinery Manufacture and Reliability, 2012, 41(4): 265-269.
[4] KOCH P M, KESTEVEN M, NISHIOKA H, et al. The AMiBA Hexapod Telescope Mount[J]. Astrophysical Journal, 2009, 694(2): 1670-1684.
[5] 侯雨雷, 段艳宾, 窦玉超, 等. 65米射电望远镜天线副面调整机构标定研究[J]. 中国机械工程, 2013, 24(24): 3318-3322.
HOU Yulei, DUAN Yanbin, DOU Yuchao, et al. Calibration of Adjusting Mechanism for Subreflector of a 65 Meters Radio Telescope[J]. China Mechanical Engineering, 2013, 24(24): 3318-3322.
[6] 姚蕊, 李庆伟, 孙京海, 等. FAST望远镜馈源舱精度分析研究[J]. 机械工程学报, 2017, 53(17): 36-42.
YAO Rui, LI Qingwei, SUN Jinghai, et al. Accuracy Analysis on Focus Cabin of FAST[J]. Journal of Mechanical Engineering, 2017, 53(17): 36-42.
[7] 段艳宾, 贾彦辉, 李建军, 等. 应用于天线座的并联机构构型设计[J]. 机械制造, 2014, 52(8): 26-29.
DUAN Yanbin, JIA Yanhui, LI Jianjun, et al. Configuration Design of Parallel Mechanism Applied to Antenna Pedestal[J]. Machinery, 2014, 52(8): 26-29.
[8] 陈兵奎, 赵骧, 王永波. 并联机构卫星通讯稳定平台运动学分析[J]. 重庆大学学报, 2008, 31(9): 982-987.
CHEN Bingkui, ZHAO Xiang, WANG Yongbo. Kinematic Analysis of a Stabilized Parallel Mechanism Platform for Satellite Communication[J]. Journal of Chongqing University, 2008, 31(9): 982-987.
[9] 华为实. 基于3-RSR并联机器人机构的天线支撑[J]. 机械, 2000, 27(5): 10-11.
HUA Weishi. Antenna Support Based on 3-RSR Parallel Robot Mechanism[J]. Mechanics, 2000, 27(5): 10-11.
[10] NOVACEK Z. Radiation of a Whip Antenna on the Car Body[C]// 17th International Conference Radioelektronika. Brno, 2007: 1-4.
[11] 姚嘉凌, 史文库, 陈志勇, 等. 基于车载导航的半主动悬架路况协调控制[J]. 机械强度, 2015, 37(4): 587-592.
YAO Jialing, SHI Wenku, CHEN Zhiyong, et al. Coordinated Control Algorithm for Semi-active Suspension in Various Roud Conditions Based on Navigation[J]. Journal of Mechanical Strength,2015, 37(4): 587-592.
[12] 任克亮, 李志刚. 行驶状态下的车载雷达动力学研究[J]. 环境装备工程,2013, 10(2): 62-66.
REN Keliang, LI Zhigang. Study on Dynamics of Running Vehicle Radar[J]. Equipment Environmental Engineering,2013, 10(2): 62-66.
[13] LI X, JI Y C, LU W, et al. Analysis of GPR Antenna System Mounted on a Vehicle[J]. IEEE Antennas & Wireless Propagation Letters,2013, 12(1): 575-578.
[14] 鹿玲, 姚建涛, 顾伟栋, 等. 基于Kane方程的冗余驱动5UPS/PRPU并联机床动力学分析[J]. 农业机械学报, 2016, 47(6): 366-372.
LU Ling, YAO Jiantao, GU Weidong, et al. Dynamics Analysis of 5UPS/PRPU Parallel Machine Tool with Redundant Actuation Based on Kane Equation[J]. Transactions of the Chinese Society for Agricultural Machinery,2016, 47(6): 366-372.
[15] CHEN B, YU J J, ZONG G H, et al. Dynamic Modeling and Sliding Mode Control of a 2-DOF Spherical Parallel Mechanism with a Passive Branch[C]// 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Buffalo, United states, 2014: 17-20.
[16] TSAI L W. Solving the Inverse Dynamics of a Stewart-Gough Manipulator by the Principle of Virtual Work[J]. Journal of Mechanical Design, 2000, 122(1):3-9.
[17] 宋雪萍, 李鹤, 李小彭, 等. 基于面向对象的机械产品的动态设计建模[J]. 机械设计,2014, 21: 75-77.
SONG Xueping, LI He, LI Xiaopeng, et al. Dynamic Design Modeling of Mechanical Products Based on Object Oriented[J]. Journal of Machine Design,2014, 21: 75-77.
[18] 冯霏, 刘挺, 闻邦椿. 基于传递矩阵法的振动筛动态设计研究[J]. 机械制造,2009, 47(10): 22-24.
FENG Fei, LIU Ting, WEN Bangchun. Dynamic Design of Vibrating Screen Based on Transfer Matrix Method[J]. Machinery, 2009, 47(10): 22-24.
[19] 张楠, 侯晓林, 闻邦椿. 基于动态优化设计方法振动筛设计的研究[J]. 煤矿机械, 2008, 29(3): 12-15.
ZHANG Nan, HOU Xiaolin, WEN Bangchun. Research for Design of Vibration Screen Based on Dynamic Optimization Design[J]. Coal Mine Machinery, 2008, 29(3): 12-15.
[20] 张利敏, 梅江平, 赵学满, 等. Delta机械手动力尺度综合[J]. 机械工程学报,2010, 46(3): 1-7.
ZHANG Limin, MEI Jiangping, ZHAO Xueman, et al. Dynamic Dimensional Synthesis of Delta Robot[J]. Journal of Mechanical Engineering, 2010, 46(3): 1-7.
[21] 乔山林, 顾吉丰. 风载荷对雷达天线座的影响与评估[J]. 现代雷达,2017, 39(10): 95-99.
QIAO Shanlin, GU Jifeng.Effect and Evaluation of Wind-load to Radar Pedestal[J]. Modern Radar, 2017, 39(10): 95-99.
[22] 潘双夏, 陈助碧, 冯培恩. M-file S-函数在时域路面不平度建模中的应用[J].中国工程机械学报,2006, 4(4): 379-384.
PAN Shuangxia, CHEN Zhubi, FENG Peien. Investigating M-file S-function on Time-domain Road Roughness Modeling[J]. Chinese Journal of Construction Machinery, 2006, 4(4): 379-384.
