0 引言
动量轮轴承组件是滚动轴承的一种,也是卫星姿态控制的关键执行部件,其工作动态性能及可靠性直接影响到卫星的控制精度与寿命[1-3]。轴承摩擦力矩是指滚动摩擦、滑动摩擦和润滑剂摩擦的总和产生的阻滞轴承运转的阻力矩,是评价轴承运转灵活性及寿命的重要指标[4];性能可靠度是指在未来时间滚动轴承运行保持最佳性能状态的程度[5]。
长期以来,轴承性能试验主要进行疲劳寿命及其可靠度的统计分析,并以威布尔分布为基本假设。CHEN等[6]基于L-P理论和Tallian模型建立了分离轴承新寿命预测模型,其研究结果表明,新型离合器分离轴承寿命预测模型更接近汽车离合器的实际情况;OSWALD等[7]分析了在3种轴承钢存在高环向应力的情况下,残余应力对滚动轴承疲劳寿命的影响;朱德馨等[8]从轴承疲劳寿命服从的分布入手,采用贝叶斯多层估计法对无失效试验数据进行处理,建立了高速列车轴承的可靠性寿命评估模型。但是航空、航天、新能源、新材料等领域的快速发展,对轴承摩擦力矩及其可靠度提出了新要求,使传统的轴承性能评估理论面临新挑战。主要原因有:①受诸多因素的影响,无法推导出摩擦力矩的精确计算公式;②摩擦力矩具有不确定的强烈波动和趋势变化,属于概率分布与趋势规律均未知的问题;③轴承摩擦力矩的研究属于动力学方程未知的非线性问题,难以找到确定的非线性模型[9-11];④现有的性能可靠性预测方法通常需要事先设定阈值,阈值的设定受主观因素的影响,缺乏说服力[12-13]。由此可知,如何对滚动轴承摩擦力矩性能可靠性进行动态预测已成为亟待解决的问题。
鉴于以上问题,本文针对卫星动量轮轴承摩擦力矩性能可靠性动态预测展开了研究。将采集到的轴承摩擦力矩原始数据进行分组得到样本,并选定本征样本;提出了用灰置信水平求解各样本变异强度的新方法,该方法既不需要数据概率分布已知,也不需要事先设定阈值;通过自助-最小二乘法和最大熵原理将紧邻的5个样本变异强度进行线性拟合,持续更新紧邻的5个变异强度,不断舍弃旧数据,引入新数据,从而得到了各样本摩擦力矩性能可靠度预测值并完成验证,最终实现了滚动轴承摩擦力矩性能可靠性的动态预测。
1 动态预测模型
1.1 本征样本
在滚动轴承服役期间,对其摩擦力矩信号进行定期采样,设采样周期为t,共采集S个数据。将S个数据均匀分组,设获得M个样本,记为X1~XM,样本含量均为N(即S=MN)。本征样本是指滚动轴承处于最佳运行状态时期的样本,该时期轴承的运转状态良好且稳定,几乎无性能失效的可能性。将本征样本记为第1个样本,即
X1=(x1(1),x1(2),…,x1(k),…,x1(N))
(1)
式中,x1(k)为X1的第k个数据;k(k=1,2,…,N)为数据序号;N为样本含量。
1.2 基于灰置信水平的变异强度和可靠度
设上述任一样本为Xi(i=1,2,…,M),将样本X1和Xi中的数据均从小到大排序,通过排序可以得到样本X1和Xi的数据序列分布特征,进而建立X1与Xi之间属性的灰关系[14]。
设X1和Xi排序后分别为Y1和Yi,其元素分别为y1(k)和yi(k)。设
(2)
令
(3)
对式(3)进行归一化处理:
(4)
则有
Zh=(zh(1),zh(2),…,zh(k),…,zh(N))
(5)
zh(k)∈[0,1] zh(1)=0 zh(N)=1
式中,Zh为Yh的规范化排序生成序列。
在最少量信息原理下,对于任意的k(k=1,2,…,N),若Zh为规范化排序序列,则参考序列Z0中的元素可以为常数0,即
z0(k)=z1(1)=0
(6)
定义灰关联度为
(7)
取分辨系数ξ∈[0,1],得到灰关联系数为
(8)
Δ0h(k)=|zh(k)-z0(k)|
式中,Δ0h(k)为灰差异信息。
定义样本X1和Xi的灰差为
d1i=|γ01-γ0i|
(9)
则得到样本X1和Xi的基于灰关联度的相似系数(即灰相似系数)可表示为
r1i=1-d1i
(10)
定义灰相似矩阵(即灰关系属性)为
(11)
式中,r11为本征样本X1与其本身的灰相似系数,则r11=1;rii为样本Xi与其本身的灰相似系数,则rii=1;r1i、ri1为本征样本X1与任一样本Xi的灰相似系数,且有0≤r1i,ri1≤1。
给定样本X1和Xi,对于ξ∈[0,1],总存在唯一的实数dmax=d1imax,使得d1i≤dmax,则称dmax为最大灰差,此时对应的ξ称为基于最大灰差的最优分辨系数。
设基于样本X1和Xi之间的灰关系属性权重可表示为
(12)
式中,f1i为属性权重,f1i∈[0,1];η为参数,η∈[0,1]。
根据白化原理和对称原理,若没有理由否认边界参数θ为真元,则在给定的准则下,默认θ为真元的代表。在给定样本X1和Xi中,取参数θ∈[0,1]为水平,若存在一个映射f1i≥θ,则表明样本X1和Xi具有相同的属性。这里取f1i=θ=0.5,即认为样本X1和Xi具有相同的属性。
设η∈[0,0.5],由式(12)可得
dmax=(1-f1i)η
(13)
灰置信水平描述了样本X1和Xi属性相同的可信度(概率),其表达式如下:
P1i=1-(1-θ)η=(1-0.5η)×100%
(14)
由于P1i描述的是任一样本Xi相对本征样本X1属性的相似度,故定义Xi相对X1的属性变异度(即变异强度)为
λi=1-P1i
(15)
变异强度λi的传统求法是通过计数过程统计得到S个数据中超出设定阈值的数据有v个,则λi=v/S,即数据波动幅值超过设定阈值的概率,但传统求法的缺点是需要事先设定阈值,若设定的阈值不同,则得到的结果也不同。本文变异强度λi的获取是基于灰置信水平P1i,不需要事先设定阈值。
任何计数过程均可由Possion过程描述,其表达式如下:
(16)
式中,Q为失效事件发生m次的概率;m (m=0,1,…)为失效事件发生的次数(即滚动轴承性能失效的次数)。
当式(16)中取m=0时,得到滚动轴承未发生性能失效的概率(即表示当前滚动轴承性能可靠度),可表示为
Ri=exp(-λi)
(17)
由于变异强度λi两种求法的区别仅在于是否需要事先设定阈值,故可将本文中变异强度λi代入式(17)求得任一样本Xi的性能可靠度Ri。
1.3 动态预测模型的建立
1.3.1 基于自助-最小二乘法的变异强度线性拟合
自助-最小二乘法是将自助法和最小二乘法进行融合。运用自助法,将紧邻5个样本Xi,Xi+1,Xi+2,Xi+3,Xi+4的5个变异强度λi,λi+1,λi+2,λi+3,λi+4(i=1,2,…,M-4)等概率可放回地随机抽取q次,得到一个自助样本Vb,其表达式如下:
Vb=(v1,v2,…,vq)
(18)
式中,Vb为第b个自助样本;vl为Vb的第l个数据,l=1,2,…,q;q为Vb的样本含量。
对自助样本Vb进行均值处理,即
(19)
式中,Vb为自助样本Vb的样本均值。
自助样本Vb重复B次得到VB,VB由样本均值Vb(b=1,2,…,B)组成,即
VB=(V1,V2,…,VB)
(20)
运用最小二乘法对样本均值Vb进行线性拟合,其表达式如下:
Vb=abil+cb
(21)
I={i1,i2,…,iq}
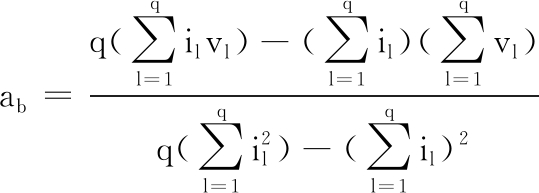

式中,I为预测步长;ab、cb为最小二乘解系数。
线性拟合共进行B次,则获得的最小二乘解系数向量为
a=(a1,a2,…,aB)
(22)
c=(c1,c2,…,cB)
(23)
1.3.2 基于最大熵原理的概率密度函数
最大熵原理可对概率分布未知数据作出主观偏见为最小的最佳估计[15]。以最小二乘解系数ab为例进行其概率密度函数f(ab)的求取,为了叙述方便,将式(22)中离散数据连续化,定义最大熵的表达式为
(24)
式中,f(ab)为系数ab的概率密度函数;S为积分区间。
积分区间S的约束条件为
(25)
式中,β为原点矩阶次;mβ为第β阶原点矩。
由式(22)可知,B可以是一个很大的数,故得到第β阶原点矩:
(26)
通过调整f(ab)可使熵达到最大值,此时可通过Lagrange乘子法进行求解,其表达式如下:
(27)
式中,m为最高原点矩阶次;σ0为首个Lagrange乘子;σβ为第β+1个Lagrange乘子。
首个Lagrange乘子σ0应满足:
(28)
其余Lagrange乘子应满足:
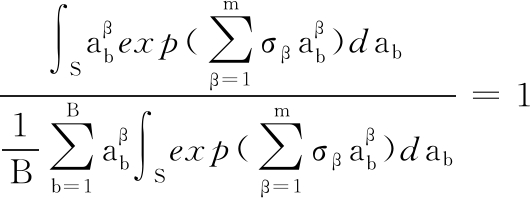
(29)
同理,可求出系数cb的概率密度函数f(cb)。
1.3.3 基于概率密度函数的系数ab和cb估计
根据f(ab),由统计原理可得系数ab的估计真值a0为
a0=![]() abf(ab)dab
abf(ab)dab
(30)
若δ∈[0,1]存在,使
P(ab<aδ)=![]() f(ab)dab=δ
f(ab)dab=δ
(31)
式中,δ为显著水平(即最小二乘系数ab<aδ的概率);aδ为f(ab)的δ分位数。
为求取最小二乘解系数ab的上下界值,需先求出双侧分位数,则有
P(ab<aU)=δ/2
(32)
P(ab≥aL)=δ/2
(33)
式中,aU、aL分别为系数ab的上界值和下界值;[aL,aU]为δ水平下的上下区间。
同理,可求得系数cb的估计真值c0与上下区间[cL,cU]。
1.3.4 可靠度的动态预测
将上述所求估计真值a0、c0和上下区间[aL,aU]、[cL,cU]代入式(21),设预测步长il=6,即可预测紧邻的下一个样本Xi+5的变异强度![]() 及其上下区间[λL,λU];并将其代入式(17)进而可得到样本Xi+5的性能可靠度预测值
及其上下区间[λL,λU];并将其代入式(17)进而可得到样本Xi+5的性能可靠度预测值![]() 及其上下区间预测值[RL,RU];持续更新紧邻的5个原始变异强度,不断舍弃旧数据,引入新数据,最终实现滚动轴承摩擦力矩性能可靠性的动态预测。
及其上下区间预测值[RL,RU];持续更新紧邻的5个原始变异强度,不断舍弃旧数据,引入新数据,最终实现滚动轴承摩擦力矩性能可靠性的动态预测。
2 试验分析
2.1 恒转速卫星动量轮轴承摩擦力矩稳态电流试验
本研究是一个恒转速卫星动量轮轴承摩擦力矩稳态电流试验,在室内温度20~25 ℃、相对湿度大于55%条件下完成,试验台建立在真空罩内的受控清洁和无振动的地基上。卫星动量轮轴承A稳态转速为3 500 r/min,试验数据采集周期t=1 d,共采集S=450个(15个月)数据,见图1。
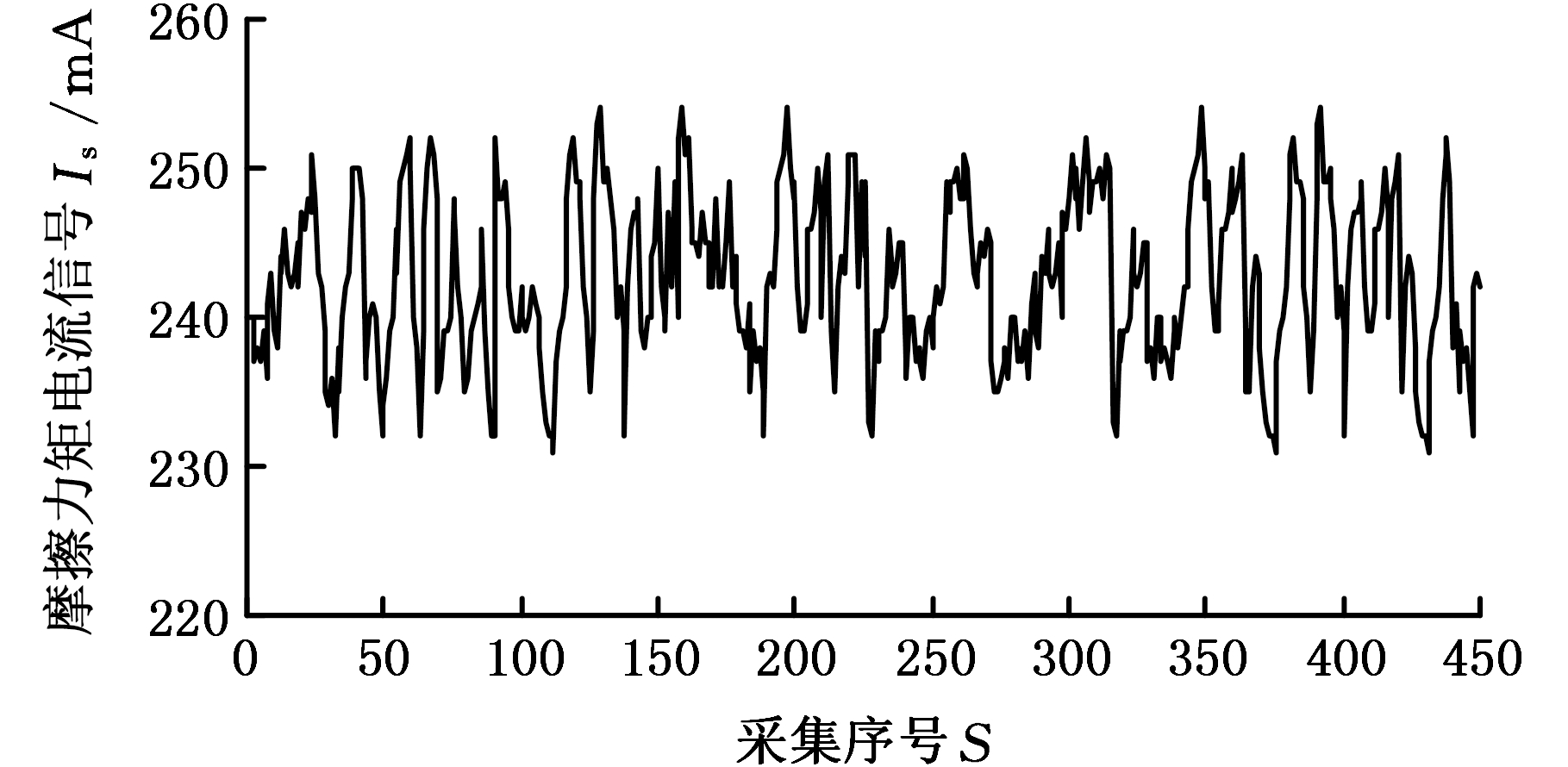
图1 卫星动量轮轴承A摩擦力矩稳态电流信号
Fig.1 Steady-state current signal of friction torque of satellite momentum wheel bearing A
采集的450个数据均分为15个样本X1~X15(即M=15),样本含量均为30(即N=30)。将采集的数据均分为15个时间段,每个时间段为1个月。设样本X1为本征样本,得到样本X1~X15的灰置信水平P1i(i=1,2,…,15),见表1。
表1 样本X1~X15的灰置信水平
Tab.1 Gray confidence level of X1~X15

样本X1X2X3X4X5灰置信水平P1i1.0000.9670.9330.9870.943样本X6X7X8X9X10灰置信水平P1i0.9360.9720.9670.9640.941样本X11X12X13X14X15灰置信水平P1i0.9250.9310.9880.9130.944
由表1可知,P11=1,表明同一个样本与其本身属性完全相同,样本X1~X15与本征样本X1的属性相同的可信度均在0.9以上,表明各时间段内卫星动量轮轴承A摩擦力矩稳态电流信号波动情况较为相似,这与对原始数据直接分析具有一致性。将表1中的P1i(i=1,2,…,15)代入式(15)得到样本X1~X15相对本征样本X1的变异强度λi(i=1,2,…,15)的实际值,见表2。
表2 样本X1~X15的变异强度(实际值)
Tab. 2 Variation intensity of X1~X15(actual values)

样本X1X2X3X4X5变异强度λi00.0330.0670.0130.058样本X6X7X8X9X10变异强度λi0.0640.0230.0330.0360.059样本X11X12X13X14X15变异强度λi0.0750.0690.0120.0880.056
由表2可知,λ1=0,表明同一个样本与其本身之间没有任何变异;λi(i=2,3,…,15)的值均很小,表明试验过程中的卫星动量轮轴承A摩擦力矩性能未发生明显变异,轴承一直处于良好的运转状态。将表2中的λi(i=1,2,…,15)代入式(17)得到各时间段内卫星动量轮轴承A摩擦力矩性能可靠度Ri(i=1,2,…,15)的实际值,见表3。
表3 卫星动量轮轴承A摩擦力矩性能可靠度(实际值)
Tab.3 Friction torque performance reliability of satellite momentum wheel bearing A(actual values)

样本X1X2X3X4X5可靠度Ri(%)100.0096.7293.5598.6894.41样本X6X7X8X9X10可靠度Ri(%)93.7897.2796.7296.5094.27样本X11X12X13X14X15可靠度Ri(%)92.7593.3698.7791.6294.52
由表3可知,各时间段内卫星动量轮轴承A摩擦力矩性能可靠度均大于91%,表明试验过程中轴承A摩擦力矩性能一直保持较高水平,再次验证了轴承处于良好的运转状态。
以上变异强度λi和性能可靠度Ri都是由原始采集数据运算得到的实际静态值,为了对卫星动量轮轴承A摩擦力矩性能可靠性进行动态预测,基于自助法将表2中前5个样本的变异强度(0,0.033,0.067,0.013,0.058)等概率可放回地随机抽取5次,得到一个自助样本V1,样本含量q=5,重复B=10 000次,可得到VB;运用最小二乘法对VB进行线性拟合,可得到最小二乘解系数 ab和cb(b=1,2,…,B),分别见图2和图3。

图2 最小二乘解系数ab
Fig.2 The coefficient ab of least square solution

图3 最小二乘解系数cb
Fig.3 The coefficient cb of least square solution
为了得到最小二乘解系数ab和cb的估计真值a0、c0及上下区间[aL,aU]、[cL,cU],基于最大熵原理可先求得系数ab和cb的概率密度函数f(ab)和f(cb),分别见图4和图5。
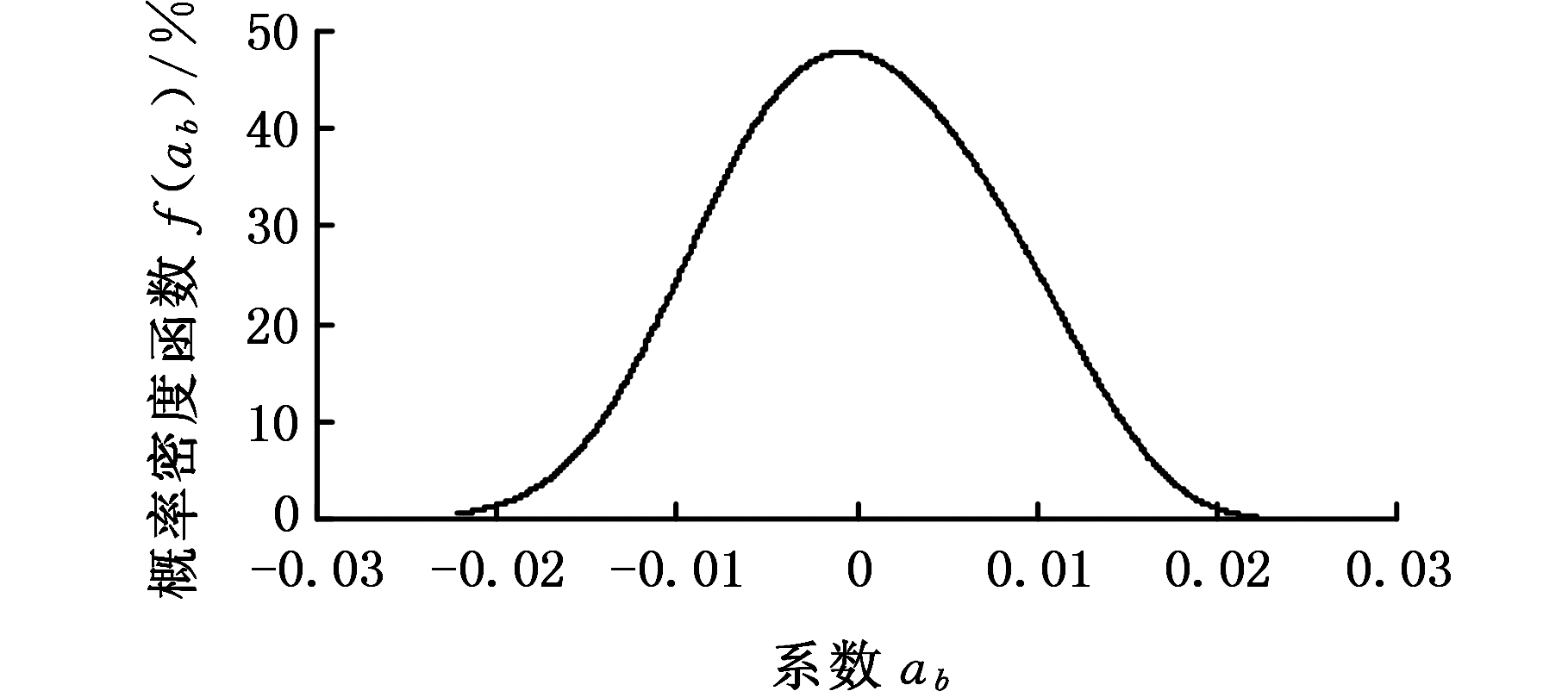
图4 概率密度函数f(ab)
Fig.4 The probability density function f(ab)

图5 概率密度函数f(cb)
Fig.5 The probability density function f(cb)
将所求概率密度函数f(ab)和f(cb)代入式(30)~式(33),设定δ=0.1,即在置信度为90%的情况下,求得最小二乘解系数ab和cb的估计真值a0、c0及上下区间[aL,aU]、[cL,cU],见表4。
表4 估计真值a0、c0及上下区间[aL,aU]、[cL,cU]
Tab. 4 The estimation true values a0, c0 and upper and lower interval [aL,aU], [cL,cU]

最小二乘解系数估计真值上下区间ab0.000 086[-0.012 508,0.012 819]cb0.035 614[-0.006 138,0.077 769]
表4所示为前5个时间段的变异强度λ1~λ5通过自助-最小二乘法所得拟合系数的估计真值和上下区间,将a0、c0及[aL,aU]、[cL,cU]代入式(21)中,令预测步长il=6,则可得到第6个时间段卫星动量轮轴承A摩擦力矩性能变异强度的预测值![]() 及其上下区间预测值[λL,λU];同理,可通过自助-最小二乘法对λ2~λ6进行线性拟合,令预测步长il=6,则可得到第7个时间段变异强度预测值
及其上下区间预测值[λL,λU];同理,可通过自助-最小二乘法对λ2~λ6进行线性拟合,令预测步长il=6,则可得到第7个时间段变异强度预测值![]() 及其上下区间预测值[λL,λU];依此类推,可分别得到第1~5,2~6,…,10~14时间段变异强度拟合系数的估计真值和上下区间,见表5。
及其上下区间预测值[λL,λU];依此类推,可分别得到第1~5,2~6,…,10~14时间段变异强度拟合系数的估计真值和上下区间,见表5。
由于自助样本由5个相邻样本及其变异强度得到,因此可将表5中各时间段变异强度拟合系数的估计真值及其上下区间代入式(21),令预测步长il=6,即![]() 则可得到第6~15个时间段卫星动量轮轴承A摩擦力矩性能变异强度预测值
则可得到第6~15个时间段卫星动量轮轴承A摩擦力矩性能变异强度预测值![]() 及其上下区间预测值[λL,λU],见图6。其中,第1~10次预测结果分别对应第6~15个时间段卫星动量轮轴承A摩擦力矩性能变异强度预测值及其上下区间预测值。
及其上下区间预测值[λL,λU],见图6。其中,第1~10次预测结果分别对应第6~15个时间段卫星动量轮轴承A摩擦力矩性能变异强度预测值及其上下区间预测值。
由图6可以看出,变异强度的实际值和预测值均在[0,0.1],变化范围很小,表明各时间段轴承A摩擦力矩性能稳定良好。其中,第1~5次(第6~10个时间段)和第10次(第15个时间段)变异强度预测值和实际值几乎相等;第6~9次(第11~14个时间段)预测误差稍微偏大,最大预测误差出现在第8次(第13个时间段);但所有的预测值和实际值均包络在上下区间内,预测范围准确率达100%。
表5 各时间段变异强度拟合系数的估计真值和上下区间
Tab.5 The estimated true value and upper and lower interval of fitting coefficient of each time period variation intensity

时间段a0c0[aL,aU][cL,cU]1~5 0.000 0860.035 614[-0.012 508,0.012 819][-0.006 138,0.077 769]2~6 0.000 0580.046 325[-0.011 219,0.011 361][0.006 061,0.080 498]3~7-0.000 0040.045 462[-0.011 290,0.011 397][0.005 349,0.079 905]4~8-0.000 1040.043 470[-0.009 888,0.009 752][0.010 397,0.074 886]5~9-0.000 0780.043 131[-0.007 903,0.007 903][0.018 738,0.070 285]6~10-0.000 0710.039 700[-0.006 976,0.006 830][0.019 714,0.065 651]7~11-0.000 0750.044 714[-0.008 608,0.008 545][0.019 326,0.075 323]8~12-0.000 1180.055 492[-0.008 907,0.008 710][0.025 759,0.083 792]9~13 0.000 0320.056 675[-0.011 048,0.011 216][0.014 419,0.088 074]10~14 0.000 0040.080 243[-0.014 443,0.014 744][0.022 416,0.156 370]
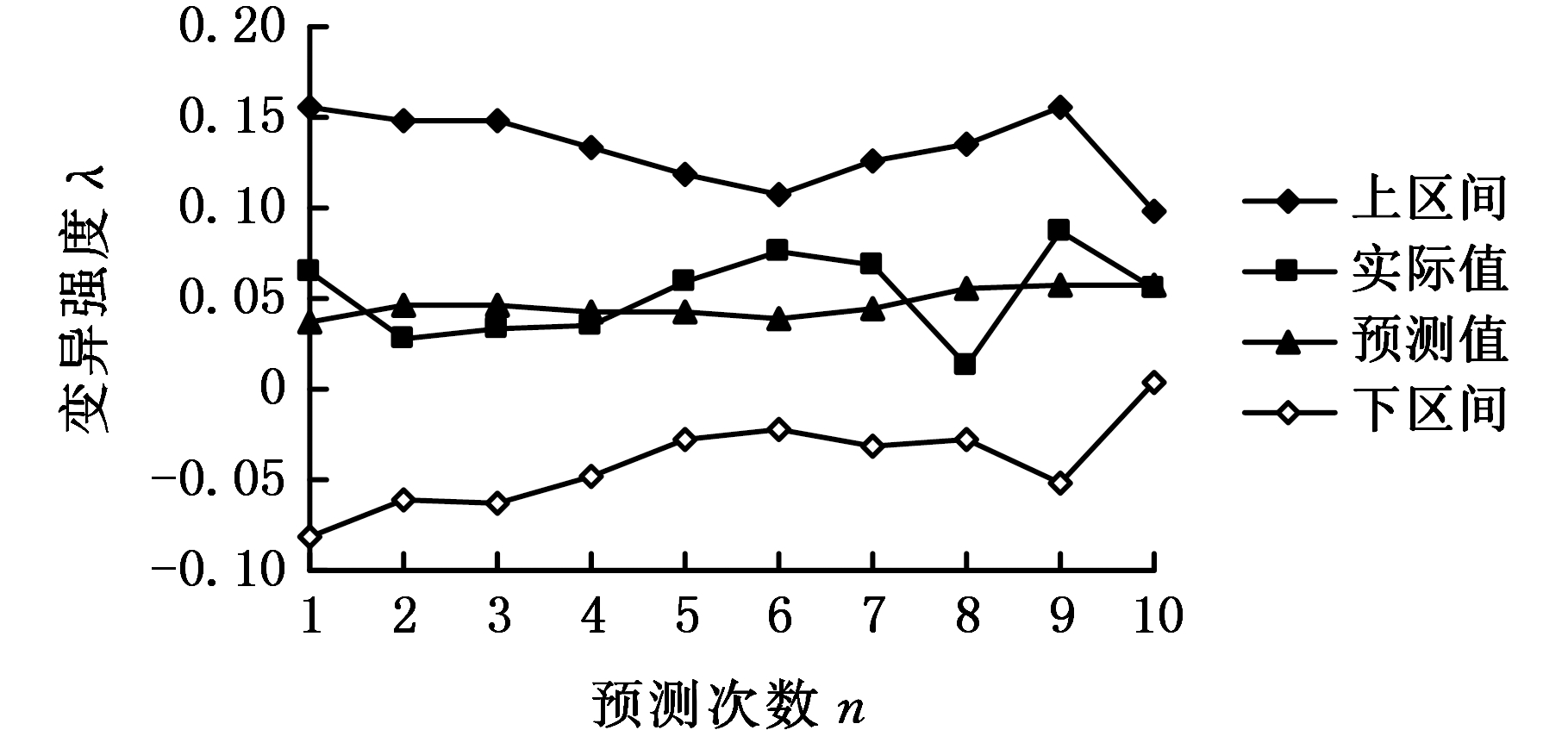
图6 各时间段摩擦力矩性能变异强度预测结果
Fig.6 Prediction results of friction torque performance variation intensity of each time period
将图6中数据代入式(17),即可得到卫星动量轮轴承A摩擦力矩性能可靠度预测值![]() 及其上下区间预测值[RL,RU]。由于式(16)中λi∈[0,1],故将图6中小于0的变异强度记作0代入式(17),并与灰色预测模型GM(1,1)[16]预测结果进行对比,见图7。其中,第1~10次预测结果分别对应第6~15个时间段卫星动量轮轴承A摩擦力矩性能可靠度预测结果。
及其上下区间预测值[RL,RU]。由于式(16)中λi∈[0,1],故将图6中小于0的变异强度记作0代入式(17),并与灰色预测模型GM(1,1)[16]预测结果进行对比,见图7。其中,第1~10次预测结果分别对应第6~15个时间段卫星动量轮轴承A摩擦力矩性能可靠度预测结果。
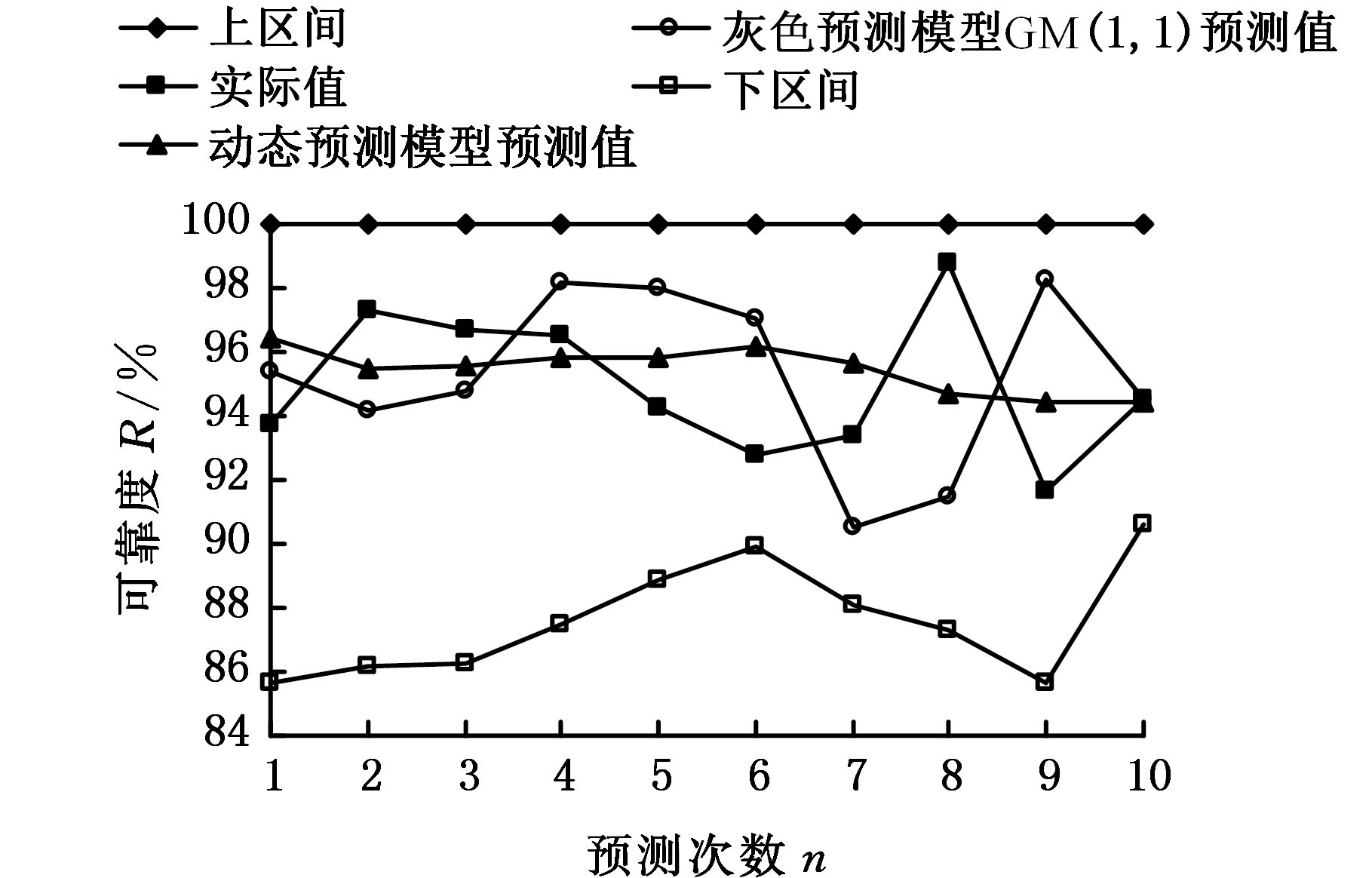
图7 各时间段摩擦力矩性能可靠度预测结果
Fig.7 Prediction results of friction torque performance reliability of each time period
由图7可以看出,可靠度的实际值和预测值均在91%以上,再次验证了试验过程中卫星动量轮轴承A摩擦力矩性能良好,可靠性较高。其中,第1~5次(第6~10个时间段)可靠度的预测值和实际值相差较小,尤其第10次(第15个时间段)可靠度的预测值和实际值几乎相同;第6~9次(第11~14个时间段)预测误差稍微偏大,最大预测误差出现在第8次(第13个时间段);其可靠度预测值上区间的数值达到了100%,且可靠度预测值下区间的数值也在84%以上,且所有可靠度的实际值和预测值均包络在上下区间内,预测范围准确率达100%。灰色预测模型GM(1,1)预测结果表明,与实际值相比,其前3次预测结果较为准确,随着预测次数的增加,预测误差相对增大,尤其在第5~9次预测,预测误差较大。这是因为随着时间的推移,旧信息数据对系统的影响越来越小,新信息数据则反映系统的最新发展状态,而灰色预测模型GM(1,1)在迭代预测过程中并未及时舍弃旧信息和引入新信息。同时也验证了所提数学模型用于轴承摩擦力矩性能可靠性动态预测的可行性和正确性。
为了更加直观地评价所提出动态预测模型的预测效果,计算得到各时间段卫星动量轮轴承A摩擦力矩性能可靠度预测值和实际值的相对误差,见图8。
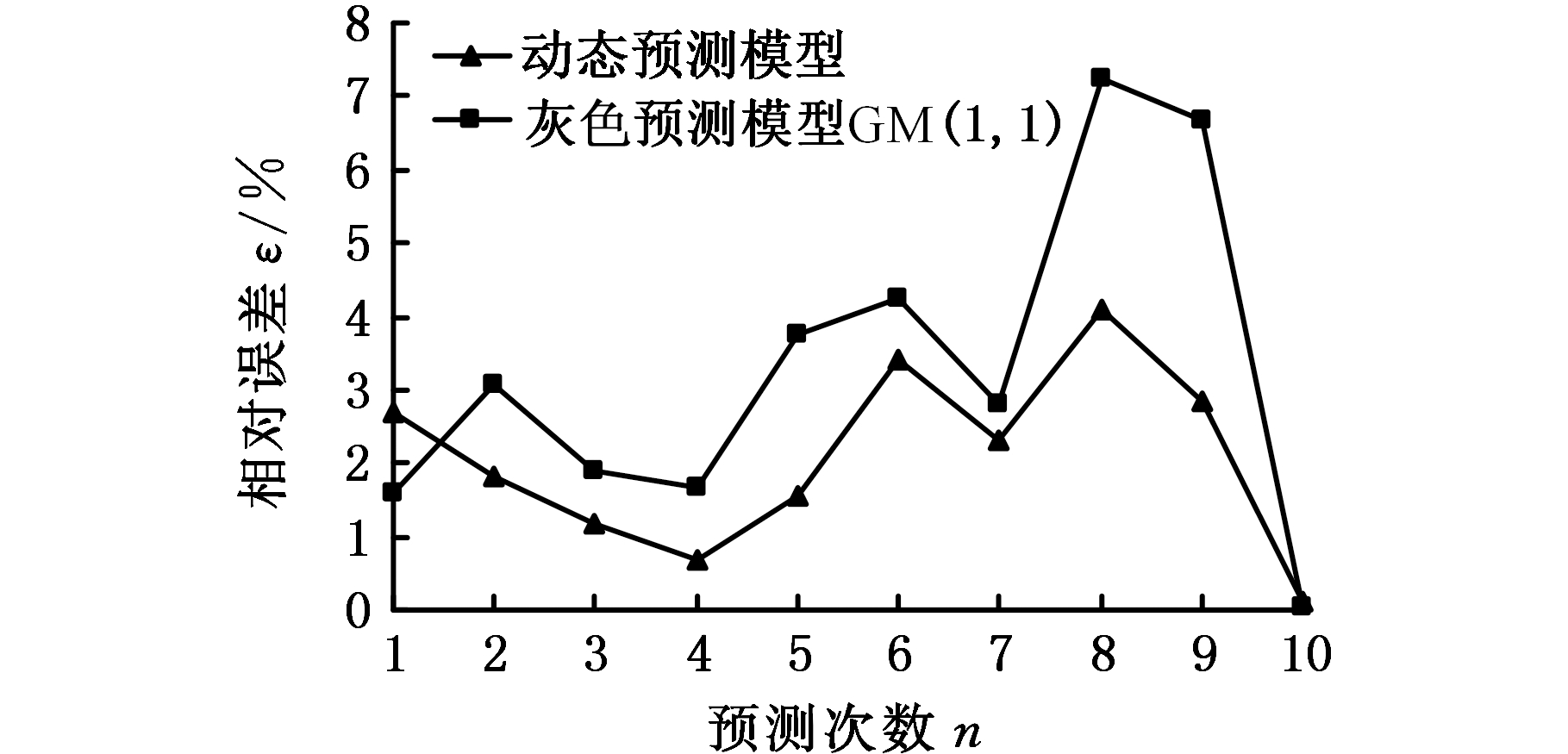
图8 各时间段可靠度实际值和预测值的相对误差
Fig.8 Relative errors of actual and predicted values of reliability for each time period
由图8可以看出,各时间段轴承A摩擦力矩性能可靠度实际值与动态预测模型预测值的相对误差均小于4.1%,其中,第1~5次(第6~10个时间段)、第7次(第12个时间段)和第10次(第15个时间段)的可靠度预测误差均小于3%,最小的预测误差出现在第10次(第15个时间段),仅为0.1%,动态预测模型的预测值和实际值几乎完全相等;而灰色预测模型GM(1,1)预测相对误差几乎均大于动态预测模型预测误差,且后期预测误差相对增大。上述研究结果再次验证了所提出动态预测模型的正确性。
2.2 变转速卫星动量轮轴承摩擦力矩仿真分析
随着轴承转速的变化,摩擦力矩电流信号将出现随机波动,且随着转速的增大,这种波动将越来越剧烈。为了模拟出这种电流信号变化趋势,本文采用蒙特卡罗法仿真出15个正态分布样本X1~X15(样本基本值均为240 mA,样本标准差从1逐渐增加到15),样本含量均为30,共450个仿真数据,见图9。
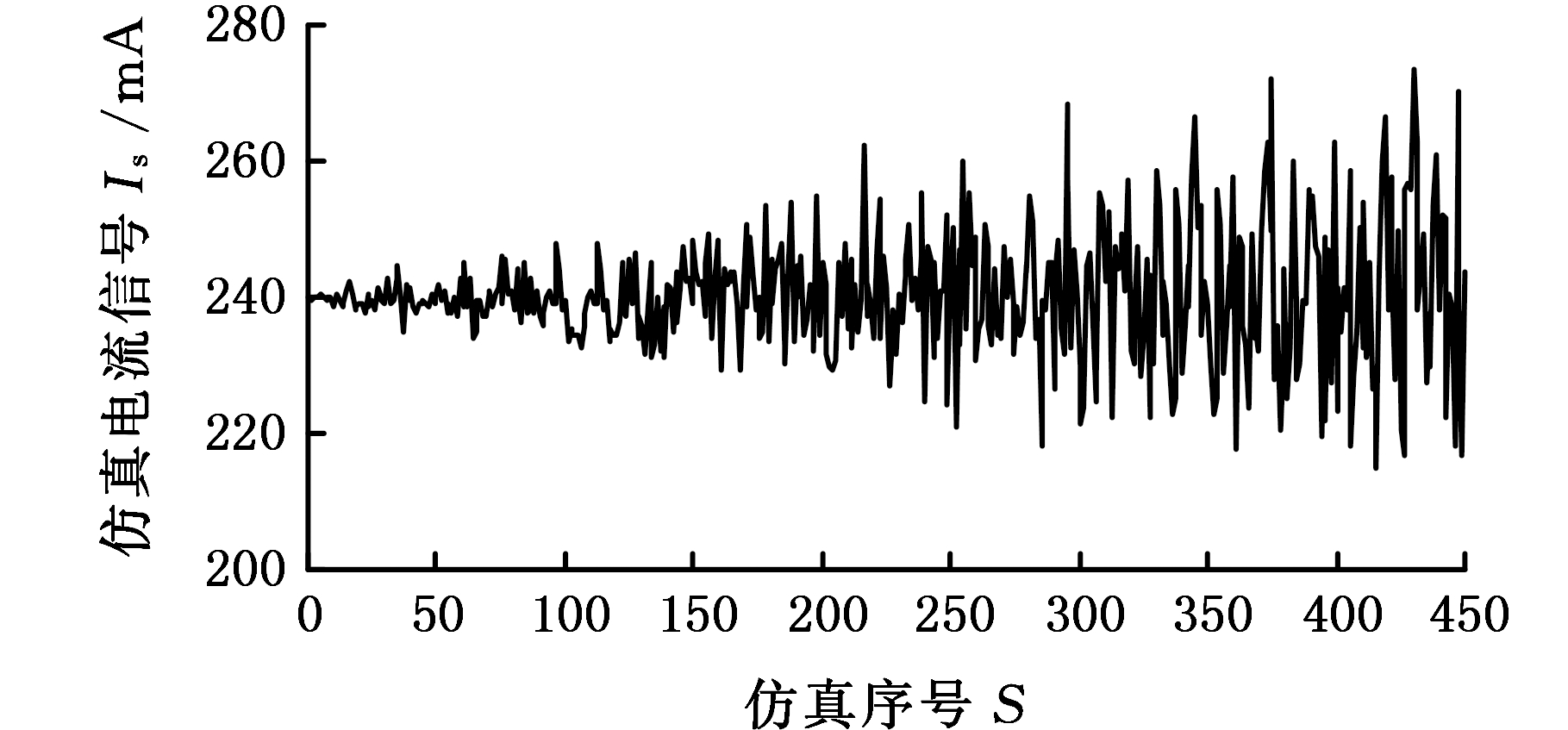
图9 仿真电流信号
Fig.9 Simulated current signal
由图9可以看出,仿真电流信号随机波动越来越强烈,可模拟出轴承摩擦力矩电流信号随轴承转速变化的越来越不稳定的变化趋势。轴承摩擦力矩性能可靠度预测过程如下。
以X1为本征样本,由式(2)~式(17)计算得到X1~X15各时间段轴承摩擦力矩性能变异强度和可靠度,分别见表6和表7。
表6 样本X1~X15的变异强度(预测值)
Tab.6 Variation intensity of X1~X15(predicted values)
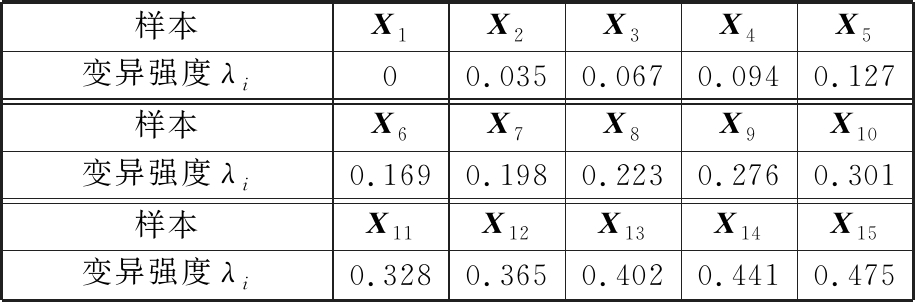
样本X1X2X3X4X5变异强度λi00.0350.0670.0940.127样本X6X7X8X9X10变异强度λi0.1690.1980.2230.2760.301样本X11X12X13X14X15变异强度λi0.3280.3650.4020.4410.475
由表7可知,X1~X15各时间段轴承摩擦力矩性能可靠度逐渐降低,这与原始数据波动越来越剧烈相一致。
将表6中的λ1~λ5进行迭代预测,可得到轴承摩擦力矩性能可靠度预测结果及预测值与实际值的相对误差,分别见图10和图11。
表7 轴承摩擦力矩性能可靠度(预测值)
Tab. 7 Friction torque performance reliability of bearing(predicted values)
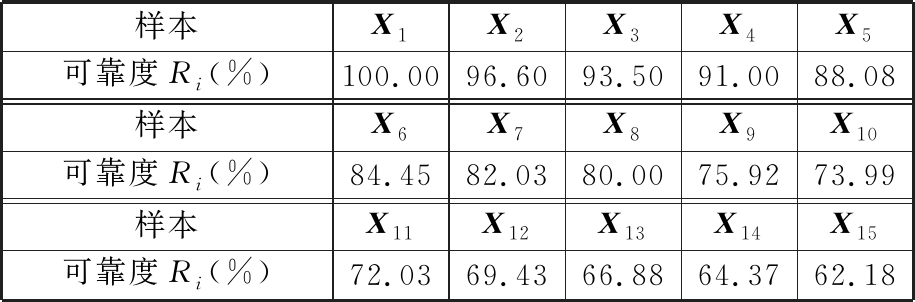
样本X1X2X3X4X5可靠度Ri(%)100.0096.6093.5091.0088.08样本X6X7X8X9X10可靠度Ri(%)84.4582.0380.0075.9273.99样本X11X12X13X14X15可靠度Ri(%)72.0369.4366.8864.3762.18
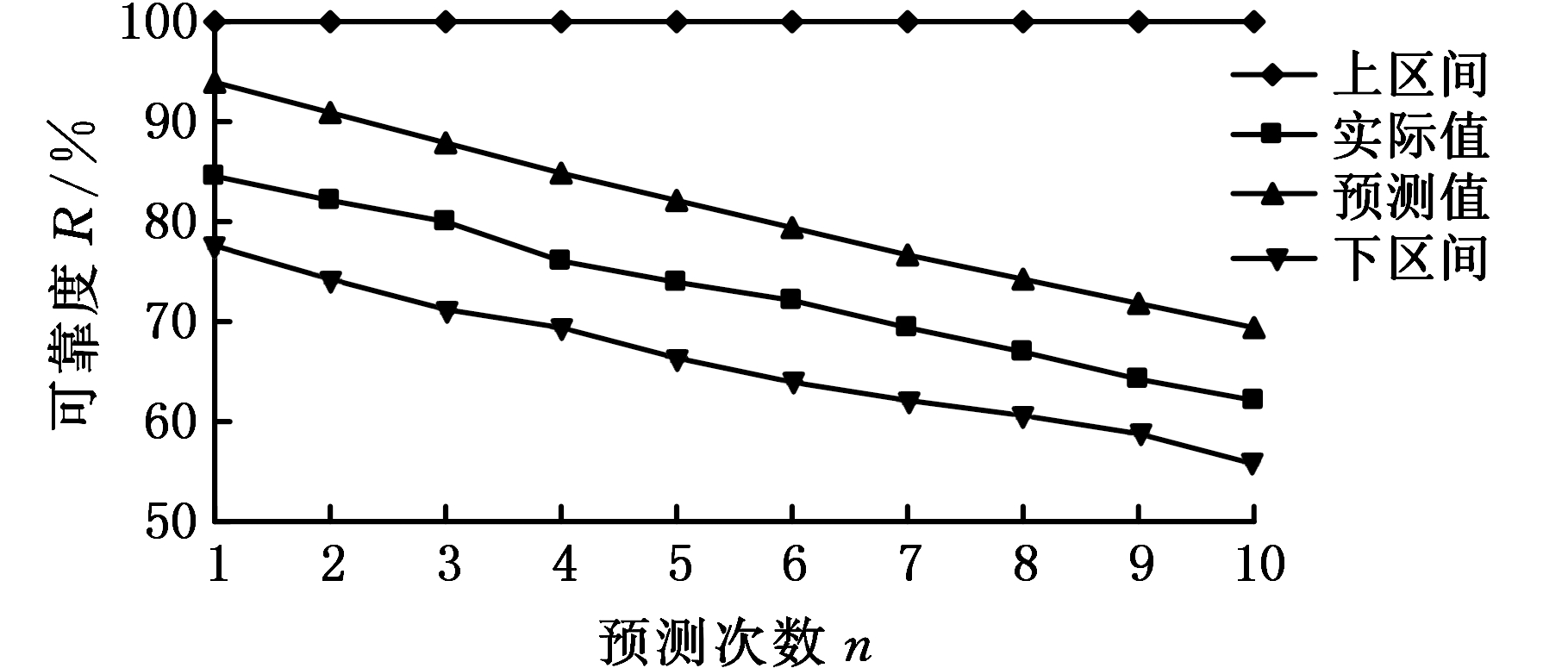
图10 仿真摩擦力矩性能可靠度预测
Fig.10 Reliability prediction of simulated friction torque
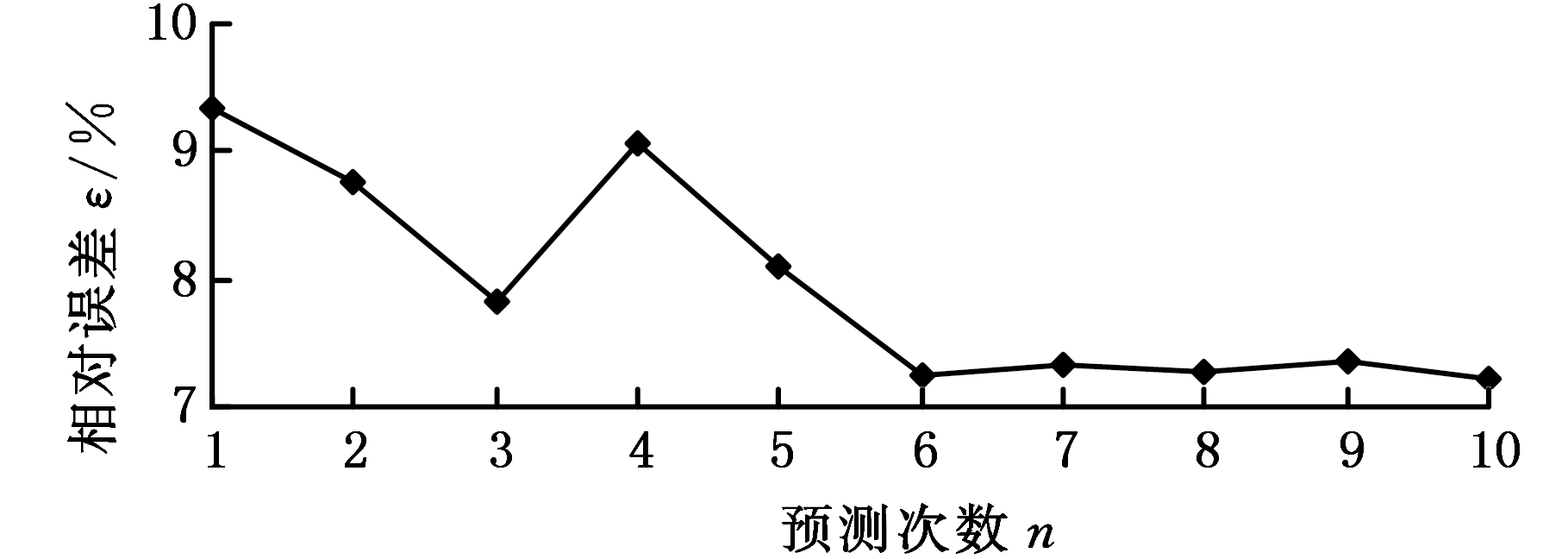
图11 可靠度实际值和预测值的相对误差
Fig.11 Relative errors of actual and predicted values of reliability
由图10可以看出,轴承摩擦力矩性能可靠度实际值和预测值保持几乎相同的减小趋势,表明原始仿真电流信号波动越来越强烈,轴承摩擦力矩性能可靠度越来越低;可靠度预测值上区间的数值达到了100%,可靠度预测值下区间的数值持续减小至60%左右,且所有可靠度实际值和预测值均包络在上下区间内,预测范围准确度100%。由图11可以看出,可靠度预测值与实际值的相对误差均在9.4%以内,较大误差出现在第1次和第4次预测,分别为9.34%和9.07%;第6~10次预测结果的预测误差稳定在7.2%~7.4%。
3 结论
(1)将灰置信水平、自助-最小二乘法和最大熵原理融合,并应用到卫星动量轮轴承摩擦力矩性能可靠性动态预测中;提出了用灰置信水平求解变异强度的新思路,弥补了变异强度传统求法中需要事先设定阈值的缺点。
(2)所提出动态预测模型是对原始试验数据本身计算得到的客观规律,对数据概率分布特征没有任何要求,弥补了传统统计学中需要事先已知数据概率分布的不足。
(3)试验分析结果表明:所提出动态预测模型可实现各时间段卫星动量轮轴承A摩擦力矩性能可靠度预测结果的验证;恒转速条件下可靠度预测误差均小于4.1%,变转速条件下可靠度预测误差也不超过9.4%。
(4)可通过改变自变量I的取值,更改预测步长,为实现超精密滚动轴承在线监控及故障诊断提供参考。
[1] 刘胜南,陆宁云,程月华,等. 基于多退化量的动量轮剩余寿命预测方法[J]. 南京航空航天大学学报, 2015, 47(3):360-366.
LIU Shengnan, LU Ningyun, CHENG Yuehua, et al. Remaining Lifetime Prediction for Momentum Wheel Based on Multiple Degradation Parameters[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(3):360-366.
[2] BELLAR A, MOHAMMED A M S, FELLAH M K, et al. Fuzzy Thruster Wheel Momentum Damping Applied under Actuated Low Earth Orbit Microsatellite[J]. Revue Roumaine des Sciences Techniques-serie Électro Technique et Énérgetique, 2017, 62(3):311-317.
[3] XIA Xintao, CHANG Zhen, YE Liang, et al. Variation Analysis of Sensitivity for Satellite Momentum Wheel[J]. Journal of Aerospace Power, 2017, 32(3):704-713.
[4] 李迎春,邱明,苗艳伟. PTFE/芳纶纤维编织衬垫自润滑关节轴承的黏接性能及摩擦学性能[J]. 中国机械工程,2016, 27(2):222-229.
LI Yingchun, QIU Ming, MIAO Yanwei. Bonding Behavior and Tribological Property for Self-lubricating Spherical Plain Bearings with PTFE/Kevlar Woven Liners[J]. China Mechanical Engineering, 2016, 27(2):222-229.
[5] LI Wei, CHEN Ming. Reliability Analysis and Evaluation for Flux-switching Permanent Magnet Machine[J]. IEEE Transaction on Industrial Electronics, 2018, 66(3):1760-1769.
[6] CHEN Guoliang, CHEN Xiaoyang. Research on Commercial Vehicle Clutch Release Bearing Fatigue Life Prediction Model[J]. Applied Mechanics and Materials, 2013, 423/426:1853-1857.
[7] OSWALD F B, ZARETSKY E V, POPLAWSKI J V. Relation between Residual and Hoop Stresses and Rolling Bearing Fatigue Life[J]. Tribology Transactions, 2014, 57(4):749-765.
[8] 朱德馨,刘宏昭,原大宁,等. 高速列车轴承可靠性试验时间的确定及可靠性寿命评估[J]. 中国机械工程, 2014, 25(21):2886-2891.
ZHU Dexin, LIU Hongzhao, YUAN Daning, et al. Time Determination and Life Assessment of High-speed Railway Bearing Reliability Test[J]. China Mechanical Engineering, 2014, 25(21):2886-2891.
[9] ALEXANDER J, STEFAN S, ALFONSO F U C, et al. Effect of Bearing Friction Torques on the Primary Stability of Press-fit Acetabular Cups:a Novel in Vitro Method[J]. Journal of Orthopaedic Research, 2018, 36(10):2745-2753.
[10] ZHOU Changguang, FENG Hutian, OU Yi. A New Model for Predicting the Mechanical Efficiency of Ball Screws Based on the Empirical Equations for the Friction Torque of Rolling Bearings[J]. Advances in Mechanical Engineering, 2018, 10(9):168781401880017.
[11] SCHERER S.The Effect of Outer Ring Distortion on Wheel Bearing Friction Torque[J]. SAE International Journal of Passenger Cars:Electronic and Electrical Systems, 2017, 10(3):786-790.
[12] ZHU Dexin, CUI Nan. Reliability Analysis of High-speed Train Bearing Based on Wiener Process[J]. International Journal of Mechatronics and Applied Mechanics, 2018,9(1):15.
[13] XU Zhaoping, MO Yuchang, LIU Yu, et al. Reliability Assessment of Multi-state Phased-mission Systems by Fusing Observation Data from Multiple Phases of Operation[J]. Mechanical Systems and Signal Processing, 2018, 118(8):603-622.
[14] 王中宇,夏新涛,朱坚民. 非统计原理及其工程应用[M]. 北京:科学出版社,2005:152-154.
WANG Zhongyu, XIA Xintao, ZHU Jianmin. Non-statistical Principles and Engineering Applications [M]. Beijing:Science Press, 2005:152-154.
[15] YANO J I, HEYMSFIELD A J, PHILLIPS V T J. Size Distributions of Hydrometeors:Analysis with the Maximum Entropy Principle[J]. Journal of the Atmospheric Sciences, 2016, 73(1):95-108.
[16] 夏新涛,陈晓阳,张永振,等. 滚动轴承乏信息试验分析与评估[M]. 北京:科学出版社,2007:38-39.
XIA Xintao, CHEN Xiaoyang, ZHANG Yongzhen, et al. Analysis and Evaluation of Poor Information of Rolling Bearing[M]. Beijing:Science Press, 2007:38-39.
