0 引言
裂纹扩展中的应力强度因子不仅体现了裂纹尖端的应力奇异性,还反映了应力与几何缺陷之间的关系,是表征裂纹尖端应力场与位移场的关键参数[1]。研究动态裂纹扩展中应力强度因子的计算方法,分析影响计算精度的关键参数并确定其参考范围,对提高应力强度因子计算精度与效率、实现关键结构裂纹扩展剩余寿命预测具有重要的科学意义与应用价值。
计算应力强度因子的常用方法有解析法、实验法和数值法。解析法和实验法受条件所限,一般用在简单几何结构和静载条件;有限元法[2]、无网格法[3]及边界元法[4]等数值法因不受几何结构或载荷情况的影响,可模拟出一般带裂纹件,受到了国内外的关注。
常规的有限元方法求解非连续位移场时依赖于单元边界,进行裂纹扩展模拟时往往需要预定裂纹扩展路径或进行网格重划分。BELYTSCHKO等[5]在有限元法基础上提出的扩展有限元法(extended finite element method,XFEM),不仅保留了传统有限元法的优点,还很好地解决了因材料和几何结构而带来的不连续问题,故XFEM得到了迅速发展,已成为裂纹扩展分析最主要的方法之一。由于存在裂纹尖端坐标、裂纹与单元切割点难以精确确定以及裂纹在单元内会发生转折等问题,采用有效方法精确计算XFEM模型中的应力强度因子一直是国内外研究的热点。NEHAR等[6]通过XFEM来模拟脆性和双材料界面的裂纹扩展,利用位移跳跃法计算应力强度因子,该计算值与理论值能很好地吻合 。周博等[7]采用基于XFEM的应力外推法对平板裂纹的应力强度因子进行计算,他们发现,纯Ⅰ型裂纹的精度较高且易于实现。GUO等[8]通过相互作用积分法计算非均质材料受热载荷下的应力强度因子,其结果与理论解有较好的一致性。ZHENG等[9]利用相互作用积分法与XFEM结合计算了带孔裂纹平板准静态下裂纹尖端的应力强度因子,并引入再分析技术,显著地减少了计算过程中的迭代次数,但缺乏实验验证。艾书民等[10]利用Franc3D软件求解裂纹扩展过程中的应力强度因子,通过疲劳寿命预测得到了验证,但其基本原理还是基于有限元法,需对网格进行加密及重复网格划分。
目前,国内外针对XFEM模型应力强度因子的计算大多集中在某型断裂模式下的准静态裂纹,有关在不同断裂模式下动态裂纹扩展应力强度因子计算方面的报道较少,有学者虽探讨了计算参数对应力强度因子计算结果的影响,但并未提出明确的计算参数范围。为此,本文基于ABAQUS软件的XFEM模块分析,采用相互作用积分法,通过Fortran语言开发urdfil用户子程序,分别对中心裂纹平板Ⅰ型断裂模式、三点弯曲Ⅱ型断裂模式下动态裂纹扩展过程的应力强度因子进行了计算,研究了网格密度和积分半径对应力强度因子计算精度的影响规律,确定了较优的计算参数范围;在对单边带孔疲劳扩展试样的应力强度因子计算的基础上,基于Paris公式预测了单边带孔试样的剩余寿命,并进行了试验验证。
1 扩展有限元法的基本理论
扩展有限元法(XFEM)在传统有限元法的框架上引入富集函数,以反映裂纹扩展带来的非连续位移场,只有少数裂纹附近的单元被富集,大部分单元都保持传统有限元单元位移模式。为此,需在有限元位移函数的表达式中增加反映局部特性的附加函数来间接模拟局部不连续性[11],其描述裂纹含裂纹面的近似位移插值矢量函数可表示为

(1)
式中,N(x)表示单元的形函数;Ns为常规节点的集合;Ncut为贯穿单元的节点集合;Ntip为裂纹尖端周围单元的节点集合;![]() 分别为常规节点位移矢量、贯穿节点位移矢量和裂纹尖端节点位移矢量;H(x)为跳跃函数,反映裂纹体的不连续性;φα(x)为裂纹尖端渐进位移场附加函数,反映裂纹尖端主要的奇异项和各种应力状态。
分别为常规节点位移矢量、贯穿节点位移矢量和裂纹尖端节点位移矢量;H(x)为跳跃函数,反映裂纹体的不连续性;φα(x)为裂纹尖端渐进位移场附加函数,反映裂纹尖端主要的奇异项和各种应力状态。
对于各项同性材料,裂纹尖端渐进位移场附加函数φα的向量表达形式如下[12]:

(2)
式中,s、θ分别为积分点在极坐标系下裂纹尖端到节点的距离和角度。
图1所示为裂纹尖端采用单层加强时(即对裂纹尖端附近的一层节点进行加强)的加强节点分布,其中,“○”表示裂纹尖端节点,“□”表示贯穿节点,其余为常规节点(图中未标出)。

图1 加强节点分布
Fig.1 Enriched nodes distribution
对于含有两种或两种以上节点的混合单元,在式(1)位移模式下得到的节点处计算值不等于真实节点位移,需通过平移加强函数来纠正,相应的位移插值矢量函数可表示为
(3)
2 基于相互作用积分法的应力强度因子计算
2.1 相互作用积分法基本理论
相互作用积分法通过建立辅助应力场和辅助位移场来获取和分离真实场中的Ⅰ型和Ⅱ型应力强度因子[13]。辅助应力场、辅助位移场是满足平衡方程、物理方程和几何方程关系的任一应力场和位移场;真实场则是物体待求裂纹尖端的应力场和位移场。
以二维裂纹扩展问题为例,如图 2所示,裂纹用一条线段表示,在其尖端建立一个局部正交坐标系,其中,Г、C0分别为绕裂纹尖端的内圆和外圆周线;nj、mj分别为路径Г和C0外法线的方向余弦;x1、x2分别表示方向1和方向2。
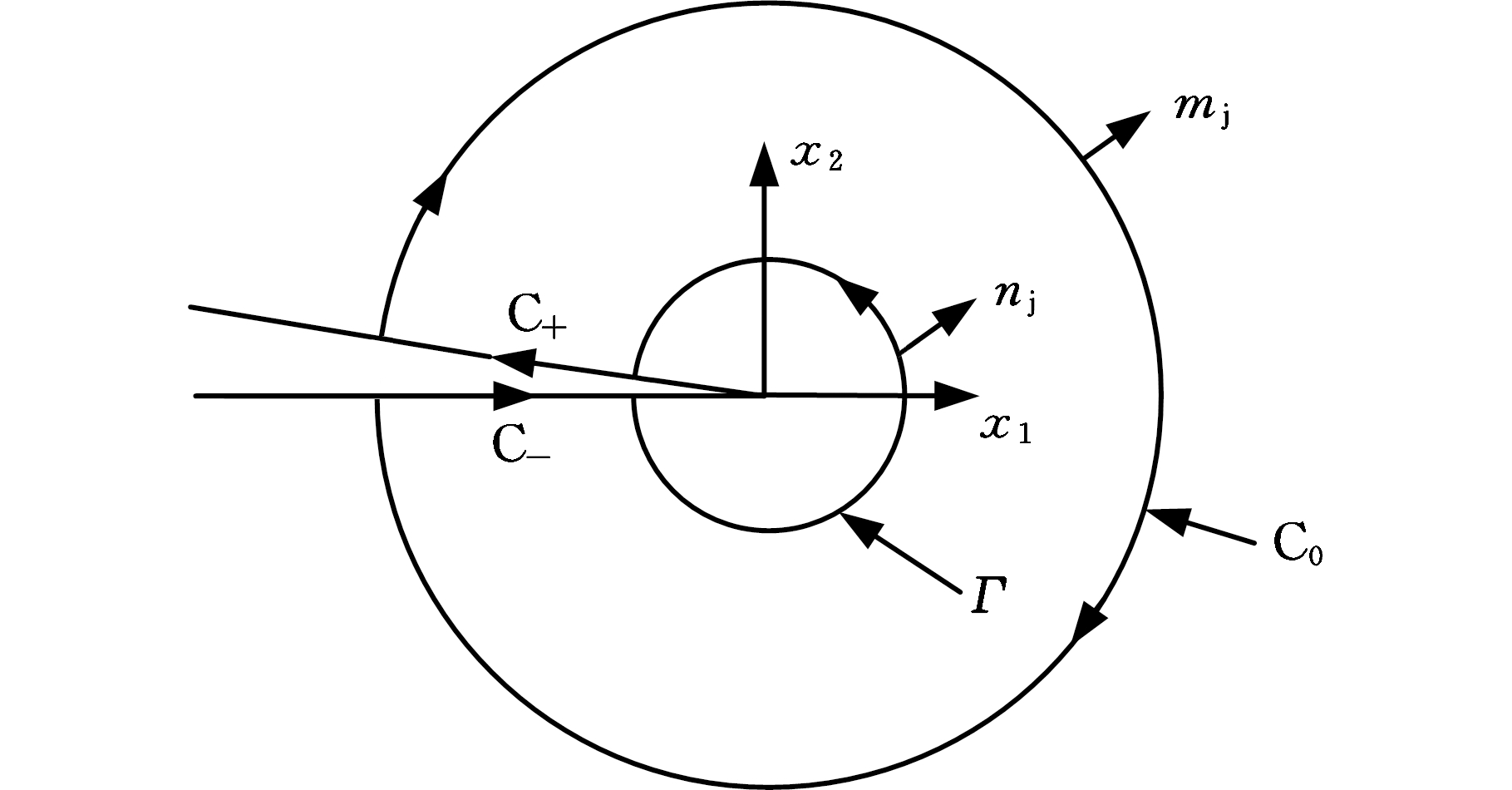
图2 局部正交坐标系
Fig.2 Local orthogonal coordinate system
定义J积分如下[14]:
![]() Г
Г
(4)
式中,w为应变能密度;δij为Kronecker函数;σij为应力分量;μi,1为方向i对方向1的位移偏导数。
为了分离混合模式下的应力强度因子KⅠ和KⅡ,利用叠加原理,选两个独立的平衡态,状态1为真实场状态,状态2为辅助场状态。将真实状态和辅助状态叠加后可得
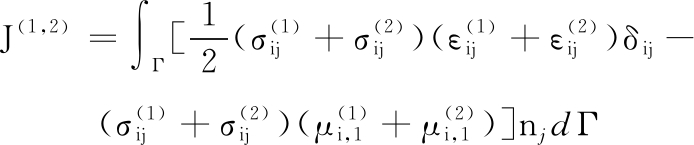
(5)
式中,![]() 分别为真实场和辅助场的应力分量;
分别为真实场和辅助场的应力分量;![]() 分别为真实场和辅助场的应变分量;
分别为真实场和辅助场的应变分量;![]() 分别为真实场和辅助场的位移偏导数。
分别为真实场和辅助场的位移偏导数。
将式(5)转换为
J(1,2)=J(1)+J(2)+I(1,2)
(6)
(7)
式中,I(1,2)为真实场和辅助场的交互积分;w(1,2)为真实场和辅助场的交互应变能密度。
各向同性材料的J积分与应力强度因子之间的关系可表示为
(8)
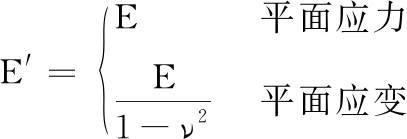
式中,E′为等效模量;E为材料的弹性模量,ν为材料的泊松比。
将两个平衡态线性叠加可得第三个平衡态,并将第三个平衡态代入式(8)可得
(9)
取状态2纯Ⅰ型、纯Ⅱ型的渐进应力场和位移场分别为f1、f2,由式(6)和式(9)分别可得
KⅠ![]()
(10)
KⅡ![]()
(11)
2.2 应力强度因子计算流程
采用ABAQUS软件建立各试样裂纹扩展的有限元模型,通过用户子程序urdfil读取运算后的单元编号以及对应的节点信息,包括当前增量步、节点编号、坐标和位移等,裂纹尖端坐标可根据单元节点的水平集插值得到;通过指定J积分区域,判断单元是否在积分区域内,并对落于积分区域内的单元节点赋予权函数;基于相互作用积分理论,构造辅助场并计算辅助场的应力应变,将真实场与辅助场的应力应变代入式(5)~式(11)分别计算得到J(1)、J(2)和KⅠ、KⅡ,并更新增量步直至计算完成。交互计算的流程见图3,用户子程序以及相互作用积分过程通过Fortran语言编写相应代码来完成。
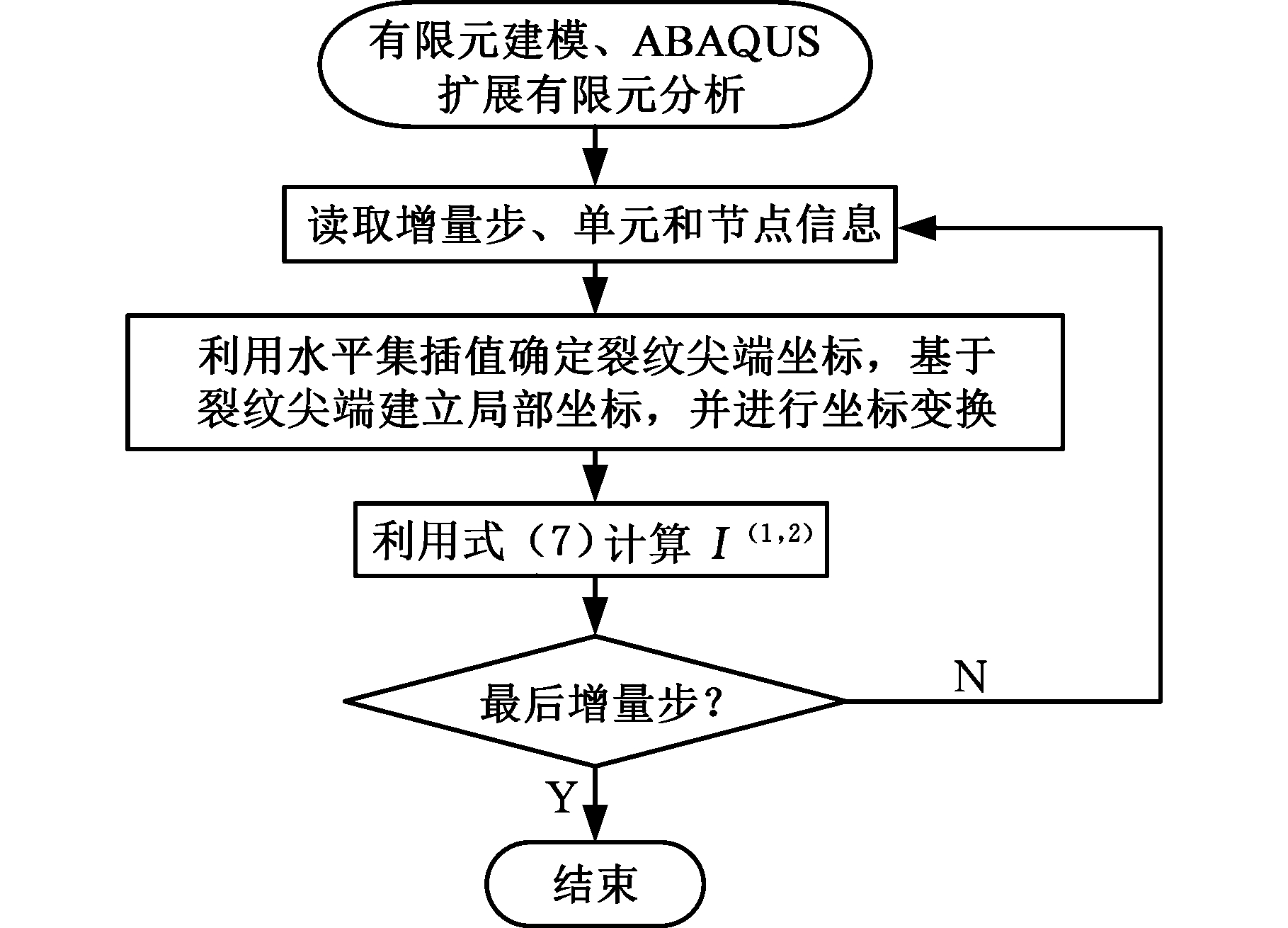
图3 算法流程
Fig.3 Algorithm flow
积分区域的指定是计算流程的一个关键步骤,图4所示阴影部分为拟指定的积分区域,其中R为绕裂纹尖端圆的半径(即积分半径),定义相对积分半径为
Rk=R/r
(12)
式中,r为单元特征长度;S为单元面积。

图4 积分区域
Fig.4 Integration area
当单元落于指定积分区域内时,为明确积分点的权函数q(x),定义:当积分区域内节点到裂纹尖端的距离大于或等于半径R时,节点权函数q(x)=1(x为方形节点);当积分区域内节点到裂纹尖端的距离小于R时,其他节点权函数q(x)=0(x为圆形节点)。
3 应力强度因子计算精度与影响因素分析
3.1 不同裂纹扩展模式下应力强度因子的计算精度
受轴向拉伸载荷作用的中心裂纹平板试样 和受集中载荷作用的三点弯曲试样常用于Ⅰ型和Ⅱ型断裂模式下的裂纹扩展规律的研究。分别制作满足解析解获得条件的中心裂纹平板标准试样和三点弯曲标准试样,并建立裂纹扩展规律分析的XFEM模型,如图5所示。
图5a所示为中心裂纹平板试样,高度H=400 mm,宽度W=200 mm,上下两端承受均布载荷σ=30 MPa的作用,裂纹长度定义为2a。图5c所示为三点弯曲试样,宽度W=20 mm,支撑点距作用点距离L=40 mm,受集中力FP=1 N的作用,裂纹长度定义为a。两种试样材料均为2024铝合金,材料属性如下[14]:弹性模量E=68 GPa,泊松比ν=0.33,主应力σmax=280 MPa。建立XFEM模型时,均采用四边形平面应力单元、结构化网格划分,两种试样的XFEM模型分别见图5b和图5d。

(a)中心裂纹平板几何尺寸 (b)中心裂纹平板扩展有限元模型

(c)三点弯曲试样几何尺寸

(d)三点弯曲试样扩展有限元模型
图5 不同断裂模式下应力强度因子的计算模型
Fig.5 The calculation model of stress intensity factors under different fracture modes
由文献[15]可知,受轴向拉伸载荷作用的中心裂纹平板的应力强度因子的理论计算表达式如下:
KⅠ![]()
![]()
(13)
当L=2W时,三点弯曲试件的应力强度因子计算表达式如下:
KⅡ![]()
(14)
式中,FV为支撑点的支持力;B为板厚。
两种试样基于相互作用积分法的应力强度因子计算值与理论值对比结果以及计算误差分别见表1和表2。由表1可知,在中心裂纹平板试样的裂纹动态扩展过程中,程序计算值与理论值的偏差不超过3%;由表2可知,在三点弯曲试样的裂纹动态扩展过程中,程序计算值与理论值的偏差不超过2%。这表明本文所提方法和程序合理,可准确地进行不同裂纹扩展模式下应力强度因子的计算。
表1 中心裂纹平板计算误差
Tab.1 Calculation errors of center crack plate

裂宽比2a/W程序计算值KXFEMⅠ(MPa·mm1/2)理论值KEXACTⅠ(MPa·mm1/2)相对误差ε(%)0.1172.3168.22.430.2246.8244.01.150.3314.2306.82.410.4381.6370.82.910.5455.2444.52.410.6550.8536.52.670.7670.6654.72.430.8827.7808.72.35
表2 三点弯曲试样计算误差
Tab.2 Calculation errors of three-point bending specimen

裂长比a/L程序计算值KXFEMⅡ(MPa·mm1/2)理论值KEXACTⅡ(MPa·mm1/2)相对误差ε(%)0.30.288 30.283 81.610.40.348 70.344 31.580.50.410 50.404 91.390.60.468 50.465 50.65
3.2 网格密度与积分半径对计算精度的影响
积分半径和网格密度是影响计算精度的主要因素,为确定合适的积分半径与网格密度,研究了不同参数对应力强度因子计算精度的影响规律。
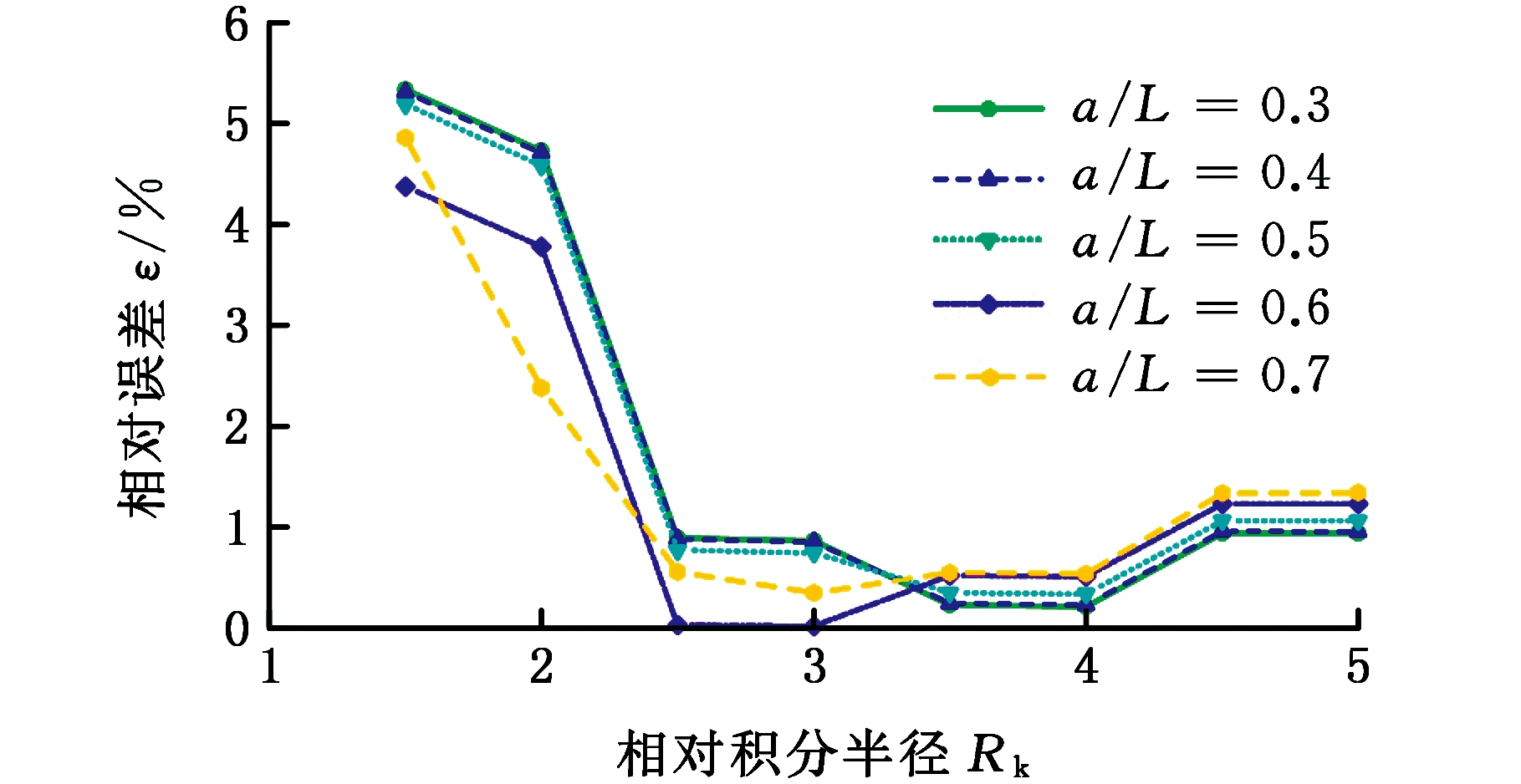
中心裂纹平板试样和三点弯曲试样在不同裂宽比(裂长比)、不同积分半径下,应力强度因子计算值与理论值的相对误差分别见图6a和图6b。由图6可以看出,对于两种试样,当相对积分半径Rk< 3时,计算误差波动较大;当相对积分半径Rk≥3时,中心裂纹平板试样和三点弯曲试样的应力强度因子计算误差分别控制在3%和2%以内,满足计算要求。

(a)中心平板裂纹试样
(b)三点弯曲试样
图6 积分半径对应力强度因子的影响
Fig.6 Effect of integral radius on stress intensity factors
对于图6a所示的裂宽比为0.1的中心裂纹平板试样,当相对积分半径Rk=4.5时,对应的积分半径R=20 mm, 积分边界正好经过裂纹另一端点,裂纹尖端的应力奇异性导致应力强度因子过大,因此出现了应力强度因子突然增大的现象,但其计算精度仍然控制在3%以内。
为研究网格密度对计算精度的要求,定义网格密度因子为
m=r/l
(15)
式中,l为平板的特征长度。
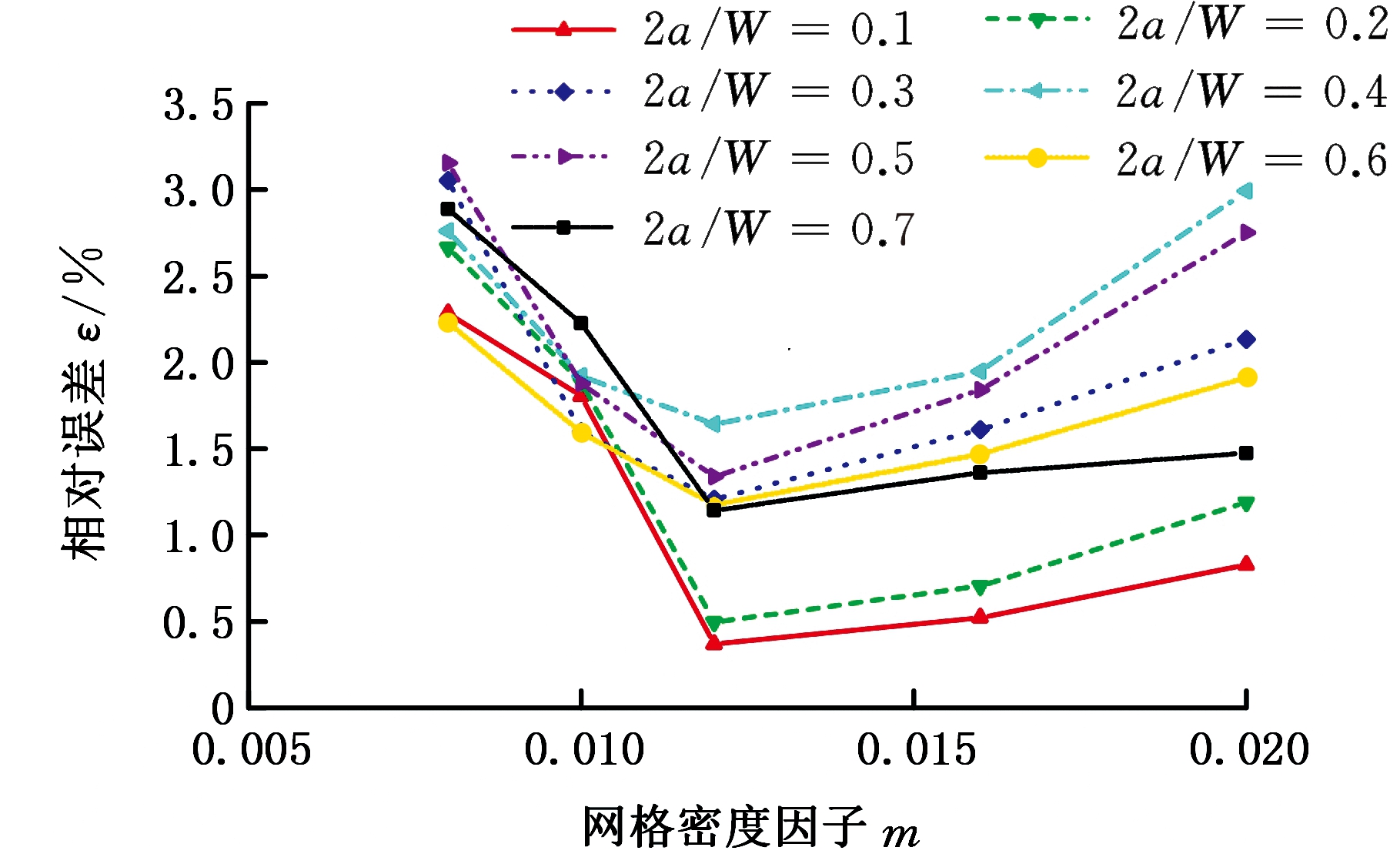
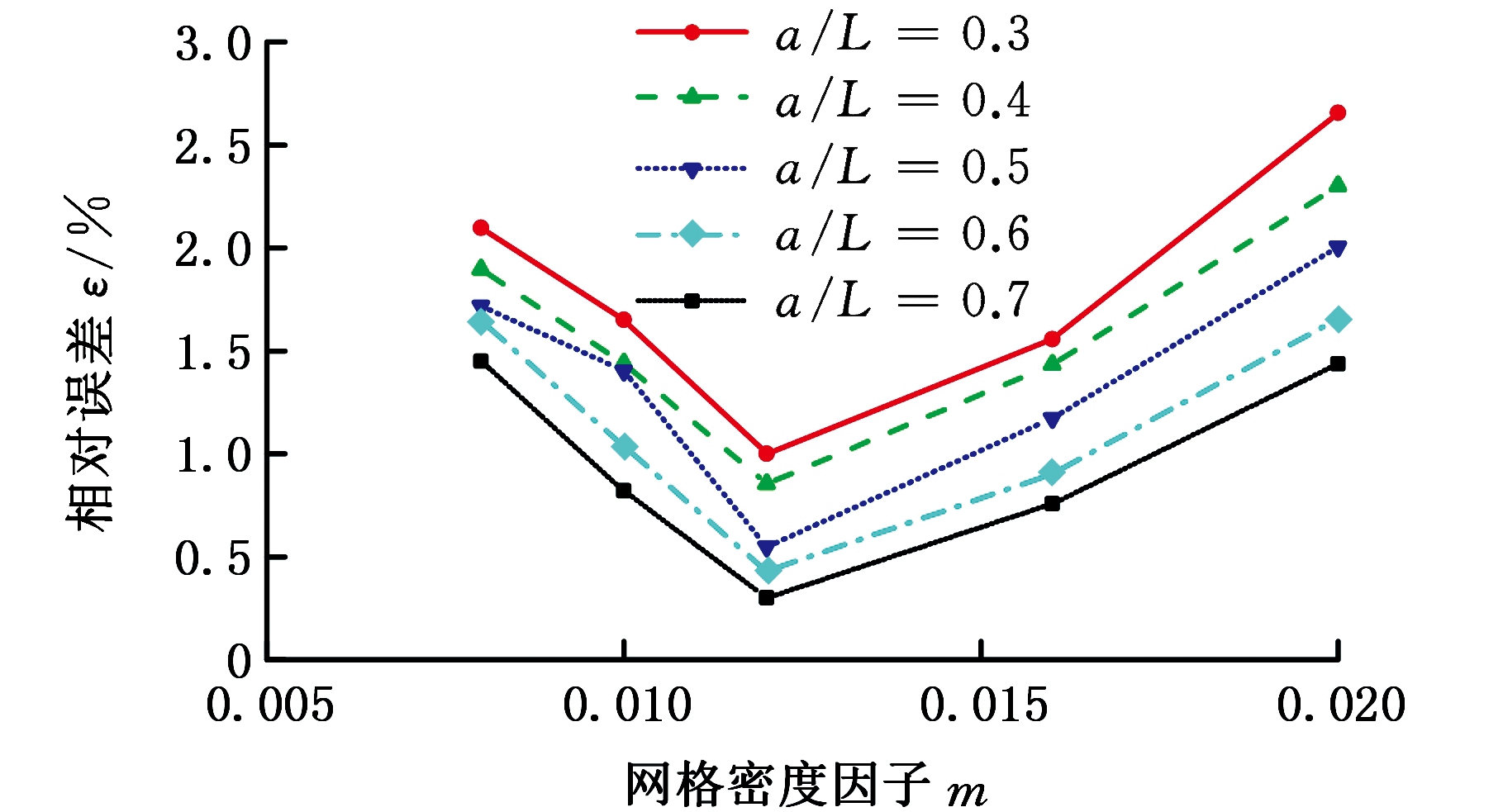
中心裂纹平板试样和三点弯曲试样在不同裂宽比(裂长比)、不同网格密度下,应力强度因子计算值与理论值的相对误差分别见图7a和图7b。由图7可以看出,当m≥0.012时,随着网格越密(即m越小),计算误差越小,求解精度越高;当m<0.012时,随着网格越密,计算误差越大。这是因为当网格过密时,积分区域是绕裂纹尖端很小的一个区域,计算值受裂尖奇异性的影响,误差偏大。当网格密度因子m在0.012~0.016范围内时,可得到较为准确的计算结果。
(a)中心裂纹平板试样
(b)三点弯曲试样
图7 网格密度对应力强度因子的影响
Fig.7 Effect of mesh density on stress intensity factors
4 典型试样动态裂纹扩展应力强度因子计算与剩余寿命预测
非标准试样动态裂纹扩展过程应力强度因子没有解析解,无法直接验证应力强度因子计算结果的准确性。将应力强度因子代入Paris公式实现各类试样剩余寿命的预测,是应力强度因子的一个典型应用,同时也可间接地验证动态裂纹扩展应力强度因子计算的准确性。
Paris公式计算疲劳裂纹扩展的寿命模型可表示为[16]
da/dN=C(ΔK)n
(16)
ΔK=Kmax-Kmin
式中,N为循环次数;C、n为材料常数,本文所用参数由文献[17]给出,C=1.484×10-10 mm/周次、n=2.761;ΔK为应力强度因子的变化,MPa·mm1/2;Kmax、Kmin分别为循坏载荷下应力强度因子的最大值和最小值。
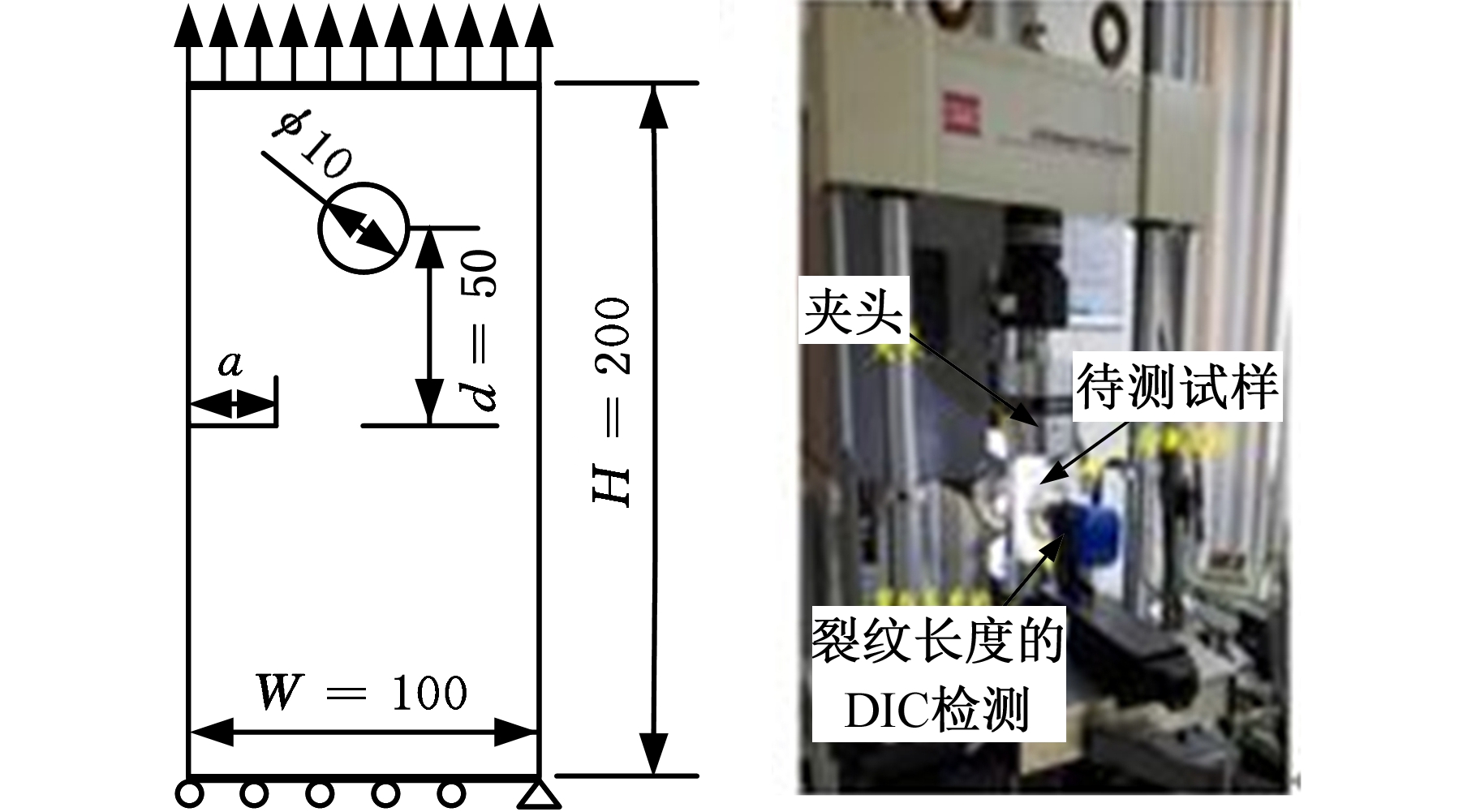
本研究的对象为非标准带孔单边裂纹扩展试样,其形状和尺寸见图8a。其中,试样高度H=200 mm、宽度W=100 mm,圆孔直径为10 mm,试样预制初始裂纹长度a=17 mm。试样受轴向应力均值为36 MPa、应力比为0.1的循环载荷σ作用,试验在MTS 810材料试验机上进行,裂纹扩展长度采用显微镜直读法来获取,测量误差不超过0.01 mm,见图8b。在ABAQUS软件中利用本文所提方法及程序建立非标试样裂纹扩展的XFEM模型(图8c)并计算应力强度因子,相关材料参数同前文2024铝合金的材料属性参数。建模时的网格密度因子为0.012,相对积分半径为3。
(a)试样几何尺寸 (b) 裂纹扩展试验

(c)XFEM模型
图8 单边带孔平板模型
Fig.8 Single side hole plate model
图9所示为裂纹扩展过程的仿真计算结果与试验实测结果,可以看出,仿真计算与试验测定的裂纹扩展路径基本一致。图10所示为计算得到的动态裂纹扩展应力强度因子变化规律,可以看出,应力强度因子KⅠ随着裂纹的扩展不断增大;应力强度因子KⅡ要小于KⅠ两个数量级以上,这表明单边裂纹带孔平板疲劳扩展以Ⅰ型为主,与实际情况相符(图9)。

(a)疲劳仿真结果 (b)疲劳试验结果
图9 疲劳仿真与试验的扩展路径
Fig.9 Extended path of fatigue simulation and test
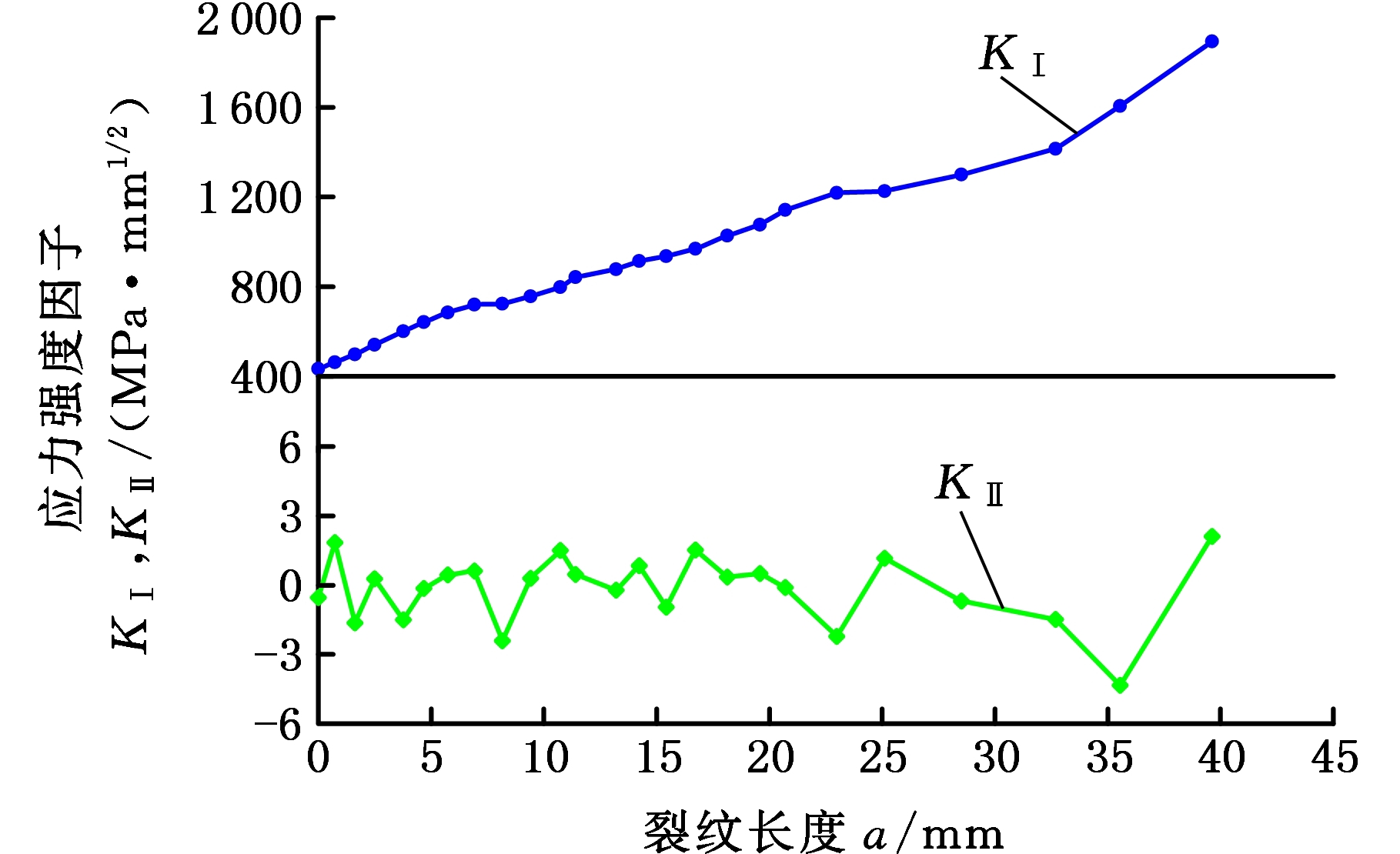
图10 应力强度因子
Fig.10 Stress intensity factors

(a)疲劳裂纹扩展a-N曲线
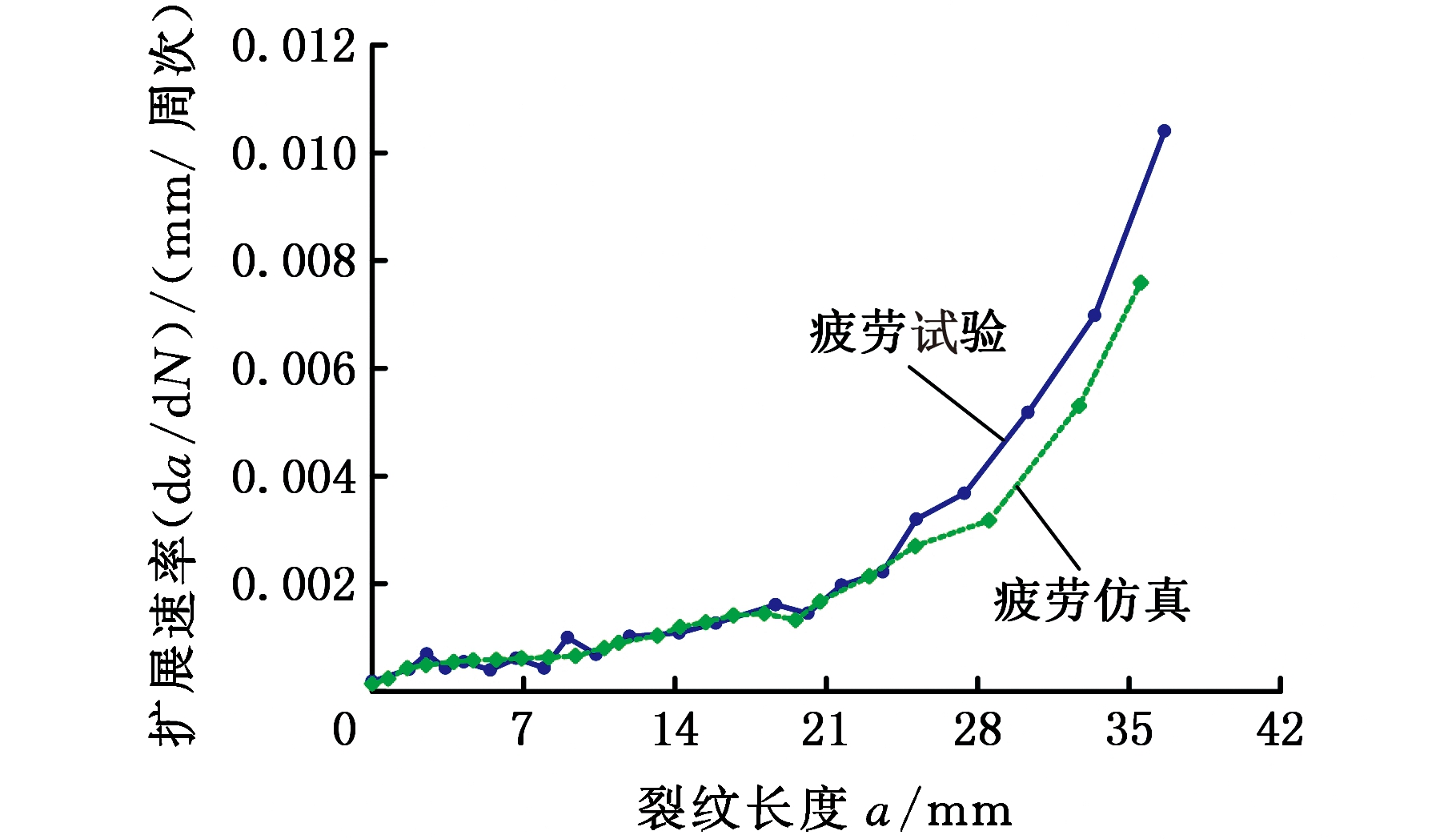
(b)疲劳裂纹扩展速率da/dN曲线
图11 单边带孔平板试样的疲劳寿命预测
Fig.11 Fatigue life prediction of single side hole plate specimens
单边带孔平板试样的疲劳寿命预测结果见图11。图11a为依据应力强度因子变化规律所计算得到的试样a-N曲线,可以看出,理论预测与试验检测结果具有较好的一致性,试样疲劳裂纹扩展的预测寿命与实测寿命分别为42 085周次和39 857周次,两者相差5.3%,在许用误差范围内。图11b为疲劳裂纹扩展速率da/dN曲线 ,可以看出,由应力强度因子计算得到的扩展速率与试验得到的疲劳扩展速率基本一致,进一步验证了应力强度因子的计算精度能够满足工程要求。
5 结论
(1)在ABAQUS软件中建立了典型试样动态裂纹扩展的XFEM模型;基于相互作用积分方法,通过Fortran语言编制用户子程序,实现了动态裂纹扩展XFEM模型应力强度因子的计算。
(2)中心裂纹平板标准试样和三点弯曲标准试样的动态裂纹扩展中应力强度因子计算值与理论值的对比分析结果表明:所提方法与所编制的程序可用于Ⅰ型、Ⅱ型裂纹扩展应力强度因子的准确计算,计算误差分别小于3%和2%。
(3)探讨了网格密度和积分半径对计算精度的影响规律,结果表明:当网格密度因子为0.012~0.016、相对积分半径Rk=3时,计算结果收敛于稳定值,计算误差控制在3%内。
(4)利用所提方法与程序对非标带孔单边裂纹扩展试样的动态应力强度因子进行了计算,基于Paris公式预测了非标准试样的疲劳裂纹扩展寿命。疲劳裂纹扩展实测结果验证了模型与所提方法的正确性,仿真值与试验值的偏差为5.3%,在许用误差范围内。
[1] 文龙飞, 王理想, 田荣. 动载下裂纹应力强度因子计算的改进型扩展有限元法[J]. 力学学报, 2018, 50(3):599-610.
WEN Longfei, WANG Lixiang, TIAN Rong. Accurate Computation on Dynamic SIFs Using Improved XFEM[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(3):599-610.
[2] BRANCO R, ANTUNES F V. Finite Element Modeling and Analysis of Crack Shape Evolution in Mode-Ⅰ Fatigue Middle Cracked Tension Specimens[J]. Engineering Fracture Mechanics, 2008,75(10):3020-3037.
[3] SAGERESAN N, DRATHI R. Crack Propagation in Concrete Using Meshless Method[J]. CMES Computer Modeling in Engineering & Sciences, 2008, 32(2):103-112.
[4] WEN P H, ALIABADI M H. Dual Boundary Element Method for Modelling Curved Crack Paths[J]. International Journal of Fracture, 2012, 176(1):127-133.
[5] BELYTSCHKO T, BLACK T. Elastic Crack Growth in Finite Elements with Minimal Remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45(5):601-620.
[6] NEHAR K C, HACHI B E, CAZES F, et al. Evaluation of Stress Intensity Factors for Bi-material Interface Cracks Using Displacement Jump Methods[J]. Acta Mechanica Sinica, 2017,33(6):1-14.
[7] 周博,薛世峰. 基于扩展有限元的应力强度因子的位移外推法[J]. 力学与实践,2017(4):371-378.
ZHOU Bo, XUE Shifeng. Displacement Extrapolation Method for Stress Intensity Factor Based on Extended Finite Method[J]. Mechanics in Engineering, 2017(4):371-378.
[8] GUO Licheng, GUO Fengnan, YU Hongjun, et al. An Interaction Energy Integral Method for Nonhomogeneous Materials with Interfaces under Thermal Loading[J]. International Journal of Solids & Structures, 2012, 49(2):355-365.
[9] ZHENG Anxing, LUO Xianqi. Numerical Study of Quasi-static Crack Growth Problems Based on Extended Finite Element Method[J]. Journal of Shanghai Jiaotong University (Science), 2014, 19(6):736-746.
[10] 艾书民,于明,成晓鸣,等. 基于Franc3D软件的三维裂纹扩展分析与应用[J]. 机械强度, 2018,40(1):251-254.
AI Shumin, YU ming, CHENG Xiaoming, et al.Analysis and Application of Three-dimensional Crack Growth Based on Franc3D[J]. Journal of Mechanical Strength, 2018,40(1):251-254.
[11] 龚迪光, 曲占庆, 李建雄, 等. 基于ABAQUS平台的水力裂缝扩展有限元模拟研究[J]. 岩土力学, 2016, 37(5):1512-1520.
GONG Diguang, QU Zhanqing, LI Jianxiong, et al. Extended Finite Element Simulation of Hydraulic Fracture Based on ABAQUS Platform[J]. Rock and Soil Mechanics, 2016, 37(5):1512-1520.
[12] ZHU Zhenyang, CHEN Weiming, ZHANG Guoxing. Cracking Propagation of Hardening Concrete Based on the Extended Finite Element Method[J]. Journal of Wuhan University of Technology(Materials Science), 2017(5):1132-1139.
[13] WEI Mingdong, DAI Feng, XU Nuwen, et al. Fracture Prediction of Rocks under Mode Ⅰ and Mode Ⅱ Loading Using the Generalized Maximum Tangential Strain Criterion[J]. Engineering Fracture Mechanics,2017,186:21-38.
[14] BENVENUTI E. An Effective XFEM with Equi- valent Eigenstrain for Stress Intensity Factors of Homogeneous Plates[J]. Computer Methods in Applied Mechanics and Engineering, 2017,4(5):427-454.
[15] 王自东,陈少华. 高等断裂力学[M]. 北京:科学出版社,2009.
WANG Zidong, CHEN Shaohua. Advanced Fracture Mechanics[M]. Beijing:China Science Publication, 2009.
[16] 申杰斌,唐东林. 一种考虑应力梯度的疲劳寿命预测方法[J]. 中国机械工程, 2017, 28(1):40-44.
SHEN Jiebin, TANG Donglin. Predicting Method for Fatigue Life with Stress Gradient[J]. China Mechanical Engineering, 2017, 28(1):40-44.
[17] LIAO Yashi, LI Yibo, PAN Qing, et al. Residual Fatigue Life Analysis and Comparison of an Aluminum Lithium Alloy Structural Repair for Aviation Applications[J]. Engineering Fracture Mechanics, 2018,194:262-280.
