0 引言
工程结构和设备运行时的安全性是重大的科技、经济和社会问题。裂纹的产生和扩展可能会影响结构的完整性,造成严重的人员和财产损失。结构中的裂纹危害大且隐蔽性强,因此如何高效地对疲劳裂纹进行检测,一直是损伤识别研究中的热点和难点问题。胡家顺等[1-2]建立了呼吸裂纹梁结构的二维有限元模型,提出系统频率的相对幅值可以作为损伤指标表征裂纹梁的损伤程度。张小五等[3]提出了应用于裂纹梁的基于能量密度的结构损伤识别方法。刘文光等[4]在假定裂纹梁刚度是幅值的非线性函数基础上,建立了呼吸裂纹梁的多项式刚度模型,提出了一种基于固有频率的呼吸裂纹梁损伤识别方法,并使用脉冲信号作为激励验证了该方法的有效性。NGUYEN[5]提出了基于模态分析的裂纹损伤识别方法。SCALERANDI等[6-10]开展了应用比例缩减法识别非线性损伤的实验研究。然而上述方法均采用低频或者脉冲信号作为激励,没有涉及到对裂纹等微小损伤更加敏感的高频频段激励。本文采用高频扫频信号作为激励,利用疲劳裂纹引发的非线性特征表征非线性损伤,提出了一种基于高频频响函数的疲劳裂纹损伤识别方法。
频响函数因其测量方便、成本低、误差小、包含信息丰富被广泛用于损伤检测领域。高频频响函数对结构局部细微变化敏感,对边界特性引起的非线性不敏感,适合作为损伤识别的参考指标。SHIN等[11]通过实验验证了频响函数对损伤检测的有效性,拓展了频响函数在结构损伤检测中的应用。CACCESE[12]研究了高频频响函数在螺栓连接结构损伤检测中的应用,给出了损伤检测的最佳参数设置。JOHNSON等[13]应用频响函数对多层框架结构进行了结构损伤检测,并对直升机驾驶舱进行了损伤识别和定位实验。NOEL等[14]探讨了飞行器的复杂非线性力学特性,研究了非线性结构的频响函数特征。
上述应用频响函数进行损伤识别的研究均需将当前结构的频响函数与健康状态下的基准进行对比,而实际工程结构的初始健康状态一般是未知的,难以得到健康基准,从而限制了频响函数方法的应用范围。本文利用激励电压幅值不同情况下非线性系统频响函数不同的特性,在无基准的情况下识别疲劳裂纹,提出了一种无需健康基准的疲劳裂纹损伤检测方法(即非线性频响差值提取法),并通过构造损伤指标分析了不同频段对非线性损伤的敏感程度。结果表明该方法能够在无基准情况下有效识别结构中的疲劳裂纹。
1 非线性频响差值提取法原理
本文将线性结构简化为单自由度线性刚度模型,如图1所示。振子由一个附着在集中质量块上的线性弹簧和线性阻尼构成,施加幅值为A、角频率为ω的持续激励f。模型运动方程为
(1)
式中,m为振子质量;c为系统阻尼;k为系统线性刚度;x、f为时间t的函数。

图1 单自由度线性模型
Fig.1 Single-degree-of-freedom linear model
对式(1)两边进行傅里叶变换可得
(m(jω)2+c(jω)+k)X=F
(2)
式中,j为虚数单位;X、F为x、f对应频域中jω的函数。
构造jω的函数H,使得
X=FH(jω)
(3)
成立。将式(3)代入式(2)得
H(jω)=(m(jω)2+c(jω)+k)-1
(4)
其中,H(jω)即为频响函数。由式(4)可知,线性结构频响函数只与结构m、c、k和激励频率有关,与激励幅值无关,所以不同激励电压下,线性结构频响函数应相同。对于非线性结构,其模型可以简化为带有三次非线性刚度kn的非线性系统,如图2所示。振子由一个附着在集中质量块上的三次非线性弹簧和线性阻尼构成。

图2 单自由度非线性模型
Fig.2 Single degree-of-freedom nonlinear model
非线性系统模型运动方程为
(5)
f=Asin(ωt+Φ)
(6)
由于出现了x的立方项,所以不能简单进行如式(2)的变换,一般采用谐波平衡法求解该方程,设试探解为
x(t)=Xsinωt
(7)
代入动力学方程(式(5))中得到
-mω2Xsinωt+cωXcosωt+kXsinωt+![]()
AsinωtcosΦ-AcosωtsinΦ
(8)
比较谐波系数后,得到系统近似频响函数为
(9)
式(9)表示,对于非线性系统,其频响函数与响应x的幅值X有关,即与激励幅值A有关。因此,可以通过对比不同电压下的频响函数来判断结构是否出现了非线性损伤。
由于实际结构本身具有多自由度的特性,所以求解结构频响函数的解析解非常复杂,而对于实际的非线性结构,通过m、c、k求频响函数精确解析解几乎不可能,因此,通常需要经过实验来测得响应信号。分别对激励信号和响应信号进行傅里叶变换,然后通过下式得到结构的频响函数:
H(jω)=X(jω)/F(jω)
(10)
非线性频响差值提取法是利用非线性结构频响函数对激励幅值的依赖性来识别非线性损伤的一种方法。给待测结构输入一系列幅值Ai(i=0,1,…,N)不同、频率相位均相同的激励,由式(10)可得出相应的频响函数Hi (i=0,1,…,N)。利用直接相减的方法将不同激励幅值下的频响函数减去最小激励幅值下的频响函数,记为
Hm,i=Hi-Hj
(11)
式中,Hj为最小激励幅值对应的频响函数。
然后将得到的差值求和取平均值,得到能代表结构非线性强弱的差值曲线,将该曲线称为非线性频响差值特性曲线,记为Hm,即
(12)
式中,N为不同幅值激励的数量。
将Hm函数的能量密度作为损伤指标可以有效地表征结构非线性损伤,其计算公式如下:
(13)
式中,n为数据点数量。
2 实验及讨论
2.1 实验装置
为了验证非线性频响差值提取法可以有效识别非线性损伤,对裂纹梁进行了非线性损伤识别实验。实验装置如图3所示。本实验对象为1块500 mm×100 mm×2 mm的铝梁,在梁中央处通过INSTRONG公司材料试验机加载循环载荷产生一长度为12 mm的疲劳裂纹。在梁表面裂纹两端粘贴两个STEMINC公司的压电片,压电片直径为12 mm,厚度为0.6 mm,两个压电片之间间隔240 mm,裂纹处于两个压电片正中央。梁两端置于海绵上已模拟自由边界,采用任意函数发生器(Agilent33522A)产生激励信号,通过电压放大器(TEGAM2350)放大后施加给一个压电片,用示波器(Agilent D50-X3014A)从另一个压电片采集电压响应信号进行分析。
2.2 实验过程与结果分析
2.2.1 裂纹梁非线性损伤识别
实验中依次给裂纹梁接入频率范围为25~60 kHz,幅值分别为0.6 V、50 V、70 V、100 V、150 V的线性扫频激励。记录示波器接收到的响应信号,通过MATLAB处理数据,得到相应的频响函数记为H0、H1、H2、H3、H4,根据式(12)计算裂纹梁的非线性频响差值函数Hm。

图3 实验装置
Fig.3 Experimental equipment
为使得图像清晰,此处仅将裂纹梁在0.6 V、50 V、150 V激励电压下的频响函数绘成曲线,如图4a所示。可以看出不同电压下裂纹梁的频响函数峰值和对应频率都有差别。将频响函数曲线局部放大后如图4b所示。50 V激励电压与150 V激励电压下的频响函数在峰值处差值可达0.7 dB,而0.6 V激励电压下与50 V激励电压下频响函数在峰值处差值为0.2 dB,说明激励电压的幅值差异越大,对应的频响函数曲线差异也越大,当激励电压的幅值存在数量级差异时,对应的频响函数差异显著。
为了验证非线性频响差值提取法的有效性,对一完整铝梁输入同样的激励做对比,得到完整梁在不同激励电压下的频响函数曲线,并根据式(12)计算完整梁的非线性频响差值函数H′m。将得到的不同激励电压下完整梁的频响函数绘成曲线,如图5a所示,不同激励电压下完整梁的频响函数曲线几乎重叠。将频响函数曲线局部放大后,如图5b所示,图像上仍无显著差异,说明不同激励电压下频响函数不同确实可以有效表征非线性损伤。
根据Hm和H′m绘制两组非线性频响差值曲线,如图6所示。由于受环境和边界状态引起的非线性影响,完整梁的非线性频响差值函数并不为零,但幅值远远小于裂纹梁的非线性频响差值函数。在低频(25~35 kHz)条件下,两组曲线幅值差异较小,而在高频(35~60 kHz)时,两组曲线幅值差异显著,说明非线性频响差值函数在高频范围对疲劳裂纹引发的非线性损伤更为敏感。
在频率范围为25~60 kHz、采样时间间隔为6.25 μs时,由式(13)计算出裂纹梁损伤指标数值D=0.91%,相应完整梁损伤指标D′=0.36%。需要指出的是,由于受环境和边界状态影响,完整梁的非线性频响差值函数不为零,导致相应的损伤指标也不为零,但与裂纹梁的损伤指标数值相比较小。这说明非线性频响差值提取法能有效识别非线性损伤。由于扫频范围包含了对局部非线性损伤不敏感区域,所以指标值较小。非线性频响差值提取法对不同频率段敏感度不一,因此需要进一步实验确定最佳的扫频范围。

(a)完整图

(b)局部放大图
图4 不同激励电压下裂纹梁频响函数曲线
Fig.4 Frequency response function curve under different excitation voltage of the cracked beam

(a)完整图
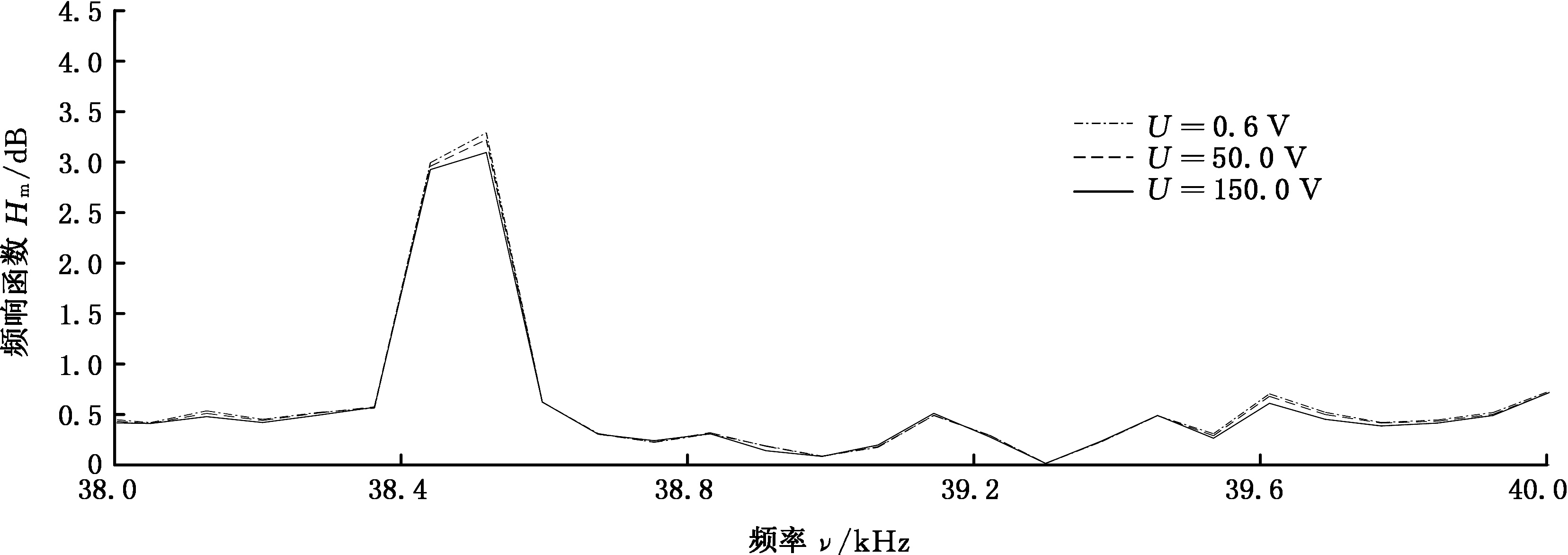
(b)局部放大图
图5 不同激励电压下完整梁频响函数曲线
Fig.5 Frequency response function curve under different excitation voltage of the intact beam

图6 非线性频响差值特性曲线对比
Fig.6 Comparison of nonlinear frequency response difference characteristic curves
2.2.2 最佳扫频范围确定
本节针对不同扫频范围对裂纹梁进行了非线性频响差值提取实验研究。为了削弱环境工况以及放大器长时间工作对实验准确度可能造成的影响,对实验过程进行了简化,只选取激励幅值为0.6 V与100 V进行对比。
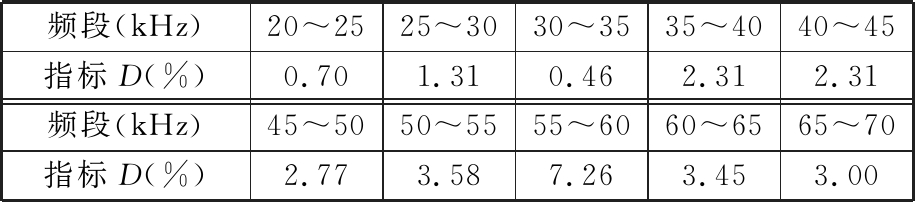
实验结果如表1所示。低频频响函数对局部细微损伤不敏感,所以频率在35 kHz以下时,损伤指标数值较小,难以有效识别非线性损伤。在频率大于35 kHz时,损伤指标数值较大,非线性频响差值提取法可以有效地识别非线性损伤。当频率范围在55~60 kHz时,损伤指标值达到最大,为7.26%,该频率段下非线性频响差值提取法可以显著识别非线性损伤。所以本实验选定最佳扫频范围为55~60 kHz。非线性频响差值提取法采用35 kHz以上的激励频率范围可以有效识别疲劳裂纹。在进一步的实验研究或对相似结构进行疲劳裂纹损伤识别时,宜选取包含55~60 kHz频率段的扫频信号作为激励。需要注意的是,对于不同的疲劳裂纹长度,应用该方法进行损伤识别的最佳频率范围不同。
表1 裂纹梁损伤指标汇总
Tab.1 The damage index of cracked beam
频段(kHz)20~2525~3030~3535~4040~45指标D(%)0.701.310.462.312.31频段(kHz)45~5050~5555~6060~6565~70指标D(%)2.773.587.263.453.00
3 结语
本文提出了一种基于高频频响函数的无基准疲劳裂纹识别方法,即非线性频响差值提取法,该方法通过计算不同电压下频响函数差值来识别疲劳裂纹引起的非线性损伤,无需健康基准。本文通过裂纹梁实验验证了该方法的有效性,构造了相应的损伤指标,并找到了应用该方法进行疲劳裂纹识别的最佳频率段,结果表明,非线性频响差值提取法可以作为疲劳裂纹识别的有效手段。需要说明的是,对于不同的结构,应用该方法进行疲劳裂纹损伤识别的判别标准仍需进一步研究。
[1] 胡家顺, 冯新, 周晶. 呼吸裂纹梁非线性动力特性研究[J]. 振动与冲击, 2009, 28(1):76-80.
HU Jiashun, FENG Xin, ZHOU Jing. Study on Nonlinear Dynamic Response of a Beam with a Breathing Crack [J]. Journal of Vibration and Shock, 2009, 28 (1): 76-80.
[2] 胡家顺, 冯新, 李昕,等. 裂纹梁振动分析和裂纹识别方法研究进展[J]. 振动与冲击, 2007, 26(11):146-152.
HU Jiashun, FENG Xin, LI Xin, et al. State-of-Art of Vibration Analysis and Crack Identification of Cracked Beams [J]. Journal of Vibration and Shock, 2007, 26 (11): 146-152.
[3] 张小五, 马文来, 王坤. 裂纹梁损伤识别的一种新型方法[J]. 装备环境工程, 2013, 10(1):73-78.
ZHANG Xiaowu, MA Wenlai, WANG Kun. A New Method of Cracked Beam Damage Identification [J]. Equipment Environmental Engineering, 2013, 10 (1): 73-78.
[4] 刘文光,郭隆清,贺红林,等. 基于固有频率的呼吸式裂纹梁损伤识别方法[J]. 中国机械工程, 2017, 28(6): 702-707.
LIU Wenguang, GUO Longqing, HE Honglin, et al. A Damage Identification Method of a Breathing Cracked Beam by Natural Frequency[J]. China Mechanical Engineering, 2017, 28(6): 702-707.
[5] NGUYEN K V. Mode Shapes Analysis of a Cracked Beam and Its Application for Crack Detection[J]. Journal of Sound & Vibration, 2014, 333(3):848-872.
[6] SCALERANDI M. Power Laws and Elastic Nonlinearity in Materials with Complex Microstructure[J]. Physics Letters A, 2016,380:413-421.
[7] SCALERANDI M, GLIOZZI A S, BRUNO C L E, et al. A Scaling Method to Enhance Detection of a Nonlinear Elastic Response[J]. Applied Physics Letters, 2008, 92(10):795.
[8] BRUNO C L E, GLIOZZI A S, SCALERANDI M, et al. Analysis of Elastic Nonlinearity Using the Scaling Subtraction Method[J]. Physical Review B, 2009, 79(6):7715-7722.
[9] GLIOZZI A S, SCALERANDI M, ANTONACI P, et al. Conditioning-induced Elastic Nonlinearity in Hysteretic Media[J]. Applied Physics A, 2010, 100(2):421-424.
[10] BENTAHAR M, GUERJOUMA R E, IDIJMARENE S, et al. Influence of Noise on the Threshold for Detection of Elastic Nonlinearity[J]. Journal of Applied Physics, 2013, 113(4):30-36.
[11] SHIN H J, YUN C Y, PARK G. Assessing Joint Integrity of a Lug Assembly Using Piezoelectric Active Sensors[J]. Structrual Control and Health Monitoring, 2012,19:621-631.
[12] CACCESE V. Detection of Bolt Load Loss in Hybrid Composite/Metal Bolted Connections[J]. Engineering Structures, 2004,26: 895-906.
[13] JOHNSON T J, BROWN R L, ADAMS D E. Distributed Structural Health Monitoring with a Smart Sensor Array[J]. Mechanical Systems and Signal Processing, 2004,18: 555-572.
[14] NOEL J P, RENSON L, KERSCHEN G. Complex Dynamics of a Nonlinear Aerospace Structure: Experimental Identification and Modal Interactions[J]. Journal of Sound & Vibration, 2014, 333(12):2588-2607.
