0 引言
滚刀磨损是盾构机施工过程中的一个重要问题,滚刀磨损量的计算基本是基于工程或试验现场的施工参数[1],如贯入度、刀间距、掘进机掘进速度以及滚刀破岩单位体积耗能等。滚刀磨损是滚刀在重载作用下的持续损伤过程,工程中刀圈磨损形式随时间、工况和地质的变化而变化,往往是多种磨损形式并存,磨损形式主要为磨料磨损和疲劳磨损[2],但通常是一种磨损形式起主导作用。大量研究表明,盘形滚刀刀圈磨损的主要机理为磨料磨损,该磨损分为塑性变形和脆性断裂两种磨损去除机制[3]。
磨损是涉及材料、几何尺寸以及接触等非线性的复杂动态过程。不同的工程、施工方法和地质环境都会使隧道有所差异,致使刀具磨损情况不同。赵战欣[4]通过分析秦岭隧道施工数据,定性地研究了掘进距离、刀具位置和地质参数对刀具磨损的影响,得出滚刀磨损量与掘进距离线性相关,刀具位置对滚刀磨损有较大影响,且刀圈磨损速度与地质因素有较大关系的结论。岩石材料一般具有各向异性和非均质等性质,围岩磨蚀性通常通过试验或经验得出[5]。
本文为了准确计算盘形滚刀磨损量,首先求解破岩弧长和基于CSM(Colorado school of mines)模型的破岩力,对磨损机理进行分析;然后建立了基于塑性与脆性断裂去除机制的磨损模型,采用粒子群算法对磨损占比进行优化;最后通过有限元分析软件计算了磨损量,并与理论结果进行了对比。
1 盘形滚刀磨损机理
1.1 滚刀破岩轨迹分析
滚刀刀圈的磨损是在与岩石的接触摩擦过程中产生的,刀圈各点接触时间越长,接触距离越长,磨损量就越大,因此,滚刀的破岩轨迹直接影响着滚刀的磨损量。
滚刀刀圈正面上各点距离滚刀中心距离相等,接触区的运动轨迹也相同,因此,对滚刀破岩轨迹进行分析[6],如图1所示。

图1 滚刀破岩运动
Fig.1 Rotary rock breaking motion
假设滚刀半径为R,贯入度为h,安装半径为Ri,取刀圈正面上点P为研究对象,其转动角为φ,点P转到与破岩最深点夹角为θ时,它与岩石接触点的距离为y,在X、Y、Z轴上的位移分别为
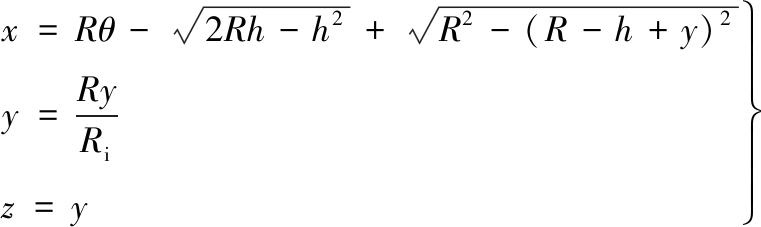
(1)
因此,滚刀正面上一点在滚刀转动一圈后所走过的弧长s为
(2)
将式(1)代入式(2)得到滚刀正面所走过的弧长
(3)
对于滚刀侧面上任意一点P,设该点到滚刀中心的距离为RP,刀圈侧面上的点只有满足R-RP<h时,才会与岩石产生接触磨损。把P点等效为贯入度h′=RP-(R-h)的破碎点,则点P在滚刀转动一圈后所走过的弧长
(4)
1.2 滚刀受力分析
岩石与刀圈接触时,岩石表面上的凸起和硬质颗粒不断碾压或划伤刀圈,导致刀圈表面材料被去除,从而产生磨损,滚刀磨损与刀圈表面的受力状况相关。
滚刀在破岩过程中受到的外力主要是岩石对刀刃的作用力,可以分解为垂直于岩石开挖面的法向力、平行于岩面的切向力以及平行于刀轴的侧向力,而滚刀侧向力一般可略去不计。在盘形滚刀破岩切削力计算模型中,CSM模型[7]是最著名、应用最广的模型,其表达式为

(5)
式中,Ft为滚刀正面所受合力,kN;P(0)为破碎区压力;T为滚刀刀刃宽度;α为刀尖压力分布系数,它随刀尖宽度增大而减小,一般α取-0.2~0.2;q为量纲一系数,一般取2.12;S为刀间距;σc为岩石单轴抗压强度,MPa;σt为岩石抗拉强度,MPa。
滚刀力学分布如图2所示,Fv和Fr分别为垂直力和滚动力,表达式为


图2 滚刀刀圈压力分布
Fig.2 Pressure distribution of the hob cutter ring
在垂直力和滚动力作用下,刀圈对岩石产生挤压、剪切、拉裂等作用。起初,岩石会产生小破碎体,破碎体在刀刃下被压碎,然后被压实成密实核,随后,密实核将滚刀压力施加到围岩,围岩产生径向裂纹,其中有一条或多条延伸到刀刃两侧,到达自由面或相邻裂纹交汇后形成岩石碎片。
通过分析岩石的破碎形式,基于摩尔-库仑定律建立刀圈侧面的接触应力模型[8],得到岩石接触面的正应力
(6)
式中,pn为滚刀侧面上某点的接触应力;c为岩石内聚力;φb为岩石内摩擦角;θh为滚刀刀刃角;β为岩石与滚刀表面的摩擦角;ψ为岩石破碎角。
1.3 磨料磨损机理
为了建立磨损计算模型,必须清楚磨损机理,分析材料在磨损过程中的状态。一般有两种材料去除机制,一种为塑性变形引起的去除机制,另一种为脆性断裂引起的去除机制,总磨损量由这两部分组成。塑性变形去除机制主要有犁沟和微观切削两种材料去除过程[3]。当材料硬度和载荷较大时,磨粒磨损主要表现为脆性断裂。
基于微量切削假说,ERNEST[9]建立了圆锥体的滑动犁沟磨料磨损模型,如图3所示。假定单颗磨料形状为圆锥体,锥底半径为r,半角为θg,法向载荷为Pg,磨料压入深度为hg,滑动距离为L,受压屈服极限为σs,则磨料在垂直方向的投影面积A=πr2。假设每个颗粒完全被压入磨损面,法向载荷仅作用于磨料前进方向的半个锥面,接触面上有n个磨料,其受到的法向载荷为

图3 简化磨料磨损模型
Fig.3 Simplified abrasive wear model
犁去的体积即磨损体积,则滑动单位距离的磨损体积为
考虑到凸体相互作用产生磨料的概率为K,则单位滑动距离的磨损体积Q′0=KQ0,滑动距离为L时,塑性去除机制下的线磨损体积为
式中,Ks为磨料磨损系数。
σs通常用刀圈硬度H表示,因此得到塑性去除机制下滑动单位距离的线磨损率
(7)
基于断裂力学,MOORE等[10]推导出了脆性断裂机制下滑动单位距离的线磨损率公式:
(8)
式中,K1为磨料形状和分布系数,一般取2;p为被磨材料所受应力,MPa;d为磨料直径,mm;Kc为断裂韧性,MPa·m1/2。
2 滚刀单圈磨损计算模型
滚刀刀圈的单圈磨料总磨损量由塑性变形与脆性断裂形成,结合正侧面磨损量,建立磨损模型

(9)
式中,Q为总磨损量;Qz、Qc分别为正侧面磨损量;Qsz、Qdz分别为基于塑性去除和脆性断裂机制下的正面磨损量;Qsc、Qdc分别为基于塑性去除和脆性断裂机制下的侧面磨损量;a为塑性去除的系数,0<a<1;b为正面磨损的系数,0<b<1。
2.1 基于塑性去除机制的磨损量计算
将式(5)代入式(7)得到刀圈正面线磨损率
(10)
结合破岩轨迹分析,由式(3)、式(10)得到某点完成一次破岩的正面线磨损量
wsz=![]() qszds=
qszds=![]()
(11)
刀圈正面由塑性去除产生的体积磨损量为
Qsz=2πRTwsz=
同理,将式(6)代入式(7)得到刀圈侧面线磨损率为
滚刀侧面上与刀圈中心距离为RP的一点由塑性去除机制所产生的线磨损量为
wsc=![]() qscds=
qscds=
距离刀圈中心为RP的一点一次完整切割的磨损体积微元ΔW=2πRPwdy。
设初始RP=R-h,由塑性去除引起的刀圈侧面所有与岩石接触的点的体积磨损量为
Qsc=2![]() 2πwsc(RP+y)dy=
2πwsc(RP+y)dy=![]()
![]()
2.2 基于断裂去除机制的磨损量计算
将式(5)代入式(8)得到断裂去除机制引起的刀圈正面线磨损率

则某点完成一次破岩的线磨损量
wdz=![]() qdzds=
qdzds=![]()
刀圈正面由断裂去除机制产生的体积磨损量为
Qdz=2πRTwdz=![]()
![]()
同理,将式(6)代入式(8),得到刀圈侧面线磨损率

滚刀侧面上与刀圈中心距离为RP的一点由断裂去除机制所产生的线磨损量为
wdc=![]() qdcds=
qdcds=![]()
![]()
刀圈侧面所有与岩石接触的点体积磨损量为
Qdc=2![]() 2πwdc(RP+y)dy=
2πwdc(RP+y)dy=![]()
![]()
3 磨损占比系数优化
为了提高磨损模型的准确率,采用粒子群优化算法[11](particle swarm optimization,PSO)对占比系数进行迭代寻优。优化占比系数的最终目的是使实际工程数据与理论计算数据的误差最小。PSO算法流程如图4所示。

图4 基于PSO的寻优算法流程图
Fig.4 Flow chart of PSO-based optimization algorithm
将占比系数a和b看作粒子,在M维解空间中,由n个粒子组成的种群X=(X1,X2,…,Xn),给初始粒子位置和速度分配随机值[12]。粒子在解空间中运动,通过个体极值和全局极值更新个体的速度和位置,更新公式如下:
m=1,2,…,M i=1,2,…,n
式中,ω为惯性权重;k为当前的迭代次数;Vim为粒子的速度;![]() 为当前个体最优粒子位置;
为当前个体最优粒子位置;![]() 为当前粒子位置;
为当前粒子位置;![]() 为全局最优粒子位置;c1、c2为被称为加速度因子的非负常数;r1、r2为分布于[0,1]之间的随机数。
为全局最优粒子位置;c1、c2为被称为加速度因子的非负常数;r1、r2为分布于[0,1]之间的随机数。
为了防止粒子的盲目搜索,粒子的位置和速度限制在[-Xmax,-Xmin]、[-Vmax,-Vmin]区间内。
粒子每更新一次速度和位置,就计算一次适应度值。目标函数可以计算出对应于每个粒子位置Xi的适应度值。建立目标函数:
f(x)=min(Q(Xi)-k)2
式中,Q为磨损计算量;Xi表示第i个粒子;k为工程实际磨损量。
通过对比新粒子的适应度值实现个体在解空间中的优化。
4 实例分析
4.1 磨损量的计算
选用陕西某隧道施工中不同厂家刀具进行施工的刀具磨损消耗分析。不同的刀具,其刀盘分布不同,刀关数量也不同,本文选用MB266-395敞开式岩石隧道掘进机(TBM),对1~8号刀进行分析,这些刀均为19英寸盘形滚刀,其刀圈直径D=482.6 mm(19英寸),刀刃宽度T=19 mm,岩石破碎角ψ=140°,刀圈尺寸参数如图5所示。本文所选用滚刀刀圈硬度为57.8 HRC,掘进深度为21.464 m,掘进时间为15.4 h,转速为4.5 r/min,推力为24 MPa,贯入度为 5 mm/r,试验段围岩强度为172 MPa。
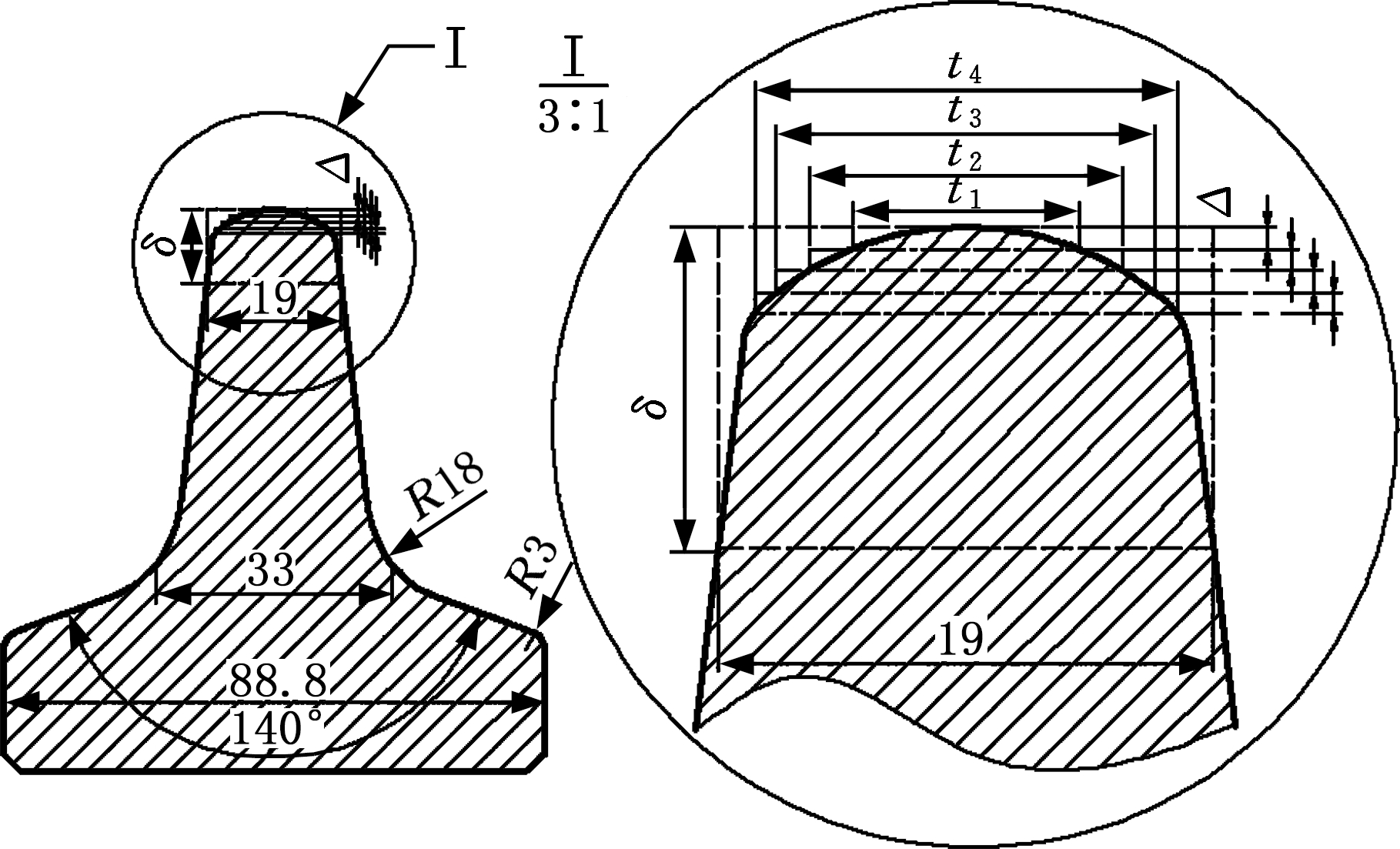
图5 刀圈尺寸参数示意图
Fig.5 Schematic diagram of the cutter ring size parameters
根据理论分析,取![]() 把刀在刀盘的分布位置参数如表1所示。
把刀在刀盘的分布位置参数如表1所示。
根据磨损公式对不同磨损机制下的磨损量进行计算,取距离刀尖2 mm处计算正侧面磨损体积,结果如表2所示。表3和表4分别为不同磨损机制下的磨损量和工程实际磨损量。
表1 各刀的位置参数
Tab.1 Position parameters of each knife

刀位号1234安装半径(mm)3 540.283 620.123 699.33 773.64刀间距(mm)82.3579.8479.1874.34刀位号5678安装半径(mm)3 840.953 898.383 944.793 979.97刀间距(mm)67.2157.5346.4135.18
表2 1~8号刀正侧面磨损量
Tab.2 1~8 knife the front and side wear

刀位号1234正面体积磨损量Qz(mm3)1 394.861 377.741 339.141 286.69侧面体积磨损量Qc(mm3)635.82635.756635.65635.60刀位号5678正面体积磨损量Qz(mm3)1 209.881 111.38996.191 339.14侧面体积磨损量Qc(mm3)635.57635.54635.52635.65
表3 不同磨损机制的磨损量
Tab.3 Wear of different wear mechanisms
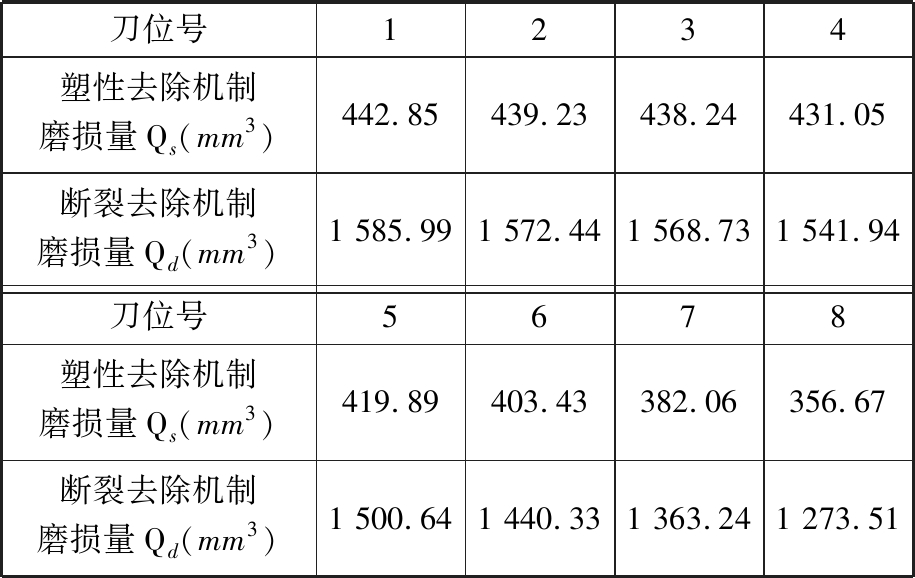
刀位号1234塑性去除机制磨损量Qs(mm3)442.85439.23438.24431.05断裂去除机制磨损量Qd(mm3)1 585.991 572.441 568.731 541.94刀位号5678塑性去除机制磨损量Qs(mm3)419.89403.43382.06356.67断裂去除机制磨损量Qd(mm3)1 500.641 440.331 363.241 273.51
表4 工程实际磨损量
Tab.4 Engineering data wear

刀位号1234径向磨损量(mm)1213-15滚刀转动一圈磨损量(mm)0.002 90.002 1-0.003 6累计磨损量(mm3)83.1490.06-103.92刀位号5678径向磨损量(mm)151077滚刀转动一圈磨损量(mm)0.003 60.002 40.001 70.001 7累计磨损量(mm3)103.9269.2848.5048.50
图6和图7分别为正侧面及两种不同去除机制下的磨损量对比图。可以看出,磨损量随着安装半径的增大而增大,主要是断裂去除机制下磨损量较大。1~8号刀为正滚刀,其正面磨损量较大。

图6 滚刀正侧面磨损量对比
Fig.6 Comparison of the amount of wear on the front and side

图7 两种去除机制下的滚刀磨损量对比
Fig.7 Comparison of wear under two removal mechanisms of the hob
4.2 基于PSO算法的系数优化
为了使理论值与工程实际值的误差最小,即求误差绝对值的最小值,基于PSO算法,设置种群规模为30,初始惯性权值ωstart=0.9,迭代至最大次数时惯性权值ωend=0.4,速度最大值Vmax=0.5,速度最小值Vmin=-0.5,个体最大值pmax=1,个体最小值pmin=0。通过粒子群优化算法反复迭代300次后,进化过程中最优个体适应度值变化如图8所示。
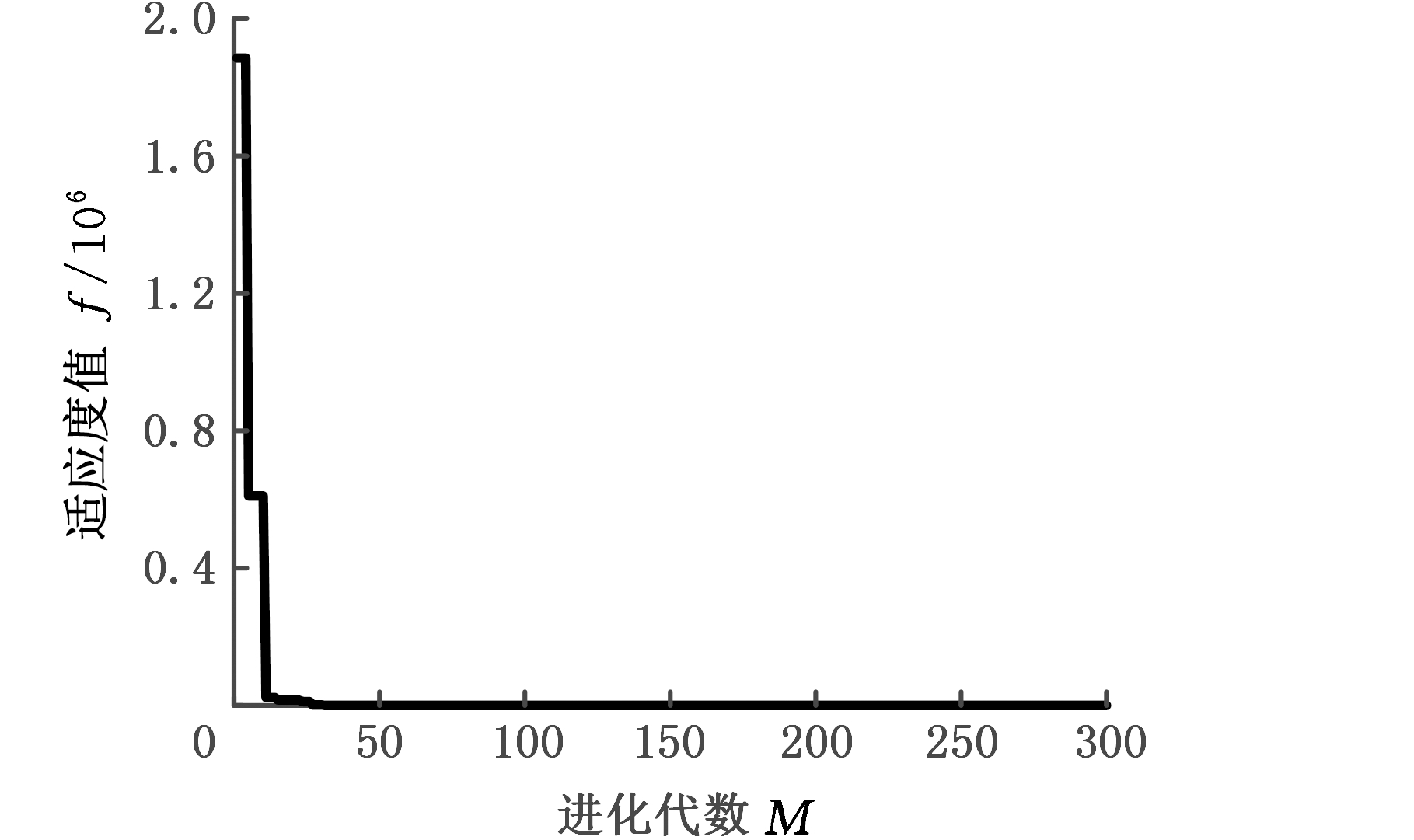
图8 进化过程
Fig.8 Evolutionary process
经20次寻优得到的最优个体适应度值为21.384 9,对应的粒子位置为(0.872 1,0.004 2),求得式(9)中的系数a=0.872 1,b=0.004 2。
4.3 计算结果对比
由于工况4下3号刀崩刃,故忽略不计。采用粒子群算法对上述数据进行局部寻优,利用MATLAB求得滚刀滚动一圈时不同磨损机制的系数占比。表5所示工况下,对每把刀具进行分析,将结果代入式(9)可以得到各刀的磨损量。
表5 工况参数
Tab.5 Working condition parameters

工况掘进距离(m)掘进时间(h)推力(MPa)转速(r/min)贯入度h(mm/r)18.33513.0306.02.824.7018.3295.42.5313.43012.0285.14.1421.46415.4244.55.0
通常工程实际磨损量受工况条件、环境条件、测量方法等多方面因素影响,如在掘进过程中一刀崩刃可能会影响其余刀具的磨损。另外,由于磨损模型是在滚刀单圈计算公式的基础上以理论刀刃宽进行计算的,而刀圈磨损呈非线性变化,即随着掘进距离增大,磨损时刀刃会逐渐变宽,因此,与工程数据相比,磨损模型的误差大。
如图5所示,按Δ=1 mm为磨损深度单位,离散拟合刀刃曲线,将其看作矩形截面,各矩形的体积磨损量的累积和即为刀具磨损量,其结果与实际工程数据误差的对比如图9所示。由图9可知磨损误差未超过20%,在误差范围内,故认为该模型相对准确。

1.工况1的拟合磨损量 2.工况1的累计磨损量 3.工况1的误差磨损量 4.工况2的拟合磨损量 5.工况2的累计磨损量 6.工况2的误差磨损量 7.工况3的拟合磨损量 8.工况3的累计磨损量 9.工况3的误差磨损量 10.工况4的拟合磨损量 11.工况4的累计磨损量 12.工况4的误差磨损量
图9 工况1~4下刀具磨损误差结果对比
Fig.9 Comparison of tool wear error results
5 DEFORM仿真
在全断面隧道掘进机施工过程中,刀盘上的盘形滚刀挤压切割岩石,形成同心圆沟槽。在理想条件下,沟槽之间的岩石将被完全破碎,但破岩过程复杂多变,其受到的磨损也随工作环境的变化而动态变化。利用DEFORM-3D软件,选用岩石的Johnson-Cook本构模型,模拟滚刀在挤压和破岩过程中的磨损情况,以此获得滚刀在破岩时的磨损深度等数据。Johnson-Cook模型应力公式为
式中,A、B、C、n、m为模型参数; εeq为等效塑性应变;![]() 为量纲一等效塑性应变; T*为量纲一温度。
为量纲一等效塑性应变; T*为量纲一温度。
5.1 滚刀和岩石模型的建立
采用的滚刀模型材料为H13热作模具钢,其弹性模量E=180 GPa,泊松比μ=0.31,质量密度ρ=7 850 kg/m3。为了简化计算,提高计算效率,分析中不考虑由于滚刀在刀盘上的位置不同而导致的差异,可认为滚刀与岩石接触的路径近似直线。划分网格时,刀刃处相对较密,最小单元尺寸为进给量的1/3,表面曲率为0.5,应变分布和应变速度分布为0.25,网格窗口为1。
岩石有多种类型,相互之间的差异性很大,由于很难得到岩石的流动应力应变曲线,故选用砂轮材料进行模拟。砂轮主要成分有Al2O3、SiC和立方氮化硼,将其作为仿真的岩石材料,取密度为3 100 kg/m3,单轴抗压强度为224 MPa,抗拉强度为25 MPa,弹性模量为210 GPa,泊松比为0.3,A=982,B=643.5,n=0.227,C=0.015,m=1.223。在不影响分析结果的前提下,尽可能减小模型的尺寸和网格数量以缩短计算时间,确定岩石模型为1 500 mm×500 mm×80 mm的长方体。由于切削深度一般在2~8 mm之间,相对于整个岩石模型的厚度较小,为了精确分析岩石的破碎状况,将与刀圈接触的网格进行局部细化,网格划分如图10所示。
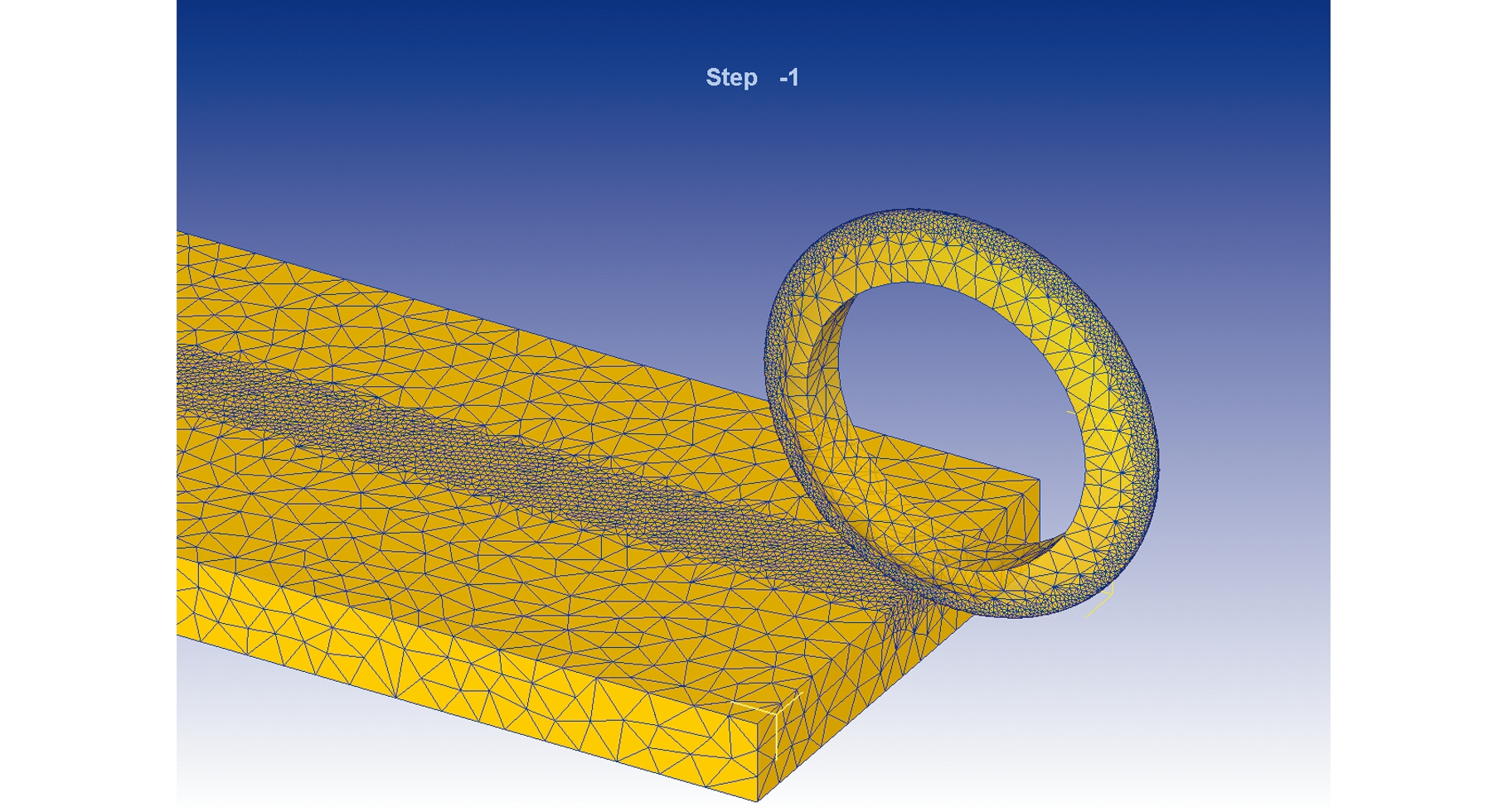
图10 模型网格
Fig.10 Model grid
5.2 仿真分析
模拟滚刀挤压破碎1 m岩石的动态过程,步长为最小网格的1/4,根据滚刀线速度求出每步所需要的时长,然后根据破岩长度得到总步数。模拟岩石的受力变形和滚刀的磨损时,设定刀圈和岩石均为塑性体。选择刀圈接触面为主面,岩石接触面为次面,其摩擦因数设置为0.3,在模拟中约束岩石面所有自由度,其他五面不做任何约束,滚刀采用恒定速度载荷加载,并施加径向压力。在MATLAB环境下计算不同贯入度下刀具的磨损深度,得出贯入度与磨损深度的计算量,如表6所示。
表6 贯入度与磨损深度的计算量
Tab.6 Calculation of penetration and wear depth

贯入度(mm/r)234磨损深度(mm)0.000 246 50.000 930 30.002 0贯入度(mm/r)5678磨损深度(mm)0.003 60.005 60.008 60.010 9
由表6可以看出,随着滚刀贯入度的增大,相应的磨损深度也不断增大。图11为滚刀挤压岩石时不同贯入度下滚刀磨损仿真图。根据云图可知,在应力加载过程中磨损始终产生在刀圈的刀尖处,其最大磨损深度值如表7所示。

(a)h=2 mm/r

(b)h=4 mm/r

(c)h=6 mm/r

(d)h=8 mm/r
图11 不同贯入度下滚刀磨损仿真图
Fig.11 Simulation of hob wear with different penetrations
表7 不同贯入度下仿真得到的最大磨损深度
Tab.7 Calculated amount of simulated maximum wear depth for different penetrations

贯入度(mm/r)234最大磨损深度(mm)0.000 4910.001 30.002 7贯入度(mm/r)5678最大磨损深度(mm)0.004 40.006 50.009 100.012 0
从磨损模拟结果可知:随着滚刀贯入度的增大,盘形滚刀与岩石接触面积也增大,与此同时,刀具表面受磨料的挤压向沟槽两侧产生隆起,形成如刨削一样的切屑过程,使得滚刀表面产生裂纹或与基体材料发生分离,从而导致磨损,因此,随着贯入度的增大,磨损量也增大。
图12为仿真与理论磨损深度对比图,可以看出,理论值和仿真值很接近,其贯入度与磨损深度的关系都是一致的,且误差较小,表明该数学模型具有一定的适用性,可计算不同工况下不同刀具的磨损量。

图12 仿真与理论磨损深度对比图
Fig.12 Comparison of simulation and theoretical wear depth
6 结语
(1)通过对破岩弧长、破岩力和磨损机理分析,建立了基于塑性去除机制和断裂去除机制的磨损模型,基于工程数据,采用PSO算法对模型磨损占比系数进行了优化;利用有限元分析软件DEFORM计算了盘形滚刀磨损量的仿真结果。
(2)掘进机在掘进过程中,滚刀刀圈的主要磨损形式为磨料磨损,以塑性去除机制为主,且正面磨损量较大。
(3)建立了盘形滚刀刀具磨损模型,并通过实际工程数据进行了验证,在同一施工条件下,刀圈磨损量与刀具的安装半径、贯入度成正比。
(4)将实际工程数据与磨损模型计算值进行对比分析,得到了模型计算值与实际工程值的误差小于20%的结论,表明滚刀磨损模型较准确。
(5)该磨损模型可以用于计算不同工况下不同刀盘分布的磨损量,可通过参数优化得到不同工况下最优施工参数和结构参数,对减少成本具有一定的理论指导意义。
[1] 林赉贶,夏毅敏,贾连辉,等.安装参数与掘进参数对滚刀破岩阻力的影响[J].浙江大学学报(工学版),2018,52(6):1209-1215.
LIN Laikuang, XIA Yimin, JIA Lianhui, et al.Effects of Installation Parameters and Excavation Parameters on Rock Breaking Resistance of Hob[J]. Journal of Zhejiang University(Engineering Science), 2018, 52(6):1209-1215.
[2] 吴俊,袁大军,李兴高.盾构刀具磨损机理及预测分析[J]中国公路学报,2017,30(8):109-116.
WU Jun, YUAN Dajun, LI Xinggao. Wear Mechanism and Prediction Analysis of Shield Tools[J] Chinese Journal of Highway, 2017,30(8):109-116.
[3] 赵海鸣,舒标,夏毅敏,等.基于磨料磨损的TBM滚刀磨损预测研究[J].铁道科学与工程学报, 2014,11(4):152-158.
ZHAO Haiming, SHU Biao, XIA Yimin, et al.Study on Wear Prediction of TBM Hob Based on Abrasive Wear[J]. Journal of Railway Science and Engineering, 2014, 11(4): 152-158.
[4] 赵战欣.TBM盘形滚刀在山岭隧道掘进过程中的磨损研究[J].地下空间与工程学报,2015,7(11):367-372.
ZHAO Zhanxin. Research on Wear of TBM Disc Hob in Tunneling Process of Mountain Tunnel[J].Chinese Journal of Underground Space and Engineering, 2015,7(11):367-372.
[5] 孙振川,杨延栋,陈馈,等.引汉济渭岭南TBM工程二长花岗岩地层滚刀磨损研究[J].隧道建设,2017,37(9):1167-1172.
SUN Zhenchuan, YANG Yandong, CHEN Kui, et al.Study on the Hob Wear of the Second Granite Formation in the TBM Project of the South of the Han Dynasty[J].Tunnel Construction, 2017,37(9):1167-1172.
[6] 舒标.基于磨料磨损的TBM滚刀磨损预测研究[J].铁道科学与工程学报,2014,11(4):152-158.
SHU Biao.Study on Wear Prediction of TBM Hob Based on Abrasive Wear[J].Journal of Railway Science and Engineering, 2014,11(4):152-158.
[7] 毕明洋,应华,张树丽.硬岩TBM盘形滚刀破岩力的一种计算分析方法[J].机电工程技术,2018,47(4):83-85.
BI Mingyang, YING Hua, ZHANG Shuli. A Calculation and Analysis Method for Rock Breaking Force of Hard Rock TBM Disc Cutter[J]. Mechanical & Electrical Engineering Technology, 2018, 47(4):83-85.
[8] 祝和意,杨延栋,陈馈.盾构滚刀破岩力及磨损速率预测模型推导[J].现代隧道技术,2016,53(5):131-136.
ZHU Heyi, YANG Yandong, CHEN Kui. Derivation of Prediction Model for Rock Breaking Force and Wear Rate of Shield Hob[J]. Modern Tunnel Technology, 2016,53(5):131-136.
[9] ERNEST R. Friction and Wear of Materials[M]. 2nd ed. New York: John Wiley & Sons Inc,1995.
[10] MOORE M A, KING F S. Abrasive Wear of Brittle Solids[J]. Wear,1980,60:123-140.
[11] 赵婷婷,程奇峰,王志丰.改进粒子群算法优化的非线性模型预测控制[J].辽宁工程技术大学学报(自然科学版),2015,34(4):517-522.
ZHAO Tingting, CHENG Qifeng, WANG Zhifeng. Predictive Control of Nonlinear Model Based on Improved Particle Swarm Optimization Algorithm[J]. Journal of Liaoning Technical University(Natural Science Edition), 2015,34(4):517-522.
[12] KENNEDY J, EBERHART R C. Particle Swarm Optimization[C]∥Proceedings of IEEE International Conference on Neural Nerworks. New York: Springer, 1995:1942-1948.
