0 引言
目前,利用核能发电来代替燃煤发电是全球控制温室效应加剧的一种重要途径。为大力发展核能发电,我国自主研发了华龙一号核电系统[1]。核主泵是核电站系统的“心脏”部件,必须确保其可靠运行,而主泵电机轴承又是核主泵系统的重要零件,它需要承受主泵转子合力及电机工作附加载荷,工作条件苛刻,是核主泵可靠稳定运行的关键因素[2]。核主泵电机轴承是一种自主研发的新型特种轴承,没有足够的运行数据,针对这种情况,需要一种适合工程实际的特种轴承可靠性分析方法。
何正嘉等[3]对机械设备可靠性评估方法进行了评述。王兆伍等[4]、常振等[5]对滚动轴承及滑动轴承可靠性进了探究。朱德馨等[6]采用Bayes多层估计法对无失效试验数据进行处理,建立了高速列车轴承的可靠性寿命评估模型。金光[7]将Bayes方法和MCMC(Markov chain Monte Carto)方法相结合,对航天轴承可靠性进行了评估。孙剑萍等[8]研究了结构的强度退化、累积损伤和电化学腐蚀对结构可靠性的影响。何成兵等[9]把故障模式及影响分析(failure mode and effects analysis,FMEA)法应用到风电机组可靠性分析中。姚灿江等[10]使用故障树分析(fault tree analysis,FAT)及FMEA对RV减速器进行了可靠性分析。杨立健等[11]基于应力-强度干涉理论对O形密封结构进行了可靠性分析。
本文主要针对少子样电机滑动轴承的可靠性研究,结合轴承特定结构和实际工况,选择理论计算和试验研究的方法,对承力构件采用手册法及应力-强度干涉法评估可靠性,并进行轴瓦磨损试验和冷却器性能试验。
1 核主泵电机滑动轴承总体结构
核主泵电机滑动轴承是核主泵系统的关键部件,作为一个独立单元,安装在主循环泵上部的支承座内,主泵电机轴承承力构件三维图见图1。

图1 核主泵电机轴承承力构件
Fig.1 Components of nuclear main pump motor bearing
该轴承的各组件结构三维总装图见图2。承力构件由推力头、推力瓦、支枢、弹性板、承板、导瓦座、导瓦和壳体等组成,它能承受泵转子传递的合力,形成动压润滑油膜以隔离推力头和轴瓦(推力瓦+导瓦),并将力传递到机座。油水冷却装置内有循环水,以确保将油膜润滑所产生的热量带出,进而保证推力瓦、导瓦与推力头之间的油膜温度在32~40 ℃范围内,以维持良好的润滑条件;测温元件作为状态监控元件,实时监控轴承内润滑油温度;液位开关为浮筒滑杆的机械结构,实时显示轴承内部润滑油液面高度;另外还有一些辅助装置,起到支承、固定或限位作用。冷却装置、测温元件、液位开关及其他辅助装置共同保证轴承具有良好的润滑作用。

1.推力头 2.壳体 3.油水冷却器 4.承板 5.推力瓦 6.支枢 7.弹性盘 8.接油盆 9.副推力瓦 10.测温元件 11.盖板 12.导瓦座 13.导瓦 14.上密封盖 15.液位开关
图2 轴承三维总装图
Fig.2 Three dimensional assembly drawing of bearing
本文研究对象为核主泵电机滑动轴承,其具体可靠性要求为10年寿命周期内可靠度不低于0.999 9,设计壳体寿命大于40年,检修间隔周期为5年,启停次数大于200次/年,寿命期内启停次数大于3 500。
2 主泵电机轴承可靠性分析
2.1 故障分析及解决方法
核主泵电机轴承为立式推力滑动轴承,为了对其进行故障分析,提前收集了近8年的相似产品的售后服务数据,统计数据见表1。
表1 轴承故障统计表
Tab.1 Bearing failure statistics table
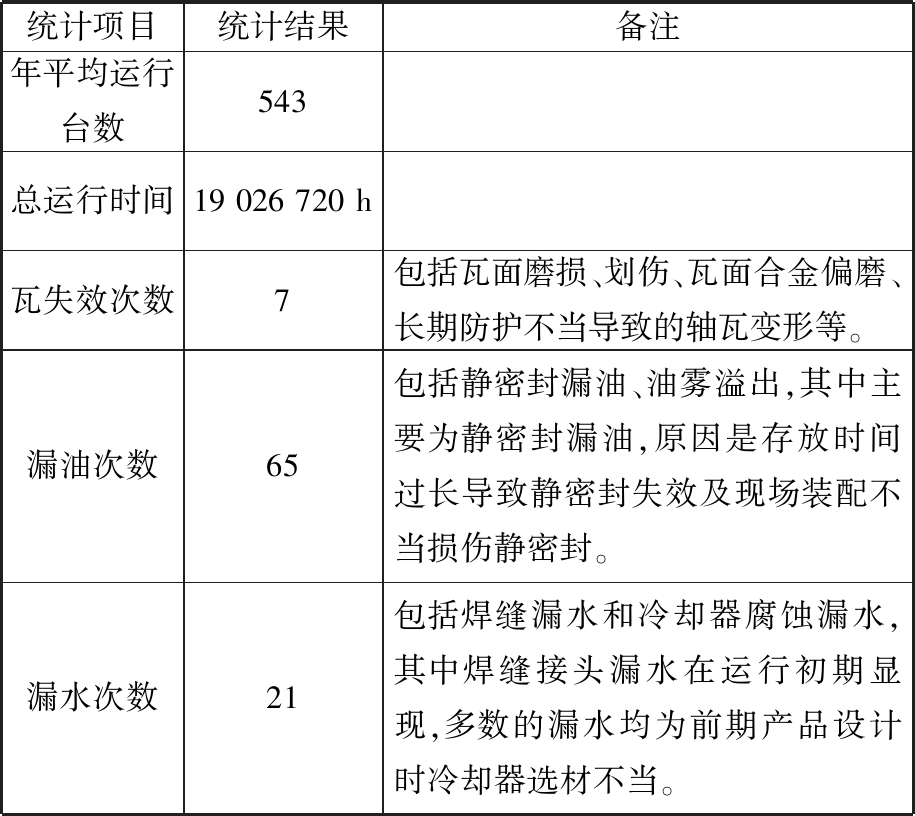
统计项目统计结果备注年平均运行台数543总运行时间19 026 720 h瓦失效次数7包括瓦面磨损、划伤、瓦面合金偏磨、长期防护不当导致的轴瓦变形等。漏油次数65包括静密封漏油、油雾溢出,其中主要为静密封漏油,原因是存放时间过长导致静密封失效及现场装配不当损伤静密封。漏水次数21包括焊缝漏水和冷却器腐蚀漏水,其中焊缝接头漏水在运行初期显现,多数的漏水均为前期产品设计时冷却器选材不当。
综合分析反馈数据,需重点关注:①轴瓦的使用寿命和更换周期;②静密封使用寿命及更换周期;③冷却器选材与冷却水水质的匹配。
根据收集的相似产品的售后服务数据及此种轴承的主要功能,确定轴承易发生故障的部件,分析故障模式,并采取对应的解决措施,表2列出了详细信息。
2.2 对应的可靠性体系
根据2.1节内容,总结出了轴承失效的关键因素,轴承故障的最终体现就是轴瓦损坏,为了更清晰地表达故障间的逻辑关系,绘制该立式推力轴承的故障树,将烧瓦作为故障树顶层事件。图3和图4是烧瓦后的轴瓦实物。绘制的故障树如图5所示。
表2 主要故障模式及解决方法
Tab.2 Main failure modes and solutions

项目故障模式解决措施弹性盘断裂根据负载计算,确保弹性板的强度和刚度。推力瓦磨损减小加工及安装误差,实时监测瓦温,进行磨损试验,按期换瓦。壳体静密封位置过大针对密封间隙匹配进行相应计算,控制静密封部件质量,按标准设计密封,选择抗老化耐辐照的材料,按照供应商提供的寿命数据规定更换周期。静密封失效防尘设计,进油过滤,油室放置磁铁,保证腔室密封间隙,控制泄油量,增加冷却器循环水流量,油位摸底试验,进行润滑及热平衡计算。导瓦磨损减小装配误差,保证导瓦组均匀磨损;重新进行匹配间隙计算,耐久性仿真;开展启停磨损试验和最低转速验证试验。冷却器漏水依据标准及实际结构设计合理接头结构形式,提高密封部件静密封质量,进行耐压防漏试验。

图3 烧瓦后的轴瓦
Fig.3 Bearing bush after firing tile bush

图4 轴瓦局部
Fig.4 Part of axle

图5 轴承故障树
Fig.5 Bearing fault tree diagram
故障树中各编号对应的内容以表格形式列出,如表3所示。
表3 故障树编号对应表
Tab.3 Fault tree number corresponding table
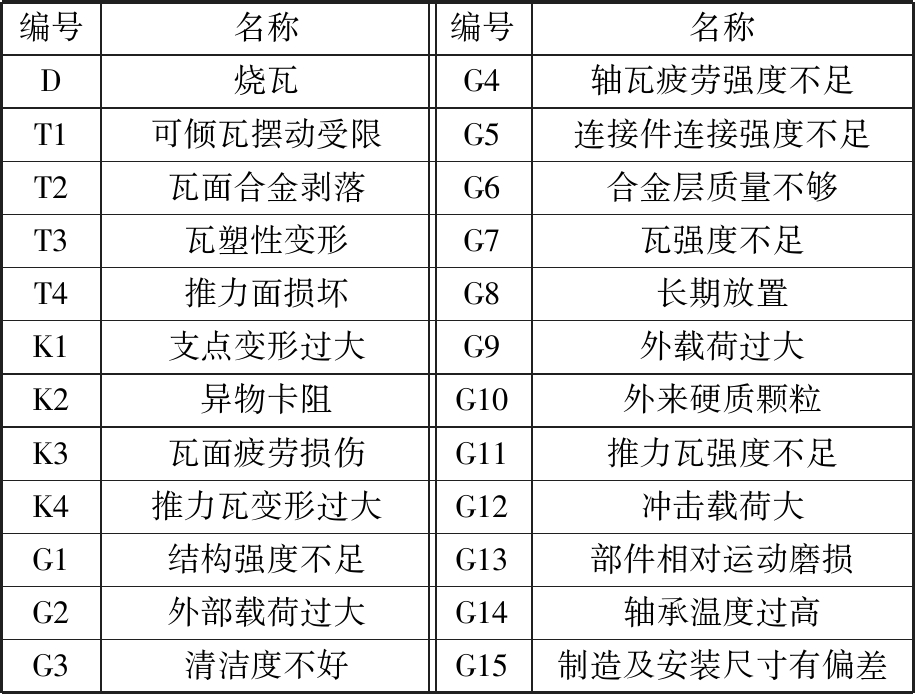
编号名称编号名称D烧瓦G4轴瓦疲劳强度不足T1可倾瓦摆动受限G5连接件连接强度不足T2瓦面合金剥落G6合金层质量不够T3瓦塑性变形G7瓦强度不足T4推力面损坏G8长期放置K1支点变形过大G9外载荷过大K2异物卡阻G10外来硬质颗粒K3瓦面疲劳损伤G11推力瓦强度不足K4推力瓦变形过大G12冲击载荷大G1结构强度不足G13部件相对运动磨损G2外部载荷过大G14轴承温度过高G3清洁度不好G15制造及安装尺寸有偏差
在建立故障树的基础上,为了更好地收集故障数据,解决问题,达到故障信息的相互分享,明确信息交互的需要,更大限度地确保产品的可靠性,必须要有一个功能齐全的可靠性体系。图6所示即是为了保证轴承产品性能所采用的可靠性体系。

图6 轴承可靠性体系
Fig.6 Bearing reliability system
3 可靠性预测
在没有大量整机试验数据的前提下,可靠性预测体现出其重要价值。可靠性预测关注的是影响轴承功能实现的各单元,电机轴承整体的可靠度是各单元组件可靠度值的乘积。零件单元的可靠性预测,按照具体要求,分别采用数据手册法和应力-强度干涉法计算求得。
3.1 可靠性计算方法
NSWC-2009可靠性设计手册[12]是美国海军为设计更好性能、更高可靠性的产品,结合大量的试验数据和领域专家的知识,编撰的一本用于机械设计的手册,得到行业普遍认可。
轴承组件中的固定螺栓组和冷却器在NSWC-2009中Threaded和Fluid Conductors章节有对应的计算模型。其中螺栓失效率计算模型为
λF=λF,BCSZCLCTCICSCCK
(1)
λF,B=1/σe,S-N
式中,λF,B为基础故障率;σe,S-N为S-N试样的耐久性或疲劳极限;CSZ、CL、CT、CI、CSC、CK分别为尺寸偏差、加载方式、温度因素、循环载荷冲击、表面涂层及加工方式对基础故障率的影响系数。
冷却器失效率计算模型为
λP=λP,BCECrCp
(2)
式中,λP,B为管路组件基本失效率;CE为环境因素影响系数;Cr为温度因素影响系数;Cp为故障发生概率因素影响系数。
螺栓组和冷却器采用手册法计算其可靠度,而其他的壳体、推力瓦、弹性盘、推力头、导座、承板、支枢及导瓦均采用应力-强度干涉法,基于有限元分析及材料数据手册的经验总结计算其可靠度。此种方法无需大量整机试验,从而避免了大量试验带来的经济投入。
对于过载和疲劳情况下的可靠度计算,由于零件工作时的结构应力服从正态分布,因此根据零件的设计尺寸偏差及有限元分析,确定其应力分布的参数,再对照零件材料的屈服强度分布及P-S-N曲线(概率-应力-寿命曲线)确定强度分布。最后,再采用Monte-Carlo抽样方法,得到过载或疲劳情况下的可靠度。
3.1.1 零件应力分布的确定方法
对于应力S~(μ,σ2),取零件尺寸变动范围内的中值对零件建模,然后进行有限元分析,得到的应力最大值S0即为μ,接下来确定σ(标准方差)。
由于
S~(μ,σ2)
则
根据标准正态分布3σ原则,认为零件尺寸变动范围内的应力最大值S1在z=0+3×1=3处取得,组合零件尺寸极限值,对零件建模,然后进行有限元分析,得到S1。此时
(3)
S1和S0的值已通过有限元分析得到,则由式(3)可求得σ,最终得到该零件的应力分布。
对于磨损情况下的可靠度计算,由于零件工作时的磨损量服从正态分布,因此根据零件的设计尺寸偏差及Archard磨损计算模型[13-14],确定其磨损量分布的参数,再对照设计要求的磨损范围,确定磨损允许量分布。最后采用Monte-Carlo抽样方法得到磨损情况下的可靠度。
3.1.2 零件磨损量分布的确定方法
对于磨损量h~(μ′,(σ′)2),取零件尺寸变动范围内的中值,然后对零件建模,进行有限元分析,得到的应力最大值h0即为μ′,接下来确定σ′。Archard磨损计算模型为
(4)
h~(μ′,(σ′)2)
则
式中,Ks为计算磨损系数;P0为最大接触力;N为启停数;L为每次启停磨损行程;H为材料硬度;A为磨损面积。
根据标准正态分布3σ原则,组合零件尺寸极限值,对零件建模,然后进行有限元分析,得到零件尺寸变动范围内的应力最大值,代入式(4),得到最大磨损量h1并认为在z′=0+3×1=3处取得。此时
(5)
h1和h0的值已通过有限元分析得到,则由式(5)可求得σ′,最终得到该零件的磨损量分布。
3.2 可靠性的计算
3.2.1 螺栓组及冷却器
采用式(1)的计算方法,根据螺栓使用情况及查NSWC-2009手册确定λF的计算参数。本系统采用的螺栓为8.8级,经计算σe,S-N值为46 410,λF,B为0.000 021 5/106。其他参数CSZ=1.0,CL=1.09,CT=1.011,CI=1,CSC=1,CK=2.2。计算得到螺栓失效率λF=0.000 052,可靠度R0=1-0.000 052=0.999 948。由于采用螺栓组固定的方法,即单个螺栓组内螺栓都失效,整体螺栓工作才会受影响,因此可靠度计算模型采用组内并联组间串联的方式,结合实际螺栓布置方式计算螺栓组1的可靠度R1=0.999 999 99,螺栓组2的可靠度R2=0.999 999 99。
采用式(2)的计算方法,根据冷却器使用情况及查NSWC-2009手册确定λP的参数。经查,λP,B为0.47/106,CE=1.0,Cr=0.21,Cp=0.076 9。计算得到冷却器工作失效率λP=0.007 59,再根据实际冷却进出油口布置个数,最终计算得到冷却器10年的可靠度R3=0.999 975 336 986 387。
3.2.2 弹性盘
弹性盘的材料为50CrVA。依照前文提到的故障模式分析,弹性盘的主要失效模式包括过载引起的断裂和循环应力引起的疲劳裂纹,并以此按照强度失效计算弹性盘的任务可靠度,具体计算过程如下。
基于有限元分析方法,在给定载荷作用下,计算零件最大结构应力值在表4所示各尺寸变量均取中值时的最大值,如图7所示,最大值为371.93 MPa。依照式(3)的计算方法,利用有限元方法计算尺寸公差范围内的应力极值并求得应力标准差为3.378 337 MPa,则最大结构应力的分布为(371.93,3.378 337 2)MPa。
表4 弹性盘尺寸变量表
Tab.4 Elastic disk size variable table mm

变量变量设计值变量最小值变量最大值弹性盘高度10.009.9910.01圆台内径50.049.750.3圆台外径58.057.758.0圆台高6.56.36.7
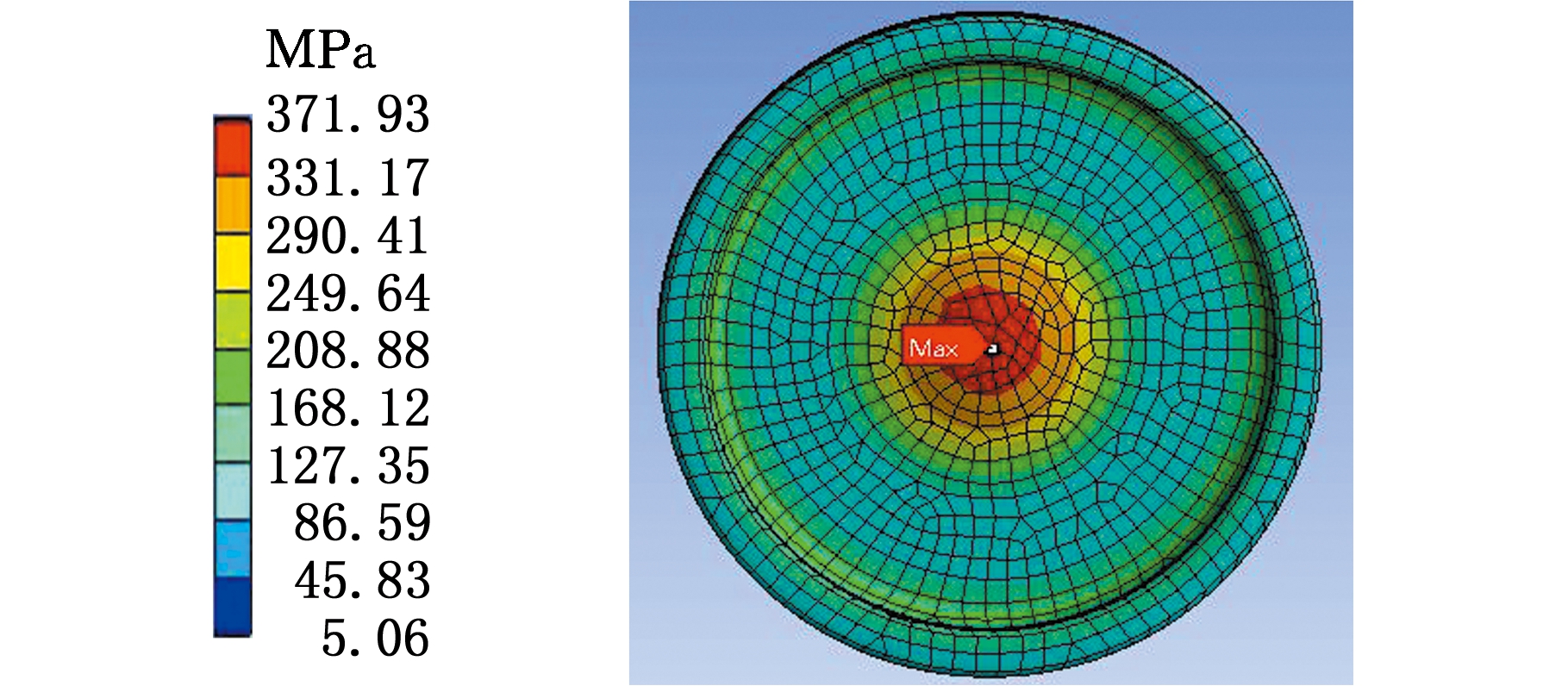
图7 弹性盘尺寸变量取中值时结构应力分析
Fig.7 Structural stress analysis of elastic plate with variable mean value
先计算强度失效形式,查找《机械工程材料性能数据手册》可得50CrVA的屈服强度σs许用值的分布为(751.3,71.832)MPa。采用Monte-Carlo抽样方法,经过1015次抽样,得到弹性盘的可靠度R′4=0.999 999 933 86,再查找手册,图8所示为50CrVA的P-S-N曲线,可得疲劳失效强度分布为(681,43.322)MPa。

图8 50CrVA光滑试样P-S-N曲线
Fig.8 P-S-N curve of 50CrVA smooth specimen
同样采用Monte-Carlo抽样方法,经过1015次抽样,可靠度R″4=0.999 999 999 999 991。弹性盘主要的失效模式为过载和疲劳,依据可靠性的相关理论,R4=R′4R″4,故经应力-强度干涉法计算,弹性盘的10年寿命期内可靠度R4=0.999 999 93。
3.2.3 推力瓦
推力瓦的材料为锻钢20,耐磨表面镀层为ZSnSb11Cu6,按照强度失效及磨损失效计算推力瓦的任务可靠度,具体计算过程如下。
基于有限元方法,在给定载荷作用下,计算零件最大结构应力值在各尺寸变量(表5)均取中值时的最大值为3.281 MPa,计算结果参见图9。依照前文所述的应力分布计算方法,采用有限元方法计算尺寸公差范围内的应力极值并求得应力标准差为0.000 066 669 MPa,则最大结构应力的分布为(3.281,0.000 066 669 2)MPa。
表5 推力瓦的尺寸变量表
Tab.5 Dimension variable table of thrust pad mm

变量位置变量基本尺寸变量最小值变量最大值推力瓦高度40.00039.98440.000测温孔到边距15.015.314.7固定端宽度45.00045.00044.984瓦面外圆半径312.5312.0313.0瓦面内圆半径220.0219.5220.5固定端厚度13.012.813.2镀层最薄处厚度0.30.20.4

图9 推力瓦尺寸变量取中值时结构应力分析
Fig.9 Structural stress analysis of thrust bearing shoe with variable mean value
查找手册,锻钢20的屈服强度σs的许用值分布为(163.3,20.662)MPa。采用Monte-Carlo抽样方法,经过1015次抽样,得到推力瓦的可靠度R′5=0.999 999 999 999 995。
采用有限元方法,计算得到施加的外载荷和各尺寸变量均取中值时零件最大接触力P0=8 678.8 N,计算结果参见图9,结合文献[15],零件磨损量中值
施加的载荷变量波动和零件的各尺寸变量均在公差范围内,零件最大接触力值P0=8 729.3 N。根据Archard磨损计算模型,零件磨损量最大值
磨损量的相关系数Ks=3.3×10-7,磨损区域表面硬度H=27 HB、每次启停磨损行程L=11 778 mm、磨损面积A=8 374.2 mm2,5年内的启停数N=5年×200次/年=1 000次。依照前文可得,磨损量的分布为(0.149 189 4,0.000 289 367 2)mm。
依照设计要求,推力瓦的表面镀层ZSnSb11Cu6厚度范围为(0.2,0.4)mm。推力瓦镀层厚度的分布为(0.3,0.033 333 332)mm。采用Monte-Carlo抽样方法,经过1015次抽样,推力瓦的可靠度R″5=0.999 996 968 029 208。经应力-强度干涉法计算,推力瓦的5年寿命可靠度R5=R′5R″5=0.999 996 969。
推力瓦、壳体、推力头、导座、承板、支枢及导瓦的计算过程不再赘述。
由有限元仿真和查阅数据手册得出,承板的最大结构应力的分布为(3.086,0.002 966 667 2),Q345B的屈服强度许用值的分布为(345,222);支枢的最大结构应力的分布为(102.85,0.298 2);50CrVA的屈服强度许用值的分布为(751.3,71.832);导瓦的最大结构应力分布为(19.229,0.004 633 333 2),锻钢20的屈服强度许用值分布为(245,20.662);壳体的最大结构应力分布为(30.589,0.707 333 333 2),Q345B的屈服强度许用值分布为(345,222);推力头的最大结构应力分布为(10.143,0.032 916 666 672),锻钢35的屈服强度许用值分布为(210,40.883 92)。采用Monte-Carlo抽样方法,经过1015次抽样,依次计算各单元的可靠度,由于系统中存在组件,在对组件进行可靠度计算时,采用组内并联,组间串联的可靠度计算模型,计算结果见表6。最终计算出主泵电机滑动轴承的可靠度为0.999 961,大于工程要求的0.999 9。
表6 可靠度结果统计
Tab.6 Reliability result statistics
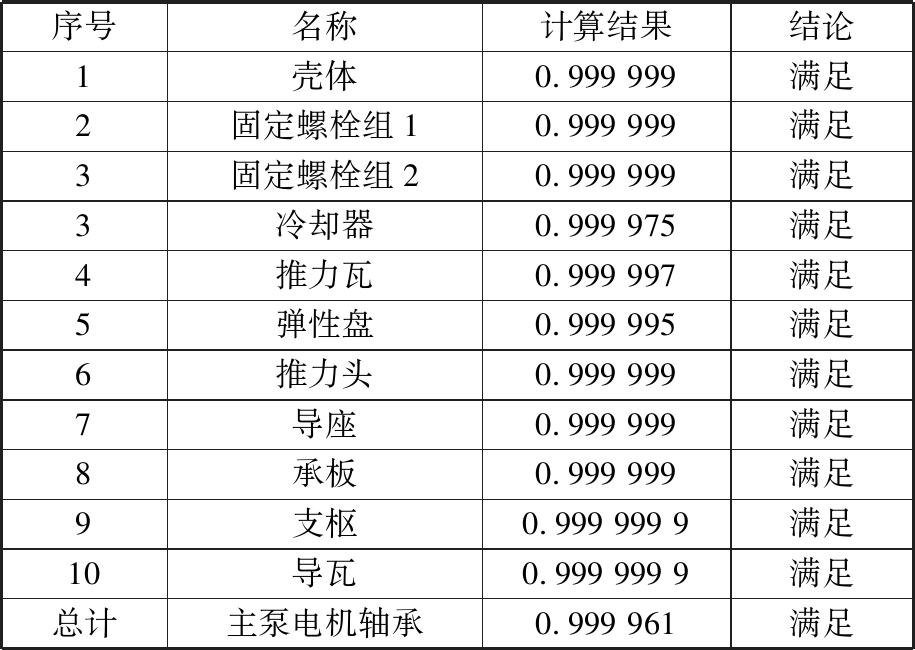
序号名称计算结果结论1壳体0.999 999满足2固定螺栓组10.999 999满足3固定螺栓组20.999 999满足3冷却器0.999 975满足4推力瓦0.999 997满足5弹性盘0.999 995满足6推力头0.999 999满足7导座0.999 999满足8承板0.999 999满足9支枢0.999 999 9满足10导瓦0.999 999 9满足总计主泵电机轴承0.999 961满足
4 推力瓦磨损及冷却器试验
推力瓦和油水冷却器是两个可靠性薄弱的部件,要分别搭建专用试验台,针对推力瓦磨损情况,确定加速试验方法[15],通过分散系数法确定试验次数,然后按照试验方案,对推力瓦进行试验。针对冷却器换热失效的情况,采用持续性试验,并记录试验数据。
4.1 推力瓦磨损试验
滑动轴承由于长期使用,特别在启停阶段会造成轴瓦磨损,并可能最终导致烧瓦,因此通过加速试验确定轴瓦磨损量。
试验是采用一定比例缩小的推力瓦模型进行磨损试验的,缩小轴承的比压(轴和轴瓦之间油膜的压力)为1.75 MPa,与产品一致,启停的升速与降速与实际一样。
通过轴承磨损寿命试验确定轴承的磨损寿命,验证其是否满足寿命指标要求,据此确定合理的轴瓦检修、更换周期。按照使用要求,轴瓦至少需要满足5年寿命,现实条件无法满足5年的破坏性试验要求,所以采用加速试验的方法完成试验。图10所示为搭建的推力瓦启停磨损试验台,试验过程中实时监测扭矩及加载压力。

图10 推力瓦启停试验台
Fig.10 Thrust bearing shoe test stand
试验中被试件推力瓦外径为200 mm;轴向载荷(向下)为5~30 kN;转速为50~1 000 r/min;扭矩范围为0~200 N·m;油温为60 ℃。电机启停时间内转速曲线见图11。

图11 启停试验单运行转速曲线
Fig.11 Start and stop test run speed curve
本试验属于重复、周期性试验,单套轴瓦的启停试验次数为3 500,试验分成4个周期进行,每次试验的内容如下。
加载载荷,保证轴承比压为1.75 MPa,并开始周期性运转,分别以500次、1 500次、2 500次和3 500次为一个试验周期,后拆检推力瓦的磨损情况,在每个试验周期结束后,分别进行一次742 r/min的性能验证试验,记录试验中轴瓦的温度;在每个试验周期的性能验证试验结束后拆检轴瓦的磨损状况,直至单副轴瓦完成3 500次启停试验或试验过程中轴瓦磨损失效,按以上方案进行第二、第三套轴承的试验。测试结果如表7及图12所示。
表7 轴瓦试验磨损结果记录
Tab.7 Bearing test wear results record

瓦块编号瓦块厚度(mm)第一次拆瓦(mm)第二次拆瓦(mm)第三次拆瓦(mm)第四次拆瓦(mm)1-113.50-0.0113.49413.49313.49213.4921-213.50-0.0113.49313.49213.49013.4911-313.50-0.0113.49413.49613.49313.4911-413.50-0.0113.49213.49113.48913.4881-513.50-0.0113.49713.49613.49413.4931-613.50-0.0113.49513.49513.49113.4891-713.50-0.0113.49713.49113.49013.491-813.50-0.0113.49013.48913.48513.482

(a)500次无测温元件 (b)500次有测温元件

(c)1 500次无测温元件 (d)1 500次有测温元件
(e)2 500次无测温元件 (f)2 500次有测温元件

(g)3 500次无测温元件 (h)3 500次有测温元件
图12 推力瓦磨损图片
Fig.12 Thrust bearing shoe wear pictures
按照试验方案,依次进行了三组推力瓦的启停磨损试验,三套瓦在3 500次启停之后均未发生失效,轴瓦温度及磨损量也在允许范围内,满足可靠性要求。
4.2 油水冷却器试验
根据故障模式分析得出冷却器主要失效模式为泄漏或冷却性能退化并最终导致轴承润滑失效,需要针对油水冷却器设计可靠性验证试验,保证冷却器的安全性和冷却器的换热性能。油水冷却器换热性能试验台如图13所示。

图13 油水冷却器换热性能试验台
Fig.13 Oil water cooler heat transfer performance test-bed
控制冷却器进油温度为40 ℃,将冷却器装配在试验专用油箱中,轴承润滑油流量为310 L/min,轴承冷却水管分别通水,其中冷却器流量控制在450 L/min进行试验,进水温度都控制为同一个自然室温,在额定流量下稳定运行试验,记录实时进出油温、油流量及压力、进出水温、水流量,计算进出油热交换量。
验收准则如下:轴承上冷却水流量为450 L/min时,换热功率大于或等于65 kW。
通过测控系统记录试验数据,列举出部分油水冷却器性能验证试验数据,如表8所示。
表8 油温统计
Tab.8 Oil temperature statistics

进油温度(℃)出油温度a(℃)出油温度b(℃)出油温度c(℃)出油温度d(℃)油流量(L/min)进水温度(℃)出水温度(℃)水流量(L/min)40.232.132.533.032.7311.528.930.3449.340.933.734.031.839312.329.130.5448.242.032.232.532.837.7313.029.230.5449.544.032.234.434.038.0314.029.030.1447.945.833.935.835.540.8314.029.330.6450.2
收集试验数据,根据下式依次计算出冷却器的冷却功率:
Pc=qV(Tc-Tr)eρ/60
(6)
式中,qV为体积流量;Tc为润滑油出口温度;Tr为润滑油进口温度;e为润滑油质量热容,2.09 kJ/(kg·℃);ρ为润滑油密度,0.9 kg/L。
验证冷却器的冷却效率是否满足水流量为450 L/min时,润滑油的换热功率大于或等于65 kW。试验总计进行100 h,经过计算冷却器的换热功率均达到要求,但仍需要进一步试验,预计工作500 h,以保证冷却器换热性能的可靠性。
5 结论
(1)根据核主泵电机轴承的主要功能特点及相似产品历史使用数据,确定了轴瓦磨损、静密封及冷却器失效为轴承故障的主要原因,针对不同的故障模式,提出了相应的解决方案。采用故障树分析该电机轴承的故障发生原因,并建立了一种可靠性保障体系流程。
(2)针对轴承上的螺栓组及冷却器,查阅NSWC-2009手册,根据零件工作特点,计算其可靠性。通过有限元方法及Archard磨损计算模型,采用Monte-Carlo抽样法,计算弹性盘、推力瓦、壳体、推力头、导座、承板、支枢及导瓦的可靠性,结果显示轴承的可靠性满足设计要求的0.999 9。
(3)对推力瓦和油水冷却器两个可靠性薄弱部件分别搭建专用试验台,针对推力瓦磨损情况,采用加速试验方法,对推力瓦进行试验。针对冷却器换热失效的情况,采用持续性试验方法。由试验统计数据的计算结果可知,设计的轴承推力瓦满足极限磨损量,冷却器冷却效率同样满足设计要求。
(4)理论和数值仿真结合得到的可靠度和少子样的可靠性试验结果得以相互验证。研究结果对于轴承的可靠度评估具有工程价值。
[1] 梁国亮. 华龙一号核电工程造价及控制措施研究[J].建筑经济, 2017, 38(3):66-68.
LIANG Guoliang. Hualong No.1 Nuclear Power Project Cost and Control Measures[J]. Building Economy, 2017, 38 (3): 66-68.
[2] 潘晓峰, 杨宝.主泵电机润滑油损失异常的分析和处理[J].中国核电, 2011, 4(2):150-159.
PAN Xiaofeng, YANG Bao. Analysis and Treatment of Abnormal Lubricant Loss of Main Pump Motor[J]. China Nuclear Power, 2011, 4(2): 150-159.
[3] 何正嘉, 曹宏瑞, 訾艳阳,等. 机械设备运行可靠性评估的发展与思考[J]. 机械工程学报, 2014, 50(2):171-186.
HE Zhengjia, CAO Hongrui, ZI Yanyang,et al. Development and Consideration of Operational Reliability Assessment of Machinery and Equipment[J]. Journal of Mechanical Engineering, 2014, 50(2): 171-186.
[4] 王兆伍, 许尚贤. 滑动轴承的可靠性分析[J]. 中国机械工程, 1995,6(增刊1): 25-28.
WANG Zhaowu, XU Shangxian. Reliability Analysis of Sliding Bearings[J]. China Mechanical Engineering, 1995,6(S1): 25-28.
[5] 常振, 夏新涛, 李云飞,等. 滚动轴承性能不确定性与可靠性评估[J]. 中国机械工程, 2017, 28(18): 2209-2216.
CHANG Zhen, XIA Xintao, LI Yunfei, et al. Evaluation of Uncertainty and Reliability of Rolling Bearing Performance[J]. China Mechanical Engineering, 2017, 28(18): 2209-2216.
[6] 朱德馨, 刘宏昭, 原大宁,等. 高速列车轴承可靠性试验时间的确定及可靠性寿命评估[J]. 中国机械工程, 2014, 25(21): 2886-2891.
ZHU Dexin, LIU Hongzhao, YUAN Daning, et al. Determination of Reliability Test Time and Reliability Life Evaluation of Bearings for High-speed Trains[J]. China Mechanical Engineering, 2014, 25(21): 2886-2891.
[7] 金光. 小子样条件下航天轴承性能可靠性建模与评估[J]. 国防科技大学学报, 2010, 32(1): 133-137.
JIN Guang. Modeling and Evaluation of Aerospace Bearing Performance Reliability under Small Sample Conditions[J]. Journal of National University of Defense Science and Technology, 2010, 32(1): 133-137.
[8] 孙剑萍, 汤兆平, 罗意平. 多级载荷累积损伤下结构的动态可靠性分析[J]. 中国机械工程, 2018, 29(7): 794-803.
SUN Jianping, TANG Zhaoping, LUO Yiping. Dynamic Reliability Analysis of Structures under Cumulative Damage of Multistage Loads[J]. China Mechanical Engineering, 2018, 29(7): 794-803.
[9] 何成兵, 顾煜炯, 邢诚.基于FMEA法的风力发电机组故障模式分析[J].可再生能源, 2011, 29(3): 120-126.
HE Chengbing, GU Yujiong, XING Cheng. Fault Mode Analysis of Wind Turbine Based on FMEA[J]. Renewable Energy, 2011, 29(3): 120-126.
[10] 姚灿江, 魏领会, 王海龙. 基于FTA和FMEA的RV减速器可靠性分析[J].现代制造工程, 2018(1): 136-140.
YAO Canjiang, WEI Linghui, WANG Hailong. Reliability Analysis of RV Reducer Based on FTA and FMEA[J]. Modern Manufacturing Engineering, 2018(1): 136-140.
[11] 杨立健, 甘祖旺, 付云飞. 基于应力-强度干涉理论的O形密封结构可靠性分析[J].水下无人系统学报, 2017, 25(3): 188-192.
YANG Lijian, GAN Zuwang, FU Yunfei. Reliability Analysis of O-shaped Sealing Structure Based on Stress-strength Interference Theory[J]. Journal of Underwater Unmanned Systems, 2017, 25(3): 188-192.
[12] Naval Surface Warfare Center Carderock Division. Handbook of Reliability Prediction Procedures for Mechanical Equipment[M]. West Bethesda, Maryland: Carderock Division, NSWC-09, 2009.
[13] 桂长林. Archard的磨损设计计算模型及其应用方法[J]. 润滑与密封, 1990(1):12-21.
GUI Changlin. Archard’s Wear Design Calculation Model and Its Application Method[J]. Lubrication and Sealing, 1990(1): 12-21.
[14] 王雷刚,黄瑶,孙宪萍,等. 基于修正Archard磨损理论的挤压模具磨损分析[J]. 润滑与密封, 2006(3):10-12.
WANG Leigang, HUANG Yao, SUN Xianping, et al. Analysis of Extrusion Die Wear Based on Modified Archard Wear Theory[J]. Lubrication and Sealing, 2006(3):10-12.
[15] 张祖明.推力滑动轴承的加速磨损试验和可靠性研究[J]. 应用科学学报,1996(2): 191-198.
ZHANG Zuming. Accelerated Wear Test of Thrust Sliding Bearing and Reliability Research[J]. Reliability Engineering Annual Meeting, 1996(2): 191-198.
