0 引言
制动器是曳引电梯重要的安全装置，它的安全、可靠是保证电梯安全运行的重要因素之一。磁流变液(magneto-rheological fluid，MRF)作为场控智能材料，不仅在磁场的控制作用下其流体属性发生改变，而且其器件在工作过程中受到磁场、流场和机构装置运动学等多方面的相互影响。GÜTH等[1]设计了通过磁力作用控制磁流变液由工作间隙向非工作间隙流动的具有双重工作间隙的新型磁流变制动装置(magneto-rheological brake, MRB)，使装置在非制动工作状态时可有效减小零场黏性力矩，提高了装置工作效率。ROSSA等[2]研制了直径60 mm、宽度39 mm、最大制动力矩5.3 N·m的微小型多盘式磁流变制动装置，通过实验验证了该制动装置可广泛应用于微机电系统。JEDRYCZKA等[3]研制了一种基于永磁铁与励磁线圈混合激励的磁流变制动装置，该装置断电后可实现自动执行制动的安全保护模式。RUSSO等[4]通过一个新型的磁流变液限滑差速器实现了车辆扭矩的合理分配，以此提高汽车驱动性、通过性及操纵稳定性。PATIL等[5]通过数值计算方法研究温度对磁流变制动装置应用于汽车的影响，通过典型实验工况验证汽车用的磁流变制动装置的热场满足材料温度使用要求。郑祥盘等[6]通过有热场的有限元分析和试验研究了曳引电梯磁流变制动装置温度特性。CHEN等[7]利用计算流体动力学方法分别对基于电磁流变技术的平面(间隙固定)和波纹面(间隙变化)双圆桶式离合器的性能进行了分析。李斌等[8]提出了一种具有多工作间隙及可获得良好多级非线性扭转刚度的新型多间隙磁流变液双质量飞轮。以往设计分析磁流变制动装置时，常采取简化的、静态的制动力矩计算公式进行计算，如圆筒形磁流变制动装置力矩计算公式[9-10]，这种方法既忽略了磁场的不均匀、流场的变化和磁流变液所受体积力的影响，又没有考虑流场的变化和制动过程中转速对制动力的动态影响，与实际结果的误差较大。
本文根据曳引电梯制动装置工作特性设计了双线圈磁流变制动装置的结构，采用多物理场耦合分析方法研究曳引电梯磁流变制动装置。这种耦合分析建立在数学物理方法之上，利用COMSOL软件在多物理场数学建模上的灵活性，描述磁流变制动装置所受的不同物理场之间的相互关系与影响，使模型更贴近实际。
1 双线圈磁流变制动装置的工作原理及结构设计
图1 双线圈磁流变制动装置的结构
Fig.1 Structure of dual coil MRB
曳引电梯磁流变制动装置以磁流变液作为工作介质，通过改变其外加磁场强度使磁流变液的剪切屈服应力发生变化，产生可控的制动力矩，实现电梯制停。设计的曳引式电梯磁流变制动装置结构见图1，主要由磁流变液、双线圈、转轴、磁轭等组成。为了保证曳引电梯磁流变制动装置磁流变液间隙的磁感应强度与磁场均匀性，装置采用双线圈轴向并排结构，可增加磁流变液工作面积，以产生足够的制动力矩。
根据GB7588—2003《电梯制造与安装安全规范》，以额定载重质量320 kg、额定速度1 m/s为基本设计参数，具体参数见表1。
表1 曳引电梯磁流变制动装置的设计参数
Tab.1 Calculation parameters of elevator MRB
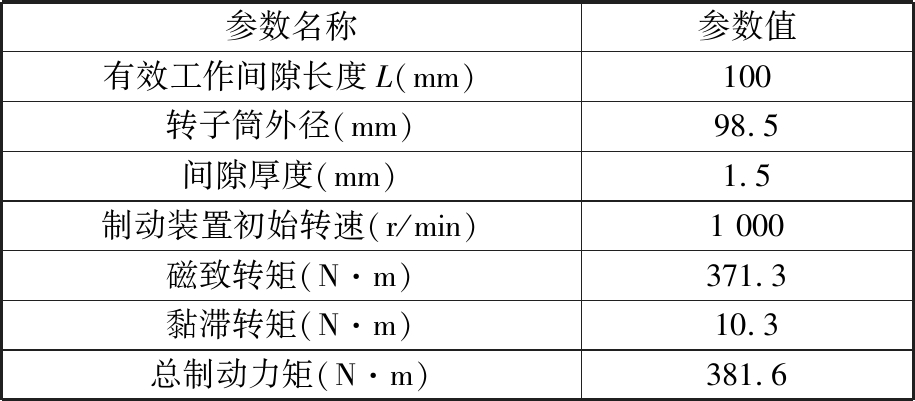
参数名称参数值有效工作间隙长度L(mm)100转子筒外径(mm)98.5间隙厚度(mm)1.5制动装置初始转速(r/min)1 000磁致转矩(N·m)371.3黏滞转矩(N·m)10.3总制动力矩(N·m)381.6
磁流变制动装置配置有一个直流电源。曳引电梯运行时，磁流变制动装置不通电即未加磁场作用，此时制动装置不处于制动工作状态，传递力矩可以被顺利地传递至蜗杆蜗轮的整个曳引系统，从而曳引轮带动电梯轿厢正常运转。电梯要停止运行时，磁流变制动装置处于制动状态，保证轿厢不运动。电梯电磁制动装置的控制和工作特点可为曳引电梯制动系统提供双重保护，保证了电梯运行的安全性。
双线圈磁流变制动装置的磁感应强度可通过装置中励磁线圈的电流大小来衡量，装置的制动力矩通过系统中的力矩传感器测出，由此，可确定曳引电梯制动装置的制动力矩与磁场强度的关系。
2 磁流变制动装置多物理场仿真分析
数学物理方程中，用麦克斯韦方程组分析装置的磁场强度分布，用Navier-Stokes方程描述磁流变液的流动，用牛顿力学常微分方程刻画刚体运动[11]，它们之间的相互影响可以通过建立不同参数之间的函数关系进行描述，即建立不同物理场之间的相互关系。于是，求解多物理场耦合问题也就转化为对不同物理场的方程组及其参数耦合关系的联立方程组进行求解。
对于磁流变制动装置，磁场从空间分布和数值上影响着磁流变液，不同旋转速度下磁流变液受到的离心力也不同，同时温度等其他因素也影响磁流变液及其装置。由此，磁流变制动装置是一个复杂的分析对象，存在不同物理场间的相互作用。磁流变制动过程在工作中主要受到磁场、流场以及转子运动规律的影响，图2说明了磁流变制动装置的场间耦合关系。图2中，B为磁感应强度，r为转子外径，l为转子轴向长度，g表示黏度μ与磁感应强度B的函数关系，h表示剪切应变率
与角速度ω的函数关系。制动力矩可表示为剪切力在转子外表面S上的积分。
图2 磁流变制动装置场间关系
Fig.2 Field relation of MRB
首先，磁场对磁流变液的流场有较大影响，反过来，磁流变液对磁场的影响不大，可以看作单向耦合,可以通过流变特性测试来建立磁流变液流体属性参数与磁场参数的函数关系式，描述磁流变制动装置磁场与流场的相互关系;其次，流场和转子的刚体运动相互影响，流场的剪切应变率由运动方程中角速度ω决定，反过来，由剪切应变率与黏度μ的乘积在转子外表面S的积分得到的制动力矩T又是常微分运动方程的参数[11]。
在COMSOL中设置如下：首先，对磁流变制动装置进行静磁场分析，得到磁场在制动装置中的分布；其次，为体现磁流变液的流变特性，在流场模块中使用磁感应强度表达式定义黏度，得到磁流变液黏度分布，并且附加磁场和旋转运动对磁流变液作用的体积力；之后，参照图2，通过剪切应变率将流场和运动方程联系起来。
耦合求解的分析过程分为三步：第一步，求解静态磁场；第二步，求解磁场耦合下的流场初值；第三步，求解流场和转子运动的动态耦合过程。
2.1 电磁场仿真结果分析
磁场分析中，为降低求解难度，忽略电流的瞬变过程和转子在磁场运动中产生的微弱涡流，按静磁场进行分析，即只对磁流变制动装置磁场稳定后的制动状态进行分析。磁场强度由麦克斯韦方程的简化形式表示[11]，运行求解后，得到图3所示的装置的磁场磁感应强度分布和图4所示的磁流变液中点沿轴向的磁通密度分布情况。
图3 装置的磁场磁感应强度分布
Fig.3 The distribution pattern of magnetic induction intensity of MRB
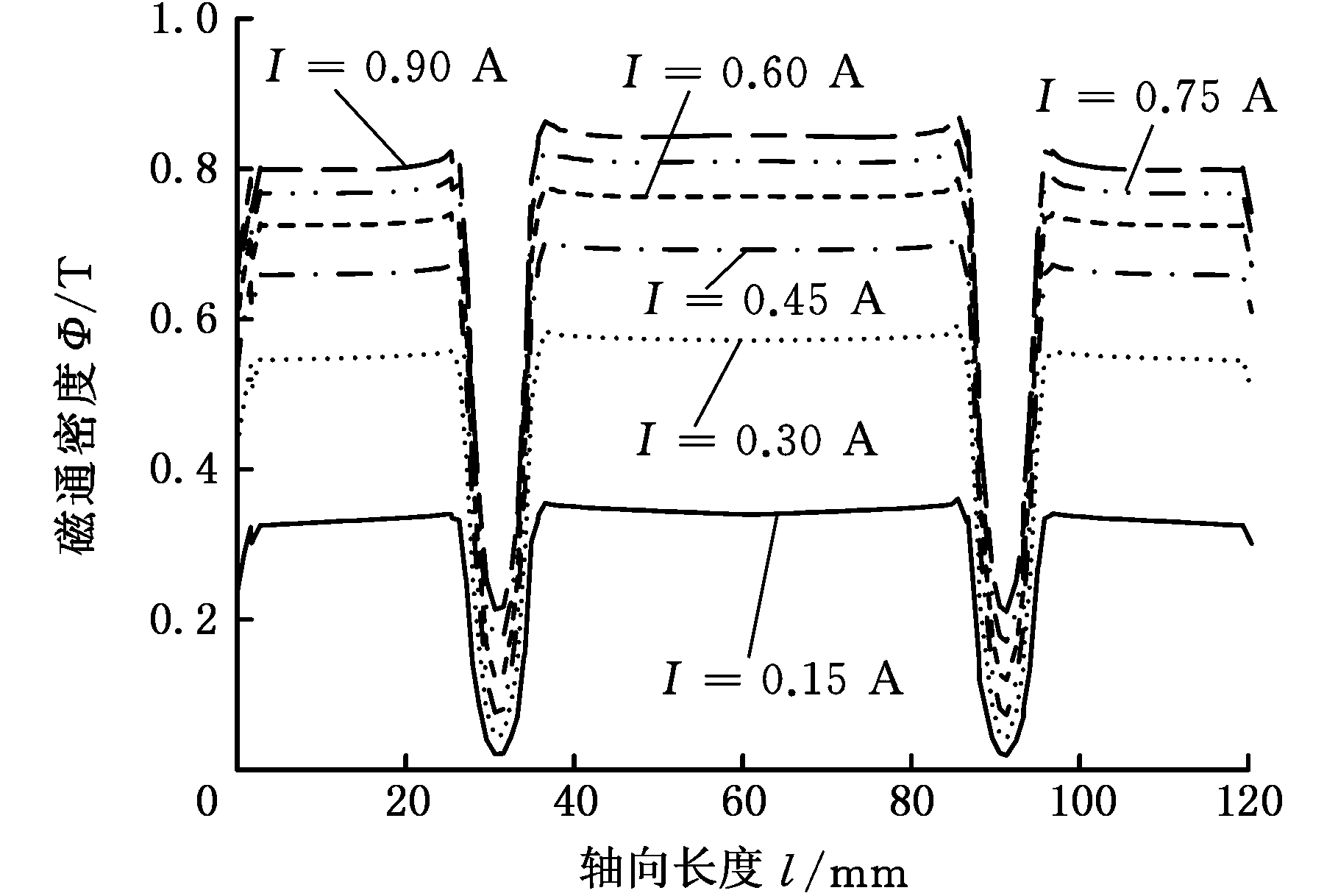
图4 磁流变液中点沿轴向的磁通密度分布
Fig.4 Magnetic induction intensity distribution of MRB midpoint in axial direction
图3显示了磁流变制动装置2个线圈分别通以0.9 A电流时的磁场分布情况。由图3可知，电流的增加使装置中磁轭部分与磁流变液中的磁感应强度增大；磁轭中的磁通密度最大值为2.0 T，磁流变液中的磁通密度最大值为0.8 T。进一步分析可以看出，装置中磁流变液中的磁感应强度的轴向分布较为均匀，而在转子侧板和隔磁环中几乎没有磁通，说明隔磁环的尺寸和位置设计合理，成功地将磁力线“引导”通过磁流变液，且与转子筒基本保持垂直，充分利用了线圈产生的磁动势，使得磁流变液可以产生足够的剪切应力。
由图4可看出，不同的激励电流I下，曲线的走向基本一致，磁感应强度随着激励电流的增大而增大。但是，激励电流越大，磁感应强度的增大趋势越缓，这也反映了装置随激励电流增大趋于饱和的事实。
2.2 流场仿真结果分析
根据曳引电梯磁流变制动装置的设计参数与磁流变液的属性参数估算雷诺数可知，流体处于层流状态。将磁流变液体视为不受温度影响的不可压缩流体，则可由Navier-Stokes方程描述[11]。实际上，磁流变液黏度不仅与磁感应强度B有关，还与剪切应变率有关。由于高剪切速率时，对黏度的影响很小，故暂且忽略。
根据磁流变材料试验测试的数据进行多项式拟合，采用的磁流变液数学模型为
τM=266 370B4-497 460B3+313 000B2+11 912B+1 722.6
(1)
式中，τM为磁致剪切应力。
磁流变液受到的体积力F为磁场梯度引起的对流体的作用力与离心力Fe之和：
F=μ′0M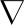
H+Fe
(2)
式中，μ′0为真空磁导率；M为磁流变液磁化强度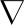；H为磁场强度的梯度。
F可在3个方向上分解，且其中Fe(|Fe|=
的方向为径向：
(3)
其中，ρ为磁流变液的密度；v为磁流变液的线速度。B、M、H值均在之前的静磁场分析中求得，在CFD模块中设置黏度和体积力时，只需将它们设定为以B、M、H为变量名的表达式，便可将磁场参数与流场参数联系起来了，也就建立了磁场与流场的耦合关系。从磁场与流场的方程中也可以看出磁场对流场参数的影响。
图5所示为磁流变制动装置在制动初始时拐角处的流场分布情况，可以看出，在拐角处流速较低，这是由液体材料的附着抑制作用引起的。
图5 流场速度云图
Fig.5 The flow field distribution
转子中点处，磁流变液剪切应变速率沿径向的变化如图6所示。由图6可知，制动开始时磁流变液的剪切应变速率较大，随制动过程转速下降而减小；对比图6a和图6b可知，电流越大，磁流变液体的屈服区域越紧靠转子表面；随着电流减小，屈服区域剪切应变速率的梯度减小。
(a)I=0.3 A
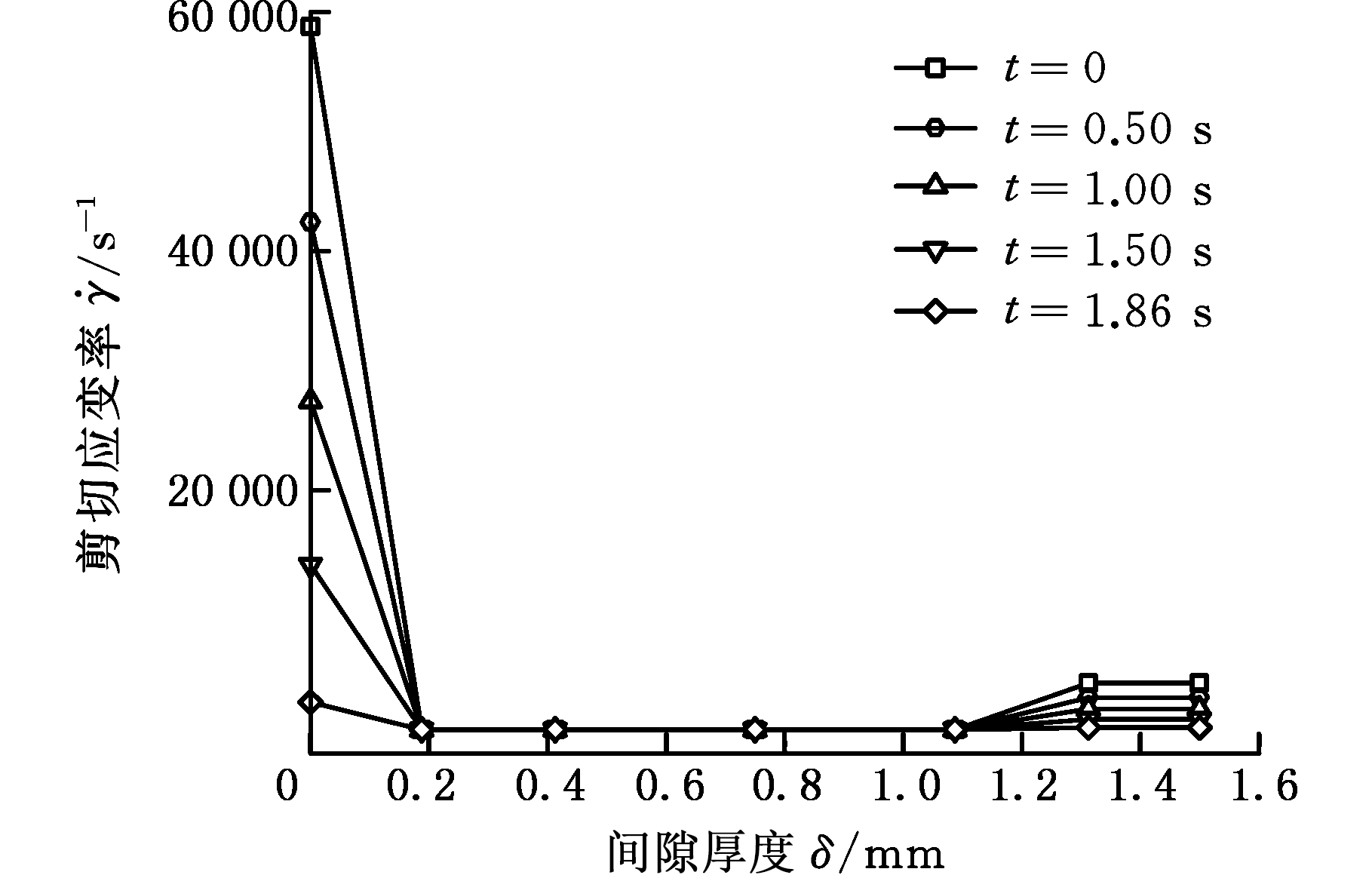
(b)I=0.6 A
图6 转子中点磁流变液剪切应变速率沿径向分布
Fig.6 The shear strain rate along the thickness direction variation of MRF
2.3 磁流耦合下的刚体动力学分析
模型中转子运动常微分方程(ODE)如下：
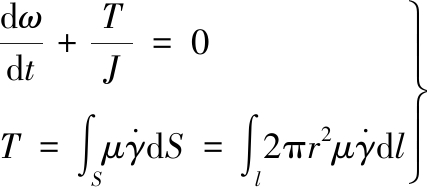
(4)
式中,t为制动时间；J为转子转动惯量。
设置转速、转子的转动惯量，电流激励I=0.6 A，仿真结果如图7所示。由图7可知，制动时间随着电流的增大而缩短，这是由于磁场趋于饱和，时间变化量也随之缩短；同时，角速度的减小并非线性，这说明磁流变制动装置并不具备绝对的恒转矩特性。角速度斜率的变化即为制动力矩的变化，即制动过程中制动力矩随时间的变化。
2.4 热场有限元分析
(a)角速度变化
(b)制动力矩变化
图7 不同电流下制动角速度、制动力矩变化
Fig.7 The changes of braking angular velocity and braking moment under different current
图8 水冷散热下装置的稳态温度场分布
Fig.8 The temperature field cloud diagarm of MRB during the water cooling
图9 紧急制动磁流变液最高温度和励磁线圈温度变化
Fig.9 The external surface temperature variation curve of the rotor midpoint
在水冷散热条件下，装置空载运行的稳态温度场分布见图8。由图8可知，靠近冷却水道的隔磁壳体外侧的温度较低，而转子筒外侧的温度较高；最高温度为34.3 ℃，位于磁流变液内；最低温度为25.0 ℃，位于外壳等地方；励磁线圈的温度为28 ℃左右。显然，磁流变液和励磁线圈的工作温度较低，且远低于磁流变液和励磁线圈的最高许可工作温度，能确保在工作过程中装置具有足够的制动与传动热容量。
图9所示为曳引电梯磁流变制动装置在紧急制动后6 s内磁流变最高温度和励磁线圈的温度变化规律。由图9可知，制动开始时刻磁流变液温度迅速升高，在1.25 s左右达到最高温度116 ℃；随着制动功率的下降，温度开始下降；至2 s左右制动完成后，装置处于散热状态，温度继续下降，到6 s左右温度已降到52 ℃以下。对于励磁线圈，开始制动后线圈温度缓慢上升，在2.25 s后，上升趋势趋于平缓，稳定在32 ℃左右，水冷却后装置的散热效果明显。
3 试验验证
曳引电梯磁流变制动装置测试平台见图10，它主要由被测磁流变制动装置、曳引主机-负载曳引机共直流母线互馈对拖测试平台、电梯井道仿真试验台、测试仪器等组成。曳引主机-负载曳引机共直流母线互馈对拖测试平台采用矢量控制方式对被测设备和负载设备进行速度和转矩控制，通过该测试平台可以模拟电梯在各种负荷加载装置和各工作条件下的动静态性能。
图10 曳引电梯磁流变制动装置性能试验平台
Fig.10 Performance test of elevator MRB
3.1 空载力矩特性测试
电梯在正常运行情况下，制动装置处于空转状态。空转转矩的大小决定了制动装置的损耗大小，该值越小越好。磁流变制动装置在没有外加磁场下，空转转矩是由磁流变液零场黏度与制动装置本身的摩擦力(如密封圈、轴承的摩擦)所产生的转矩，这个转矩在工作中相当于阻力，是装置的额外负载，其中磁流变液的零场黏度产生的黏滞力矩为空转转矩的主要部分。
如图11所示，制动装置的空转转矩仿真值随转速的增大线性增大。试验结果也显示出这种变化趋势。试验结果在不同转速下与仿真结果存在误差，分析其原因主要是：①试验中不同转速下，磁流变材料稠化程度不同，此过程具有不可逆的复杂稠化现象，导致磁流变液的零场黏度和剪切应力变大；②装置的实际散热功能未达到仿真分析中的冷却条件，空转转矩在100～300 r/min的转速范围时误差较大，这是由于此时曳引电梯制动装置温升而冷却作用不明显，导致此时空转转矩最大误差值接近于10 N·m；③仿真分析中忽略了机械摩擦转矩因素。
图11 空转转矩试验结果与仿真结果对比图
Fig.11 The contrast figure of experiment and theoretical result during empty torque
3.2 恒转矩特性测试
固定电流激励即磁场强度保持不变，测试曳引主机不同转速条件下(100～1 000 r/min)装置的转矩特性，结果如图12所示。
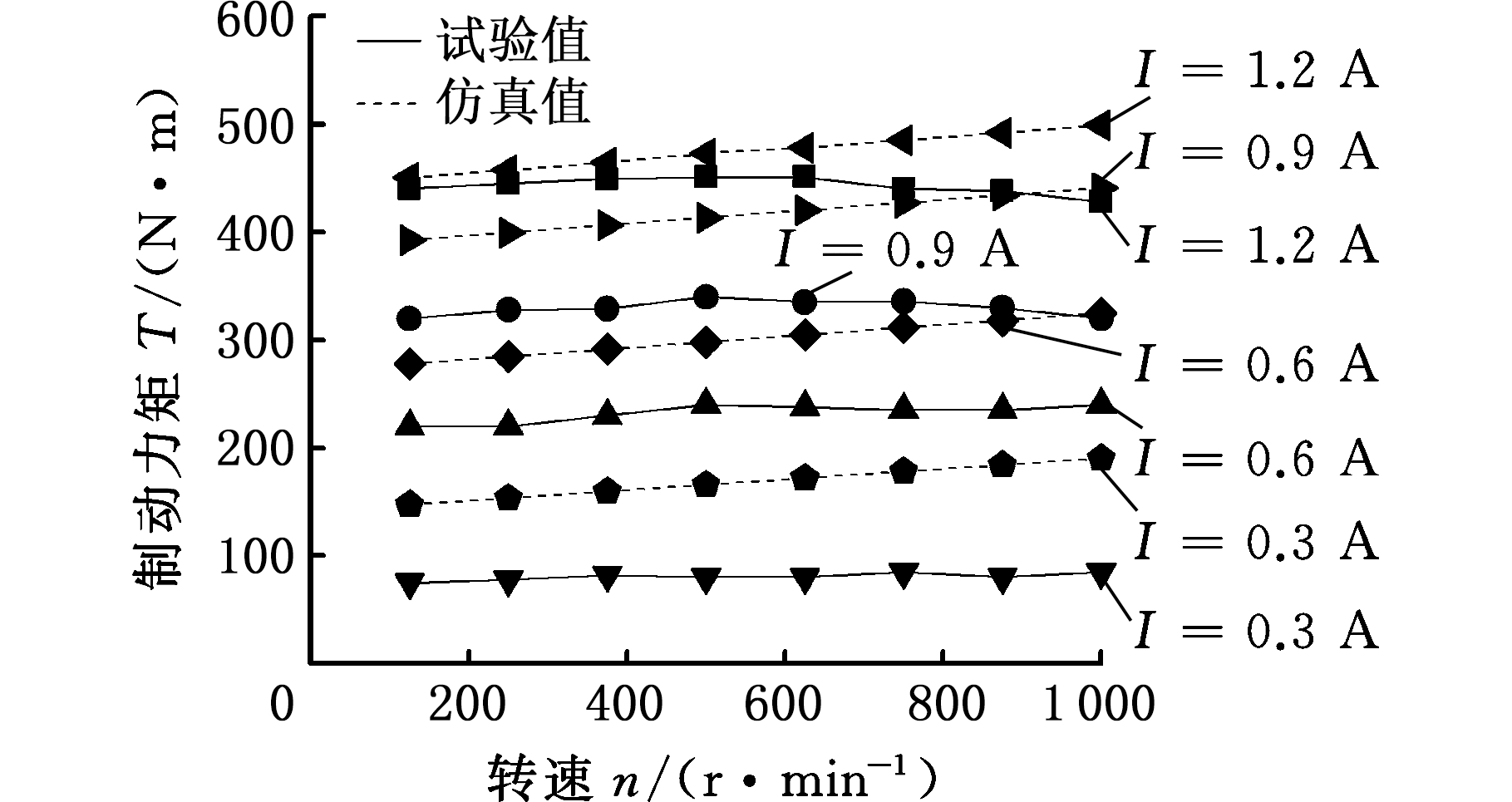
图12 恒转矩试验结果与仿真结果对比图
Fig.12 The contrast figure of experiment and theoretical result during constant torque
由图12可以看出，在不同的电流激励下，仿真与试验得到的制动力矩都较为稳定，说明装置具备较好的恒转矩特性，符合电梯运行中载荷和转速变化不引起转矩变化的需求。由于装置试验中磁流变液会受温度影响，故未出现仿真结果中制动力矩随转速微弱上升的趋势。就数值来看，试验结果均小于仿真结果，主要原因在于：在仿真分析中，忽略磁场的磁漏可能导致实际在中磁流变液产生的磁感应强度低于试验情况，致使试验中制动力矩较小。但只要保证电流超过1.2 A，就能满足该型号电梯的制动力矩达到450 N·m左右，保障电梯安全制动。
3.3 制动特性测试
静载荷试验制动性能结果如图13所示，试验结果表明，电流增大使制动力矩增大，在不同转速下，转矩值重合较好，也证明了上述试验中，装置恒转矩特性较好的特点。相比仿真分析结果，试验结果没有仿真结果规律整齐，且数值上整体略小于仿真值。主要原因在于仿真分析中，忽略了磁流变材料沉淀和磁场的磁漏，导致实际在液体产生的磁感应强度低于试验值，致使试验中制动力矩较小。
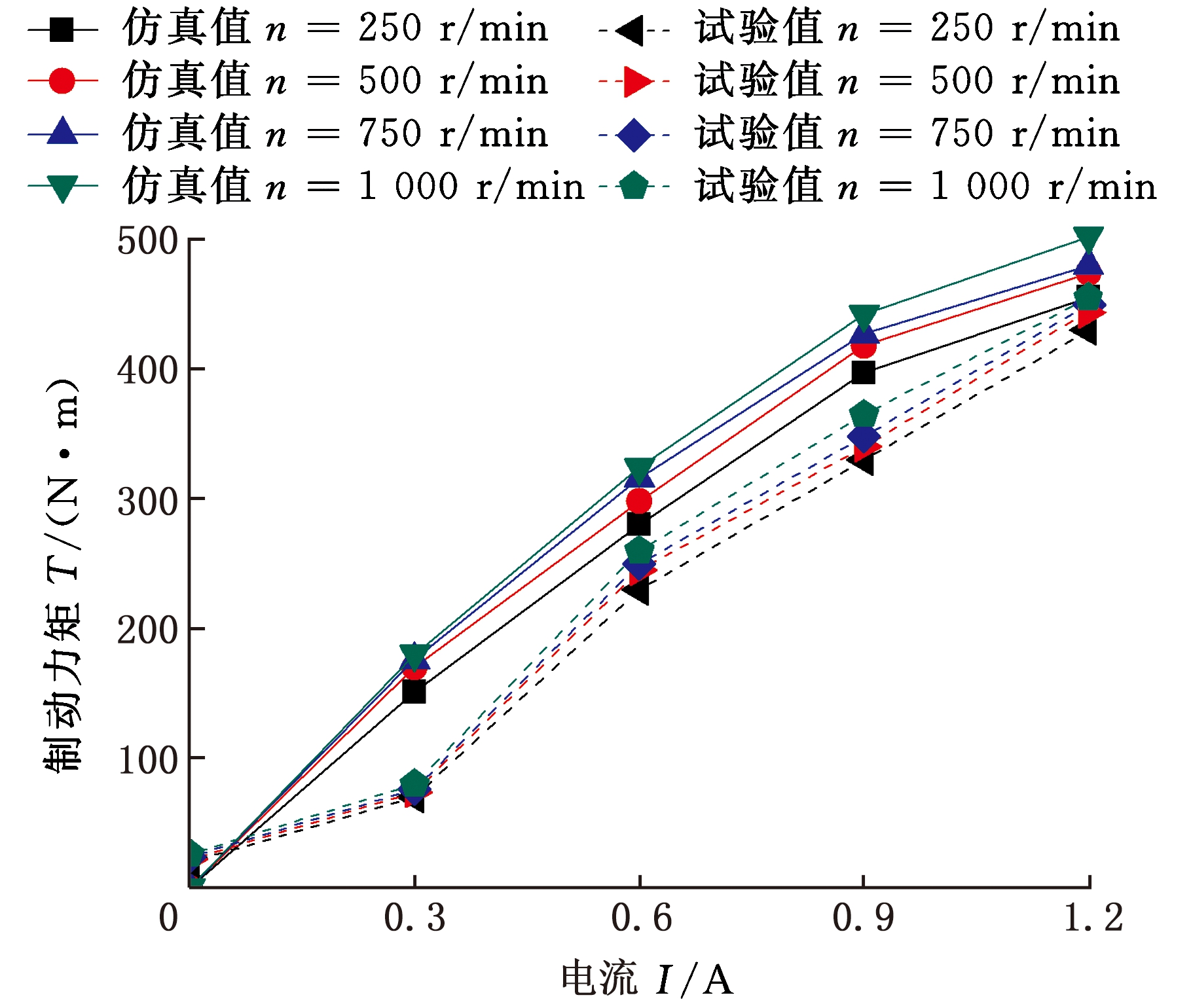
图13 静载荷试验制动性能结果对比
Fig.13 The braking performance curve of static load
3.4 温度特性测试
表2所示为点温计所测得的制动装置水冷却条件下稳定工作状态时外表面温度，图14为装置在水冷却条件下电梯空载运行20 min后，用红外热成像仪所拍摄的其外表面红外热成像图。表2中温度测量结果符合转速越高温度越高的变化规律，但是对比仿真结果温度偏高，说明实际散热情况没有仿真情况好。但是即便在此工作条件下，磁流变液和制动装置依然能保证稳定的工作状态，其表面最高温度为54.8 ℃，未超过磁流变液服役工作要求。
表2 电梯运行状态下的装置外表面温度值
Tab.2 The temperature of the device surface elevator under at steady state of elevator
转速n(r/min)温度θ(℃)017.210025.320032.530040.840049.3
图14 水冷散热下空载运行中装置的整体温度变化
Fig.14 The temperature changes in empty running under water cooling
4 结论
(1)线圈通电后，在磁流变液中产生的磁感应强度能达到要求，使得制动器产生足够的制动力矩，沿轴向方向较为均匀(除隔磁环处外)，磁场得到了充分的利用，制动装置在1.2 A的电流下能达到约400 N·m的制动力矩，满足设计的曳引电梯制动力矩要求。
(2)将流场与磁场耦合后，流场中的磁流变液黏度根据磁场的分布而分布，制动过程中磁流变液的屈服面、剪切应变率、流速都随着转速的变化而变化；耦合了流场的运动方程，得到了制动过程中角速度和制动力矩的变化规律。
(3)采用多物理场耦合分析方法，仿真得到了流场和运动方程的动态联系与相互影响，利于分析电梯磁流变液制动器制动过程中重要参数的变化规律。通过试验验证了水冷散热方式下，磁流变制动器满足电梯运行工况的设计温度要求。
[1] GÜTH D, SCHAMONI M, MAAS J. Magnetic Fluid Control for Viscous Loss Reduction of High-speed MRF Brakes and Clutches with Well-defined Fail-safe Behavior[J]. Smart Materials and Structures, 2013, 22(9): 94010.
[2] ROSSA C, JAEGY A, MICAELLI A, et al. Development of a Multilayered Wide-ranged Torque Magnetorheological Brake[J]. Smart Materials and Structures, 2014, 23(2): 25028.
[3] JEDRYCZKA C, SZELAG W, WOJCIECHOWSKI R M.FE Analysis of Magnetorheological Brake with HYBRID EXCITATION[C]// International Symposium on Electrodynamic and Mechatronic System (SELM). Opole-Zawiercie, Poland， 2013:69-70.
[4] RUSSO R, STRANO S, TERZO M. Enhancement of Vehicle Dynamics via an Innovative Magnetorheological Fluid Limited Slip Differential[J]. Mechanical Systems and Signal Processing, 2016, 70: 1193-1208.
[5] PATIL S R, POWAR K P, SAWANT S M. Thermal Analysis of Magnetorheological Brake for Automotive Application[J]. Applied Thermal Engineering, 2016, 98: 238-245.
[6] 郑祥盘, 陈凯峰, 陈淑梅. 曳引电梯磁流变制动装置的温度特性研究[J]. 中国机械工程, 2016, 27(16):2141-2147.
ZHENG Xiangpan, CHEN Kaifeng, CHEN Shumei. Investigation on Temperature Properties of Elevator Magnetorheological Brake[J]. China Mechanical Engineering, 2016, 27(16): 2141-2147.
[7] CHEN Shumei, WEI Chenguan. Experimental Study on Percolation Structure of Electrorheological Suspensions[J]. Int. J. of Applied Mechanics and Engineering, 2007, 12(1):299-230.
[8] 李斌,李华,姚进. 新型磁流变液多间隙双质量飞轮研究[J]. 中国机械工程, 2017, 28(16): 1928-1936.
LI Bin,LI Hua,YAO Jin. Research on a Novel MRF-MDMF[J].China Mechanical Engineering, 2017, 28(16): 1928-1936.
[9] TOMORI H, MIDORIKAWA Y, NAKAMURA T. Construction of a Nonlinear Dynamic Characteristic Model of Pneumatic Artificial Rubber Muscle Manipulator Using the Magneto-rheological (MR) Brake[J]. Journal of Intelligent Material Systems & Structures, 2012, 23(9):1011-1018.
[10] 郑军. 磁流变传动理论与试验研究[D]. 重庆：重庆大学, 2008.
ZHENG Jun. Theoretical and Experimental Study of Magnetorheological Transmission [D].Chongqing：Chongqing University, 2008.
[11] 刘国勇. 流体力学数值方法[M]. 北京：冶金工业出版社, 2016.
LIU Guoyong. Numerical Method of Fluid Mechanics[M]. Beijing：Metallurgical Industry Press, 2016.
