0 引言
研究表明制造业加工过程能源效率通常小于30%[1-2],GUTOWSKI等[3]指出生产线能源效率只有14.8%。目前,中国已成为全球最大的铝型材生产国,2015年我国铝加工材料达到3亿吨,铝合金挤压材料产量达到1.4亿吨 [4-5],铝挤压企业超过820家,其中4.5~250 MN的挤压机超过5 800台,占世界总台数的85%以上[6]。热挤压是铝及铝合金加工的核心工艺之一,具有高效、无切屑、材料利用率高等优点,但目前能耗强度偏高。我国主要铝加工厂挤压材生产的能耗是欧洲的1.43倍,温室效应是欧洲的2.33倍[7]。
随着挤压成形技术在交通运输、航空航天等领域应用越来越广泛,挤压成形工艺能耗问题受到越来越多关注。INGARAO等[8-9]基于生命周期清单,对比分析了热挤压成形与传统车削工艺加工同一种轴对称铝合金零件的能源效率,并分析了零件批量、尺寸变化对单产能耗的影响。BUIS等[10]建立了挤压成形工艺生命周期清单模型,分析了不同工艺参量与加工条件对能耗性能的影响。JEONG等[11]针对分流挤压的铝棒加热效率问题,提出铝棒匀质热处理与铝棒预热过程融合法,并评估了该方法能耗性能情况。王安哲等[12]对铜管热挤压与冷挤压工艺能耗、碳排放进行了对比评估,并分析了关键工艺参数对挤压工艺能耗及碳排放的影响。石建业[13]分析了电阻加热炉与工频感应加热炉在铝及铝合金热挤压中的加热效果和能源消耗情况,并指出工频感应加热具有较好的节能效果。然而,挤压成形过程属于复杂的热力耦合过程,对挤压过程热平衡要求严格,而且挤压成形过程受挤压速度、温度、铝棒长度、挤压模具几何尺寸、材料性能等多种参数影响,现有研究更强调对挤压设备或挤压工艺能耗的宏观统计分析或局部改进技术的研究,对挤压成形能耗优化、控制方法研究仍较匮乏。
本文以降低挤压成形比能耗为目标,建立热平衡约束条件等价方程,以铝棒起始温度、铝棒长度、挤压速度、挤压筒温度、模角等为控制变量,以热导率、材料强度系数为扰动变量,集成利用实验设计(DOE)、方差分析等方法构建热平衡约束的挤压成形比能耗鲁棒优化模型,在保证挤压稳定的情况下,降低挤压成形能耗。
1 挤压成形过程能耗与热流平衡特征
热挤压是高度非线性的热力耦合过程,能源消耗用于满足金属塑性变形条件,以实现物质转移,达到工件形状、尺寸变化以及改善组织、性能的要求,金属成形过程如图1所示。

图1 挤压成形过程能耗与热流平衡
Fig.1 Energy balance and heat flow balance of heat extrusion forming
从能耗输入视角来看,铝合金热挤压前先对铝棒、模具、挤压筒进行加热,电能经电动机、液压系统提供挤压力,挤压力会用于材料变形做功和克服摩擦做功。根据能量守恒定律,挤压成形能耗可以表达为
(1)
式中,P为挤压力;vin为挤压速度;Wcf为金属流动过程中克服与挤压筒摩擦力所做的功;Wdf为金属流动过程中克服模具摩擦力做的功;Wform为金属变形做的功。
在材料塑性变形过程中,从力平衡的角度看,变形区入口球面的应力是与包括挤压模锥面或死区界面上的摩擦力在内的其他应力相平衡的,因此金属变形功Wform包括了模锥面或死区界面上的摩擦功消耗。为了计算该部分的功,本文将根据文献[14]提出的挤压变形球面坐标系(图2),基于圆棒挤压功计算模型,采用系数修正法获取变形功。

图2 挤压变形时球面坐标系及应力应变状态[14]
Fig.2 Spherical coordinate system and stress-strain state during extrusion deformation [14]
为实现塑性变形而消耗在变形区内的功率,可由变形区入口球面上的应力与速度分布通过积分求得:

(2)
εe=lnλ
式中,vj为挤压变形入口处的速度,本文假设该速度等于挤压速度vin;At为挤压筒的横截面积;Dt为挤压筒内部直径;σk为与挤压条件有关的金属变形抗力;α为模角;λ为挤压比;mz为变形区模锥面或死区界面上的摩擦因子(取值范围为0≤mz≤1.0,无润滑热挤压或产生死区时,mz=1.0;带润滑热挤压无死区时,mz=0.5;冷挤压无死区时,mz=0.2~0.3[14])。
材料与挤压筒接触面的摩擦功Wcf可根据摩擦力做功进行计算:
Wcf=Fcfvj
(3)
其中摩擦力Fcf可由下式计算:
Fcf=πτDtL
(4)
式中,L为铝锭与挤压筒的接触长度;τ为铝棒与挤压筒接触面上的摩擦剪切应力。
综合式(3)与式(4),材料与挤压筒接触面的摩擦功Wcf可以表示为
(5)
式中,![]() 为常规流动应力;mt为挤压材料与挤压筒的摩擦因子。
为常规流动应力;mt为挤压材料与挤压筒的摩擦因子。
Wcf可以看成是接触长度L的线性函数。在材料挤压过程中,材料会填充到整个模具中,此时材料与模具的接触面是固定的,材料与模具接触面的摩擦功Wdf可以视为常数,通过下式计算:
(6)
式中,vf为产品出口处速度;d为产品直径;Ld为定径带长度;md为挤压材料与模具接触面的摩擦因子。
研究表明,无论何种形式的做功最终都会转化成热,而且模具载热、铝棒载热、变形生热、摩擦生热伴随着坯料与模具、挤压筒、垫片的热传导,使挤压成形存在复杂的热行为,当热流不平衡时,即净热量不为零时,挤压产品头、中、尾部的组织和性能极不均匀,易导致扭拧、弯曲、波浪、收口、扩口等缺陷,质量不能满足使用要求。挤压工艺能耗与产品质量呈现出复杂强耦合关系,能耗的调控会引起产品质量的变化,因此挤压成形过程中要保持热流平衡,如下式所示:
ΔQ=Qcf+Qdf+Qform-Qd1-Qd2-Qd3
(7)
式中,ΔQ为净生热量,等温挤压时,理想值为0;Qcf为坯料与挤压筒之间的摩擦生热量;Qdf为坯料与模具之间的摩擦生热量;Qform为金属变形区的变形生热量;Qd1为坯料与挤压垫片之间的传热量;Qd2为坯料与挤压筒之间的传热量;Qd3为坯料与模具之间的传热量。
式(7)中,Qd1、Qd2、Qd3均可根据材料热传导方程进行计算确定。
2 热平衡约束等价方程
根据挤压过程中热流平衡机理,假设变形区内的金属发生塑性变形产生的热全部作用在模孔出口处的挤压产品上,并引起模孔出口处挤压产品温度升高,即可假设模孔出口处产品的温度T是坯料进入变形区时的温度T0与变形区内塑性变形热导致的温升ΔT之和,即
T=T0+ΔT
(8)
其中,ΔT可以看作是热挤压过程中塑性变形生热导致的温升,已有研究通过机理分析、经验等解析出了温升预测公式[14]:

(9)
式中,Af为产品断面面积,cm2;l为铝棒长度,cm;vout为产品流出速度,cm/s;Q为挤压模附近塑性变形区内产生的热量,J;K为经由挤压筒和挤压模的热流系数,J/(s·℃);T0为初始坯料温度加上剪切变形所产生的温升,再减去挤压模初始温度所得的值,℃;c为金属的质量热容,J/(g·℃);ρ为金属的密度,g/cm3。
任何一种铝合金材料都有一个最佳挤出温度,实际温度与最佳挤出温度之间的波动量越小,挤出产品质量越稳定。假设某种产品最佳挤出温度为Tbest,则产品挤出温度的波动量
δT=T-Tbest
(10)
综合以上分析,热平衡约束条件可以定义为
δT→min(T-Tbest)
(11)
3 成形比能耗鲁棒优化模型
3.1 比能耗优化流程
本文采用图3所示的成形比能耗优化模型来优化成形能耗,该模型是建立在挤压成形能耗平衡与热平衡机理分析基础上的,从该模型中可知,若要实现能效的鲁棒性优化,需进行以下几个方面研究。

图3 成形能耗的优化过程
Fig.3 Optimization process of forming energy
(1)成形过程能耗平衡、热平衡机理分析。该部分主要是根据金属挤压变形过程,通过对挤压力受力状态、挤压力影响因素等进行分析,一方面确定挤压过程能耗平衡机制,另一方面确定挤压过程热生成、传递、转换机理,确定热平衡机制。
(2)热平衡控制原则分析。根据挤压过程中金属的传热行为特征,建立挤压过程的热流平衡关系,明确挤压控制变量对热平衡及出模孔产品温度的影响规律,在此基础上确定挤压成形过程中热平衡控制原则,即确定工艺控制变量的选择基准。
(3)变量类型及范围设定。根据挤压过程特点,将关键工艺参数、设计参数、扰动参数定义为挤压成形过程的控制变量集,并确定不同变量的取值范围。本文选取模角、铝棒长度、铝棒起始温度为设计变量(DV),挤压速度、挤压温度为工艺变量(PV),而描述挤压工艺设备、产品设计参数的变量定义为固定变量(FV), 对影响成形能耗但难以控制的变量集定义为扰动变量(NV)。
(4)能效优化模型。将挤压成形比能耗定义为优化目标,构建能效的优化模型,并基于DOE构建鲁棒性优化算法,实现能效的优化,其中比能耗可采用下式计算:
(12)
F(DV,PV,NV)为单位时间内产品挤出量与能耗的比值,定义为产品挤出速度与产品成形功耗的比值,单位为mm/J,该值越大表明挤压成形能效越高。
(5)能效鲁棒优化算法的构建。主要基于DOE构建能效的鲁棒性算法,在挤压热平衡约束下实现能效的鲁棒优化。
3.2 能效鲁棒性优化算法
根据图1对成形能耗的分析,构建了能效鲁棒性优化算法,如图4所示。其中,步骤(3)为比能耗、热约束评价指标的计算模拟。基于挤压成形能耗分析模型以及控制变量、扰动变量的正交矩阵确定不同输入模式下(工艺参数、设计参数不同组合方案确定了不同输入模式)成形比能耗、温度波动量的评价指标的均值、方差以及变异系数等。其中变异系数可采用下式计算:
η=-10lg{(1/μ2)·[1+3(σ2/μ2)]}
(13)
式中,μ为成形比能耗或温升的均值;σ为成形比能耗或温升的方差。
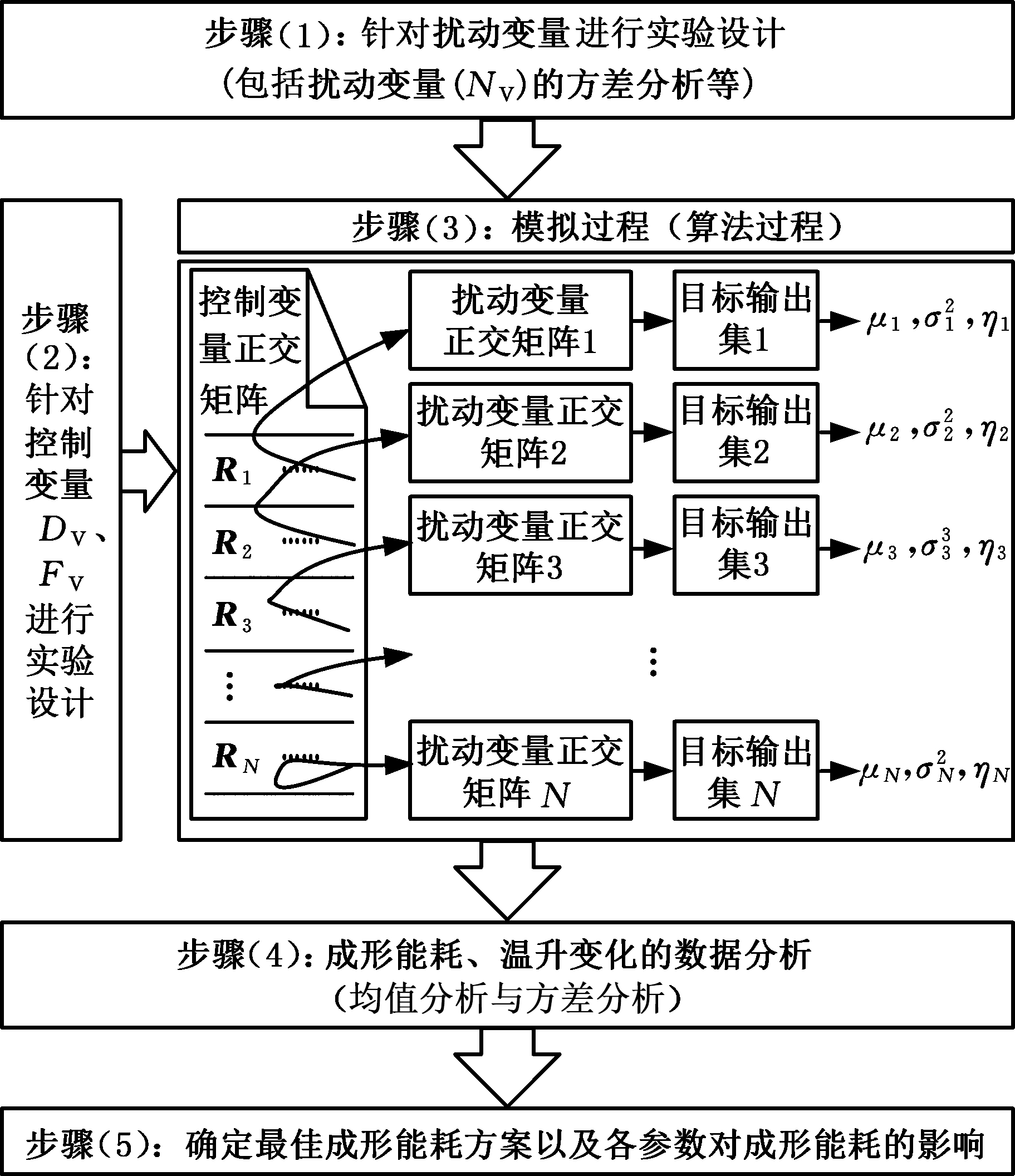
图4 鲁棒优化算法过程
Fig.4 Robust optimization algorithm
4 案例研究
4.1 实验设计
实验选取图5所示的铝合金零部件为研究对象,该零部件材料为6063铝合金,其材料性能参数如表1所示。为了加工该铝合金件,采用图6所示的挤压模具。上模尺寸为φ100 mm×50 mm,上模设有4个分流孔;下模尺寸为φ100 mm×50 mm,焊合高度为20 mm,设有一级空刀槽,空刀槽起到支撑工作带和避免模具与型材之间的接触减少摩擦的作用。铝合金零部件的挤压条件如表2所示。

图5 零件尺寸
Fig.5 Parameters of aluminum profile
表1 6063铝合金零件材料性能参数
Tab.1 Material parameters of 6063 aluminum alloy

序号性能参数数值1弹性模量(MPa)4.0×1042密度(kg/m3)2.7×1033泊松比0.3334铝棒与模具传热系数(W/(m2·K))3 0005热导率(W/(m·K))1986质量热容(J/(kg·K))9007材料极限强度(MPa)375

图6 挤压模具结构
Fig.6 Parameters of extrusion dies
4.2 实验结果分析
针对本文所给出的实验对象的加工要求可确定优化模型中的固定变量、控制变量、扰动变量类型及范围分别如表3~表5所示。
表2 铝合金零件挤压条件
Tab.2 Aluminum alloy parts extrusion condition

序号条件参数数值1模具起始温度(℃)4503挤压筒直径(mm)1304挤压比115润滑方式无润滑6铝棒直径(mm)1207模具材料H13热作模具钢8上模尺寸(直径×高)(mm)100×509下模尺寸(直径×高)(mm)100×50
表3 固定变量
Tab.3 Fixed variables

序号变量类型数值1截面上端宽度(mm)252截面下端宽度(mm)453截面上端夹角(°)454材料类型6063铝合金5截面下端高度(mm)15
表4 控制变量类型及范围
Tab.4 Type and range of control variables

序号类型控制变量范围1DV铝棒起始温度T0(℃)[320,480]2DV铝棒长度l(mm)[500,580]3PV挤压速度vin(mm/s)[330,550]4PV挤压筒温度Tc(℃)[340,440]5DV模角α(°)[45,60]
表5 扰动变量
Tab.5 Noise variables

序号变量名称平均值1金属与挤压筒摩擦因数μ0.312热导率λ(W/(m·K))1983极限强度系数s(MPa)3754铝棒与模具传热系数h(W/(m2·K))3 000
扰动变量包括金属-挤压筒摩擦因数、金属热导率、金属极限强度系数、金属-模具的传热系数等,该类变量都非常难控制,如金属-挤压筒摩擦因数会随润滑条件等随机波动,金属热导率与金属极限强度系数会随每批材料质量的差异波动等。本实验将各个变量的经验值作为平均值,并假设所有变量都满足正态分布,通过正交矩阵模拟的方法确定其方差、标准差等,然后基于方差、标准差等进一步确定扰动变量的取值范围,结果如表6、表7所示。
表6 扰动变量的值、差值及标准差
Tab.6 Values, difference, and standard deviations for NV
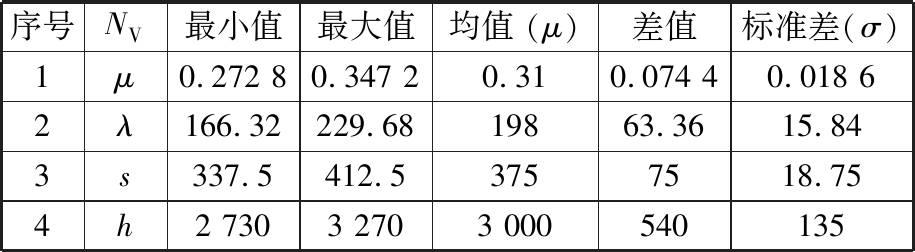
序号NV最小值最大值均值 (μ)差值标准差(σ)1μ0.272 80.347 20.310.074 40.018 62λ166.32229.6819863.3615.843s337.5412.53757518.754h2 7303 2703 000540135
表7 正交试验中扰动变量的水平值
Tab.7 Level of noise variables in orthogonal test

变量均值方差试验水平值μ-3/(2σ)μμ+3/(2σ)μ0.310.018 60.198 6450.310.421 355λ19815.84194.750 4198201.249 6s37518.75371.464 5375378.535 5h3 0001352 990.5133 0003 009.487
根据表3~表7给出的各变量的取值范围,利用Minitab17软件可确定控制变量与扰动变量的正交矩阵,计算结果如表8、表9所示。根据上述数据,采用MATLAB平台对鲁棒优化过程进行模拟计算,可以确定表10所示的成形比能耗的平均值、方差以及变异数。
表8 控制变量的L16(45)正交矩阵
Tab.8 L16 (45) orthogonal array for control variables

序号因素T0lvinTcα1320500330340452320530400375503320560480405554320580550440605370500400405606370530330440557370560550340508370580480375459420500480440501042053055040545114205603303756012420580400340551348050055037555144805304803406015480560400440451648058033040550
表9 扰动变量的L16(43)正交矩阵
Tab.9 L16(43) orthogonal array for noise variables
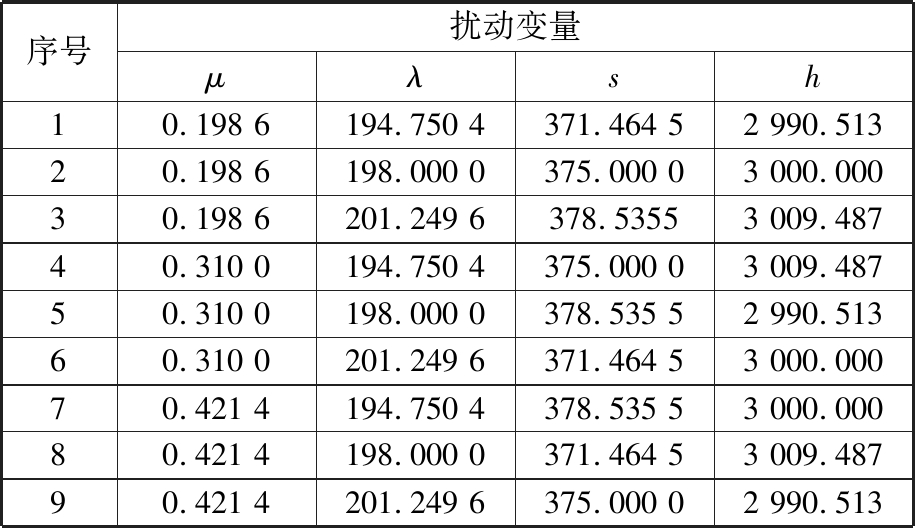
序号扰动变量μλsh10.198 6194.750 4371.464 52 990.51320.198 6198.000 0375.000 03 000.00030.198 6201.249 6378.53553 009.48740.310 0194.750 4375.000 03 009.48750.310 0198.000 0378.535 52 990.51360.310 0201.249 6371.464 53 000.00070.421 4194.750 4378.535 53 000.00080.421 4198.000 0371.464 53 009.48790.421 4201.249 6375.000 02 990.513
根据表10可以确定最佳比能耗方案,当T0=420 ℃,l=560 mm,vin=330 mm/s,Tc=375 ℃,α=60°时,最佳比成形能耗为95.88 mm/J,温度波动量为1.78 ℃。如图7所示,本文利用效应曲线图进一步揭示了控制变量对比能耗的影响。当T0增大时,比能耗存在一定的波动性,且存在一个最佳值,铝棒温度过低会导致金属挤压变形应力增大,比能耗降低;为保证挤压产品出口
表10 成形比能耗的均值、方差及变异系数
Tab.10 Mean, variance, and variation coefficient for specific energy

控制变量矩阵行均值μ方差σ2变异系数η190.320.000 096 2039.236280.590.000 124 6038.096367.180.000 082 5036.823457.990.000 024 8035.189585.660.000 324 0038.52680.610.000 086 6637.95760.550.000 055 4435.64860.920.000 032 1435.45965.020.000 218 7037.031059.760.000 212 4035.791195.880.000 025 2039.831276.860.000 032 9437.801362.720.000 034 1835.801474.050.000 016 8036.991576.40.000 021 6837.221679.940.000 014 8938.53

图7 控制变量的效应曲线图分析
Fig.7 Effect curve of control variables
处的温度,铝棒温度过高时,应减小挤压速度vin;此时比能耗也减少;l的增大会导致比能耗降低,主要是因为铝棒长度增大,铝棒与挤压筒之间的摩擦阻力增大,能耗增大;Tc的增大会导致挤压比能耗降低,Tc增大意味着加热能耗的增加,但对比能耗的影响并不是很大;随着模角α的增大,挤压比能耗升高,主要原因是模角增大,金属与模具的摩擦力减小,能耗需求降低,同时也增大了产品出口处的速度。
5 结论
本文揭示了挤压成形过程热平衡与能耗平衡机制,建立了热平衡的等价约束方程。以优化挤压成形比能耗为目标,提出了热平衡约束的挤压成形比能耗鲁棒优化模型,并基于实验设计、方差分析等方法提出比能耗鲁棒算法。以某6063铝合金零件的热挤压为例,确定当初始温度为420 ℃、铝棒长度为560 mm、挤压速度为330 mm/s、挤压筒温度为375 ℃、模角为60°时,最佳比成形能耗为95.88 mm/J,温度波动量为1.78 ℃。而且根据各控制变量的效应曲线,铝棒初始温度与挤压速度对挤压比能耗的影响最大。但由于生产实际中影响因素更复杂,需要进一步结合所提方法与工程试验,确定最佳参量的可信度范围,以便更好支撑生产实际。
[1] WANG Q, LIU F, LI C. An Integrated Method for Assessing the Energy Efficiency of Machining Workshop[J]. Journal of Cleaner Production, 2013, 52: 122-133.
[2] MOUZON G, YILDIRIM M B, TWOMER J. Operational Methods for Minimization of Energy Consumption of Manufacturing Equipment[J]. International Journal of Production Research, 2007, 45(18/19): 4247-4271.
[3] GUTOWSKI T G, BRANHAM M S, DAHMUS J B, et al. Thermodynamic Analysis of Resources Used in Manufacturing Processes[J]. Environmental Science & Technology, 2009, 43(5):1584.
[4] 刘静安, 何梅琼, 左其福,等. 推广国产优质模具钢促进铝挤压工业与技术发展-SRM-1高强韧高温耐磨特种合金钢的特性及性价比分析 [J]. 铝加工, 2016(4):57-62.
LIU Jing’an, HE Meiqiong, ZUO Qifu, et al. Propotion of Domestic High-quality Steel, Promotion of Development of Aluminum Extrusion Industry and Technology [J].Aluminium Fabrication, 2016, (4):57-62.
[5] 项胜前, 罗铭强, 陈文泗,等. 铝合金一模多出(孔)挤压的特点及关键技术[J]. 铝加工, 2015(5):9-14.
XIANG Shengqian, LOU Mingqiang, CHEN Wensi, et al. Characteristics and Key Technical Analysis for Porous Mold Extrusion of Aluminum Alloy [J]. Aluminium Fabrication, 2015, (5):9-14.
[6] 王祝堂. 中国铝挤压工业现状[J]. 有色金属加工, 2016, 45(1):1-3.
WANG Zhutang. Present Situation of Aluminum Extrusion Industry in China [J]. Nonferrous Metals Processing, 2016, 45(1):1-3
[7] 丁宁,高峰,王志宏,等. 铝挤压材生产的能耗和温室效应分析[J].轻金属,2011(增刊1):320-324.
DING Ning, GAO Feng, WANG Zhihong,et al. Analysis of the Energy Consumption and Greenhouse Gas Emissions in Aluminum Extrusion Production [J]. Light Metals, 2011(S1):320-324.
[8] INGARAO G, PRIARONE P C, GAGLIARDI F, et al. Subtractive Versus Mass Conserving Metal Shaping Technologies: an Environmental Impact Comparison[J]. Journal of Cleaner Production, 2015, 87: 862-873.
[9] INGARAO G, PRIARONE P C , LORENZO D R, et al. A Methodology for Evaluating the Influence of Batch Size and Part Geometry on the Environmental Performance of Machining and Forming Process [J]. Journal of Cleaner Production, 2016, 135:1611-1622.
[10] BUIS J J , SUTHERLAND J W , ZHAO F. Unit Process Life Cycle Inventory Models of Hot Forming Processes[C]//Proceedings of the ASME 2013 International Manufacturing Science and Engineering Conference. Madison, Wisconsin, 2013: V002T04A011.
[11] JEONG M S , LEE S Y , LEE I K , et al. Green Alternative Aluminum Extrusion Process through Process Convergence [J]. International Journal of Precision Engineering and Manufacturing, 2014, 15(6):1173-1177.
[12] 王安哲,陈忠家,张哲,等.铜管挤压加工工艺能耗及碳排放研究[J].金属功能材料,2014,21(3):30-33.
WANG Anzhe, CHEN Zhongjia, ZHANG Zhe,et al. Research of the Energy Consumption and Carbon Emissisons for Copper Tube Extursion Process [J].Metallic Functional Materials, 2014 (3):30-33.
[13] 石建业.感应炉加热铸锭在铝及铝合金热挤压种的节能分析[J].有色金属加工,2011,40 (5): 57-59.
SHI Jianye. Analysis on Saving in Energy for Induction Heating Billet in Induction Heating Furnace [J].Nonferrous Metals Processing, 2011, 40(5):57-59.
[14] 谢建新,刘静安. 金属挤压理论与技术[M].北京:冶金工业出版社,2012.
XIE Jianxin, LIU Jing’an. Theory and Technology of Metals Extrusion[M].Beijing: Metallurgical Industry Press, 2012.
