0 引言
工程结构优化分析中，常常会遇到结构参数域是凸集的情况，如椭圆凸集、椭球凸集或超椭球凸集(本文统称为椭球凸集)[1-2]，利用有限元法离散工程结构后，采用合适的优化算法，通常能很好地解决这类问题[3-4]。然而，当工程结构呈现出大型且复杂的状态时，为提高结构分析计算的精度，采用有限元法时往往会离散出更细致的网格，使获得的结构离散系统趋于庞大，从而导致产生许多自由度，故结合有限元法的结构优化算法虽然有效，但因结构平衡方程的计算量过大而显得耗时不菲，进而影响工程分析的时效性。由此可知，拥有众多自由度的椭球凸集参数域结构的高效优化分析，是一个值得研究的掣肘问题，需找到合适的解决方法。减基法是一种高效解决问题的方法，它源于连续函数的伽辽金映射逼近分析，多拓展用于偏微分方程的快速数值计算[5-7]，但在结构分析等领域因工程计算的复杂性而较少使用[8-10]。文献[11]直接从矩阵逼近理论出发进行列式推导，提出了能够在合理构建的减基空间中高精度、高速率地计算结构静态响应的减基方法。文献[12]研究了基于减基法的结构静态最优极值响应算法，并获得了高效的减基优化算法。然而，目前尚未有相关文献报道减基法高效处理椭球凸集参数域结构优化问题的方法，因此结合减基法研究椭球凸集参数域结构的快速优化问题将是有价值的和有必要的。
本文提出了一种针对椭球凸集参数域结构的高效减基优化方法，并给出了对应的结构减基优化流程。该方法在椭球凸集参数域通过基变换、选边界及伽辽金映射降阶来构建合适的减基计算模型及列式，进而构建相应的结构减基优化模型。本文通过对结构算例进行数值运算，来验证所提方法在保证计算精度的前提下能够获得较佳的优化效率。
1 优化问题描述
参数化结构静态平衡方程的有限元表达式如下：
K(μ)u(μ)=F μ∈Ω
(1)
式中，K为结构的刚度矩阵；u为结构的位移响应逼近解；F为结构的载荷向量，结构方程的自由度数记为n；μ为结构的参数向量，其维数记为m；Ω为结构的参数域。
在椭球凸集参数域条件下，研究的结构优化问题可描述为
(2)
式中，f(u(μ))表示结构优化的目标函数；“∶=”表示“定义为”； b为标量；
为椭球凸集参数域的中心点向量；W为椭球凸集参数域的特征矩阵，且为正定矩阵。
在式(2)中，
为结构椭球凸集参数域的表达式，若结构平衡方程的维数过于庞大，则该结构优化问题的计算求解过程将会过于耗时。
2 减基优化方法
2.1 减基法的构筑
椭球凸集参数域的特征矩阵为正定矩阵，可对其进行舒尔变换[13]，变基处理后可得
W=QTΛQ
(3)
式中，Q为正交矩阵；Λ为正定的对角矩阵；
为W的特征值。
结合式(3)，结构的椭球凸集参数域可变为标准的椭球凸集参数域，即
(4)
将式(4)进行变换得到
(5)
将变换后的标准椭球凸集参数域记为
(6)
(7)
将式(7)进行变换得到
(8)
式中，
为参数域变基处理后的参数向量(即在新坐标体系下的参数向量形式)。
由此可知，经过基变换后的参数域仍是椭球凸集而非通常意义下的矩形凸集，故不便于进行结构响应的减基空间建构。但新坐标体系下的标准椭球凸集参数域呈现出新的数学特征，其各个维度的轴长为1/ai(i=1,2，…,m)。对于标准的椭球凸集参数域，采用能将其包裹的标准矩形凸集参数域
作为结构减基计算的参数域，标准矩形凸集参数域的边界线平行于新坐标体系下的坐标轴，并大于或等于相应维度的椭球轴长，将新产生的标准矩形参数域
以及与之匹配的参数向量
记为
[-r1,r1]×[-r2,r2]×…×
[-ri,ri]×…×[-rm,rm]
(9)
ri≥1/ai i=1,2，…,m
式中，ri为标准矩形凸集参数域边界线对应的坐标值。
依据式(8)，新坐标系下的参数向量
与原参数域的参数向量μ∈Ω之间的对应关系为
(10)
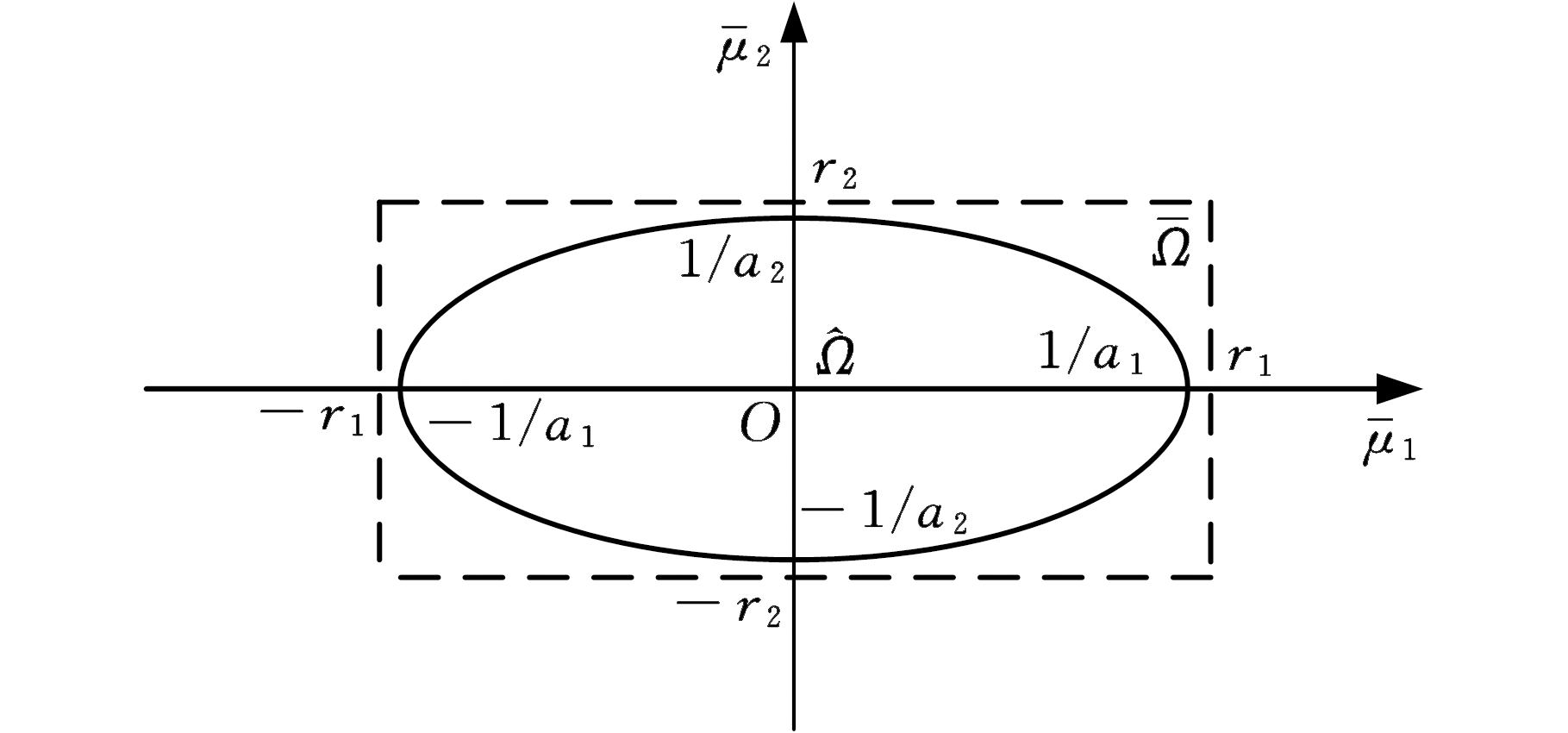
图1 二维椭球凸集参数域的矩形边界
Fig.1 The rectangular boundary of two-dimensional ellipsoidal convex parameter domain
以二维参数域为例，其作变基处理后的标准矩形凸集参数域的取值示意图见图1。由图1可以看出，新坐标系中标准的矩形凸集参数域覆盖了标准的椭球凸集参数域
故可在变基处理之后的标准矩形凸集参数域中进行有效采样并获得一组具有N个参数样本点向量的集合
同时依据式(10)得到原结构参数域下的采样点集合SN。针对集合SN，依据式(1)计算得到对应的结构位移响应，进而获得N维减基空间的减基矩阵：
ZN=[u(μ1) u(μ2) … u(μN)]
(11)
将结构的刚度矩阵K(μ)进行参数分离，并在减基空间中将结构的平衡方程(式(1))通过伽辽金映射进行降阶减缩，从而可获得椭球凸集参数域结构的位移响应减基计算表达式：
(12)
式中，uN(μ)为N维减基空间中的结构位移响应逼近解；αN(μ)为N维减基空间中的权系数向量；p为刚度矩阵K(μ)的参数分离数；σj(μ)为与参数相关的标量函数，并随着参数向量μ的变化而变化；Kj为分离参数获得的刚度矩阵;BN,j、FN分别为与参数无关的N阶矩阵和向量，可将其存储于计算机中。
2.2 优化模型的建立
利用上述减基法的构筑方式，在椭球凸集参数域条件下，可将原结构优化问题(式(2))转变为如下结构减基优化问题：
(13)
由式(13)可知，通过在标准的矩形凸集参数域中采样用来建立优化问题的低维减基空间，以及在原结构参数域Ω中进行有效的减基模拟和优化计算，能够高效率地求解获得目标函数的最优值。
2.3 减基优化流程
将结构的减基优化算法分为离线处理阶段和在线计算阶段，离线处理阶段为构建减基空间及其减基列式的流程，在线计算阶段为快速求解减基优化模型的流程。
(1)离线处理阶段。将结构的椭球凸集参数域Ω变为标准的椭球凸集参数域并获得标准的矩形凸集参数域及其边界±ri(i=1,2,…,m)；采用合适的抽样方法，在标准的矩形凸集参数域中采样得到样本点集合
并依据式(1)和式(10)建立减基空间并获得能存储于计算机中的减基矩阵ZN以及矩阵Kj、BN,j(j=1,2,…,p)和向量FN。
(2)在线计算阶段。由结构减基优化问题(式(13))可知，在结构的椭球凸集参数域Ω中，可借助减基列式(式(12))快速地计算得到结构位移响应逼近解uN(μ)，并在此基础上选用通用的优化算法高效地求解优化目标函数f(uN(μ))。
3 结构算例分析
考虑图2所示的应力结构算例，结构两端呈固定状态，施加竖直向下的力载荷f1=f2=f3=800 kN。相应的结构长度l=1.6 m，宽度w=0.5 m，厚度为0.02 m。将此结构算例进行有限元离散，形成拥有n=2 066个自由度的结构系统。将结构的材料参数记为向量形式μ=(μ1,μ2)=(E,ν)，其中E为弹性模量(102GPa)，ν为泊松比。结构的椭球凸集参数域可表示为
(14)
图2 结构算例
Fig.2 The example of a structure
结构算例对应的参数域形态如图3所示。对此结构算例进行分析，将图2中O点的竖直向下位移绝对值|uo(μ)|作为研究对象，|uo(μ)|为结构参数的函数，该函数相应于结构参数域Ω会有一个位移响应域且有位移响应最优值。针对此结构算例，具体的优化求解问题可描述为
(15)
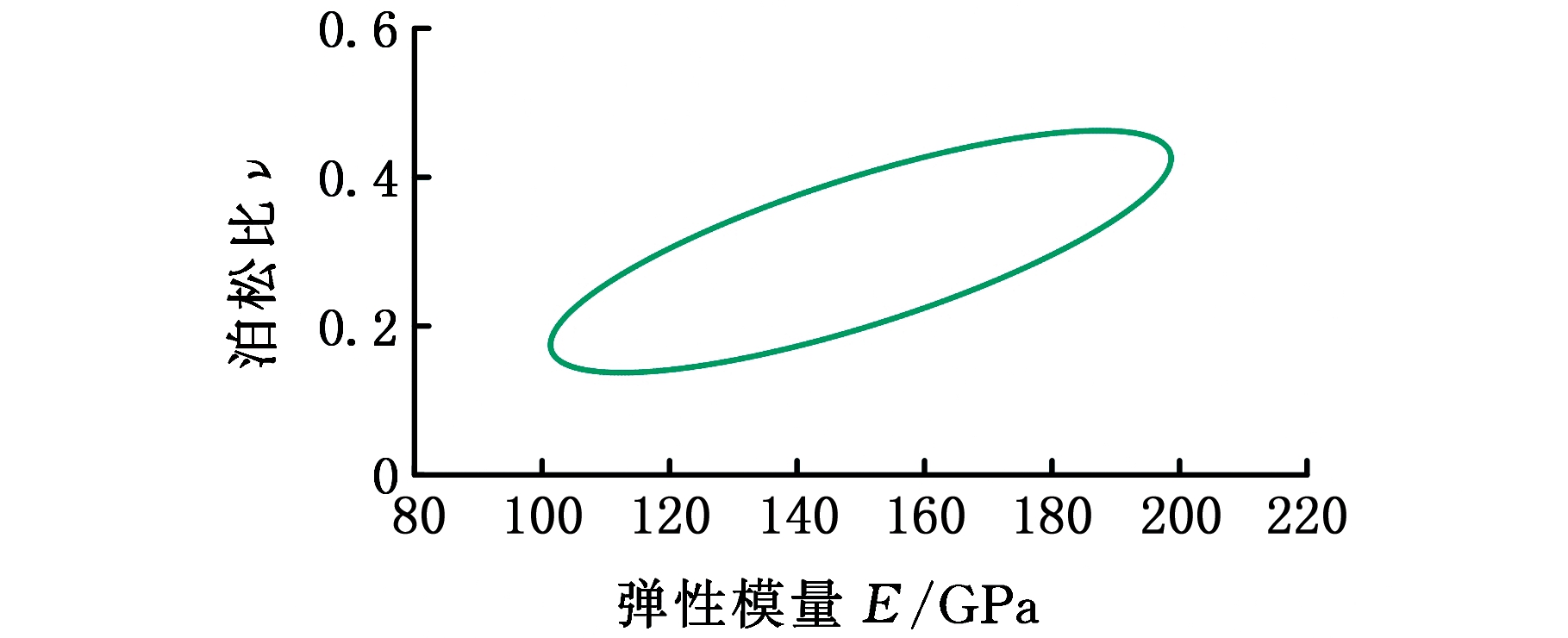
图3 结构算例的椭球凸集参数域
Fig.3 The ellipsoidal convex parameter field of the structure example
将特征矩阵W作舒尔处理，可得到其正定的对角矩阵：
(16)
依据式(9)可取r1=0.51、r2=0.1，进而得到标准矩形凸集参数域及其参数向量为
(17)
在标准矩形凸集参数域中，选用随机抽样的拉丁超立方法[14]采样N=12个参数点构建样本点集合
并根据式(10)求解得到原结构参数域Ω中的参数样本点集合S12，其分布见图4。在集合S12条件下，依据式(1)求解可得到原结构参数域Ω条件下的12维数减基空间及其表达矩阵Ζ12。同时，将结构刚度矩阵进行参数分离并在相应的减转基空间中进行伽辽金映射降阶，以此获得椭球凸集参数域条件下的减基计算表达式(式(12))，进而将结构算例的优化问题式(15)变为结构的减基优化问题，即
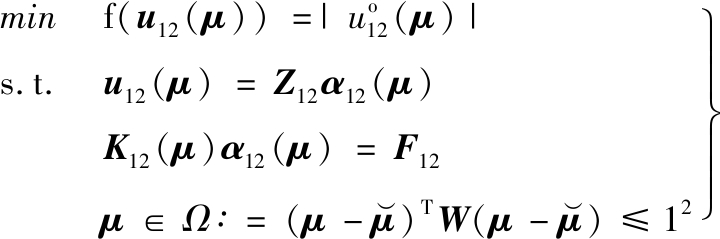
(18)
图4 结构算例的参数样本点分布
Fig.4 The distribution of parameter sample points of the structure example
针对上述结构减基优化问题(式(18))，采用基于梯度分析的优化算法进行减基优化求解。将优化迭代的起始点选取为椭球凸集参数域的中心点向量
设定最大迭代步数k=16，相应的优化迭代过程及其结果见图5。同时，采用有限元法结合相同的优化算法来求解同样的结构减基优化问题，其优化迭代过程及结果见图6。
图5 减基法的优化迭代过程
Fig.5 The optimizing iterative process for RBM
图6 有限元法的优化迭代过程
Fig.6 The optimizing iterative process for FEM
由图5和图6的迭代过程数据可知，减基法与有限元法优化结构算例的过程均是保持收敛的，而两种方法在迭代过程中的些许不同则主要是由减基法的数值计算误差造成的。由图5和图6的迭代最终优化数据可知，若将有限元法优化的结果作为精确解，则减基法优化导致的相对误差值仅为0.56%，以此可以评价两者的优化结果几乎是一致的，因此减基法优化具有较高的计算可靠性。在同一台计算机上，基于有限元法的优化算法在线求解结构算例的一次平均耗时量约为9.8 s，而采用基于减基法的优化算法在线求解结构算例则仅需0.6 s。显然，减基法的求解效率高于有限元法的求解效率，减基法计算时效的提升倍数约为16，因此减基法优化又具有较高的计算时效性。
4 结论
针对椭球凸集参数域的结构优化问题，提出了一种可靠而又高效的减基求解方法。所提方法将减基概念及其列式有机地融入到具有椭球凸集约束的优化算法中，能够高时效地解决工程结构的相关优化问题，具有一定的实践应用价值。结构算例分析验证了所提方法具有较高的计算可靠性和计算时效性。
[1] 罗阳军. 基于多椭球凸模型的结构非概率可靠性优化设计[D]. 大连:大连理工大学, 2009.
LUO Yangjun. Structural Non-probabilistic Reliability Based Design Optimization Using Multi-ellipsoid Convex Model[D]. Dalian:Dalian University of Technology, 2009.
[2] 张乾, 潘鑫, 乐培华, 等. 基于概率-凸集混合模型的汽车碰撞安全可靠性分析[J]. 机械强度, 2012, 34(6):916-920.
ZHANG Qian, PAN Xin, LE Peihua, et al. Reliability Analysis of the Vehicle Collision Safety Based Probability-convex Hybrid Model[J]. Journal of Mechanical Strength, 2012, 34(6):916-920.
[3] 陈东宁, 姚成玉. 系统可靠性评价的超椭球贝叶斯网络及其灵敏度方法[J]. 中国机械工程, 2015, 26(4):529-535.
CHEN Dongning, YAO Chengyu. System Reliability Assessment Method Based on Hyper-ellipsoid Bayesian Networks and Their Sensitivities[J]. China Mechanical Engineering, 2015, 26(4):529-535.
[4] 陈国荣. 有限单元法原理及应用[M]. 北京:科学出版社, 2009.
CHEN Guorong. The Principle and Application for the Finite Element Method[M]. Beijing:Science Press, 2009.
[5] SEN S, VEROY K, HUYNH D B P, et al. “Natural Norm” a Posteriori Error Estimators for Reduced Basis Approximations[J]. Journal of Computational Physics, 2006, 217:37-62.
[6] NGUYEN N C. A Multiscale Reduced-basis Method for Parametrized Elliptic Partial Differential Equations with Multiple Scales[J].Journal of Computational Physics, 2008, 227:9807-9822.
[7] HUYNH D B P, KNEZEVIC D J, CHEN Y, et al. A Natural-norm Successive Constraint Method for Inf-sup Lower Bounds[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199:1963-1975.
[8] LIU G R, ZAW K, WANG, Y Y. Rapid Inverse Parameter Estimation Using Reduced-basis Approximation with Asymptotic Error Estimation[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197:3898-3910.
[9] ZAW K, LIU G R, DENG B, et al. Rapid Identification of Elastic Modulus of the Interface Tissue on Dental Implants Surfaces Using Reduced-basis Method and a Neural Network[J]. Journal of Biomechanics, 2009, 42:634-641.
[10] 韩旭, 雷飞. 一种基于壳单元的自动快速计算方法及其在结构设计中的应用[J]. 计算力学学报, 2011, 28(3):332-337.
HAN Xu, LEI Fei. An Automatic and Rapid Computational Method and Its Application in Vehicle Body Design[J]. Chinese Journal of Computational Mechanics, 2011, 28(3):332-337.
[11] 张正, 韩旭, 姜潮, 等. 一种改进的减基法及其在固体结构分析中的应用[J]. 湖南大学学报(自然科学版), 2011, 38(2):30-34.
ZHANG Zheng, HAN Xu, JIANG Chao, et al. An Improved Reduced Basis Method and Its Applications in the Analysis of Solid Structures[J]. Journal of Hunan University(Natural Sciences), 2011, 38(2):30-34.
[12] 张正, 刘杰, 徐迎. 基于减基法的结构静态极值响应快速计算方法[J]. 计算力学学报, 2015, 32(1):94-98.
ZHANG Zheng, LIU Jie, XU Ying. Rapid Computation of Structural Static Extreme Response Based on Reduced Basis Method[J]. Chinese Journal of Computational Mechanics, 2015, 32(1):94-98.
[13] GOLUB G H, van LOAN C F.Matrix Computations[M]. Baltimore:John Hopkins University Press, 1996.
[14] YE K Q, LI W, SUDJIANTO A. Algorithmic Construction of Optimal Symmetric Latin Hypercube Designs[J]. Journal of Statistical Planning and Inference, 2000, 90:145-159.
