0 引言
负泊松比材料和结构受到轴向压缩时会发生横向收缩，或受到轴向拉伸时会发生横向膨胀，EVANS等[1]将这一类具有负泊松比效应的材料和结构命名为auxetics(意为拉伸膨胀)，因此负泊松比材料又被称为拉胀材料。国内外学者已对负泊松比材料和结构进行了广泛和深入的研究，研究发现，负泊松比材料和结构压痕阻力大[2]、抗冲击性能好[3]、吸声性能良好[4],且具有同向弯曲性能[5]和抗裂纹扩展性[6]等优良性能，被广泛应用于汽车、航空、船舶等工业领域。典型的负泊松比材料和结构包括泡沫聚合物、蜂窝结构、聚丙烯纤维及某些晶体结构等[7]。本文所研究的负泊松比蜂窝结构不但具有质量小、比强度高、结构简单和可设计性强等传统蜂窝结构的优良性能[8]，还具有其他独特的力学性能，近年来已成为一个新兴的研究热点。
LAKES[9]在实验室制造出了第一个人工负泊松比材料。CHOI等[10]对材料负泊松比效应的产生机理、微观结构形成方法和结构受外力作用时的变形情况进行了系统的研究。NKANSAH等[11]发现了聚四氯乙烯具有负泊松比特性。LAKES等[12]采用对传统三维结构进行转变的方法，指出了三维内凹单元的变形行为。YANG等[13]在微极弹性理论的基础上，对一种二维三角蜂窝结构的几何参数与泊松比之间的关系进行了研究。WAN等[14]基于大挠度理论对负泊松比内凹蜂窝结构的力学性能进行了研究。卢子兴等[15]基于旋转机制建立了一种具有负泊松比效应的、由部分内凹及部分规则六边形组成的二维多胞材料力学模型。GASPAR[7]基于平均线应变假设和一阶非均匀性对新型非常规负泊松比颗粒状材料进行了研究。颜芳芳等[16]将柔性蜂窝结构应用于无人机外翼，探讨了蜂窝结构各项参数的改变对蜂窝结构力学性能的影响，进而对无人机外翼的性能进行了优化。SUN等[17]提出了一种具有负泊松比子结构的多功能分层蜂窝结构，基于欧拉梁理论推导出了结构的弹性模量。郭磊[18]基于旋转刚性单元模型建立了新型多尺寸刚性矩形单元组合模型。鲁超等[19]利用柔性悬臂梁模型，给出了蜂窝壁板大变形条件下面内等效弹性模量的理论计算公式。金爱兵等[20]从微观结构角度分析了岩体特殊的负泊松比效应，研究了具有负泊松比效应的晶体材料。LI等[21]设计了一种新型负泊松比空心骨架胞元结构，采用有限元法与实验方法对结构进行了研究。蒋伟等[22]改进了传统蜂窝材料的结构设计, 提出了一种环形负泊松比结构, 运用能量法推导出了环形蜂窝芯等效弹性模量公式，并采用有限元法对环形蜂窝芯结构进行了力学性能仿真。LU等[23]设计了一种在内凹蜂窝结构中增加一个窄肋的新型蜂窝结构。FU等[24]依据梁理论推导出了一种新型负泊松比手性三维材料的等效弹性模量和泊松比的解析解。
本文基于环形蜂窝结构[22]提出了一种具有负泊松比效应的可变弧角曲边内凹蜂窝结构，该结构的曲边内凹程度可以改变，当曲边弧角为180°时即为环形蜂窝结构。利用能量法推导出了结构的等效弹性模量和等效泊松比的解析表达式，并与已有理论解和有限元结果进行了比较；讨论了等效弹性模量和等效泊松比与结构几何参数之间的关系。
1 结构建模
图1为本文所提出的曲边内凹蜂窝结构示意图，其构思源于环形蜂窝结构[22]，所提结构的曲边弧角θ可以改变。由图1可知，胞元结构在面内呈中心对称，竖直壁板长度为2h，两竖直壁板间宽度为2l，曲边圆弧半径为r，弯曲壁板为圆的部分圆弧，其对应的曲边弧角为θ，连接部分长度为m，壁板厚度为t，结构垂直于所在平面的厚度为d，当弧角θ取180°时，l=r。胞元受到横向或纵向载荷作用时，结构会产生变形。当作用载荷较小时，壁板发生弹性变形，结构的弹性模量和泊松比等力学性能由胞元的参数确定；当作用载荷较大时，壁板发生塑性变形，此时结构的力学性能随载荷大小变化。本文采用解析方法研究胞元内各几何参数对结构宏观等效力学性能的影响。
图1 曲边内凹蜂窝胞元结构示意图
Fig.1 Schematic diagram of honeycomb cell structure with curved concave sides
2 变形分析
2.1 Y轴方向受载
根据文献[22]的思路，本文对曲边内凹蜂窝模型进行受力分析(图2)。令胞元结构在上下胞元连接点处作用图2a所示的竖直方向的对称载荷FS，使得胞元内部各壁板产生拉伸、剪切和弯曲变形。本文研究的结构为梁架结构，结构中的拉伸应变能和剪切应变能相对于弯曲应变能很小，因此采用能量法求解结构各方向的位移变形时，只考虑结构的弯曲应变[22]。因不考虑拉伸应变能，故将胞元间的连接杆视为刚性杆，杆两端的位移相等，可直接研究胞元主体。对称载荷直接作用在E、F处，胞元结构为封闭梁结构。该力学问题为超静定问题，且封闭梁结构关于中心对称，因此可取结构的1/4部分进行研究，如图2b所示，自由端受竖直载荷FS/2和未知弯矩M0的作用。
(a)整体胞元结构受载示意图 (b)1/4结构的内力示意图
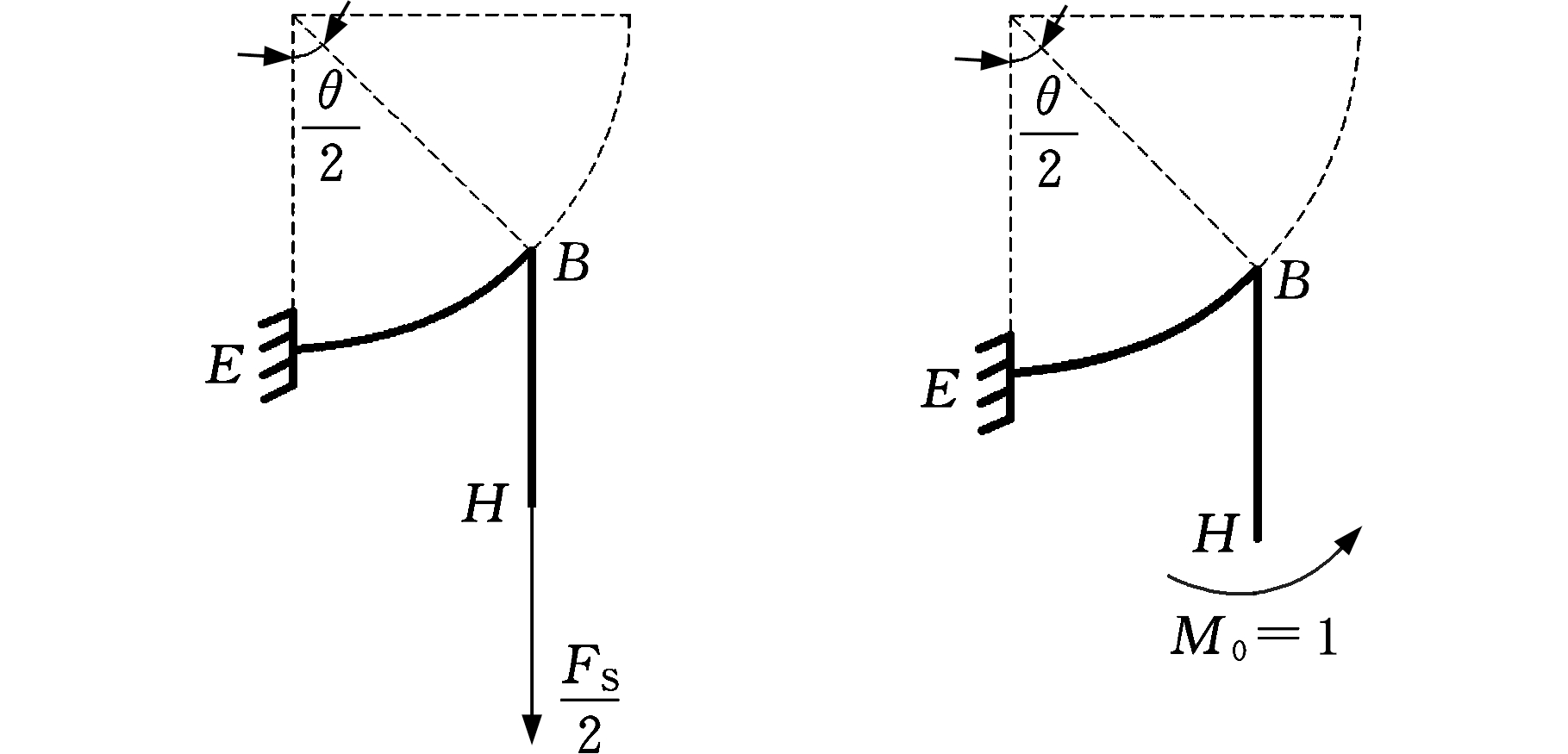
(c)只作用F/2载荷时1/4结构 (d)只作用单位弯矩时1/4结构
(e)只作用水平单位力时1/4结构
图2 Y轴方向受载时的受力分析
Fig.2 Force analysis under Y-axis load
因弯矩M0未知，故将其在下式中记作MR1，则自由端H处截面的转角变形协调条件满足：
δ11MR1+δ1F=0
(1)
式中,δ1F为仅作用载荷FN=FS/2时H所在截面的转角，如图2c所示；δ11为在H处作用单位弯矩时H所在截面的转角,如图2d所示。
当只作用载荷FN时，分别求得杆BH和杆EB的弯矩，其中直杆BH横截面上的弯矩是关于杆长x的函数M(x)，曲杆EB横截面上的弯矩是关于弧角φ的函数M(φ)。当只作用单位弯矩时,分别求得杆BH和杆EB的弯矩
和
根据下式，可分别求得δ1F和δ11：
(2)
(3)
Im=dt3/12
式中,Em为材料弹性模量;Im为截面对中性轴的惯性矩。
由式(1)可得
(4)
由式(4)可得
(5)
运用卡氏定理可求出在Y轴方向作用对称载荷FS时，胞元结构在Y轴方向的位移变形ΔYY，即为结构应变能对Y轴方向作用力FS求偏导，其表达式如下:
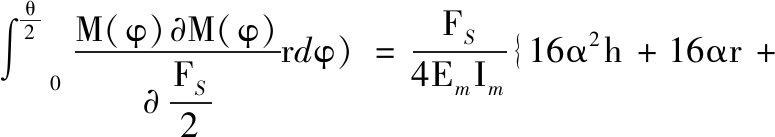
(6)
如图2e所示，利用单位力法可求出在Y轴方向作用对称载荷FS时，胞元结构在X轴方向的位移变形ΔYX；作用FN和M0时,杆BH和杆EB的弯矩分别为M(x)和M(φ)；只作用水平单位力时,杆BH和杆EB的弯矩分别为和此条件下的位移变形可表示为
(7)
2.2 X轴方向受载
如图3所示，令结构只受X方向的水平对称载荷FS作用，取其1/4结构研究，可分别求得在X轴和Y轴方向的位移变形，其表达式分别如下：
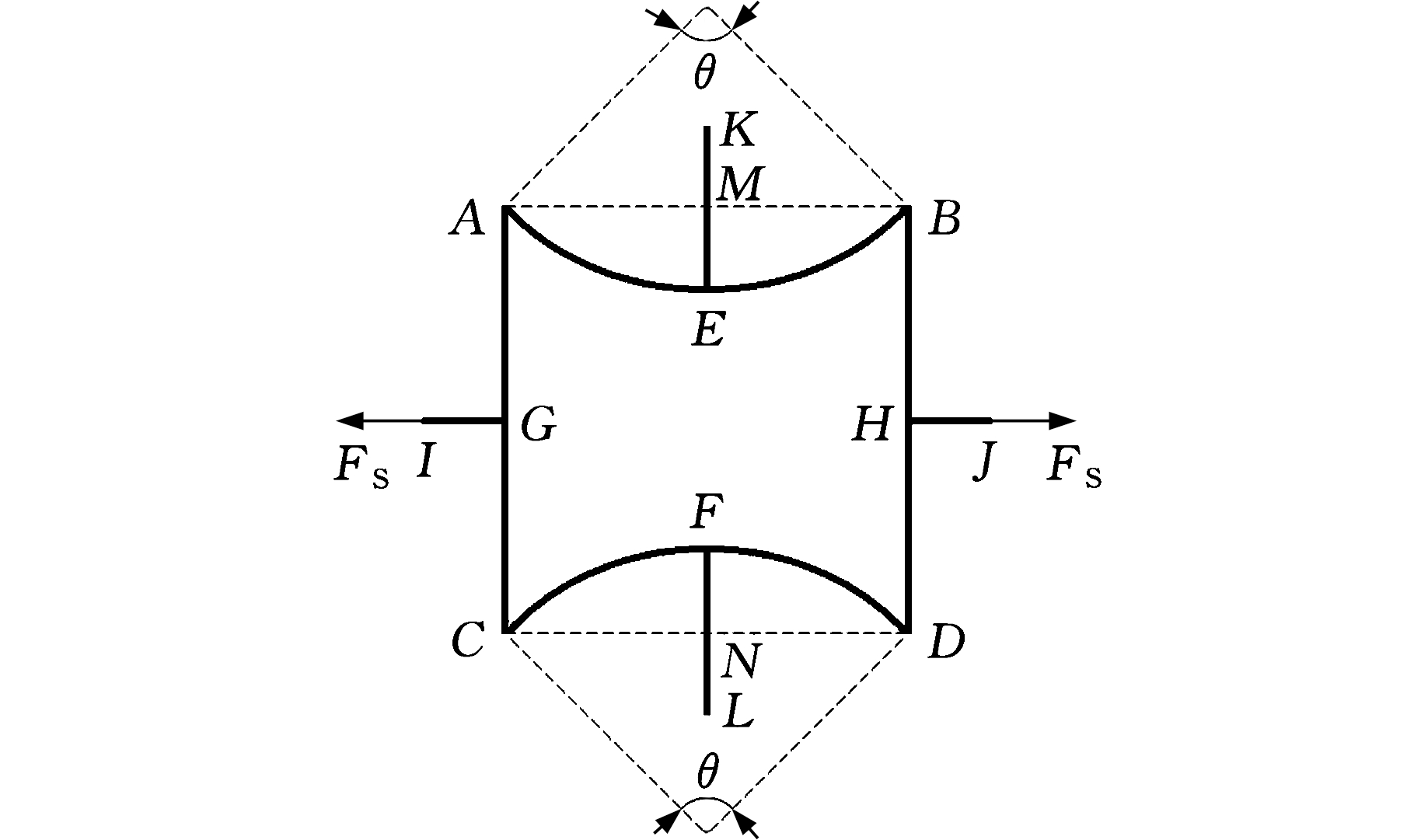
图3 X轴方向受力时结构示意图
Fig.3 Schematic diagram of structure under X-axis load
(8)
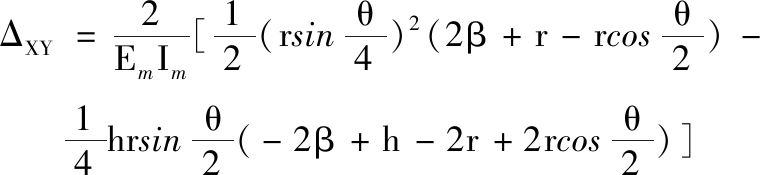
(9)
3 等效弹性模量与等效泊松比
依据Y轴受力时的位移变形公式(式(6)和式(7))，可求得Y轴方向的等效弹性模量和等效泊松比分别为
(10)
(11)
式中,εYY、εYX分别为Y方向受力时Y方向和X方向的应变；σY为Y方向应力。
同理可求得X轴方向的弹性模量和等效泊松比分别为
(12)
(13)
式中，εXX、εXY分别为X方向受力时X方向和Y方向的应变；σX为X方向应力。
4 结果分析与讨论
4.1 本文解析解与已有理论解及有限元结果比较
本文所提出的可变弧角曲边内凹蜂窝结构(图1)，在弧角θ=180°时将退化为环形蜂窝结构[22]。有限元计算模型采用5×5阵列的周期胞元结构，如图4所示，材料选取较为常见的铝合金，弹性模量Em=71 GPa，密度ρ=2 770 kg/m3，泊松比ν=0.33。算例中厚度t取定值1 mm。设置位移约束条件如下：①约束与X轴平行的结构对称中心线Y方向的位移,②约束与Y轴平行的对称中心线X方向的位移,③约束整个结构Z方向的位移。分别作用X轴方向对称载荷与Y轴方向对称载荷，求得结构位移变形后，计算等效弹性模量。
图4 有限元计算模型
Fig.4 Finite element calculation model
选取与文献[22]相同的几何参数，图5给出了环形蜂窝结构时的Y轴方向等效弹性模量EY的本文解析解、文献[22]理论解以及有限元结果的比较曲线图。从图5中可以看出，本文解析解、文献[22]理论解和有限元结果三者完全吻合，验证了本文理论推导和解析结果的正确性,同时也表明了本文在采用能量法求解时忽略拉伸应变能和剪切应变能这一假设的合理性。
图5 环形蜂窝结构时Y轴方向等效弹性模量与曲边圆弧半径的关系曲线
Fig.5 The relationship between Y-axis equivalent elastic modulus and curved arc radius in circular honeycomb structure
4.2 弧角θ对等效弹性模量和等效泊松比的影响
当弧角θ取为任意角度时，尚无其他理论解答可以进行对比。为校验本文理论推导和解析结果的有效性，在研究弧角变化对结构等效弹性模量和等效泊松比的影响时，同时给出了本文解析解和有限元结果。
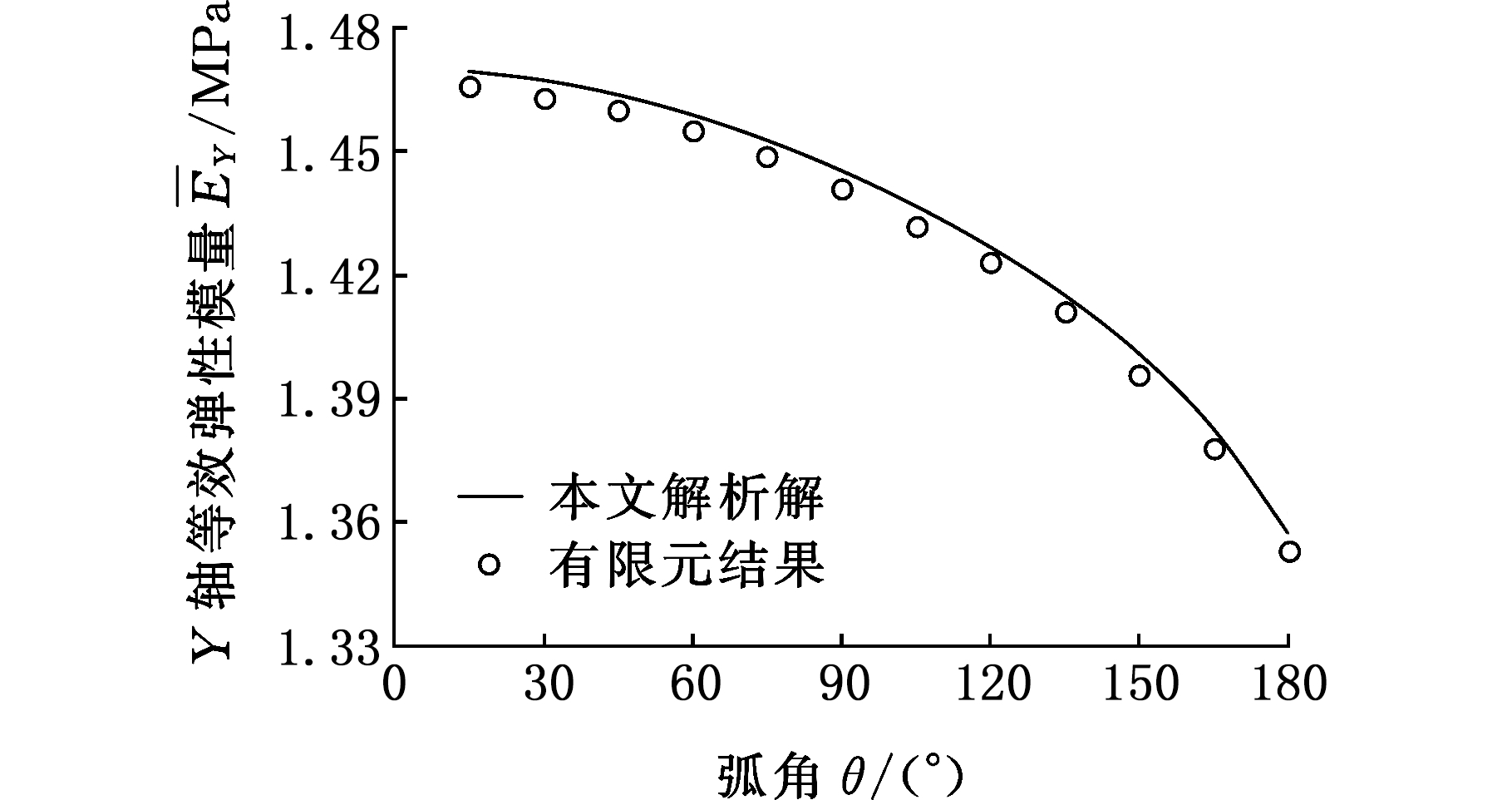
(a)Y轴方向等效弹性模量
(b)X轴方向等效弹性模量
图6 等效弹性模量随弧角的变化
Fig.6 Variations of the equivalent elastic modulus with arc angles
(a)Y向受载时等效泊松比
(b)X向受载时等效泊松比
图7 等效泊松比随弧角的变化
Fig.7 Variations of the equivalent Poisson’s ratio with arc angles
模型中的参数设置如下：h=35 mm，d=10 mm，l=28 mm，t=1 mm，m=5 mm，弧角θ在0～180°之间按间隔15°取12组数据，计算结果见图6和图7。由图6可以看出，等效弹性模量
随弧角θ的增大而逐渐减小；等效弹性模量
随弧角θ的增大先增大后减小，在θ取某一值时，等效弹性模量取得极大值。由图7可以看出，等效泊松比
随弧角θ的增大而逐渐减小，当θ超过一定角度时，该泊松比变为负值；等效泊松比
随弧角θ的增大同样逐渐减小，但变化趋势较为平缓。由图6和图7还可以看出，本文解析解与有限元结果有较好的吻合度，从而验证了解析解在不同弧角下的有效性。但注意到图6a中等效弹性模量的有限元结果始终稍小于本文解析解，这是因为理论推导时忽略了拉伸应变能和剪切应变能的影响，使得位移变形偏小，等效弹性模量偏大。
4.3 结构各参数对等效泊松比的影响
利用所得理论公式研究结构中几何参数对等效泊松比的影响规律。值得注意的是，不同弧角下的h和l中某一参数固定时，另一参数取值范围有所限制，因此在各图中不同曲线的横坐标起止值不同。
结构的等效泊松比随竖直壁板半长h的变化关系见图8，其中t=1 mm，l=28 mm，m=5 mm，θ取30°、60°、90°、120°、150°。由图8可以看出，随着h的增大，当弧角θ为钝角或直角时，等效泊松比单调递增；当弧角θ为锐角时，等效泊松比先增大而后减小，最终趋于0。不论弧角θ取何值，等效泊松比单调递增。
(a)X向受载时等效泊松比
(b)Y向受载时等效泊松比
图8 等效泊松比随竖直壁板半长的变化
Fig.8 Variations of the equivalent Poisson’s ratio with half-length of vertical wall
结构的等效泊松比随两竖直壁板半宽l的变化关系见图9，其中t=1 mm，h=35 mm，m=5 mm，θ取30°、60°、90°、120°、150°。由图9可以看出，随着l的增大，当弧角θ为钝角或直角时，等效泊松比取值从0单调递减；当弧角θ为锐角时，等效泊松比取值从0先增大而后减小。不论弧角θ如何取值，等效泊松比单调递减。
(a)X向受载时等效泊松比
(b)Y向受载时等效泊松比
图9 等效泊松比随两竖直壁板间半宽的变化
Fig.9 Variations of the equivalent Poisson’s ratio with half-width between two vertical walls
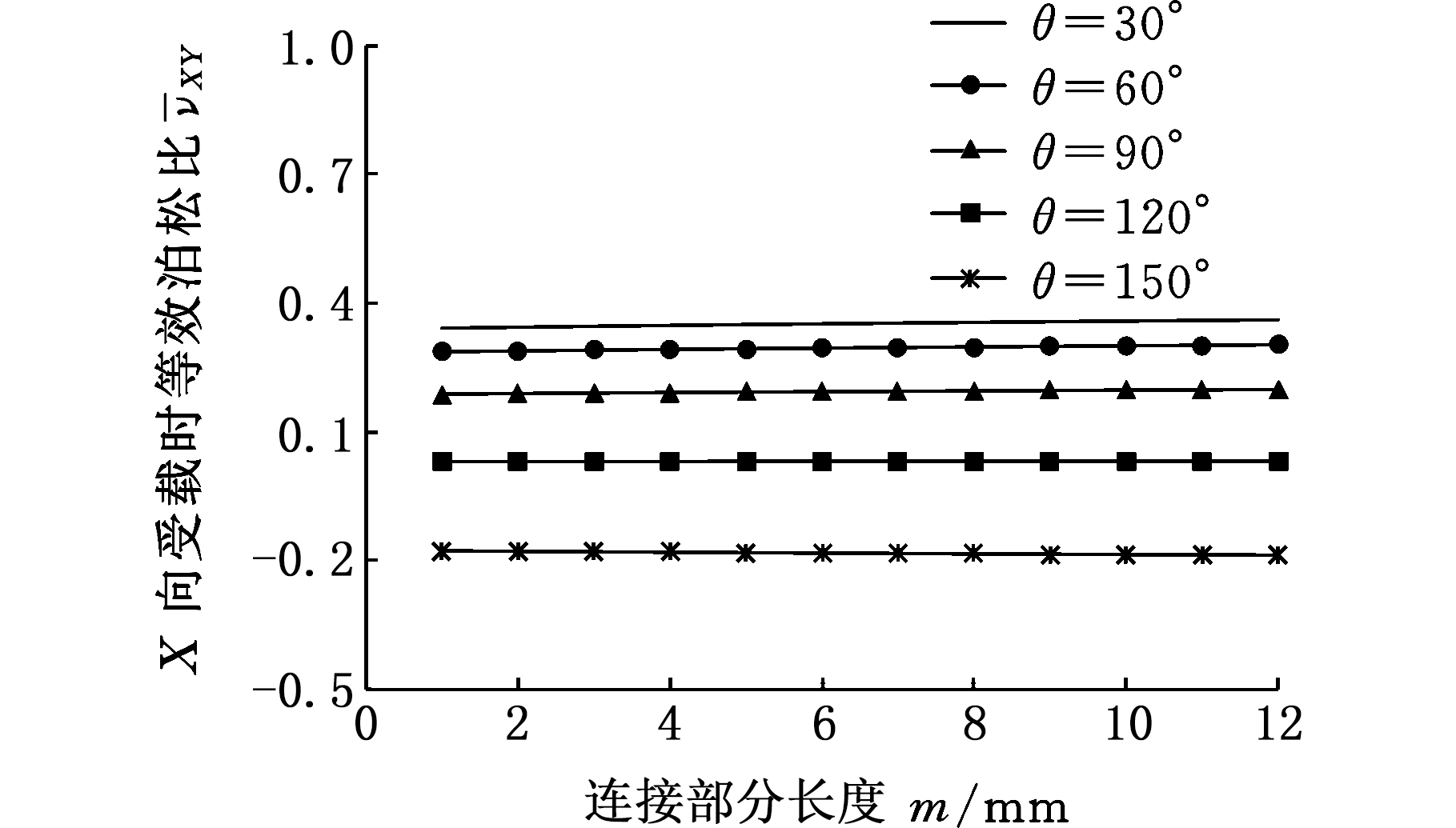
(a)X向受载时等效泊松比
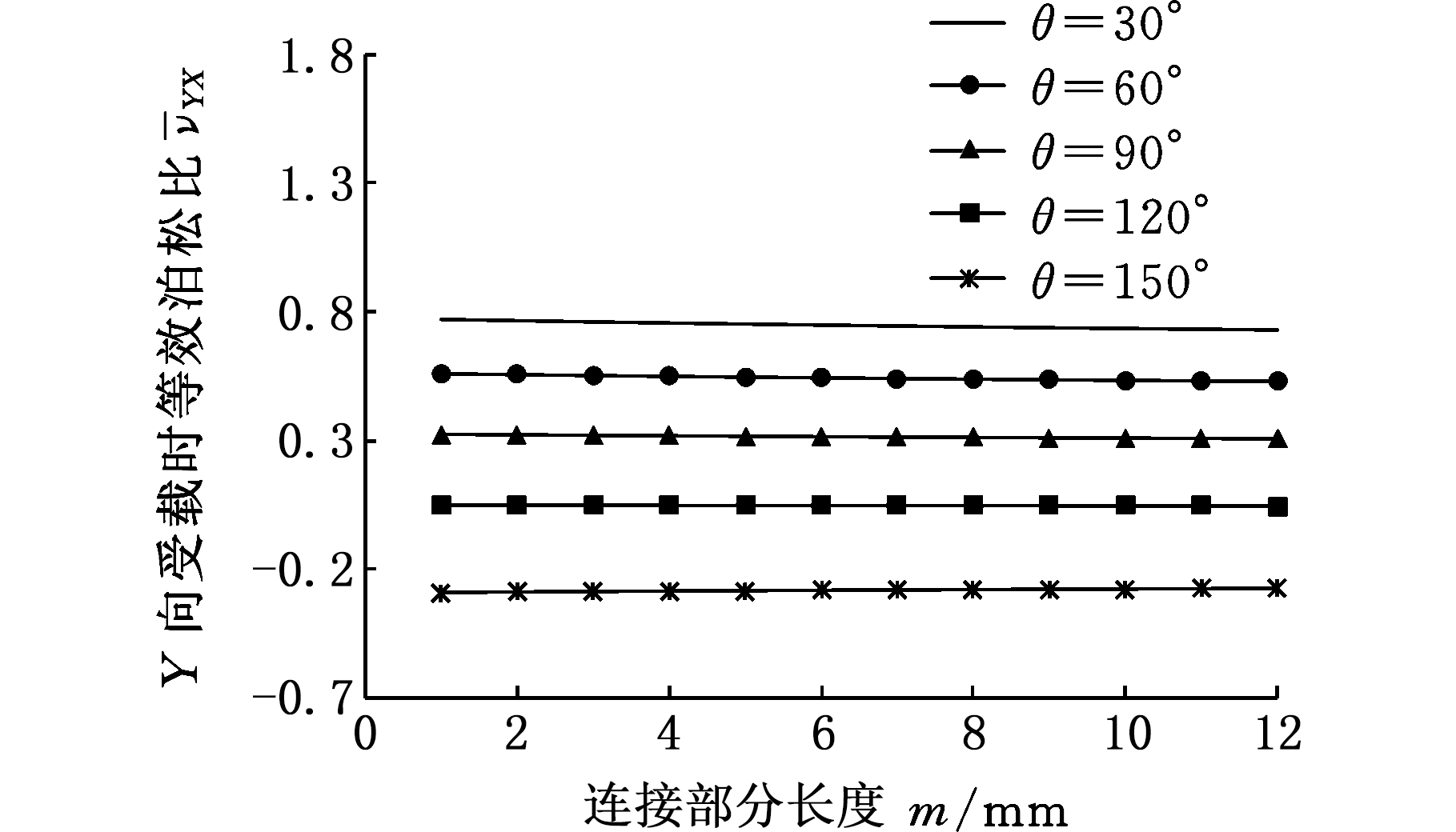
(b)Y向受载时等效泊松比
图10 等效泊松比随连接部分长度的变化
Fig.10 Variations of the equivalent Poisson’s ratio with connected past lengths
结构的等效泊松比随连接部分长度m的变化关系见图10，其中t=1 mm，h=35 mm，l=28 mm，θ取30°、60°、90°、120°、150°。由图10可以看出，随着连接部分长度m的改变，等效泊松比和基本保持不变。
由上述讨论可知，改变结构参数时，结构的等效泊松比既能取正值也能取负值，不同方向的等效泊松比随结构几何参数的改变有较大差异。
5 结论
(1)Y轴方向的等效弹性模量随弧角θ的增大而减小；X轴方向的等效弹性模量随弧角θ的增大先增大后减小，当θ取某一值时，取到最大值；Y轴方向等效弹性模量的有限元结果始终稍低于本文解析解，其原因为理论推导时忽略了拉伸应变能和剪切应变能的影响，使得位移变形偏小，等效弹性模量偏大。
(2)等效泊松比和均随弧角θ的增大从正值逐渐减小至负值，当θ取某一值时，等效泊松比取值为0。当弧角θ取锐角时，等效泊松比随竖直壁板半长h的增大先增大后减小，最终逐渐趋于
随两竖直壁板间半宽l的增大从0先增大而后减小。当弧角θ取钝角或直角时，等效泊松比随h的增大逐渐增大到随l的增大从0开始缓慢减小。不论弧角θ取何值，等效泊松比随h的增大单调递增；随l的增大单调递减。连接部分长度m的改变对等效泊松比的影响很小。
[1] EVANS K E, NKANSAH M A, HUTCHINSON I J, et al.Molecular Network Design[J].Nature, 1991, 353(6340):124.
[2] ALDERSON A.A Triumph of Lateral Thought[J].Chemistry and Industry, 1999, 318(10):384-391.
[3] 张新春, 刘颖, 李娜.具有负泊松比效应蜂窝材料的面内冲击动力学性能[J].爆炸与冲击, 2012, 32(5):475-482.
ZHANG Xinchun, LIU Ying, LI Na.In-plane Impact Dynamic Behavior of Honeycomb Materials with Negative Poisson’s Ratio Effect[J].Explosion and Shock Waves, 2012, 32(5):475-482.
[4] SCARPA F, BULLOUGH W A, LUMLEY P.Trends in Acoustic Properties of Iron Particle Seeded Auxetic Polyurethane Foam[J]. Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science, 2004,218(2):241-244.
[5] EVANS K E.Tailoring the Negative Poisson’s Ratio[J].Chemistry and Industry, 1990, 20:654-657.
[6] YANG W, LI Z M, SHI W, et al.Review on Auxetic Materials[J]. Journal of Materials Science, 2004, 39(10):3269-3279.
[7] GASPAR N.A Granular Material with a Negative Poisson’s Ratio[J].Mechanics of Materials, 2010, 42(7):673-677.
[8] 史齐.负泊松比蜂窝夹芯结构性能表征及优化设计[D].哈尔滨:哈尔滨工业大学, 2014.
SHI Qi.Characterization and Optimization Design of Negative Poisson’s Ratio Honeycomb Sandwich Structure[D].Harbin:Harbin Institute of Technology, 2014.
[9] LAKES R.Foam Structures with a Negative Poisson’s Ratio[J].Science, 1987, 235(4792):1038-1040.
[10] CHOI J B, LAKES R S.Fracture Toughness of Re-entrant Foam Materials with a Negative Poisson’s Ratio:Experiment and Analysis[J].International Journal of Fracture, 1996, 80(1):73-83.
[11] NKANSAH M A, EVANS K E, HUTCHINSON I J.Modelling the Mechanical Properties of an Auxetic Molecular Network[J].Modelling & Simulation in Materials Science & Engineering, 1999, 2(3):337-352.
[12] LAKES R S, WITT R.Making and Characterizing Negative Poisson’s Ratio Materials[J].International Journal of Mechanical Engineering Education, 2000, 30(1):73-90.
[13] YANG D U, LEE S, HUANG F Y.Geometric Effects on Micropolar Elastic Honeycomb Structure with Negative Poisson’s Ratio Using the Finite Element Method[J].Finite Elements in Analysis & Design, 2003, 39(3):187-205.
[14] WAN H, OHTAKI H, KOTOSAKA S, et al.A Study of Negative Poisson’s Ratios in Auxetic Honeycombs Based on a Large Deflection Model[J].European Journal of Mechanics A/Solids, 2004, 23(1):95-106.
[15] 卢子兴, 赵亚斌.一种有负泊松比效应的二维多胞材料力学模型[J].北京航空航天大学学报, 2006, 32(5):594-597.
LU Zixing, ZHAO Yabin.A Two-dimensional Multicellular Material Mechanical Model with Negative Poisson’s Ratio[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(5):594-597.
[16] 颜芳芳, 徐晓东.负泊松比柔性蜂窝结构在变体机翼中的应用[J].中国机械工程, 2012, 23(5):542-546.
YAN Fangfang, XU Xiaodong.Application of Negative Poisson’s Ratio Flexible Cellular Structure in Variant Wing[J].China Mechanical Engineering, 2012, 23(5):542-546.
[17] SUN Y, PUGNO N. In Plane Stiffness of Multifunctional Hierarchical Honeycombs with Negative Poisson’s Ratio Sub-structures[J]. Composite Structures, 2013,106:681-689.
[18] 郭磊.基于二维不同尺寸旋转刚性单元的负泊松比研究[J].力学季刊, 2014,35(2):321-326.
GUO Lei.Research on Negative Poisson’s Ratio Based on Two-dimensional Rotating Rigid Element with Different Size[J].Chinese Quarterly of Mechanics, 2014,35(2):321-326.
[19] 鲁超, 李永新, 吴金玺, 等.负泊松比蜂窝芯非线性等效弹性模量研究[J].中国机械工程, 2014, 25(11):1540-1544.
LU Chao, LI Yongxin, WU Jinxi, et al.Nonlinear Equivalent Modulus of Elasticity of Negative Poisson’s Ratio Honeycomb Core[J].China Mechanical Engineering, 2014, 25(11):1540-1544.
[20] 金爱兵, 王凯, 杨振伟, 等.负泊松比岩体颗粒流模型及模拟分析[J].中南大学学报(自然科学版), 2015, 46(9):3423-3428.
JIN Aibing, WANG Kai, YANG Zhenwei, et al.Particle Flow Model and Simulation Analysis of Negative Poisson’s Rock Mass[J].Journal of Central South University (Science and Technology), 2015, 46(9):3423-3428.
[21] LI D, DONG L, LAKES R S.A Unit Cell Structure with Tunable Poisson’s Ratio from Positive to Negative[J].Materials Letters, 2016, 164:456-459.
[22] 蒋伟, 马华, 王军, 等.基于环形蜂窝芯结构的负泊松比机械超材料[J].科学通报, 2016, 61(13):1421-1427.
JIANG Wei, MA Hua, WANG Jun, et al.Negative Poisson’s Ratio Mechanical Metamaterials Based on a Ring Honeycomb Core Structure[J].Chinese Science Bulletin, 2016, 61(13):1421-1427.
[23] LU Z X, LI X, YANG Z Y, et al.Novel Structure with Negative Poisson’s Ratio and Enhanced Young’s Modulus[J].Composite Structures, 2016, 138:243-252.
[24] FU M H, ZHENG B B, LI W H.A Novel Chiral Three-dimensional Material with Negative Poisson’s Ratio and the Equivalent Elastic Parameters[J].Composite Structures, 2017, 176:442-448.
