0 引言
航空发动机是飞机的心脏，其工作状态直接影响飞机的安全运行。航空发动机的结构日益复杂，工况日益恶劣，轻微的机械缺陷或损伤都会引起转子系统的强烈振动。应用故障诊断技术对航空发动机转子系统进行实时的监测和诊断[1]，能够及时发现发动机转子系统的故障，避免设备恶性事故的发生。转子系统振动信号包含了设备运行的状态特征信息，提取并识别该类信息是转子故障诊断的主要手段和目的。然而，故障状况下的振动信号，大多为非线性、非平稳时序信号，分析此类信号时应主要研究其局部特性。传统的频域分析方法如细化谱分析(zoom spectrum analysis，ZSA)[2]、全息谱分析(holospectrum analysis，HA)[3]、倒谱分析(cepstrum analysis，CA)[4]，以全局变换为基础，无法方便有效地处理该类信号。
经验模态分解(empirical mode decomposition，EMD)[5]作为典型的自适应时频分析方法，具有良好的时频聚集性，且无需构造任何匹配信号分量的基函数。但EMD存在模态混叠、端点效应等缺陷，缺乏必要的数学理论，模型复杂[6-7]。为解决EMD的问题，集合经验模态分解(ensemble empirical mode decomposition，EEMD)等方法先后被提出，但这些方法并不能完全弥补EMD的缺陷[8]。基于EMD分解理论的非参数时频分析方法如局部均值分解(local mean decomposition，LMD)、经验小波变换(empirical wavelet transform，EWT)和变分模态分解(variational mode decomposition，VMD)等方法相继被人们提出，但这些方法都存一定的缺点[9-11]。
傅里叶分解方法(Fourier decomposition method，FDM)是基于傅里叶变换(Fourier transform，FT)的时频分析方法[12]。FDM首先定义出傅里叶固有频带函数(Fourier intrinsic band functions，FIBFs)，然后利用傅里叶变换对非平稳非线性信号在傅里叶域 (Fourier domain，FD)内自适应地解析得到傅里叶固有频带解析函数(analytic FIBFs，AFIBFs)，从而将样本信号分解为一系列的AFIBFs和一个残余分量。FDM是基于傅里叶变换的完备的、正交的、自适应的和局部的时频分析方法，理论基础完整，在进行航空发动机转子故障诊断的研究中具有较强的适用性。基于此，本文通过数值仿真，验证了FDM对非线性、非平稳时序信号进行时频分析的有效性，并结合信号峭度特性，提出了基于FDM的航空发动机转子故障诊断方法。
1 FDM算法
FDM算法将多分量信号x(t)用一组特定连续单分量之和表示，即
(1)
式中，r(t)为残余分量；yi(t)为第i个单分量的信号(即信号x(t)的FIBFs)。
FIBFs定义如下：yi(t)为区间[a,b]内能量有限的函数空间变量，且满足如下条件：FIBFs为零均值函数，即
yi(t)dt=0；FIBFs分量相互正交，即i≠j时，yi(t)yj(t)dt=0；③FIBFs对应的解析函数AFIBFs的包络幅值和瞬时频率均不小于0，即假设AFIBFs为
·exp(jφi(t))，则∀t，ai(t)≥0，dφi(t)/dt≥0。
由式(1)及FIBFs的定义可知，FMD分解具有完备性、正交性、自适应性和局部性，且FIBFs为具有特定物理意义的瞬时频率单分量信号。
机械振动信号一般为特定时间区间内的非线性、非平稳信号。设信号x(t)在区间[t1,t1+T0]内满足狄里克雷条件，构造x(t)的周期信号
此时的x(t)=xT0(t)ω(t)，当t1≤t≤t1+T0时，ω(t)=1；当t<t1或t>t1+T0时，ω(t)=0。则xT0(t)的傅里叶级数展开式为
(2)
将式(2)改写为
(3)
由式(3)可以得出：
xT0(t)=a0+Re{zT0(t)}
(4)
则信号x(t)的AFIBFs为
(5)
zT0(t)的共轭复数
将Re{zT0(t)}定义为zT0(t)的实部，则可将zT0(t)改写成：
(6)
式(6)为文献[5]的广义傅里叶级数展开的简化表达，是基于纯傅里叶基的时序信号完备级数自适应解析表达，故由式(6)可以对时序信号进行广义的傅里叶展开计算。利用式(6)将序列信号扩展到有限数量的AFIBFs，基于广义傅里叶级数展开的AFIBFs求解方法不仅提高了扩展效率，而且能够适应非平稳数据的傅里叶分解计算，得到不同分量的频率与包络幅值的表达式。在实际的机械故障诊断中，常将连续时序振动信号离散化处理，相应的FDM算法也需离散化处理，基于不同的信号AFIBFs分量搜索方法有由低频到高频搜索的FDM-LTH算法和由高频到低频搜索的FDM-HTL算法，二者的区别主要如下。
假设k=Ni-1+1，信号x(t)的第i个AFIBFs分量为
为得到最小数目信号AFIBFs，FDM-LTH算法采取由低频向高频的搜索方式，该算法的信号AFIBFs分解结果如下：
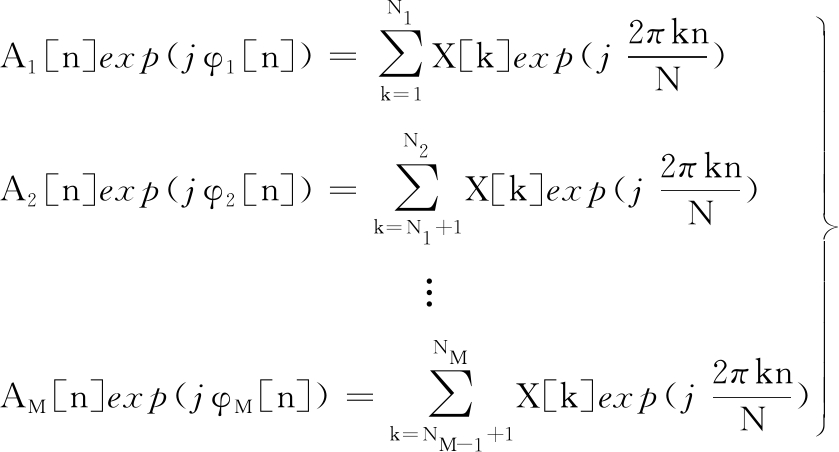
(7)
AFIBFs分解结果可写为
(8)
i=1，2，…，M N0=0 NM=N/2-1
该方法为获取信号数量最小的AFIBFs分量，对于分量AFIBFsi，由k=Ni-1+1开始，逐渐叠加至能够满足信号AFIBFsi分量假设条件的最大数Ni(Ni-1+1≤Ni≤N/2-1)，定义AFIBFsi分量假设条件为：对于∀n，存在单步差分ωi[n]=φi[n+1]-φi[n]≥0(i=1，2，…，M)，即时变幅值φi[n]为单调递增函数，或满足两步差分ωi[n]=(φi[n+1]-φi[n-1])/2≥0，对于∀n存在ai[n]≥0。由上述AFIBFs的求解过程和式(8)的求解方法可知，FDM-LTH算法的分解结果总是存在的。
FDM-HTL算法为获取最小数目的信号AFIBFs分量，对信号第i个FIBFs分量yi(t)，由Ni-1-1开始叠加信号FIBFs分量，并逐渐减小至能够满足信号AFIBFs分量条件的最小Ni(1≤Ni≤Ni-1-1)，该算法的信号AFIBFs分解结果如下：
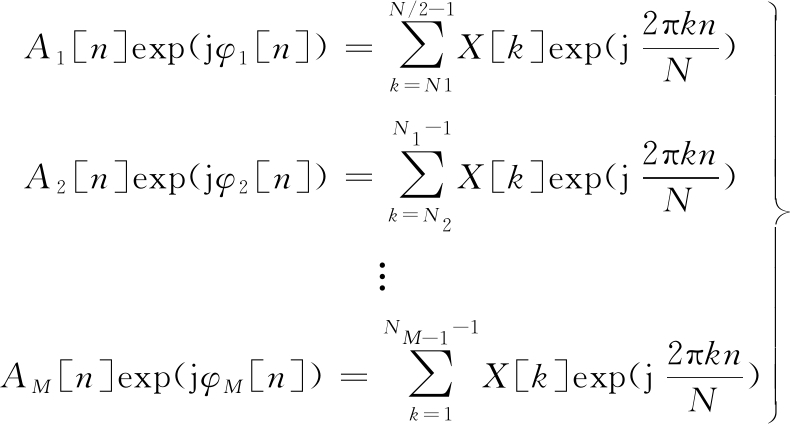
(8)
由上述分析可知，FDM算法是以傅里叶分解为基础，具备完整理论、自适应的信号分解方法，该方法通过对信号FIBFs分量的有效解析，得到不同分量对应的瞬时幅值和瞬时频率，由此揭示出原始信号包含的局部特征信息。
2 数值仿真研究
为验证FDM的有效性，构造仿真信号：
x1(t)= x11(t)+x12(t)
(9)
x11(t)=sin(400πt+180πt2)
x12(t)=(1+cos(20πt))cos(200πt+3sin(20πt))
仿真信号x1(t)包含调频信号x11(t)和调频调幅信号x12(t)，设置采样频率为1 000 Hz，图1为仿真信号x1(t)的时域波形图，图2为仿真信号分量x11(t)和x12(t)的时域波形图，利用不同的信号分解方法对仿真信号x1(t)进行分解，对比分析不同方法的分解结果，以验证FDM算法有效性。
图1 仿真信号时域波形图
Fig.1 Time-domain waveform of simulation signal
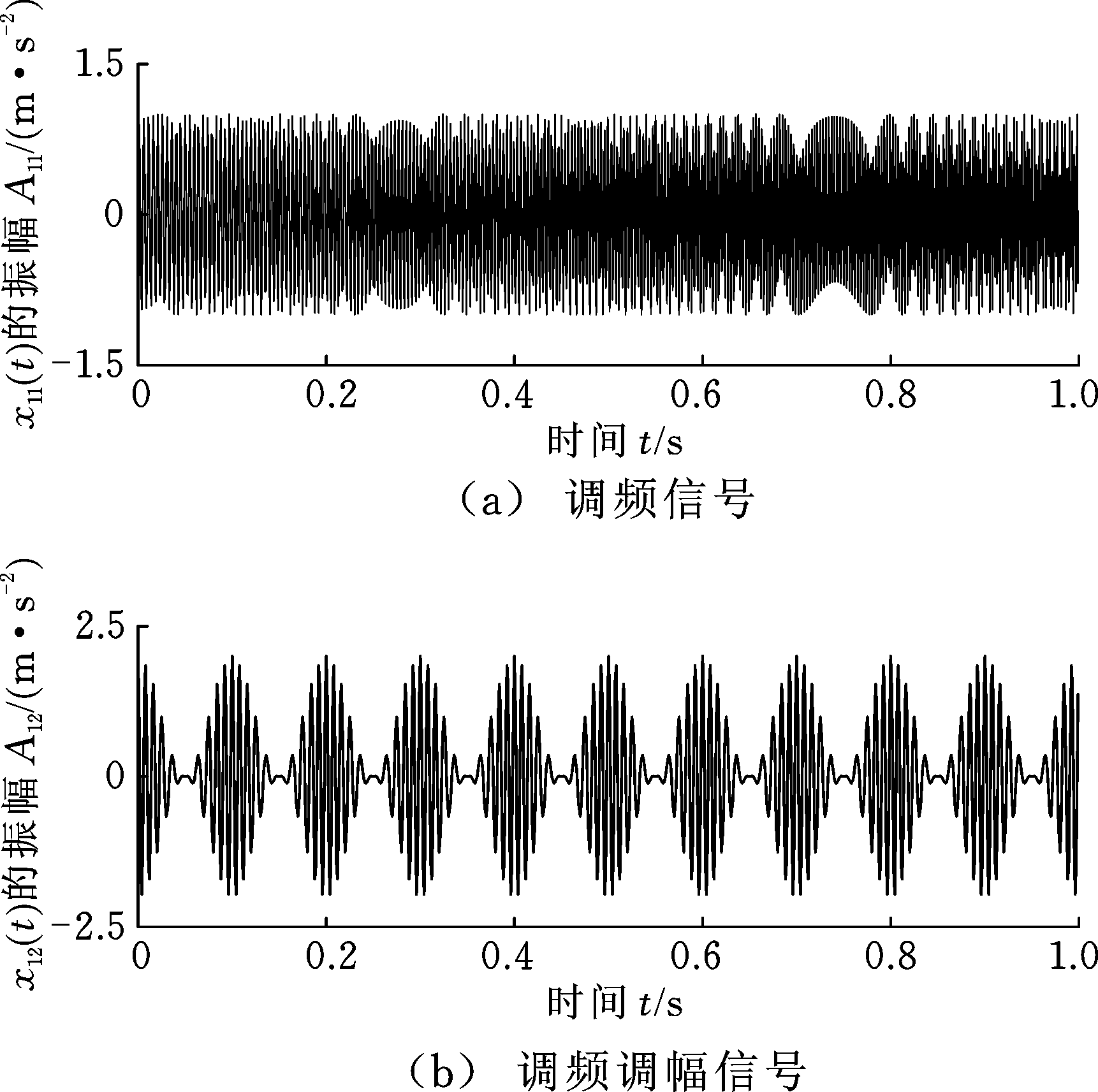
图2 分量信号时域波形图
Fig.2 Time-domain waveform of component signal
图3为仿真信号x1(t)的EEMD分解结果图，c1、c2、c3为模态分量，r为残余量。
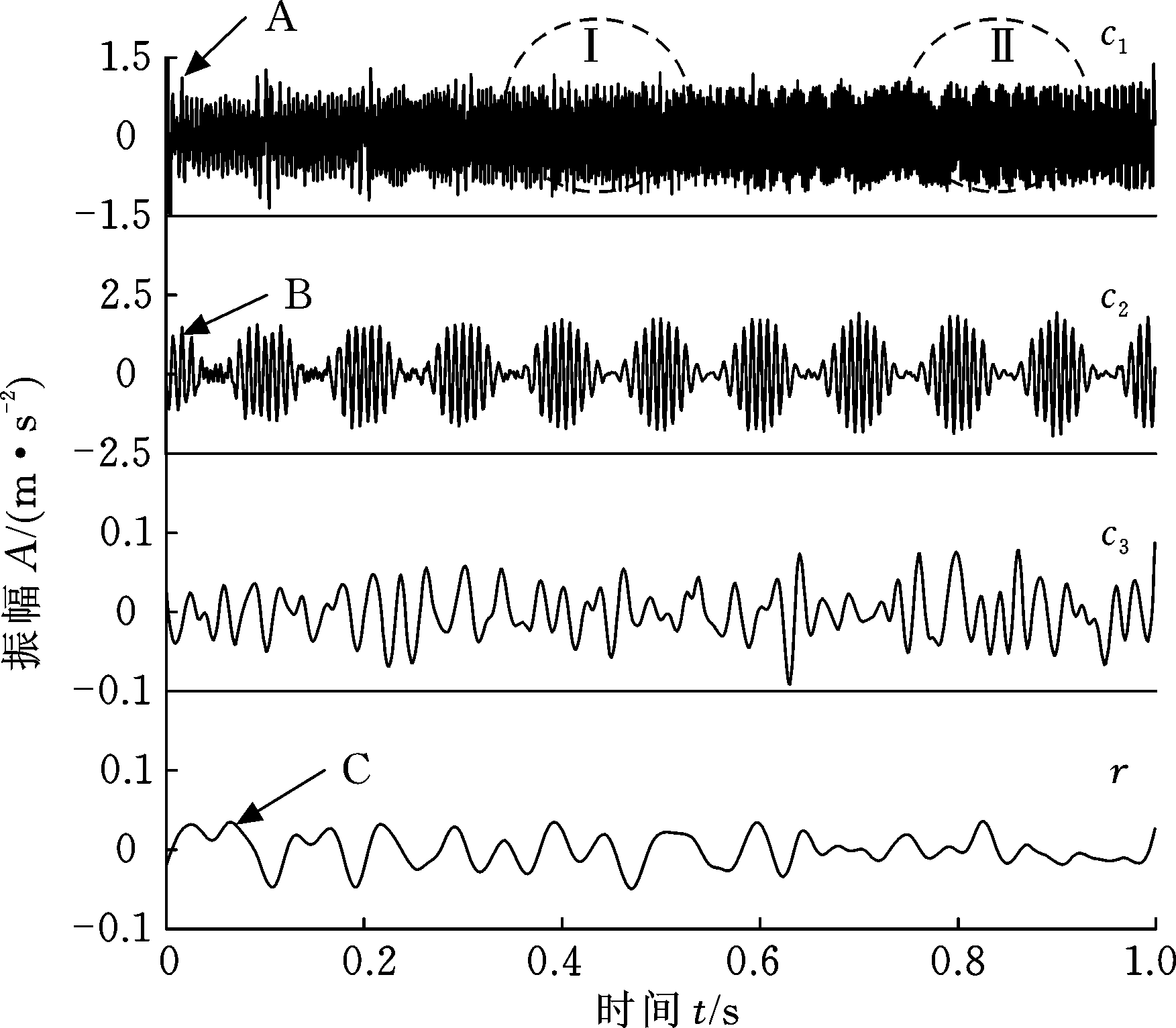
图3 仿真信号EEMD分解结果
Fig.3 EEMD decomposition result of simulation signal
图4为仿真信号x1(t)的VMD分解结果图，u1、u2为信号模态分量。
图4 仿真信号VMD分解结果
Fig.4 VMD decomposition result of simulation signal
对仿真信号进行FDM分解，得到图5、图6所示的分解结果。
图5 仿真信号FDM-LTH分解结果
Fig.5 FDM-LTH decomposition result of simulation signal
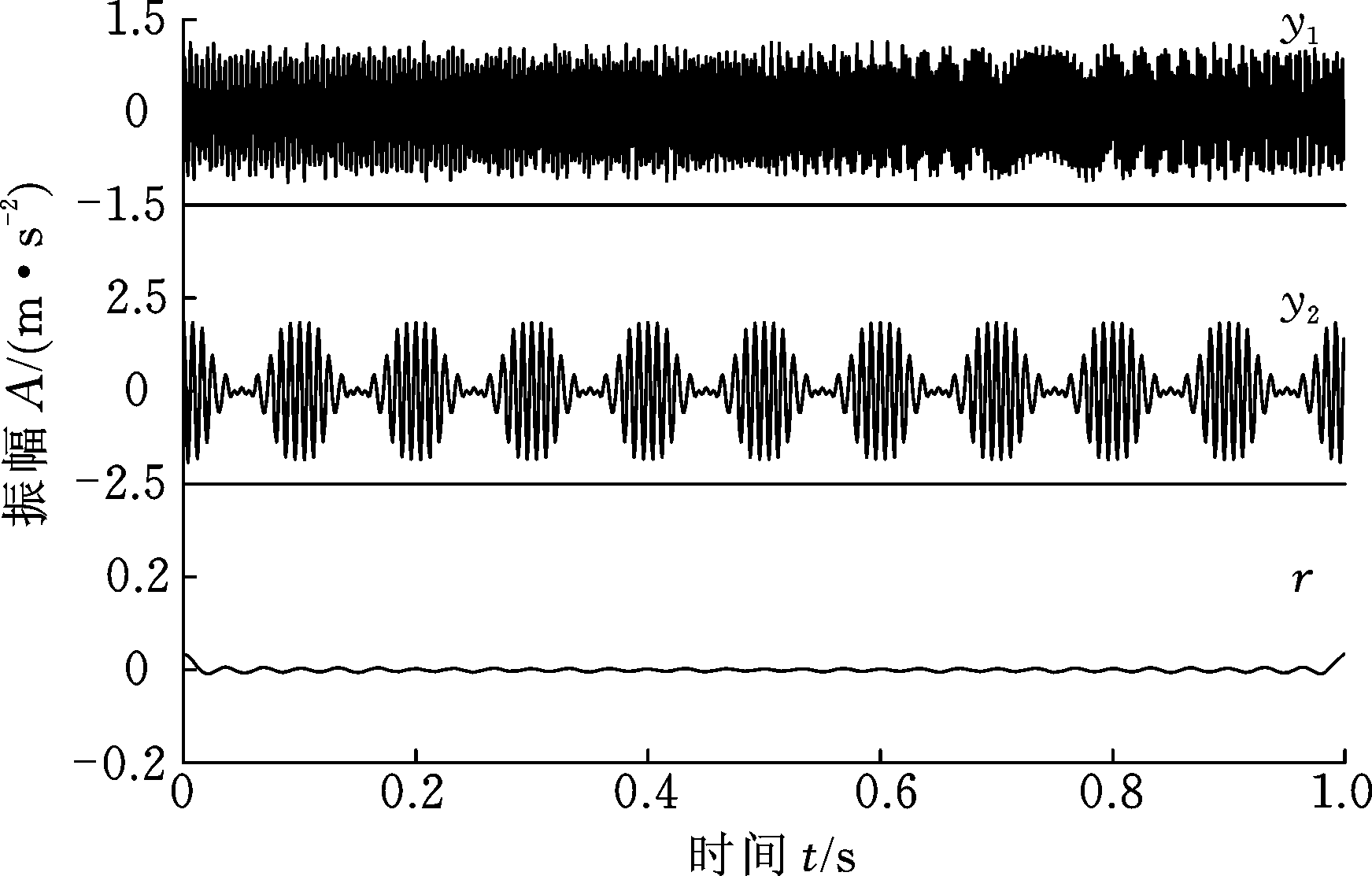
图6 仿真信号FDM-HTL分解结果
Fig.6 FDM-HTL decomposition result of simulation signal
对比仿真信号分解结果可得出：EEMD能够有效分解调频调幅仿真信号，得到模态分量c1、c2和残余分量r，分别对应仿真信号的原始分量x11(t)及x12(t)，但该结果中存在信号过分解分量c3，且在结果图的A、B和C位置存在明显的端点效应；区域Ⅰ和区域Ⅱ存在较为严重的模态混叠，残余量r也存在显著的模态混叠，故经验模态分解类信号分解方法无法实现调频调幅信号的有效分解。完全非递归自适应时频分析方法VMD实现了仿真信号的分解，得到的分量u1、u2分别对应仿真信号的原始分量x12(t)及x11(t)，该分解结果存在区域Ⅲ和区域Ⅳ所示的分解失效问题，分量u2无法合理映射原始分量x11(t)。FDM的FDM-LTH和FDM-HTL算法均能自适应地实现仿真信号的有效分解，得到合理映射仿真信号原始分量的信号FIBFs，不存在端点效应及模态混叠问题，残余量r振幅几乎为0。通过上述对比分析可知：FDM算法能够实现调频调幅类非线性非平稳信号的有效分解。
为进一步讨论FDM算法两种不同分解方法的时频分辨效果，分别作出仿真信号FDM-LTH和FDM-HTL算法分解结果的时频能量谱图(图7、图8)。由图7、图8可得出：FDM-LTH和FDM-HTL算法均具有较高的时频分辨效果，无冗余频率成分，且能直观表征仿真信号包含的时频特征信息，有效揭示仿真信号的局部时频特性；FDM-LTH在高频段具有更好的时频聚散性，FDM-HTL在低频段具有更高的时频分辨率。
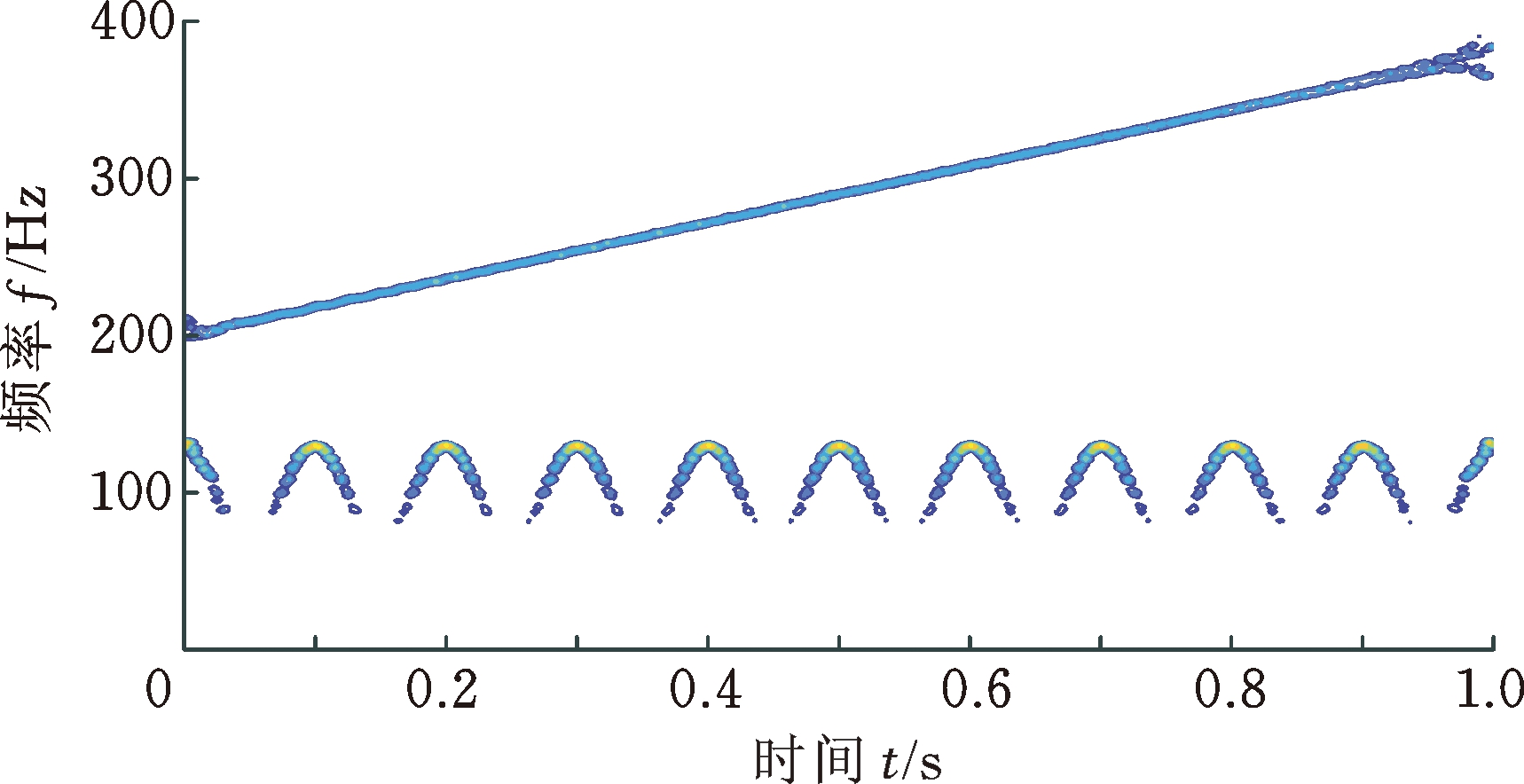
图7 仿真信号FDM-LTH分解的时频能量谱图
Fig.7 Time-frequency energy spectrum of simulation signal FDM-LTH decomposition
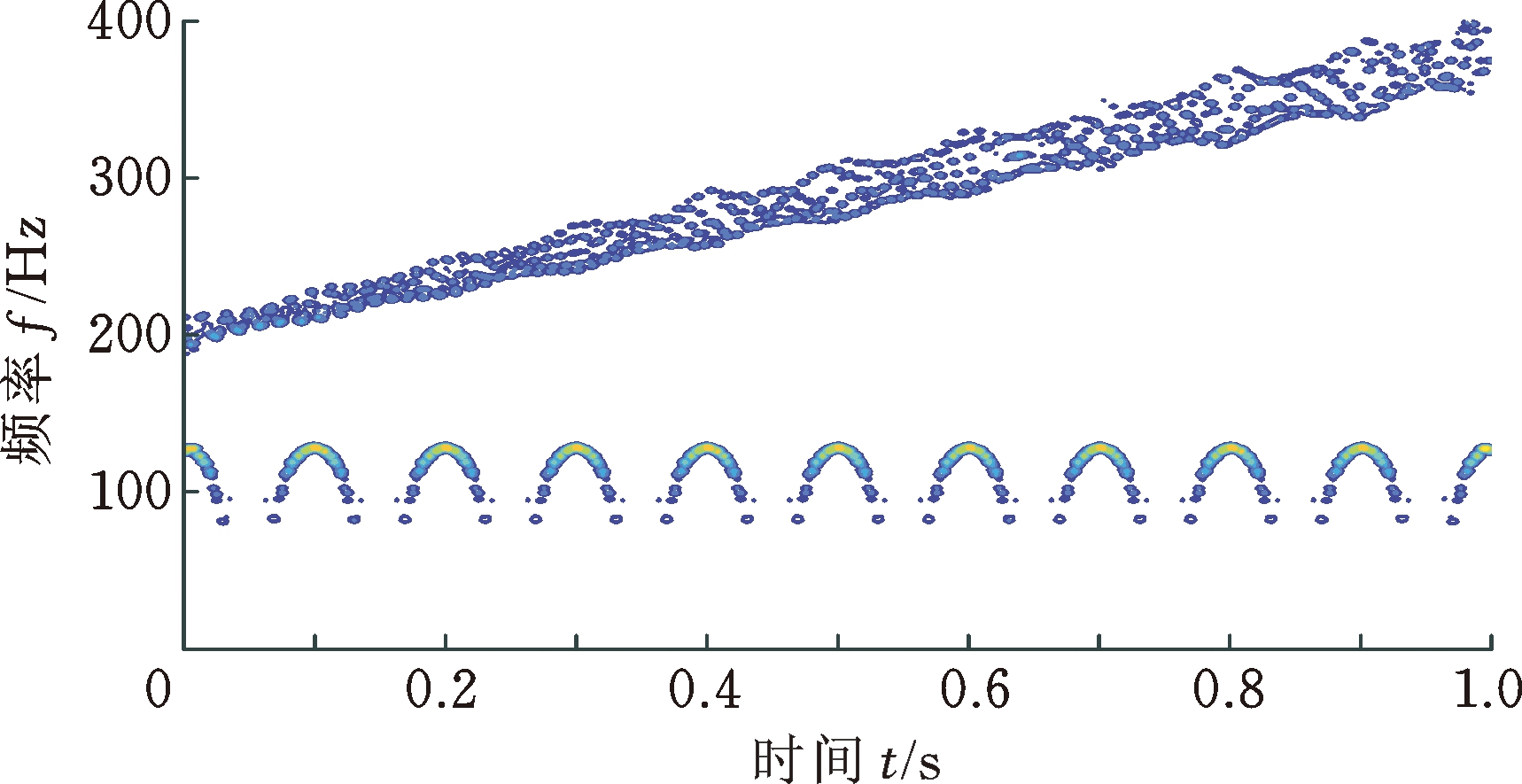
图8 仿真信号FDM-HTL分解的时频能量谱图
Fig.8 Time-frequency energy spectrum of simulation signal FDM-HTL decomposition
3 实验研究
3.1 转子碰摩实验
采集航空发动机转子试验器的机匣单点-转子全周碰摩试验故障样本数据[13]并进行FDM分解，验证FDM算法实现航空发动机转子系统碰摩故障诊断的有效性。图9为航空发动机转子试验器结构图，图10为转子碰摩试验示意图。为实现转子碰摩试验，在图10所示的转子机匣顶端位置用扳手拧紧碰摩螺钉，使螺钉无限接近涡轮叶片，产生转子机匣形变，形成涡轮叶片与机匣封严间隙处的转子机匣单点-转子全周碰摩故障。
图9 航空发动机转子试验器
Fig.9 Aeroengine rotor tester
图10 转子碰摩实验示意图
Fig.10 Rotor rubbing experiment diagram
图11为机匣单点-转子全周碰摩故障位置示意图，该图直观揭示出转子碰摩故障发生的位置。由图11可知：在转子机匣顶端碰摩螺钉位置(E处)，机匣表面碰摩螺钉与F处的转子叶片发生摩擦运动，构成转子全周碰摩故障，由此形成机匣单点-转子全周完整的碰摩过程。
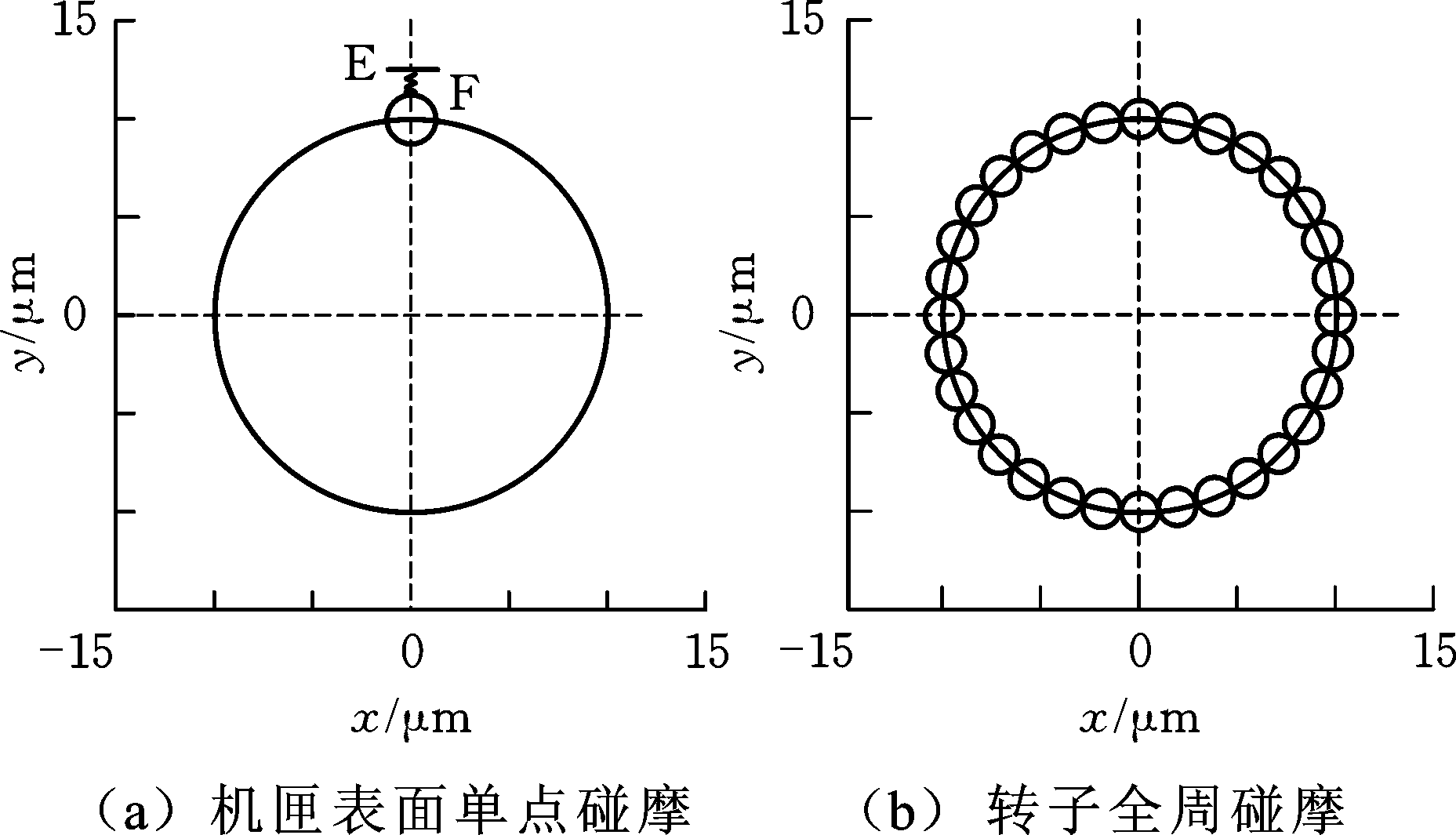
图11 转子碰摩位置
Fig.11 Rotor rubbing position diagram
3.2 碰摩振动信号频谱分析
以上述转子碰摩试验为例，设置机匣单点-转子全周碰摩实验参数：转子系统转速n0=2 700 r/min，对应的转速频率f0=45 Hz，采样频率fs=10 240 Hz，采样点数N=4 096。转子试验器的主要硬件参数如下：碰摩刚度kr=120 MN/m；涡轮叶片数N0=32；涡轮叶片与机匣封严原始间隙为0.1 mm；设置叶片机匣动静间隙减小量为0.15 mm，转静件摩擦因数为0.3，压气机与涡轮盘的偏心距为0.3 mm，以试验器机匣外测垂直方向加速度传感器采集的振动信号为研究对象，振动加速度a的单位为重力加速度g[13-14]。任取一组试验数据对其进行时频分析，得到转子碰摩加速度振动信号波形、振动信号频谱图及局部放大图。
由图12可得，转子碰摩振动信号呈现典型的非线性、非平稳调频调幅振动冲击特性，0～0.1 s信号的非平稳冲击特性更为显著。
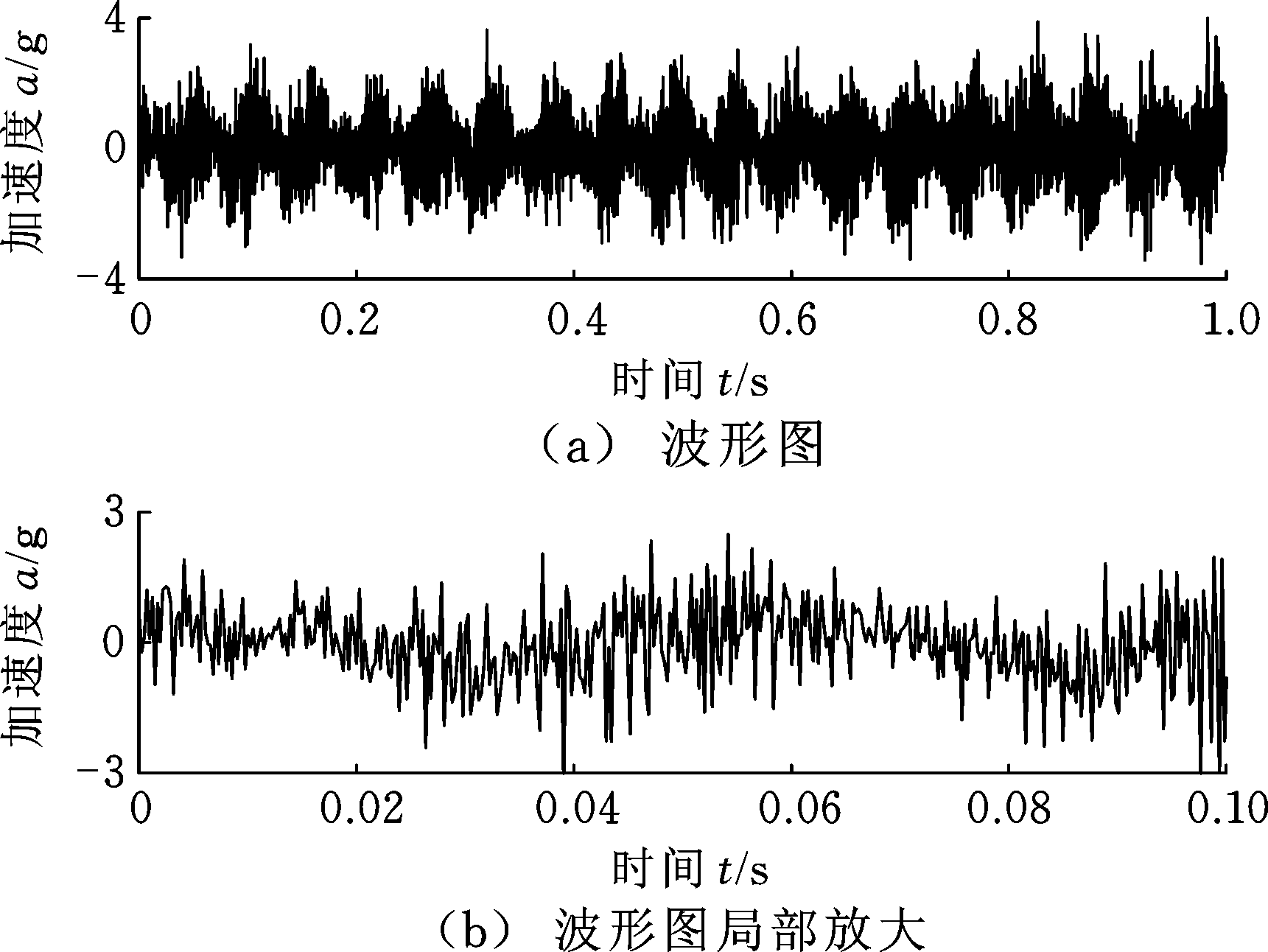
图12 转子碰摩加速度振动信号波形图
Fig.12 The waveform diagram of rotor rubbing acceleration vibration signal
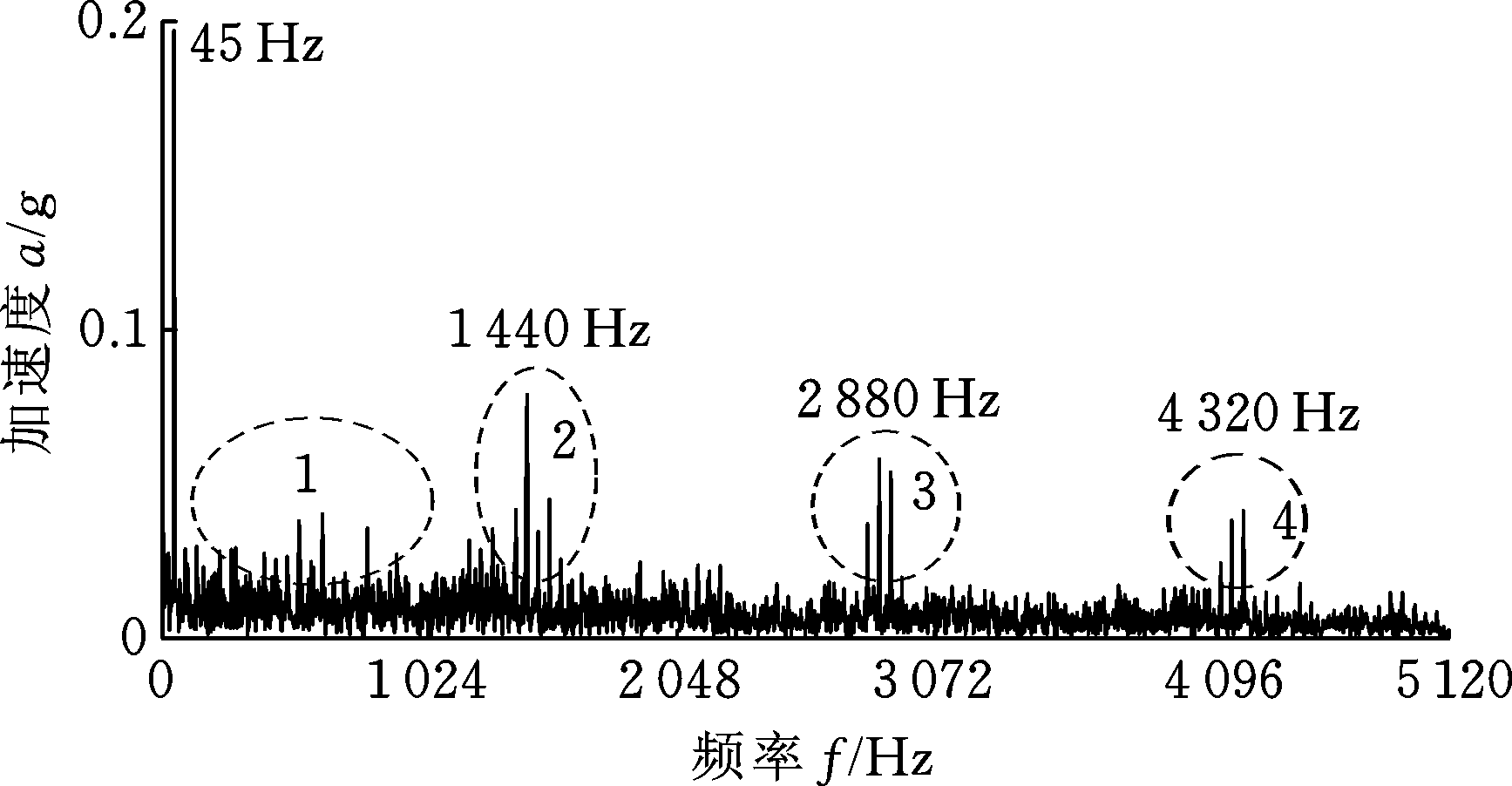
图13 转子碰摩振动信号频谱图
Fig.13 The spectrogram of rotor rubbing vibration signal
图13从信号频谱特性角度表现出转子碰摩振动信号的频域分布特点：转子系统的机匣单点-转子全周碰摩振动信号频谱冲击显著，在转速频率f0处的频谱冲击强烈，同时，在转子机匣冲击频率f1(涡轮叶片经过转子机匣，产生振动冲击的转子系统固有频率，其数值为转速频率f0与叶片总数目N0的乘积，即f1=N0f0)附近具有密集的频谱能量分布，而在频谱图高频段冲击频率f1的2倍频、3倍频附近同样具有明显的频谱冲击特性。
由图14可知：频谱图局部放大位置1存在复杂的频谱成分，转速频率f0的基频冲击显著，但其他碰摩故障特征频率淹没在复杂的背景噪声中，无法得到合理辨识；由局部放大位置2～位置4的频谱图可看出，在信号冲击频率f1的基频、2倍频和3倍频两侧均出现以转速频率f0为间隔的边谱频率带，构成了以冲击频率f1及其倍频为中心的等间隔边谱带簇，为机匣单点-转子全周特有频谱特性。
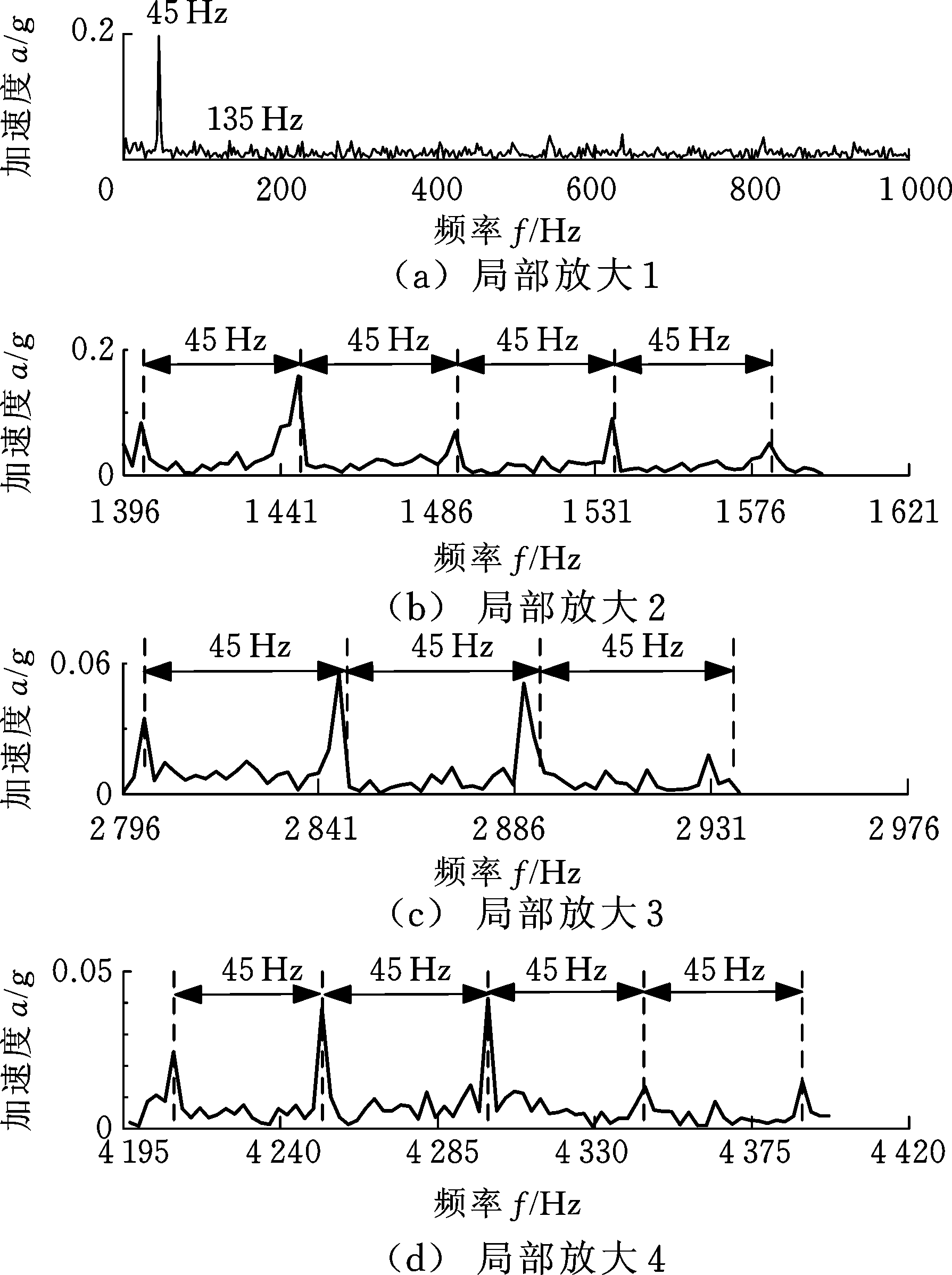
图14 转子碰摩振动信号频谱局部放大图
Fig.14 The partial enlargement spectrum of rotor rubbing vibration signal
由上述分析可知：由转子碰摩振动信号频谱图能够有效识别转子碰摩转速频率f0、冲击频率f1及其倍频，以及冲击频率等间隔边谱带簇等故障特征。但单叶片与机匣单点碰摩的故障特征明显淹没在强背景噪声信号中，如何从中提取微弱的单叶片单点碰摩故障特征频率是航空发动机转子系统碰摩故障诊断的主要目的。
3.3 碰摩振动信号分解结果
转子单叶片单点碰摩故障特征复杂，包含较多的转速频率f0的倍频分量信息，本文提出利用FDM算法在强噪声背景信号中提取转子碰摩弱故障特征频率，以验证FDM算法在航空发动机转子系统碰摩故障诊断中的有效性。利用EEMD、VMD和FDM对碰摩振动信号进行分解，通过信号分解结果的周期功率谱密度估计表征不同信号分解方法的分解效果，如图15所示。
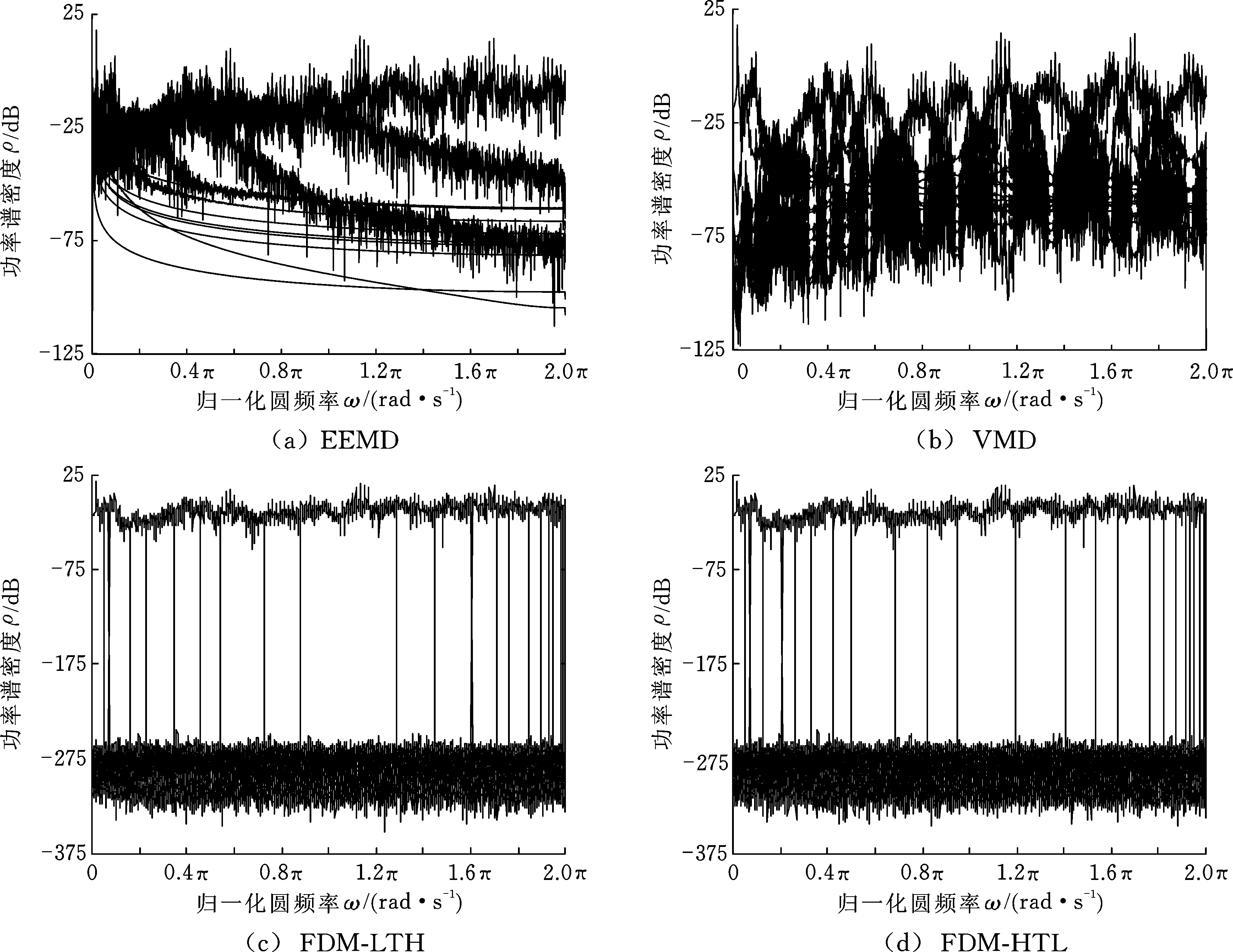
图15 不同信号分解结果的周期功率谱密度估计
Fig.15 Periodic power spectral density estimation of different signal decomposition results
对比上述功率谱密度的估计结果可以得到如下结论：EEMD算法未能实现转子碰摩振动信号的有效分解，不同频域分量间彼此混叠；VMD虽能实现振动信号的分解，但不同频率分量间存在交叉项，且信号分量数需预先设定，缺乏自适应性；FDM算法能够实现振动信号的完备分解，不同信号分量间彼此正交，功率谱密度分布均匀，无模态混叠现象，且具备自适应性。
3.4 转子碰摩故障诊断结果
峭度作为描述信号波形峰值量纲一参数，能反映机械设备故障程度，以振动信号分量的峭度准则筛选能最大限度表征转子碰摩故障特征信息的振动信号分量，对其进行包络谱分析，得到图16所示的转子碰摩故障诊断结果。
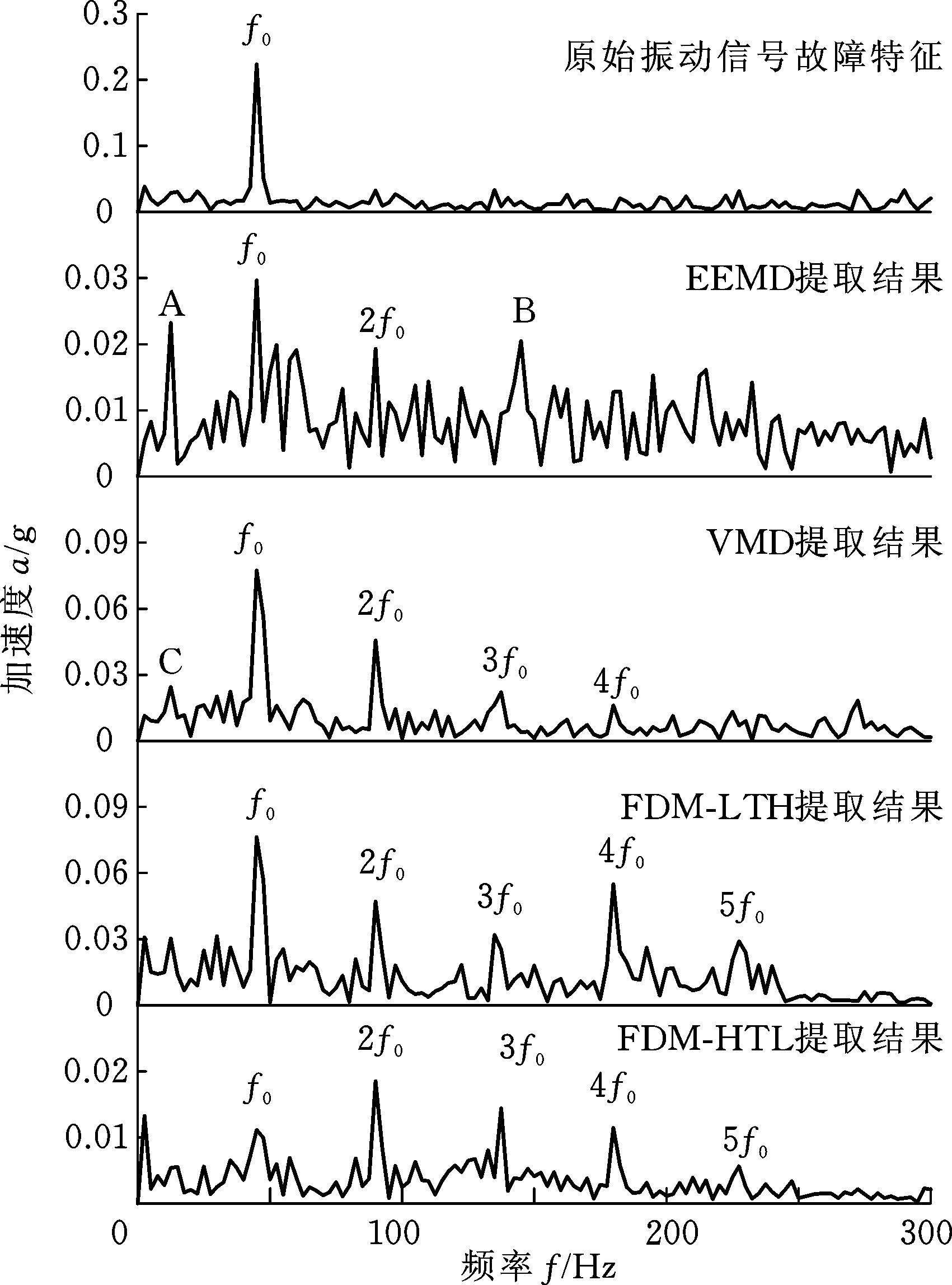
图16 转子碰摩故障特征提取结果
Fig.16 Fault feature extraction results of rotor rub-impact
由上述故障特征提取结果可知：基于EEMD和VMD算法的转子碰摩故障特征提取结果包含部分故障特征频率，如转速频率f0的基频、2倍频，但二者的提取结果均包括A、B和C位置的噪声频率(非故障特征频率)。基于FDM算法的提取结果中包含转速频率f0的基频、2倍频、3倍频、4倍频、5倍频，且无噪声频率，对比原始转子碰摩振动信号故障特征，该提取结果是较为完备的，能够有效表征转子系统存在的转子单叶片单点碰摩故障特征。
4 结论
(1)傅里叶分解方法(FDM)具有完备性、正交性、自适性和局部性等特点，仿真结果表明该算法有效避免了调频调幅信号模态分解时的端点效应和模态混叠问题，且不存在分解失效的现象。
(2)航空发动机转子系统机匣单点-转子全周碰摩故障频谱特征复杂，淹没在强噪声背景下的转子单叶片单点弱故障特征信息常无法得到有效提取，而有效的信号分解是将包含转子碰摩故障特征频率分量从原始振动信号中分离的前提，故本文利用EEMD、VMD和FDM算法对采集到的转子碰摩振动信号进行分解。对比分析信号分解结果的周期功率谱密度估计，验证了FDM实现转子碰摩故障振动信号完备分解的有效性。
(3)依据峭度准则，筛选能够最大限度表征原始振动信号故障特性的信号分量，对其进行包络谱分析，成功提取出试验采样信号包含的故障信息。对比不同信号分解方法的故障特征提取结果，验证了基于FDM算法航空发动机转子系统故障诊断方法的有效性。
[1] 范作民,孙春林,白杰.航空发动机故障诊断导论[M].北京：科学出版社,2004.
FAN Zuomin,SUN Chunlin,BAI Jie.An Introduction to Aeroengine Diagnosis[M].Beijing：Science Press,2004.
[2] 谢明,丁康.基于复解析带通滤波器的复调制细化谱分析的算法研究[J].振动工程学报,2002,15(4)：479-483.
XIE Ming,DING Kang.Algorithm of Multiple Modulation Zoom Spectrum Analysis Based on Complex Analytic Band-pass Filter[J].Journal of Vibration Engineering,2002,15 (4)：479-483.
[3] 孟建,屈梁生,刘晗.全息谱的分解及其在机械诊断中的应用[J].机械工程学报,1997,33(2)：106-110.
MENG Jian,QU Liangsheng,LIU Han.Holospectrum Decomposition and Its Application in Mechanical Diagnosis[J].Chinese Journal of Mechanical Engineering,1997,33(2)：106-110.
[4] BADAOUI M E,GUILLET F,DANI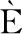
RE J.New Applications of the Real Cepstrum to Gear Signals,including Definition of a Robust Fault Indicator[J].Mechanical Systems and Signal Processing,2004,18(5)：1031-1046.
[5] HUANG N E,SHEN Z,LONG S R,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Proceedings of the Royal Society A:Mathematical,Physical and Engineering Sciences,1998,454(1971)：903-995.
[6] CHENG Junsheng,YU Dejie,TANG Jiashi,et al.Application of Frequency Family Separation Method Based upon EMD and Local Hilbert Energy Spectrum Method to Gear Fault Diagnosis[J].Mechanism and Machine Theory,2008,43(6)：712-723.
[7] YAN Jihong,LU Lei.Improved Hilbert-Huang Transform Based Weak Signal Detection Methodology and Its Application on Incipient Fault Diagnosis and ECG Signal Analysis[J].Signal Processing,2014,98：74-87.
[8] WU Zhaohua,HUANG N E.Ensemble Empirical Mode Decomposition：a Noise-assisted Data Analysis Method[J].Advances in Adaptive Data Analysis,2009,1(1)：1-41.
[9] SMITH J S.The Local Mean Decomposition and Its Application to EEG Perception Data[J].Journal of the Royal Society Interface,2005,2(5)：443-454.
[10] GILLES J.Empirical Wavelet Transform[J].IEEE Transactions on Signal Processing,2013,61(16)：3999-4010.
[11] DRAGOMIRETSKIY K,ZOSSO D.Variational Mode Decomposition[J].IEEE Transactions on Signal Processing,2014,62(3)：531-544.
[12] SINGH P,JOSHI S D,PATNEY R K,et al.The Fourier Decomposition Method for Nonlinear and Nonstationary Time Series Analysis[J].Proceedings of the Royal Society A:Mathematical,Physical and Engineering Sciences,2017,473(2199)：1-14.
[13] 陈果,王海飞,刘永泉,等.新型叶片-机匣碰摩模型及其验证[J].航空动力学报,2015,30(4)：952-965.
CHEN Guo,WANG Haifei,LIU Yongquan,et al.A New Blade-casing Rubbing Model and Its Verification[J].Journal of Aerospace Power,2015,30(4)：952-965.
[14] 南京航空航天大学智能诊断与专家系统研究室[EB/OL].南京：南京航空航天大学民航学院,[2018-01-10].http:∥ides.nuaa.edu.cn/ides/index.asp.
