0 引言
机构综合指根据给定的机构运动特性、动力学特性，设计出实现给定特性的机构,本文中利用傅里叶描述子设计耦合串联连杆机构就是典型的机构综合问题。耦合串联连杆机构指通过齿轮或绳索滑轮传动使连杆转动耦合的一类连杆机构，其优点在于通过齿轮或皮带-带轮传动来耦合各杆运动，可以使串联连杆机构的自由度减小到1，从而实现单驱动器控制，降低控制难度，同时还可实现较为复杂的末端执行器轨迹或运动位姿。
近年来，利用傅里叶级数进行机构综合的研究越来越受到重视。该方法最早由文献[1]用于连杆机构函数生成问题中，此后，文献[2-9]均将傅里叶级数方法应用到机构综合中，极大地促进了机构综合的研究发展。
在最近的机构综合问题研究中，文献[10]将傅里叶方法用于RCCC机构的轨迹综合问题，在给定目标轨迹条件下，通过建立的轨迹数值图谱和推导的机构安装参数、连杆上点的位置理论计算式解决了RCCC机构轨迹综合问题。文献[11]在此基础上进一步将傅里叶级数用于RCCC机构的运动综合问题，通过研究连杆刚体转角输出和位置输出与机构基本尺寸之间的关系，给出了进行刚体导引综合的具体步骤，实现了对RCCC机构刚体导引综合问题的求解。
文献[12]借助傅里叶变换，从球面四杆机构输入角与连杆运动的函数关系入手，发现了连杆位姿与机构基本尺寸之间的关系，并在此基础上建立了连杆运动谐波特征参数的数值图谱库，解决了球面四杆机构运动综合问题。文献[13]则将傅里叶级数用于球面四杆机构曲柄滑块机构的尺度综合问题，通过傅里叶级数对该机构的函数发生、轨迹发生和刚体导引发生这三大机构尺度综合问题进行了深入研究。
文献[14]首先将傅里叶描述子方法扩展到Clifford代数理论中的四元数映射空间，解决了四杆机构综合中的周期循环运动综合问题，通过将四杆机构的连杆运动位姿转化为映射空间中的曲线并利用傅里叶描述子进行表达，借助神经网络建立了连杆位姿傅里叶描述子与四杆机构基本尺寸参数之间的对应关系。
上述文献主要是在机构具体结构已确定的情况下进行机构的尺度综合，而本文的方法则是在已知目标机构类型为耦合串联机构而其具体拓扑结构和尺度参数均未知的情况下进行其构型尺度的融合设计。在前期的工作中[15-17]，我们已通过运动映射理论对平面目标运动进行分析，找到目标运动的几何约束，解决了RP、RR、PR等二杆组(R代表转动副，P代表移动副)的构型与尺寸融合设计问题。本文则主要通过傅里叶变换对目标运动进行谐波分析，从而确定其中的最简轨迹(包含最少数量的谐波分量)，并由这些谐波分量所包含的特征参数确定与之对应的耦合串联机构的全部拓扑和尺度信息，完成目标运动数据驱动的机构综合。
1 复数形式傅里叶变换
文献[18]指出，一个平面运动轨迹可定义为z(t)=x(t)+y(t)i，其中x(t)和y(t)分别是产生该轨迹的运动点在t时刻的横坐标和纵坐标。如果平面轨迹是封闭的，则复函数z(t)可认为是一个周期函数。假设T表示该函数的最小正周期，那么，一个连续周期复函数z(t)的傅里叶变换由下式给出：
(1)
其中，hn(t)为n阶谐波分量；Cn为hn(t)的傅里叶描述子，其值可由下式给出：
(2)
当封闭曲线由一系列的离散点构成而并非一条连续曲线时，周期函数z(t)可表示为
(3)
其中，j表示第j个点；N表示离散点的总个数。
在式(1)的谐波分量hn(t)中，傅里叶描述子C0定义了基波(0阶谐波分量)h0(t)的幅值和初始相位，在几何意义上则给出了平面轨迹的形心或几何中心，同时决定了轨迹在固定坐标系中的位置，而其他谐波分量hn(t)(n≠0)则分别对应了不同半径、初始相位以及转动速度的动态圆轨迹。例如，第k个谐波分量hk(t)表示在t从0～T的时间内以旋转角速度ω=2kπ/T旋转了k圈的动态圆轨迹，它所包含的傅里叶描述子Ck则给出了产生该圆轨迹的运动点的转动半径和起始转角。
因此，任何平面轨迹都可视为一系列不同半径、转动速度以及起始转角的动态圆轨迹依次相连而成。例如在图1中，粗实线所示的椭圆轨迹可以由两个动态圆轨迹形成，两个圆轨迹对应的谐波分量分别为h1(t)和h-1(t)，分别由对应于C1和C-1傅里叶描述子的向量C1和C-1以各自旋转速度生成。故而从机构实现角度来看，任意给定的平面轨迹均可由耦合串联连杆机构实现，并且杆的数目、尺寸及转动速度分别由动态圆轨迹的数目、半径以及角速度决定。
图1 椭圆运动轨迹
Fig.1 The elliptical motion trajectory
2 最简轨迹的确定
考虑一个相对于固定坐标系F给定的离散平面运动M(j)=(x(j),y(j),θ(j))，j=1,2,…,N，其中x、y、θ分别表示动坐标系的原点坐标和动坐标系与固定坐标系之间的夹角，图2所示为该平面运动刚体的一个瞬时位置，其中g点为动坐标系原点，p点为刚体上的任意一点，a点是要确定的最简轨迹上的瞬时位置点。
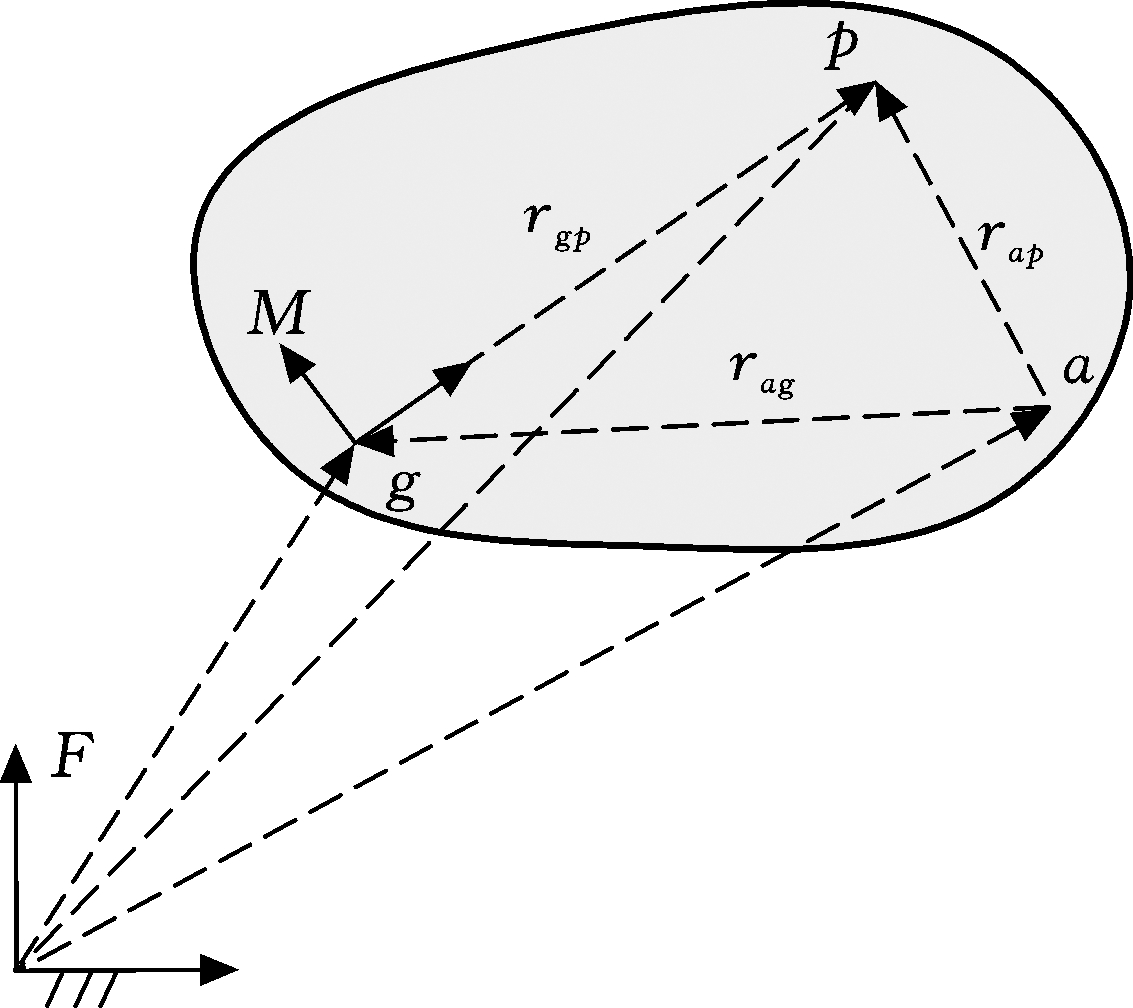
图2 平面刚体运动的一个瞬时位置
Fig.2 A momentary position of plane rigid body motion
给定的动坐标系原点轨迹按照复数形式可表示为：g(j)=x(j)+y(j)i。刚体上任意一点p的运动轨迹在固定坐标系中以复数形式可表示为p(j)=xp(j)+yp(j)i，而p点相对于动坐标系M的坐标为rgp(up,vp)，则p点运动轨迹又可以由下式给出：
(4)
改写式(4)，将其简化表达为
p(j)=g(j)+rgpeiθ(j)
(5)
式(5)中g(j)和p(j)分别表示了动坐标系原点g和刚体上任意点p的平移运动，eiθ(j)表示了刚体的旋转运动。根据式(3)和式(4)得到包含p(j)傅里叶描述子的表达式如下：
(6)
然后根据傅里叶描述子的线性性质，式(6)可以简化为
Cpn=Cgn+rgpCθn
(7)
其中，Cpn、Cgn和Cθn分别表示轨迹p、g和eiθ的第n阶谐波分量的傅里叶描述子。
需要指出的是，在动刚体上所有点的运动轨迹中，存在图2所示的轨迹a，它的傅里叶描述子中包含了最少数量的谐波分量，可以将其定义为目标运动的最简轨迹。例如，假设该最简轨迹a仅包含0阶、1阶和2阶谐波分量，这时，对于刚体上动坐标系原点g，它的第n阶傅里叶描述子可表示为
(8)
n≠0,1,2
同理，对于刚体上任意一点p，它的第n阶傅里叶描述子可表示为
(9)
n≠0,1,2
由于所给的目标运动信息中没有直接给出最简轨迹，我们需要从两点的轨迹数据中识别出该目标运动所包含的最简轨迹。由式(8)、式(9)可知，如果选定轨迹p和g并对比，能够发现它们的傅里叶描述子之间绝大部分是成比例的(除对应于最简轨迹谐波分量阶数的傅里叶描述子之外)。那么，轨迹p和g的傅里叶描述子将满足如下关系：
=k n≠0,1,2
(10)
其中，k是一个常数，它对应于p和g相对于a的相对位置。
本文的方法是通过分析所选择的2个轨迹的谐波分量来找到k，即：将每个Cgn与Cpn相除，然后得到一组复数，假设它们是Kn，n={-H,…,0,…,H}，H表示可以得到的傅里叶系数的最高阶数，构成集合{Kn}。它们的值大多等于k，只有少数不同。现在，想找出哪些元素是不同的，以便确定k的值。如果计算每个元素与其他元素之间的差的绝对值之和，这个问题就可以简化为
(11)
其中，
是新得到的实数集合
的第n个元素。
通过这一步，可以将从集合中找不同元素的问题转换为找集合中比其余元素大得多的元素的问题，因为原集合中的那些不同的元素在经过式(11)计算后将比其他的元素值大得多。
现在只需找出
中哪些元素明显大于其他元素。由于这些元素是少数，故可以计算这个新集合的平均值，对于那些大于平均值的元素，就可以将它们视为要找的元素。
由于{Kn}中的不同元素的阶数实际上对应了最简轨迹a的谐波分量的阶数，因此可以通过从{Cgn}和{Cpn}中消除这些阶数对应的傅里叶描述子来获得k的值：
(12)
其中，n不等于不同项对应的阶数。
这里求和的目的是为了提高计算精度。得到比值k后，通过式(8)～(10)导出：
其中，n等于不同项对应的阶数。
求得最简轨迹a的傅里叶系数。
至此，得到最简轨迹a包含的所有谐波分量，这意味着确定了最简轨迹a的所有信息。
3 最简轨迹的机构实现
基于前面的讨论，刚体运动时其上任意一点的轨迹均可由一系列动态圆轨迹首尾相连形成，而最简轨迹则包含了最少数量的动态圆轨迹(即最少数量的谐波分量)，相应地，最简轨迹可以由最少数量的耦合串联杆实现。第2节中给出了最简轨迹的识别方法，这里仍然假设最简轨迹a仅包含0阶、1阶、2阶谐波分量，则该最简轨迹的谐波表达式如下：
a(j)=C0e0i2πj/N+C1e1i2πj/N+C2e2i2πj/N
(14)
其中，C0为a(j)的0阶谐波分量的傅里叶描述子，决定了最简轨迹的几何中心位置，也给出了耦合串联机构的固定铰链坐标；a(j)的1阶谐波分量对应的动态圆轨迹的角速度为2π/N，代表了杆L1的转速；|C1|为旋转半径，代表杆L1的长度；起始转角为arg C1，代表杆L1相对于固定坐标系的起始转角。a(j)的2阶谐波分量对应的动态圆轨迹的角速度为4π/N，代表杆L2的转速；旋转半径为|C2|，代表杆L2的长度；起始转角为arg C2，代表杆L2相对于固定坐标系的起始转角。
因此，根据式(14)，最简轨迹可通过一个耦合串联连杆机构来实现(图3)，各杆之间的相对转动通过齿轮来耦合，其作用是使各杆的旋转速度等于各动态圆轨迹的角速度。
图3 通过耦合串联机构实现的最简轨迹
Fig.3 The simplest trajectory realized by CSM
4 实例：方法的验证
使用齿轮五杆机构连杆运动来验证本文方法的可行性。该齿轮五杆机构的初始状态如图4所示，给定的运动如图5所示。杆的参数列于表1，L1和L2的初始角度分别为120°和60°。在连杆刚体上设定一个动坐标系，并利用这个动坐标系的运动来验证所述方法。为了实施该方法，必须在动刚体上任意选择两点，由动坐标系的运动可以得到它们的轨迹p和q，该两点及两铰链点R2和R3在动坐标系中的位置信息见表2。
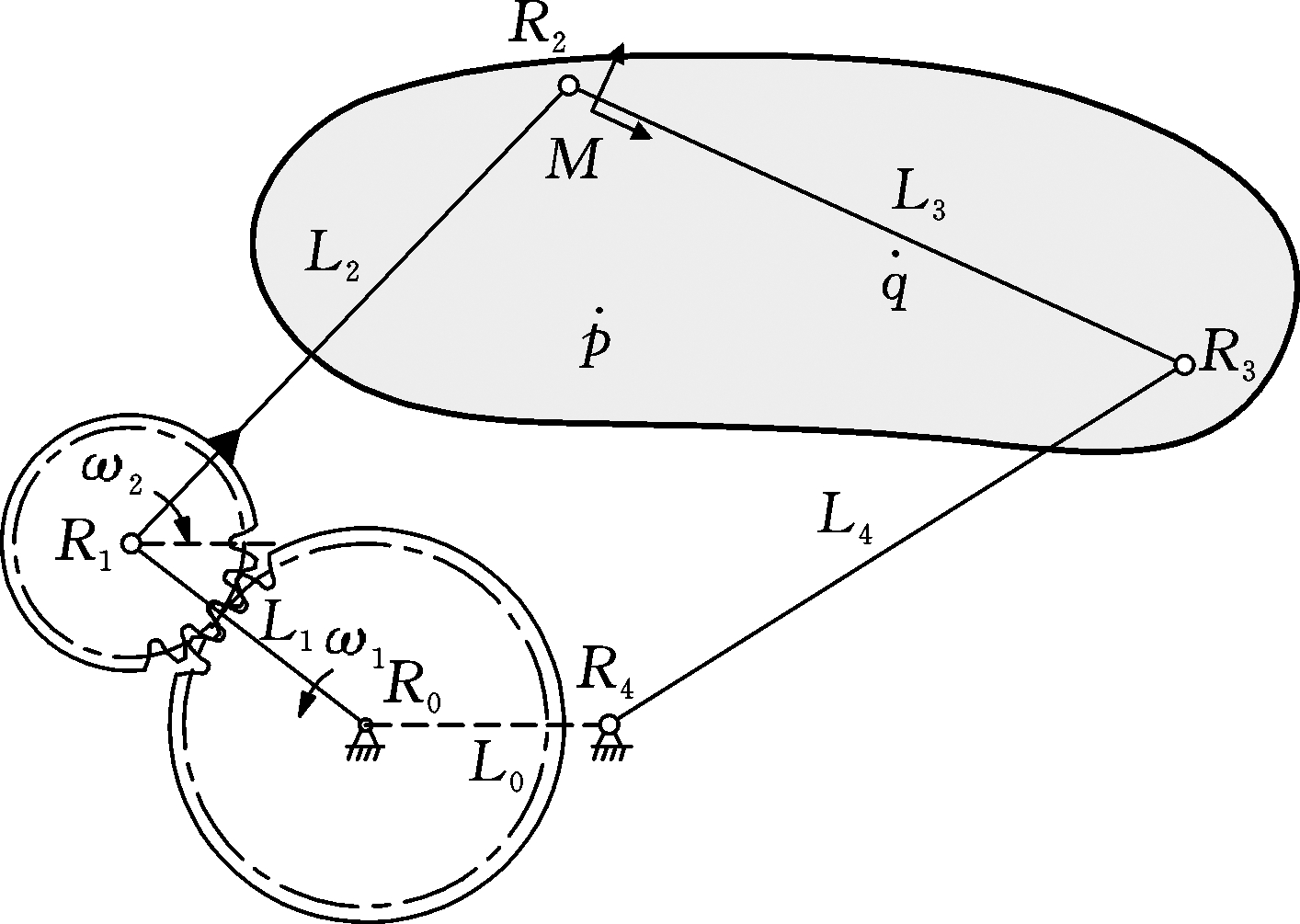
图4 齿轮五杆机构的初始状态
Fig.4 The initial status of the geared 5-bar linkage mchanism
图5 给定的连杆目标运动
Fig.5 The given motion of coupler link
表1 齿轮五杆机构相对于固定坐标系的参数
Tab.1 Parameters of gear 5-bar linkage mechanism with respect to the fixed frame
R0R4L1L2L3L4ω1ω2(0,0)(7,0)81616161 r/s-2 r/s
表2 连杆刚体相对于动坐标系的信息
Tab.2 Coupler rigid body information with respect to the moving frame
R2R3pq(-1,0)(15,0)(4,-5)(8,0)
按照以上章节中讨论的方法，首先对轨迹p和q进行傅里叶变换并进一步得到{Cpn}和{Cqn}。然后计算它们的比值Kn=Cpn/Cqn，利用式(11)将{Kn}转换为
集合{Kn}和
中元素见表3(仅给出-5阶到5阶的傅里叶描述子)。
表3 齿轮五杆机构连杆运动相关参数
Tab.3 Parameters in gear 5-bar linkage mechanism’s coupler motion
阶数CpnCqnKnKNn-50.243 2-0.221 5i0.027 24-0.338 5i0.707 7+0.661 57i1.910 9-40.260 1+0.104 7i0.269 9-0.104 3i0.707 7+0.661 57i1.910 9-3-0.161 6-0.094 41i-0.188 4+0.042 77i0.707 7+0.661 57i1.911 0-21.00 8-1.615i1.968-1.482i0.721 3-0.277 47i8.681 7-10.126 7-0.109 1i0.018 63-0.171 6i0.707 7+0.661 57i1.911 000.385 6+0.135 2i0.386 1-0.169 8i0.707 7+0.661 57i1.910 91-0.711 1-0.942 4i-0.420 5-1.114i0.951 3-0.279 17i8.975 920.076 32+0.031 44i0.079 72-0.030 09i0.707 7+0.661 57i1.911 030.028 58+0.164 4i0.137 4+0.103 8i0.707 7+0.661 57i1.910 94-0.075 41+0.077 65i-0.002 129+0.111 7i0.707 7+0.661 57i1.910 95-0.038 02+0.021 76i-0.013 33+0.043 21i0.707 7+0.661 57i1.910 9
由表3可以看出，在
中，只有-2阶和1阶明显大于其余项，因此可以确定最简轨迹只包含傅里叶系数中的-2阶和1阶谐波分量。使用式(12)求得比例系数k=0.707 7+0.661 57i，并用式(13)求出最简轨迹的-2阶和1阶傅里叶系数：
根据式(14)，可以确定一个包含两个杆的耦合串联连杆机构来实现这个最简轨迹。杆L1的长度为|C1|=7.999 9，杆L2的长度为|C-2|=15.999 9，与给定五杆的曲柄基本相同。此外，没有C0，这意味着机构的固定铰链位置在(0,0)处，也就是与R0相同。因此，所述方法是可行的。
为了形成闭链并保持机构自由度为1，还需要找到一个二杆组。由文献[15-17]可知，有一种快速有效的算法可用于二杆组综合。根据该算法，连杆长度L4、R3在动坐标系M中的位置以及R4在固定坐标系中的位置与给定数据完全相同。
5 实例：任意运动的综合
使用上述方法对任意平面刚体运动进行综合，如图6所示。选择动坐标系中两点分别为p(0,2)和q(4,4)，由式(4)和式(5)获得两点轨迹，然后，使用第2节的方法，对两轨迹进行傅里叶变换并确定最简轨迹的谐波分量。表4表明，除了0阶、-1阶和1阶谐波分量之外，
大部分是相同的。因此，最简轨迹包含0阶、-1阶和1阶傅里叶系数。再使用式(12)求出比例系数k=0.435 0+0.208 3i，并用式(13)求出最简轨迹的0阶、-1阶和1阶傅里叶系数：
图6 给定任意平面刚体运动
Fig.6 The arbitrary given motion of planar rigid body
从上文傅里叶描述子中可以提取以下信息：机构的固定铰链点R0相对于固定坐标系位于(0.165 5,-3.186 7)，耦合串联连杆机构包含两个杆，杆1以ω1=1 r/s的速度旋转，其长度大约为|C1|=3.886 6，起始转角为arg C1=-59.11°；杆2以ω2=-1 r/s的速度旋转，其长度为|C-1|=1.906 7，起始转角为arg C-1=66.39°。
表4 任意给定平面刚体运动相关参数
Tab.4 Parameters in the arbitrary given motion of plane rigid body motion
阶数CpnCqnKnKNn-5-0.060 77-0.116 3i-0.232 4-0.178 4i0.406 3+0.188 6i2.183 5-40.188 3+0.034 63i0.418 4-0.126 7i0.389 2+0.200 6i2.197 7-3-0.248 1+0.236 8i-0.248 5+0.712 8i0.404 5+0.207 1i2.158 1-2-0.114 2-0.542 9i0.747 9-0.981 0i0.406 1+0.193 2i2.166 4-12.237 5+1.859 4i3.620 5+0.637 3i0.687 1+0.3926 i4.117 70-1.095 6-1.016 9i-0.249 6+2.000 4i-0.433 3+0.601 7i9.765 51-0.888 5+4.899 2i1.475 4+5.268 7i0.818 5+0.397 8i5.174 820.094 07-0.060 4i0.136 7-0.162 5i0.502 7+0.155 9i2.707 430.167 4-0.115 0i0.222 8-0.371 9i0.426 0+0.195 0i2.201 94-0.009 91+0.007 286i-0.011 17+0.041 34i0.225 2+0.180 8i3.294 25-0.024 21-0.023 69i-0.071 06-0.010 68i0.382 2+0.275 9i2.428 0
在这个例子中，将耦合串联连杆机构与二杆组进一步综合，最终得到了一个如图7所示的闭式连杆机构。该机构包含4个活动杆件，杆1和杆2为实现最简轨迹的耦合串联连杆机构中两杆件；杆3为连杆，实现了给定的目标运动；杆4是为形成闭链找到的二杆组。该闭式连杆机构的自由度为1，同时还可以实现给定的目标运动，这进一步证明了所述方法是正确可行的。
图7 机构综合结果
Fig.7 The synthesis result of mechanism
6 结论
本文提出了一种方法对给定的平面刚体运动进行机构综合，得到耦合串联机构。通过方法叙述和实例论证，可以得到以下结论：对任意给定的平面运动，本文定义刚体运动中的包含最少数量谐波分量的轨迹为最简轨迹，并给出了确定该最简轨迹的方法。最简轨迹包含的谐波分量确定了耦合串联连杆机构的拓扑结构信息(杆件数目、齿轮数目及相互之间的连接关系)和尺度参数信息(杆件长度、齿轮齿数、固定铰链位置等)。为了形成闭链，找到一个二杆组，并最终得到了一个闭式连杆机构。实例表明，该方法在进行任意给定平面运动综合时是可行的。
[1] FREUDENSTEIN F.Harmonic Analysis of Crank-and-Rocker Mechanisms with Application[J].Journal of Applied Mechanics,1959,26：673-675.
[2] FUNABASHI H,FREUDENSTEIN F.Performance Criteria for High-speed Crank-and-Rocker Linkages,Part Ⅰ：Plane Crank-and-Rocker Linkages[J].Journal of Mechanical Design,1979,101(1)：20-25.
[3] FARHANG K,MIDHA A,BAJAJ A.Synthesis of Harmonic Motion Generating Linkages,PartⅠ：Function Generation[J].Journal of Mechanisms Transmissions and Automation in Design,1988,110(1)：16-21.
[4] FARHANG K,MIDHA A,BAJAJ A.Synthesis of Harmonic Motion Generating Linkages,PartⅡ：Path and Motion Generation[J].Journal of Mechanisms Transmissions and Automation in Design,1988,110(1)：22-27.
[5] CHU J,CAO W.Synthesis of Coupler Curves of Planar Four-bar Linkages through Fast Fourier Transform[J].Chinese Journal of Mechanical Engineering,1993,29(5)：117-122.
[6] MCGARVA J,MULLINEUX G.Harmonic Representation of Closed Curves[J].Applied Mathematical Modelling,1993,17(4)：213-218.
[7] MCGARVA J.Rapid Search and Selection of Path Generating Mechanisms from a Library[J].Mechanism and Machine Theory,1994,29(2)：223-235.
[8] ULLAH L,KOTA S.Optimal Synthesis of Mechanisms for Path Generation Using Fourier Descriptor and Global Search Methods[J].Journal of Mechanical Design,1997,119(4)：504-510.
[9] NIE X,KROVI V.Fourier Methods for Kinematic Synthesis of Coupled Serial Chain Mechanisms[J].Journal of Mechanical Design,2005,127(1):232-241.
[10] 褚金奎,孙建伟.RCCC机构轨迹综合的数值图谱法[J].中国机械工程,2009,20(9):1024-1028.
CHU Jinkui,SUN Jianwei.Research on RCCC Mechanism Path Generation by Using Numerical Atlas Method[J].China Mechanical Engineering,2009,20(9):1024-1028.
[11] CHU J,SUN J.A New Approach to Dimension Synthesis of Spatial Four-bar Linkage through Numerical Atlas Method[J].Journal of Mechanism and Robotics,2010,2(4)：041004.
[12] SUN J,CHEN L,CHU J.Motion Generation of Spherical Four-bar Mechanism Using Harmonic Characteristic Parameters[J].Mechanism and Machine Theory,2016,95：76-92.
[13] 路贺.球面四杆曲柄滑块机构尺度综合的研究[D].长春：长春工业大学,2014.
LU He.Dimensional Synthesis of Spherical Four Bar Crank Slider Mechanism[D].Changchun：Changchun University of Technology,2014.
[14] XIE J,CHEN Y.Application Backpropagation Neural Network to Synthesis of Whole Cycle Motion Generation Mechanism[C]∥12th IFToMM World Congress.Besancon,2007：dmg19969009.
[15] ZHAO P,LI X,ZHU L,et al.A Novel Motion Synthesis Approach with Expandable Solution Space for Planar Linkages Based on Kinematic-mapping[J].Mechanism and Machine Theory,2016,105:164-175.
[16] ZHAO P,LI X,PURWAR A,et al.A Task Driven Unified Synthesis of Planar Four-bar and Six-bar Linkages with R-and P-Joints for Five-position Realization[J].Journal of Mechanisms and Robotics,2016,8(6)：061003.
[17] GE Q J,PURWAR A,ZHAO P,et al.A Task-driven Approach to Unified Synthesis of Planar Four-bar Linkages Using Algebraic Fitting of a Pencil of G-manifolds[J].Journal of Computing and Information Science in Engineering,2017,17(3)：031011.
[18] WU J,GE Q J,GAO F,et al.On the Extension of a Fourier Descriptor Based Method for Planar Four-bar Linkage Synthesis for Generation of Open and Closed Paths[J].Journal of Mechanisms and Robotics,2011，3(3)：031002.
