0 引言
得益于信号采集与计算机技术的发展,在设备运行过程中获取大量的状态监测数据成为可能,这推动了数据驱动的机械设备剩余寿命预测方法研究的发展。
传统的剩余寿命预测方法需要2个基础步骤:①建立性能退化指标;②研究预测模型。性能退化指标的建立旨在从采集的振动加速度信号中得到能表征轴承性能退化过程的指标;预测模型针对性能指标的退化趋势进行预测,以达到预测寿命的目的。性能退化指标构建的一种方法是从原始信号中提取单一的统计特征并将其作为性能退化指标,如LI等[1]采用的均方根和峭度,王冰等[2]采用的基于多尺度形态分解谱熵,李洪儒等[3]采用的二元多尺度熵。使用单一的时域或时频域特征来人工构造性能退化指标,需要大量的经验与专业知识,且单一的统计特征也难以保证后续的预测精度。除此之外,还有将多种指标融合的性能退化指标构造方法,如WANG等[4]采用的主成分分析方法,王建利[5]采用自组织图谱融合构造新性能退化指标的方法。这些利用数据降维进行特征融合的方法在降维过程中会损失部分信息,且这些方法都是基于无监督学习的方法,在降维中没有加入与剩余寿命相关的约束条件,无法保证这些损失的信息都是与轴承剩余寿命相关度低的信息。在数据驱动的机械设备剩余寿命预测方法的研究中,高斯博[6]利用线性Wiener过程,LIU等[7]采用隐马尔可夫模型,李洪儒等[3]使用极限学习机,申中杰[8]使用支持向量机,陈法法等[9]使用小波支持向量机进行剩余寿命预测。以上方法均需要先人工构造特征,且所用方法在模型复杂度和学习能力上较以卷积神经网络为代表的深度学习方法存在差距,所以预测精度仍有提升空间。
以上剩余寿命预测方法的重点在于性能退化指标的构建。传统方法的性能指标需要人工提取信号的某种或某些特征,再进行筛选和融合。在这个过程中,为了提取合适的特征,需要对所采集信号的特性有相当程度的了解,并且特征的筛选和融合需要一定的经验与知识,所以合适特征的提取与融合需要投入大量的精力。另外,单一的性能退化指标往往不适用于大多数的退化过程,它在不同个体的剩余寿命预测中的表现不稳定。
针对上述问题,笔者提出基于全卷积层神经网络的轴承剩余寿命预测方法,将卷积神经网络用于轴承剩余寿命预测可以免去传统方法中的特征提取、筛选与融合等步骤,而这些步骤往往需要一定的经验与相关知识。本文方法将全连接层全部换为卷积层与池化层,利用卷积层的局部连接和权值共享的特性,简化网络的权值参数,降低对训练样本量的需求,提高网络泛化能力。直接将原始振动信号作为网络的输入时,输出的预测结果曲线中会存在大量的噪声,故本文将加权平均的方法用于预测结果的降噪,该方法只需用到当前预测点以及其前面的数据,适用于剩余寿命预测过程中的降噪。
1 神经网络介绍
1.1 卷积神经网络
卷积神经网络的核心在于特征的自主学习,与传统的寿命预测方法相比,它减少了人工的特征提取等操作。使用多层卷积神经网络时,每个卷积层将提取信号不同层次的特征,能更好地反映数据本身的特点。传统的卷积神经网络包括卷积层、池化层和全连接层,如图1所示,本文中用作参考的传统卷积神经网络表的结构共有13层,包括1个输入层、用于特征学习的3个卷积层(C1~C3)和3个池化层(P1~P3)、用于将特征展开到一维的1个扁平化层(F)、用于预测剩余寿命的5个全连接层(D1~D5)。考虑到全连接层的参数较多,采用了dropout方法防止过拟合。

图1 传统卷积神经网络结构示意图
Fig.1 Schematic diagram of traditional convolutional neural network structure
1.2 全卷积层神经网络
全卷积层神经网络将传统卷积神经网络最后的全连接层更换为卷积层和池化层,利用卷积层的权值共享、局部连接等特性,减少了网络权值等在训练中需优化参数的数量[10],在减小训练样本需求的同时提高了结果的可靠性。如图2所示,该网络共有14层,包括1个输入层、7个卷积层(C1~C7)、6个池化层(P1~P6)。首先,由输入层将原始的振动数据输入到第1个卷积层;然后,经过多个卷积层和池化层,提取信号中的特征并降低数据维度;网络的最后一个池化层输出的一个单值数据表示剩余寿命。全卷积层神经网络的前7层与传统的卷积神经网络相同,但全卷积层神经网络的后6个全连接层改为4个卷积层与3个池化层,并舍弃了dropout等正则化过程。

图2 全卷积层神经网络结构示意图
Fig.2 Schematic diagram of full convolutional neural network structure
全卷积层神经网络的核心是卷积层,它对输入的数据进行卷积运算,增强原始信号中的有效信息并抑制噪声的影响。每个卷积层都有一个卷积核,每个卷积核只与输入信号的部分区间相连,形成局部连接,而传统的全连接层要求每个输入单元与每个输出单元都产生交互。两种连接方式如图3所示,局部连接比全连接需要更少的权重参数,不仅降低了模型的存储需求,而且提高了计算效率。
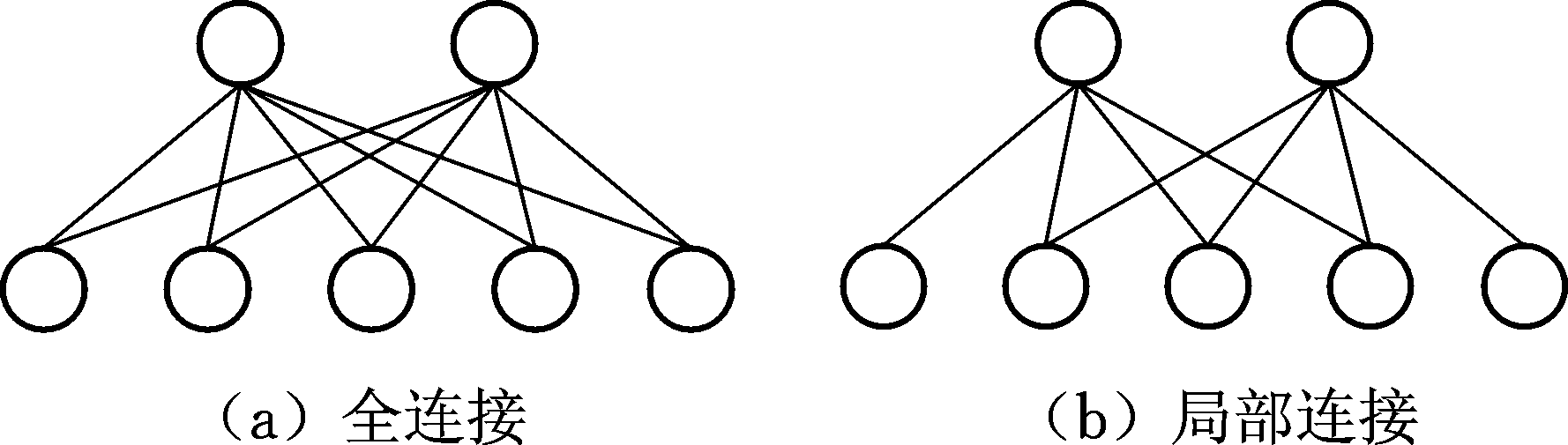
图3 网络连接方式示意图
Fig.3 Network connection diagram
每个卷积层的计算如下:
(1)
式中,*表示卷积操作;In为与卷积核相连的部分输入单元;N为该部分输入单元的数量;zi为第i个输出单元;wi,n为与第i个输出单元相连的所有输入单元中第n个单元的权重;bi为该输出单元的偏置。
由于上述卷积操作为线性变化,而线性模型的表达能力有所欠缺,所以需通过非线性激活函数来得到下一层的输入。本文选择relu(线性整流函数)作为激活函数,其定义如下:
yi=max(0,zi)
(2)
式中,yi为经过激活函数的输出。
池化层对卷积层的输出起到降采样的作用,以减少数据维度。它能够对特征进行压缩,不仅减小后续网络的计算量,并且能够突出更重要的特征。输入到池化层的数据先被分割成一系列的片段,再由池化函数计算出片段中最有价值的信息来代替这一片段的信息,从而完成对特征的压缩。本文选用的最大池化方法将片段yi-yi+1内的最大值作为特征来代替片段yi-yi+1。
建立好全卷积层神经网络模型后,需要对其输入训练样本{(xi,yi)}进行训练,其中,xi为训练的输入数据,本文中为采集到的原始振动数据;yi为训练样本的标签,本文中为振动数据对应的剩余寿命。训练时,将训练样本xi输入模型,得到计算出的剩余寿命yi,t,计算模型的剩余寿命计算值yi,t与实际剩余寿命yi间的均方误差作为损失函数,均方误差的计算公式为
(3)
式中,M为训练样本的总数。
以减小均方误差L作为优化目标,在训练集上最小化L来优化模型的参数。
2 加权平均的降噪方法
本文模型的输入为原始振动数据,将原始振动数据输入预测模型后直接得到预测值。预测值中存在相当大的噪声,导致预测的剩余寿命曲线存在相当大的波动,造成预测结果误差大。剩余寿命预测中,预测某一时刻的剩余寿命时,只有当前时刻和以前时刻的预测值,基于数据驱动的预测方法在应用时,将采集的数据作为输入才能预测剩余寿命。一般的滑动平均降噪方法需要预测时刻前后的数据,即需要使用未来的数据才能对该点进行平滑,所以滑动平均方法不适用。本文采用加权平均方法,用一个时间段内预测值的加权平均值代替最后一个时刻的预测值,靠近当前预测点的数据具有更大的权重。此外,为了取得更好的降噪效果,在计算最新时刻的结果时,采用已经降噪过的数据进行迭代计算,即在计算Ym时,用计算好的Ym-5~Ym代替Pm-5~Pm进行计算,这样,该时刻的降噪计算结果实质上是所选时间段内当前时刻的未降噪预测结果与之前时刻已降噪结果的加权平均,具体的计算方法如下:
(4)
式中,m为时间长度;wi为权重,取等差数列;Yi为已降噪结果;Pm为当前时刻未降噪的预测值。
3 实例验证
3.1 数据来源
本文的实验数据为从滚动轴承加速寿命台架试验采集的振动加速度数据,它来源于IEEE 2012年的PHM数据挑战赛[11]。该数据集包含3种工况下的17个滚动轴承的全生命周期振动数据,每10 s采集一次数据,采样频率为25.6 kHz,一次采样时间为0.1 s,所以每次采集可得到2 560个振动加速度,振动加速度的测量值达到预先设定的阈值时认为的轴承失效,轴承的剩余使用寿命结束。本文模型不考虑工况的影响,用轴承数据集中的16个构建训练样本,将剩余的1个作为测试样本进行试验。每条训练样本{(xi,yi)}中的xi为第i次采集到的振动加速数据,即0.1 s内传感器采集的数据(共有2 560个数值),图4所示为原始振动信号。yi为该次采集时所对应的剩余寿命——当前时刻与失效时刻间的时间与起始时刻和失效时刻间时间的比值。如某一轴承共有2 803条采集数据,其使用寿命为28 030 s,当前样本为其第1 500条采集数据时,剩余寿命为13 030 s,训练时的标签yi即为剩余寿命0.464 859。
图4 原始振动信号
Fig.4 Original vibration signal
3.2 验证结果
首先,对本文的全卷积层神经网络设置参数,其中,7个卷积层中的前5个卷积核的尺寸均为6,后2个卷积核的尺寸依次为3和2;7个卷积层中,卷积核的数量分别为20、40、80、40、20、10、1;6个池化层的池化窗口长度分别为4、4、4、5、4、2。建立好的模型中每层网络的输出数据如图2所示,其中,输入信号为2560×1的一维振动信号,第1个卷积层的输出数据维度为2 560×20,第1个池化层输出数据维度为640×20,以此类推,最终输出1个单值数据——预测的剩余寿命,如图5所示,可以看出有些相邻时间点的剩余寿命预测结果相差很大,整体波动明显,预测误差较大,所以需要对整个预测结果进行降噪处理。

图5 降噪处理前的预测结果
Fig.5 Prediction results before noise reduction processing
本文采用加权平均降噪方法,时间窗长度为6,即将Pi-5~Pi的加权平均值作为ti时刻的预测值,预测值不足6个时,计算所有值的加权平均,其中,权重为差是1的等差数列,Pi-n,Pi-n+1,…,Pi对应的权重为1,2,…,n(n<6);当预测值达到6个时,则Pi-5,Pi-4,…,Pi对应的权重为1,2,…,6,利用式(4)迭代求得降噪后的预测值如图6所示,可以看到噪声明显减小,降噪后的预测值曲线更加贴近实际剩余寿命线,并且原来偏离程度较大的预测点在降噪后,与实际值的偏离程度均有所减小。

图6 全卷积层神经网络剩余寿命预测结果
Fig.6 Full convolutional neural networks prediction results
3.3 结果分析
将本文预测结果与传统的支持向量回归(support vector regression ,SVR)[12]、传统卷积神经网络[13]的预测结果进行对比。SVR方法的性能退化指标为均方根和峭度,传统卷积神经网络(图1)采用与全卷积层神经网络相同的数据输入格式,即2 560×1的一维振动信号,网络每层的数据输出格式如图1所示,最终输出寿命预测值(单值)。3种模型均采用相同的方法构建训练集与测试集,将训练集输入各模型进行模型训练,对训练好的模型输入测试数据,得到测试结果,采用相同的降噪方法处理以得到最后预测结果,同一轴承的3种模型的剩余寿命预测如图6~图8所示。

图7 支持向量回归的剩余寿命预测结果
Fig.7 SVR remaining life prediction results

图8 卷积神经网络剩余寿命预测结果
Fig.8 Convolutional neural network remaining life prediction results
由图6~图8可以看出,SVR方法与其他2种方法相比,在预测精度上有较大的差距,证明了深度学习方法的优越性,并且本文方法预测值更接近实际剩余寿命。计算3个模型预测结果的平均相对误差与最大相对误差并进行对比。预测结果是剩余寿命与总寿命的比值,所以计算预测结果相对于总寿命的平均相对误差和最大相对误差分别为
(5)
em=max{Pi-Yi}
(6)
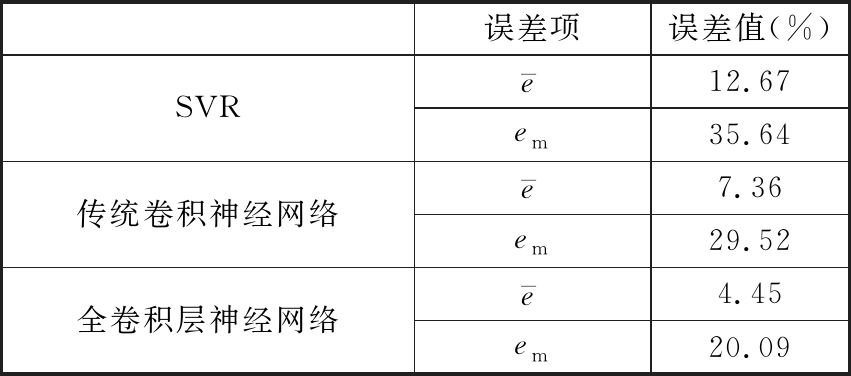
3个测试样本的误差结果如表1所示。
表1 3种模型预测误差
Tab.1 Prediction errors of 3 models
误差项误差值(%)SVRe-12.67em35.64传统卷积神经网络e-7.36em29.52全卷积层神经网络e-4.45em20.09
从误差统计可以看出,全卷积层神经网络比SVR方法的预测平均相对误差减小了64.88%,最大相对误差减小了43.63%;比传统卷积神经网络的平均相对误差降低39.54%,最大相对误差减小了31.94%。
4 结论
(1)与传统的先人工构建性能退化指标、再预测的方法相比,将卷积神经网络自学习特征用于轴承剩余寿命预测的方法,不仅减少了需要人工参与的环节,还大幅提高了预测精度。
(2)将传统卷积神经网络改进为全卷积层神经网络,可提高小样本情况下的轴承剩余寿命预测精度。
(3)引入加权平均方法对预测结果进行降噪,提高了预测精度。
[1] LI N P,LEI Y G,LIN J,et al.An Improved Exponential Model for Predicting Remaining Useful Life of Rolling Element Bearings[J].IEEE Trans.Industr.Electron.,2015,62:7762-7773.
[2] 王冰,李洪儒,许葆华.基于多尺度形态分解谱熵的电机轴承预测特征提取及退化状态评估[J].振动与冲击,2013,32(22):124-128.
WANG Bing,LI Hongru,XU Baohua.Motor Bearing Forecast Feature Extracting and Degradation Status Identification Based on Multi-scale Morphological Decomposition Spectral Entropy[J].Journal of Vibration and Shock,2013,32(22):124-128.
[3] 李洪儒,于贺,田再克,等.基于二元多尺度熵的滚动轴承退化趋势预测[J].中国机械工程,2017,28(20):2420-2425.
LI Hongru,YU He,TIAN Zaike,et al.Degradation Trend Prediction of Rolling Bearing Based on Two-element Multiscale Entropy[J].China Mechanical Engineering,2017,28(20):2420-2425.
[4] WANG F,SUN J,YAN D,et al.A Feature Extraction Method for Fault Classification of Rolling Bearing Based on PCA[J].Journal of Physics:Conference Series,2015,628:012079.
[5] 王建利.滚动轴承性能退化评价与趋势预测研究[D].大连:大连理工大学,2013.
WANG Jianli,Research on Performance Degradation Assessment and Trend Prediction of Rolling Bearing[D].Dalian:Dalian University of Technology,2013.
[6] 高斯博.基于退化数据的寿命预测中估计问题研究[D].大连:大连理工大学,2016.
GAO Sibo.Estimation Research in Remaining Useful Life Prediction Driven by Statistical Data[D].Dalian:Dalian University of Technology,2016.
[7] LIU Z,LI Q,MU C.A Hybrid LSSVR-HMM Based Prognostics Approach[J].Sensors,2013,13(5):5542-5560.
[8] 申中杰,陈雪峰,何正嘉.基于相对特征和多变量支持向量机的滚动轴承剩余寿命预测[J].机械工程学报,2013,49 (2):183-189.
SHEN Zhongjie,CHEN Xuefeng,HE Zhengjia.Remaining Life Predictions of Rolling Bearing Based on Relative Features and Multivariable Support Vector Machine[J].Journal of Mechanical Engineering,2013,49 (2):183-189.
[9] 陈法法,杨勇,陈保家,等.基于模糊信息粒化与小波支持向量机的滚动轴承性能退化趋势预测[J].中国机械工程,2016,27(12):1655-1661.
CHEN Fafa,YANG Yong,CHEN Baojia,et al.Degradation Trend Prediction of Rolling Bearing Based on Fuzzy Information Granulation and Wavelet Support Vector Machine[J].China Mechanical Engineering,2016,27(12):1655-1661.
[10] LECUN Y,BENGIO Y,HINTON G.Deep Learning[J].Nature,2015,521(7553):436-444.
[11] NECTOUX P,GOURIVEAU R,MEDJAHER K,et al.PRONOSTIA:An Experimental Platform for Bearings Accelerated Degradation Tests[C]∥IEEE International Conference on Prognostics and Health Management.Denver,2012:1-8.
[12] 雷亚国.旋转机械智能故障诊断与剩余寿命预测[M].西安:西安交通大学出版社,2017:294-299.
LEI Yaguo.Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery[M].Xi’an:Xi’an Jiaotong University Press,2017:294-299.
[13] GUO L,LEI Y G,LI N P,et al.Deep Convolution Feature Learning for Health Indicator Construction of Bearings[C]∥Prognostics and System Health Management Conference.Harbin,2017:1-6.
