0 引言
型腔铣削在模具、航空和汽车零部件的加工中占有重要地位[1]。在工艺规划阶段,需要知道切削状况,如轴向和径向切削深度、主轴转速、沿路径的进给速度等信息以生成数控加工指令,因此对于给定机床,在工艺规划阶段正确选择加工参数非常重要[2]。除此之外,数控加工过程中的切削颤振也是一个必需考虑的问题。机床操作者通常采用试切的方式来避免颤振,寻找合适的刀具或最优的加工参数,显然这将降低生产效率,增加生产成本[3-4]。
针对以上问题,本文在工艺规划阶段预测数控铣削加工过程中可能出现的颤振,进而提前修改加工工艺参数,从而避免数控铣削加工过程中产生的颤振。
文献[4-5]建立了稳定性判别的解析法,但该方法过于简单,不能预测小径向切深状况下出现的附加不稳定区域(倍周期分岔)。INSPERGER等[6-8]将半离散法(semi-discretization method,SDM)引入铣削加工稳定性的预报,由于此方法适用于小径向切深等多种工况,引起了其他学者的关注。DING等[9-11] 对SDM进行改进,提出了用于铣削稳定性预测的完全离散算法、谱方法和数值积分法。
采用上述算法或试验[12]可获得铣削加工颤振的稳定性叶瓣图(stability lobe diagram,SLD)。参照SLD选取无颤振铣削加工工艺参数,可提高加工效率。尽管人们在铣削加工动力学模型及其稳定性方面已展开了广泛的研究,但其应用仍局限于加工路径是直线的状况。型腔铣削过程当中,当铣刀进入拐角区域或加工路径是曲线时,由于铣刀刀齿与工件相互啮合状况的改变,原有针对刀具-工件啮合状况恒定的铣削加工稳定性判据将无法直接使用。为了在型腔加工时也能用SLD进行工艺规划,提高生产效率,本文在半离散法对铣削加工稳定性预测的基础上,将其与型腔铣削路径引起刀具-工件啮合状况变化相结合,提出了型腔加工时的稳定性预测判定方法,并通过铣削加工试验验证了该方法的有效性和实用性。
1 铣削加工动力学模型
如图1所示,本文以含有再生效应的两自由度铣削加工动力学模型为研究对象[6,8]。假设刀具在X、Y方向是弹性体,于是刀具和工件间相互作用的动力学方程为
(1)
式中,q(t)为铣刀刀尖在X和Y方向上的动态位移,q(t)=[x(t)y(t)]T;M、C、K分别为质量、阻尼和刚度的矩阵;F(t)为作用在铣刀上的动态切削力,F(t)=[Fx(t)Fy(t)]T。

图1 铣削加工力学模型
Fig.1 Mechanical model of milling
考虑刀具螺旋角的影响,加工时X和Y方向上动态切削力可表示为
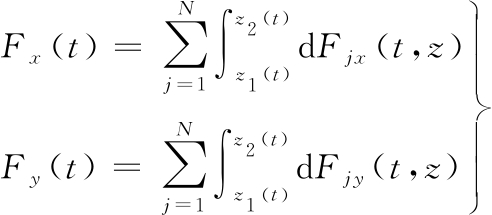
(2)
(3)
(4)
式中,N为铣刀齿数;dFjx(t,z)、dFjy(t,z)分别为第j齿在z处X和Y方向的微分力(见图2);z1 (t)、z2(t)分别为螺旋铣刀加工时切入和切出点位置;n为主轴转速;θ为刀具螺旋角;dc为铣刀直径。
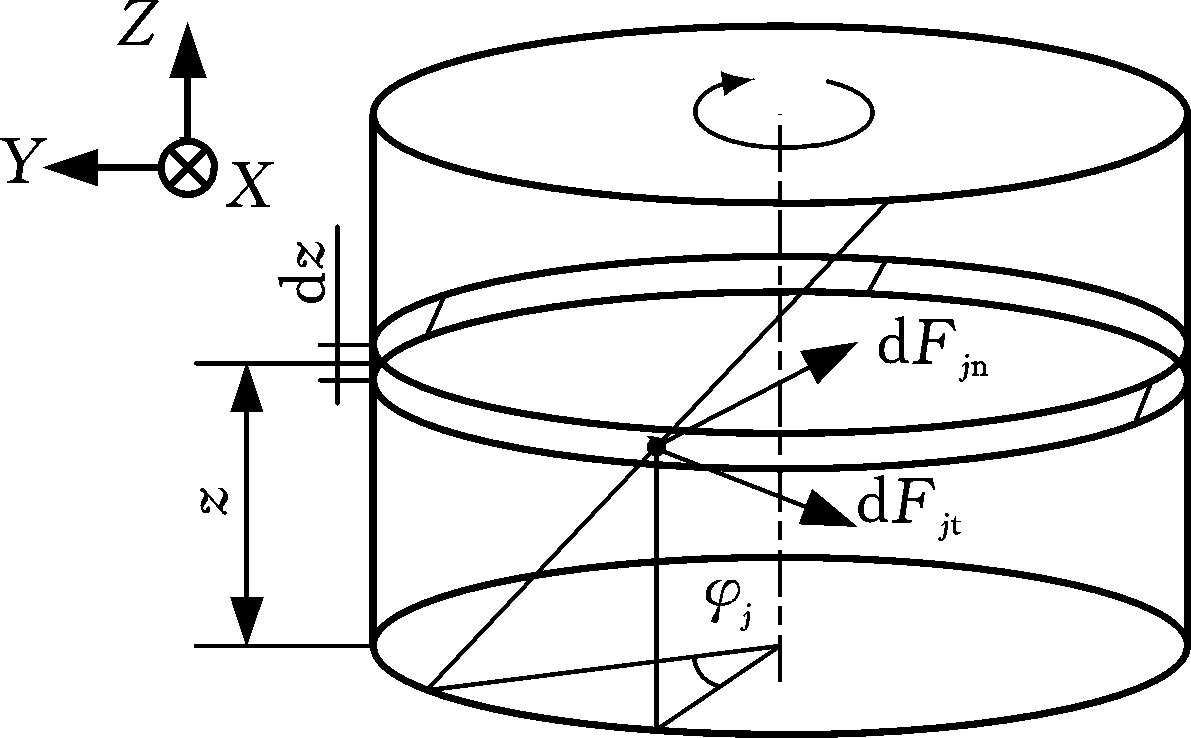
图2 螺旋铣刀切削力微元
Fig.2 Cutting force element with helix angle
微分切向力和微分法向力分别为
(5)
(6)
hj(t,z)=(x(t)-x(t-τ))sinφj(t,z)+
(y(t)-y(t-τ))cosφj(t,z)
(7)
式中,Kt、Kn分别为切向和法向的切削系数;g(φj(t,z))为窗函数;φst、φex分别为切入角和切出角;hj(t,z)为振动引起的动态切削厚度;τ为时滞项。
依据上面的分析,可以得到铣削过程的控制方程。接下来分析螺旋角对不同切削区域的影响。当计算切削力时,式(2)中的积分下限z1(t)和积分上限z2(t)可分为5种情况[13]来讨论,见图3。

图3 刀具切削过程模型示意图
Fig.3 Integral zone classification of milling process
(1)状态1。若φst<φj(t,0)<φex,则zj,1=0;若φst<φj(t,w)<φex,则zj,2= w,其中,w为轴向切削深。
(2)状态2。若φst<φj(t,0)<φex,则zj,1=0;若φj(t,w)<φst,则zj,2= (φj(t,0)-φst)/kθ,kθ=2tanθ/dc。
(3)状态3。若φj(t,0)>φex,则zj,1=(φj(t,0)-φst)/kθ;若φst<φj(t,w)<φex,则zj,2=w。
(4)状态4。若φj(t,0)>φex,则zj,1=(φj(t,0)-φex)/kθ;若φj(t,w)<φst,则zj,2=(φj(t,0)-φst)/kθ。
(5)状态5。若φj(t,0)>φex且φj(t,w)>φex,则铣刀不在切削状态。
2 基于半离散算法的稳定性预测
为了判定铣削加工动力学方程的稳定性,需将铣削动力学方程变换为状态空间方程的形式[7]。通过Cauchy变换,由式(1)可得:
(8)

![]()
Knsinφj(t,z))sinφj(t,z)dz![]()
Knsinφj(t,z))cosφj(t,z)dz![]()
Kncosφj(t,z))sinφj(t,z)dz![]()
Kncosφj(t,z))cosφj(t,z)dz
由于刀齿的周期激励作用,周期函数矩阵H(t)以相邻刀齿间隔τ=T=60/(Nn)为周期。
接下来用半离散法[7-8]来判定式(8)的稳定性。第i个离散时间区间[ti,ti+1]的时间长度Δt=T/k。时滞 τ所对应的间隔份数可近似表示为
(9)
于是在一个完整的主轴旋转周期上,可得到一个系统稳定性的数学表达式[7]:
(10)
式中,Zk、Z0 为系统状态向量;Φ为系数矩阵。
系统的稳定性可以通过Floquet理论进行判定:若传递矩阵Φ的所有特征值的绝对值小于1,则系统是稳定的,否则,系统是不稳定的。
3 型腔铣削加工稳定性预测算法
由半离散算法可以生成铣削加工SLD,但在型腔铣削加工的过程中,由于非直线加工路径的存在,铣刀刀齿与工件从相互接触到分离时的切入角、切出角将随加工路径发生改变,导致无法直接应用SLD来选择最终的加工参数。考虑到型腔铣削加工中的这一特点,判定数控型腔铣削加工过程中的稳定性问题的处理方式见图4。不失一般性,以下将以数控型腔铣削加工时有代表性的拐角处加工为例进行后续分析。如图4所示,首先,根据刀具-工件沿加工路径变化的啮合信息、模态参数和主轴转速得到SLD矩阵。铣削加工过程中,切削厚度不变时,铣削加工临界轴向切深wc将保持恒定;当切削路径为曲线或由于切削厚度变化而导致切入、切出角(如式(6)所示)变化时,对于给定的铣削装置,可得到一定主轴转速下,随加工路径变化的临界轴向切深矩阵。

图4 基于铣削路径的稳定性预测算法
Fig.4 Chatter stability prediction algorithm based on milling path
其次,刀具和工件间的接触状况可根据几何模型的边界信息通过计算得到。切入角、切出角以及轴向切深w通过CAM软件仿真得到。
最后,由铣削颤振稳定性预测算法经过计算可得沿路径变化的临界轴向切深,然后将其与加工过程选定的轴向切深进行对比。若所选轴向切深大于临界轴向切深,则发生颤振;否则,铣削加工过程稳定。当预测到加工过程中会有颤振发生时,可通过预先调整加工参数,然后重新计算加工状态变化后的加工工艺参数。再次比较轴向切深和临界轴向切深,直至采用新的工艺参数能够避免颤振的发生。这样可避免型腔铣削加工工艺规划过程中,由刀具路径变化引起的刀具工件间啮合状况的改变对SLD的重复计算。
4 铣削加工试验验证
4.1 试验装置
试验在沈阳机床厂生产的i5三轴立式加工中心上完成,该机床的最高主轴转速为20 000 r/min。试验装置如图5所示。刀具为2齿整体硬质合金螺旋铣刀,直径为10 mm。刀尖点模态参数使用Kistler 9722A2000力锤,通过锤击法,借助Modalview分析软件提取得到刀具模态参数,见表1。测试工件为85 mm×85 mm×60 mm的铝合金,装夹在Kistler 9257B压电式测力平台上。通过切削实验测得的切向切削力系数Ktc=900.8 MPa、法向切削力系数Krc=456.8 MPa。

图5 切削试验装置
Fig.5 Cutting test equipment
表1 刀具的模态测试参数
Tab.1 Modal parameters of cuttng tool
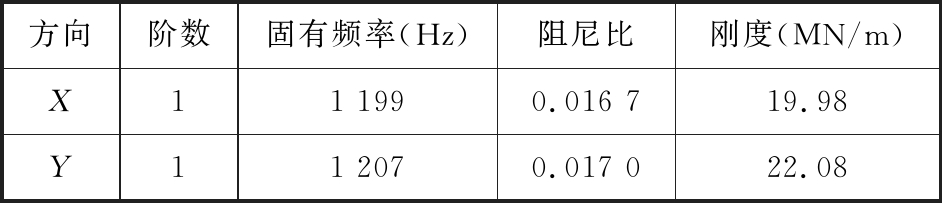
方向阶数固有频率(Hz)阻尼比刚度(MN/m)X11 1990.016 719.98Y11 2070.017 022.08
4.2 型腔铣削加工颤振预测试验
由于半离散算法用于直线走刀时的稳定性问题文献[14]已验证,本节将对型腔铣削加工拐角处的稳定性进行预测,然后通过试验进行加工验证。
铣削过程中是否发生颤振常通过观察工件表面是否有振纹,或考察傅里叶变换后切削力的幅值频谱成分来判断。宋清华[15]经过试验证明,由于铣削加工过程的复杂性,通过铣削力频谱成分判定颤振的发生不能获得准确的结果。丁烨[16]关于铣削颤振的试验也显示,颤振发生时的颤振频率表现不明显。因此拐角处的颤振试验主要通过振纹来判定,同时将试验时的切削力及其频谱作为参考。
根据4.1节测得的试验参数,得到加工时的颤振稳定性图(图6)。根据图6我们选择主轴转速为14 000 r/min、17 500 r/min,其他加工工艺参数均相同。试验加工路径如图7所示。铣刀进入拐角后,刀具的径向切深将会增加,导致轴向临界稳定切削深度下降。由图7可知,顺铣时,当铣刀进入拐角后,径向切深会增大,导致刀具的切出角逐渐变小。根据图7所示的铣削加工走刀路径和图8所示的切入角和切出角随路径变化的关系,用稳定性算法预测的结果如下:①主轴转速为14 000 r/min时,在铣刀通过拐角的过程中,切入角先减小后增大。当切入角小于1.78 rad时,临界轴向切深小于3 mm(图9),此时铣削加工过程将产生颤振;随着加工的进行,当切入角从最小值逐渐增大并超过1.78 rad时,临界轴向切深将大于3 mm,此时颤振逐渐消失。因此当主轴转速为14 000 r/min时,切削加工在直线走刀处切削稳定,在拐角处加工时会有颤振发生。②主轴转速为17 500 r/min时,由图9可知,无论切入角如何变化,其临界轴向切深始终大于3 mm,因此,整个加工过程稳定,不会有颤振发生。

图6 铣削加工稳定性叶瓣图
Fig.6 SLD of milling process

图7 走刀路径
Fig.7 Tool path

图8 切入角、切出角随铣刀进入拐角的行程变化
Fig.8 Entry and exit angle variation according to cutter movement into corner

图9 轴向临界切深和切入、切出角的关系
Fig.9 The relationship of wc and entry-exit angle
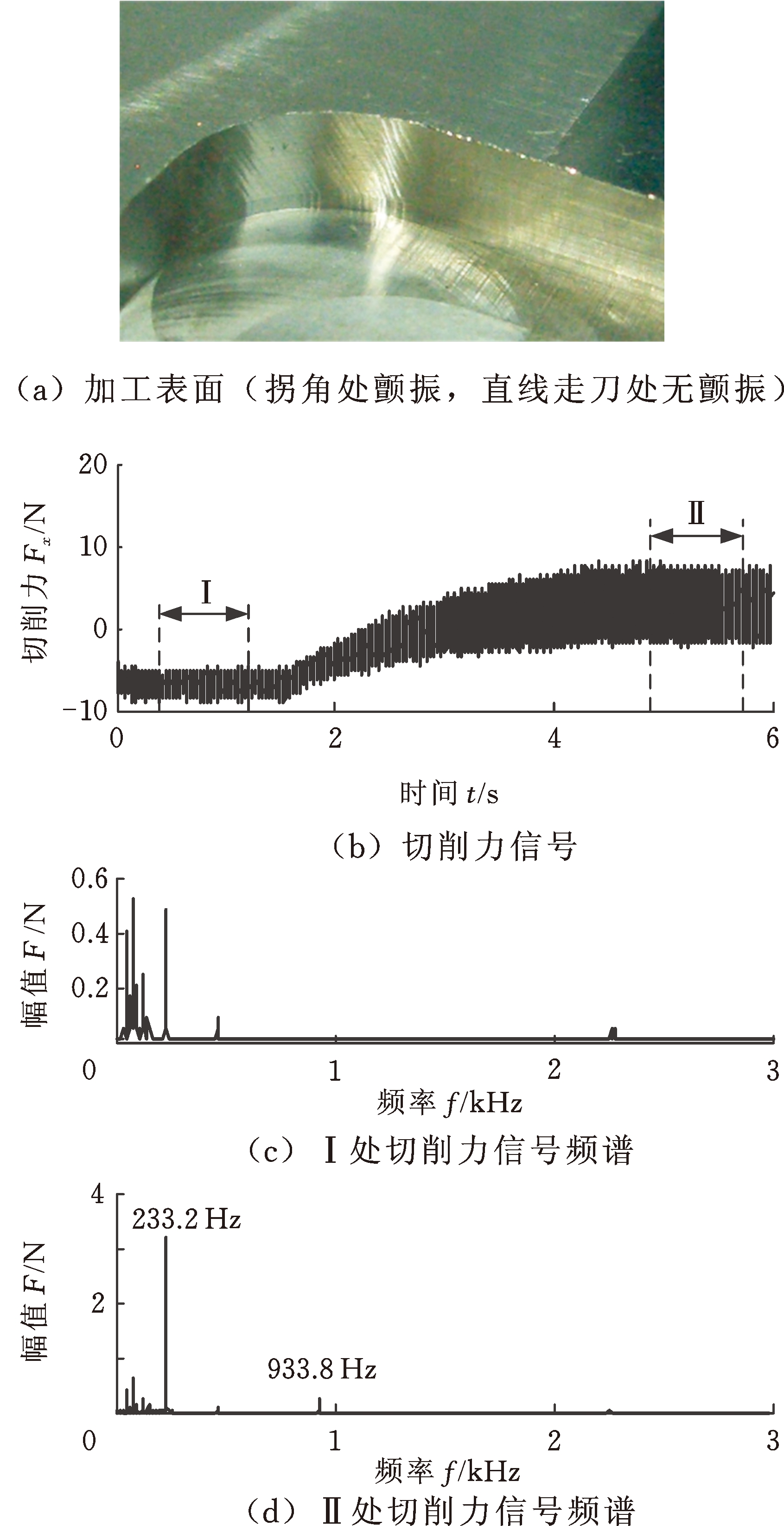
图10 型腔铣削加工表面和切削力频谱
(主轴转速14 000 r/min,拐角处颤振)
Fig.10 Surface of cutting and FFT of cutting force
(spindle speed is 14 000 r/min,chatter at cornering section)
采用上述两组工艺参数进行铣削加工试验的结果如图10、图11所示。从图10a中拐角处的振纹可知,铣刀进入拐角后颤振发生。图10b是加工过程测得的时域信号图,图10c和图10d是图10b中Ⅰ和Ⅱ处的频谱。颤振部分与直线走刀部分频谱的不同主要在于,拐角部分X向的切削力频谱出现主轴旋转频率的4倍频933.8 Hz;与直线走刀相比,主轴旋转频率233.2 Hz的幅值也明显增大。由图10b可知,加工过程中X向铣削力并不大;主轴通过频率及其谐波频率与主轴系统X方向和Y方向的固有频率相差较大,因此铣刀通过拐角处时,除了主轴旋转频率的幅值明显增大之外,刀齿通过频率466.7 Hz的2倍频表现明显。
图11为主轴转速为17 500 r/min时的铣削加工表面、时域信号及其频谱图。由第3节算法预测结果可知,在整个加工过程中无颤振发生。图11a显示,铣削表面光滑,无颤振发生,这和预测结果相一致。从时域和频谱图看,与直线走刀处的频率成分相比,拐角处X向的频谱成分中,主轴旋转频率291.7 Hz有所增大,主轴转速的二倍频584.7 Hz和三倍频876.5 Hz均有所增加,但在铣削力的频谱图中并没有激发出明显的颤振频率。

图11 型腔铣削加工表面和切削力频谱
(主轴转速17 500 r/min,无颤振)
Fig.11 Surface of cutting and FFT of cutting force
(spindle speed is 17 500 r/min,no chatter at all)
以上2次试验中,拐角处铣削加工时出现颤振的时间较短,颤振处振纹很浅(图10a),因此直接通过铣削力的频谱来判断颤振的产生比较困难。从试验结果来看,在进行铣削加工试验时,由于加工过程的复杂性,被加工表面振纹对颤振的判定也起着关键作用。
5 结论
在利用半离散算法对铣削稳定性判定的基础上,提出了型腔铣削加工时拐角处铣削稳定性判定的算法。首先,通过半离散算法得到不同主轴转速下的临界轴向切深。然后,将由半离散算法获得的稳定性叶瓣图离散化,获得一定转速下随切入角、切出角变化的轴向临界切深阵列。依加工几何模型从数控代码中提取加工参数,将一定转速下的轴向切深和临界切深比较。如果从数控加工代码中提取的轴向切深大于从临界轴向切深,则发生颤振;反之,加工过程稳定。本算法的有效性已在型腔铣削加工中经过试验验证。在更为复杂的加工路径中,该方法也可在工艺规划时对加工过程中可能产生的颤振进行预测,然后通过修改加工参数来避免颤振的产生。
[1] HELD M.VRONI:An Engineering Approach to the Reliable and Efficient Computation of Voronoi Diagrams of Points and Line Segments[J].Computational Geometry,2001,18(2):95-123.
[2] SHUNMUGAM M S,REDDY S V B,NARENDRAN T T.Selection of Optimal Conditions in Multi-pass Face-milling Using a Genetic Algorithm[J].International Journal of Machine Tools &Manufacture,2000,40(3):401-414.
[3] 汤爱民,周志雄,肖思来,等.基于铣削快速落刀法的切削颤振研究[J].中国机械工程,2011,22(19):2274-2278.
TANG Aimin,ZHOU Zhixiong,XIAO Silai,et al.Study on Cutting Chatter Based on Fast Tool-off Milling[J].China Mechanical Engineering,2011,22(19):2274-2278.
[4] ALTINTAS Y,BUDAK E.Analytical Prediction of Stability Lobes in Milling[J].CIRP Annals—Manufacturing Technology,1995,44(1):357-362.
[5] BUDAK E,ALTINTAS Y.Analytical Prediction of Chatter Stability in Milling—Part I:General Formulation[J].ASME Journal of Dynamic Systems Measurement &Control,1998,120(1):31-36.
[6] INSPERGER T,MANN B P,STEPAN G,et al.Stability of Up-milling and Down-milling,Part 1:Alternative Analytical Methods[J].International Journal of Machine Tools &Manufacture,2003,43(1):25-34.
[7] INSPERGER T,STEPAN G.Semi-discretization Method for Delayed Systems[J].International Journal for Numerical Methods in Engineering,2010,55(5):503-518.
[8] INSPERGER T,STEPAN G.Updated Semi-discretization Method for Periodic Delay-differential Equations with Discrete Delay[J].International Journal for Numerical Methods in Engineering,2010,61(1):117-141.
[9] DING Y,ZHU L M,ZHANG X J,et al.A Full-discretization Method for Prediction of Milling Stability[J].International Journal of Machine Tools &Manufacture,2010,50(5):502-509.
[10] DING Y,ZHU L M,ZHANG X J,et al.Numerical Integration Method for Prediction of Milling Stability[J].Journal of Manufacturing Science &Engineering,2011,133(3):031005.
[11] DING Y,ZHU L,ZHANG X,et al.Spectral Method for Prediction of Chatter Stability in Low Radial Immersion Milling[C]∥2011 IEEE International Conference on Robotics and Automation.Shanghai,2011:4359-4363.
[12] ISMAIL F,SOLIMAN E.A New Method for the Identification of Stability Lobes in Machining[J].International Journal of Machine Tools &Manufacture,1997,37(6):763-774.
[13] ALTINTAS Y.Manufacturing Automation:Metal Cutting Mechanics,Machine Tool Vibrations,and CNC Design[M].New York:Cambridge University Press,2012:43-47
[14] ALTINTAS Y,STEPAN G,MERDOL D,et al.Chatter Stability of Milling in Frequency and Discrete Time Domain[J].Journal of Manufacturing Science &Technology,2009,1(1):35-44.
[15] 宋清华.高速铣削稳定性及加工精度研究[D].济南:山东大学,2009.
SONG Qinghua.High Speed Milling Stability and Machining Accuracy[D].Jinan:Shandong University,2009.
[16] 丁烨.铣削动力学-稳定性分析方法与应用[D].上海:上海交通大学,2011.
DING Ye.Milling Dynamics-stability Analysis Methods and Applications[D].Shanghai:Shanghai Jiao Tong University,2011
