0 引言
大型结构物提升系统中的提升塔架是提升系统中需要钢材最多、安全性要求最高的部件，因此，通过优化设计得到满足安全性要求、轻量化的提升塔架具有实际意义。
Kriging模型作为一种代理模型技术，可以替代复杂费时的分析模型，相较于响应面模型和径向基函数模型具有无偏估计、平滑效应和响应快等特点，适用于解决参数个数少于8的复杂非线性问题，已广泛应用于机械结构优化设计等领域[1-2]。相较于静态Kriging模型，通过不断加点的动态Kriging模型具有更高的模型精度。加点准则主要有最小预测点(minimizing the predictor，MP)加点准则和期望提高(expected improvement，EI)加点准则。MP加点准则在每次迭代的最优解处进行加点，尽管模型最优解附近的局部精度不断提高，但该加点准则易使迭代收敛于局部最优解；EI加点准则在计算得到的EI最大值处进行加点[3]，模型全局精度得以提高，但最优解附近的局部精度不易得到保证。
人工蜂群算法是由KARABOGA[4]于2005年提出的一种智能全局优化算法，最初仅用于无约束优化问题的求解。随后KARABOGA等[5]于2011年通过引入Deb规则选择蜜源，根据可行解的适应度与不可行解的背离值来计算观察蜂选择蜜源的概率，并用来处理带约束的优化问题。目前Deb规则已广泛应用于带约束优化问题的求解[6]。
本文针对MP加点准则和EI加点准则的不足，综合考虑代理模型的全局精度和最优解附近的局部精度，提出了一种双加点动态Kriging模型，基于该模型和人工蜂群算法对提升塔架进行了优化设计，并将该模型的优化结果与仿真模型、静态Kriging模型和基于传统加点准则的动态Kriging模型的优化结果进行了对比分析。
1 优化问题描述
提升塔架是大型结构物提升系统中的重要支撑部件，主要由两组共4个支撑架组成，每个支撑架由主支撑架和斜支撑架组成，其结构如图1所示。其中，支撑架固定在地基上，塔顶横梁连接2个相邻的支撑架，液压提升器固定在塔顶横梁上。
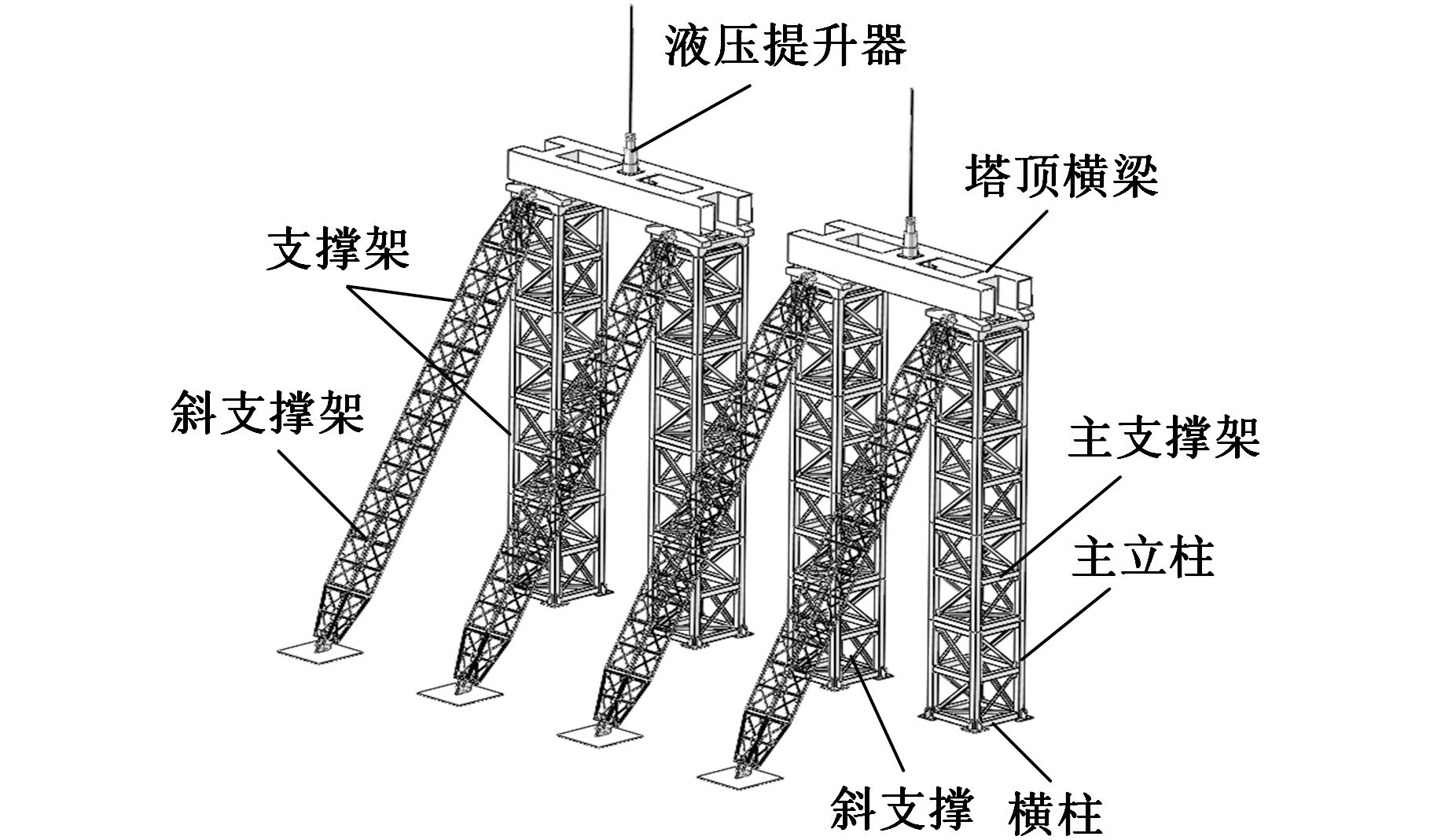
图1 提升塔架结构
Fig.1 Structure of hoist tower
为提高优化设计效率，考虑动载系数和载荷分布系数，因提升塔架具有对称结构，故本文仅对1个支撑架进行仿真分析。提升塔架材料为Q235，提升塔架的总质量为21 708 kg，其提升总质量为1 000 t，得到的分析结果见图2，其中，最大应力的绝对值为128.193 MPa。
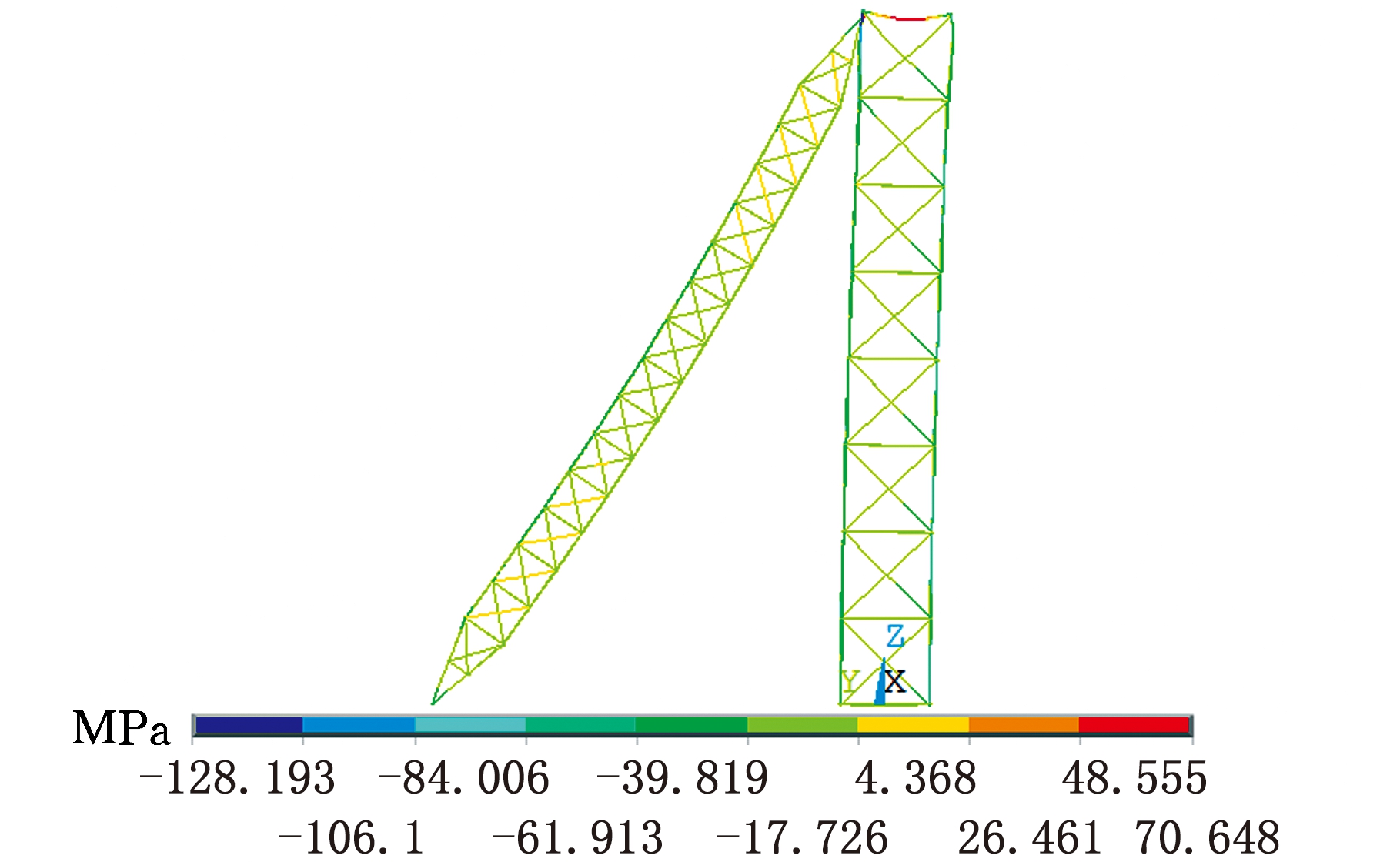
图2 提升塔架初始分析结果
Fig.2 Initial analysis results of hoist tower
为降低提升系统的制造和运输成本，需在保证最大应力不变的条件下，以主支撑架的主立柱截面宽度W1L、横柱长度D1及横柱截面宽度W1D、斜支撑截面宽度W1XZ和斜支撑架的主立柱截面宽度W2L、横柱长度D2及横柱截面宽度W2D、斜支撑截面宽度W2XZ以及主支撑架与斜支撑架之间的夹角θ为设计变量，以提升塔架的总质量为优化目标进行多参数带约束优化设计。
2 全局敏感性分析
全局敏感性分析是指分析各参数的变化对输出变量影响的敏感程度，通过全局敏感性分析可进行各参数敏感性排序，将非敏感参数设为固定值可降低优化问题的维度，以简化优化问题[7]。
2.1 Sobol指数法
基于方差的Sobol指数法是一种定量的全局敏感性分析方法[8]，其基本思想是将模型分解为单个参数和任意两个参数组合的函数，通过计算单个参数方差和任意两个参数组合的方差对总方差的影响来确定参数的总体敏感程度与参数之间的相互影响程度。通常，结构优化问题中设计变量和目标函数之间的具体函数关系未知，需采用基于蒙特卡罗方法的Sobol指数法进行全局敏感性分析。
假设设计空间参数个数为m，通过拉丁超立方试验设计在设计空间内取样两次，每次抽取n个样本点，并得到A、B两个样本矩阵：
(1)
(2)
用矩阵B的第i列替换矩阵A的第i列，得到矩阵Ci；用矩阵A的第i列替换矩阵B的第i列，得到矩阵Di，其表达式分别如下：
(3)
(4)
将矩阵中每组设计参数代入仿真模型中进行仿真分析，从而得到相应响应值，并可通过如下公式计算得到各参数敏感性指标：
(5)
f(x′k1,x′k2,…,x′k(i-1),xki,x′k(i+1),…,x′km)
(6)
f(xk1,xk2,…,xk(i-1),x′ki,xk(i+1),…,xkm)
(7)
式中，f(·)为仿真模型的响应值；
为总方差；
为偏方差。
则设计空间参数xi的主效应指标可表示为
(8)
设计空间参数xi的全效应指标可表示为
(9)
其中，主效应指标
反映了变量xi单独对输出的影响程度，全效应指标
反映了变量xi对输出的总体影响程度以及变量xi与其他变量交互作用对输出的总体影响程度。
2.2 敏感性指标求解
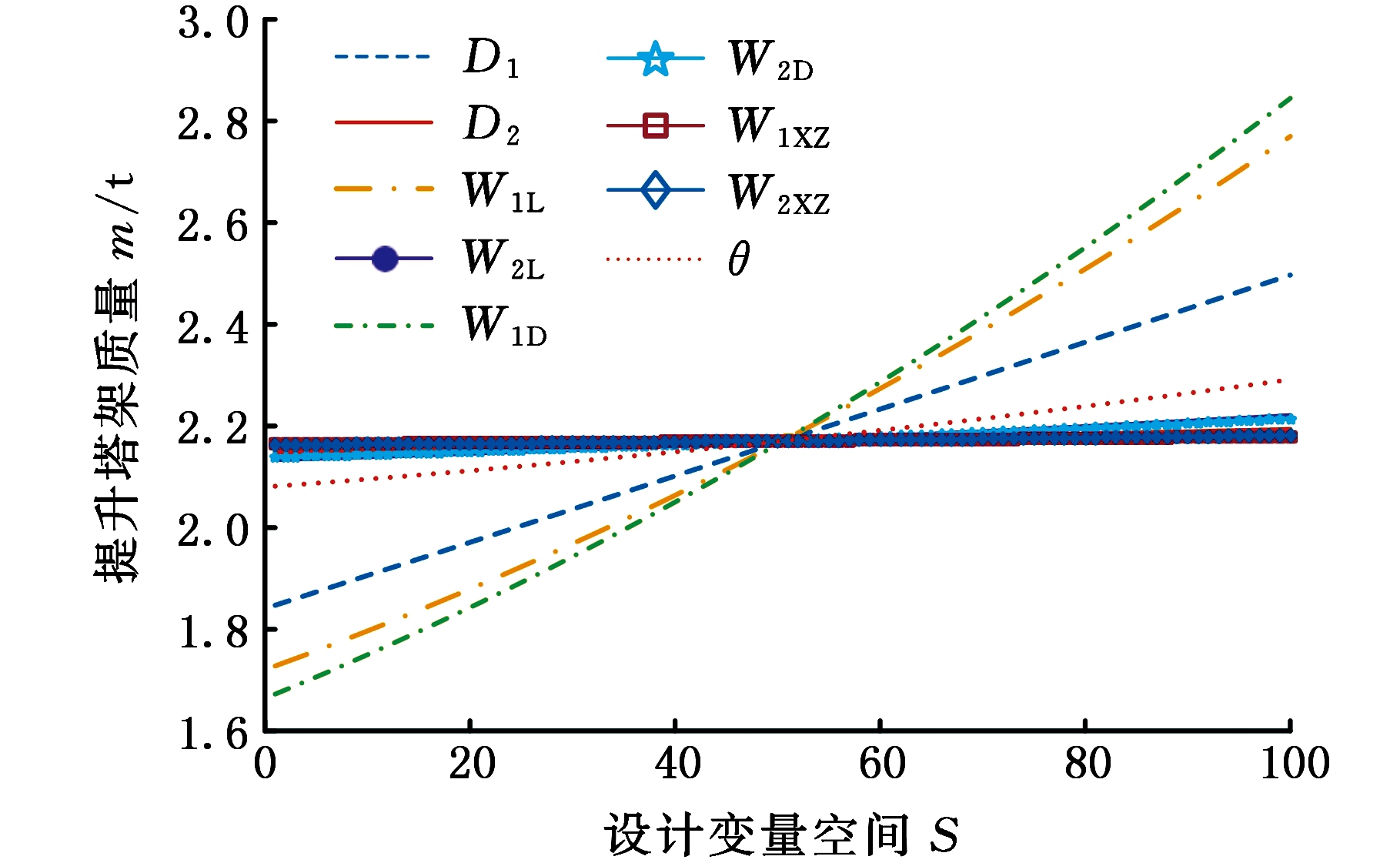
选取设计变量初始值的-30%～30%作为初始设计空间，通过拉丁超立方试验设计得到参数敏感性分析样本数据，利用ANSYS软件仿真分析得到相应响应值，并代入式(8)、式(9)，从而得到各参数敏感性指标，见表1，相应的主效应图为图3。
由全局敏感性指标计算结果和主效应图可知，参数W1D、W1L、D1和θ的敏感性较强，可选取上述4个参数作为后续优化的设计变量。这将降低优化问题的维数，使优化问题得以简化，优化效率得以提高。
表1 全局敏感性指标计算结果
Tab.1 Caculation results of global sensitivity indices
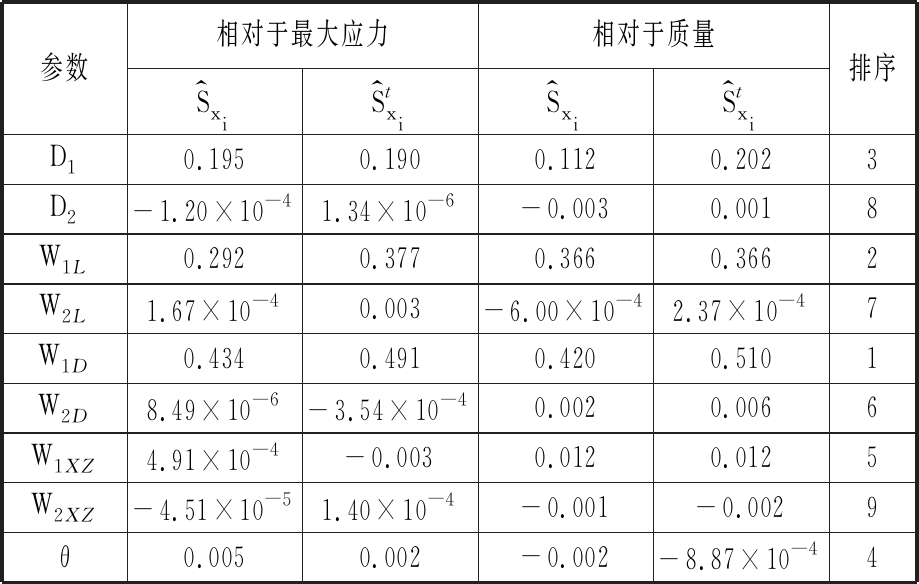
参数相对于最大应力相对于质量S^xiS^txiS^xiS^txi排序D10.1950.1900.1120.2023D2-1.20×10-41.34×10-6-0.0030.0018W1L0.2920.3770.3660.3662W2L1.67×10-40.003-6.00×10-42.37×10-47W1D0.4340.4910.4200.5101W2D8.49×10-6-3.54×10-40.0020.0066W1XZ4.91×10-4-0.0030.0120.0125W2XZ-4.51×10-51.40×10-4-0.001-0.0029θ0.0050.002-0.002-8.87×10-44
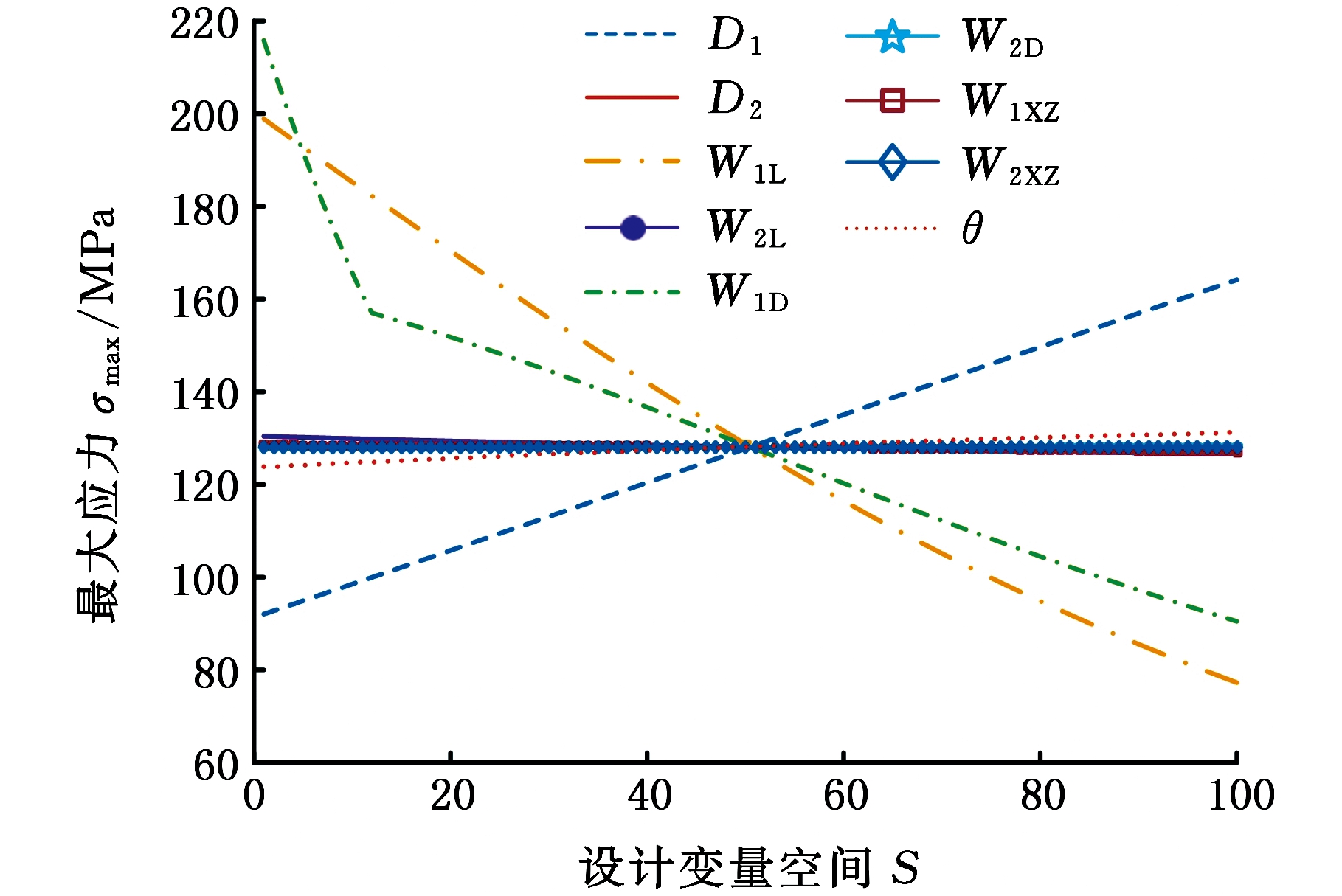
(a)相对于最大应力
(b)相对于质量
图3 主效应图
Fig.3 Graph of main effect
3 基于双加点动态Kriging模型和人工蜂群算法的提升塔架优化设计
3.1 双加点动态Kriging模型
Kriging代理模型的数学表达式如下：
(10)
其中，β为回归系数，ft(x)β表示回归模型，是一个确定成分，通常用多项式表示，是全局近似的模拟；z(x)表示一个随机过程，是局部偏差近似的模拟，z(x)满足如下统计特征：
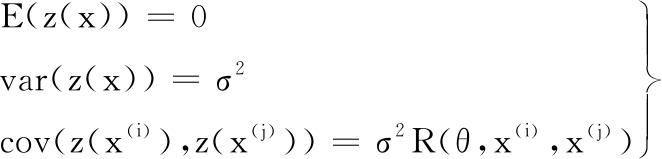
(11)
式中，E为期望；var表示方差；cov表示协方差；σ为标准差；R(θ,x(i),x(j))表示以θ为参数的样本点x(i)与x(j)之间的相关函数。
基于样本点建立Kriging模型时，使真实值和估计值之间的估计方差最小，即可得到具有无偏估计和最小估计方差的Kriging模型，进而得到设计空间任意一点的响应值和相应估计方差。
通常，由初始样本点建立得到的静态Kriging模型的全局精度较低，最优解处的局部精度更加难以得到保证。针对这一问题，本文提出了一种基于双加点准则的动态Kriging模型。双加点准则的表述如下：在每次优化迭代时分别判断最优解和预测误差最大值处的样本点是否与样本空间中的样本点重复，若两点均重复则此次迭代放弃向样本空间加点，否则就将相应点加入到样本空间中，并调用ANSYS仿真程序计算新加入的样本点处的真实响应值，从而形成新的样本空间，并重建Kriging模型。
优化过程中，采用双加点更新准则对初始Kriging模型进行多次动态更新，从而可得到全局精度、局部精度和最优解处局部精度均有大幅提高的双加点动态Kriging模型。
3.2 基于双加点动态Kriging模型和人工蜂群算法的提升塔架优化流程
结合双加点动态Kriging模型和人工蜂群优化算法，对大型结构物提升系统中的提升塔架进行了优化设计，其总体优化流程见图4。
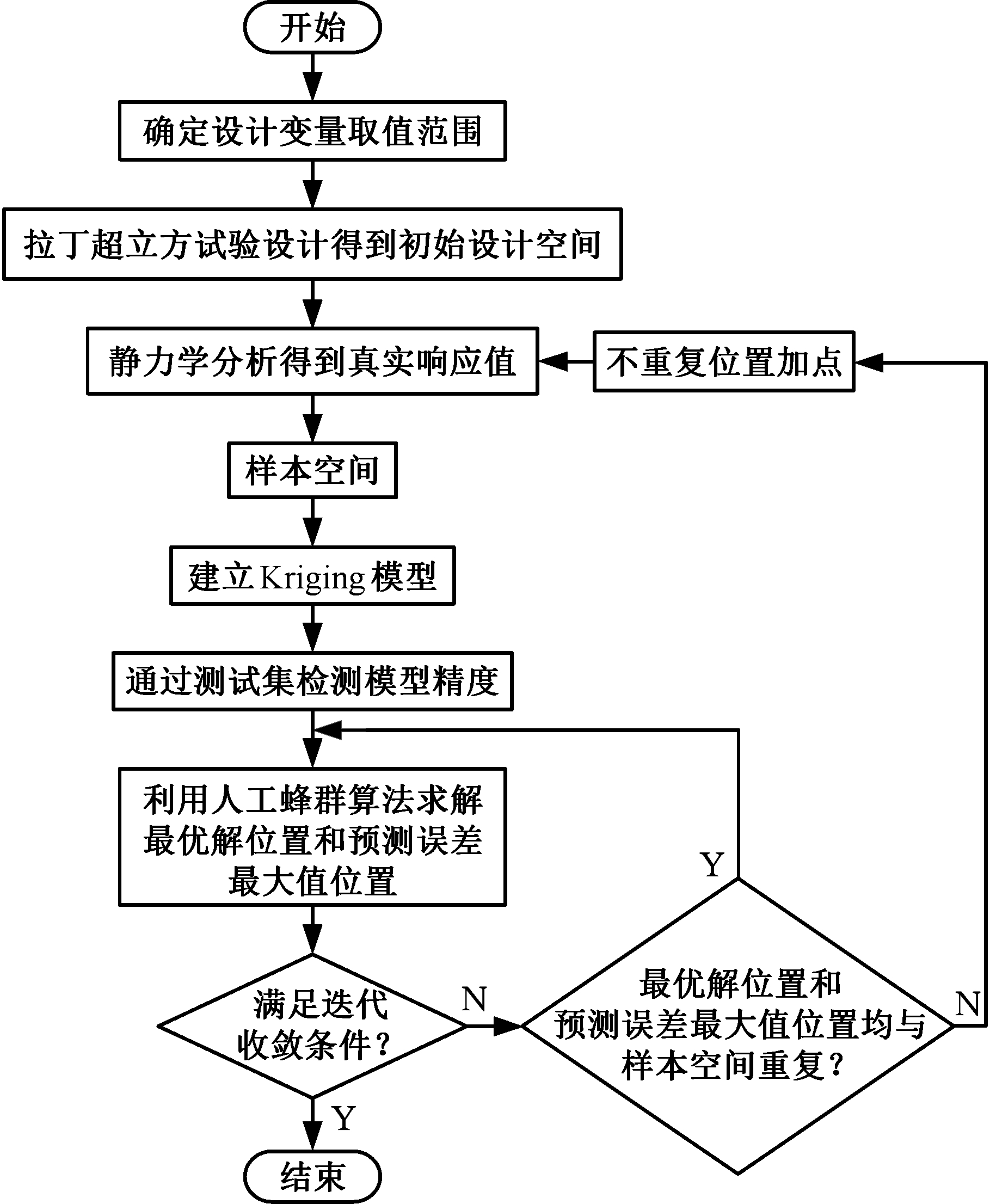
图4 提升塔架总体优化流程图
Fig.4 Optimization flow chart of hoist tower
3.2.1 确定设计变量取值范围和优化模型
根据全局敏感性分析结果，将参数D1、W1L、W1D和θ作为提升塔架优化设计的设计变量，各参数的取值范围见表2。
表2 设计变量取值范围
Tab.2 Range of design variables
参数D1(mm)W1L(mm)W1D(mm)θ(rad)上限3 2503903900.68下限1 7502102100.37
以提升塔架的质量m为优化目标函数，最大应力σmax为约束条件，从而可得到提升塔架优化数学模型：
(12)
3.2.2 建立初始Kriging模型
在设计空间内，基于拉丁超立方试验设计进行了30次抽样，并利用MATLAB软件中的DACE工具箱，选取二次多项式模型作为回归模型，选取高斯函数作为相关模型，建立了4个设计变量分别与最大应力、质量之间的Kriging模型，并得到了初始Kriging模型和精度，见表3。
表3 初始Kriging模型和精度
Tab.3 Initial Kriging model and its accuracy
Kriging模型参数R2εRMAσmaxθ=(0.248,1.403,1.984,0.035)β=(-0.264,0.442,-0.535,-0.713,-0.050,-0.019,-0.131,-0.117,0.021,0.162,0.111,-0.030,0.136,0.089,2×10-4)Tγ=(-0.160,0.025,0.060,0.026,0.506,0.340,-0.218,-0.231,-0.248,-0.653,0.252,-0.006,0.233,-0.237,-0.244,-0.169,-0.013,-0.061,0.111,0.084,0.000 5,0.316,-0.031,0.158,0.179,-0.064,-0.046,0.125,-0.131,0.094)0.859 740.998 23mθ=(0.503,0.100,17.690,2.473)β=(-0.101,0.391,0.650,0.727,0.010,-0.006,4.312×10-5,0.124,-0.011,0.059,0.002,0.004,0.064,0.002,0.002)Tγ=(0.016,-8×10-4,-0.011,-0.006,-0.004,-7×10-4,7×10-4,-0.006,1×10-4,-0.002,-4×10-4,-0.007,0.009,0.001,0.013,0.004,0.010,-0.012,-0.002,-0.002,-0.009,0.004,-0.002,-3×10-4,-0.002,-0.006,0.012,-0.001,-0.002,-0.006)0.872 160.479 41
通过测试集检验建立的模型精度，将复相关系数R2作为模型全局精度评价指标，相对最大绝对误差εRMA作为模型局部精度评价指标。R2越接近于1表明模型全局精度越高，εRMA越接近于0表明模型局部精度越高[9]。R2和εRMA的计算表达式分别如下：
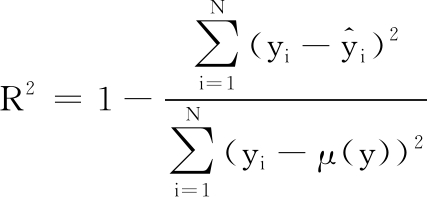
(13)
(14)
式中，yi为测试集的真实响应值;
为测试集的代理模型预测值;μ(y)为测试集的均值;σ(y)为测试集的标准差;N为测试集样本数量。
3.2.3 利用人工蜂群算法优化求解
(1)通过拉丁超立方试验设计初始化蜜源位置(蜂群大小为200，蜜源数为100)，并得到分布相对均匀的蜜源。
(2)通过初始Kriging模型预测各蜜源位置的目标函数值，记录预测误差，计算相应适应度值，分别得到目标函数值矩阵、预测误差矩阵和适应度矩阵。适应度计算表达式如下：
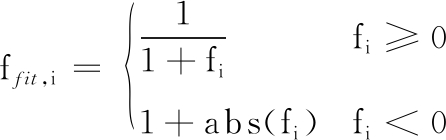
(15)
式中，fi为第i个蜜源处的模型预测值；ffit,i为第i个蜜源的适应度值；abs(fi)为fi的绝对值。
(3)雇佣蜂阶段。在各蜜源附近搜索新蜜源，其表达式如下：
vij=xij+Rand(xij-xkj)
(16)
式中，vij为新蜜源；j为均匀分布的随机整数，表示参数序号；xkj为随机选择不与xij重复的蜜源,k为不同于i的随机选择指数；Rand(·)为[-1,1]之间的随机数。
利用初始Kriging模型预测新蜜源位置目标函数值，记录预测误差，并计算相应适应度值。依据Deb规则[4]判断新蜜源是否优于原蜜源，Deb规则表述如下：①可行解优于不可行解；②可行解中适应度大的解优于适应度小的解；③不可行解中约束背离值小的解优于约束背离值大的解。其中，不可行解的约束背离值为最大应力响应值与允许的最大应力值之差。
若新蜜源优于原蜜源，则替换原蜜源，并更新相应目标函数值矩阵、预测误差矩阵和适应度矩阵。
计算蜜源变异概率，其计算表达式如下：
(17)
式中，N是蜜源个数；viol,i为第i个蜜源的约束背离值。
(4)观察蜂阶段。对于任意一个蜜源i，观察蜂有概率Pi在其附近，利用式(16)找到一个新蜜源，通过Deb规则选择蜜源，若新蜜源优于原蜜源，则替换原蜜源，并更新相应目标函数值矩阵、预测误差矩阵和适应度矩阵。
(5)侦查蜂阶段。超过限制次数(限制次数为 100)而没发生变异的蜜源对应的雇佣蜂变为侦查蜂，并在设计空间中依据下式随机产生一个新蜜源：
(18)
式中，
为超过限制次数(限制次数为 100)而没发生变异的蜜源i的第j个参数；
分别为第j个参数对应的上限和下限。
通过Kriging模型预测新蜜源位置的目标函数值，记录预测误差，计算相应适应度值，并更新相应目标函数值矩阵、预测误差矩阵和适应度矩阵。
(6)基于上文所提出的双加点准则重建Kriging模型。
(7)不断重复步骤(3)～步骤(6)，直到获得最优解。
3.3 优化结果对比分析
经过783次迭代、152次基于双加点准则的动态加点后，共计182个样本点，并得到了如下最优解：D1=1 750 mm、W1L=279.64 mm、W1D=225.66 mm、θ=0.37 rad、σmax=128.19 MPa、m=13 162 kg，最终Kriging模型和精度见表4。
在最大应力不变的条件下，优化后的提升塔架质量减小了39.37%。由表3和表4中优化前后的Kriging模型精度可知，经过基于双加点准则的动态迭代更新后，最大应力Kriging模型的全局精度提高了14.35%、局部精度提高了31.26%；质量Kriging模型全局精度提高了14.66%，局部精度提高了34.98%。
为更好地体现基于双加点动态Kriging模型优化方法的有效性和优势，将基于双加点动态Kriging模型优化得到的优化结果与初始设计、仿真模型的优化结果、基于静态Kriging模型的优化结果、分别基于MP加点准则和EI加点准则的动态Kriging模型优化结果进行综合对比，得到的对比结果见表5。其中，
分别为基于Kriging模型的最大应力和质量的预测值；σmax、m分别为基于ANSYS仿真分析的最大应力和质量的真实响应值；Eσmax、Em分别为最大应力和质量在最优解处Kriging模型预测值相对真实响应值的误差，计算表达式如下：
表4 最终Kriging模型和精度
Tab.4 Final Kriging model and its accuracy
Kriging模型参数R2εRMAσmaxθ=(0.062,17.818,3.969,0.078)β=(-0.431,0.606,-0.856,-0.965,0.035,0.015,-0.103,-0.182,0.019,0.242,0.131,-0.034,0.351,-0.008,-0.004)Tγ1×182=(0.385,0.078,0.154,0.026,0.103,0.020,-0.815,0.061,0.185,0.063,0.511,-0.229,0.212,0.153,…,-0.060,-58.031,-0.609,-0.147,0.779,-0.053,-0.811,-0.447,-2.840,-30.063,-1.227,-0.125)0.983 130.686 16mθ=(0.590,0.100,19.713,0.100)β=(-0.133,0.393,0.704,0.641,0.009,-1.84×10-4,5.88×10-5,0.126,-6.1×10-4,0.063,7.04×10-4,1.95×10-4,0.058,5×10-4,0.001)Tγ1×182=(0.005,0.012,-0.010,-0.035,0.015,-0.001,-0.007,-0.001,0.002,-0.024,-0.005,-0.016,-0.003,-0.003,…,-0.397,0.375,0.004,-0.208,-0.004,-0.008,-5.79×10-4,0.004,0.048,0.025,-0.003,0.090,-0.092,-0.012)0.999 980.311 72
(19)
式中，
为最优解处Kriging模型预测值；ybest为最优解处利用仿真模型计算得到的真实响应值。
由表5可知，所有基于Kriging模型的优化效率相较于仿真模型的优化效率，均有大幅度提高；双加点动态Kriging模型相较于相同样本数的静态Kriging模型，其最大应力Kriging模型的全局精度提高了5.55%、局部精度提高了14.62%，质量Kriging模型的全局精度提高了5.58%、局部精度提高了19.56%，最大应力Kriging模型和质量Kriging模型在最优解处模型预测值相对真实响应值的误差明显减小；双加点动态Kriging模型相较于基于MP加点准则和EI加点准则的动态Kriging模型，其全局精度、局部精度和最优解处局部精度均得到了一定改善。
表5 优化结果对比
Tab.6 Comparison of optimized results
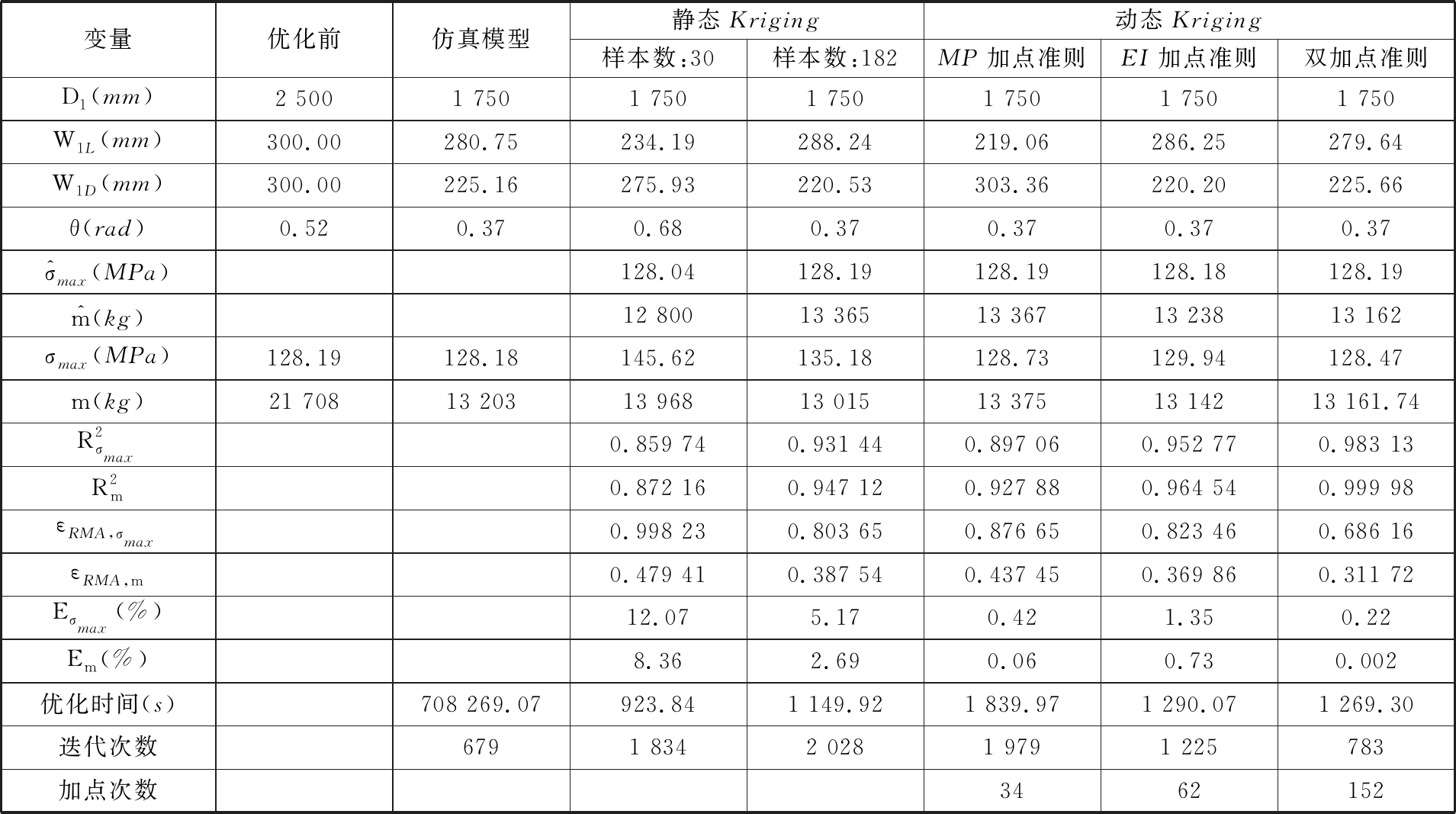
变量优化前仿真模型静态Kriging动态Kriging样本数:30样本数:182MP加点准则EI加点准则双加点准则D1(mm)2 5001 7501 7501 7501 7501 7501 750W1L(mm)300.00280.75234.19288.24219.06286.25279.64W1D(mm)300.00225.16275.93220.53303.36220.20225.66θ(rad)0.520.370.680.370.370.370.37^σmax(MPa)128.04128.19128.19128.18128.19^m(kg)12 80013 36513 36713 23813 162σmax(MPa)128.19128.18145.62135.18128.73129.94128.47m(kg)21 70813 20313 96813 01513 37513 14213 161.74R2σmax0.859 740.931 440.897 060.952 770.983 13R2m0.872 160.947 120.927 880.964 540.999 98εRMA,σmax0.998 230.803 650.876 650.823 460.686 16εRMA,m0.479 410.387 540.437 450.369 860.311 72Eσmax(%)12.075.170.421.350.22Em(%)8.362.690.060.730.002优化时间(s)708 269.07923.841 149.921 839.971 290.071 269.30迭代次数6791 8342 0281 9791 225783加点次数3462152
4 结论
(1)通过基于方差的Sobol指数法进行了全局敏感性分析，设计变量个数由9个减少为4个，降低了优化问题维数，优化问题得以简化,优化效率得以提高。
(2)优化后，最大应力为128.19 MPa、提升塔架质量为1316 2 kg，在最大应力不变的条件下，提升塔架质量减小了39.37%。
(3)基于双加点动态Kriging模型相较于仿真模型，优化设计效率得到大幅提高。
(4)双加点动态Kriging模型相较于静态Kriging模型、基于MP加点准则和EI加点准则的动态Kriging模型，具有更高的全局精度、局部精度和最优解处局部精度。
[1] 陈立娜, 张维刚. 基于Kriging模型的发动机罩多目标优化设计[J]. 中国机械工程, 2013, 24(22)：3014-3018.
CHEN Lina, ZHANG Weigang. Multi-objective Optimization Design of Engine Hood Based on Kriging Model[J]. China Mechanical Engineering, 2013, 24(22)：3014-3018.
[2] 何东海. Kriging代理模型的序列优化及其应用[D]. 上海：华东理工大学, 2015.
HE Donghai. Sequential Optimization Method Based on Kriging Surrogate Model and Its Application[D]. Shanghai：East China University of Science and Technology, 2015.
[3] JONES D R, SCHONLAU M, WELCH W J. Efficient Global Optimization of Expensive Black-box Functions[J]. Journal of Global Optimization, 1998, 13:445-492.
[4] KARABOGA D. An Idea Based on Honey Bee Swarm for Numerical Optimization[R]. Kaiseri：Erciyes University, 2005.
[5] KARABOGA D, AKAY B. A Modified Artificial Bee Colony (ABC) Algorithm for Constrained Optimization Problems[J]. Applied Soft Computing, 2011, 11：3021-3031.
[6] 罗钧, 林于晴, 刘学明, 等. 改进蜂群算法及其在圆度误差评定中的应用[J]. 机械工程学报, 2016, 52(16)：27-32.
LUO Jun, LIN Yuqing, LIU Xueming, et al. Research on Roundness Error Evaluation Based on the Improved Artificial Bee Colony Algorithm[J]. Journal of Mechanical Engineering, 2016, 52(16)：27-32.
[7] 唐皓, 段吉安, 郑煜, 等. 平面光波导精密对准平台运动误差的敏感性分析[J]. 中国机械工程, 2012, 23(8)：888-892.
TANG Hao, DUAN Ji’an, ZHENG Yu, et al. Motion Error Sensitivity Analysis of Planar Optical Waveguide Precise Aligning Stage[J]. China Mechanical Engineering, 2012, 23(8)：888-892.
[8] SOBOL I M. On Sensitivity Estimation for Nonlinear Mathematical Models[J]. Mathmaticheskoe Modelirovanie, 1990, 2(1)：112-118.
[9] 高云凯, 张朋, 吴锦妍, 等. 基于Kriging模型的大客车侧翻安全性多目标优化[J]. 同济大学学报(自然科学版), 2012, 40(12)：1882-1887.
GAO Yunkai, ZHANG Peng, WU Jinyan, et al. Multi-objective Optimization for Bus Rollover Safety Based on Kriging Model[J]. Journal of Tongji University (Natural Science), 2012, 40(12)：1882-1887.
