0 引言
计算机辅助工艺规划(computer aided process planning,CAPP)是计算机辅助制造(computer aided manufacturing,CAM)和计算机辅助设计(computer aided design,CAD)之间的桥梁[1]。装夹规划作为计算机辅助工艺规划的重要组成部分,包括以下几个重要功能:确定零件的加工特征及其分组排序,识别加工基准面和规划装夹所需的各个夹具等。装夹规划的优劣决定着零件的可加工性和加工质量,同时也关系到制造成本。但因为装夹规划本身的多因性及制造资源所具有的多样性,使得装夹规划问题具有一定的复杂性和特殊性[2]。
为了解决加工制造中的装夹规划问题,传统方法有很多,如基于图论的方法[3-4]、基于聚类分析的方法[5]等。同时,一些研究者提出运用现代智能优化算法来解决该问题,其中包括遗传算法[6-7]、粒子群算法[8]、蚁群算法[9-10]和模拟退火算法[11]等。但上述智能优化方法存在一定的局限性,如多以加工特征为主要着手点,但对制造资源间的各种约束考虑欠妥,可能存在加工顺序冲突问题;有些方法对加工特征中的加工阶段(精、粗加工等)缺乏考虑。同时,上述方法在寻求最优装夹方案的效率上不是很高,在加工资源的利用优化方面仍有改进的地方。
针对上述问题,本文在考虑装夹的可行性和连续性的前提下,提出一种基于智能水滴(intelligent water drops,IWD)算法的装夹规划方法。通过定义操作单元和构建装夹约束矩阵,利用智能水滴算法的全局搜索能力,将独特的迭代机制与装夹规划相结合来寻求较好的规划方案。
1 装夹序列规划问题的相关描述
1.1 操作单元的定义
针对加工工序较为复杂、生产批量较大的零部件,在装夹规划中,需要对这些零件不同的加工特征(如孔、槽、平面、台阶和型腔等)进行分析,结合机床和刀具等所需的加工资源,以及刀具接近方向等装夹特征,将各个加工特征拆解为加工操作单元,通过对这些操作单元进行分组来形成合理的加工次序,以此来构建零部件加工的工序及工步。
操作单元由加工阶段、备选机床、刀具接近方向以及备选刀具构成,其表达形式如下:
ui={O,M,D,T}
(1)
u={u1,u2,…,uk}
i=1,2,…,k
其中,ui表示不同的操作单元,k为操作单元的个数,O表示加工特征的各个精粗加工阶段,M表示备选机床,D表示加工特征中刀具的接近方向,T表示备选刀具。
1.2 操作单元的约束关系
装夹规划中,各操作单元之间的加工先后排序受到定位基准、几何特征、生产成本等因素的约束。同时,操作单元的排序也受到待加工零件的精度要求的影响,如精加工过程中的操作单元需放在粗加工及半精加工的后面。
综合上述约束条件,为保证装夹顺序的合理性,可构建一个n阶方阵M来表示操作单元间的顺序约束关系:
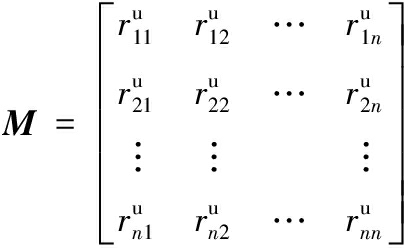
(2)
其中,![]() 为第i个操作单元ui与第j个操作单元uj是否存在优先关系的判断因子。如果第i个操作单元ui优先于第j个操作单元uj进行加工,则
为第i个操作单元ui与第j个操作单元uj是否存在优先关系的判断因子。如果第i个操作单元ui优先于第j个操作单元uj进行加工,则![]() 反之
反之![]() 如果第i个操作单元与第j个操作单元不存在优先关系约束,则
如果第i个操作单元与第j个操作单元不存在优先关系约束,则![]()
1.3 装夹序列规划的数学模型
装夹规划问题是一个典型的NP组合优化问题,通过对操作单元的分组,以实现获得最少的装夹次数以及相同加工特征尽可能分配在一次加工的目的。
假定{u1,u2,…,uk}为待加工零件的操作单元。设第m次规划后所产生的结果为集合Sm={Sm,1,Sm,2,…,Sm,n},其中n为零件的装夹次数,则装夹规划问题的目标函数如下:
f(Sm)=min n
(3)
同时,各操作单元满足以下约束条件:
u1(M)∩u2(M)∩…∩ui(M)≠Ø,∀ui∈Sm,n
(4)
u1(D)∪u2(D)∪…∪ui(D)⊆{D},∀ui∈Sm,n
(5)
(6)
式(4)表示不同操作单元可以选取同一个机床;式(5)表示所有操作单元的刀具接近方向(tool approach direction,TAD)需从刀具接近方向的集合中选取;式(6)表示各个操作单元需符合加工顺序约束条件。
2 基于智能水滴算法的装夹规划方法
2.1 智能水滴算法的基本原理
在物理界中,河流可以视为由无数个小水滴所构成,各个水滴在地球引力的作用下会持续地流动。水滴在流动过程中会改变河床,同时河床也会影响到水滴的流动[12]。在自然界中水滴所具有的特征包括:①水滴在流动过程中会冲刷掉河床中的部分泥土;②河床中被冲刷掉的泥土量与水滴的流动速度成正比;③流经路径中的泥土量越少,则水滴在该路径间获得的速度增量就越大;④水滴在面临流动路径选择时,选取泥土量更少的路径概率会更大[13]。
利用上述的水滴特征来构建虚拟模型,即基于智能水滴(IWD)算法的装夹规划方法。该方法基于水滴的流动速度和所包含的泥土量这两个重要特征,用s(IWD)表示水滴中包含的泥土量,用v(IWD)表示水滴的流动速度。在自然界中,液体的流动过程是连续不断的,但是智能水滴在移动过程中的环境假定为离散的。该环境假定由Nc个节点构成,需要从一个节点流到另一个节点。当水滴k从节点i流到下一个节点j时,这两节点间的路径上的泥土量用s(i, j)表示,同时水滴的速度会发生变化,用Δv(k)(i,j)来表示其速度增量。其中,s(i, j)和Δv(k)(i,j)存在反比的关系,其表达式如下:
(7)
式中,av、bv、cv为针对所给问题设置的恒定速度参数,均取正值;α为自定义参数,也取正值。
具有流动速度v(k)的智能水滴k从节点i流到节点j的同时,从两节点间路径上获得的泥土量也相应地增加,节点间路径上的泥土量s(i, j)相应地减少,即
s(i,j)=ρ0s(i,j)-ρnΔs(i,j)
(8)
其中,ρ0和ρn为根据所给问题从0~1之间选取的正数,在装夹规划问题中,ρ0=1-ρn。Δs(i,j)为泥土增量,其表达式如下:
(9)
其中,as、bs、cs和θ均为用户自定义的恒定参数,均取正值;t(i,j;v(k))为具有速度v(k)的智能水滴k从节点i流到节点j所花费的时间,其表达式如下:
(10)
式中,H(i, j)为根据所给问题定义的局部反向启发函数,表示智能水滴不愿选择从节点i流向节点j的程度。
2.2 基于智能水滴算法的装夹规划问题
为使智能水滴算法能够合理地解决装夹规划问题,结合智能水滴算法的定义,将待加工零件的各个操作单元设为智能水滴算法的每个节点。这样,水滴流经k个节点的路径即为某个零件拥有k个操作单元的装夹序列。图1所示为一个具体的通过智能水滴算法获得的操作单元的装夹序列。其中,操作单位ui均取自于操作单元集合u,机床Mi均取自备选机床集合M,刀具接近方向x、y、z等均取自于刀具接近方向集合D,刀具Ti均取自于备选刀具集合T。
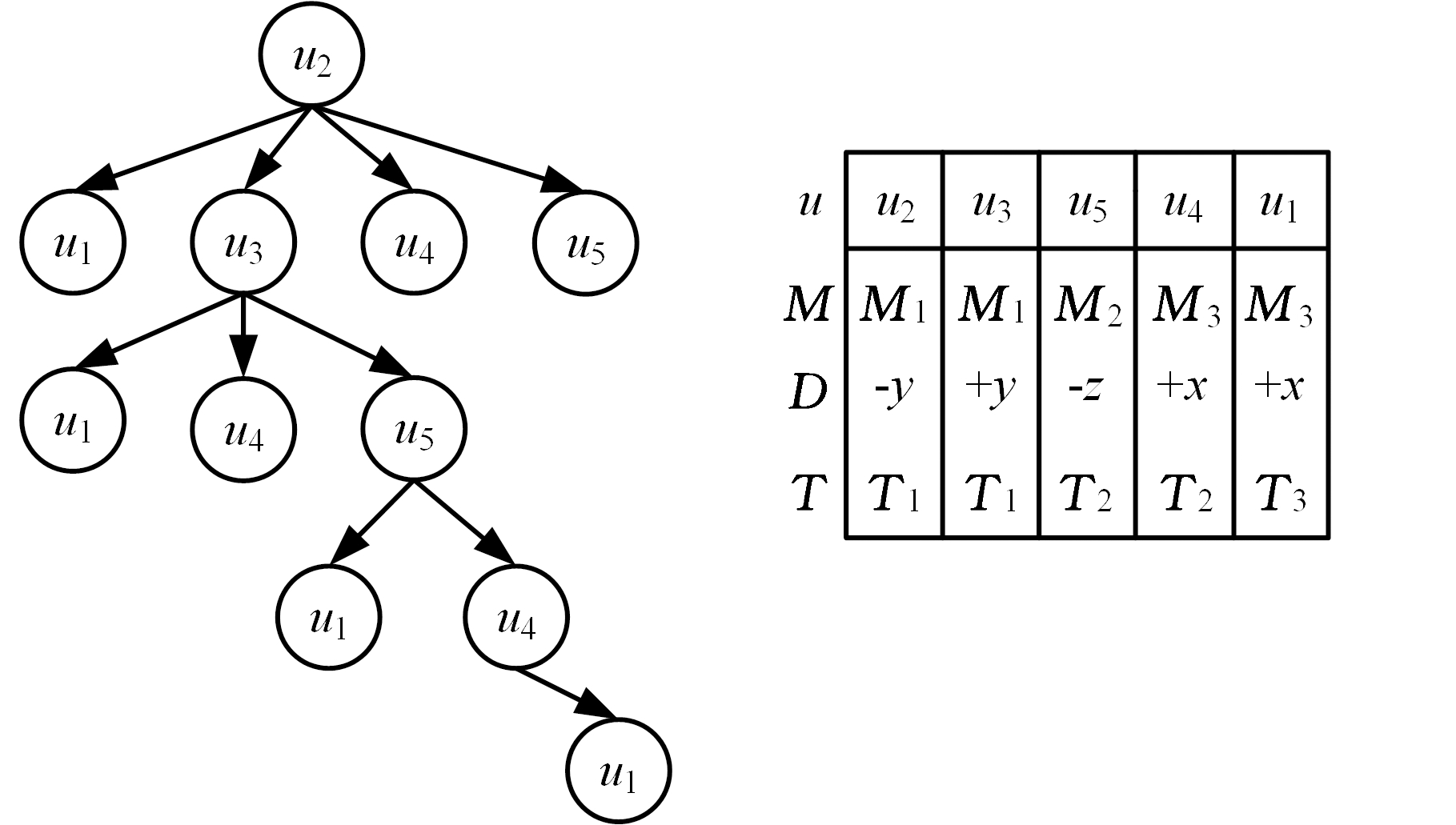
(a)水滴流经路径(b)对应路径生成的装夹序列
图1 基于智能水滴算法获得的装夹序列
Fig.1 Setup sequence obtained based o n IWD algorithm
装夹规划的优越程度由各相邻的操作单元间的相似性来决定,在满足操作单元顺序约束矩阵M的前提下,当两个操作单元具有相同的刀具接近方向、备选刀具和机床时,则它们划分到同一次装夹的概率就很大。用![]() 来表征两个操作单元间的装夹相似度,其表达式如下:
来表征两个操作单元间的装夹相似度,其表达式如下:
(11)
其中,e为各操作单元间属性值相同的变量的数量,w为各操作单位间变量的总量。即操作单元间的装夹相似度越高,划分到一次装夹的可能性越大。反之,相似度越低,划分到不同装夹分组的可能性就越大。
将智能水滴算法中节点i至节点j间路径上的泥土量s(i, j)与装夹规划中相邻的两操作单元i和j间的相似度![]() 相结合,其表达式如下:
相结合,其表达式如下:
(12)
由式(12)可以看出,两个相邻操作单元的装夹相似度越高,代表这两个操作单元的两个相邻节点间的泥土量越少。
同时,将反向启发函数H(i, j)与两节点间的泥土量s(i, j)相结合,其表达式如下:
(13)
由式(13)可知,反向启发函数H(i, j)与两节点间的泥土量s(i, j) 为正相关关系,即两节点i和j间的泥土量越多,则智能水滴越不愿从节点i流向节点j。
当智能水滴处于节点i时,从节点i流至节点j的概率为P(i,j),其表达式如下:
(14)
其中,l为水滴下一步可能选择的节点,h(s(i, j))是以节点i、j间路径中的泥土量为变量的函数,其表达式为
(15)
其中,常量εs为一个非常小的正数,以避免函数中出现分母为0的情况,这里取εs= 0.01。函数g(s(i,j))用于将节点i至节点j间路径上的泥土量转换为正值,具体如下:
g(s(i,j))=

(16)
其中,函数min(s(i,l))表示节点i与下一步可能选择的节点l之间的路径上泥土量的最小值;vc为水滴已流经过的节点集合。
2.3 基于智能水滴算法的适应度函数构造
基于智能水滴算法,将各个操作单元作为智能水滴的节点,利用节点间泥土量来表示操作单元间的相似度。由式(7)可知,两节点间的泥土量s(i,j)和智能水滴k通过下一节点后的速度增量Δv(k)(i,j)存在负相关关系,而由式(9)可知,速度增量Δv(k)(i,j)与所携带的泥土增Δs(i,j)存在正相关关系,所以,可以用智能水滴通过所有节点后最终携带的泥土量来表征装夹规划的适应度函数f:
(17)
其中,![]() 表示智能水滴k通过最后节点m所携带的泥土量,其表达式如下:
表示智能水滴k通过最后节点m所携带的泥土量,其表达式如下:
(18)
式中,s(k)为智能水滴在通过初始节点前所携带的泥土量。
综合式(17)和式(18),定义装夹规划的适应度函数:
(19)
通过智能水滴生成的每一组操作单元的序列都有其相应的适应度函数,基于适应度函数来寻求最优的装夹方案。
2.4 智能水滴算法的迭代操作
考虑用适应度函数f(ZIWD)来寻找由智能水滴算法获得的解ZIWD,即寻求操作单元的排序。在每次迭代结束时,由智能水滴寻找的迭代最优解为
(20)
其中,迭代最优解ZIB为所有解ZIWD中最终携带泥土质量最大的解。基于迭代最优解f(ZIB)的泥土质量来更新解ZIB的路径。
路径上泥土量的更新应包括一定量的质量解,具体为
s(i,j)=ρss(i,j)+ρIWDk(Nc)sIB
∀(i,j)∈ZIB
(21)
其中,sIB为迭代最优水滴的泥土量。k(Nc)为一个取决于节点数Nc的正系数,这里选取k(Nc)=1/(Nc-1)。参数ρs为一个正常数,参数ρIWD为一个负常数。
式(21)中,ρss(i,j)表示由水滴获得的当前解的质量,ρIWDk(Nc)sIB表示从上一次迭代中剩下的泥土量。因此,在式(21)中,水滴由节点i到节点j路径上从总泥土量s(i, j)中获得的泥土量的比例会减小。这样迭代最优解会不断地增强,同时会引导水滴寻找附近优秀的解,并有希望寻找到全局最优解。
算法中每次迭代完成时,总的最优解集ZTB会通过当前迭代最优解集ZIB来更新,即
(22)
如此操作可以保证ZTB拥有目前由IWD算法获得的最优解。
2.5 智能水滴算法优化装夹规划的实现步骤
智能水滴算法运用到装夹规划问题的具体步骤如下:
(1)分析加工特征。通过对待加工零件的加工特征进行分析和归类分组,将其设置为操作单元的各个变量,构建装夹信息集合。
(2)生成操作单元。基于装夹信息集合所提供的加工特征,生成各个操作单元。
(3)构建操作单元顺序约束矩阵。根据待加工零件的加工工艺和要求,记录各操作单元间的约束关系,构建操作单元顺序约束矩阵。
(4)初始化水滴静态参数。设定水滴的数量NIWD为一个正整数,水滴所要流经的节点数量Nc等于待加工零件的操作单元数量。设定水滴流动的速度更新参数av、bv、cv和泥土量的更新参数as、bs、cs,确定局部泥土量更新参数ρn,以及全局泥土量更新参数ρIWD。设定水滴的初始速度vinit,以及算法的最大迭代次数imax。
(5)更新各个水滴的信息集合。对每个水滴所经过的节点列表,将其设置为空矩阵。设定每个水滴所携带的初始泥土量s(k)为0。
(6)基于操作单元顺序约束矩阵的次序,令每个水滴随机选取节点。
(7)更新每个水滴访问过的节点列表,将已被访问过的节点依次添加进去。
(8)没有获得完整流动路径的水滴,则重复执行下列步骤:
①在符合操作单元顺序约束矩阵的前提下,从水滴未曾流经的节点列表中选取下一个需要访问的节点。根据式(14)所定义的概率P(i,j)来更新即将访问的节点。
②令式(7)中α=1。当水滴k从节点i流至j后,速度会更新,其表达式为
(23)
③根据式(9),结合式(10)和式(12),令θ=1,计算两节点间的泥土减少量Δs(i,j)。
④根据式(8),更新两节点间路径中的泥土量s(i, j),流经两节点后水滴k所携带的泥土量为
s(k)(t+1)=s(k)(t)+Δs(i,j)
(24)
(9)根据式(20),寻找迭代最优解ZIB。
(10)根据式(21),设定ρs=(1-ρIWD),更新当前迭代最优解ZIB路径中的泥土量。
(11)根据式(22),用当前迭代最优解ZIB来替代之前最优解ZTB。
(12)重复开始第(4)步,直至迭代次数达到最大。
(13)获得最终最优解ZTB即最佳的装夹方案后,终止算法。
图2所示为算法步骤的流程,图3为算法步骤(8)的具体流程。
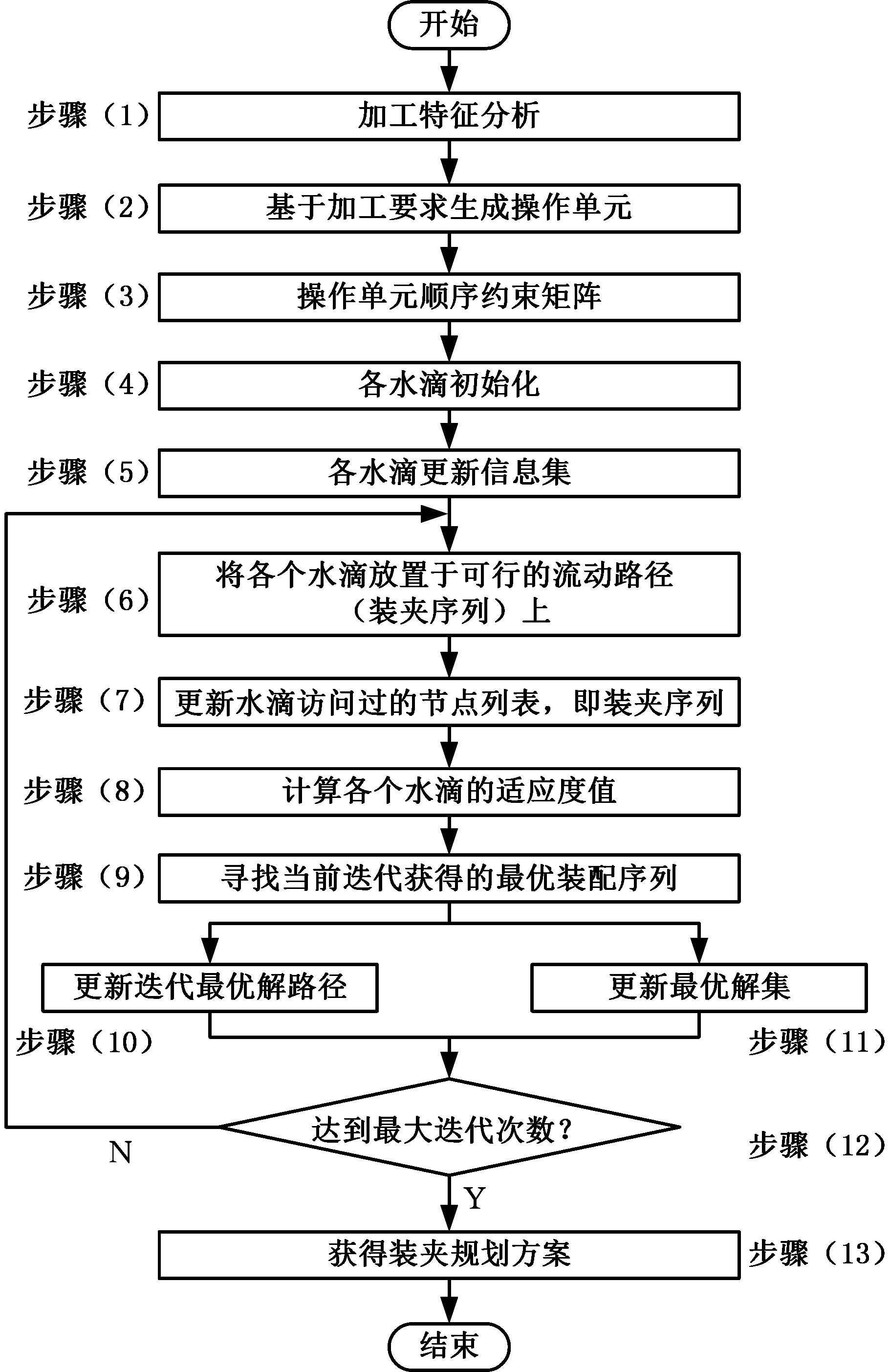
图2 利用智能水滴算法求解装夹规划的流程图
Fig.2 Flowchart for solving the setup planning b y IWD algorithm
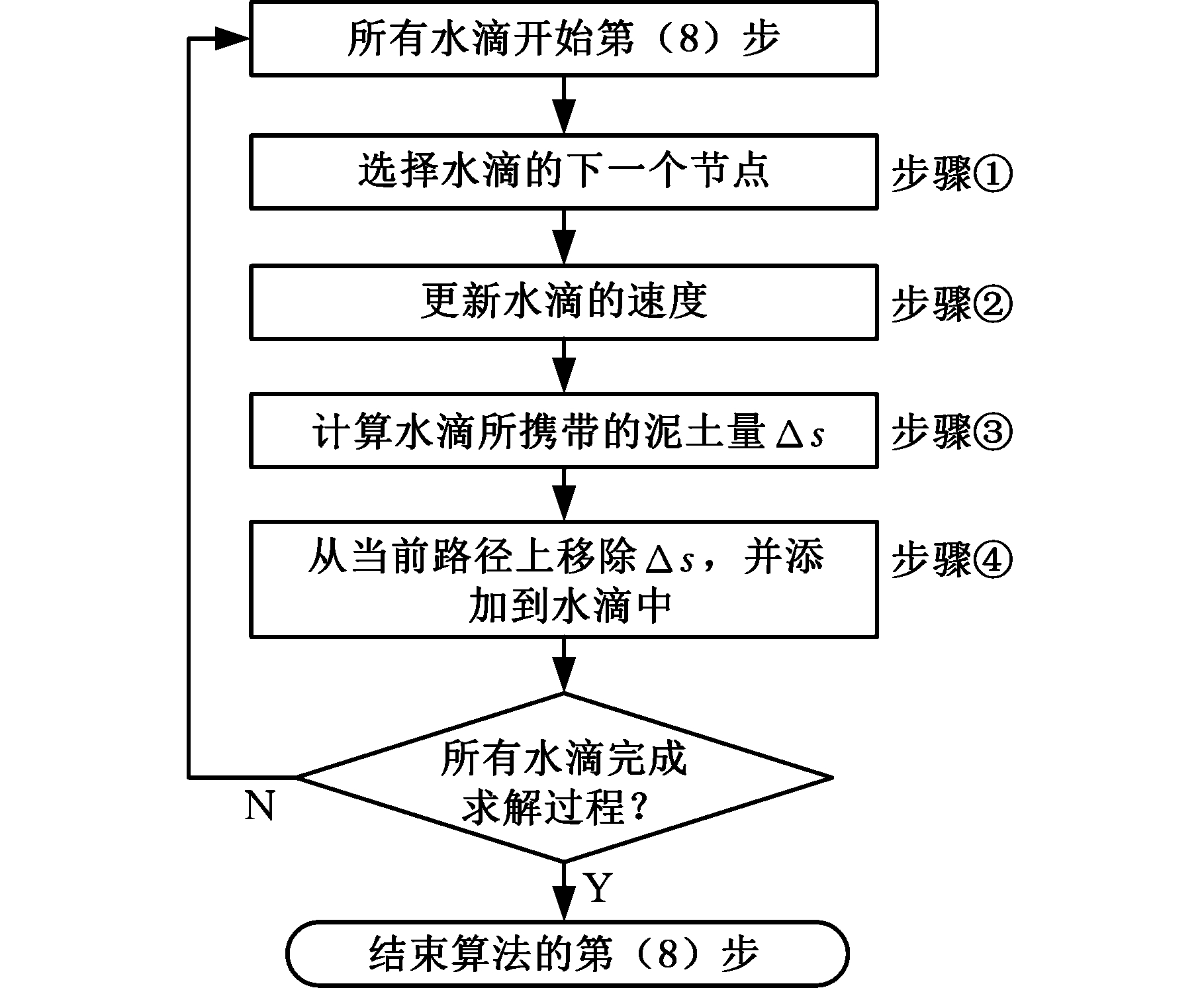
图3 智能水滴算法步骤(8)的流程图
Fig.3 Flowchart for step(8) of IWD algorithm
3 实例验证
为了验证智能水滴算法在装夹规划中的可行性及有效性,参照文献[1],本文选取图4所示的零件模型作为分析对象,将使用的刀具、刀具接近方向和功能类型相同的操作单元进行简化,使得该零件划分为14个加工特征及20个操作单元。
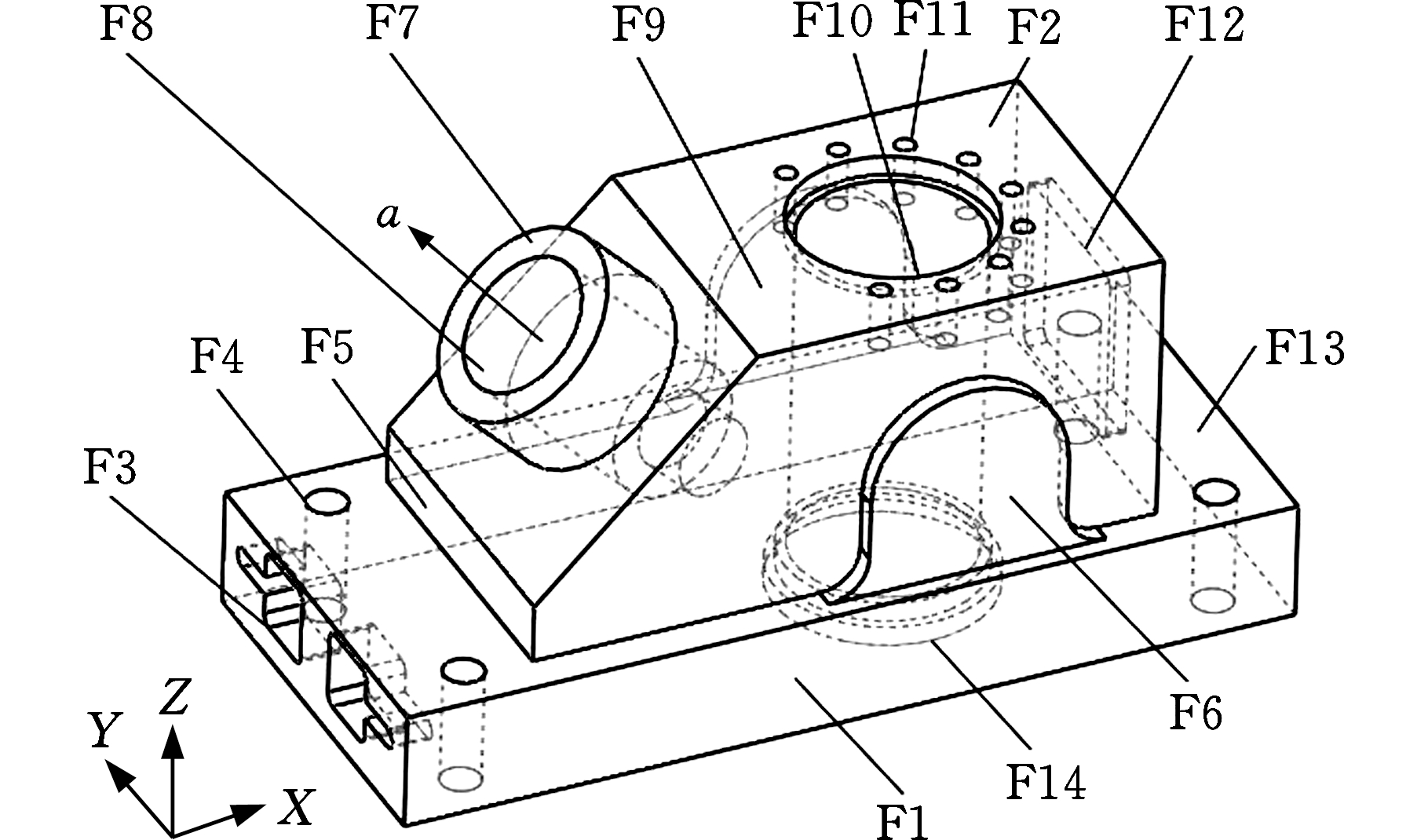
图4 零件的三维模型图
Fig.4 3D model of parts
根据零件的加工特征,细分各个不同的操作单元,将操作单元所需的机床、工具和刀具接近方向等信息汇集成加工信息集合,如表1所示。
表1 操作单元信息集
Tab.1 Feature information set of machining units
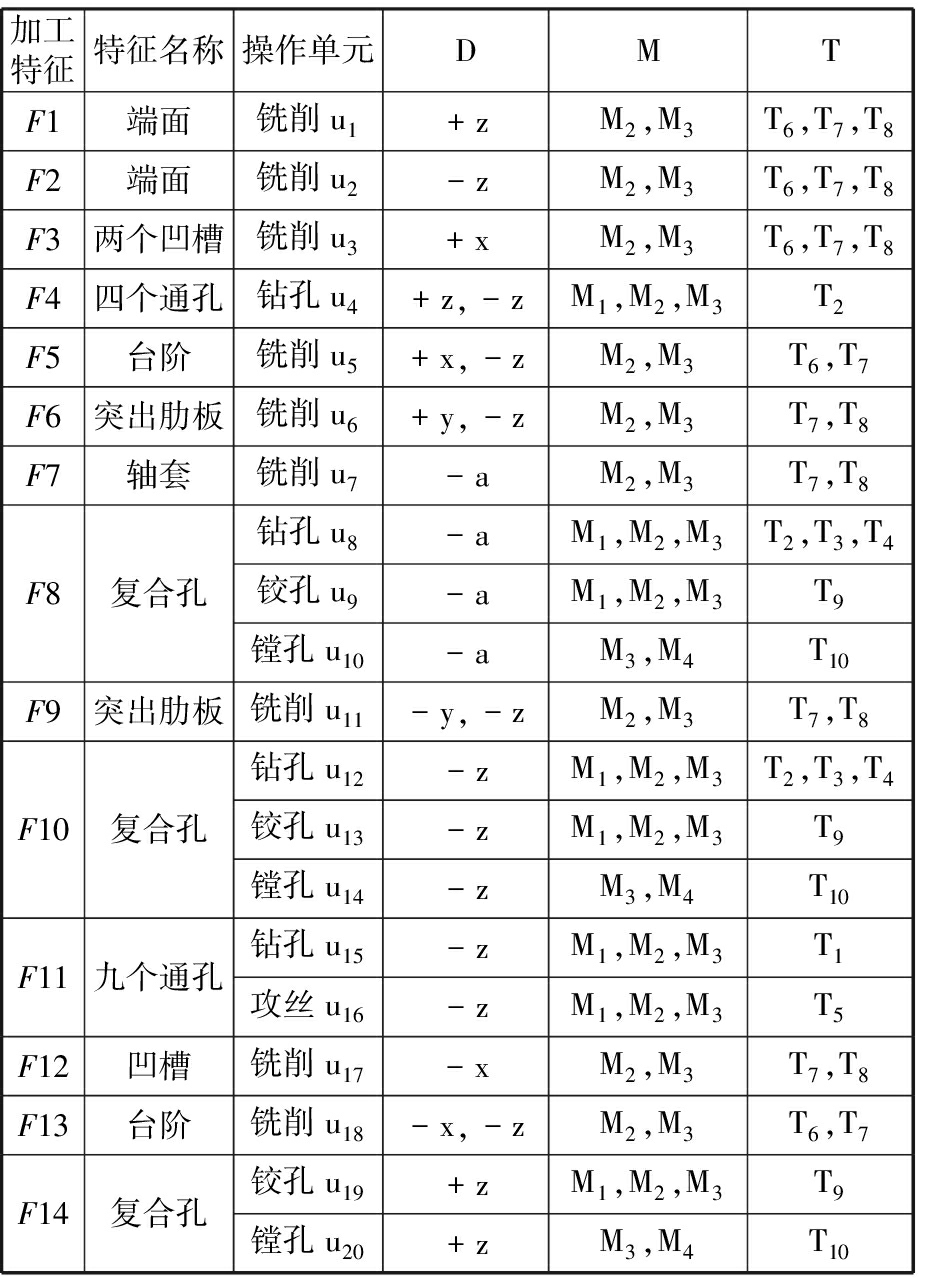
加工特征特征名称操作单元DMTF1端面铣削u1+zM2,M3T6,T7,T8F2端面铣削u2-zM2,M3T6,T7,T8F3两个凹槽铣削u3+xM2,M3T6,T7,T8F4四个通孔钻孔u4+z,-zM1,M2,M3T2F5台阶铣削u5+x,-zM2,M3T6,T7F6突出肋板铣削u6+y,-zM2,M3T7,T8F7轴套铣削u7-aM2,M3T7,T8F8复合孔钻孔u8-aM1,M2,M3T2,T3,T4铰孔u9-aM1,M2,M3T9镗孔u10-aM3,M4T10F9突出肋板铣削u11-y,-zM2,M3T7,T8F10复合孔钻孔u12-zM1,M2,M3T2,T3,T4铰孔u13-zM1,M2,M3T9镗孔u14-zM3,M4T10F11九个通孔钻孔u15-zM1,M2,M3T1攻丝u16-zM1,M2,M3T5F12凹槽铣削u17-xM2,M3T7,T8F13台阶铣削u18-x,-zM2,M3T6,T7F14复合孔铰孔u19+zM1,M2,M3T9镗孔u20+zM3,M4T10
通过对各个操作单元的定位基准、几何特征、加工精度要求以及生产成本进行综合分析,确定了各操作单元之间的加工顺序关系,由此构建加工顺序约束矩阵M:

(25)
智能水滴算法的参数设定如下:初始种群数200,迭代次数30,局部泥土量的更新参数ρn=0.9,全局泥土量的更新参数ρIWD=-0.9,水滴的初始速度vinit=4。
在经过迭代计算后,从种群集合中随机选取4个种群与最优种群进行对比,具体迭代曲线如图5所示。可见各种群的初始适应变度值较大,即由智能水滴算法获得的初始解质量较高。经过前期迭代更新后适应度值逐渐趋于稳定,最终获得最佳的流动路径,即最优的装夹规划方案。
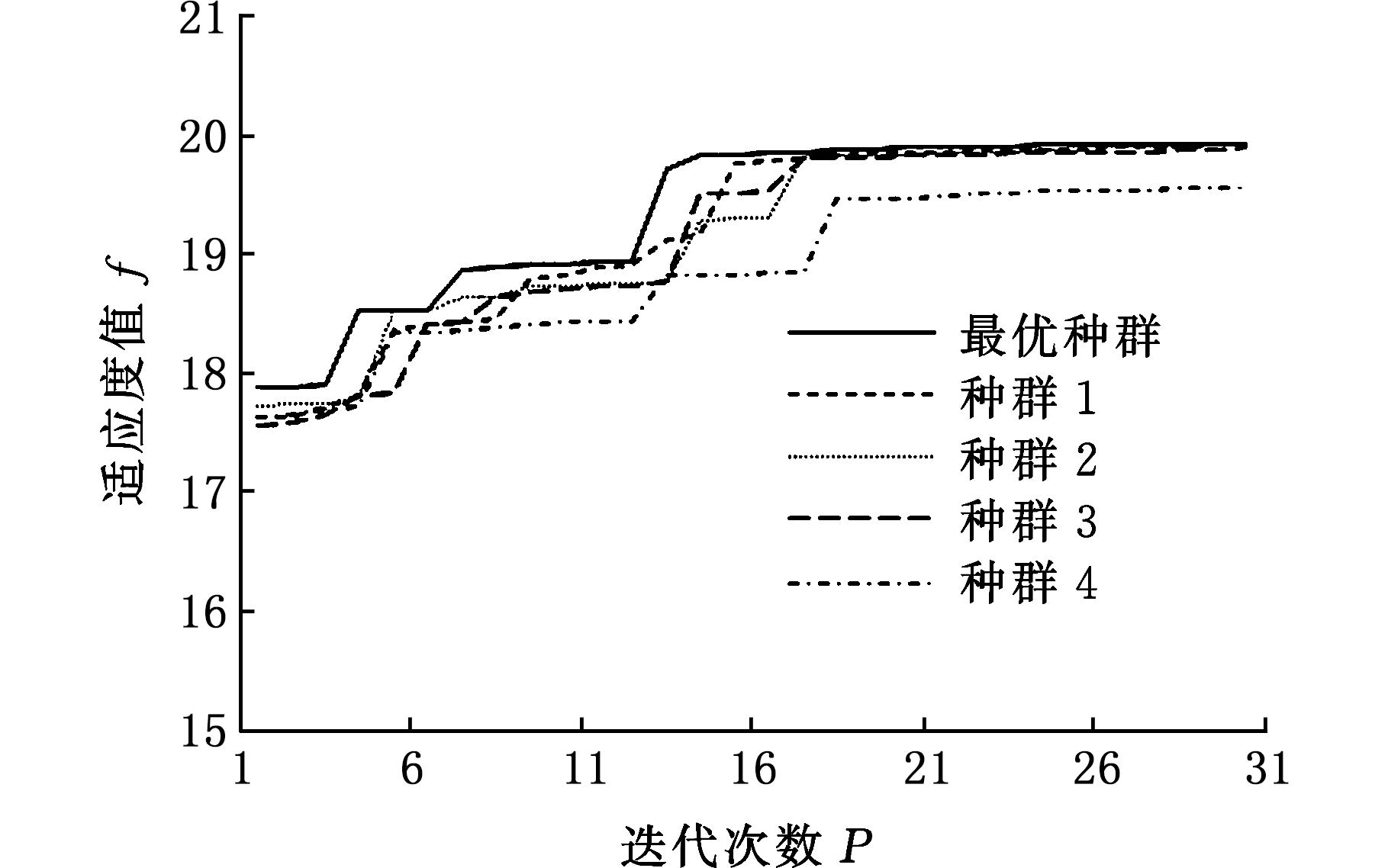
图5 智能水滴算法的适应度曲线
Fig.5 Fitness curve of IWD algorithm
将智能水滴(IWD)算法与遗传算法(GA)的装夹分组过程进行对比,其迭代结果如图6所示。
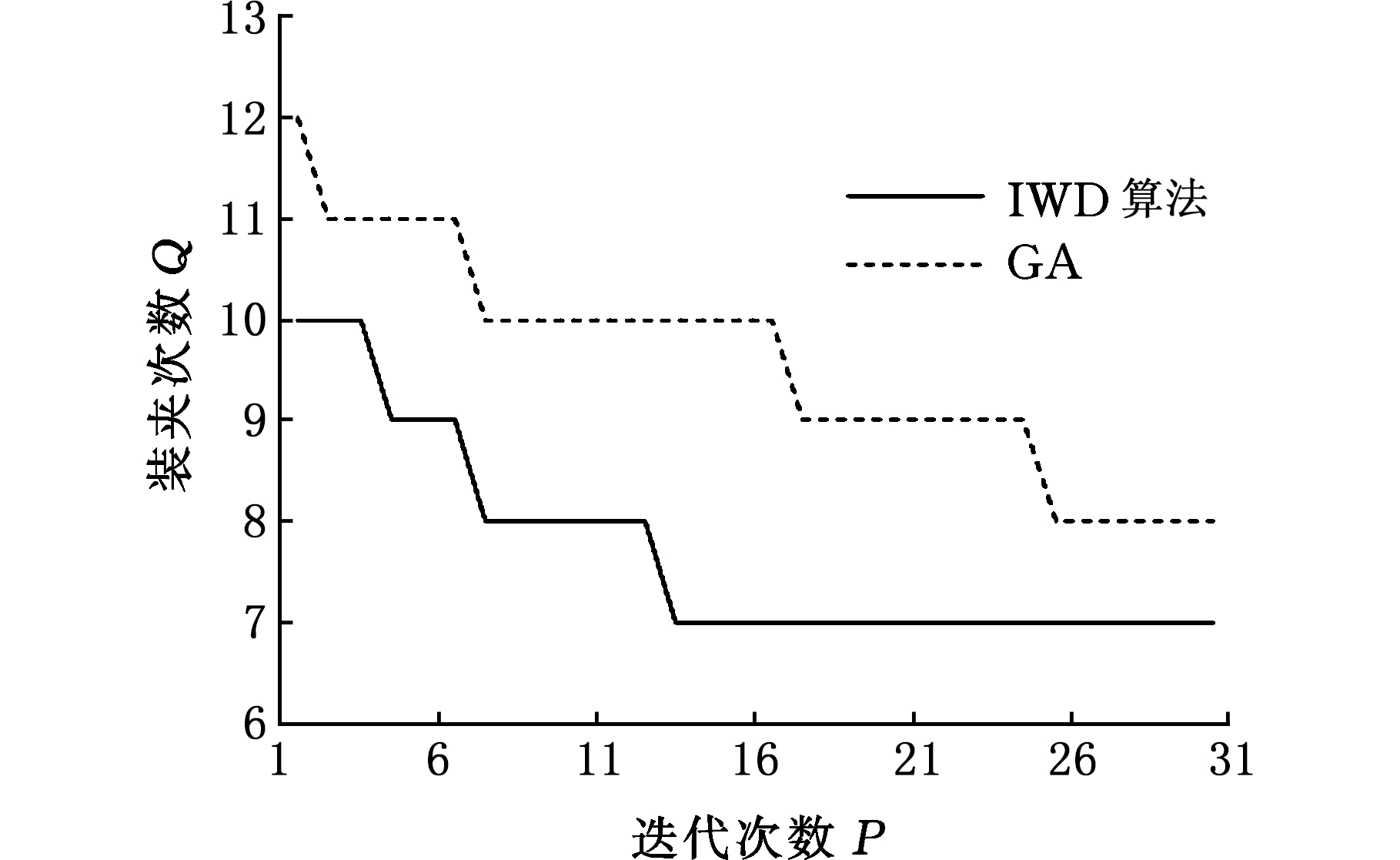
图6 不同算法的装夹分组过程
Fig.6 Grouping process of setup based o n different algorithms
在通过操作单元顺序约束矩阵对装夹规划方案进行筛选后,基于智能水滴算法的装夹规划过程中的初始装夹次数要少于遗传算法计算的初始装夹次数。同时,由于算法的迭代特性,使得迭代过程中水滴所经过的路径上的泥土量不断减少,水滴所选取的节点顺序逐渐趋于一致,算法的收敛速度提高,可以较快地获得更为优秀的装夹规划方案。
通过IWD算法的迭代计算后,得到的最优装夹规划方案如表2所示。具体的装夹分组方案如表3所示。
表2 智能水滴算法获得的最优装夹规划方案
Tab.2 Optimal setup planning scheme obtaine d by IWD algorithm
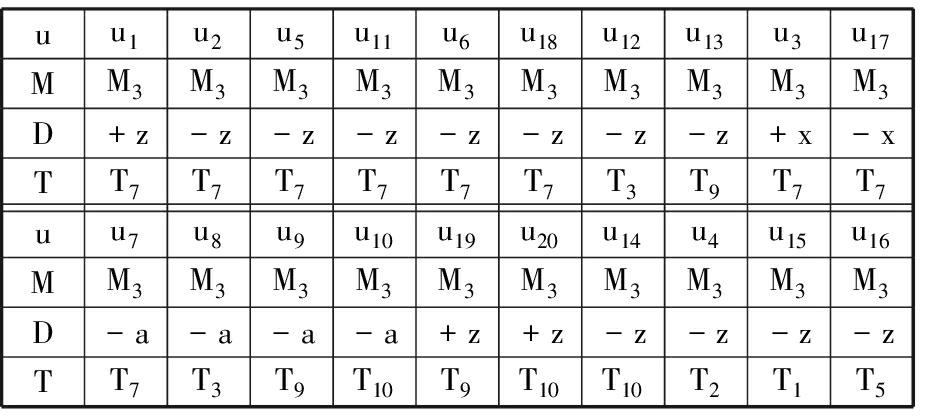
uu1u2u5u11u6u18u12u13u3u17MM3M3M3M3M3M3M3M3M3M3D+z-z-z-z-z-z-z-z+x-xTT7T7T7T7T7T7T3T9T7T7uu7u8u9u10u19u20u14u4u15u16MM3M3M3M3M3M3M3M3M3M3D-a-a-a-a+z+z-z-z-z-zTT7T3T9T10T9T10T10T2T1T5
表3 智能水滴算法获得的最优装夹分组方案
Tab.3 Optimal setup grouping scheme obtaine d by IWD algorithm
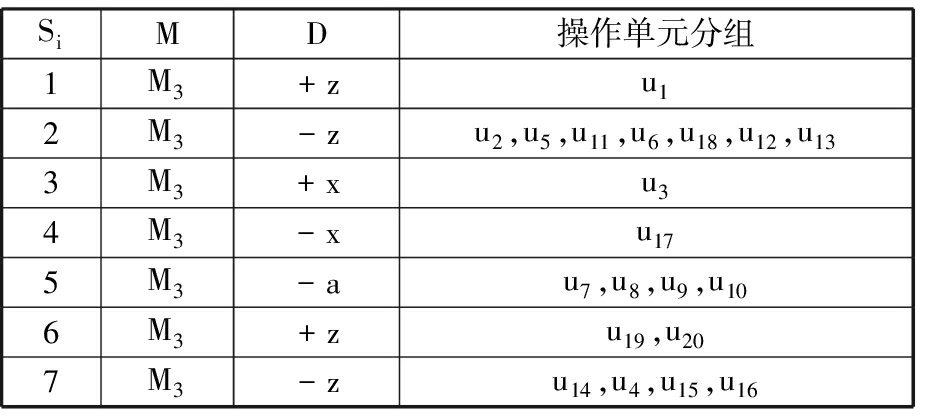
SiMD操作单元分组1M3+zu12M3-zu2,u5,u11,u6,u18,u12,u133M3+xu34M3-xu175M3-au7,u8,u9,u106M3+zu19,u207M3-zu14,u4,u15,u16
4 结论
针对计算机辅助工艺规划中的装夹规划问题,提出利用智能水滴算法来进行求解。由装夹特征来定义零件的操作单元,通过顺序约束矩阵来保证装夹规划方案的可行性。通过将智能水滴算法中流动路径的各节点与各操作单元相匹配,使得水滴的流动路径即为操作单元的排序。同时,将各节点间的泥土量与操作单元间的相似性相结合来构建适应度函数,符合装夹规划过程中的信息处理机制,提高了算法的搜索效率。基于智能水滴算法的特性,通过在迭代过程中使流动路径上的泥土量不断减少,使得水滴所选取的节点顺序逐渐趋于一致,提高了算法的收敛速度,同时保证了所获得的最优装夹规划方案的质量。
[1] SU Y, CHU X, CHEN D, et al. A Genetic Algorithm for Operation Sequencing in CAPP Using Edge Selection Based Encoding Strategy[J]. Journal of Intelligent Manufacturing, 2017(9/10):1-20.
[2] 高博,阎艳,张发平,等. 基于文化基因算法的装夹规划方法[J]. 机械工程学报,2015,51(3):162-169.
GAO Bo, YAN Yan, ZHANG Faping, et al. Setup Planning Method Based on Memetic Algorithm[J]. Journal of Mechanical Engineering, 2015, 51(3):162-169.
[3] YAO S, HAN X, YANG Y, et al. Computer Aided Manufacturing Planning for Mass Customization: Part 2, Automated Setup Planning[J]. International Journal of Advanced Manufacturing Technology, 2007, 32(1/2):205-217.
[4] SUN X W, CHU X N, SU Y L, et al. A New Directed Graph Approach for Automated Setup Planning in CAPP[J]. International Journal of Production Research, 2010, 48(22):6583-6612.
[5] 高博,阎艳,张发平,等. 基于公差推理的零件聚类装夹规划方法研究[J]. 北京理工大学学报,2015,35(3):236-241.
GAO Bo, YAN Yan, ZHANG Faping, et al. Research on Clustering Setup Planning of Part Based on Tolerance Reasoning[J]. Transactions of Beijing Institute of Technology, 2015, 35(3):236-241.
[6] HUANG W, HU Y, CAI L. An Effective Hybrid Graph and Genetic Algorithm Approach to Process Planning Optimization for Prismatic Parts[J]. International Journal of Advanced Manufacturing Technology, 2012, 62(9/12):1219-1232.
[7] KAFASHI S. Integrated Setup Planning and Operation Sequencing(ISOS) Using Genetic Algorithm[J]. International Journal of Advanced Manufacturing Technology, 2011, 56(5/8):589-600.
[8] GUO Y W, LI W D, MILEHAM A R, et al. Applications of Particle Swarm Optimisation in Integrated Process Planning and Scheduling[J]. Robotics and Computer-integrated Manufacturing, 2009, 25(2):280-288.
[9] 常智勇,杨建新,赵杰,等. 基于自适应蚁群算法的工艺路线优化[J]. 机械工程学报,2012,48(9):163-169.
CHANG Zhiyong, YANG Jianxin, ZHAO Jie, et al. Optimization of Process Based on Adaptive Ant Colony Algorithm[J]. Journal of Mechanical Engineering, 2012, 48(9):163-169.
[10] 黄风立,左春柽,顾金梅,等. 基于加工操作单元的多态蚁群装夹规划方法[J]. 机械工程学报,2017,53(7):164-172.
HUANG Fengli, ZUO Chuncheng, GU Jinmei, et al. Polymorphic Ant Colony Clamping Planning Method Based on the Machining Operation Unit[J]. Journal of Mechanical Engineering, 2017, 53(7):164-172.
[11] LI W D, ONG S K, NEE A Y C. Hybrid Genetic Algorithm and Simulated Annealing Approach for the Optimization of Process Plans for Prismatic Parts[J]. International Journal of Production Research, 2002, 40(8):1899-1922.
[12] 宋晓琳,潘鲁彬,曹昊天. 基于改进智能水滴算法的汽车避障局部路径规划[J]. 汽车工程,2016,38(2):185-191.
SONG Xiaolin, PAN Lubin, CAO Haotian. Local Path Planning for Vehicle Obstacle Avoidance Based on Improved Intelligent Water Drops Algorithm[J]. Automotive Engineering, 2016, 38(2):185-191.
[13] SHAH-HOSSEINI H. Intelligent Water Drops Algorithm: A New Optimization Method for Solving the Multiple Knapsack Problem[J]. International Journal of Intelligent Computing and Cybernetics, 2008, 1(2):193-212.
