0 引言
活齿传动具有结构紧凑、传动效率高、传动范围广和承载能力大等优点,可用于机器人关节、航空航天、精密仪器、油井勘探等技术领域。20世纪八十年代以来,美国学者相继提出了无齿轮减速器、消减和添加差动齿轮减速系统 [1-2];日本学者研究了单摆线活齿传动的运动原理,强度设计,曲率、压力角的计算和传动效率 [3-6]。21世纪以来,学者们对活齿传动的研究更加深入。LI等 [7]进行了正弦活齿传动的失效分析。TERADA等[8-9]提出了两段式摆线钢球减速器,完成了驱动轮廓的计算,并将其成功应用到机器人关节中。LIANG等 [10]对摆线活齿传动的齿廓特性和强度计算进行了研究。SAPSALEV等 [11]开发出了循环无齿电机驱动减速器,并对其进行了优化和改进。NAM等 [12]设计了活齿薄板式减速器,并将其应用于机器人领域。NISHIBE等 [13]研究了偏心活齿驱动系统,并将其用于驱动机器人手臂。XU等 [14-15]设计了电磁谐波活齿传动系统,该系统大大减小了机电驱动系统的整体尺寸,随后XU等 [16]又提出了双级正弦活齿传动系统。
在上述提到的活齿传动中,双级正弦活齿传动在传动比相同的情况下具有最小的径向尺寸,特别适用于石油钻机和机器人手臂等技术领域。然而,随着传动尺寸的减小,轴承等处的摩擦损耗占比提高,显著影响了传动系统的工作效率。因此,本文对该种传动系统的工作效率进行研究,分析不同结构参数对传动效率的影响规律。
1 工作原理
双级正弦活齿传动系统主要由5个基本元件组成 (图1):①带有外正弦滚道的输入轴,其滚道周期数用Z1表示(图中 Z1=1) ;②带有活齿槽和外正弦滚道的一级导架,其滚道周期数用Z2表示(图中 Z2=1) ;③带有两排内正弦滚道的壳体,其滚道周期数分别用Z3 和 Z4表示(图中Z3=5,Z4=5 );④二级导架(输出端);⑤活齿(12个滚珠,每级导架6个)。

图1 双级正弦活齿传动模型
Fig.1 Two-step sine movable tooth drive
当中心输入轴转动时,第一排活齿在外正弦滚道的推动作用下运动,同时受到壳体内正弦滚道的约束而绕中心输入轴与壳体的公共轴线做等速圆周运动。同时活齿推动一级导架输出运动与动力;第二排活齿在一级导架外正弦滚道的推动作用下运动,受到壳体内正弦滚道的约束而绕一级导架与壳体的公共轴线做等速圆周运动,将输出的动力输入到第二级传动上,最终通过二级导架输出整个传动机构的运动与动力。应用UG10.0运动仿真模块对设计的双级正弦活齿传动系统进行运动仿真,该传动系统能够按要求正常运转,验证了该种传动原理的正确性。图1所示双级正弦活齿传动系统的主要参数见表1。
表1 双级正弦活齿传动系统参数
Tab.1 Main parameters for two-step sin e movable tooth drive

名称及单位数值传动比i=i1×i26×6活齿中心圆周方向旋转半径R(mm)10.5活齿半径r(mm)2正弦滚道半径r′(mm)2.2正弦滚道幅值A(mm)1.5输入轴、一级导架外正弦滚道周期数Zi(i=1,2)1壳体内正弦滚道周期数Zi(i=3,4)5
2 效率公式
在不计活齿啮合副之间的摩擦力与活齿重力情况下,建立空间活齿的局部坐标系σ(Oxyz),活齿球心为坐标原点,x轴、y轴和z轴分别代表活齿啮合传动的径向、周向和轴向,则各构件对活齿的接触力都通过活齿的球心并沿活齿齿面的法线方向。图2所示为作用在活齿上的各接触力的位置关系。

(a)活齿受力(b)输入轴对活齿的接触力
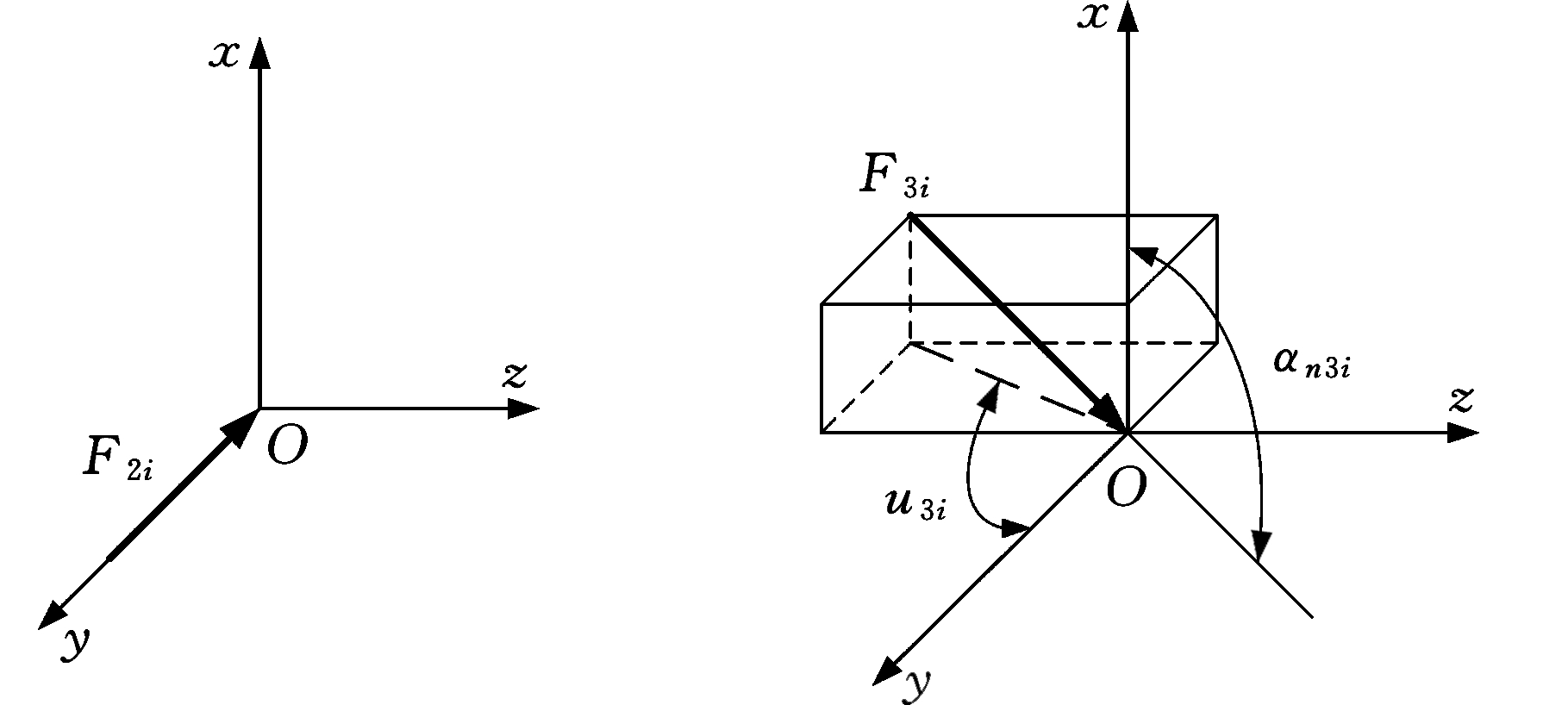
(c)导架对活齿的接触力(d)壳体对活齿的接触力
图2 活齿受力关系图
Fig.2 Forces on movable tooth
根据图2中各接触力的空间位置关系,对活齿列力平衡方程如下:

(1)
其中输入轴的外正弦滚道对活齿的接触力为F1i,接触角为αn1i;导架的活齿槽对活齿的接触力为F2i;壳体内正弦滚道对活齿的接触力为F3i,接触角为αn3i;各啮合副间瞬时接触线的方向角为uji (j=1,3)。
将活齿与输入轴之间的接触力F1i分解为径向力F1ix和径向法截面方向的力F1iyz,假定输入轴瞬时不发生运动,给活齿施加一个顺时针方向的力矩T1(输入力矩)。在该输入力矩作用下,各个活齿与输入轴滚道接触处都会受到力的作用,从而产生弹性变形,使活齿中心转过一个微角度Δφ,则各活齿中心相应地发生一个相同的微周向位移Δs。由变形协调条件知,Δs在F1iyz方向上的分量与F1iyz成正比,即F1iyz∝Δscosu1i,故有下式成立[16]:
(2)
F1iyz=F1isinαn1 u1max=arctan(R1/(AZ1))
式中,R1为输入轴外正弦滚道空间径向半径;A为空间正弦滚道的幅值。
对输入轴列力矩平衡方程如下:
(3)
式中,T1为输入力矩,即电机输出力矩Tem;n1为第一级传动系统的活齿个数。
联立式(2)和式(3)得
(4)
利用平均法求和式得到
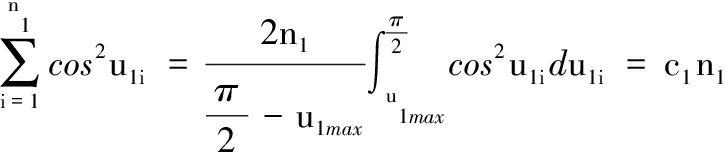
(5)

则由式(4)和式(5)可得
(6)
(7)
根据正弦活齿传动中的空间几何关系,有
(r′-r)(cosαn1i-cosαn3i)=R1-R3
(8)
式中,r、 r′分别为活齿半径和正弦滚道半径;R3为壳体内正弦滚道空间径向半径。
联立式(1)、式(7)、式(8)得

(9)
化简整理得到
(10)
由正弦活齿传动原理可知,动力由主动轴输入,活齿在固定的壳体内正弦滚道和转动的外正弦滚道的共同约束下与导架啮合,将运动和动力从导架输出。通过对活齿的受力分析可知,导架对单个活齿的作用力为F2i。由牛顿第三定律可知,单个活齿对导架的作用力大小也为F2i。设有n1个活齿参与啮合的传动,对导架列力矩平衡方程,得到系统的输出力矩为
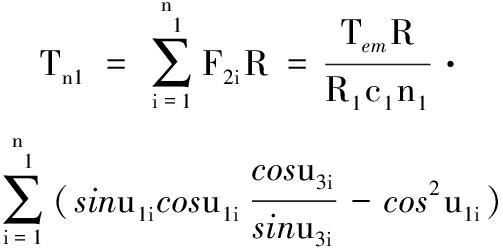
(11)
对于第二级传动而言,活齿受力方程组与式(9)相同,仅仅是输入力矩发生了变化。将第一级传动系统的输出力矩Tn1作为第二级传动系统的输入力矩,就能得到第二级传动系统的受力方程。设第二级传动的活齿数为n2,一级导架和壳体对活齿的接触角分别为αn2i和αn4i,各作用力含义与前文类似,仅加上标“(2)”作为区分,因此得到第二级传动的活齿受力方程为

(12)

ujmax=arctan(Rj/(AZj)) j=2,4
式中,R2为一级导架外正弦滚道空间径向半径;R4为壳体内正弦滚道空间径向半径。
对式(12)整理化简,可得二级导架对活齿作用力的解析式:
(13)
则双级正弦活齿传动的总输出力矩

(14)
传动效率的表达式为
(15)
式中, T1为输入转矩;T2为输出转矩;i为传动比。
将式(11)中的Tn1作为第一级传动的输出力矩,Tem为输入力矩,代入式(15)得到第一级活齿传动效率公式

(16)
对于第二级传动来讲,将式(14)中的Tn2作为第二级传动的输出力矩,Tn1为输入力矩,代入式(15)得到二级活齿传动效率公式:

(17)
3 效率计算与实验
应用以上方程,将表1中参数代入式(16)、式(17)中,得到双级正弦活齿传动系统的传动效率如图3所示。由图3可知:
(1)在双级正弦活齿传动系统中,传动效率呈周期性变化,这是因为系统输出力矩随着输入轴转角周期性变化,变化周期为活齿受力周期。对于第一级活齿传动,其变化周期为6π/5,由于第一级传动比为6,故第二级变化周期相对于第一级扩大了6倍,其周期为36π/5。
(2)对于第一级活齿传动,当φ=0和φ=6π/5时,瞬时效率取得最小值,最小值为66.87%,当φ=3π/5时,瞬时效率取得最大值,最大值为92.41%,其平均值为79.59%。因输出力矩是在6个活齿共同作用下产生的,故第一级传动效率呈现正弦性周期波动。

图3 双级正弦活齿传动系统传动效率
Fig.3 Efficiency of the two-step sine movable
drive system
(3)对于第二级活齿传动,当φ=18π/5时,瞬时效率取得最小值,最小值为46.29%,当φ=33π/5时,瞬时效率取得最大值,最大值为82.05%,其平均值为62.65%,波动比为30.9%。第一级传动的输出力矩Tn1作为第二级传动的输入力矩,相对于初始力矩Tem增大的同时,呈现正弦周期性变化,因此第二级活齿传动效率不再是标准的正弦曲线。
从表1中可以发现,双级正弦活齿传动的主要设计参数有正弦滚道幅值A,活齿中心圆周方向旋转半径R 和传动比i,其中传动比与内外正弦滚道周期数有关。本文通过改变A、R和i 在两级间的分配研究参数变化对传动效率的影响。传动效率η随A、R和i分配的变化曲线如图4~图6所示。由图4~图6可知:

图4 η随A的变化曲线
Fig.4 Changes of efficiency along with A
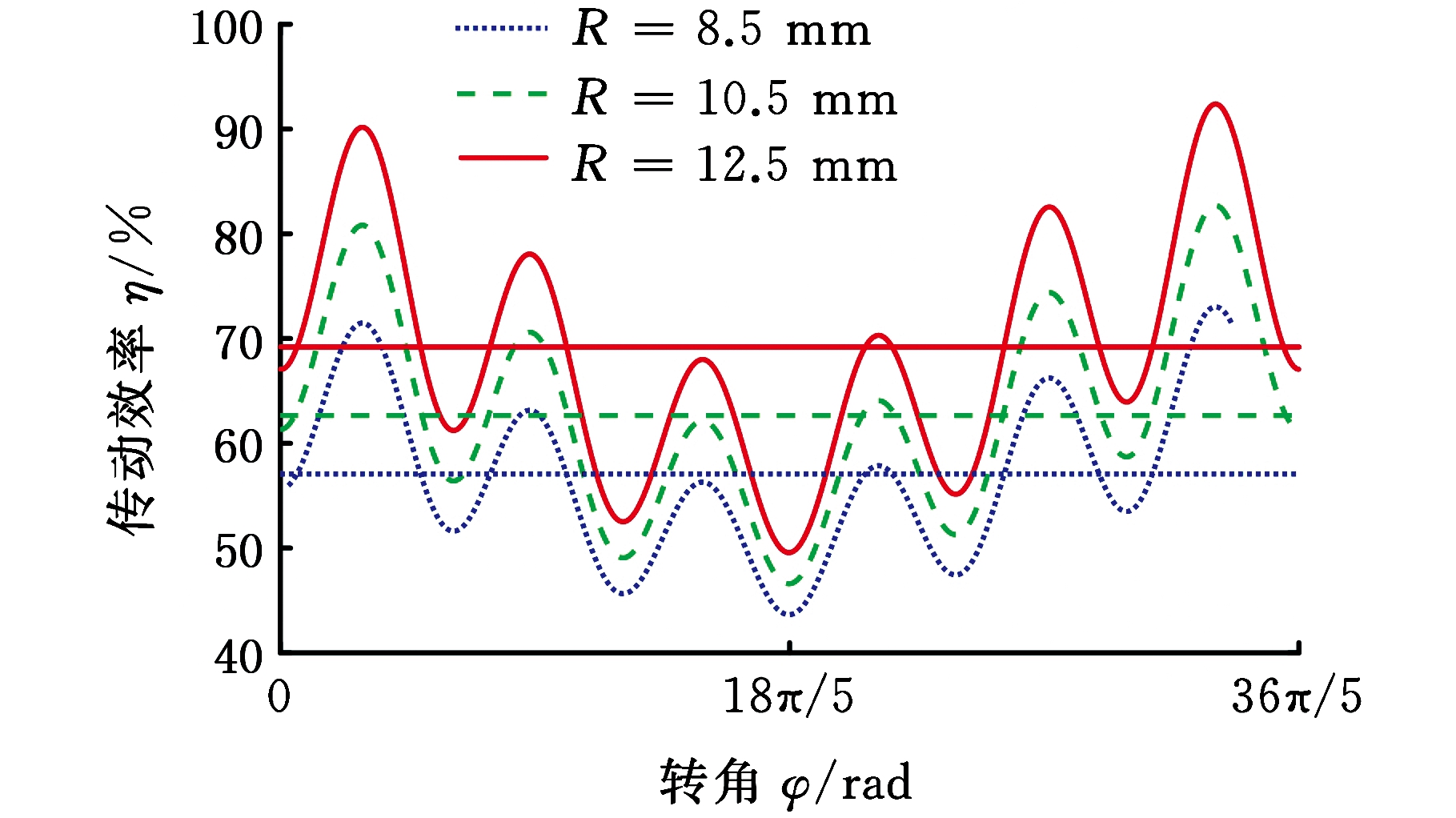
图5 η随R的变化曲线
Fig.5 Changes of efficiency along with R

图6 η随i1×i2的变化曲线
Fig.6 Changes of efficiency along with i1×i2
(1)随着正弦滚道幅值A的增大,传动效率的最大值和平均值增大,但增加幅度不大,产生瞬时效率最值的位置不变。当A为0.5,1.5和2.5 mm时,其传动效率的平均值分别为60.56%,62.65%和64.74%,但其波动比不变,仍为30.9%。
(2)随着活齿中心旋转半径R的增大,传动效率的最大值和平均值增大,且增大幅度明显,产生瞬时效率极值的位置不变。当R为8.5,10.5和12.5 mm时,其传动效率的平均值分别为57.07%,62.65%和69.19%,波动比略有增大。当R=12.5 mm时,其传动效率最大值和平均值分别为91.39%和69.19%,波动比为32%,变化幅度不大。
(3)当总传动比一定时,传动效率可以随着两级传动比的不同分配得到提高。当第一级传动比大于第二级传动比时,传动效率得到提高且波动比减小,输出更平稳。当传动比分配分别为9×4和4×9时,其传动效率的平均值分别为72.27%和35.7%,波动比分别为30.9%和55.1%,可以看出,传动比分配为9×4时的传动效率近似为传动比分配为4×9时的两倍,且波动比减小了近一半。
通过以上分析可知,为了得到效率更高的传动系统,在满足设计要求的情况下,应适当提高正弦滚道幅值A、活齿中心旋转半径R和合理的传动比分配,在总传动比一定的情况下,第一级传动比越大,传动效率越高,波动越小,输出更稳定。
为了验证以上分析,设计了双级正弦活齿传动实验样机(参数见表1)。样机采用德国DMU 60 monoBLOCK五轴立式加工中心对内外正弦滚道进行加工制造。因输入轴和一级导架外正弦滚道周期数仅为1,故在加工时难度较低,在保证对刀精度的情况下,按照设计好的滚道加工程序进行加工。图7所示为主动轴外正弦滚道加工实况,为保证样机在运转过程中更加连续,对加工完之后的滚道边缘进行0.3 mm的圆角处理,以保证活齿在滚道面运转过程中更加光滑连续。一级导架外正弦滚道的设计参数与主动轴外正弦滚道设计参数相同,故外正弦滚道加工过程与主动轴相同。图8所示为双级正弦活齿传动系统的主要零件。图9为双级正弦活齿传动系统装配完成图。

图7 主动轴外正弦滚道加工
Fig.7 Manufacture for outer sine ball track

图8 双级正弦活齿传动主要零件
Fig.8 Main parts for two-step sine movable tooth drive

图9 双级正弦活齿传动样机
Fig.9 Drive model machine of two-step sin e movable tooth
图10所示为测量传动效率的实验装置,该实验装置主要由双级正弦活齿传动样机、输入电机、电机控制器、扭矩传感器、 CHB型测力仪表、 磁粉制动器、磁粉传感器控制仪表组成。

图10 测量传动效率的实验装置
Fig.10 Experimental apparatus of testin g transmission efficiency
将双级正弦活齿传动样机在低速下空载跑合后,测量该传动样机在输入转速分别为180,240,300,360和420 r/min时的实验数据。应用MATLAB软件对所测数据进行整合,得到该传动样机在不同转速下的传动效率随负载之间的变化曲线,见图11。由图11可知:
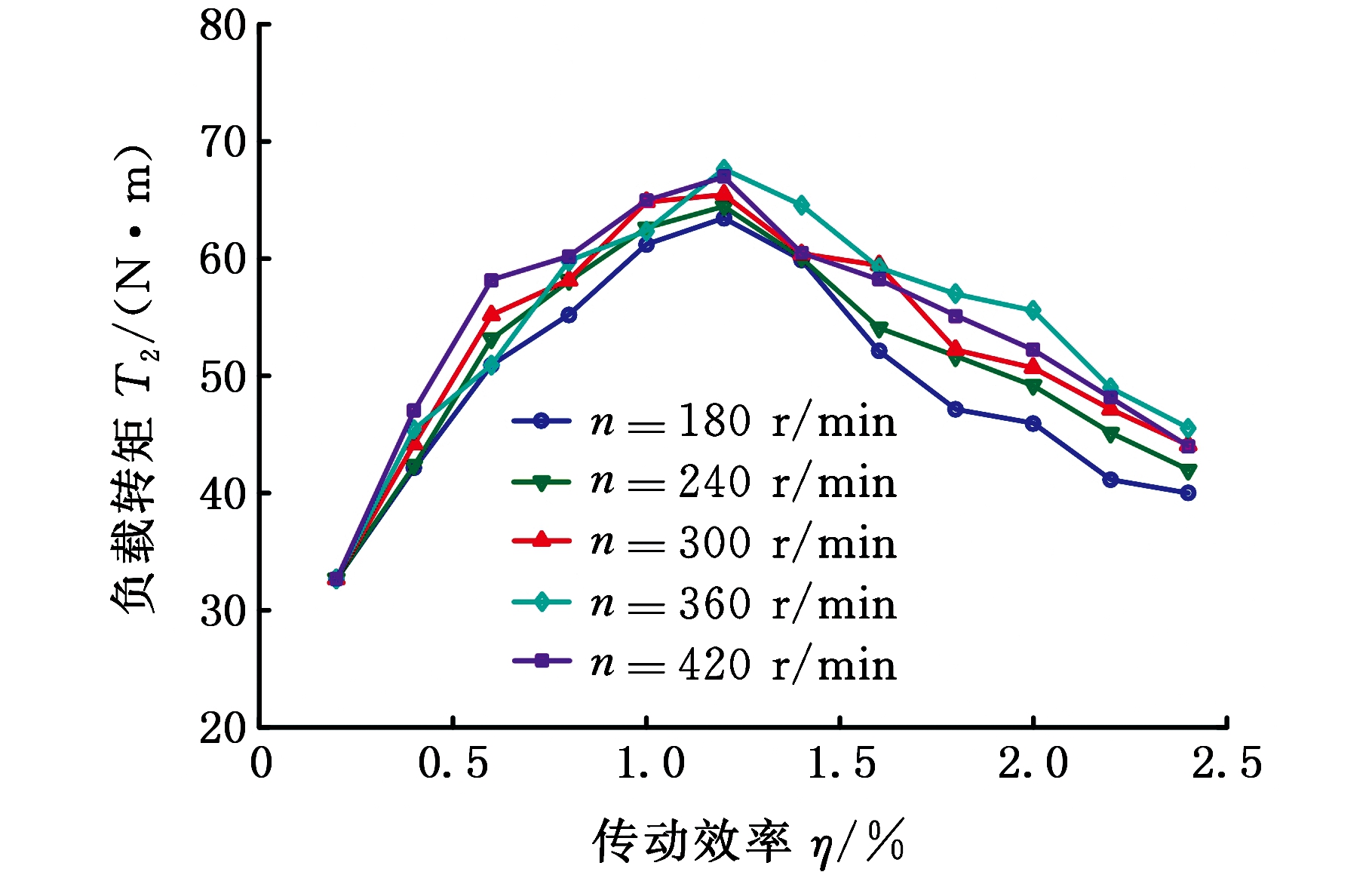
图11 样机传动效率
Fig.11 Efficiency for the model machine
(1)在相同转速下,样机的传动效率η先随负载转矩T2的增大而增大,当负载转矩达到一定数值时,传动效率开始减小,当负载转矩继续增大达到一定数值时,传动效率基本保持不变。
(2)对于该传动样机,当输入转速分别为180,240,300,360和420 r/min时,传动效率最大值均出现在负载转矩T2=1.2 N·m处。不同转速下的最大传动效率如表2所示。最大效率值随转速变化曲线见图12。根据表2和图12可以看出,当输入转速n1=360 r/min时,最大传动效率η′达到67.66%,在转速为360 r/min附近,不管转速是增大还是减小,最大传动效率均略有减小,可知n1=360 r/min时得到的双级正弦活齿传动的效率为最大传动效率。随着转速的增大,效率最大值稳定在65%左右。
表2 最大传动效率η′
Tab.2 The maximum transmission efficiency η′

输入转速n1(r/min)最大传动效率η′(%)6060.6312062.5818063.4624064.4630065.3836067.6642066.92

图12 最大传动效率随输入转速变化曲线
Fig.12 Changes of the maximum efficiency alon g with speed
(3)随着负载转矩的增大,传动效率保持在40%左右不再改变,说明高负载情况下,传动效率受其负载影响不明显。
(4)当n=60,120,180,240,300,360和420 r/min时,实验测得最大传动效率与理论效率平均值相差分别为2.9%,0.1%,1.3%,2.9%,4.4%,7.9%和6.8%。效率实验结果与理论计算值接近,验证了本文理论分析的正确性。其中当转速较低时,实验值与理论值偏差很小;当转速较高时,实验值与理论值偏差相对较大(达到7.9%和6.8%)。其主要原因在于:①速度增大会导致输入轴及输出轴力矩波动性增大,影响力矩传感器读数精度,由此而产生一定的测量误差;②速度增大还会导致传动系统中附加内部动载荷以及附加外部动载荷的增大,影响传动系统的瞬时效率。本文所推导的效率公式尚未考虑动载荷对传动系统工作效率的实际影响。考虑动载荷因素进一步提升双级正弦活齿传动效率的计算精度是下一步研究的重点。
4 结论
本文针对双级正弦活齿传动系统,推导出了传动效率计算公式,计算得到了该传动系统的平均传动效率为62.65%。分析了不同结构参数对传动效率的影响,结果表明:为了提高传动效率,应该增大正弦滚道幅值、增大活齿中心圆周方向旋转半径以及合理分配传动比。按照设计参数研制出了双级正弦活齿传动样机,进行了传动效率实验,结果表明:计算效率与实验效率结果接近。研究结果对于该种传动系统的设计与制造具有参考价值。
[1] KEITH S. Subtractive and Additive Differential Gear Reduction System:US4338830A[P]. 1982-07-02.
[2] IMASE K. Ball-rolling Type Torque Transmission Device:US5683323A[P]. 1997-11-04.
[3] TERADA H, MAKINO H, IMASE K. Fundamental Analysis of Cycloid Ball Reducer (1st Report) Motion Principle[J]. JSPE, 1988, 54(11): 1705-1709.
[4] TERADA H, MAKINO H, IMASE K. Fundamental Analysis of Cycloid Ball Reducer (2nd Report) Radius of Curvature and Pressure Angle[J]. JSPE, 1990, 56(4): 751-756.
[5] TERADA H, MAKINO H, IMASE K. Fundamental Analysis of Cycloid Ball Reducer(3rd Report) Strength Design[J]. JSPE, 1995, 61(12): 1705-1709.
[6] TERADA H, MAKINO H, IMASE K. Fundamental Analysis of Cycloid Ball Reducer (4th Report) Efficiency Analysis and Development of the Oldham’s Type Output Mechanism[J]. JSPE, 1997, 63(6): 834-838.
[7] LI Guixian, SUN Yu. Application of Grey-relational Theory in Fault Tree Analysis of Miniature Sine Oscillating Tooth Geardrive[J]. Chinese Journal of Construction Machinary, 2006,4(2):127-132.
[8] TERADA H, IMASE K. Fundamental Analysis of a Cycloid Ball Reducer (5th Report)—Development of a Two Stage Type Reduction Mechanism[J]. JSPE, 2009, 75(12): 1418-1422.
[9] TERADA H. The Development of Gearless Reducers with Rolling Balls[J]. Journal of Mechanical Science and Technology, 2010, 24(1): 189-195.
[10] LIANG Shangming, FU Bo, WANG Dongmei. Tooth Profile Synthesis and Strength Computation of Swing Movable Teeth Drives[J]. Key Engineering Materials, 2011, 474/476:162-167.
[11] SAPSALEV A V. Optimizing Cyclic Gearless Electric Drives with a Reduced-speed Section[J]. Allerton Press Inc., 2012, 32(5/6): 438-443.
[12] NAM W, SHIN J, OH S. Design of Thin Plate-type Speed Reducers Using Balls for Robots[J]. Journal of Mechanical Science and Technology, 2013, 27(2):519-524.
[13] NISHIBE S, MITSUFUJI S, NISHITANI Y. Eccentric Oscillating Reduction Gear for Joint Drive of Robot:JP2014161952A[P].2014-05-16.
[14] XU Lizhong, LIANG Yongli. Free Vibration for an Electromagnetic Harmonic Movable Tooth Drive System[J]. Open Mechanical Engineering Journal, 2015, 9(1):15-21.
[15] XU Lizhong, LIANG Yongli. Torque for an Electromagnetic Harmonic Movable Tooth Drive System[J]. Mechanism and Machine Theory, 2016, 98:190-198.
[16] XU Lizhong, SONG Wentao. Two-step Sine Movable Tooth Drive[J]. Advances in Mechanical Engineering, 2017, 9(6):1-9.
