0 引言
增材制造与传统制造技术的区别在于“逐层累加”材料的构造方式,这使得增材制造可以快速地制造出复杂化、整体化和个性化结构的零件[1]。尽管如此,在零件设计时仍需考虑增材制造的限制因素和条件。例如,许多学者研究了各种增材制造工艺的成形过程及打印特征,以便将用户的需求和可用的增材制造工艺相匹配[2-5];开发了特定的方法或者解决方案,以辅助增材制造设计过程[6-10]等。
在增材制造设计时需要考虑的因素主要有[11]:①用户的设计需要;②各工艺的制造约束;③零件的几何和拓扑形状。设计的第一步是获取用户的设计需求。设计需求的获取一方面可以帮助用户更多地了解增材制造的打印过程,另一方面可让设计人员更精准地理解用户的需求。第二步是考虑制造工艺约束。当用户的设计需求明确后,需考虑增材制造工艺的打印能力、零件的可成形性,如打印体积、可用材料、可打印的最大/最小特征、打印零件的机械特性、构建时间和打印成本等[12-13]。第三步是细节设计,即优化零件的几何结构,利用拓扑优化[14-15]、仿生设计[16-17]等方法对现有零件结构进行优化设计,同时,考虑零件的几何形状或拓扑结构对增材制造工艺规划的影响,如打印方向、分层切片、支撑和路径规划等。
上述考虑因素可以被归纳为宏观和微观两级规划内容。宏观规划包括用户需求分析、零件结构优化、可成形性分析、制造工艺选择和打印参数设置等。微观规划对应零件的打印阶段,包括3D模型的数据检查、修复与缩放,零件打印方向设计,多部件放置策略,支撑结构设计,分层切片方式,路径扫描策略以及打印零件的后处理等。微观规划内容决定零件的打印效果。
1 宏微一体的综合决策框架
综合决策流程见图1。具体过程描述如下:①分析用户需求,实施零件建模;②优化设计零件几何形状,生成打印用STL文件;③优选增材制造工艺;④结合零件的几何特征推荐最适宜的打印工艺;⑤调整零件的打印方向,使得打印零件各项指标达到设计要求。

图1 宏微一体综合决策流程图
Fig.1 Macro and micro integrated decision flow chart
决策框架的两个层次分别与增材制造宏/微观工艺规划内容相对应。决策设计的信息或知识直接来自工艺规划结果。先执行宏观决策,再执行微观决策。在宏观决策阶段,包括可适性指标AI和鉴别性指标DI;在微观决策阶段,指标包括打印表面粗糙度Ra、支撑结构体积Vs和打印时间Tbuild。
2 综合决策指标定量化建模
2.1 宏观决策指标
宏观决策的目的是判断零件的可成形性并决策出最佳打印工艺。可适性指标AI用于设计零件的可成形性分析,鉴别性指标DI用于在一组可用的增材制造工艺中选择最佳工艺。在可适性指标AI中,将设计规范(或制造要求)与可用增材制造工艺间的匹配程度作为决策标准,为了定量化计算该值,用具有相同尺度的矢量描述设计规范和增材制造工艺,记为设计向量和制造向量,分别由描述设计规范和制造工艺主要特征的属性集构成。匹配程度即设计向量和制造向量的相似性程度,公式化表示为
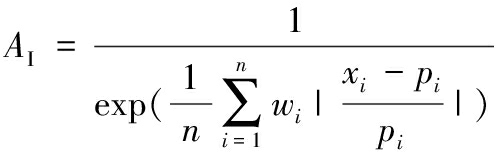
(1)
其中,xi、pi分别表示设计向量和制造向量的特征属性,wi表示设计向量和制造向量特征属性间的权重信息。xi和pi包括增材制造的打印成本和效率、打印零件的表面粗糙度和强度等指标,如何选择特征属性取决于用户的具体需求和各种增材制造的工艺特点,没有固定形式。由式(1)可知,可适性指标AI的取值范围为(0,1)。AI越大,表示设计向量和制造向量相似性越大,设计与工艺匹配度越高。在实际应用中可能存在通过AI指标评估后有一系列满足预定要求的增材制造工艺,且各工艺的AI非常接近,从AI的大小很难判断何种制造工艺是最佳的,为此,提出鉴别性指标DI,用于在系列备选增材制造工艺中确定出最佳工艺方案,公式化表达为
(2)
其中,AI,max表示备选方案中最大的AI,AI,i表示备选方案中除AI,max外其余的某个值。DI越小,说明工艺制造特征与打印要求的差距越小,工艺的匹配程度越高。若所有方案的AI非常接近,说明设计没有利用任何一种工艺的优势,需重新考虑设计本身的合理性。
2.2 微观决策指标
2.2.1 表面粗糙度评估模型
由分层制造原理可知,增材制造中零件倾斜平面和曲面上会产生不同程度的台阶效应,是影响零件表面质量的重要因素之一[18],此外,打印参数和材料参数也会影响表面质量。但是,不同条件千差万别,考虑到统一性和定量化表达,在微观决策指标中,仅采用由于分层制造引起的台阶效应来评估零件的表面质量:
(3)
其中,lt为层厚,θi为第i个三角面片的法向量与打印方向单位向量的夹角(图2),其表达式为
(4)
式中,n为三角面片的法向量,n=(A,B,C);e为打印方向的单位向量,e=(e1,e2,e3)。

图2 三角面片法向量与打印方向单位向量
Fig.2 Triangle face normal vector and the direction o f the printing direction unit vector
除了表面质量,支撑结构的体积也作为微观决策指标,因此需考虑支撑体对表面质量的影响。假设支撑体与零件表面接触处有恒定的粗糙度Rs,则表面粗糙度Ra可表达为

(5)
式中,Ai为三角面片的面积;As为支撑体与零件表面接触点的总面积;nf为切片层数。
表面粗糙度Ra越小,零件的表面质量越好。
2.2.2 支撑结构体积评估模型
在设计零件的打印方向时,当零件表面与水平面夹角小于45°时,认为该表面为悬垂表面,在打印过程中需要添加支撑结构以防止材料发生坍塌或者变形[19-20]。在微观决策指标中,通过计算悬垂面上每个三角面片的支撑结构体积来评估总体支撑结构的体积。其中,每个三角面片的支撑结构体积由其投影所构成的三棱锥和三棱柱计算(图3),其表达式为
Vi=Aicosθi(zmin+hs)+Aicosθi(zmax-zmin)/3
(6)
式中,zmax和zmin分别为三角面片z方向的最大值和最小值;hs为零件与打印基台之间的距离。

图3 单个三角面片的支撑结构体积
Fig.3 Supporting structure volume of a singl e triangular patch
支撑结构的总体积为所有悬垂表面的三角面片的三棱锥与三棱柱的体积之和:
(7)
式中,nd为所有悬垂表面的三角面片的数量。
在实际打印过程中,一般会在零件底层铺设一层打印基台,防止打印零件粘到打印机底板上并可减小零件的变形和翘曲。该部分所用的材料算到支撑结构体积中,可借助打印零件的最小包围盒计算:
Vbase=lbSaabb
(8)
式中,lb为基台厚度;Saabb为所打印零件的最小包围盒在水平面上的投影面积。
因此,支撑结构的体积VS可表达为
(9)
2.2.3 打印时间评估模型
增材制造打印时间可以由4个子过程时间来计算[21],分别为外轮廓打印时间TC、内部填充时间TH、支撑结构打印时间TS和机器运动时间TM。在微观决策指标中,考虑外轮廓打印时间TC和支撑结构打印时间TS来评估打印时间,则总打印时间Tbuild表示为
Tbuild=TC+TS
(10)
外轮廓打印时间TC通过横截面轮廓的总长度除以轮廓扫描速度计算:

(11)
式中,Cj为横截面轮廓长度;vTC为轮廓扫描速度;nl为横截面总轮廓数。
支撑结构打印时间TS由下式计算:
(12)
其中,vTS表示打印支撑结构的扫描速度;Hx、Hy分别为x方向和y方向的扫描间距。
3 综合决策模型
通过宏观决策阶段可以确定零件的可成形性以及可用的增材制造工艺。微观决策以表面粗糙度、支撑结构体积、打印时间为决策指标,优化出最佳打印方向,最大程度满足用户需求。
有序加权平均算子为由YAGER[22]提出的一种用于多属性综合决策的信息集结算子。本文利用有序加权平均算子对2.2节提出的3个微观决策指标进行集结处理,以此评估不同打印方向的综合决策结果,其表达式为
(13)
其中,a1、a2、a3表示2.2节提出的表面粗糙度、支撑结构体积和打印时间3个决策指标,j表示上述三个指标按降序重新排列后的位置,bj表示按降序重新排列的决策指标,wj为各指标对应的权重,wj∈[0,1]且![]() 因为所用的三个指标均为消耗型指标,所以综合决策结果的数值越小说明工艺的合理性越强。
因为所用的三个指标均为消耗型指标,所以综合决策结果的数值越小说明工艺的合理性越强。
4 决策模型的算例预估与验证
本节以拓扑优化的梁结构为测试对象,验证所提出的宏微一体综合决策模型的有效性。梁结构的STL模型见图4。
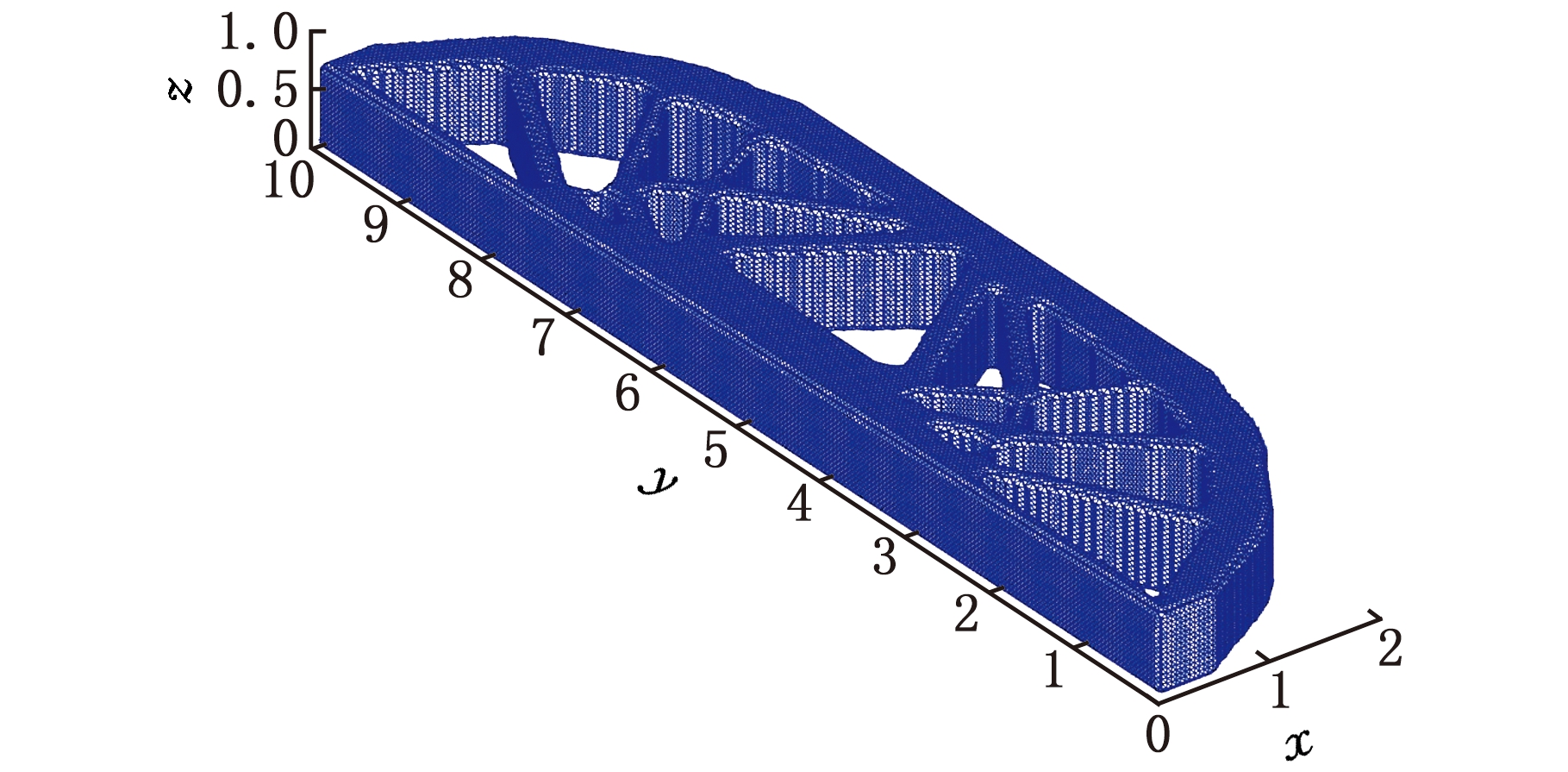
图4 MBB梁STL文件
Fig.4 MBB beam STL file
4.1 宏观工艺匹配性评估
以熔融沉积成形(FDM)和立体光固化成形(SLA)两种增材制造工艺为例,测试宏观决策的效果。图5所示为MakerBot公司的Replicator2型FDM打印机和Formlabs公司的Form2型SLA打印机,其打印参数见表1。

(a)FDM工艺 (b)SLA工艺
图5 两种不同3D打印机
Fig.5 Two different 3D printers
表1 FDM及SLA工艺打印参数
Tab.1 FDM and SLA process printing parameters

打印类型打印成本(元/cm3)打印效率(min/cm3)表面粗糙度(μm)抗拉强度(MPa)FDM62.836.9238.59SLA155.362.4768.38
假设用户打印需求如下:打印成本控制在5~10元/cm3,打印效率控制在3~4 min/cm3,表面粗糙度控制在2~4 μm,抗拉强度控制在40~60 MPa。基于上述打印要求,设计向量和制造向量选定打印成本、打印效率、表面粗糙度和抗拉强度四个特征值,结合表1中的打印参数可表示为(需求特征取中间值):

(14)
其中,设计向量取设计要求区间范围的平均值,各项指标的权重信息wi=1,i=1,2,3,4。根据式(1),计算得到FDM工艺的可适性指标AI为0.637 9,SLA工艺的AI为0.641 8。两种工艺的AI值非常接近,很难判断何种工艺更加适宜。为此,根据式(2)计算得到FDM工艺的DI为5.047 0,SLA工艺的DI为3.816 1。综合AI和DI,SLA工艺更符合上述打印要求。
4.2 微观工艺适应性评估
在微观工艺规划阶段,通过表面粗糙度、支撑结构体积和打印时间三个指标综合决策出打印方向。设计图6所示两种打印方法验证建立模型的适用性。设定打印方向1为原始打印方向沿旋转轴t=(7,3,9)逆时针旋转30°,打印方向2为原始打印方向沿旋转轴t=(1,3,1)逆时针旋转20°。表2为工艺参数值,并设三个决策指标对应的权重w=(0.6,0.3,0.1)。
根据表2中数据,由式(5)、式(9)和式(10)计算表面粗糙度、支撑结构体积和打印时间。打印成本为梁结构体积与支撑结构体积的和乘以打印材料的单价。计算得出的微观决策指标如表3所示。将结果代入式(13),得出打印方向1的综合决策结果为90.812 0,打印方向2为60.996 3,打印方向2更优。

(a)打印方向1

(b)打印方向2
图6 设定的两种打印方向
Fig.6 Sets the two printing directions
表2 微观决策参数设置
Tab.2 Micro decision parameters setting
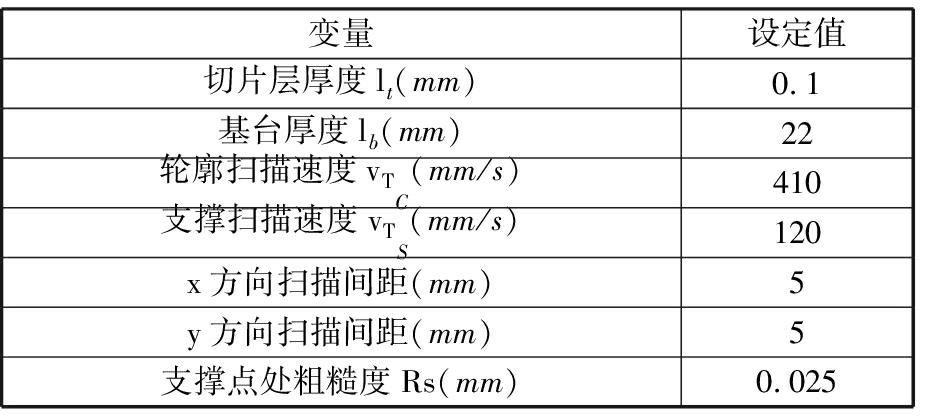
变量设定值切片层厚度lt(mm)0.1基台厚度lb(mm)22轮廓扫描速度vTC(mm/s)410支撑扫描速度vTS(mm/s)120x方向扫描间距(mm)5y方向扫描间距(mm)5支撑点处粗糙度Rs(mm)0.025
表3 微观决策指标数值
Tab.3 Micro-decision indicator values

打印方向表面粗糙度(μm)打印时间(min)打印成本(元/cm3)157.522 994.796 693.939 3263.862 457.731 853.592 9
4.3 评估结果验证
图7所示为按图6设定打印方向用Formlabs公司Preform软件模拟的打印结果。

(a)打印方向1 (b)打印方向2
图7 Preform软件模拟结果
Fig.7 Preform software simulation results
两个打印方向的切片层数均为379。打印方向1的模拟打印结果为:消耗材料体积9.59 mL,预计打印时间2h30min;打印方向2的模拟打印结果为:消耗材料体积7.07mL,预计打印时间1h49min。综合考虑可知,打印方向2在节省材料和节省打印时间方面更具优势,与模型预测结果一致。但是,该结果与预测模型的计算数值存在一定偏差,实际打印时间较预测时间更长,究其原因主要是本文的预测模型目前仅考虑了零件外轮廓和支撑结构的打印,暂没有考虑零件内部填充打印和材料铺送、机器空转等相关耗时。这些参数与具体打印机参数密切相关,根据实际情况完善打印时间计算公式(10)有望获得更高的预测精度。
5 结论
建立了评估宏观和微观两级规划的增材制造工艺匹配性和合理性定量化计算模型,为增材制造工艺选择提供了量化方法。宏观模型抽象了设计需求与制造工艺的数学表达,从可成形性角度评判工艺的匹配程度。微观模型建立了表面粗糙度、支撑结构体积和打印时间的计算模型,从打印质量的角度优化打印工艺。以拓扑优化的梁结构零件为例,利用建立的综合决策模型优化了其打印工艺,结果与模拟打印相一致,验证了模型的有效性。但是,预测模型在打印特征量的选取与计算方法上还有待完善,并需在金属打印等主流工艺上验证。
[1] GIBSON I, ROSEN D W, STUCKER B. Additive Manufacturing Technologies[M]. New York: Springer, 2014.
[2] NGO T D, KASHANI A, IMBALZANO G, et al. Additive Manufacturing (3D Printing): a Review of Materials, Methods, Applications and Challenges[J]. Composites Part B: Engineering, 2018, 143: 172-196.
[3] FRAZIER W E. Metal Additive Manufacturing: a Review[J]. Journal of Materials Engineering and Performance, 2014, 23(6): 1917-1928.
[4] HERZOG D, SEYDA V, WYCISK E, et al. Additive Manufacturing of Metals[J]. Acta Materialia, 2016, 117: 371-392.
[5] DEBROY T, WEI H L, ZUBACK J S, et al. Additive Manufacturing of Metallic Components—Process, Structure and Properties[J]. Progress in Materials Science, 2018, 92: 112-224.
[6] ZHANG Y, XU Y, BERNARD A. A New Decision Support Method for the Selection of RP Process: Knowledge Value Measuring[J]. International Journal of Computer Integrated Manufacturing, 2014, 27(8):12.
[7] CHU C, GRAF G, ROSEN D W, et al. Design for Additive Manufacturing of Cellular Structures[J]. Computer-aided Design and Applications, 2008, 5(5): 686-696.
[8] THOMPSON M K, MORONI G, VANEKER T, et al. Design for Additive Manufacturing: Trends, Opportunities, Considerations, and Constraints[J]. CIRP Annals, 2016, 65(2): 737-760.
[9] ADAM G A O, ZIMMER D. Design for Additive Manufacturing—Element Transitions and Aggregated Structures[J]. CIRP Journal of Manufacturing Science and Technology, 2014, 7(1): 20-28.
[10] YANG S, ZHAO Y F. Additive Manufacturing-enabled Design Theory and Methodology: a Critical Review[J]. The International Journal of Advanced Manufacturing Technology, 2015, 80(1/4): 327-342.
[11] TURNER B N, STRONG R, GOLD S A. A Review of Melt Extrusion Additive Manufacturing Processes: Ⅰ. Process Design and Modeling[J]. Rapid Prototyping Journal, 2014, 20(3): 192-204.
[12] PONCHE R, KERBRAT O, MOGNOL P, et al. A Novel Methodology of Design for Additive Manufacturing Applied to Additive Laser Manufacturing Process[J]. Robotics and Computer Integrated Manufacturing, 2014, 30(4): 389-398.
[13] 曾达幸,张星, 樊明洲, 等. 3-CUR解耦并联3D打印机结构优化与动力学分析[J]. 中国机械工程, 2017,28(12):1413-1420.
ZENG Daxing, ZHANG Xing, FAN Mingzhou,et al. Structure Optimization and Dynamics Analysis of 3-CUR Decoupling Parallel 3D Printer[J]. China Mechanical Engineering,2017,28(12):1413-1420.
[14] BRACKETT D, ASHCROFT I, HAGUE R. Topology Optimization for Additive Manufacturing[C]∥Proceedings of the Solid Freeform Fabrication Symposium. Austin, 2011, 1: 348-362.
[15] ZEGARD T, PAULINO G H. Bridging Topology Optimization and Additive Manufacturing[J]. Structural and Multidisciplinary Optimization, 2016, 53(1): 175-192.
[16] EMMELMANN C, SANDER P, KRANZ J, et al. Laser Additive Manufacturing and Bionics: Redefining Lightweight Design[J]. Physics Procedia, 2011, 12: 364-368.
[17] KRANZ J, HERZOG D, EMMELMANN C. Design Guidelines for Laser Additive Manufacturing of Lightweight Structures in TiAl6V4[J]. Journal of Laser Applications, 2015, 27(S1): S14001.
[18] ALMANGOUR B, YANG J M. Improving the Surface Quality and Mechanical Properties by Shot-peening of 17-4 Stainless Steel Fabricated by Additive Manufacturing[J]. Materials & Design, 2016, 110: 914-924.
[19] STRANO G, HAO L, EVERSON R M, et al. A New Approach to the Design and Optimization of Support Structures in Additive Manufacturing[J]. The International Journal of Advanced Manufacturing Technology, 2013, 66(9/12): 1247-1254.
[20] 吴根丽, 刘婷婷, 张长东, 等. Ti6Al4V激光选区熔化成形悬垂结构的质量研究[J]. 中国机械工程, 2016, 27(13):1810-1815.
WU Genli, LIU Tingting, ZHANG Changdong,et al. Study on the Quality of Ti6Al4V Laser Selective Melting and Forming Overhang Structure[J].China Mechanical Engineering,2016, 27(13):1810-1815.
[21] YIM S, ROSEN D. Build Time and Cost Models for Additive Manufacturing Process Selection[C]∥ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. New York: American Society of Mechanical Engineers, 2012: 375-382.
[22] YAGER R R. On Ordered Weighted Averaging Aggregation Operations in Multicriteria Decision Making [J].IEEE Trans. Systems Man Cybernet,1988, 18(1):80-87.
