0 引言
火箭弹的初始扰动是指火箭弹在脱离定向器约束的瞬间实际弹道与理想弹道的偏差。对于无控火箭弹而言，初始扰动直接影响其发射精度和散布；对有控火箭弹而言，初始扰动是影响其发射精度的重要因素，过大的初始扰动会增加火箭弹超出制导系统可控域的危险，甚至造成制导系统不能截获火箭弹而失控的局面[1]。因此对初始扰动的成因及其影响因素进行分析研究，寻求减小和控制初始扰动的方法十分必要。
理论和实践表明，火箭弹在发射过程中定心部与导轨产生的相互作用是影响其发射精度的重要原因[1]，为此已有许多学者采用不同的动力学模型和分析方法对弹-架系统的动力学特性进行研究[2-5]，揭示了影响初始扰动的各种因素及基本规律,但目前对减小火箭弹初始扰动的理论及仿真研究相对较少。冯勇等[6]采用多岛遗传算法通过优化发射间隔及与之相匹配的变刚度、阻尼来减小初始扰动；陈阵等[7]对影响火箭初始扰动的弹管间隙开展了优化设计；李彦君[8]以火箭弹发射过程中的振动幅值最小为条件，计算出了火箭弹振动响应最小的间隙量，并对发射装置进行了优化。以上研究为发射系统的研制提供了参考，但对火箭弹结构设计尤其定心部结构参数选择方面提供的指导意义却十分有限。
本文以固定基础倾斜发射不同时离轨的火箭弹为研究对象，采用发射动力学仿真方法，以减小初始扰动为目标，以弹-轨不发生碰撞为约束，开展了火箭弹定心部结构参数优化分析，得到了定心部宽度及布局的优化设计结果，为火箭弹定心部的结构设计提供了参考。
1 火箭弹的初始扰动
发射过程中，火箭弹在定向器上的运动姿态由于受各种因素的影响而产生扰动，使弹从导轨上滑离时产生非零的俯仰角和俯仰角速度(即初始扰动)，该扰动将作为无控飞行弹道的起始条件使火箭弹进入无控飞行阶段。
为获得初始扰动，需建立火箭弹离轨过程中的运动学模型，为使问题简化且不失一般性，对发射装置作合理简化：发射架底盘、回转台均与大地视为一体，定向器与起落架视为一体并简化成一个绕固定轴转动的刚体导轨，液压作动筒简化成弹性体，并假设：①导轨平直；②发动机推力无偏心；③火箭弹定心部与导轨存在间隙，不计摩擦；④发射过程中弹的质量不变；⑤不计燃气流作用。
建立的发射动力学模型如图1所示，oxy为固定坐标系，表示发射架的初始位置；ox1y1为发射架坐标系，固定在发射架上，与发射架一起运动。根据发射动力学模型，建立发射系统火箭弹滑离时的运动方程[9]如下：
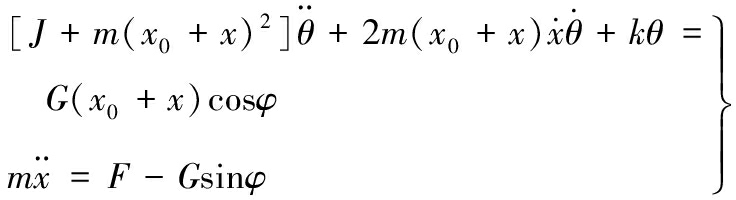
(1)
式中，G为火箭弹重力；m为火箭弹质量；J为发射架和导弹的转动惯量；k为发射架等效扭转刚度；F为发动机推力；θ为发射架的振动角；(x0,y0)为火箭弹质心的初始位置；x为质心在x1轴上的位移；φ为发射角。
图1 火箭弹发射动力学模型
Fig.1 Launch dynamics model of rocket
设火箭弹前定心部与后定心部间的距离为lB，质心到后定心部的距离为lR，定心部回转半径为RA，则火箭弹在铅垂面内的初始扰动角速度为[10]
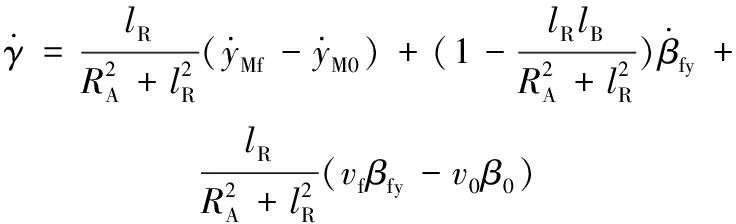
(2)
式中，
分别为中定心部离轨时导轨振动角速率及振动角位移的垂向分量；β0为后定心部离轨时导轨振动角位移的垂向分量；vf、v0分别为中后定心部离轨速度；
分别为中后定心部离轨时导轨振动线速度的垂向分量。
2 火箭弹发射模型的建立
火箭弹发射系统结构较为复杂，在建立仿真模型时，应当结合实际情况，分析和选取主要影响因素。经简化后建立的从固定基础发射火箭弹的多体动力学模型主要包括大地(含发射架底盘、回转台)、导轨(含起落架、定向器)、火箭弹(含弹体、定心部)、液压作动筒(等效为弹簧连接)等构件，其拓扑结构如图2所示。第i个构件记为Bi(i=1，2，…，N)，N为多体系统中构件的个数，Bij(j=1，2，…，M)表示第i个构件的第j个部分。用有向线段表示连接相邻构件的约束，记为Jk(k=1，2，…，P)。
图2 火箭弹发射模型拓扑结构
Fig.2 The topology of rocket launch model
大地B0与底盘B01、回转台B02间通过固定副J0、J1连接；定向器B11与起落架B12、导轨B1间通过固定副J4、J5连接；回转台B02与起落架B12间通过转动副J2连接，发射架的弹性通过液压作动筒等效成的弹簧J3实现；弹体B2与定心部B21、B22、B23以及定向钮B24、B25分别通过固定约束J11～J15组成火箭弹；三个定心部、两个定向钮分别与导轨B1间通过J6～J10建立接触。因火箭弹质心离轨是影响初始扰动及下沉量的主要因素[1,10]，同时是导致弹体与导轨发生碰撞的主要原因，因此模型中建立弹体的虚拟构件B3与弹体B2通过固定副J17连接，并与导轨B1间建立接触J16，用以实现仿真过程中弹体与导轨间碰撞的实时检测。发动机推力沿弹轴线施加于弹体尾部，推力-时间曲线由样条曲线拟合。为获得火箭弹的初始扰动，仿真结束时刻设置为火箭弹脱离导轨的瞬间。
3 定心部优化模型的建立及分析
3.1 优化模型建立
火箭弹在导轨上运动期间，通过定心部与导轨产生的剧烈接触作用，以及在质心离轨过程中产生的弹体转动是影响初始扰动的主要因素，而火箭弹定心部的宽度和布局直接影响了火箭弹与导轨的相互作用以及质心离轨的过程。为此选取的设计变量为定心部的布局参数(距弹头顶点的距离)La、Lb、Lc，以及定心部的宽度w。设计变量的约束分为边界约束和性能约束，边界约束根据火箭弹自身的结构特点确定，如应避开舱段连接处、测试窗口及焊缝位置等；性能约束可为弹-轨碰撞力、定心部与导轨间的应力、定向钮与导轨间的应力等，本文考虑火箭弹在离轨过程中弹体与导轨的碰撞力F1=0。综上所述，为减小初始扰动的火箭弹定心部结构参数优化问题的数学模型为
(3)
式中，
为目标函数，分别表示初始扰动角和初始扰动角速度；
分别为定心部位置的下限和上限；wL、wU分别为定心部宽度的下限和上限；G(·)表示其他边界约束；F1(·)表示弹体与导轨间的碰撞力。
3.2 优化问题实现
本文以某型固定基础倾斜发射不同时离轨火箭弹为例建立发射动力学仿真模型，对定心部的位置和宽度进行参数化设计，以初始扰动角和初始扰动角速度作为目标函数，进行火箭弹发射动力学仿真优化，可直接得到定心部宽度和布局的优化设计结果。在本优化问题中，设计变量除满足边界约束外，还要满足实时仿真过程中弹-轨不发生碰撞的性能约束。火箭弹定心部结构设计变量的取值范围如表1所示。
表1 设计变量取值范围
Tab.1 Values range of design parameters mm
项目初始值下限值上限值La1 7161 6862 865Lb4 3434 3007 175Lc7 0005 7507 175w10050200
3.3 优化结果分析
采用上述方法对本文的优化问题进行了求解，得到定心部宽度和布局的优化设计结果如表2所示。由优化前后设计变量值对比可知，定心部宽度变化率最大，通过对设计参数进行灵敏度分析亦可知，定心部宽度对初始扰动的影响较大。
表2 优化前后设计变量值对比
Tab.2 Design parameters values compariso n before-and-after optimal design
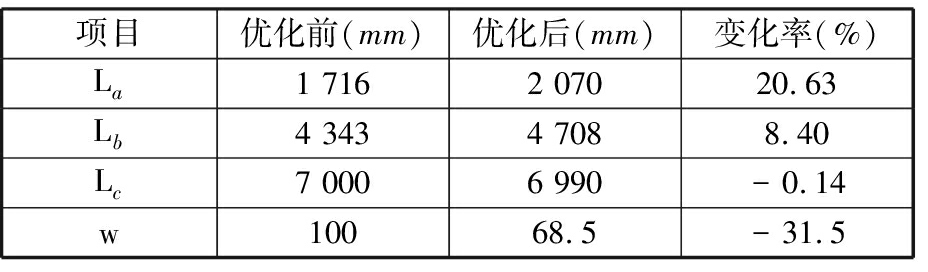
项目优化前(mm)优化后(mm)变化率(%)La1 7162 07020.63Lb4 3434 7088.40Lc7 0006 990-0.14w10068.5-31.5
优化前后火箭弹初始扰动角和初始扰动角速度对比情况如表3所示，由对比结果可见，优化后火箭弹的初始扰动量明显减小，表明本文采用的优化方法有效，优化得到的设计参数可行，可为火箭弹定心部的设计提供理论参考。
表3 优化前后离轨姿态参数对比
Tab.3 Take-off attitude parameters compariso n before-and-after optimal design
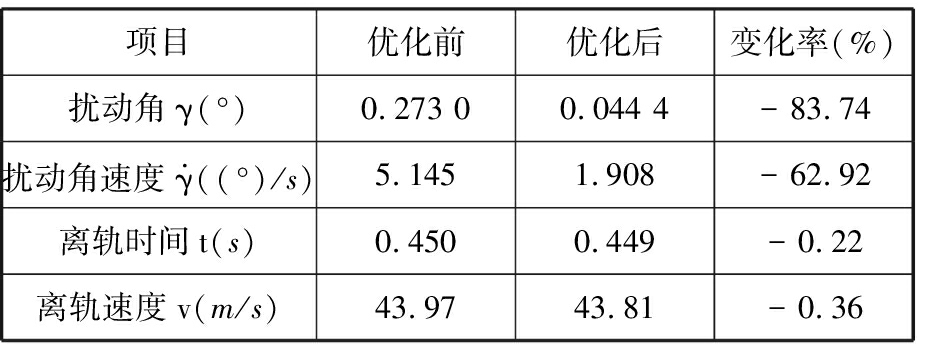
项目优化前优化后变化率(%)扰动角γ(°)0.273 00.044 4-83.74扰动角速度γ·((°)/s)5.1451.908-62.92离轨时间t(s)0.4500.449-0.22离轨速度v(m/s)43.9743.81-0.36
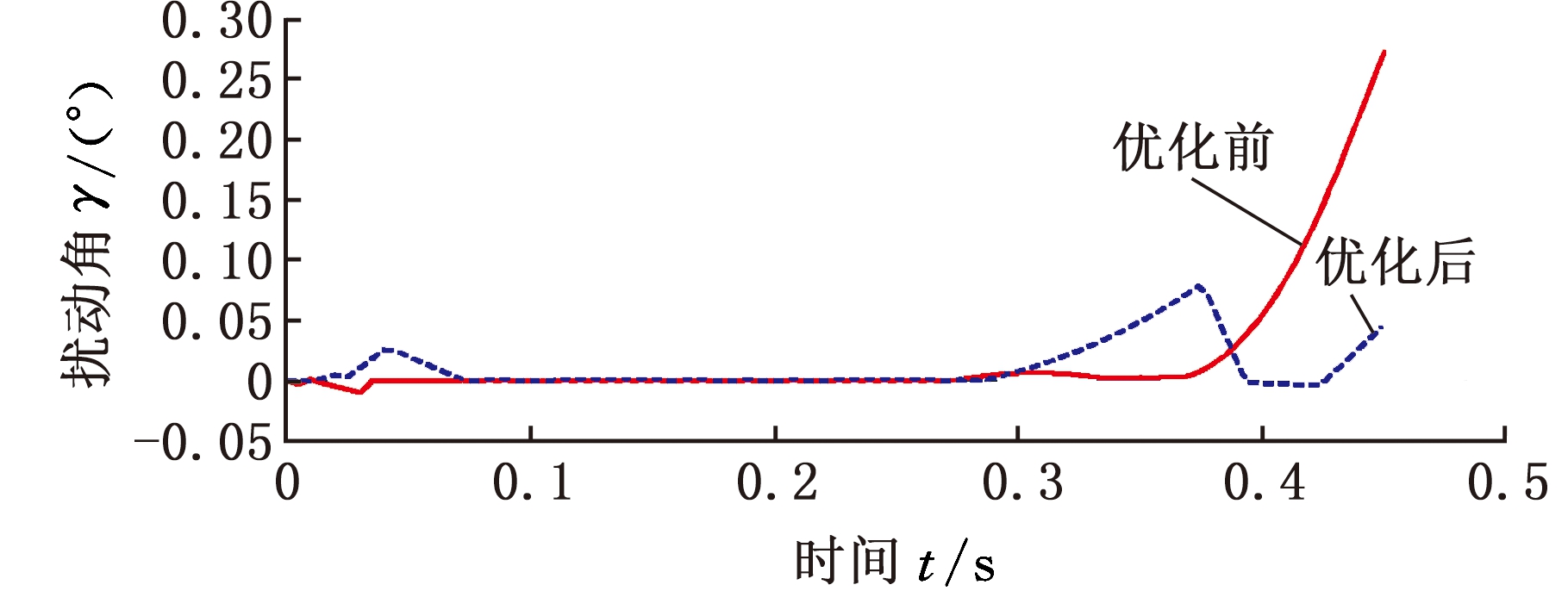
图3 优化前后扰动角对比
Fig.3 Disturbance angle compariso n before-and-after optimization
图4 优化前后扰动角速度对比
Fig.4 Disturbance angular velocity compariso n before-and-after optimization
优化前后火箭弹发射过程中扰动角及扰动角速度变化对比如图3、图4所示。由对比曲线可知，优化前扰动角及角速度在火箭弹离轨前以较大斜率呈上升趋势，在离轨瞬间达到最大值；优化后扰动角及角速度在火箭弹离轨前出现先增大再减小再增大的波动，最终得到的初始扰动相比于优化前明显减小。
在选择优化设计参数情况下，发射过程中弹与导轨间碰撞力约束情况如图5所示，表明在发射过程中弹与导轨间没有碰撞现象发生，满足性能约束条件。优化前后火箭弹速度对比如图6所示，表明火箭弹发射过程中速度变化在定心部设计参数优化前后基本一致。火箭离轨姿态参数在优化前后的对比情况如表3所示，由对比结果可知，在以初始扰动为优化目标得到的定心部优化设计参数下，火箭弹的离轨速度、离轨时间几乎无变化。
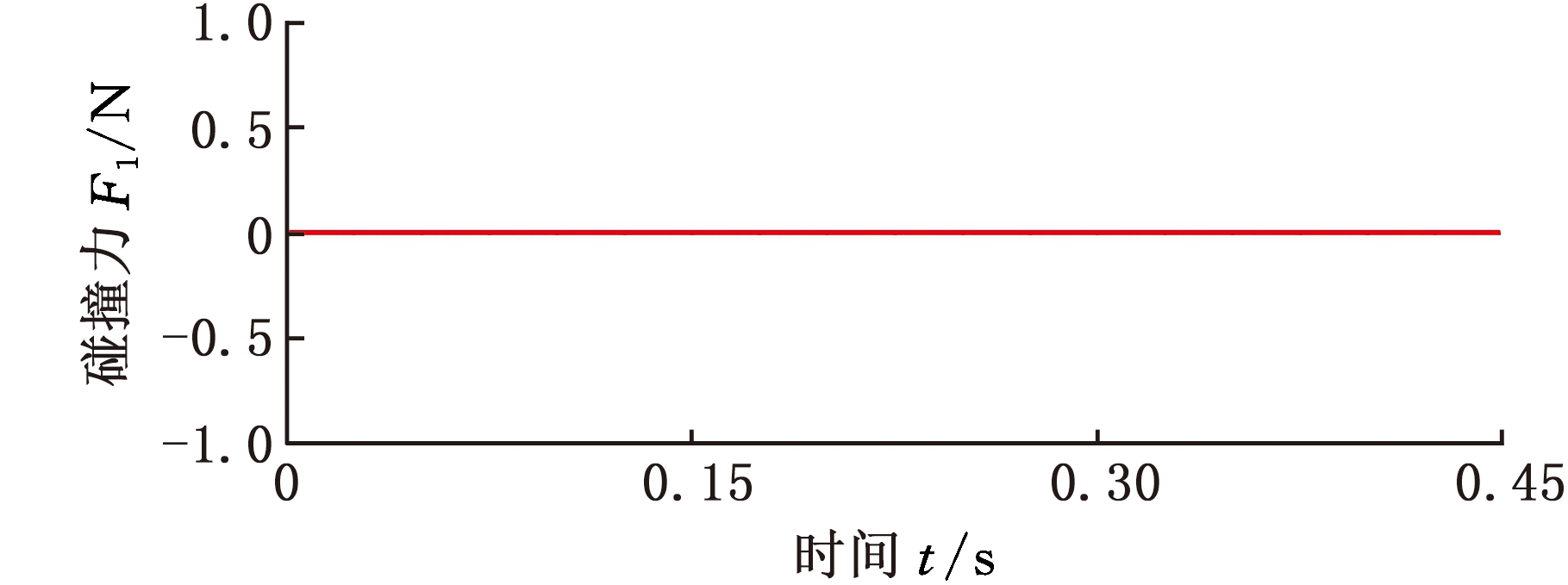
图5 优化后的弹体与导轨间碰撞力
Fig.5 Impact force between rocket body an d rail after optimization
图6 优化前后速度对比
Fig.6 Velocity comparison before-and-after optimization
由上述结果可知，火箭弹定心部结构参数优化设计值满足约束条件，在几乎不影响离轨时间、速度的同时，使火箭弹的初始扰动角减小了83.74%，初始扰动角速度减小了62.92%，且发射过程弹体与导轨间无碰撞现象发生，获得了良好的优化效果。
4 结论
(1)火箭弹在发射过程中，定心部的宽度和布局是影响初始扰动的灵敏因素，定心部的宽度对初始扰动的影响尤其大。
(2)通过火箭弹发射动力学仿真对定心部结构参数进行优化设计的方法，使得算例中的初始扰动角减小了83.74%，初始扰动角速度减小了62.92%，优化效果良好。因此，合理地选取定心部结构参数能够在较大程度上改善火箭弹的离轨姿态，降低初始扰动量。
[1] 姚昌仁，唐国梁，宋廷伦．火箭导弹发射动力学[M]．北京：北京理工大学出版社，1996：5-22.
YAO Changren, TANG Guoliang, SONG Tinglun. Launching System Dynamics for Rockets or Missiles[M]. Beijing: Beijing Institute of Technology Press, 1996:5-22.
[2] 关宏，徐世杰．基于FLUENT计算的火箭离轨姿态运动仿真与分析[J]．航天控制，2012，30(3)：93-98.
GUAN Hong，XU Shijie. The Analysis and Simulation of Attitude Motion for a Deorbit Rocket Based on FLUENT Flow Field Calculation[J]. Aerospace Control, 2012, 30(3): 93-98.
[3] 朱保义．某多管火箭炮的动力学特性分析[J]．舰船科学技术，2012，34(9)：51-55.
ZHU Baoyi. Dynamic Characteristics of Multiple Rockets Gun[J]. Ship Science and Technology, 2012, 34(9):51-55.
[4] 曾永辉，王洪亮，刘君．某导弹发射系统动力学特性仿真研究[J]．战术导弹技术，2013(1)：32-37．
ZENG Yonghui, WANG Hongliang, LIU Jun.Research on Dynamic Characteristics of Missile Launching System[J]. Tactical Missile Technology, 2013 (1):32-37.
[5] 洪亚军，曹岩枫，尹强，等．火炮身管-反后坐装置集成优化设计方法研究[J]．中国机械工程，2013，24(1)：15-20．
HONG Yajun, CAO Yanfeng, YIN Qiang, et al.Research on Integrated Optimization Method of Barrel and Recoil Mechanisms[J]. China Mechanical Engineering, 2013, 24(1):15-20.
[6] 冯勇，徐振钦．基于多岛遗传算法的火箭炮初始扰动综合优化分析[J]．振动与冲击，2014，33(9)：168-172．
FENG Yong, XU Zhenqin. Comprehensive Optimization of Initial Perturbation of a Rocket System with Multi-island Genetic Algorithms[J]. Journal of Vibration and Shock, 2014, 33(9):168-172.
[7] 陈阵，毕世华．基于减小初始扰动的弹管间隙优化设计方法[J]．固体火箭技术，2010，33(2)：135-137．
CHEN Zhen，BI Shihua. An Optimum Design Method for Clearances between Rockets and Launching Tubes Based on Minimizing Initial Disturbances[J]. Journal of Solid Rocket Technology, 2010, 33(2):135-137.
[8] 李彦君．发射装置与火箭弹间相互作用非线性动力学分析[D]．南京：南京理工大学，2012．
LI Yanjun. Nonlinear Dynamics Analysis on the Interaction between Emission Devices and Rockets[D]. Nanjing: Nanjing University of Science and Technology, 2012.
[9] 李喜仁．防空导弹发射装置[M]．北京：中国宇航出版社，1993：406-481．
LI Xiren. Air Defense Missile Launcher[M]. Beijing: China Astronautic Publishing House, 1993:406-481.
[10] 李军．火箭发射系统设计[M]．北京：国防工业出版社，2008：162-189．
LI Jun. Rocket Launching System Design[M].Beijing: National Defense Industry Press, 2008:162-189.
