0 引言
机床的加工精度和加工效率决定于机床整机的静动态特性,而床身的支撑方式直接影响机床整机的静动态特性[1],垫铁作为联结基础和床身的重要部件,对精密机床的加工精度有着重要的影响。目前国内机床厂商一般根据设计经验选择垫铁数量并布置垫铁位置,垫铁位置通常均匀布置于床身底面。事实上,不同的垫铁布置方案会使床身在实际加工过程中获得不同的静动态特性[2],影响着机床的加工精度,合理的垫铁位置分布可以提高加工精度,延长机床使用寿命。目前,对机床垫铁位置的确定已引起国内外学者的关注。赵秋红[3]提出了三种布置床身垫铁的方式,分别为对称方式、横向对称方式、非对称方式,根据实际的研究对象每种方式列举了3种布置情况,随后对这9种情况分别进行了静力分析和模态分析,结果显示在垫铁以对称方式布置情况下床身低阶固有频率最佳,固有频率随垫铁数量增加缓慢增大。BUHI[4]以一个微型夹持机构为例,将其支撑位置参数化并通过几何非线性分析模拟不同工况,最终使用连续型拓扑优化方法确定支撑位置,结果表明该机构刚度显著提高。
另一方面,机床的调平对加工稳定性及精度有着重要的影响,调平不当会导致机床振动,加工质量下降,设备使用寿命缩短。传统床身由多个垫铁支撑,接触点多,不利于床身调平。三点支撑利用三点确定一个平面的原理,可以有效提高机床可调平性、稳定性,且明显缩短安装时间。三点支撑方式相对于多点支撑具有精度保持性好、内应力小、易于调平、便于安装等优点[5],已在国内外机床企业得到应用,如德国德玛吉公司的NHC 4000卧式加工中心、瑞士克林伯格公司的部分机床已使用三点支撑,并获得了较高的机床加工精度[6-7]。云青等[5]结合中心复合试验、响应面模型和多目标遗传算法,针对三点支撑下的床身结构开展了多目标优化设计,提高了床身的静动态性能。
对垫铁位置进行优化设计,寻求垫铁最优支撑位置,可以在不改变床身结构的情况下,仅通过移动垫铁支撑位置就能达到提高机床性能的目的,在机床实际设计和使用中具有重要价值。目前对机床支撑布置方式的研究,多是在位置确定情况下,或者人为改变支撑位置情况下对机床进行优化设计,很少有文献研究三点支撑位置的最优布置方法。三点支撑位置的设计,需尽量保证床身上各部件总质心在床身底面的投影与三点支撑所围成的三角形形心相重合,但在实际使用过程中由于机床工况复杂,机床在加工过程中质心时刻在发生变化,因此很难直接确定三点支撑的最优位置。针对这种情况,本文提出了一种机床三点支撑位置多目标优化设计方法,并以某型号精密外圆磨床的T形床身为例,开展三点支撑位置优化设计。
1 三点支撑床身初始模型的确定
图1a所示为某型号磨床的主要结构,主要由五大部分组成:床身、头架、尾架、工作台和砂轮架;图1b所示为该型号床身结构,该床身为典型的T形结构,床身的总体尺寸为2 760 mm×1 680 mm×690 mm。根据床身结构形式,可将床身分为前后床身两部分。前床身主要支撑工作台、头架和尾架等部件,其上从前至后分布两条导轨,分别为平导轨和V形导轨;后床身用于支撑砂轮架、主轴箱等部件。
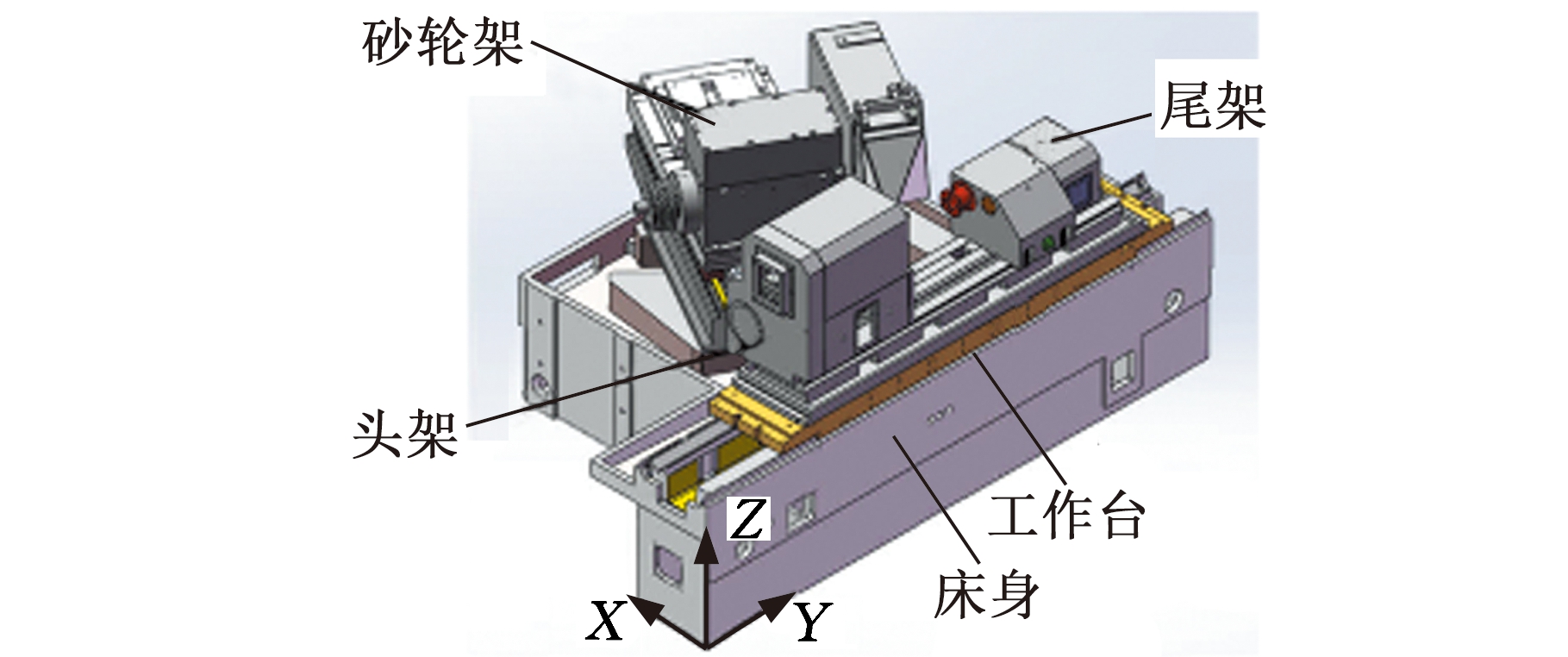
(a)磨床部件

(b)床身结构示意图
图1 某型磨床结构
Fig.1 A type of grinding machine structure
1.1 载荷工况分析
在工作状态下,磨床工作台等移动部件在床身上做直线往复运动,使得床身的受力情况变得十分复杂,因此如何选择载荷工况以尽可能全面地反映其实际的工作状况,不仅影响床身静动态性能分析,而且对后续支撑件位置优化有直接影响[8]。磨床导轨上的移动部件可在工作行程内沿直线任意移动,因此床身受到移动载荷的作用。磨床受力最恶劣的磨削位置分别为左右两个极限位置以及最常用的工作行程中间位置,因此可以将这三个位置作为待研究的载荷工况来近似模拟实际的工作过程[9]。
为了充分模拟床身受载荷情况,对床身三个位置(工作台在前床身的左极限位置;工作台位于导轨的正中间位置;工作台在前床身的右极限位置)进行加载。这三个位置按三种工况来处理。图2所示为床身不同工况的示意图(三种工况下砂轮架的位置均保持不变)。

图2 不同工况示意图
Fig.2 Different working conditions
1.2 三点支撑床身垫铁初始位置
目前,T形床身的垫铁位置一般按照床身底面的形状来布置,其布置原则为:在8个角点上布置8块垫铁,在长边1/3点上再布置两块垫铁,一共10块垫铁,如图3中的T1~T10所示。用三点支撑代替原有布置,可按照以下方法来确定三个支点的初始位置。

图3 床身底面分区示意图
Fig.3 Bed bottom partition diagram
三点支撑位置的确定主要有两个原则,要保证:①床身上各部件总质心在床身底面的投影时刻在三点支撑所围成的三角形区域内;②三个支撑点围成三角形的面积较大,以保证支撑的稳定性。因此首先对床身进行分区,分别为T1T2T8T7、T3T4T5T6围成的四边形区域和T7T9T10、T6T9T10围成的三角形区域,见图3。因为要使三点支撑围成三角形的面积尽量大,因此中心区域部分可以不选择,只选择四周的区域即可。T7T9T10、T6T9T10两块区域有所重合且重合部分靠近后床身边缘,主要是为了将后床身支撑点布置在后床身关于Z向对称的中轴线上,同时使该支撑点在一定程度上靠近后床身后边缘线T9T10来尽量保证床身的稳定性。对4块区域编号,如表1所示。
表1 分区编号
Tab.1 Partition number
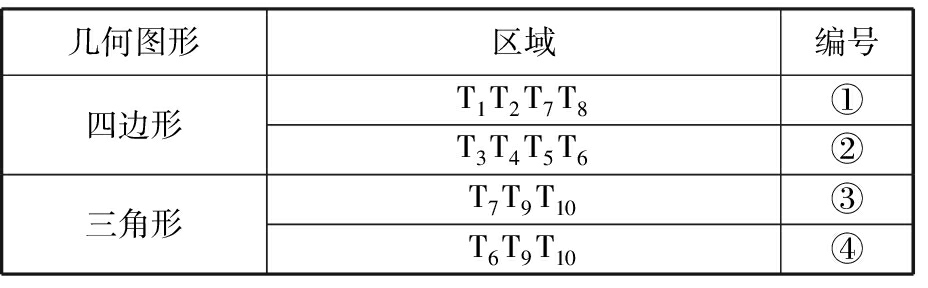
几何图形区域编号四边形T1T2T7T8①T3T4T5T6②三角形T7T9T10③T6T9T10④
如图4所示,点A、B、C、D分别为区域①、②、③、④的形心,连接CD,取线段CD中点E,三个黑点A、B、E为三点支撑垫铁初始位置。连接AE、AB、BE,△ABE为三点支撑所围成的三角形区域。在图2所述的三种工况下,磨床总质心在床身底面投影位置分别为a1、a2、a3,且均在△ABE内部,初步保证了床身静态性能。因此,三点支撑3个垫铁的初始位置确定为A、B、E。本文将三个初始点支撑下的T形床身称之为“原型”,在原型的基础上进行垫铁位置优化。

图4 三点支撑床身垫铁初始位置
Fig.4 Prototype of three-point support be d pad-iron position
以点O为原点建立平面直角坐标系,横轴为Z轴,纵轴为X轴,易知线段AB为水平线,即垫铁A和垫铁B的纵坐标相同。得到三垫铁A、B、E初始位置坐标如表2所示。
表2 垫铁A、B、E初始位置
Tab.2 Initial position of pad-iron A,B,E mm

垫铁位置(Z , X)A(2 370,1 500)B(390,1 500)E(1 350,430)
1.3 设计变量取值范围的确定

图5 设计变量示意图
Fig.5 Design variable diagram
图5为设计变量在磨床床身底面示意图,A、B、E为垫铁,a1、a2、a3为床身及其以上部件在左极限工况、中间位置工况和右极限工况下的重心投影点。在OZX平面直角坐标系中,因为垫铁A、B在同一水平线上,即它们的X轴坐标相等,所以3个垫铁的位置可用5个设计变量表示:E垫铁X轴方向位置XE;E垫铁Z轴方向位置ZE;A垫铁Z轴方向位置ZA;B垫铁Z轴方向位置ZB;A、B垫铁X轴方向位置XA(XB)。设计变量如表3所示。
表3 OZX坐标系下三个垫铁的参数化位置
Tab.3 Parameterized position of three pad-iron s in OZX coordinate system

垫铁位置(Z,X)A(ZA,XA)B(ZB,XB)E(ZE,XE)
以三种工况的重心a1、a2、a3必须在三个垫铁围成的△ABE中为设计原则,考虑垫铁不超出床身边缘线的情况,讨论5个设计变量ZA、XA(XB)、ZB、ZE、XE的取值上下限。
图6中,粗实线为床身边缘线,内部细实线为考虑垫铁不超出床身边缘线情况下垫铁位置设计范围的包络线。连接Aa1交包络线于K,连接Ba3交包络线于L。测得K点X轴坐标小于L点X轴坐标,为保证机床三个工况的重心在△ABE内,选K点X轴坐标为E垫铁X轴方向的最大值。为了保证支撑的稳定性,后床身支撑应尽量靠近中线,过K点作水平线交EB、EA于K1、K2,考虑到T7T8比T5T6长80 mm,过K2沿Z轴正方向延长水平线80 mm至K3,则K1K3即为E垫铁Z方向的设计长度。Z轴到K1K3距离为562 mm,因此XE最大取值为562 mm。
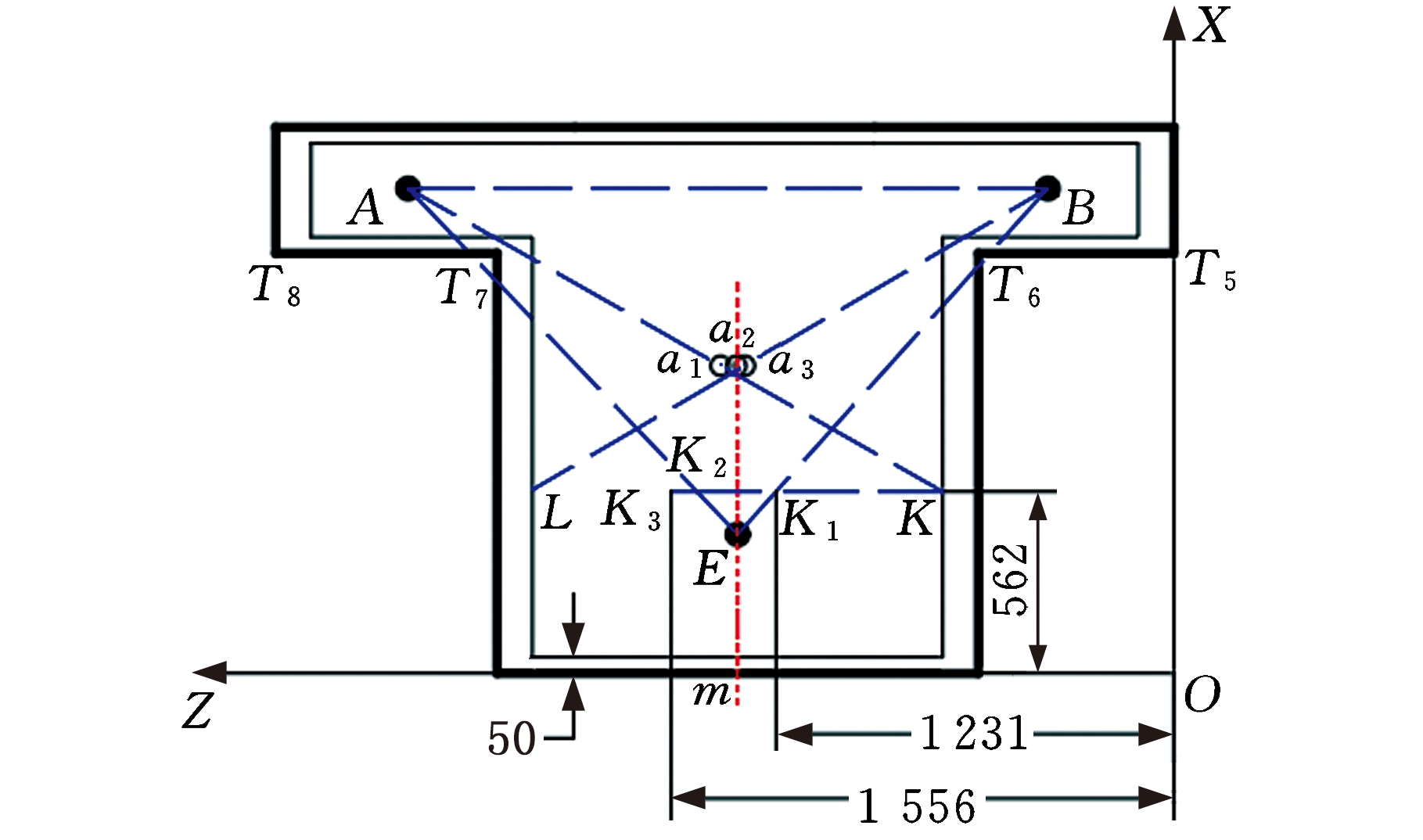
图6 E垫铁设计范围的确定
Fig.6 Determination of E pad-iron design range
如图7所示,同样考虑极限情况,连接Ea1交线段AB于K′,连接Ea3交线段AB于L′,测得K′点Z坐标为1 459 mm,L′点Z坐标为1 305 mm。△EK′L′为机床在左右极限位置工况下能保证结构重心在三个支撑位置所围成三角形内的最小三角形。为了保证支撑的稳定性,以1.4为安全系数增大K′横坐标,减小L′横坐标,取整得:K′Z=2 043 mm,L′Z=932 mm。XA(XB)的取值范围不超过包络线。
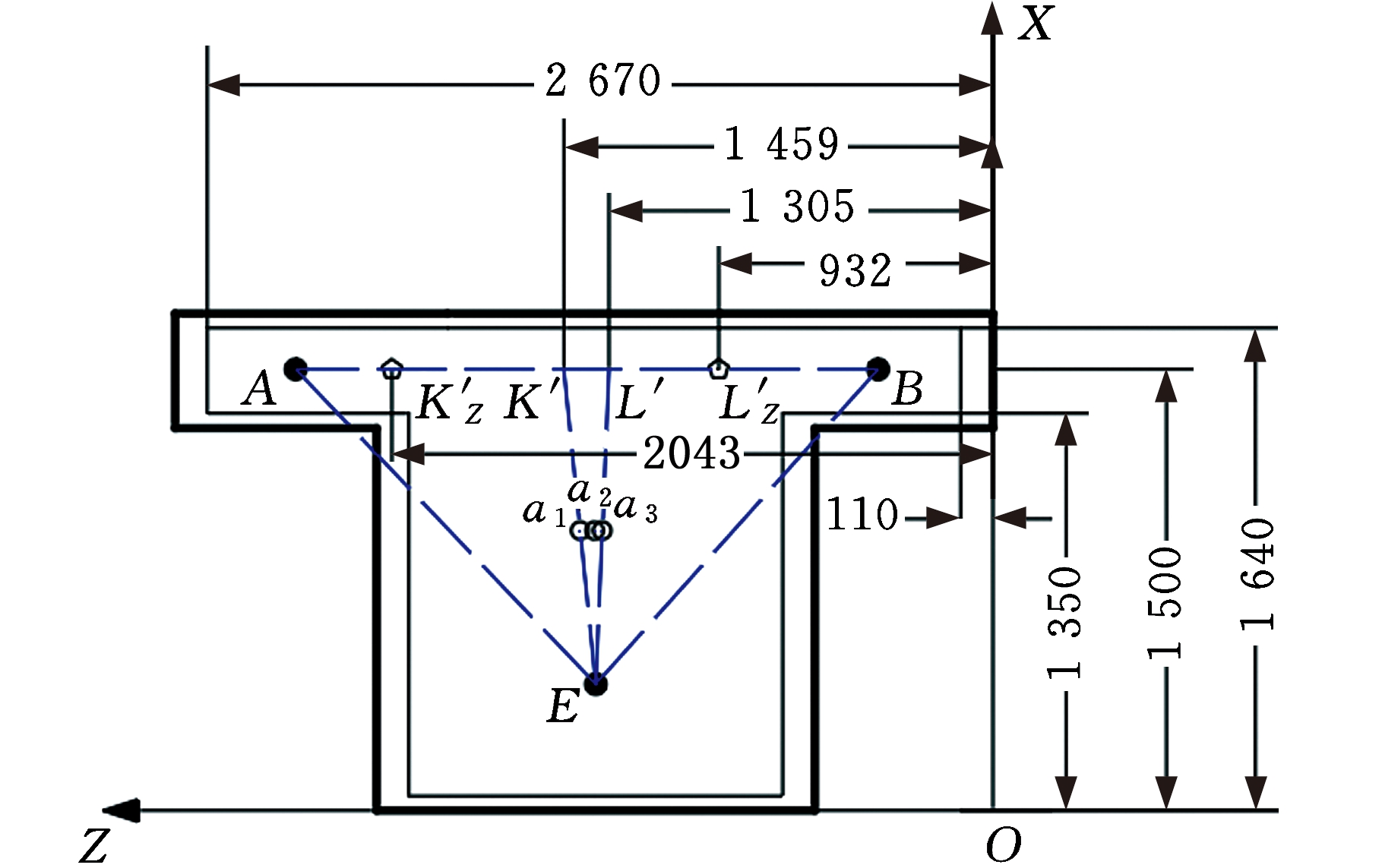
图7 A、B垫铁设计范围的确定
Fig.7 Determination of A,B pad-irons design range
得到5个设计变量在平面OZX坐标系下的取值范围如表4所示。
表4 在OZX坐标系中设计变量取值范围的确定
Tab.4 Determination of design variable range in OZXcoordinate system mm
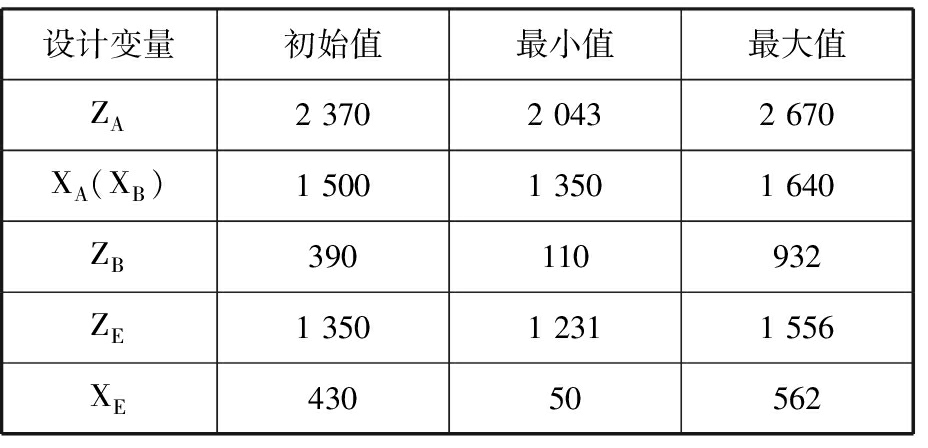
设计变量初始值最小值最大值ZA2 3702 0432 670XA(XB)1 5001 3501 640ZB390110932ZE1 3501 2311 556XE43050562
2 基于静动态性能的垫铁位置优化
2.1 多目标优化数学模型
垫铁位置优化旨在提高床身的静动态性能,通过调整三个垫铁支撑位置使床身静动态性能最优。考虑以床身结构动刚度和静刚度最大为目标函数,分别选择一阶固有频率最大和床身上V形导轨的最大变形最小来综合反映床身静动态刚度。
以一阶固有频率最大和床身上V形导轨的最大变形最小为目标函数,以垫铁位置为设计变量,对垫铁位置进行多目标优化设计。其中,优化一阶固有频率用于提高床身动态性能,优化V形导轨最大变形为改善床身静态性能。
多目标优化设计数学模型如下:
find G=(ZA,XA(XB),ZB,ZE,XE)
min D&(-f1)
s.t. Gmin≤G≤Gmax
式中,G为设计变量集;D为床身在中间位置工况下V形导轨最大变形量;f1为床身结构的第一阶固有频率;Gmin、Gmax为设计变量下限和上限。
采用邻域培植遗传算法(neighborhood cultivation genetic algorithm,NCGA)[10-11]在设计区域上进行多目标优化,在Pareto优化解集中根据实际情况选择一个优化结果,如表5所示。图8所示为目标函数的迭代历程。
表5 设计变量优化值
Tab.5 Design variable optimization value mm
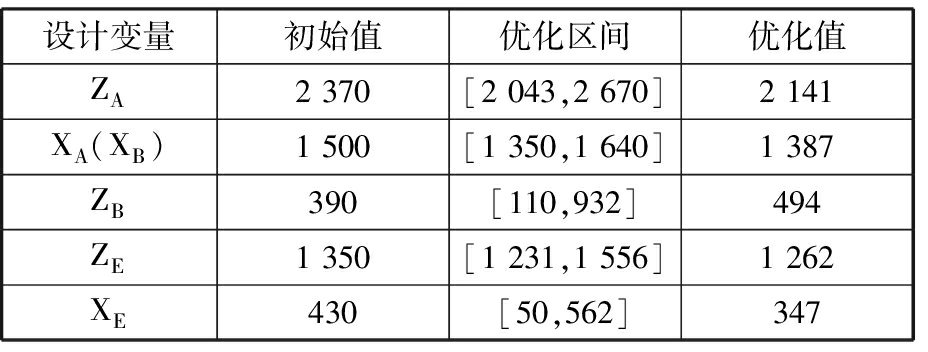
设计变量初始值优化区间优化值ZA2 370[2 043,2 670]2 141XA(XB)1 500[1 350,1 640]1 387ZB390[110,932]494ZE1 350[1 231,1 556]1 262XE430[50,562]347

图8 多目标优化迭代曲线
Fig.8 Multi-objective optimization iterativehistory
表6所示为优化前后垫铁位置,图9为优化前后垫铁位置分布示意图,其中,A、B、E为优化前垫铁位置,A3、B3、E3为优化后垫铁位置。由图9可知,垫铁A、B、E均向Z轴靠近,在Z方向上垫铁A、B同时往导轨中部移动,且垫铁A移动幅度明显大于垫铁B的移动幅度。
表6 优化前后三点支撑床身垫铁位置
Tab.6 Three positions of supporting bed pad-iro n before and after optimization mm

垫铁编号原型(Z,X)优化后(Z,X)A(2 370,1 500)(2 141,1 387)B(390,1 500)(494,1 387)E(1 350,430)(1 262,347)
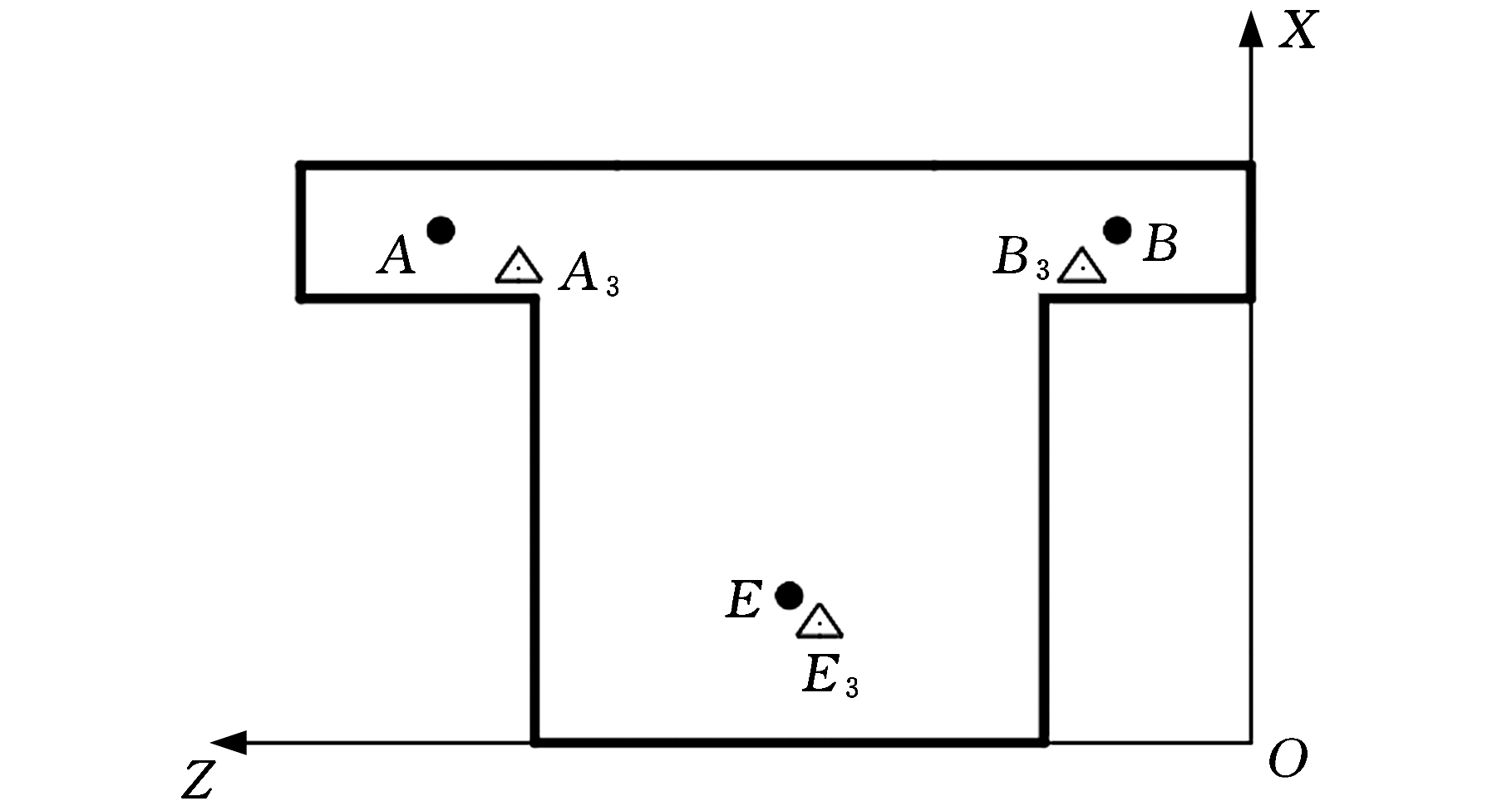
图9 优化前后垫铁位置分布示意图
Fig.9 Schematic diagram of position distribution o f pad-irons before and after optimization
2.2 多目标优化结果验证
根据优化结果对三点支撑床身垫铁位置重新进行参数化建模。在此基础上,对床身的三种工况进行静动态性能分析,分析结果与原型床身分析结果对比如表7所示。
表7 优化前后三种工况下V形导轨位移最大变形量对比
Tab.7 Comparison of maximum displacemen t of V-rail under three working conditions before an d after optimization
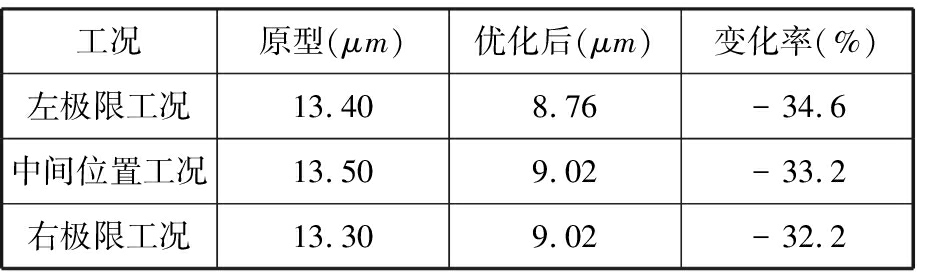
工况原型(μm)优化后(μm)变化率(%)左极限工况13.408.76-34.6中间位置工况13.509.02-33.2右极限工况13.309.02-32.2
表7可以看出,左极限位置工况、中间位置工况和右极限位置工况下,V形导轨最大变形量分别减小34.6%、33.2%和32.2%,平均减小率为33.3%。从V形导轨最大变形评价指标看,床身结构静态性能得到提高,加工精度有所提高。
图10所示为中间位置工况下原型及多目标优化后V形导轨位移变形量沿Z坐标方向变化情况。图10横坐标为选取的V形导轨沿Z方向直线的节点,直线具体位置如图11所示。由图10可以看出,多目标优化后V形导轨变形曲线在原型床身变形曲线的下方,且优化后V形导轨变形量显著减小,最大变形差(最大变形量减去最小变形量)为5 μm。进一步引入V形导轨变形方差作为评价床身静态性能的指标,由图10所示的数据点计算得到优化前后工作台在中间位置工况下V形导轨变形方差如表8所示。

图10 优化前后V形导轨Z方向变形曲线对比
Fig.10 Comparison of V-rail Z-direction deformatio n curves before and after optimization
表9所示为优化前后磨床床身结构前6阶固有频率对比,可以看出三个垫铁位置优化后,除了床身第3阶固有频率减小外,其余前5阶固有频率均增大。由于在对床身进行多目标优化时,最大化一阶固有频率为其中一个优化目标,故一阶固有频率上升值为8.7%。
综上所述,垫铁位置优化后,V形导轨最大变形、变形方差和一阶固有频率均得到改善,实现了优化床身静动态性能的目标。

图11 选取的V形导轨沿Z方向直线
Fig.11 The line selected on the V-rail along Z direction
表8 优化前后V形导轨变形方差
Tab.8 V-rail deformation variance before an d after optimization
原型优化后变化率(%)变形量方差S27.153.03-57.6
表9 优化前后床身前6阶固有频率对比
Tab.9 A comparison of the first six natural frequencie s of the bed before and after optimization

阶数固有频率(Hz)原型优化后变化率(%)1123.26133.988.72168.45178.696.13190.74183.52-3.84210.06250.6719.35255.15258.051.16274.55280.962.3
3 三点支撑床身垫铁位置布置准则探讨
利用NCGA算法对三点支撑床身垫铁位置进行多目标优化得到的Pareto最优解集和Pareto前沿如图12所示,图中,圆点为Pareto最优解集;曲线为Pareto前沿;方点为优化迭代过程后得到的优化解。接近Pareto前沿的解更优。

图12 三点支撑床身垫铁位置的Pareto最优解集
Fig.12 Pareto optimal solution set of three-poin t supporting bed pad-iron position
根据图12的Pareto前沿可画出三个垫铁优化位置的散点集,如图13所示。黑点表示垫铁的优化位置;圆圈表示三个工况下机床重心在床身底面的投影点;粗实线为床身边缘线;内部细实线为考虑垫铁不超出床身边缘线情况下垫铁位置设计范围的包络线。

图13 垫铁优化位置散点图
Fig.13 Scatterplot of optimized pad-iron location
为了便于得到三个垫铁优化位置的关系,用包含垫铁A、B、E的最小矩形优化位置散点,用线段a代表机床质心位置,如图14所示。

图14 垫铁优化位置与床身尺寸位置关系图
Fig.14 Optimal pad-iron positions and bed size
通过探究Pareto最优解集下三点支撑床身垫铁位置与机床重心及床身总体尺寸之间的关系得出T形床身垫铁布置原则如下:
(1)不同位置工况下机床重心在底面的投影均必须在三点支撑围成的三角形内;
(2)三点支撑围成三角形的形心沿X轴负方向到机床重心连线的垂直距离取尺寸w的4.0%~10.5%较好;
(3)三点支撑围成三角形的形心到X轴垂直距离取尺寸l的44.2%~48.2%较好;
(4)垫铁A到X轴垂直距离取尺寸l的73.2%~78.5%较好;
(5)垫铁A到Z轴垂直距离取尺寸w的82.1%~89.3%较好;
(6)垫铁A、B之间的Z向距离取尺寸l的54.2%~63.4%较好;
(7)垫铁E到X轴垂直距离取尺寸l的44.7%~46.6%较好;
(8)垫铁E到AB连线的垂直距离取尺寸w的60.6%~72.1%较好。
4 结论
(1)本文以随工作台运动的机床整机质心在床身底面投影点落在三个支撑点围成的三角形内和垫铁不超出床身边缘线为设计原则,运用极限位置法确定设计变量取值范围。建立多目标优化数学模型,采用NCGA算法对三个垫铁位置进行基于床身静动态性能的多目标优化。以V形导轨最大变形量和一阶固有频率为评价指标,对三点支撑垫铁位置进行优化设计,优化后的床身静动态性能均得到了提升。
(2)经过多目标优化得到Pareto解集后,以最小矩形包围优化三个垫铁位置散点集,通过计算最小矩形、三个支撑点所围成三角形的形心和床身总体尺寸的关系确定T形床身三点支撑位置布置原则,为三点支撑床身垫铁位置设计提供一种新思路。
[1] ZHANG Heng, DING Xiaohong, DONG Xiaohu, et al. Optimal Topology Design of Internal Stiffeners for Machine Pedestal Structures Using Biological Branching Phenomena[J]. Structural and Multidisciplinary Optimization, 2018, 57(6): 2323-2338.
[2] ZHU Jihong, ZHANG Weihong. Maximization of Structural Natural Frequency with Optimal Support Layout[J]. Structural and Multidisciplinary Optimization, 2006,31: 462-469.
[3] 赵秋红. 涡轮增压器喷嘴环叶片专用机床整体布局与支撑部件优化设计[D].武汉: 武汉理工大学,2013.
ZHAO Qiuhong.Optimization Design of Overall Layout and Supporting Parts for Turbocharger Nozzle Ring Blades[D]. Wuhan: Wuhan University of Technology, 2013.
[4] BUHI T. Simultaneous Topology Optimization of Structure and Supports[J]. Structural and Multidisciplinary Optimization, 2002, 23:336-346.
[5] 云青,牛文铁,王俊强. 精密机床床身结构三点支撑的多目标优化设计[J].机械设计,2015,32(7): 1-7.
YUN Qing, NIU Wentie, WANG Junqiang.Multi-objective Optimization Design of Three-point Support for Precision Machine Tool Bed Structure[J]. Mechanical Design, 2015,32(7): 1-7.
[6] 德玛吉机床有限公司.NHC 4000高稳定性、高精度和高动态性能的卧式加工中心[DB/OL].[2018-06-20]. https:∥cn.dmgmori.com/products/machines/milling/horizontal-milling/nhc/nhc-4000.
DMG MORI. NHC 400 Horizontal Machining Center with High Stability, High Precision and High Dynamic Performance[DB/OL]. [2018-06-20]. https:∥cn.dmgmori.com/products/machines/milling/horizontal-milling/nhc/nhc-4000.
[7] Kellenberger. KEL-VITA Product Documents [DB/OL]. [2018-06-20]. http:∥www.hardinge.com/ProductCatalog/Product/ProductId/142.
[8] LAW M, ALTINTASN Y, PHANI A S. Rapid Evaluation and Optimization of Machine Tools with Position-dependent Stability[J]. International Journal of Machine Tools & Manufacture, 2013,68(3): 81-90.
[9] LAW M, IHLENFELDT S, WABNER M, et al. Position-dependent Dynamics and Stability of Serial-parallel Kinematic Machines[J]. CIRP Annals—Manufacturing Technology, 2013, 62(1):375-378.
[10] DAI Xiaoming,SUN Rong,ZOU Runmin. Global Convergence Analysis of Non-crossover Genetic Algorithm and Its Application to Optimization[J]. Journal of Systems Engineering and Electronics,2002,13(2): 84-91.
[11] 银波,徐典,安亦然,等. 基于iSIGHT平台的三维机翼气动优化设计[J]. 应用数学和力学,2008,29(5):544-549.
YIN Bo, XU Dian, AN Yiran, et al. 3D Wing Aerodynamic Optimization Design Based on iSIGHT Platform[J]. Applied Mathematics and Mechanics, 2008,29(5):544-549.
