0 引言
近年来，随着传感器技术的发展及其在汽车领域中的广泛应用，使高级驾驶员辅助与自动驾驶技术得以快速发展[1-2]。作为未来改善道路交通与驾驶安全最具前途的技术，自动驾驶技术日益受到学术界与工业界的广泛关注[3]，研究热点主要包括智能车自适应巡航、车道保持、主动避障、主动变道等[4]。变道作为最传统的驾驶行为之一，相比其他智能车相关技术的研究成果，主动变道的研究是滞后的。然而，所有驾驶行为中，变道是最复杂的，因为需要同时考虑纵向与横向控制[3-5]。文献[6-8]充分说明了不安全的变道行为是发生交通拥堵和交通事故的关键原因。
智能车主动变道主要涉及变道决策机制、变道轨迹规划和变道轨迹跟踪三方面的关键技术。在智能车自主变道轨迹跟踪方面，人们期望在未来的控制研究中能够充分利用优秀驾驶员的驾驶控制方法和习惯[9]。文献[10]提出了一种基于改进的预瞄跟随驾驶员模型的电动汽车智能转向控制策略。针对自动驾驶车辆的大曲率转向控制问题，文献[11]研究了拟人转向控制模型，并设计了并联的模糊控制器；文献[12]提出了一种动态双点预瞄策略，设计了横纵向模糊控制器。但上述文献中的模糊规则难以建立，高控制精度条件下控制器的实时性难以保证。
为充分考虑智能车变道过程中道路的动力学特性, 本文建立了车辆二自由度简化模型及道路模型；基于“预瞄-跟随”理论建立了智能车自主变道过程中多点最优预瞄轨迹跟踪控制模型，并利用线性二次型调节器(linear quadratic regulator,LQR)理论设计了轨迹跟踪控制器，以实现智能车变道过程中的转向控制；在MATLAB/Simulink中建立了自主变道的决策模块、参考轨迹模块及轨迹跟踪控制模块，在CarSim中建立了驾驶场景与传感器模型，并设置了仿真工况，从而实现了基于MATLAB/Simulink和CarSim的智能车自主变道的联合仿真，且结合实车测试结果验证了所设计控制器的控制效果。
1 车辆动力学建模
构建一个精确且能够反映车辆运动学与动力学特性的模型是进行智能车变道轨迹跟踪控制的前提。由于车辆是一个非常复杂的非线性时变系统，建立一个可完整地反映各方面特性的动力学模型既不现实也没有必要。为使汽车横向换道模型计算不至于过于复杂，将汽车简化为二自由度模型进行研究[13]。在分析的过程中作了如下的假设：①忽略悬架的影响，认为汽车的运动在一个平面上；②汽车纵向速度恒定；③汽车只有沿y 轴的横向运动和绕z 轴的横摆运动两个自由度。
在进行智能车变道轨迹跟踪的控制中，实际上是通过控制转向盘实现对车辆行驶轨迹的控制。所以，考虑车辆横向与横摆运动两个自由度的车辆动力学模型就可满足要求，如图1所示。
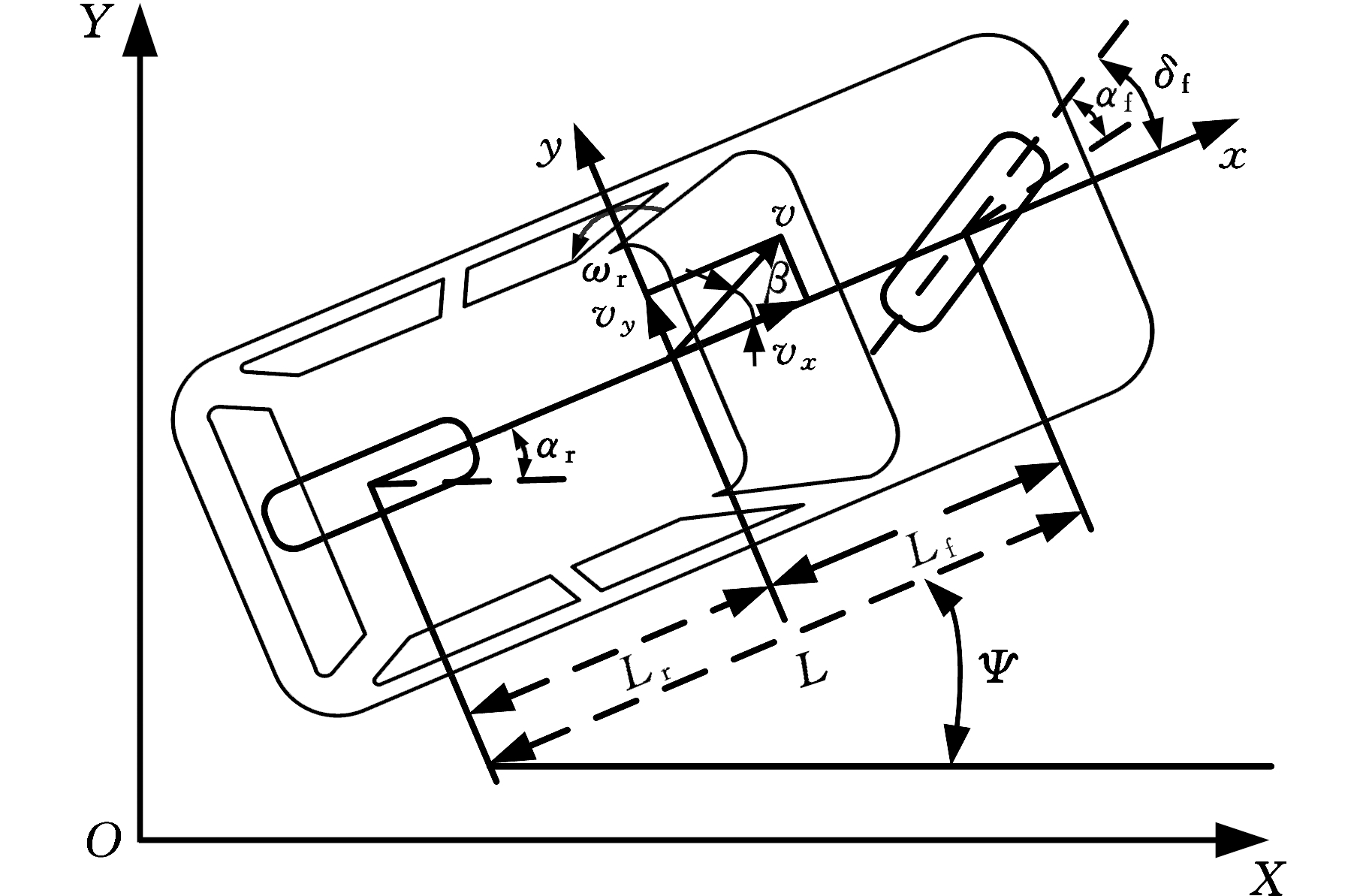
图1 车辆动力学模型
Fig.1 Vehicle dynamics model
二自由度车辆模型状态空间方程为
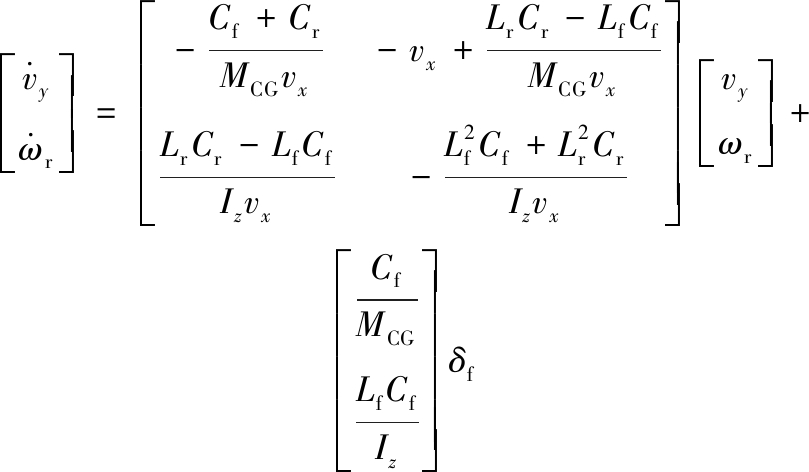
(1)
式中，MCG为整车质量；vx为汽车纵向行驶速度；vy为汽车的横向速度；β为汽车质心侧偏角；ωr为汽车横摆角速度；δf为汽车前轮转角；L为轴距；Lf为质心到前轴的距离；Lr为质心到后轴的距离；Iz为车辆绕z轴横摆转动惯量；Cf、Cr分别为前后轮胎的侧偏刚度。
式(1)表示的车辆模型状态空间方程是以车辆坐标系为参考坐标系建立的,而在变道轨迹跟踪过程中，期望的路径是以大地坐标系为参考的，所以为得到车辆位置在大地坐标系下的坐标(图1)，应对其坐标系进行转换：
(2)
(3)
式中，X、Y为大地坐标系下车辆的位置坐标；Ψ为大地坐标系下车辆的实际航向角。
综上，可得到以转向盘转角θ为输入，以车辆横向速度vy、横摆角速度ωr、横向位移y和航向角Ψ为状态变量的状态空间方程：
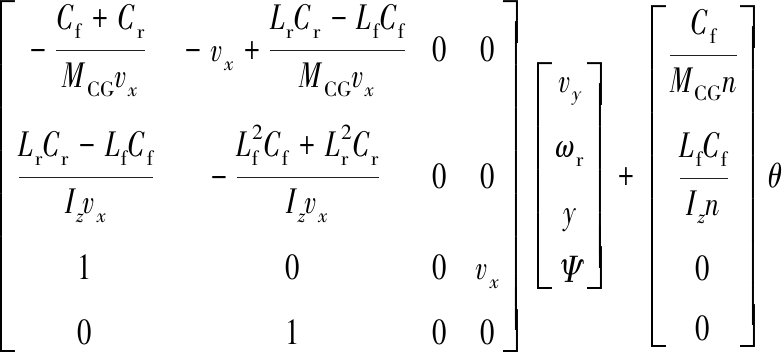
(4)
式中，n为转向盘到车轮的传动比。
将状态空间方程(式(4))写成标准形式，并离散后得到：
x(k+1)=Adx(k)+Bdθ(k)
(5)
x(k)=[vy(k) ωr(k) y(k) Ψ(k)]
式中，x(k)为状态变量；θ(k)为控制变量；Ad为系统矩阵；Bd为控制矩阵。
2 轨迹跟踪控制器设计
2.1 “预瞄-跟随”理论
“预瞄-跟随”理论描述了系统中参考未来输入信息而进行的控制方法，从系统构成而言可理解为预瞄器和跟随器两者串联组成的系统。最优预瞄的理论依据是驾驶员开车过程中，通过对道路前方信息进行预估，使得车辆实际轨迹与理论轨迹的偏差最小，从而得到一个最优的转向盘转角输入[14-16]。
2.2 道路预瞄模型
在建立道路预瞄模型时，通过采样将连续的道路中心线转换为离散形式。其具体的转换过程类似于“队列”：选择N个离散点，并将其作为系统的状态变量。新的离散点继续进入系统，先进先出，然后重复上述方式，直到所有道路采样点逐渐进入系统[17]。随着时间的推移，这些离散点将逐渐靠近车辆，如图2所示。
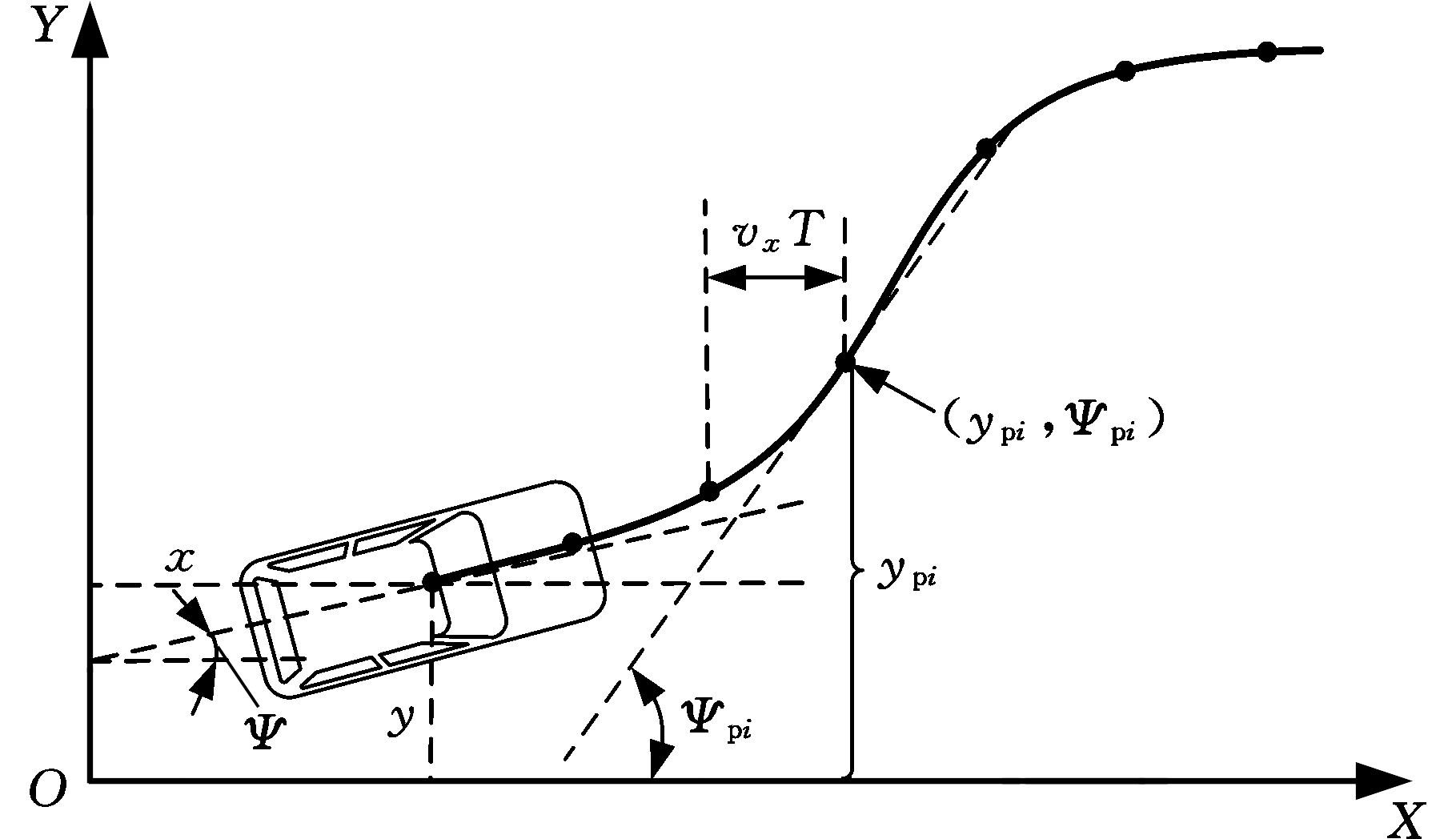
图2 大地坐标系下的道路预瞄模型
Fig.2 Road preview model in geodetic coordinate system
图2中，T为时间步长，ypi为大地坐标系下道路点 i 的横向位置，Ψpi为大地坐标系下道路点i上的期望航向角。假设前面的道路被分成N个等距点(即共有N个道路点)，则道路预瞄模型可表示为
y(k+1)=Dy(k)+Eyp(k)
(6)
yp(k)=[yp1(k) yp2(k) … ypN(k)]T
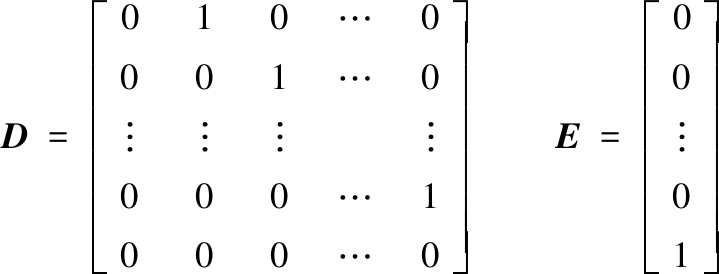
式中，yp(k)表示道路输入；D、E为道路预瞄模型的系统矩阵。
在实际情况下，驾驶员在决策时使用的信息是基于车辆坐标系观察到的，如图3所示，其中Ψri为车辆坐标系下道路点i上的期望航向角。驾驶员获得的道路信息是车辆坐标系下的观测值yri(k)(即驾驶员使用车辆与预瞄道路之间的相对误差)，而不是大地坐标系中的观测值ypi(k)。
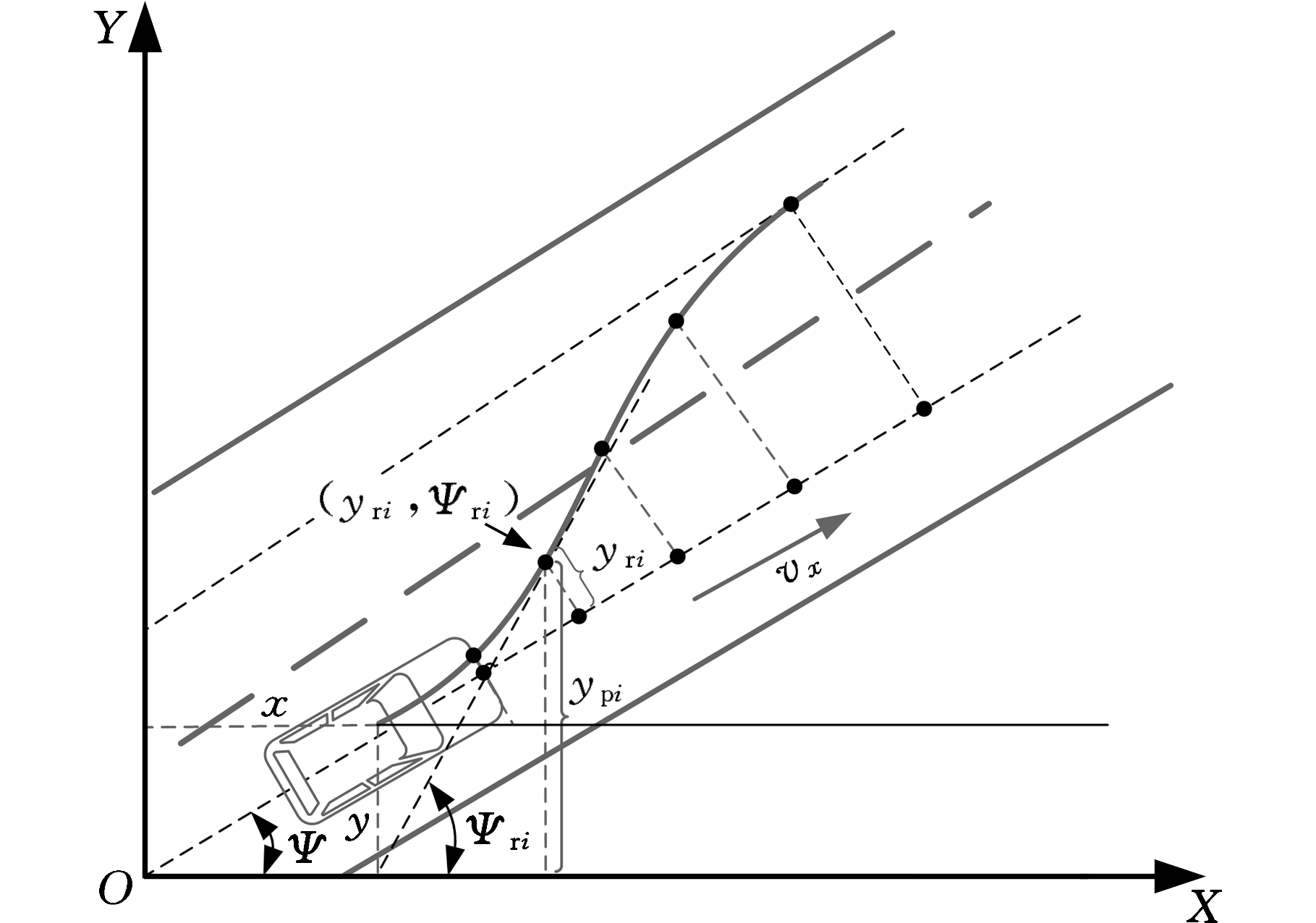
图3 车辆坐标系下的道路预瞄模型
Fig.3 Road preview model in vehicle coordinate system
假定航向角非常小，在大地坐标系中，车辆横向位移可定义为
ypi(k)=y(k)+yri(k)+ivxTΨ(k)
(7)
2.3 控制器设计
本文基于上述“预瞄-跟随”理论和“车辆-道路”模型，提出了最优预瞄轨迹跟踪控制模型。基于LQR理论，充分考虑道路信息，设计了轨迹跟踪控制器，可将车辆与道路整合为一体[18]。图3显示了“道路-车辆”系统，其状态空间方程如下：
(8)
构造的代价函数可表示为
(Ψe(k))TQΨΨe(k)+(θ(k))TQθθ(k)]
(9)
Ψe(k)=Ψri(k)-Ψ(k)
式中，Qy、QΨ和Qθ分别为横向位移偏差、航向角偏差和转向盘转角输入误差的权重矩阵。
当代价函数 J 达到最小值时，可获得状态反馈增益矩阵：
KG=[kx kp]
(10)
其中，kx=[k1 k2 k3 k4]为与车辆状态变量x(k)=[vy(k) ωr(k) y(k) Ψ(k)]相关的状态增益矩阵，kp=[kp1 kp2 … kpN]为与道路信息相关的预瞄增益矩阵。从而可得到最优的转向盘转角控制输入：
(11)
其中，大地坐标系下最优转向盘转角可表示为
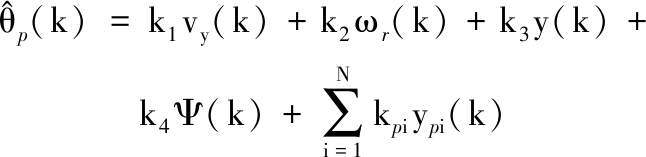
(12)
车辆坐标系下的最优转向盘转角可表示为
(13)
由式(12)和式(13)可得
3 仿真分析
3.1 仿真模型的建立
为验证所设计控制器的有效性，本文采用联合仿真对所构建的控制模型进行仿真验证。CarSim仿真软件可方便灵活地定义试验环境和试验过程，详细地定义整车各系统的性能参数与特性文件，且CarSim与MATLAB/Simulink可实现无缝连接。目前，CarSim软件已在国内外各大汽车制造厂和零部件公司得到了广泛的应用，并已成为汽车行业的标准软件。
本文的仿真过程主要涉及如下5个步骤：
(1)交通环境仿真建模。建立智能车及交通参与车辆的模型，其中智能车模型的参数见表1；单车道宽度为3.5 m的五车道道路示意图见图4。
表1 整车参数
Tab.1 Vehicle parameters
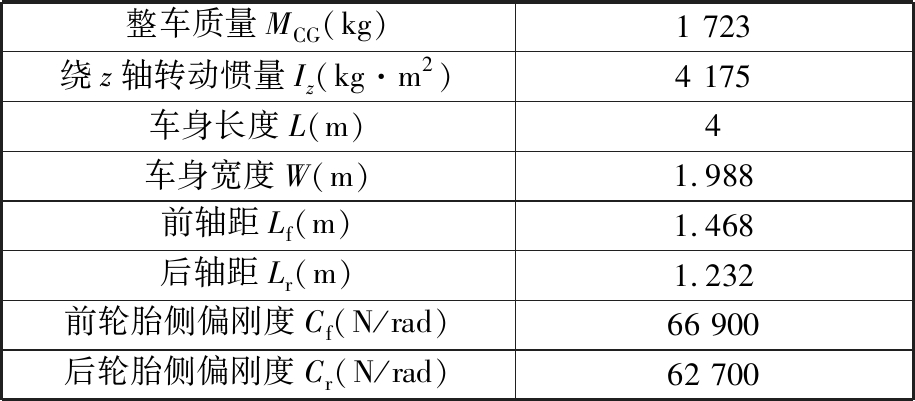
整车质量MCG(kg)1 723绕z轴转动惯量Iz(kg·m2)4 175车身长度L(m)4车身宽度W(m)1.988前轴距Lf(m)1.468后轴距Lr(m)1.232前轮胎侧偏刚度Cf(N/rad)66 900后轮胎侧偏刚度Cr(N/rad)62 700
图4 仿真环境模型
Fig.4 Simulation environment model
(2)传感器仿真建模。该模型包括1个前向测距雷达传感器和4个角雷达测距传感器。
(3)控制系统仿真建模。基于MATLAB/Simulink软件建立控制系统仿真模型，包括变道决策模块、变道参考轨迹模块和轨迹跟踪控制模块，如图5所示。
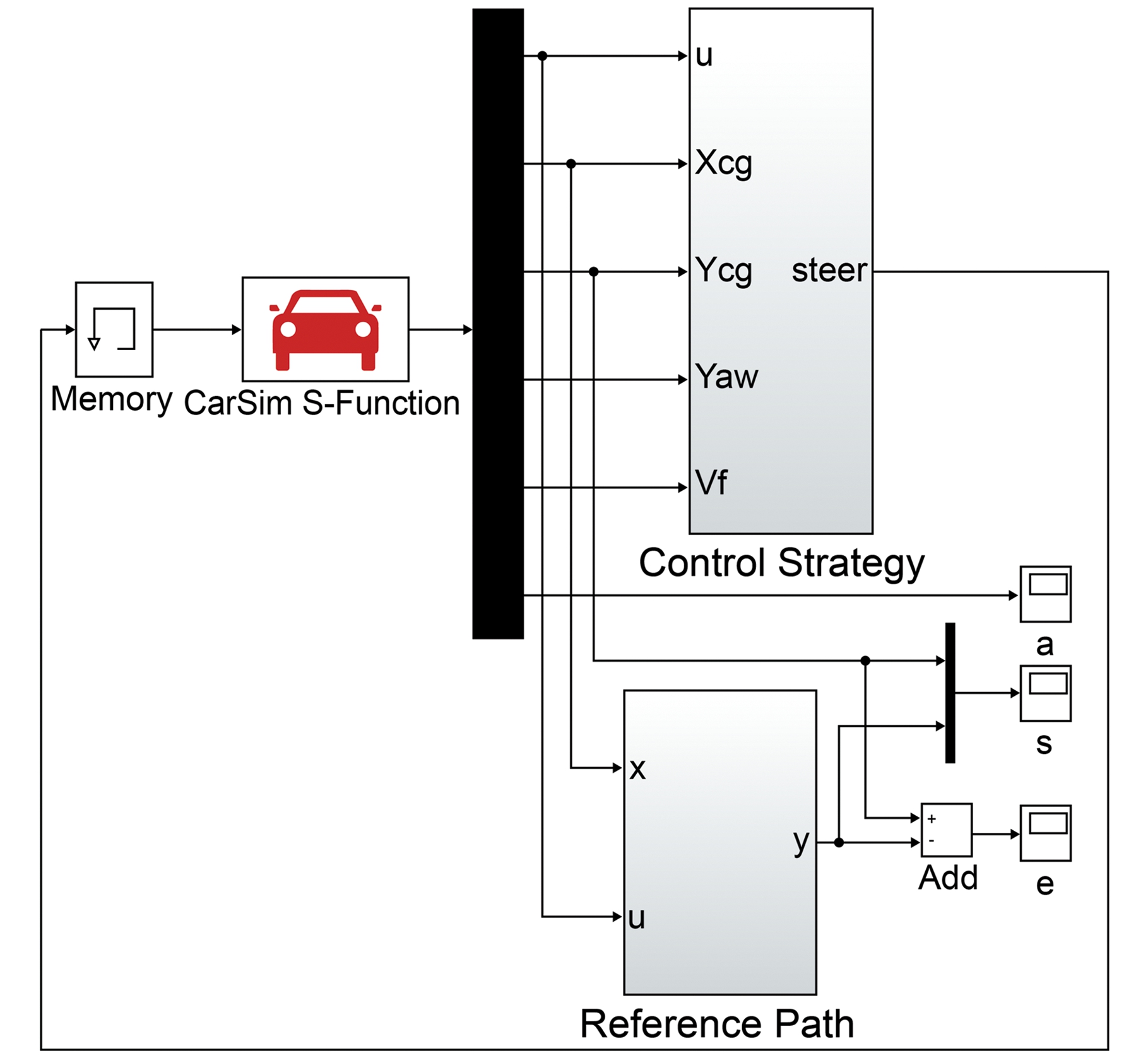
图5 控制系统仿真模型
Fig.5 Control system simulation model
(4)运行仿真工况。仿真工况的参数包括智能车与交通参与车辆的行驶状态参数、仿真时间等。
(5)仿真结果后处理。依据仿真结果生成仿真动画与曲线。
3.2 变道轨迹的选取
建立智能车主动变道跟踪控制过程中的仿真系统时，需选择一条合适的实际车道变换轨迹作为智能车变道控制过程中的参考轨迹。本文采用基于sin函数的变道轨迹作为智能车换道的参考轨迹，其数学表达式如下：
(14)
式中，S为变道结束时的横向距离；d为变道结束时的纵向距离。
3.3 仿真结果分析
在MATLAB/Simulink环境中，将上述所建立的智能车变道控制过程中的系统模型与CarSim和MATLAB/Simulink连接时生成的S-Function模块相连接，以完成仿真模型的建立。在本研究过程中，假设智能车是匀速行驶的，分别设置智能车在30 km/h、50 km/h和70 km/h的速度下匀速行驶，设定变道横向距离为3.5 m，并对控制模型的性能进行了仿真验证。将仿真得到的变道行驶轨迹与依据式(14)得到的参考变道行驶轨迹进行了对比，上述3种速度下的变道轨迹见图6，横向偏差见图7，横摆角速度见图8。
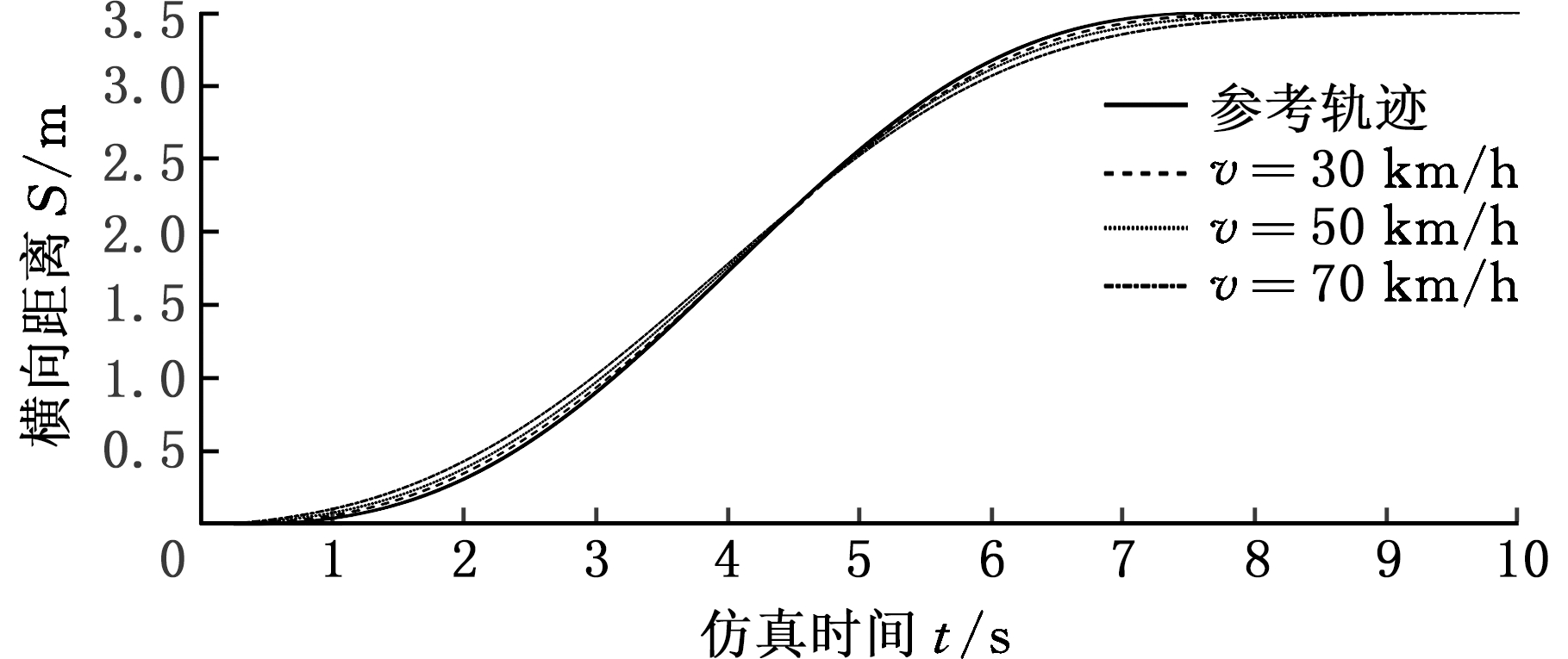
图6 变道轨迹
Fig.6 Lane-change trajectory
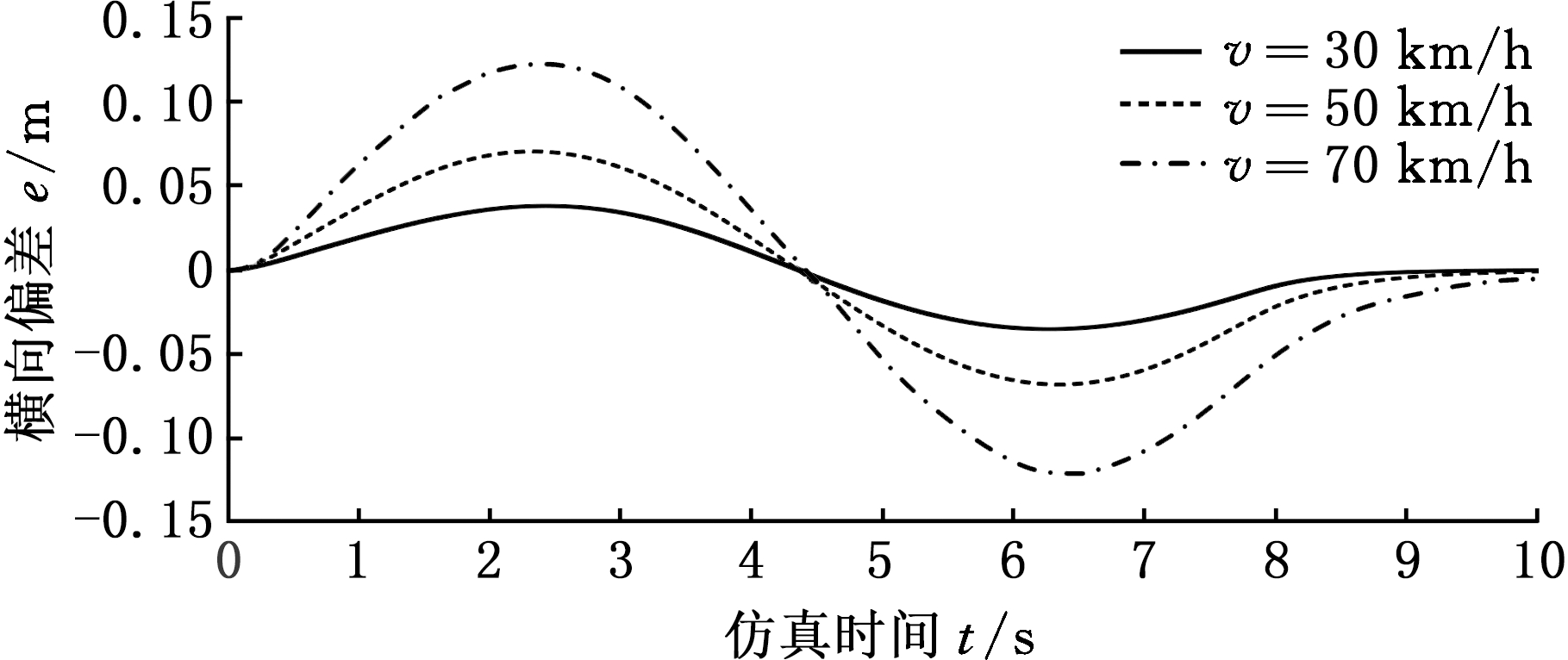
图7 横向偏差
Fig.7 Lateral deviation
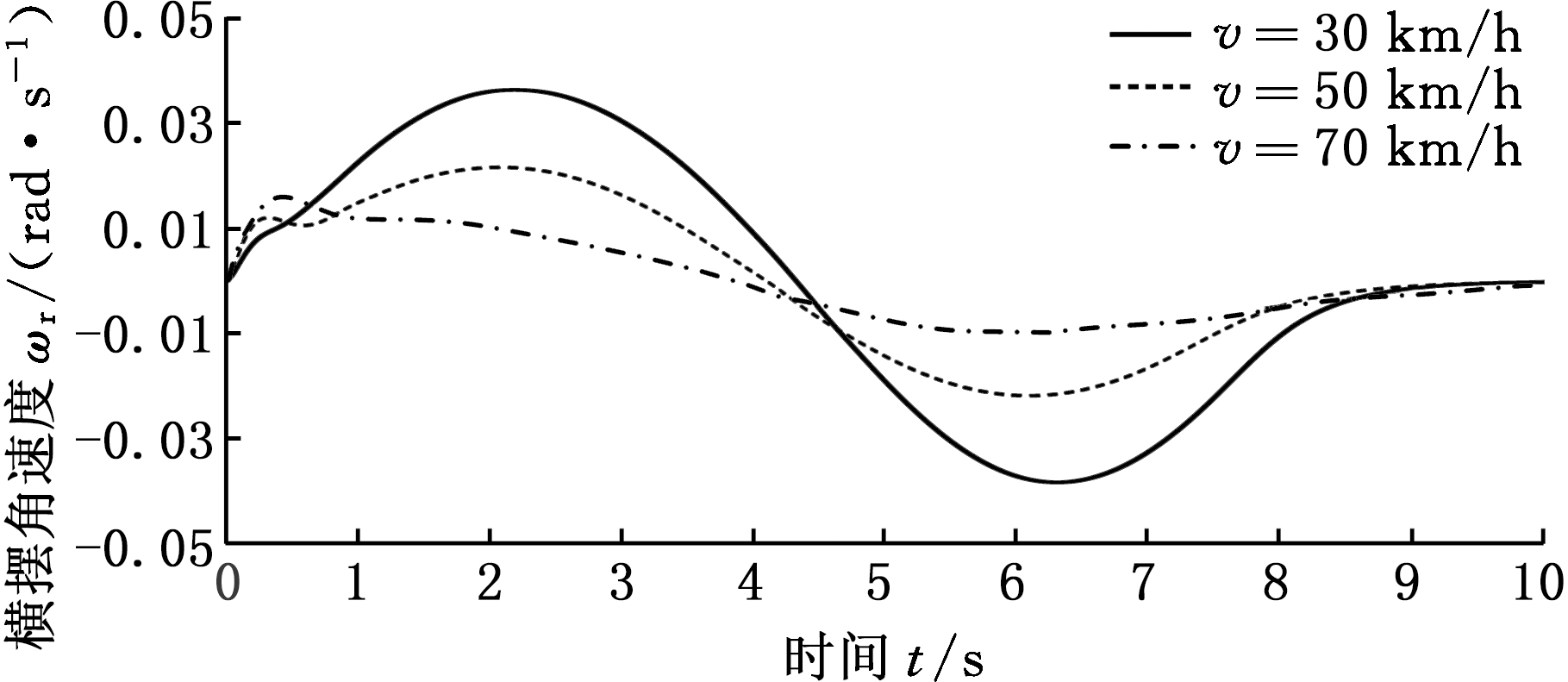
图8 横摆角速度
Fig.8 Yaw rate
由图6和图7可以看出，智能车变道过程中，仿真得到的变道行驶轨迹与参考变道行驶轨迹的偏差呈先变大、再变小、再变大、再变小的变化趋势；当智能车车速为30 km/h时，仿真得到的变道轨迹与参考变道轨迹基本重合，可很好地跟踪参考轨迹行驶；当智能车车速为70 km/h时，仿真得到的变道轨迹与参考变道轨迹在变道过程中的偏差变大，两者变道轨迹的最大偏差为0.15 m；变道过程中，随着速度的增大和仿真过程的进行，变道纵向距离也在增大，控制模型随着速度的变化而进行了调整，具备很好的鲁棒性。
由图8可以看出，仿真过程中智能车的最大横摆角速度约为0.04 rad/s。根据文献[19]可计算出本研究设置的3种速度下车辆期望横摆角速度的最小约束值约为0.4 rad/s，所以本研究中3种工况下智能车的横摆角速度均满足条件，在变道过程中车辆具备良好的稳定性。
4 实车测试
为更好地验证所设计控制器的控制效果，本文将所设计的控制器部署到样车上并进行实车测试，测试系统如图9所示。试验过程中拨动转向灯操纵杆来触发变道指令。试验具体过程如下：①采集试验环境下的基线位置信息;②测试车辆在车道线清晰且平坦的直道上分别以30 km/h、50 km/h和70 km/h的速度匀速行驶;③当目标车道无车时触发变道，并采集变道时测试车辆的位置信息;④对每个速度值分别向左和向右变道测试5次;⑤对试验数据进行处理，并得到测试车辆的变道轨迹。以30 km/h速度下向左变道的变道轨迹为例，其处理结果见图10。
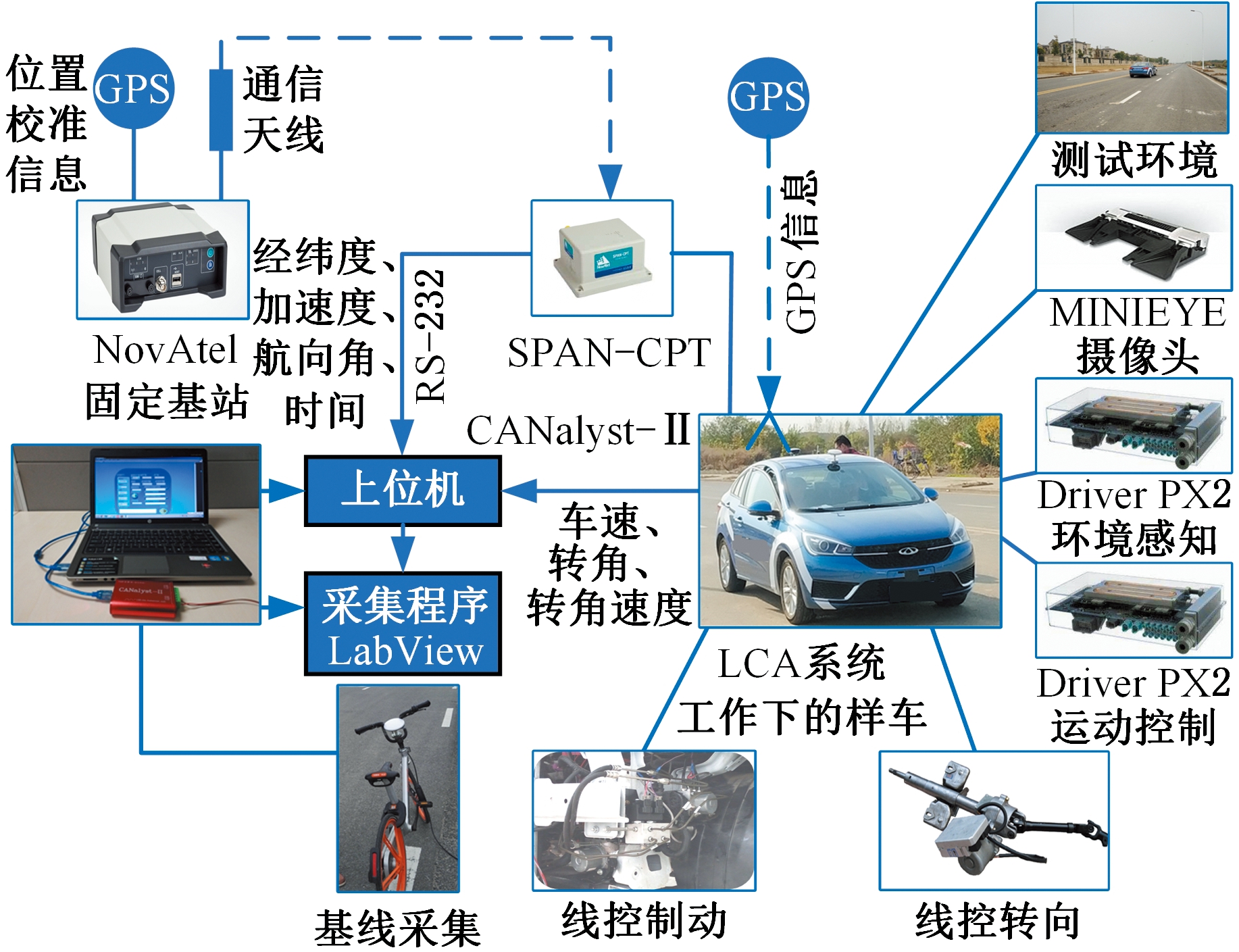
图9 测试系统原理图
Fig.9 Schematic diagram of test system
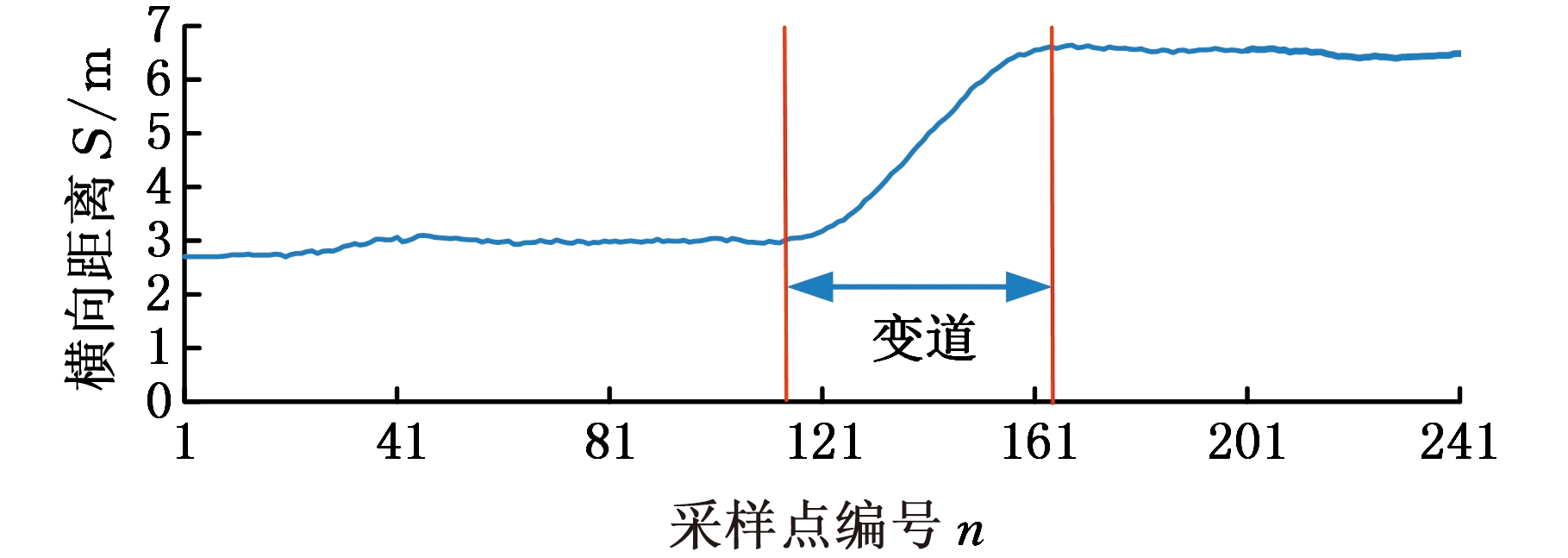
图10 30 km/h向左变道
Fig.10 Lane-change to left at 30 km/h
图11为30 km/h、50 km/h和70 km/h速度下的仿真结果与实车测试结果的对比曲线。
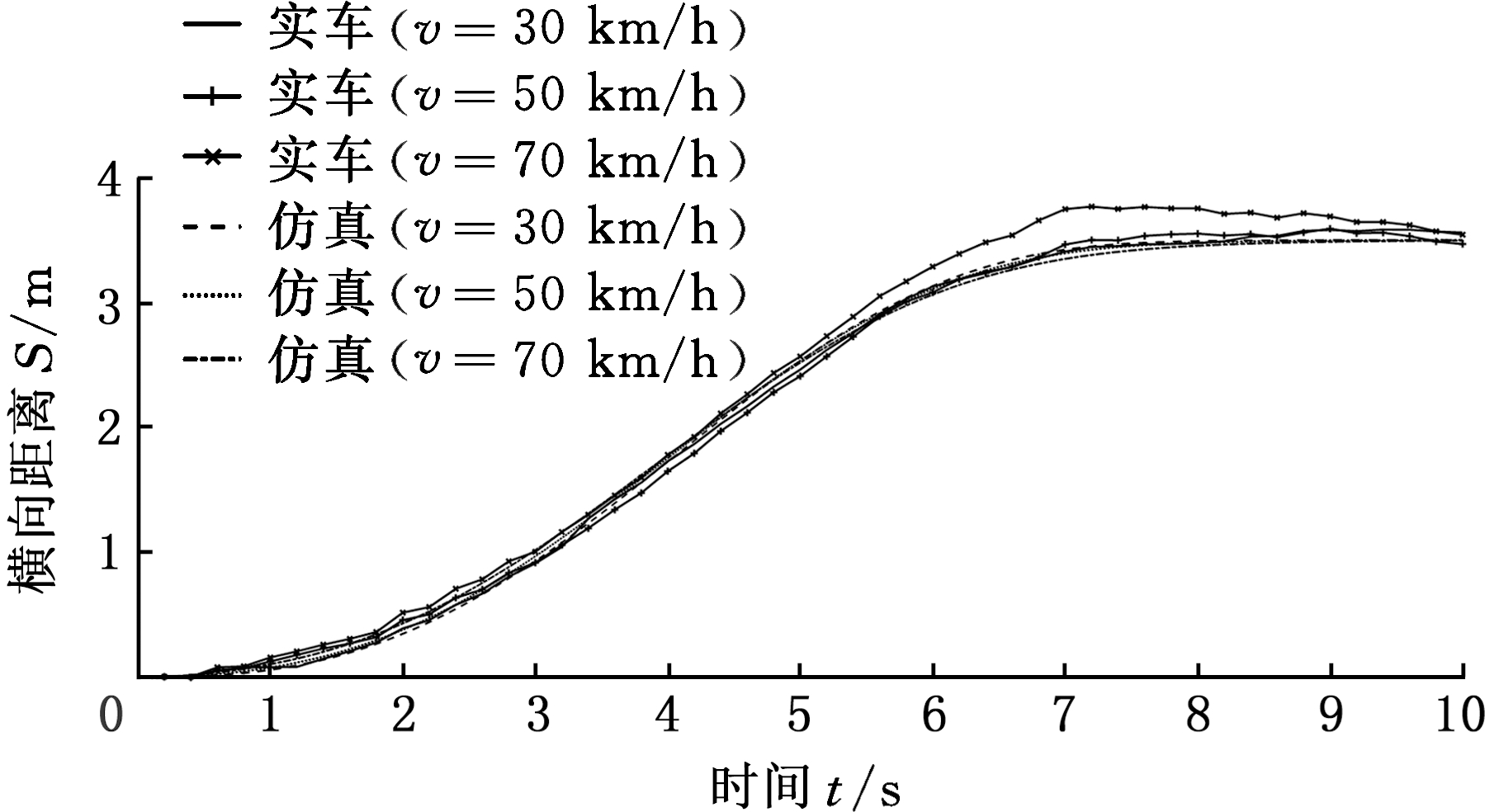
图11 仿真与实车测试的对比
Fig.11 Comparison of simulation and vehicle test
总体而言，虽然不同车速下的仿真结果存在一定差异性，但与实车变道测试相比较，本文所建立的仿真模型能够正确控制智能车的横向运动过程，仿真得到的横向运动轨迹值与实测变道轨迹值较为接近，仿真曲线与实测曲线走势相同，且总体比较接近，这表明本文所设计的智能车变道控制器具有较好的精确度。
5 结论
(1)基于“预瞄-跟随”理论建立了智能车辆在变道过程中的最优预瞄轨迹跟踪控制模型，并依据LQR理论设计了轨迹跟踪控制器。
(2)在MATLAB/Simulink和CarSim的联合仿真环境下，建立了智能车变道过程中的变道策略模块、变道参考轨迹模块和轨迹跟踪控制模块。分别对智能车在30 km/h、50 km/h、70 km/h匀速运行下的变道轨迹进行了虚拟仿真和实车测试，结果表明：虚拟仿真轨迹与实车变道轨迹的变化趋势接近，且大部分的虚拟仿真轨迹与实际轨迹相重合，从而验证了所设计的轨道跟踪控制器具有较好的精确度，适用于智能车的自动变道控制功能。
(3)该控制模型的建立过程以实际车道变换轨迹为参考对象，并基于实车进行了相应工况下的测试验证，因此基于该控制模型所设计的智能车自动变道控制器可体现驾驶员的真实驾驶行为，这将在很大程度上提高智能车的行驶稳定性。
[1] NILSSON P, LAINE L, JACOBSON B. A Simulator Study Comparing Characteristics of Manual and Automated Driving During Lane Changes of Long Combination Vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(9):2514-2524.
[2] HOU Y, EDARA P, SUN C. Situation Assessment and Decision Making for Lane Change Assistance Usingensemble Learning Methods[J]. Expert Systems with Applications, 2015, 42(8):3875-3882.
[3] LUO Y, XIANG Y, CAO K, et al. A Dynamic Automated Lane Change Maneuver Based on Vehicle-to-Vehicle Communication[J]. Transportation Research：Part C, 2016, 62:87-102.
[4] YOU F, ZHANG R, GUO L, et al. Trajectory Planning and Tracking Control for Autonomous Lane Change Maneuver Based on the Cooperative Vehicle Infrastructure System[J]. Expert Systems with Applications, 2015, 42(14):5932-5946.
[5] WU X, YANG H. A Lane Change Model with the Consideration of Car Following Behavior[J]. Procedia-Social and Behavioral Sciences, 2013, 96:2354-2361.
[6] AHN S, CASSIDY M J. Freeway Traffic Oscillations and Vehicle Lane-change Maneuvers[C]∥17th International Symposium on Transportation & Traffic Theory. London, 2007:691-710.
[7] RODEMERK C, HABENICHT S, WEITZEL A, et al. Development of a General Criticality Criterion for the Risk Estimation of Driving Situations and Its Application to a Maneuver-based Lane Change Assistance System[C]∥Intelligent Vehicles Symposium. Alcala de Henares：IEEE，2013：264-269.
[8] HABEL L C , SCHRECKENBERG M. Asymmetric Lane Change Rules for a Microscopic Highway Traffic Model[J]. Lecture Notes in Computer Science, 2014, 8751:620-629.
[9] MACADAM C C. Understanding and Modeling the Human Driver[J]. Vehicle System Dynamics, 2003, 40(1/3):101-134.
[10] 黄锡昌, 宗志坚. 基于改进预瞄跟随算法的电动车智能转向控制[J]. 中国机械工程, 2014, 25(14):1984-1987.
HUANG Xichang, ZONG Zhijian. Intelligent Steering Control Strategy of EV Based on Improved Preview Following Algorithm[J]. China Mechanical Engineering,2014, 25(14):1984-1987.
[11] 沈峘, 凌锐, 李舜酩. 基于预瞄最优曲率模型的大曲率转向控制方法[J]. 中国机械工程, 2012, 23(17):2111-2116.
SHEN Huan, LING Rui, LI Shunming. SteeringControl on Large Curvature Road Based on Preview Optimal Curvature Model[J]. China Mechanical Engineering, 2012, 23(17):2111-2116.
[12] 刁勤晴, 张雅妮, 朱凌云. 双预瞄点智能车大曲率路径的横纵向模糊控制[J]. 中国机械工程, 2019, 30(12):1445-1452.
DIAO Qinqing, ZHANG Yani, ZHU Lingyun. A Lateral and Longitudinal Fuzzy Control of Intelligent Vehicles with Double Preview Points for Large Curvature Roads[J]. China Mechanical Engineering,2019, 30(12):1445-1452.
[13] 王畅, 秦加合, 郭明华,等. 智能汽车换道控制算法的仿真研究[J]. 计算机工程与设计, 2013, 34(7):2528-2532.
WANG Chang, QIN Jiahe, GUO Minghua, et al. Simulation of Lane Change Control Algorithm for Intelligent Vehicle[J]. Computer Engineering and Design, 2013, 34(7): 2528-2532.
[14] 郭孔辉. 驾驶员—汽车闭环系统操纵运动的预瞄最优曲率模型[J]. 汽车工程, 1984(3):3-18.
GUO Konghui. The Optimal Curvature Model for the Control Movement of the Driver-automobile Closed-loop System[J]. Automotive Engineering， 1984(3): 3-18.
[15] 郭孔辉. 预瞄跟随理论与人-车闭环系统大角度操纵运动仿真[J]. 汽车工程, 1992(1):1-11.
GUO Konghui. Preview-following Theory and Simulation of Large Angle Maneuvering Motion of Human-vehicle Closed-loop System[J]. Automotive Engineering，1992(1):1-11.
[16] 管欣, 高振海, 郭孔辉. 驾驶员稳态预瞄动态校正假说[J]. 汽车工程, 2003, 25(3):227-231.
GUAN Xin, GAO Zhenhai, GUO Konghui. A Hypothesis of Steady Preview and Dynamic Correction for Driver Model[J]. Automotive Engineering, 2003, 25(3):227-231.
[17] GU J , MA A . Research on Optimal Driver Steering Model Based on Multi-point Preview[J]. Journal of Physics: Conference Series, 2017, 887:012024.
[18] MING T , DENG W , ZHANG S , et al. MPC-Based Trajectory Tracking Control for Intelligent Vehicles[C]∥SAE 2016 World Congress and Exhibition.Detroit，2016：2016-01-0452.
[19] 张凤娇, 魏民祥, 黄丽琼,等. 基于模型预测控制的汽车紧急换道控制研究[J]. 现代制造工程, 2017(3):57-64.
ZHANG Fengjiao, WEI Minxiang, HUANG Liqiong, et al. Study of Vehicle Emergent Lane-change Control Based on Model Predictive Control[J]. Mod. Manuf. Eng., 2017(3): 57-64.
