0 引言
GCr15是一种高碳铬轴承钢,含碳量高,经淬火、回火等热处理后能够得到稳定、均匀的金相组织,表现出优越的材料性能,目前被广泛应用于轴承、精密量具等高精度零件[1]。轴承钢在轴承等机械产品的应用中需要进行外圆磨削,为兼顾其加工质量和加工效率,有必要开展高速外圆磨削加工研究。
磨削加工时,磨削参数与磨削结果并不成线性关系。选择合理的磨削参数可提高加工表面质量和生产效率,并能降低加工成本。人们常用正交法[2]、田口法[3]、响应曲面法(response surface method,RSM)[4]等试验设计优化方法,以及遗传算法[5]、神经网络[5]等智能算法来对磨削参数进行优选。RSM法通过对因子与响应关系进行多项式近似拟合,分析单个因子与响应之间的独立影响和多个因子与响应之间的交互影响,并找出最优的因子组合[6]。
本文采用对GCr15高速外圆磨削结果影响较大的3个加工工艺参数(砂轮线速度、工件速度、磨削深度),进行RSM法中适合三水平的Box-Behnken试验设计。
1 磨削试验
1.1 工件材料
高速外圆磨削(high speed cylindrical grinding,HSCG)试验所用的工件材料是GCr15,工件毛坯为圆柱形,其外径、内径、宽度分别为60 mm、32 mm、19 mm,如图1所示。GCr15的主要材料性能如下:抗拉强度值650 MPa,屈服强度值365 MPa,硬度值188HV。

图1 GCr15工件毛坯
Fig.1 GCr15 workpiece
1.2 试验设备

图2 HSCG试验系统
Fig.2 Experimental system of HSCG
在CNC8325高速数控磨床上进行GCr15的HSCG试验,试验系统如图2所示。选用陶瓷CBN砂轮,砂轮粒径为75/80 μm、磨粒体积分数为37.5%,砂轮的直径、宽度分别为400 mm、25 mm。利用SDC-CG2测力仪、FLIR-SC325红外测温仪实时检测与采集整个磨削过程的磨削力、磨削温度。由VHX-500FE显微系统检测GCr15工件外圆表面形貌与变质层形貌,利用HVS-1000硬度探测计采集变质层硬度值。
1.3 试验方案
采用逆磨方式进行GCr15的HSCG试验。为提高试验效率,同时确保其有效性,采用RSM法的Box-Behnken方法进行试验设计。采用对加工结果影响较大的3个加工工艺参数(砂轮线速度vs、工件速度vw、磨削深度ap)进行3因子3水平试验设计,各磨削参数取值如表1所示。Box-Behnken试验设计为17组,有5组参数相同合为1组,则进行13组试验,具体试验方案如表2所示。
表1 磨削参数取值
Tab.1 Values of grinding parameters

水平vs(m/s)vw(mm/s)ap(μm)-160126100752202019031430
表2 磨削试验方案与结果
Tab.2 Grinding experimental scheme and results
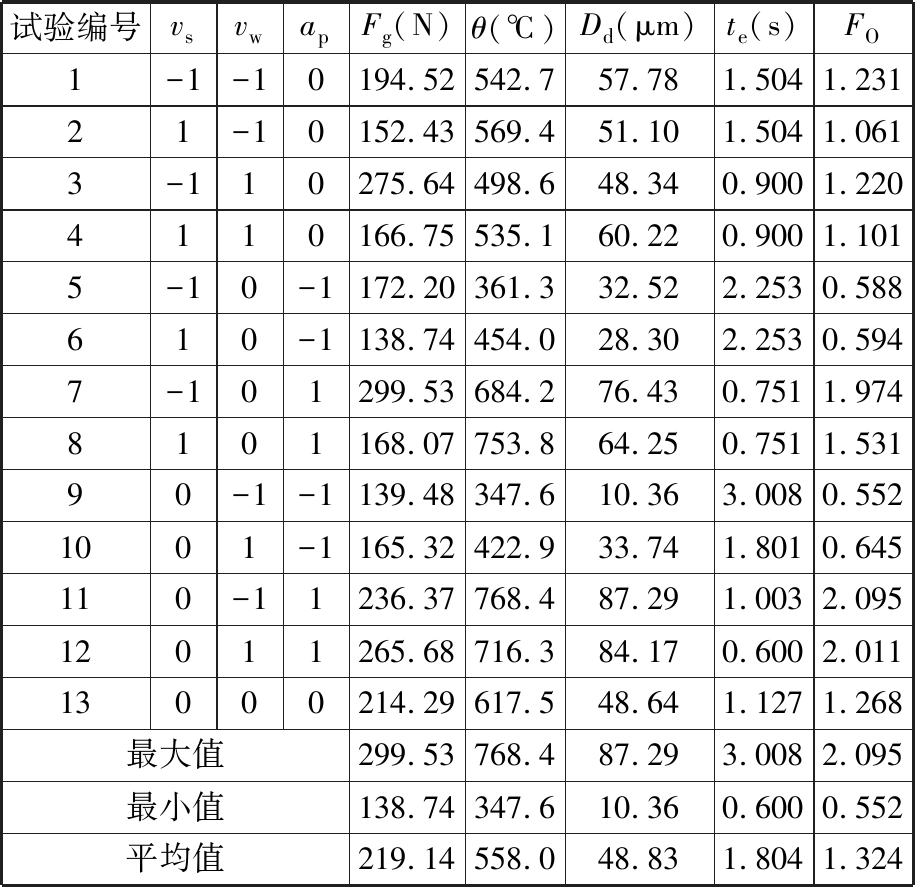
试验编号vsvwapFg(N)θ(℃)Dd(μm)te(s)FO1-1-10194.52542.757.781.5041.23121-10152.43569.451.101.5041.0613-110275.64498.648.340.9001.2204110166.75535.160.220.9001.1015-10-1172.20361.332.522.2530.588610-1138.74454.028.302.2530.5947-101299.53684.276.430.7511.9748101168.07753.864.250.7511.53190-1-1139.48347.610.363.0080.5521001-1165.32422.933.741.8010.645110-11236.37768.487.291.0032.09512011265.68716.384.170.6002.01113000214.29617.548.641.1271.268最大值299.53768.487.293.0082.095最小值138.74347.610.360.6000.552平均值219.14558.048.831.8041.324
为了保证材料去除量一定,记录每组试验的实际加工时间t,然后等效到磨削深度为30 μm的等效加工时间te,不考虑进退刀时间,计算公式为
te=30t/ap
(1)
t=πdw/vw
(2)
式中,dw为工件直径。
由式(1)、式(2)可知,等效加工时间te随着工件速度vw、磨削深度ap的增大而减小,与砂轮线速度vs无关。
1.4 试验结果
为保证磨削温度的检测精度,左磨削试验前进行GCr15热辐射率值的标定。选取试验中FLIR-SC325红外测温仪检测得到的最高温度作为磨削温度。
图3所示为6号试验的工件表面形貌。图3a中工件表面光滑,划痕平直清晰。图3b中亚表面存在由白层、暗层组成的变质层[7-8],对它进行不同区域的硬度检测,结果如图4所示,两个黑点分别表示暗层与白层的分界、暗层与基体的分界。白层硬度最大,但硬度下降快;暗层硬度缓慢下降。白层与暗层即为加工硬化的变质层,由磨削力和磨削温度共同作用所致[7-8]。根据工件变质层硬度变化,当材料硬度下降为工件毛坯硬度时,该处深度定义为变质层深度。

(a)表面形貌 (b)亚表面形貌
图3 工件表面形貌与亚表面形貌
Fig.3 Surface and sub-surface topographies of wokpiece
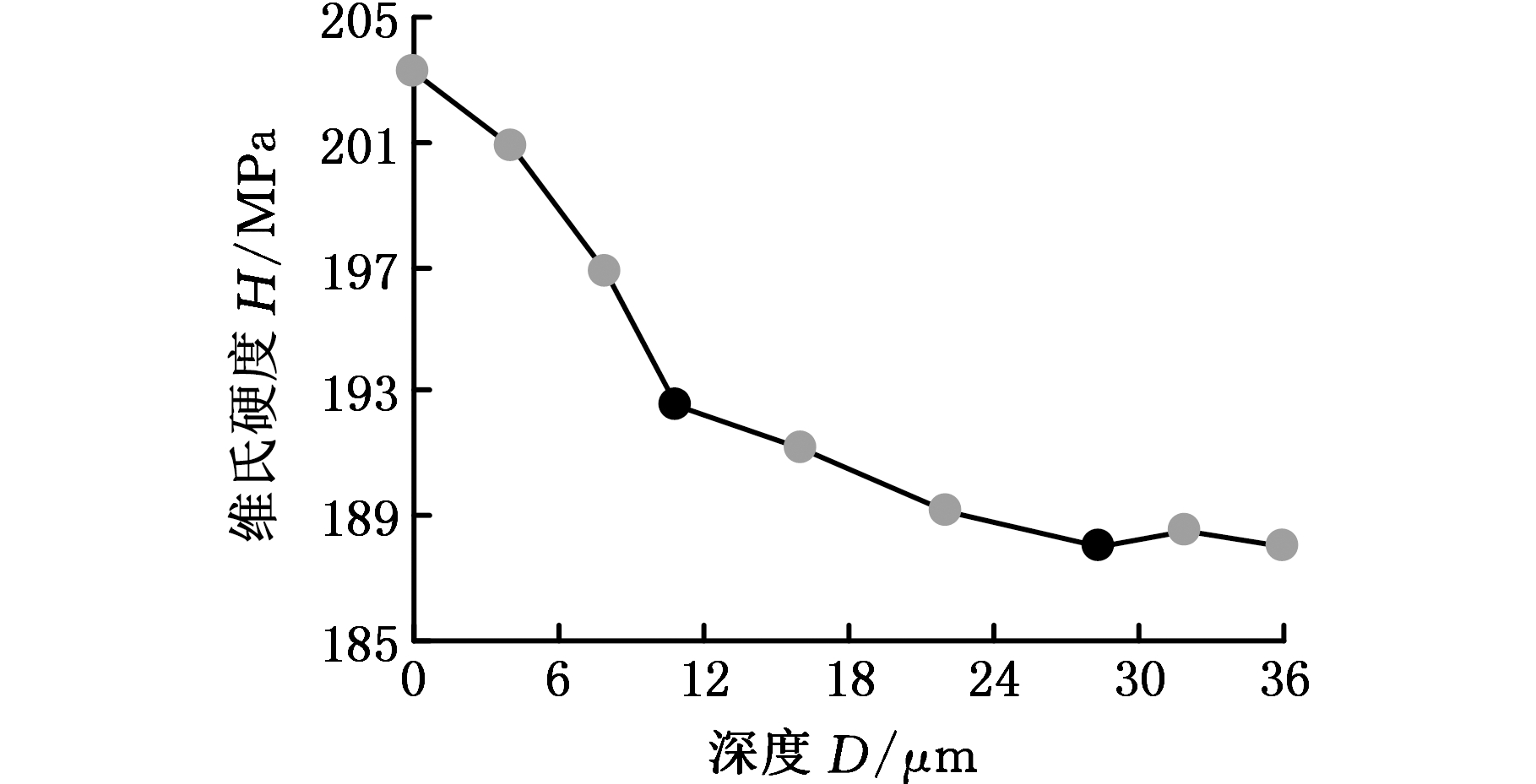
图4 变质层硬度变化曲线
Fig.4 Hardness curve of deterioration layer
各组加工参数试验均开展3次,并对每组的磨削加工数据进行平均值计算,以确保GCr15的HSCG试验结果的准确度与可信度。每组试验对应的磨削力Fg、磨削温度θ、变质层深度Dd和等效加工时间te具体响应参数数值如表2所示,其中FO表示综合目标。
2 试验分析
2.1 回归方程的建立及其显著性验证
采用Design-Expert软件,对表2中各响应进行模拟、建模、比对,优选出最佳数学模型。磨削力选择2因素交互关系模型2FI,磨削温度和变质层深度选择线性模型Linear。对表2中试验检测的结果进行多项式线性拟合,获得GCr15的HSCG磨削力Fg、磨削温度θ和变质层深度Dd的回归模型:
Fg=-337.649+5.069vs+1.597vw+16.329ap- 0.018vsvw-0.163vsap+1.377×10-3vwap
(3)
θ=111.697+1.879vs-0.109vw+16.711ap
(4)
Dd=-2.186-0.093vs+0.039vw+2.590ap
(5)
等效加工时间te的模型即为式(1)。
对回归模型进行方差分析(即显著性检验)来验证模型的正确性。采用方差法对GCr15的HSCG回归模型进行分析,各项目结果如表3所示。可知:①磨削力模型式(3)的显著性F大于F0.01(6, 6)=8.47(0.01表示显著性水平,前一个6表示自由度,后一个6表示自变量数目),表明模型是显著的,模型中3个一次项与交互项(vwap除外)的相伴概率P都小于0.05,属于显著项;②磨削温度和变质层深度模型式(4)、式(5)的显著性F大于F0.01(9, 3)=6.99,表明模型是显著的,两个模型中仅一次项ap的相伴概率P小于0.05,属于显著项;③3个模型的R-squared分别为0.977 8、0.945 0、0.882 2(表3中未列出),皆大于0.80,表明所建立模型满足拟合要求。
表3 模型方差分析
Tab.3 Variance analysis for models
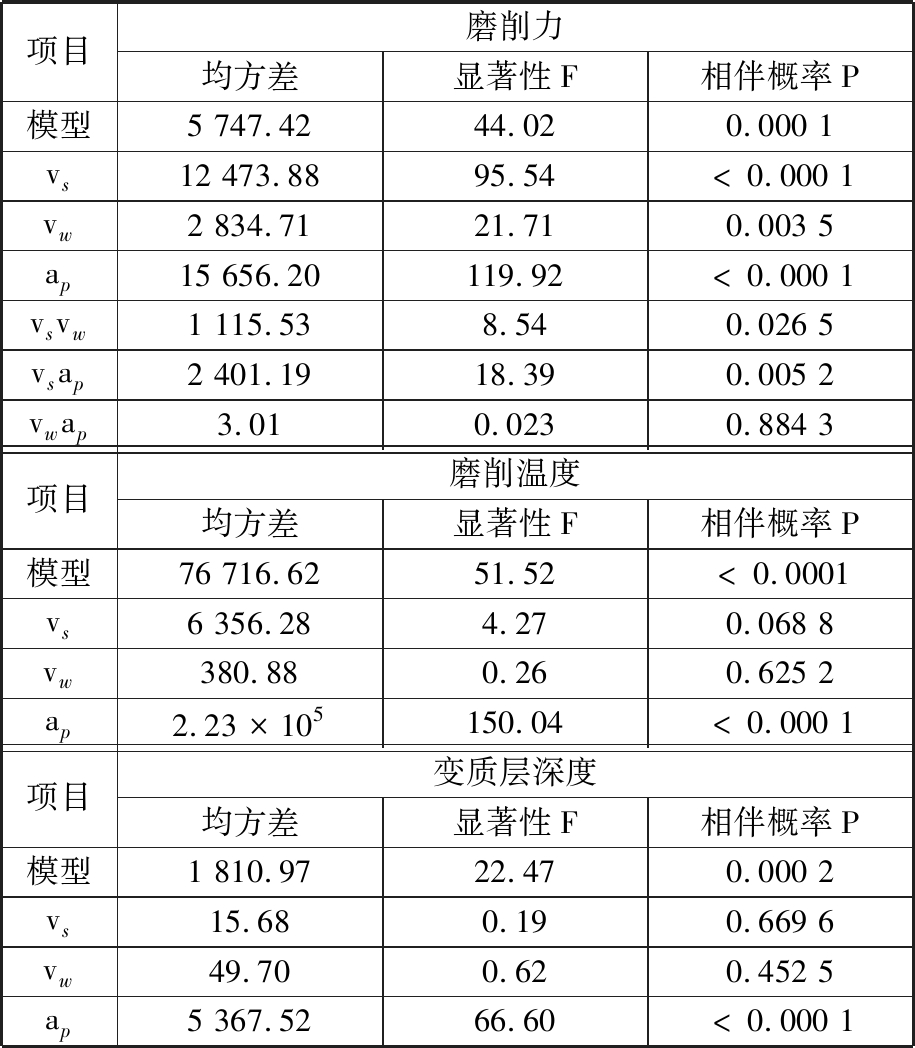
项目磨削力均方差显著性F相伴概率P模型5 747.4244.020.000 1vs12 473.8895.54<0.000 1vw2 834.7121.710.003 5ap15 656.20119.92<0.000 1vsvw1 115.538.540.026 5vsap2 401.1918.390.005 2vwap3.010.0230.884 3项目磨削温度均方差显著性F相伴概率P模型76 716.6251.52<0.0001vs6 356.284.270.068 8vw380.880.260.625 2ap2.23×105150.04<0.000 1项目变质层深度均方差显著性F相伴概率P模型1 810.9722.470.000 2vs15.680.190.669 6vw49.700.620.452 5ap5 367.5266.60<0.000 1
2.2 响应曲面分析
为了分析砂轮线速度vs、工件速度vw、磨削深度ap中任意2个因子对磨削结果的影响,进行图5~图7所示的GCr15的HSCG的响应曲面分析。由图5~图7可知:①其他参数不变,提高砂轮线速度vs,磨削力Fg和变质层深度Dd会随之减小,磨削温度θ则略微提高;②其他参数不变,提高工件速度vw,磨削力Fg明显增大,磨削温度θ略微减小,变质层深度Dd略微增大;③其他参数不变,加大磨削深度ap,磨削力Fg、磨削温度θ、变质层深度Dd都明显增大;④随砂轮线速度vs的提高和工件速度vw的加快,两者的影响是相反的,使得磨削力Fg先增大后减小,交互作用比较显著,磨削温度θ、变质层深度Dd都增大,交互作用不显著;⑤随着砂轮线速度vs和磨削深度ap增大,两者的影响基本相反,使得磨削力Fg先增大后减小,交互作用比较显著,磨削温度θ、变质层深度Dd都增大,交互作用不显著;⑥随着工件速度vw和磨削深度ap增大,两者的影响基本相同,使得磨削力Fg、磨削温度θ、变质层深度Dd都增大。各因子对响应的影响程度与方差分析的结果是一致的,如表4所示,其中“↑”、“↓”分别表示明显增大、减小,“ ”、“
”、“ ”分别表示略微增大、减小,“/”表示无影响。
”分别表示略微增大、减小,“/”表示无影响。

(a)vs-vw(ap=20 μm) (b)vs-ap(vw=251 mm/s) (c)vw-ap(vs=75 m/s)
图5 磨削力Fg的响应曲面图
Fig.5 Response surface of grinding force Fg
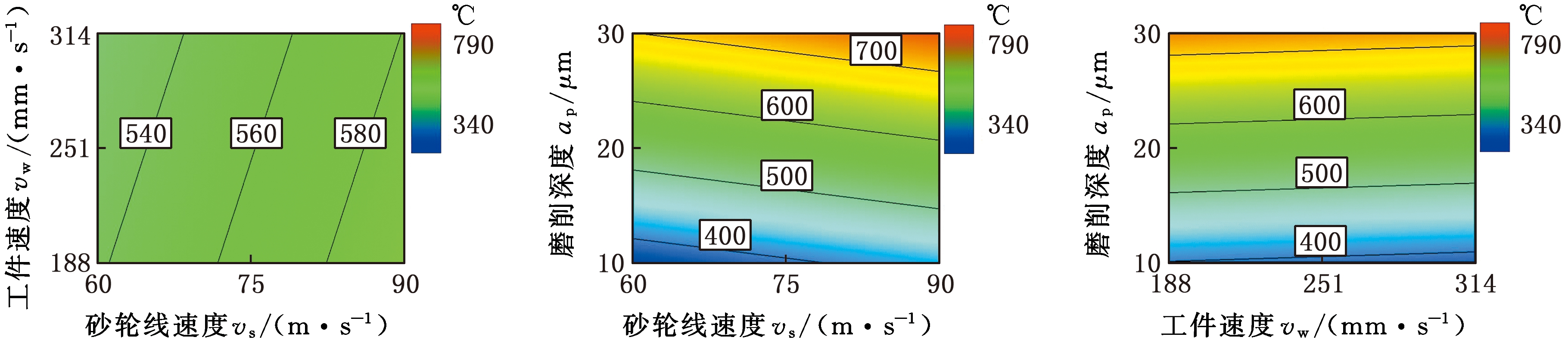
(a)vs-vw(ap=20 μm) (b)vs-ap(vw=251 mm/s) (c)vw-ap(vs=75 m/s)
图6 磨削温度θ的响应曲面图
Fig.6 Response surface of grinding temperature θ
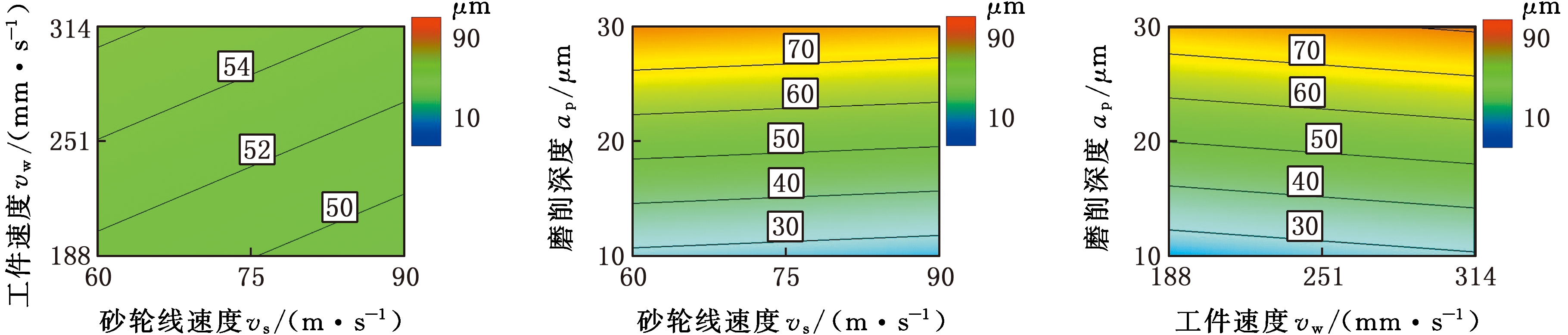
(a)vs-vw(ap=20 μm) (b)vs-ap(vw=251 mm/s) (c)vw-ap(vs=75 m/s)
图7 变质层深度Dd的响应曲面图
Fig.7 Response surface of deterioration layer depth Dd
表4 磨削试验结果分析
Tab.4 Analysis for grinding experimental results
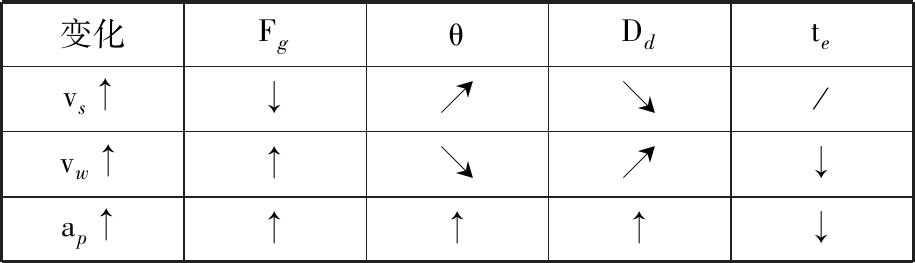
变化FgθDdtevs↑↓↗↘/vw↑↑↘↗↓ap↑↑↑↑↓
2.3 综合分析
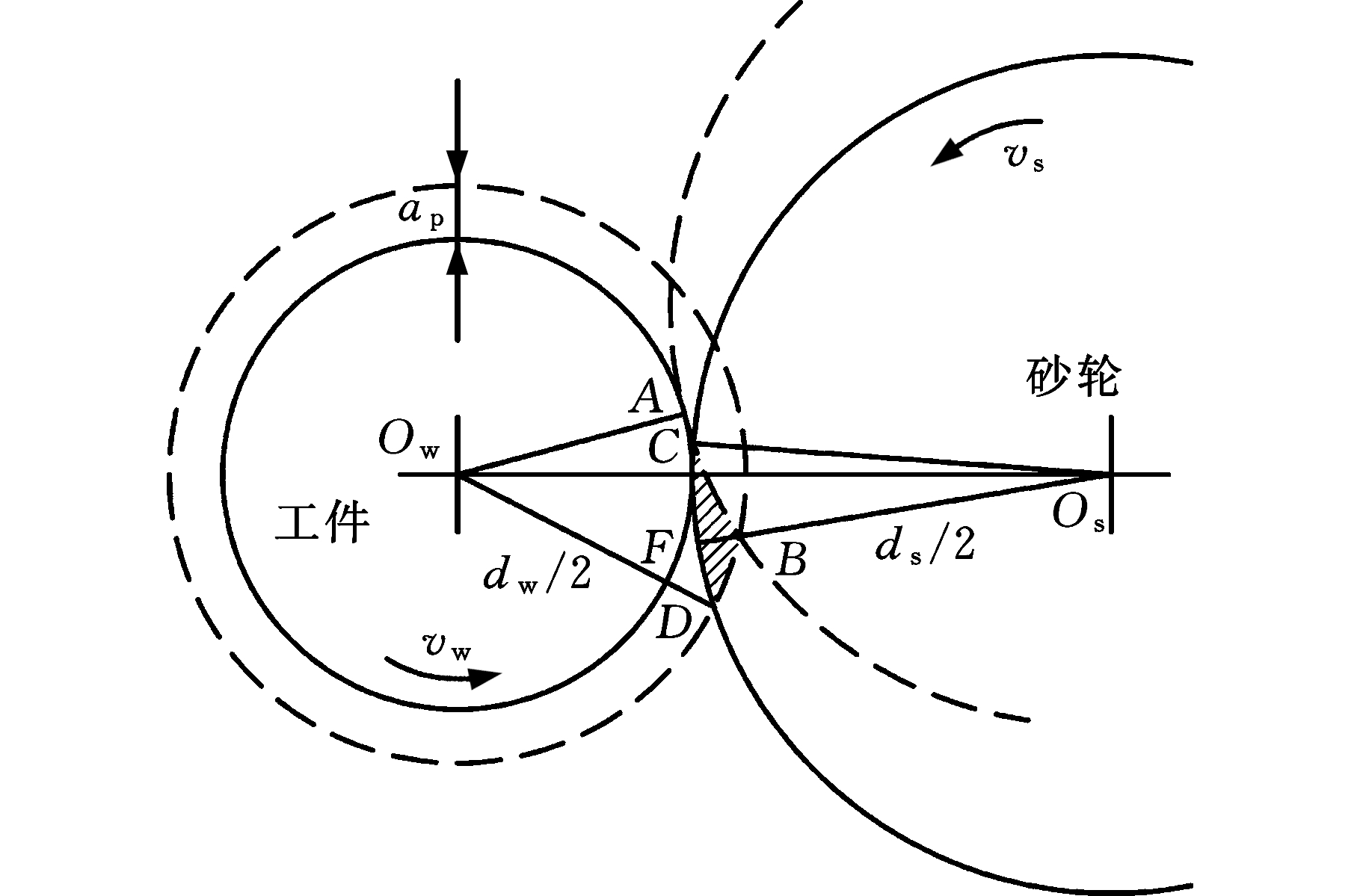
图8 磨粒的最大未变形切削厚度
Fig.8 Maximum undeformed chip thickness of grain
GCr15的HSCG磨削参数对加工结果的影响是由磨粒的最大未变形切削厚度agmax的变化所致的,如图8所示。外圆磨削时,砂轮表面任一动态有效磨粒的磨削轨迹为![]() 其下一个动态有效磨粒的磨削轨迹为
其下一个动态有效磨粒的磨削轨迹为![]() 剖面线部分即切屑形成部分,其厚度从零逐渐增大,然后减小为零;其中
剖面线部分即切屑形成部分,其厚度从零逐渐增大,然后减小为零;其中![]() 即为agmax,计算公式如下:
即为agmax,计算公式如下:
(6)
式中,λ为砂轮表面动态有效磨粒间距;ds为砂轮直径。
由式(6)可知:磨削参数的变化导致磨粒的agmax改变,则磨削力Fg、磨削温度θ、变质层深度Dd等试验检测结果随之发生改变。
磨削温度的变化可以基于ROWE等[9]提出的经典模型进行解释,工件最大磨削温度θmax计算如下:
(7)
式中,C为常数,一般取1;qw为进入工件的热通量;βw为工件材料的热性质;lc为砂轮与工件之间的接触弧长。
随着vs提高,单位时间内通过磨削区的磨粒数会增多,使agmax减小,从而导致磨削力Fg减小。vw提高,材料去除率(material removal rate,MRR)和agmax增大,从而使得磨削力Fg增大。ap增大,使得agmax增大,介入磨削区域的有效磨粒数增加,进而使得磨削力Fg增大。
vs提高,在一方面,加工过程中消耗的磨削功率增多,MRR值无变化,导致能量转化成热能的比例增大;在另一方面,介入磨削区域的砂轮有效磨粒数量增加,agmax减小,磨粒在滑擦阶段与耕犁阶段的比例相应增大,工件与砂轮产生激烈的相互摩擦,从而增加产热;最后qw增大,使得磨削温度θ升高。工件速度vw的增大使得磨粒与工件作用时间缩短,单位面积材料与砂轮的磨削时间缩短,qw减小,以及工件速度平方根的反比例作用,使得磨削温度θ降低。ap提高,一方面MRR值、agmax增大,介入磨削区域的有效磨粒数增加,qw增大;另一方面lc增大,使得热量不容易散发,从而导致磨削温度θ升高。
3 试验优化与验证
借鉴RSM的优化策略[10],以GCr15的HSCG的磨削力Fg、磨削温度θ、变质层深度Dd、等效加工时间te这4个响应综合最小为目标,对砂轮线速度vs、工件速度vw、磨削深度ap等加工参数进行多目标参数优化。由于4个响应的量级与取值范围不同,根据加工经验对响应的重要度分别取其权重系数为0.5、0.75、1、0.25。优化目标函数与约束函数定义为
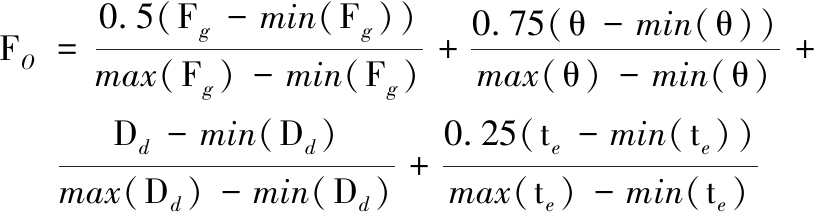
(8)
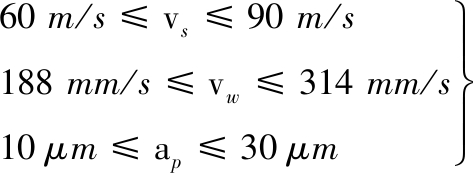
(9)
由表2可知式(8)中4个响应的最大值与最小值。综合式(1)、式(3)~式(5)、式(9)求解式(8)的最小值min(FO),可得优化的工艺参数组合为vs=90 m/s、vw=314 mm/s、ap=10 μm,对应的预测结果如表5所示。采用优化的工艺参数组合进行GCr15的HSCG试验,试验后工件表面形貌如图9所示,具体结果如表5所示。
表5 磨削优化结果
Tab.5 Results of optimized grinding process
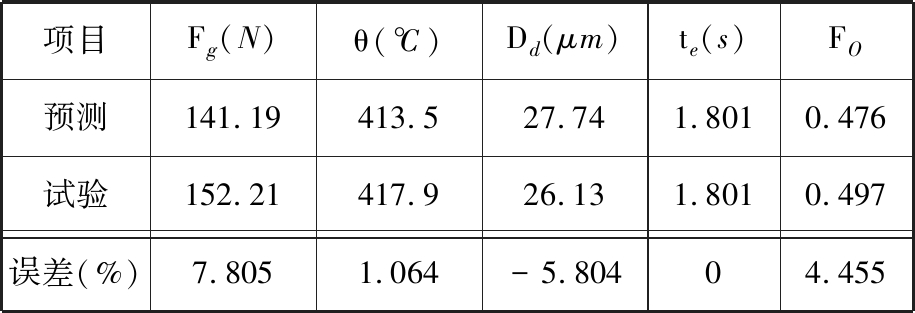
项目Fg(N)θ(℃)Dd(μm)te(s)FO预测141.19413.527.741.8010.476试验152.21417.926.131.8010.497误差(%)7.8051.064-5.80404.455

图9 优化试验工件表面形貌
Fig.9 Surface topography by optimized experiment
根据表5可知,4个响应的相对误差分别为7.8%、1.1%、-5.8%、0,都小于±8%,预测结果和试验结果相差不大,再次证明了式(3)~式(5)所示模型是正确的,表明该模型可以用于GCr15的HSCG预测。与表2的原始试验结果相比,表5的优化试验结果的4个响应的取值都小于各响应的平均值,且综合目标FO是最小的,表明加工结果得到了优化,该优化方法是有效的。
4 结论
(1)采用响应曲面法的Box-Behnken方法设计了GCr15的高速外圆磨削试验,根据试验结果建立了磨削力、磨削温度、变质层深度的回归模型,该模型显著,且拟合程度良好,可用于磨削结果预测。
(2)提高砂轮线速度vs,磨削力Fg和变质层深度Dd减小,磨削温度θ提高;提高工件速度vw,磨削力Fg、变质层深度Dd增大,磨削温度θ减小;加大磨削深度ap,磨削力Fg、磨削温度θ、变质层深度Dd都增大。
(3)以磨削力、磨削温度、变质层深度、等效加工时间这4个响应综合最小为目标,建立了GCr15高速外圆磨削的3个磨削参数因子的多目标参数优化模型,通过试验验证了优化模型和结果的正确性,表明该优化模型可用于磨削参数优化。
[1] YUAN Z J, HU Z H, KOBAYASHI A. Surface Integrity of Grinding of Bearing Steel GCr15 with CBN Wheels[J]. CIRP Annals—Manufacturing Technology, 1989, 38(1): 553-556.
[2] 刘伟, 邓朝晖, 万林林, 等. 基于正交试验-遗传神经网络的陶瓷球面精密磨削参数优化[J]. 中国机械工程, 2014, 25(4): 451-455.
LIU Wei, DENG Zhaohui, WAN Linlin, et al. Parameters Optimization on Precision Grinding of Ceramic Sphere Using Orthogonal Experiment and Genetic Neural Network[J]. China Mechanical Engineering, 2014, 25(4): 451-455.
[3] WAN L L, DENG Z H, WANG C D, et al. Process Parameters Optimisation for Si3N4 in Chemical-mechanical Polishing via Taguchi Technique[J]. International Journal of Nanomanufacturing, 2016, 12(2): 143-153.
[4] 卿启湘, 陈哲吾, 刘杰, 等. 基于Kriging插值和回归响应面法的冲压成形参数的优化及对比[J]. 中国机械工程, 2013, 24(11): 1447-1452.
QING Qixiang, CHEN Zhewu, LIU jie, et al. Study on Comparison and Optimization of Sheet Forming Parameters Using Kringing Interpolation and Regression Response Surface Metamodeling Techniques[J]. China Mechanical Engineering, 2013, 24(11): 1447-1452.
[5] 汪定伟, 王俊伟, 王洪峰, 等. 智能优化方法[M]. 北京: 高等教育出版社, 2007.
WANG Dingwei, WANG Junwei, WANG Hongfeng, et al. Intelligent Optimization Methods[M]. Beijing: Higher Education Press, 2007.
[6] 李云雁, 胡传荣. 试验设计与数据处理[M]. 北京: 化学工业出版社, 2005.
LI Yunyan, HU Chuanrong. Experiment Design and Data Processing [M]. Beijing: Chemical Industry Press, 2005.
[7] VENKATACHALAPATHY V S K, RAJMOHAN B. Experimental Studies on the Grind-hardening Effect in Cylindrical Grinding[J]. Materials and Manufacturing Processes, 2003, 18(2): 245-259.
[8] HUANG X M, REN Y H, ZHOU Z X, et al. Experimental Study on White Layers in High-speed Grinding of AISI52100 Hardened Steel[J]. Journal of Mechanical Science and Technology, 2015, 29(3): 1257-1263.
[9] ROWE W B. Principles of Modern Grinding Technology[M]. Waltham: William Andrew, 2009.
[10] SRIVASTAVA S, GARG R K. Process Parameter Optimization of Gas Metal Arc Welding on IS:2062 Mild Steel Using Response Surface Methodology[J]. Journal of Manufacturing Processes, 2017, 25: 296-305.
