0 引言
相比传统齿轮，面齿轮传动具有重合度更高、结构更加紧凑、传动噪声更小、承载能力更强的优点，已广泛应用于机器人、汽车及航空等领域[1-2]。面齿轮按照其齿顶线的不同可分为直齿面齿轮、斜齿面齿轮和曲齿面齿轮三种类型。直齿面齿轮和斜齿面齿轮因其齿形相对简单，已有许多研究人员提出了可行的加工方法。STADTFELD[3]采用高阶滚比多项式法使直廓刀具模拟出近似的渐开线产形轮齿廓，利用Coniflex 直廓刀具在Phoenix 机床上进行了直齿面齿轮的粗切和磨削实验。王延忠等[4]提出了面齿轮的插齿刀齿形设计方法。赵宁等[5]提出了利用球形滚刀滚切加工面齿轮的加工方法。为实现硬齿面面齿轮的加工，王晓军等[6]研究了磨齿加工过程中的蜗杆砂轮设计方法及磨损蜗杆砂轮的修正方法。董皓等[7]采用增材制造的方法加工斜齿面齿轮，为斜齿面齿轮的快速成形加工提供了依据。
本文所涉及的偏置圆柱蜗杆传动是由圆柱蜗杆与蜗杆面齿轮(是曲齿面齿轮的一种)构成的一类传递交错轴运动的传动，蜗杆面齿轮是由阿基米德蜗杆依据齿轮啮合原理包络而成的，相比其他类型的面齿轮，优点更加突出，传动更加平稳[8]。但蜗杆面齿轮的缺点是齿面比较复杂，上述加工直齿或斜齿面齿轮的方法都无法运用到该类面齿轮的加工中。目前加工该类面齿轮的方法有三种：①蜗杆滚刀滚切加工[9-11]；②Freeform自由曲面加工[12]；③压铸加工[1]。三种方法各有弊端：对于蜗杆滚刀滚切加工，一方面滚刀制造和刃磨比较复杂，另一方面，在加工小模数面齿轮时，与之相匹配的蜗杆滚刀十分纤小，其强度无法满足加工要求；对于Freeform自由曲面加工，加工所需机床设备的成本高昂，最重要的是加工效率低，仅适用于单件小批量生产；对于压铸加工，其加工精度较低，加工出的齿轮仅适用于低速轻载的场合，无法发挥出蜗杆面齿轮的优势[13-15]。
本文以四轴数控镗床为加工平台，提出了一种蜗杆面齿轮加工的新方法，基于齿面共轭原理，利用阿基米德蜗杆轴截面作为飞刀的刃形，使得所提方法能够快速精确地完成面齿轮齿面的加工，并可分为如下两个阶段：①飞刀做螺旋运动模拟出蜗杆，形成加工蜗杆面齿轮的假想产形轮；②该假想产形轮在齿坯上做滚切运动完成分度加工。本文的主要任务是整合上述加工过程，求解飞刀的轨迹，编制蜗杆面齿轮的加工程序，并完成加工。
1 偏置圆柱蜗杆传动的理论建模
1.1 传动空间坐标系
为得到蜗杆面齿轮传动的理论模型，建立了偏置圆柱蜗杆传动的空间坐标系，各坐标系的空间位置关系如图1所示。
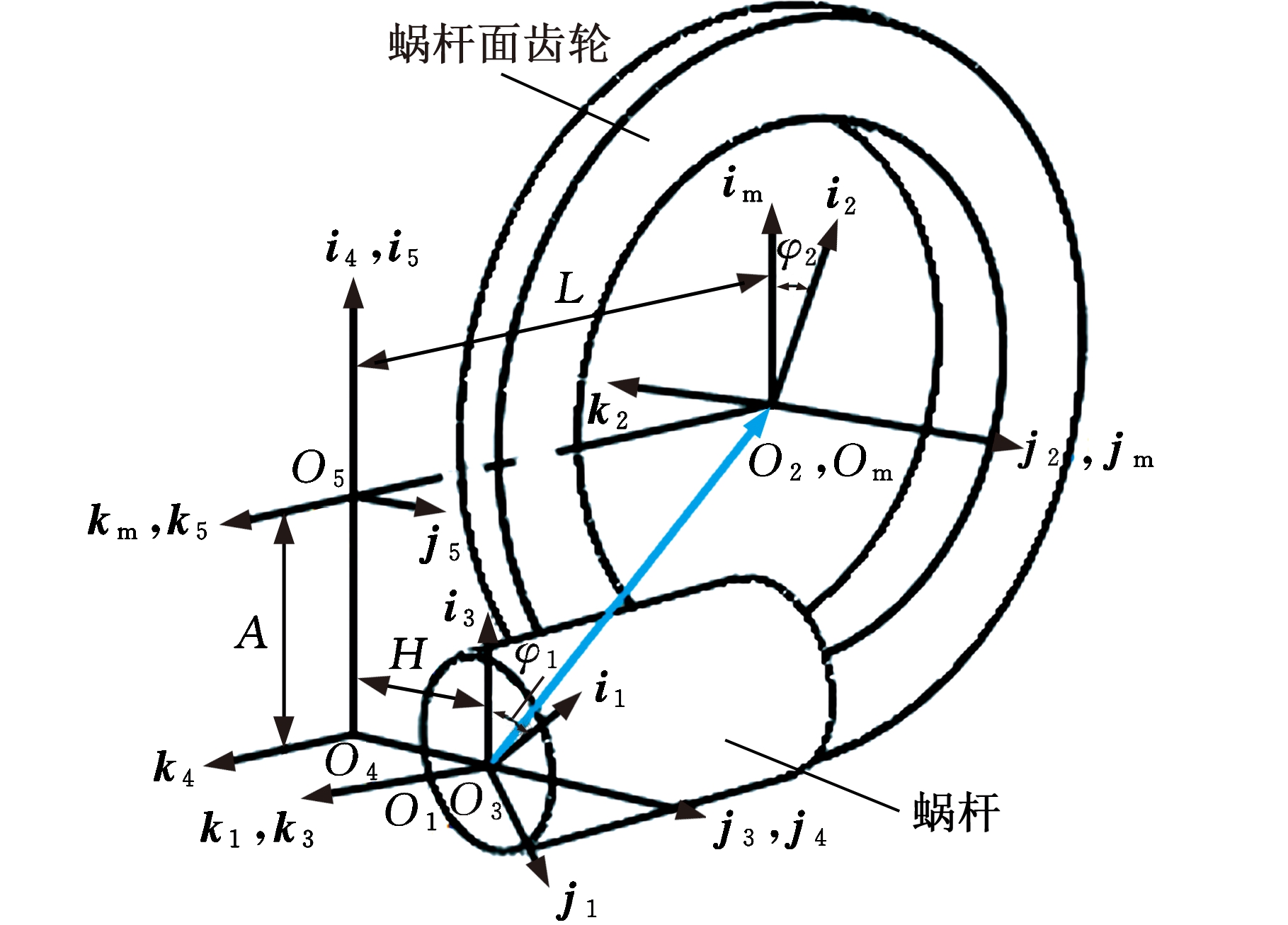
图1 偏置圆柱蜗杆传动空间坐标系
Fig.1 Space coordinate systems of the offset cylindrical worm drive
图1中，坐标系{S1}、{S2}分别与蜗杆和面齿轮固连；{S3}、{Sm}为空间固定坐标系，分别表示蜗杆和面齿轮的初始位置；其他坐标系{S4}、{S5}为辅助坐标系。i、j、k为坐标轴的单位矢量。从坐标系{S1}到{S2}的变换矩阵为
M21=M2m·Mm5·M54·M43·M31=
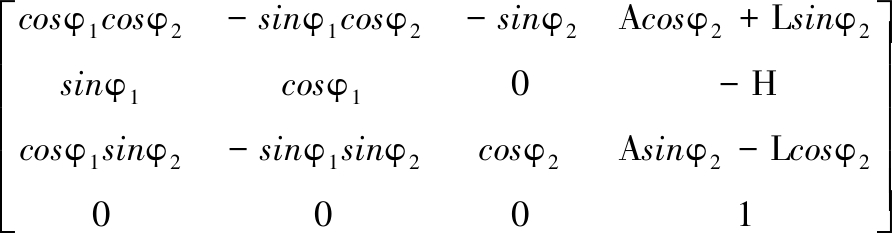
(1)
式中，M31为坐标系{S1}到{S3}的变换矩阵，其他类同；φ1、φ2分别为蜗杆及面齿轮的转角；A、H、L为安装参数，分别表示各坐标系原点间的距离。
1.2 啮合点处相对速度
为了运用齿轮啮合原理求出面齿轮的齿面方程，需先求出啮合点的单位法线矢量及两齿面的相对速度。文献[15]已给出了阿基米德蜗杆的齿面方程及齿面的单位法线矢量，以右旋蜗杆为例，其轮齿两侧面分别记为Ⅰ和Ⅱ，齿面方程可分别表示为
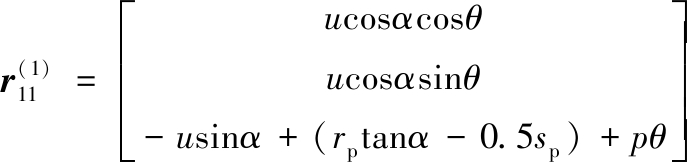
(2)
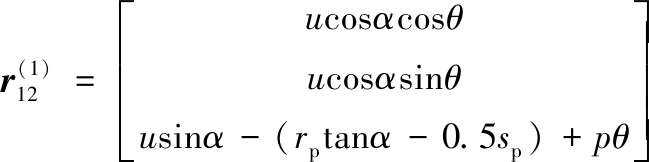
(3)
式中，u为参数，表示产形线上流动点的位置；θ为产形线做螺旋运动的回转角；α、rp、p、sp为蜗杆的设计参数，分别表示蜗杆的压力角、分度圆半径、螺旋参数及蜗杆轴截面齿槽宽；
下标表示蜗杆齿侧Ⅰ，上标表示坐标系{S1}中的坐标，其他类同。
右旋蜗杆两侧齿面的单位法线矢量可分别表示为
(4)
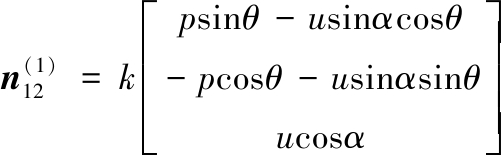
(5)
k=1/(p2+u2)0.5
啮合点处两齿面的相对速度可表示为[16]
v(1)=[(ω1-ω2)×r]-(β×ω2)
(6)
ω1=ω1k1
(7)
(8)
i12=ω1/ω2=φ1/φ2
β=Ai3-Hj3-Lk1= (Acosφ1-Hsinφ1)i1-(Asinφ1+Hcosφ1)j1-Lk1
(9)
式中，r为啮合点在坐标系{S1}中的位置矢量;ω1、ω2分别为蜗杆和面齿轮的角速度；i12为传动比；β为坐标系{S2}的坐标原点O2在坐标系{S1}中的位置矢量。
将式(2) 、式(7)～式(9)代入式(6)中，便可求出啮合点处的相对速度：
(10)
当σ=σ1=-usinα+(rptanα-0.5sp)+pθ时，v(1)为蜗杆齿侧Ⅰ处啮合点的相对速度；当σ=σ2=usinα-(rptanα-0.5sp)+pθ时，v(1)为蜗杆齿侧Ⅱ处啮合点的相对速度。
1.3 面齿轮理论模型
蜗杆与面齿轮啮合时两齿面不能相互脱离或是嵌入，这就要求相互接触的两齿面在接触点处有公共的切平面和法向量，因此，两齿面接触点的相对速度方向必须与公共法向量方向垂直，即两齿面必须满足如下啮合方程[15]：
n·v=0
(11)
将式(4)、式(10)代入式(11)中，便可得到蜗杆齿侧Ⅰ与面齿轮的啮合方程：
u(σ1+L)sinαcos(θ+φ1)+pi12ucosα- u2cos2αcos(θ+φ1)+uAcosα=0
(12)
同理，将式(5)、式(10)代入式(11)中，可得到蜗杆齿侧Ⅱ与面齿轮的啮合方程：
u(σ2+L)sinαcos(θ+φ1)+pi12ucosα- u2cos2αcos(θ+φ1)+uAcosα=0
(13)
面齿轮由蜗杆包络而成，其齿面上的点不仅要满足啮合方程，还需要与蜗杆上的对应点相重合。蜗杆齿面对应点在坐标系{S2}中可表示为
(14)
当
时，表示蜗杆齿侧Ⅰ；当
时，表示蜗杆齿侧Ⅱ。
依据啮合原理，面齿轮的两齿面可分别表示为
(15)
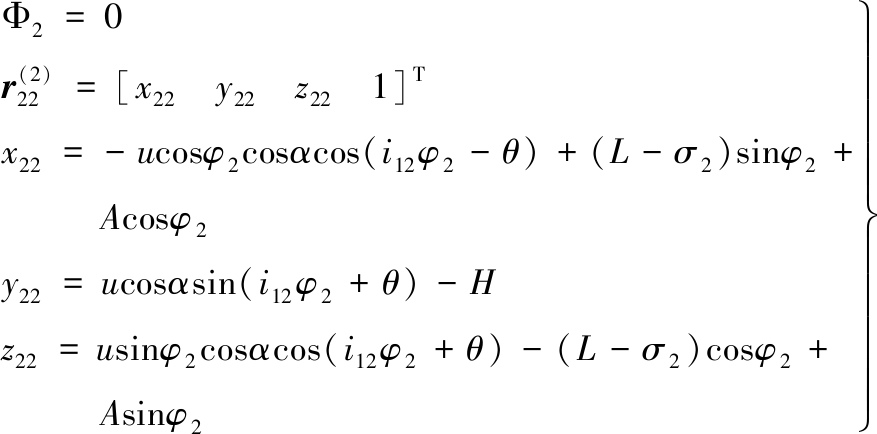
(16)
选取适当的参数可得到偏置圆柱蜗杆传动的CAD模型(图2)，偏置圆柱蜗杆传动的参数见表2。
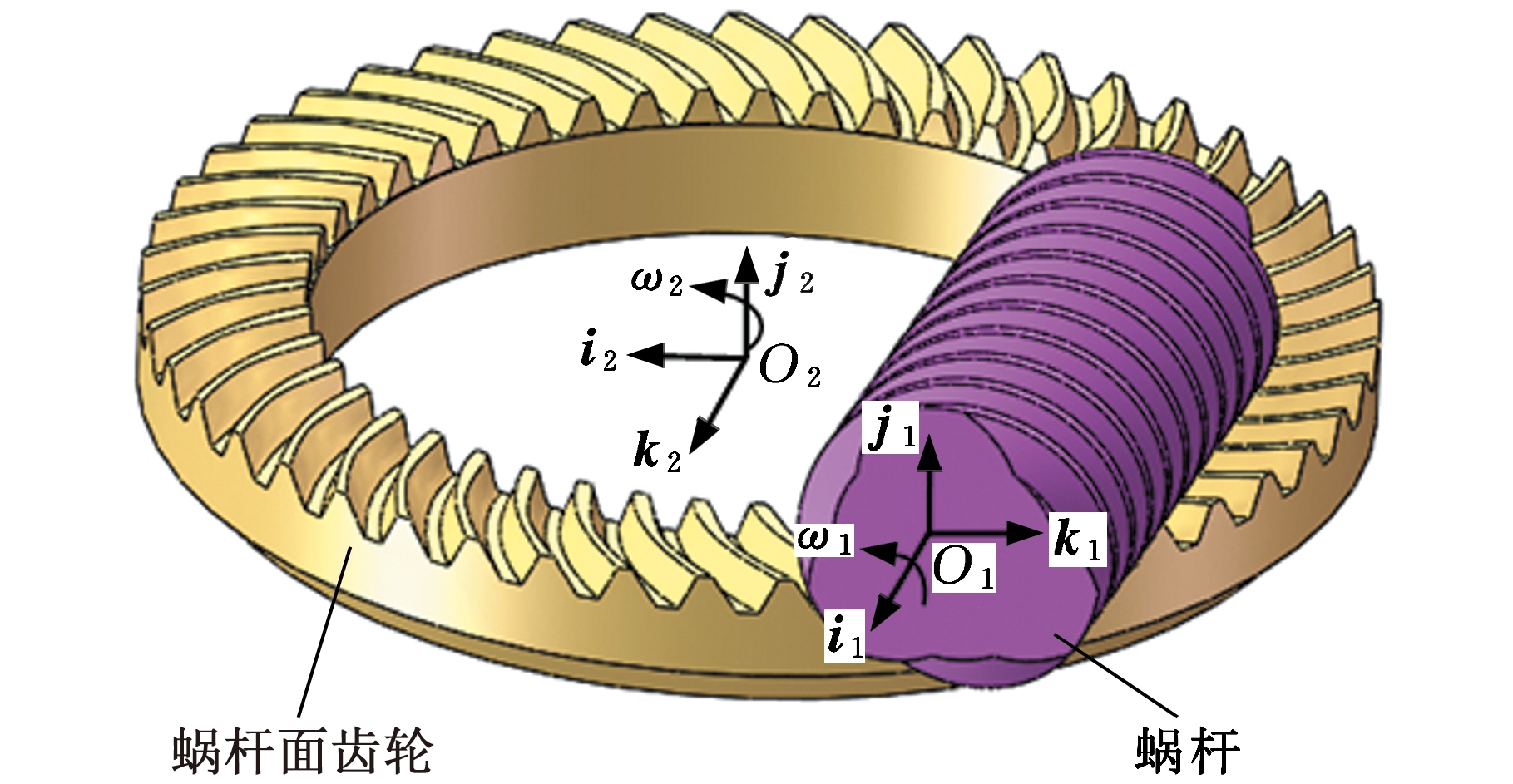
图2 偏置圆柱蜗杆传动CAD模型
Fig.2 The CAD model of offset cylindrical worm drive
表1 偏置圆柱蜗杆传动的参数
Tab.1 Parameters of offset cylindrical worm drive
基本参数数值蜗杆头数z13面齿轮齿数z248A(mm)32H(mm)21.94L(mm)62压力角α (°)20传动比i1216模数m(mm)1.5蜗杆直径系数q14.89蜗杆导程Px(mm)13.92面齿轮小端半径R1(mm)35面齿轮大端半径R2(mm)48
2 加工机理分析
根据文献[1]，蜗杆面齿轮可由与之相匹配的蜗杆滚刀加工而成(图3)，而蜗杆可由车刀车削产生。为寻求一种利用简单刀具快速加工该类型面齿轮的方法，基于共轭原理，将上述两个过程进行整合，将面齿轮的加工分成两个阶段：第一阶段为蜗杆轴截面飞刀做螺旋运动模拟出蜗杆，形成假想产形轮(即仿形阶段)；第二阶段为飞刀模拟蜗杆滚刀滚切面齿轮(即分度加工阶段)，该阶段是为了使假想产形轮做展成运动切削整个面齿轮。通过坐标变换，可求解出蜗杆轴截面飞刀加工面齿轮的切触轨迹线。依据机床的切削运动关系，分解切触轨迹线，使其转化为刀具主轴、工件轴及Z轴(进给方向)之间的关联运动。为了求解刀具的轨迹，建立了图4所示的坐标系。坐标系{S}与刀具固连，其他坐标系含义与图1相同。
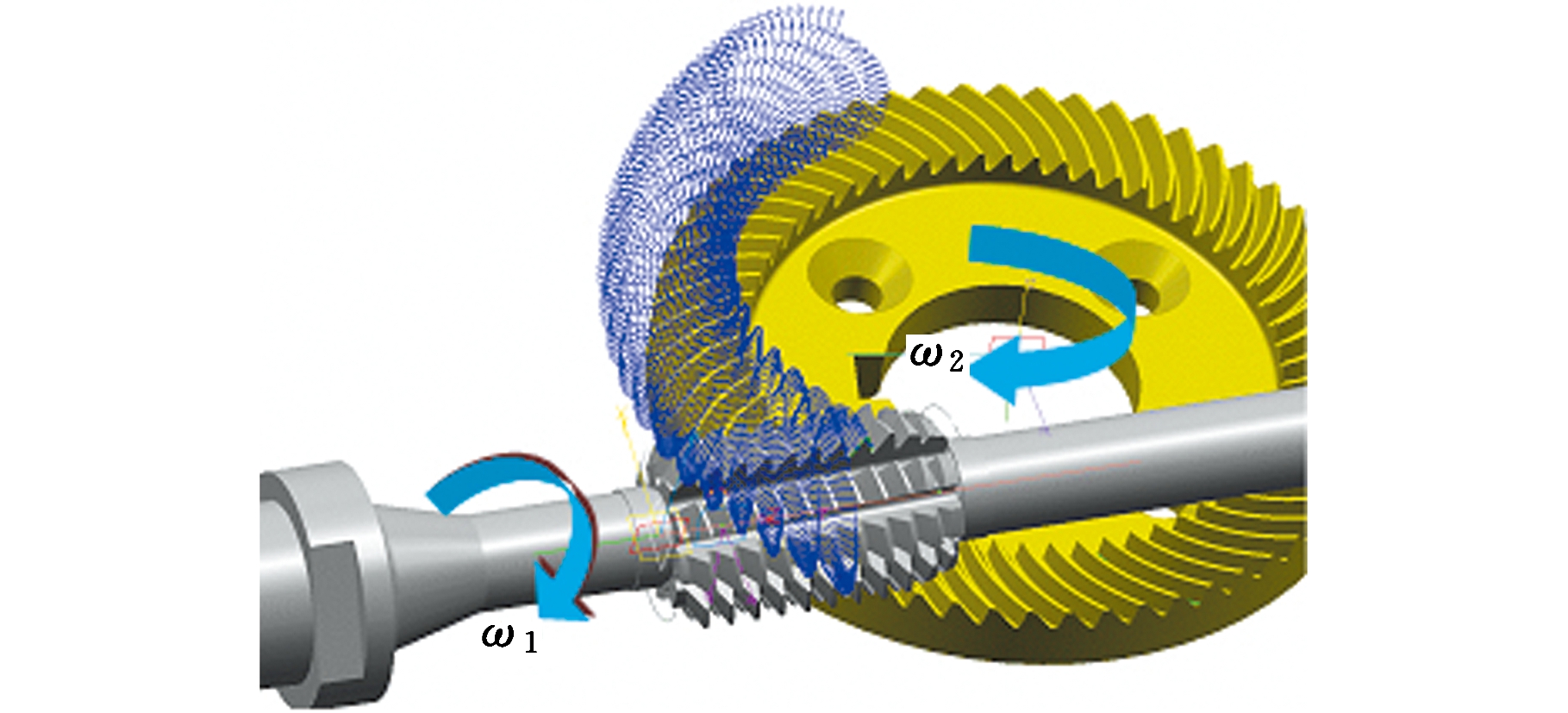
图3 蜗杆滚刀滚切加工蜗杆面齿轮示意图
Fig.3 Schematic diagram of cutting worm-face gear by worm hob
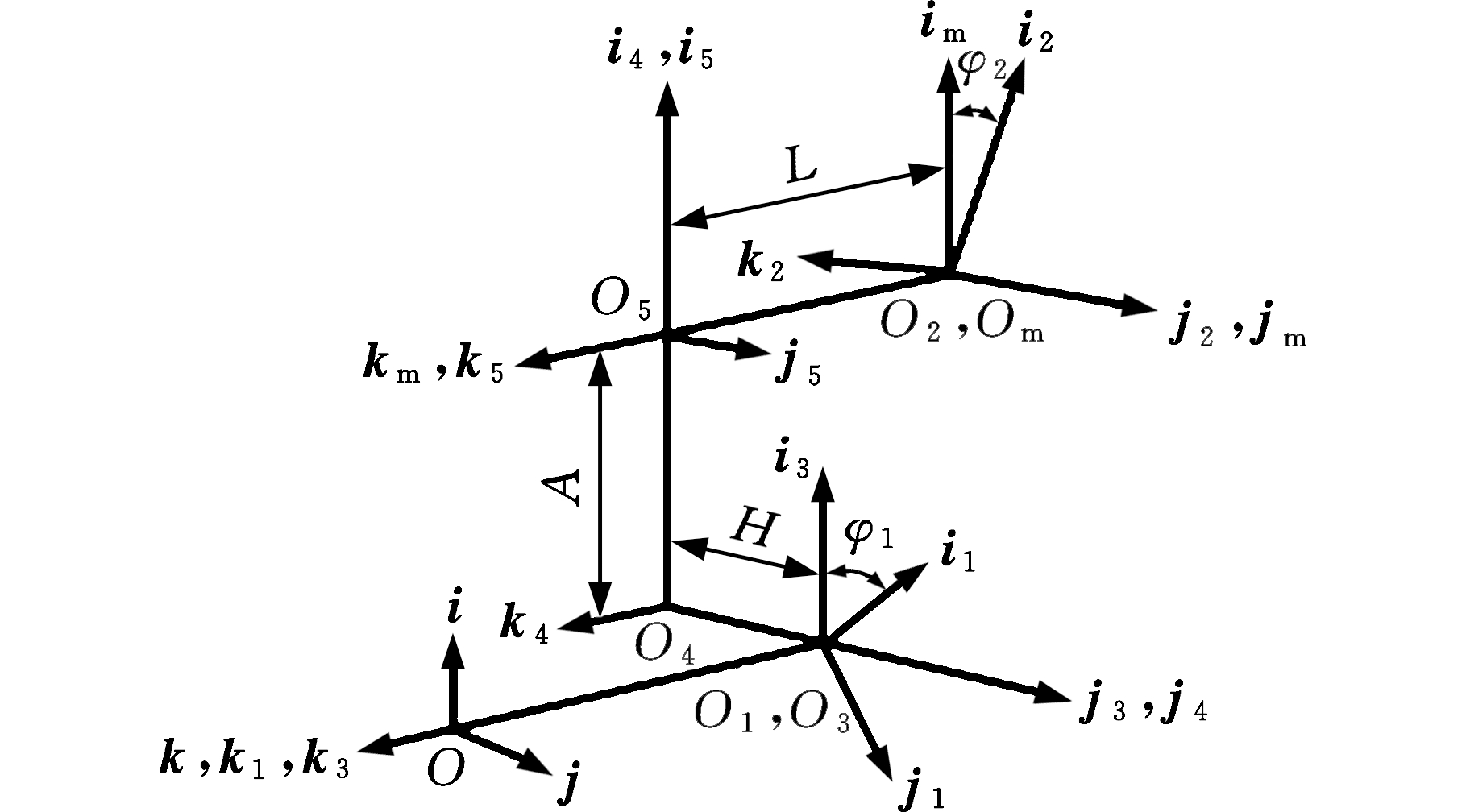
图4 蜗杆面齿轮加工坐标系
Fig.4 Machining coordinate systems of worm-face gear
2.1 仿形阶段
为产生假想产形轮，需要求解飞刀的刃形及其运动规律，本文根据蜗杆的形成原理，选取蜗杆的轴截面作为飞刀的刃形。阿基米德蜗杆在轴截面上的齿廓为直线，如图5所示，该直线为阿基米德蜗杆的产形线。
图5 阿基米德蜗杆轴截面示意图
Fig.5 Schematic diagram of the shaft section of ZA worm
假定坐标系{S}的k轴与蜗杆的轴线重合，i轴穿过蜗杆轴截面齿廓的中心，点M为蜗杆节圆与轴截面齿廓的交点，其坐标可表示为(mq/2，0,πm/4)，则直线齿廓ab上某点在坐标系{S}中的位置矢量可表示为
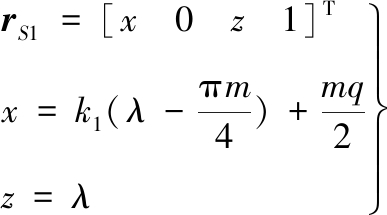
(17)
k1=tan(π/2+α)
式中，λ为参变量。
同理，直线齿廓cd上某点的位置矢量可表示为
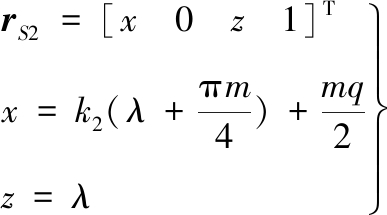
(18)
k2=tan(π/2-α)
仿形阶段的目的是模拟出蜗杆螺旋齿面(假想产形轮)，因此，该过程中面齿轮齿坯静止不动，飞刀做螺旋运动，刀具沿k轴负方向的进给运动需要与绕k轴的旋转运动保持对应的比例关系。图6给出了阿基米德蜗杆螺旋线展开角γ与导程Px之间的对应关系，由此得出刀具的轴向位移量与转角之间的关系：
(19)
式中，Fs为刀具的轴向位移量；φs1为刀具在仿形加工阶段时的转角。
图6 蜗杆螺旋线展开角与导程的关系
Fig.6 Relationship between the expansion angle and lead of thread line
刀具在坐标系{S1}中的轨迹可表示为
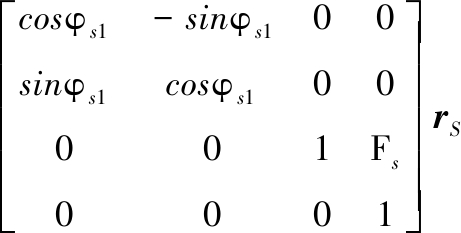
(20)
式中，M为坐标系{S}到{S1}的变换矩阵；rS为刀具齿廓在坐标系{S}中的坐标。
将式(17)、式(19)代入式(20)中，可得到齿廓ab在坐标系{S1}中的轨迹方程：
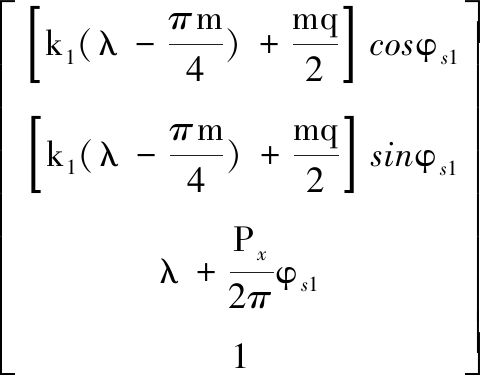
(21)
同理，将式(18)、式(19)代入式(20)中，可得到齿廓cd在坐标系{S1}中的轨迹方程：
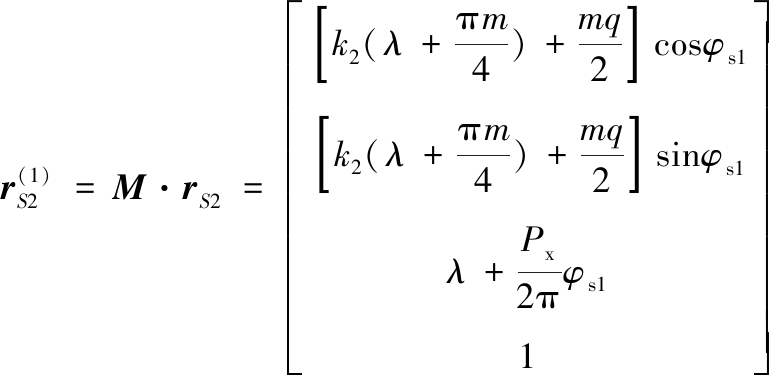
(22)
将表1中的参数代入式(21)、式(22)中，可以得到坐标系{S1}中刀具的轨迹图像,见图7a，其中vf为刀具进给速度，该轨迹即飞刀模拟出的产形轮。仿形阶段刀具走刀一次切削后的面齿轮齿廓见图7b。
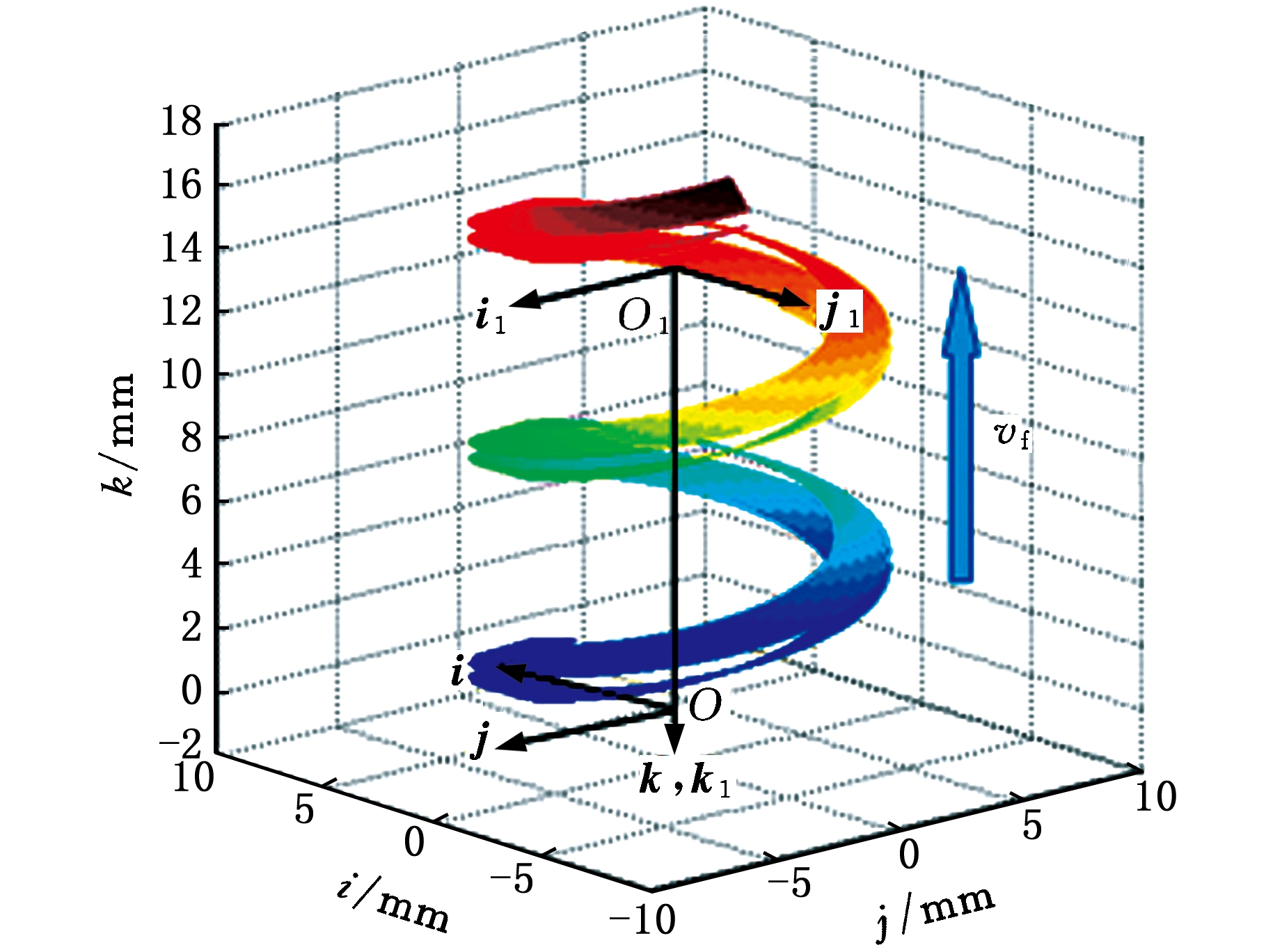
(a)刀具轨迹
(b)面齿轮齿廓
图7 仿形阶段
Fig.7 Imitation stage
2.2 分度加工阶段
在仿形阶段，飞刀模拟出了产形轮，当刀具的轨迹穿过面齿轮齿坯时，切出的齿形只能满足在某一特定时刻蜗杆与面齿轮的啮合，要想加工出完整的面齿轮齿面，保证蜗杆与面齿轮连续的啮合传动，就需要产形轮做展成运动来完成，上述过程称之为分度加工过程。分度加工过程是为了模拟蜗杆滚刀滚切加工面齿轮，过程中飞刀和面齿轮齿坯分别做旋转运动，刀具主轴与工件轴的转角则需满足如下比例关系:
φs2=i12φb
(23)
式中，φb为面齿轮齿坯绕其轴线的转角；φs2为刀具在分度加工阶段绕其轴线的转角。
假定面齿轮齿坯静止不动，根据相对运动关系，刀具在绕自身轴线旋转的同时，还要绕面齿轮齿坯的轴线做旋转运动，刀具齿廓ab在坐标系{S2}中的运动轨迹可表示为
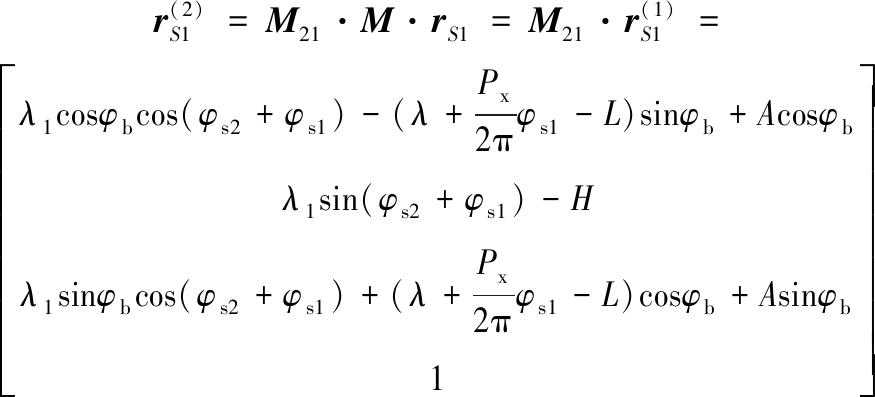
(24)
λ1=k1(λ-πm/4)+mq/2
同理，刀具齿廓cd的运动轨迹可以表示为
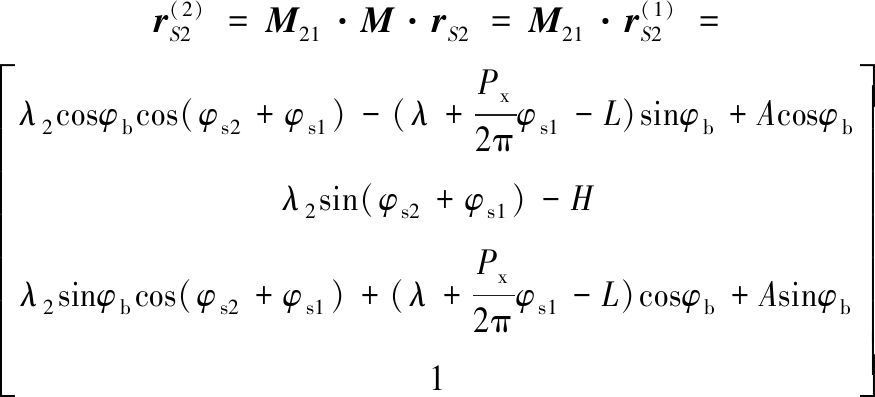
(25)
λ2=k2(λ+πm/4)+mq/2
由式(24)、式(25)可知，刀具齿廓在坐标系{S2}中的轨迹方程包含3个独立变量：λ、φs1、φb，无法直接获得刀具的轨迹，因此需要选定一系列φb的值来构建刀具的三维轨迹。当φb取值为0°，20°，40°，…，360°时，得到的刀具轨迹如图8所示。该轨迹实质为假想产形轮对面齿轮齿坯的包络线。
图8 分度加工阶段刀具轨迹
Fig.8 Trajectory of cutter in rolling cutting stage
3 仿真加工
3.1 仿真加工环境
利用VERICUT仿真加工软件来验证所提出的蜗杆面齿轮新型加工方法的有效性和可行性。由于该加工方法中的两个阶段分别是联动的，因此选择进行仿真加工的机床必须能够实现工件轴与刀具主轴之间、机床坐标系Z轴(与km轴方向一致)与刀具主轴之间的精确联动。该新型面齿轮加工方法的目的是通过上述联动作用来完成面齿轮的加工。仿真加工所用的数控机床如图9所示，该机床为四轴数控镗床，可满足上述加工要求。
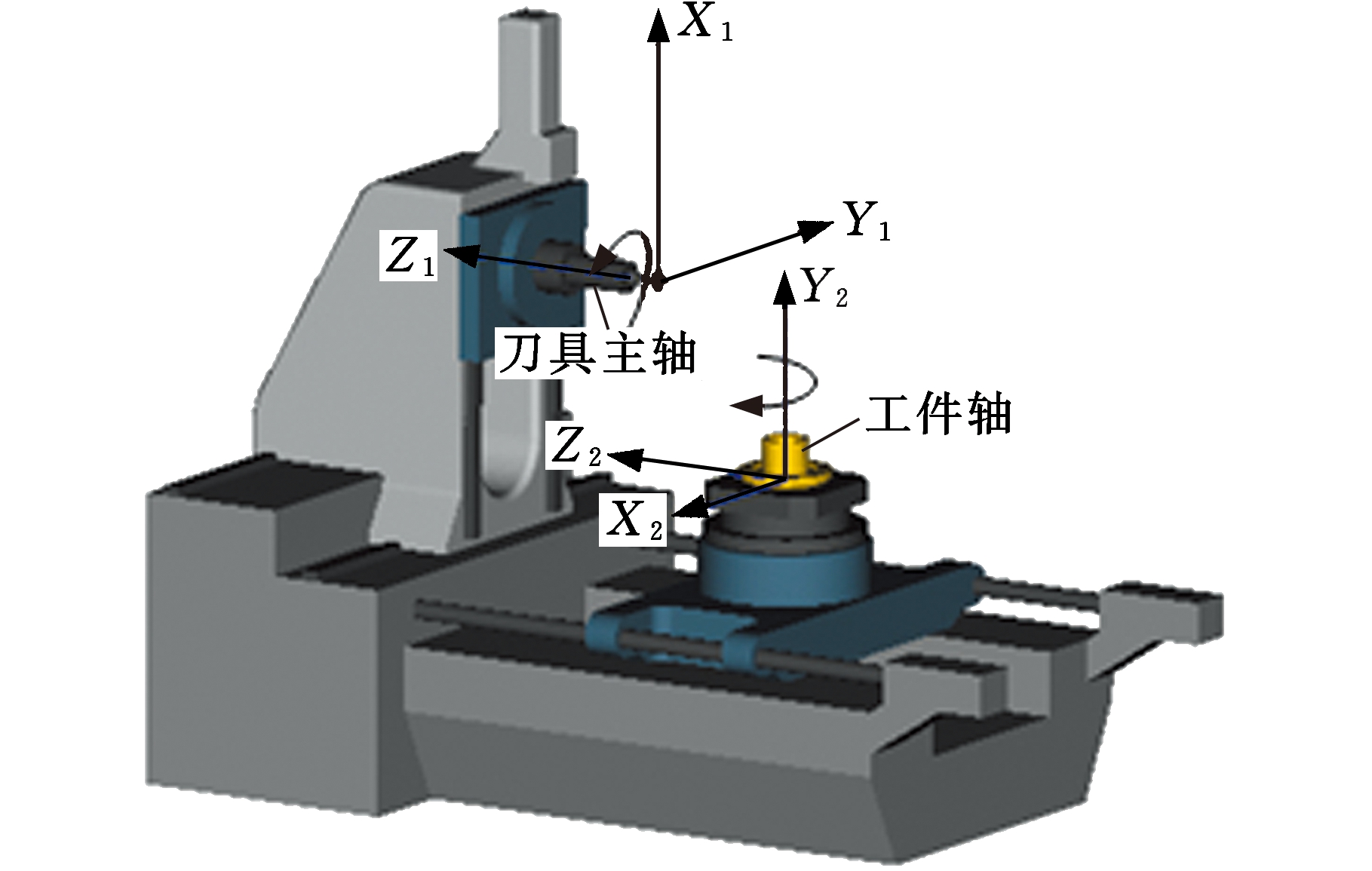
图9 VERICUT仿真加工环境
Fig.9 Simulation machining environment in VERICUT
仿真加工刀具为直廓飞刀，刀具刃形为阿基米德蜗杆轴截面齿廓,如图10所示，其具体参数与图5一致。仿真加工时的刀具不考虑前角、后角及刃倾角等参数的取值，也不考虑安装误差及受力变形的影响。
图10 仿真加工刀具示意图
Fig.10 Schematic diagram of the cutter in simulation process
3.2 仿真加工程序
由刀具轨迹(图8)可以看出，刀路是十分复杂的，仿形阶段飞刀轨迹形成假想产形轮，分度加工阶段完成包络运动，来进行面齿轮圆周方向的加工。为了在数控机床上完成上述过程，必须将两个过程进行整合。刀具主轴与工件轴按固定传动比进行转动，刀具先进行滚切运动，采用刀具轴向进给的方式来加工，飞刀滚切面齿轮毛坯一周后，沿刀具轴向进给的同时进行螺旋进给，如此循环，直至切削整个面齿轮齿长。该方法的加工程序可由两个循环来完成。取分度加工阶段齿坯转角φb=0.4°，仿形阶段刀具轴向进给量Fs=0.01 mm。该方法仿形阶段中的轴向进给量应足够小，以便获得表面粗糙度值较小的齿面。蜗杆面齿轮的具体加工流程见图11，其中I1为面轮转角角度值计数，I2为刀具轴向进给次数计数。
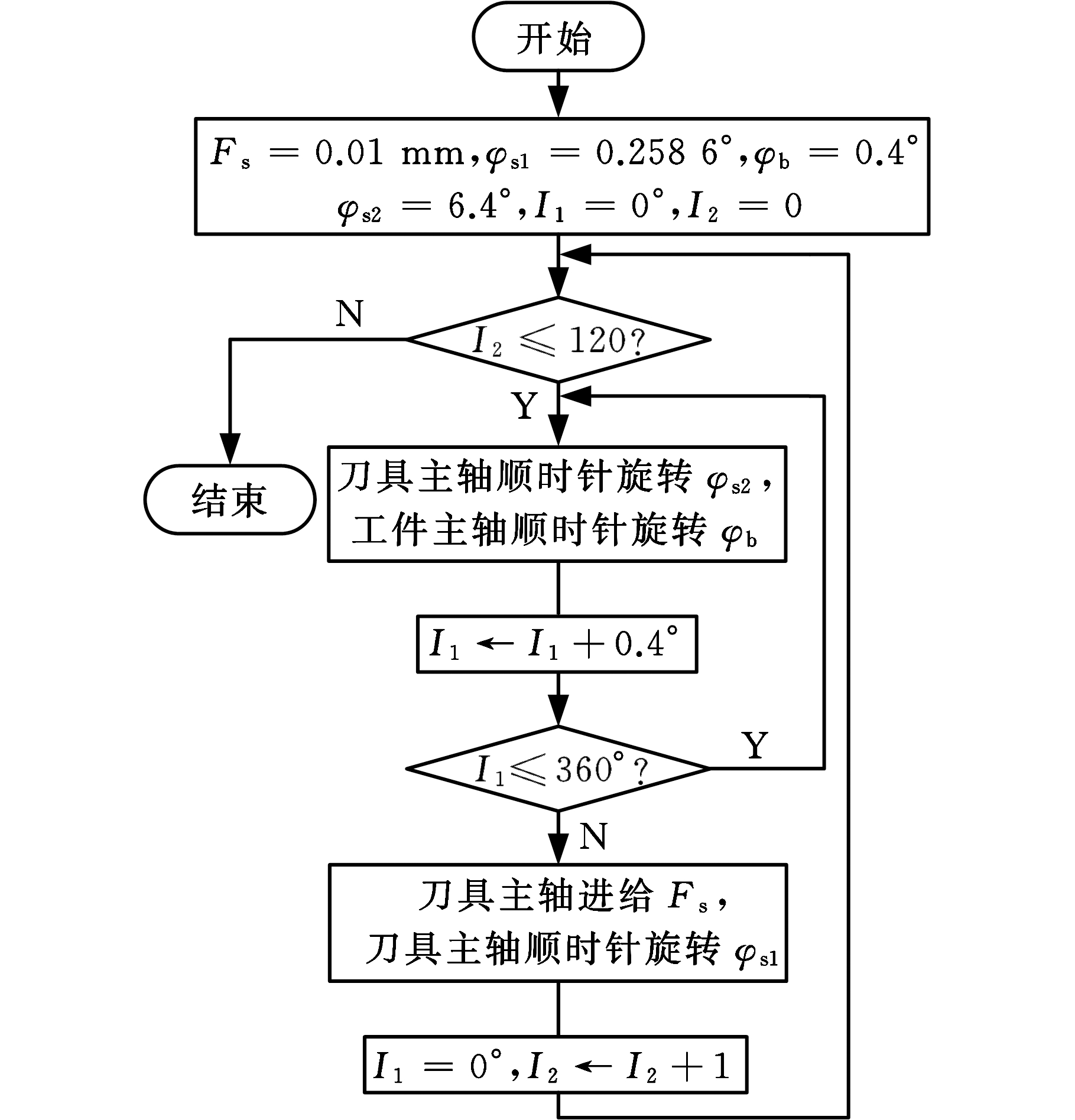
图11 蜗杆面齿轮加工流程
Fig.11 Machining process of worm-face gear
在VERICUT仿真加工时，为了模拟刀具主轴与工件轴的联动，需要对机床模型稍作修改，删除机床主轴，并添加刀具主轴，通过对刀具主轴及工件轴的角度控制完成分度加工运动，通过对刀具主轴及Z轴的联动控制实现仿形运动，进而完成进给加工。由于涉及循环和联动控制，因此选用宏程序，具体加工程序如下：
N1 %0001 ∥主程序
N2CGTECH_MACRO “BroaChModeOnOff” “” 1 ∥开启拉削模式
N3 T03 M06 ∥选择03号刀具
N4 G90 G01 G54 Y21.94 X32 Z76 ∥调整刀具到加工位置
N5 A0 C0 ∥刀具主轴与工件轴初始化
N6 #1=-0.4 ∥工件轴转角赋初值
N7 #2=6.4 ∥刀具主轴转角赋初值
N8 #3=0.4 ∥圆周方法转角计数赋初值
N9 #4=-0.01 ∥进给量
N10 #5=1 ∥进给次数计数赋初值
N11 WHILE #5 LE 120 ∥仿形加工循环120次
N12 M98 P0002 ∥分度加工
N13 #1=-0.4 ∥工件轴转角赋初值
N14 #2=6.4 ∥刀具主轴转角赋初值
N15 #3=0 ∥圆周方法转角计数初始化
N16 #5=#5+1 ∥刀具轴向进给次数计数(即I2)
N17 #4=#4-0.01 ∥进给量
N18 G91 A[#4*360/13.92] Z[#4] ∥螺旋进给
N19 ENDW
N20 M30 ∥主程序结束
N21 %0002 ∥子程序
N22 WHILE #3 LE 360 ∥分度加工循环
N23 G91 C[#1] A[#2] ∥分度加工
N24 #3=#3+0.4 ∥面轮转角角度值计数(即I1)
N25 ENDW
N26 M99 ∥子程序结束
3.4 仿真加工结果
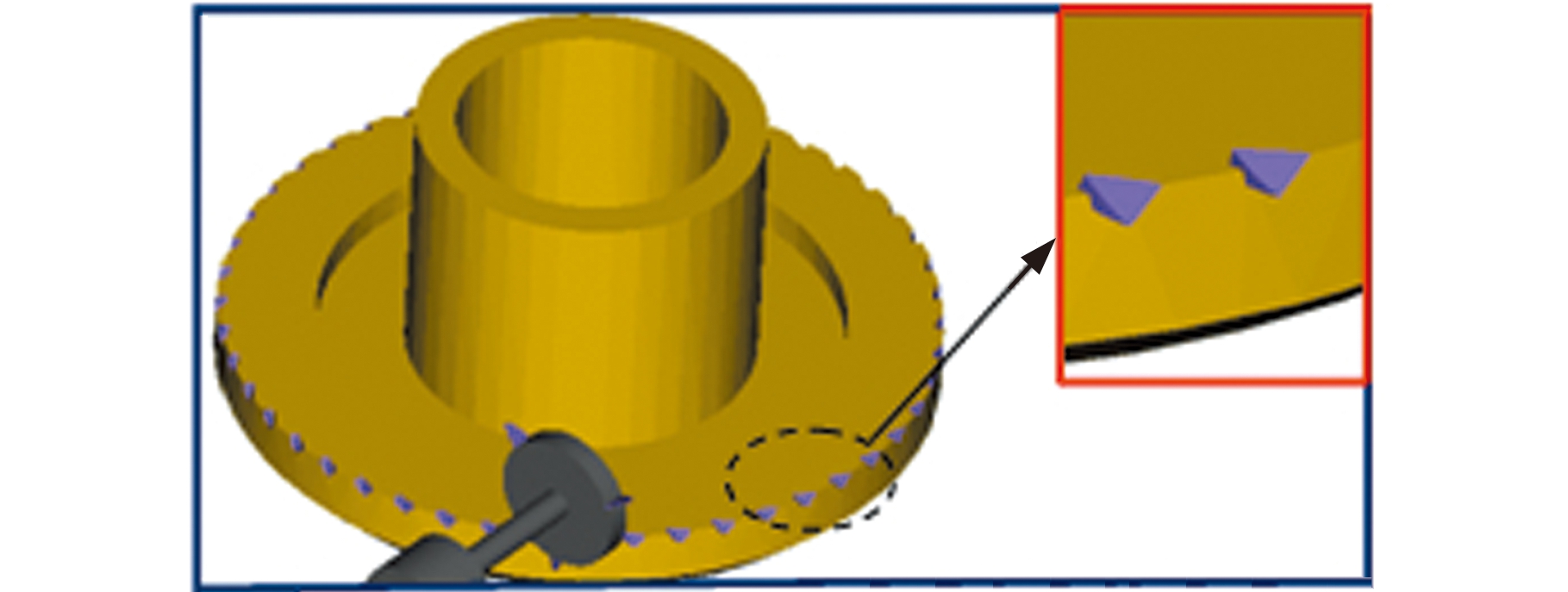
(a)开始
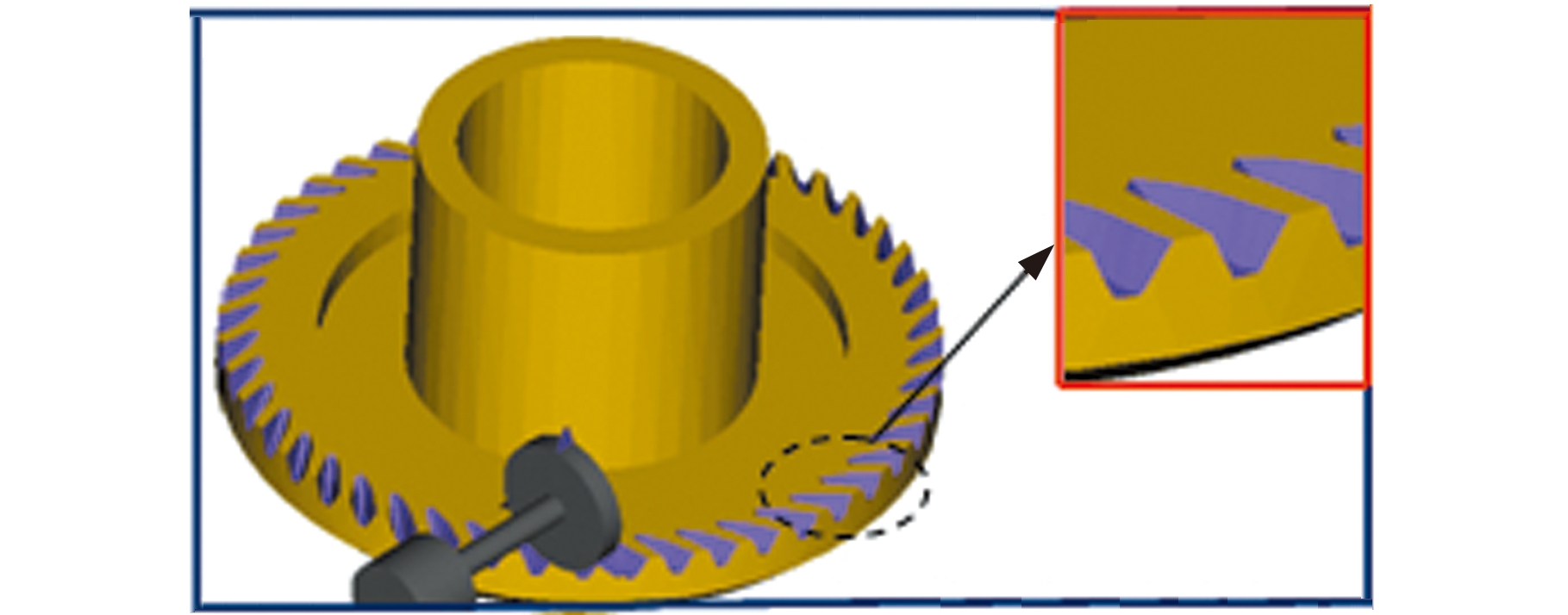
(b)中间
(c)结束
图12 VERICUT仿真加工蜗杆面齿轮
Fig.12 Simulation machining of worm-face gear in VERICUT
(a)凸面模型对比 (b)凹面模型对比
图13 切削模型与理论模型误差比较
Fig.13 Error comparison of cutting and theoretical model
通过仿真可快速并精确地完成蜗杆面齿轮的加工，加工过程如图12所示。将面齿轮理论模型导入VERICUT并与切削模型进行比较，得到的结果见图13,结果表明：当刀具轴向进给量取0.01 mm时，最大过切量为0.09 mm，最大残余量为0.12 mm，两者均在误差允许范围内。该误差与仿真过程中进给量的取值有关，在实际加工时，选用具有电子齿轮箱功能的数控机床可实现各轴之间的精确联动，从而消除此类误差。
4 加工实验
为进一步验证所提加工方法的可行性，在四轴CNC数控机床上进行了加工实验，如图14所示。加工刀具见图14b，为了使刀具结构简单、易于制造，用单齿飞刀代替仿真时使用的三齿飞刀(图10)。在加工过程中，使用单齿飞刀按上述方法进行加工，每完成一个加工循环，飞刀转动120°，并继续进行加工，这样三个循环即可完成整个面齿轮的加工。
(a)加工现场 (b)加工刀具
(c)面齿轮试件
图14 蜗杆面齿轮加工实验
Fig.14 Machining experiment of worm-face gear
图15 蜗杆面齿轮检测过程
Fig.15 Detection process of worm-face gear
在DAISY三坐标测量机上对面齿轮试件进行检测，如图15所示，测得了面齿轮轮齿凸面和凹面离散点的坐标值，并经过坐标变换后与理论坐标值进行了对比，得到的齿面法向偏差见图16，可以看出，最大误差出现在轮齿的凹面，为99.2 μm。该误差是由刀具的制造误差及切削过程中飞刀的变形所造成的。
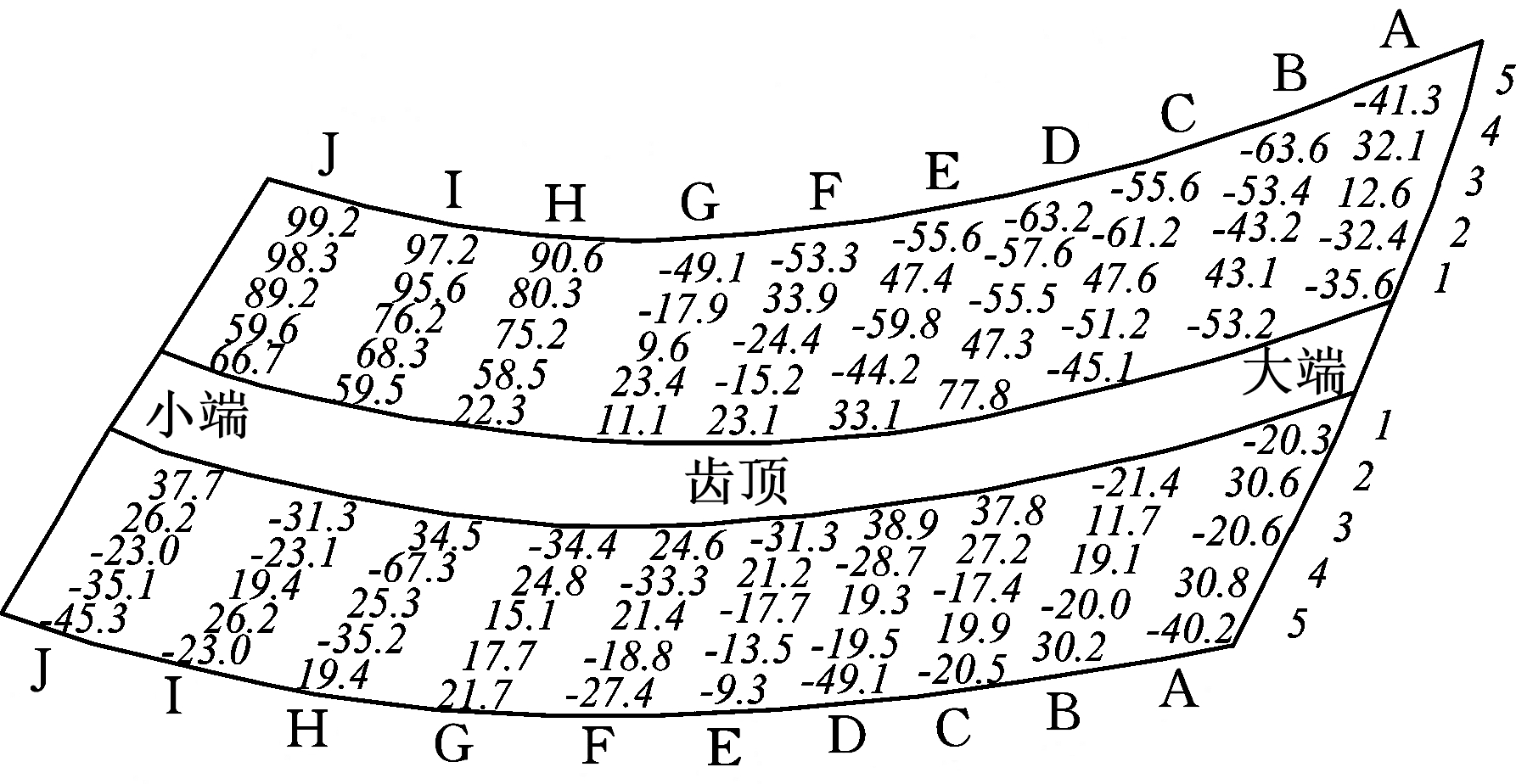
图16 蜗杆面齿轮齿面法向偏差示意图(μm)
Fig.16 Schematic diagram of normal deviation of the tooth surface for worm-face gear(μm)
5 结论
(1)本文提出了一种全新的蜗杆面齿轮加工方法，该方法可利用蜗杆轴截面作为刀具的刃形，快速并精确地完成面齿轮的加工，特别是在加工小模数蜗杆面齿轮时，该方法具有重要的参考价值。
(2)分析了蜗杆面齿轮加工所包含的两个加工阶段，分别求解了两个加工阶段中刀具的轨迹，并根据机床的运动关系将两个阶段进行整合，转化为刀具主轴、工件轴及Z轴的关联运动。
(3)对所提出的方法进行了加工实验并对加工误差进行了检测，齿面最大误差为99.2 μm，检测结果表明该飞刀加工法是可行的。
飞刀加工法所需的机床结构较为简单，可对三轴数控车床稍加改装变为专用机床，这对该类面齿轮的广泛应用非常有利。
[1] 傅则绍. 新型蜗杆传动[M].西安：陕西科学技术出版社，1990.
FU Zeshao. New Worm Drive[M]. Xi’an:Shaanxi Science & Technology Press, 1990.
[2] LITVIN F L，VECCHIATO D，GUROVICH E，et al. Computerized Developments in Design, Generation， Simulation of Meshing， and Stress Analysis of Gear Drives[J]. Meccanica，2005，40(3):291-324.
[3] STADTFELD H J. CONIFACE Face Gear Cutting and Grinding[J]. Gear Solutions,2010(9)：38-47.
[4] 王延忠，吴灿辉，葛旭阳，等.面齿轮滚刀基本蜗杆的设计方法[J].北京航空航天大学学报, 2009, 35(2):166-169.
WANG Yanzhong, WU Canhui, GE Xuyang, et al. Design Method of the Basic Worm of Surface Gear Hob[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(2):166-169.
[5] 赵宁，郭辉，方宗德，等.用球形滚刀滚切面齿轮的理论误差[J].航空动力学报, 2009, 24(3):677-682.
ZHAO Ning, GUO Hui, FANG Zongde, et al. Theoretical Error of Using Spherical Hob to Roll Shear Surface Gear[J]. Journal of Aerospace Power, 2009, 24(3):677-682.
[6] 王晓军，李晓贞，叶闻.面齿轮磨齿加工中蜗杆砂的设计及修整[J]，机械传动，2016, 40(12):65-68.
WANG Xiaojun, LI Xiaozhen, YE Wen. Design and Modification of Worm Sand in Gear Grinding Process[J]. Journal of Mechanical Transmission, 2016, 40(12):65-68.
[7] 董皓，赵晓龙，方舟，等.考虑数字齿面的斜齿面齿轮增材制造加工方法[J],工艺与检测,2016(7):113-117.
DONG Hao, ZHAO Xiaolong, FANG Zhou, et al. Considering the Processing Method for the Manufacturing of Helical Tooth Surface Gear with Digital Tooth Surface[J]. Process and Detection, 2016(7):113-117.
[8] 户立杰.蜗杆面齿轮铣削加工方法研究[D]. 天津:天津大学, 2016.
HU Lijie.Research on Milling Method of Curved Tooth Face Gear[D]. Tianjin:Tianjin University, 2016.
[9] NAPAU I D, MATIES V, NAPAU I, et al. A New Orthogonal Skew-axis Drive with Face Gear and Cylindrical Worm: Mathematical Model, Geometric Synthesis and Generation Method[C]∥ASME 2005 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Long Beach, 2005:615-624.
[10] NAPAU I, NAPAU I D, NAPAU M, et al. Computerized Modeling and Simulation of Duplex Worm-face Gear Drives Manufacturing Process[C]∥ASME 2006 International Mechanical Engineering Congress and Exposition. Chicago, 2006:1095-1104.
[11] NAPAU M, NAPAU I D, NAPAU I, et al. Computerized Modeling and Simulation of Idle and Loaded Multi-tooth Contact Analysis in Worm-face Gear Drives[C]∥ASME 2007 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference. Las Vegas, 2007：1103-1112.
[12] MALGORZATA P. Free-form Surface Machining Error Compensation Applying 3D CAD Machining Pattern Model[J]. Computer-Aided Design, 2015, 62:227-235.
[13] 
BOLOS V. The Mathematical Model of Generating Kinematic for the Worm Face Gear with Modified Geometry[J]. Procedia Technology 2014, 12:442-447.
[14] 
I, BOLOS V. Experimental Research Concerning Relation Between Contact Patch and Lapping Operation of Worm Face Gear[J]. Procedia Technology, 2015, 19:120-127.
[15] F.L.李特文.齿轮几何学与应用理论[M].国楷，叶凌云，范琳，等译. 上海:上海科学技术出版社, 2008.
LITVIN F L. Gear Geometry and Applied Theory[M]. GUO Kai, YE Lingyun, FAN Lin, et al, Trans. Shanghai :Shanghai Scientific and Technical Publishers, 2008.
[16] F.L. 李特文. 齿轮啮合原理[M].2版.卢贤占，高业田，王树人，译.上海:上海科学技术出版社, 1984.
LIYVIN F L. Principle of Gear Meshing [M]. 2nd ed. LU Xianzhan, GAO Yetian, WANG Shuren, Trans. Shanghai :Shanghai Scientific and Technical Publishers, 1984.
