0 引言
齿轮作为机械设备中常用的动力传递装置，对其进行状态监测与故障诊断具有重要意义。齿轮故障机理研究是故障诊断的基础，目前对齿轮进行故障机理的研究方法主要是将齿轮看作一个振动系统，对其建立各种相应的动力学模型来揭示齿轮故障演变规律。作为齿轮系统振动特性的主要激励，齿轮啮合刚度具有时变性，其参数变化直接影响齿轮动力学行为，因此，研究啮合刚度的变化对齿轮故障机理研究具有深刻的意义。
目前啮合刚度的计算主要有传统法、有限元法(finite element method, FEM)和解析计算等方法。其中，应用于啮合刚度计算的石川算法、ISO6336-1-2006标准、ROMAX软件等传统方法都具有很大的局限性[1]。针对有限元法和解析法，目前国内外学者进行了大量研究。CHAARI等[2]提出了一种计算齿轮啮合刚度的解析计算方法，并研究了齿裂纹深度扩展对齿轮啮合刚度的影响。万志国等[3]通过改进齿根圆与基圆不重合现象，对势能法求解啮合刚度进行了改进，显著减小了计算误差。RINCON等[4]运用有限元分析方法和赫兹接触理论分析方法描述了齿轮啮合传动过程中齿轮啮合刚度的变化过程。LIANG等[5]将齿轮简化为一个变截面悬臂梁，利用解析法求取齿轮啮合刚度随啮合点变化的曲线，提供了一种简单有效的时变啮合刚度计算方法。MOHAMMED等[6]运用解析法求解齿轮裂纹故障时变啮合刚度并分析了3种不同裂纹扩展状况的齿轮早期故障现象。PANDYA等[7]采用有限元法和势能法研究了齿轮不同的裂纹扩展路径对齿轮啮合刚度变化的影响。CHEN等[8]在考虑齿根裂纹沿齿宽和裂纹深度的扩展的前提下模拟齿轮齿根裂纹，特别是齿根裂纹处于非常早期时的啮合刚度计算方法。HE等[9]运用有限元方法建立了直齿圆柱齿轮的啮合模型，对不同裂纹层次的齿轮故障进行定量诊断。然而，解析法和有限元法虽然能够通过计算得到齿轮时变啮合刚度，但依然存在局限性，如解析法计算过程复杂，不能准确反映齿轮局部微小变化；有限元法计算量大、建模困难且无法验证等。
针对目前啮合刚度计算存在的问题，本文将现代测试方法、优化方法与有限元法相结合，提出了基于参数反求的时变啮合刚度计算方法。考虑到齿根动态应力与啮合刚度之间存在隐式的映射关系，即啮合刚度的变化会引起裂纹部位的齿根动态应力发生相应的变化[10]，该方法通过对各种不同裂纹状态下的齿根动态应力进行检测，在构建考虑时变啮合刚度的齿根弯曲应力正问题模型的基础上，采用优化方法反向求解时变啮合刚度。将计算结果与其他方法对比来验证该方法的有效性。同时构建多自由度齿轮系统动力学模型，将本文计算结果代入模型，模拟齿根裂纹故障下的动力学响应，通过对动力学响应进行时域及频域分析来揭示齿轮裂纹故障机理。
1 齿轮啮合刚度计算反求方法
1.1 时变啮合刚度正问题建模
正问题模型包含齿轮啮合刚度与齿根应力之间的隐式映射关系，不同工作状态的齿轮弯曲强度可通过有限元法进行构建。齿轮工作过程中，轮齿的啮合作用可以简化为一个在啮合线方向上的时变弹簧，即弹簧刚度为不同时刻的齿轮啮合刚度，在不考虑惯性力的基础上齿轮啮合刚度可表示为
(1)
其中，N为法向载荷，Cm为齿轮啮合黏性阻尼，δn为法向综合弹性形变。根据轮齿传递误差原理，实际转动位移与理想转动位移之差
XT.E=θg-zpθp/zg
(2)
其中，θg、θp分别为大齿轮与小齿轮的转角，zp、zg分别为大齿轮与小齿轮的齿数。将传递误差转换成啮合线方向上的位移，故受载传递误差(load transfer error, LTE)为
XLTE=Rbgθg-Rbpθp
(3)
其中，Rbp、Rbg分别为主动轮、从动轮的基圆半径。当有齿形误差时，产生无负载传递误差。在不考虑制造误差的情况下，综合弹性形变可定义为
δn=Rbpθp-Rbgθg+xp-xg
(4)
式中，xp、xg分别为齿轮沿啮合线方向上的位移误差。
如图1所示，啮合齿接触时，实际作用于齿面的力包含法向载荷N和垂直于法向载荷的摩擦力Nf，故接触点的载荷分力可以表示为
(5)
其中，根据库仑定律Nf=μN，α为法向载荷与水平面的夹角，μ为齿面摩擦因数。则式(5)可表示为
(6)
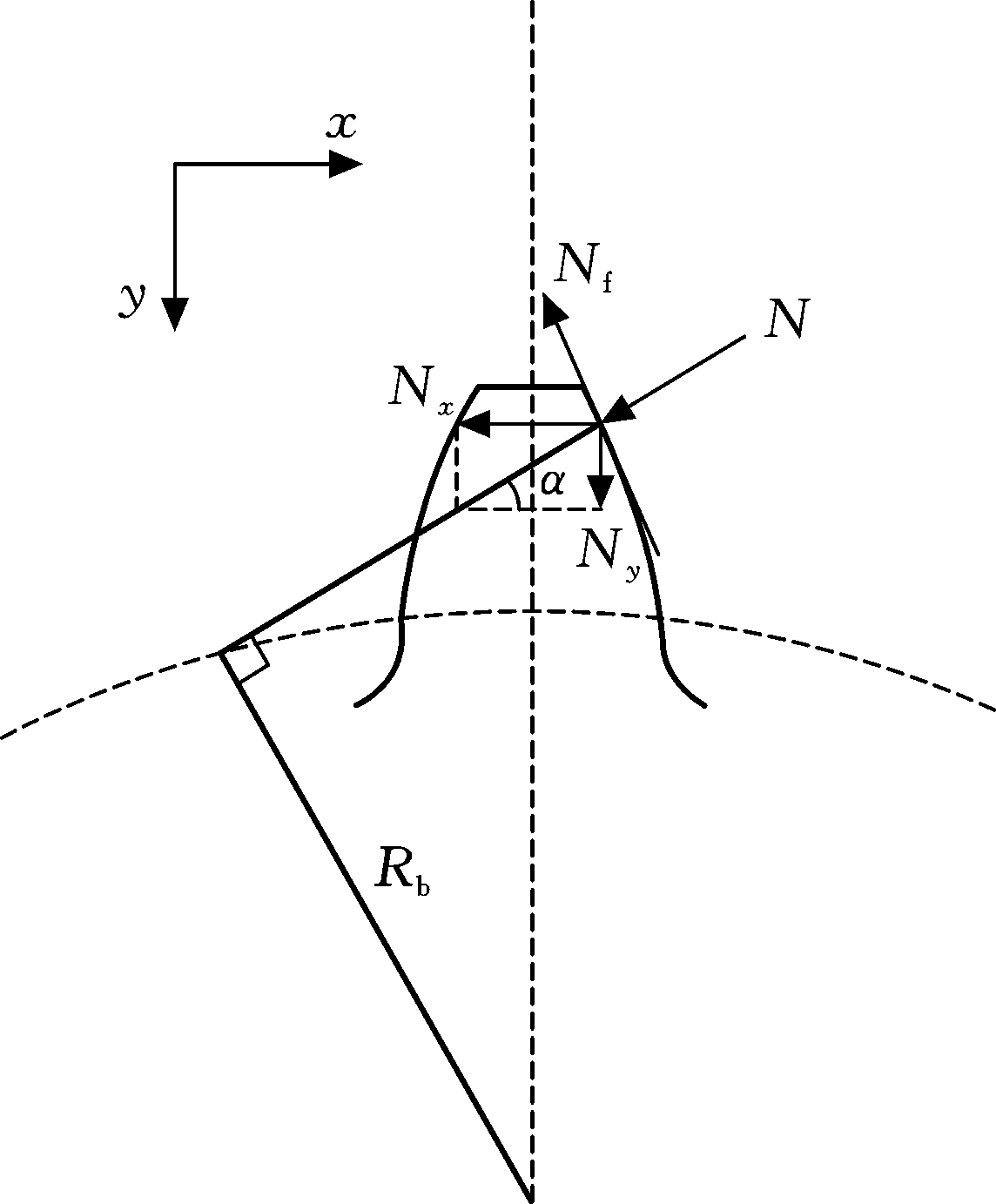
图1 齿轮齿面接触示意图
Fig.1 The schematic diagram of gear surface contact
考虑到在有限元仿真中，齿根部位的应力变化受到载荷分量Nx和Ny的影响，有
σc=σ(Nx,Ny)
(7)
其中，σc表示齿根动态计算应力。依据弹性力学，σ=Eε，E表示弹性模量，ε表示应变，因此，结合式(1)、式(6)、式(7)可得齿轮啮合刚度与齿根动态应变之间的正问题模型：
εc=ε(N(t),k(t))
(8)
1.2 时变啮合刚度反问题建模
时变啮合刚度的反求过程实际上为一参数优化过程。通过在齿轮根部应力集中区域布置应变片组，获得齿根动态测量应变εm，结合数值仿真技术模拟实验条件建立求解模型，得到相应位置的齿根动态计算应变εc，将计算应变εc与测量应变εm相比较，构建以齿轮啮合刚度k为自变量的目标函数，进而建立以优化模型为基础的反问题模型：
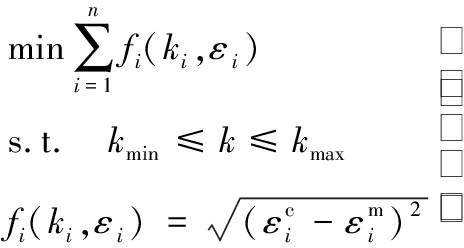
(9)
式中，ki为第i个采样点的啮合刚度值；kmin=0.1kmax，kmax为正常齿轮的双齿啮合刚度值；
分别为第i个采样点仿真计算获得的应变和实验测量获得的应变；n为实验和计算采样点的数目，实验和计算采样点n的个数必须大于反求参数的数目，以保证求解过程的超静定。
基于参数反求的齿轮时变啮合刚度计算方法步骤如下：①将应变片粘贴在齿根的位置，即最大应力区域。然后通过与虚拟仪器动态数据采集系统连接的应变片获得齿根的测量应变。②通过FEM计算模拟齿根应变。仿真模型具有与实验相同的约束条件，齿根部位应变采样点为应变片粘贴位置，与实验设置相同。③采用优化模型，以齿轮啮合刚度、测量应变和仿真应变为目标函数自变量，根据时变啮合刚度与齿根应变的关系，使FEM计算出的齿根应力与实际测量的齿根应变保持接近，最后得到实际齿轮裂纹状态下的时变啮合刚度。整个齿轮啮合刚度反求的基本流程如图2所示。
图2 齿轮啮合刚度反求流程图
Fig.2 The flow chart of the inverse calculation of TVMS
2 基于参数反求的齿轮裂纹啮合刚度计算实例
2.1 齿根应变测试
实验装置由变频电机、转矩传感器、齿轮箱、应变片、负载电机和数据采集系统组成。实验开始前，根据啮合齿之间的可用空间，应使应变计尽可能小；此外，在安装应变片期间，应先使用丙酮溶液清洁齿根表面；根据有限元云图的齿根应力分布，将应变片粘贴在齿轮轴向最大应力区域，通过轴上的孔将应变片连接到齿轮轴伸出端的滑环，然后连接到数据采集系统。旋转机械实验台如图3所示，变速箱的内部细节如图4所示。
1.负载电机 2.转速转矩传感器 3.齿轮箱
4.转速转矩传感器 5.驱动电机
图3 齿轮系统实验台
Fig.3 Gear system rig
图4 齿轮裂纹应变片测量实验台内部细节
Fig.4 The internal details of the gearbox
实验中，齿轮系统与仿真模型参数相同，均是模数为2.5 mm、齿数分别为40、80的标准直齿轮，裂纹故障通过人工在齿根切割0.5 mm、1.0 mm、1.5 mm、2.0 mm深度的裂纹，裂纹倾斜角为90°。故障齿轮如图5所示。
图5 四种裂纹故障齿轮
Fig.5 Four kinds of crack fault gears
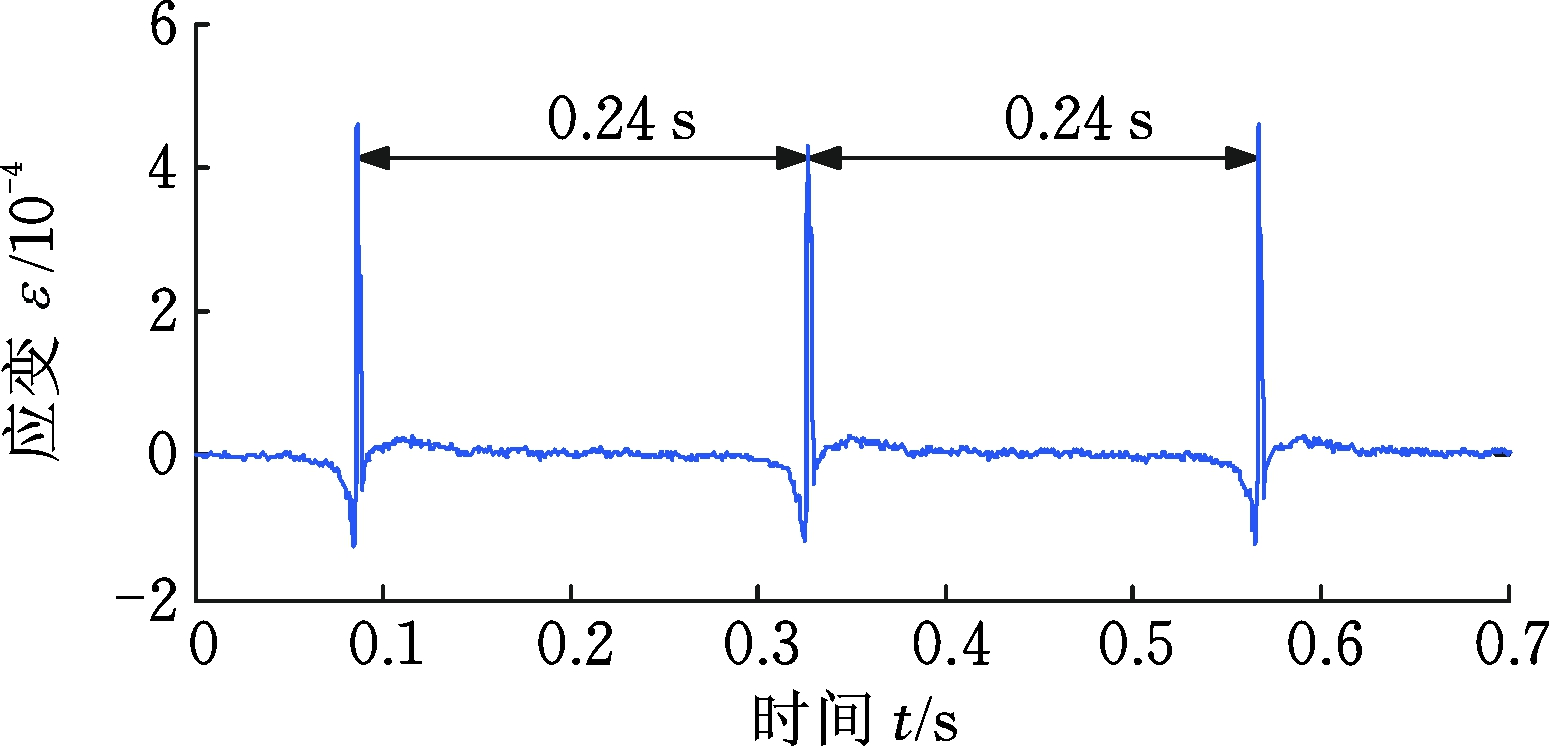
实验时，驱动电机转速为500 r/min，负载电机扭矩为50 N·m，应变信号采样频率为2 500 Hz。5种不同齿根裂纹深度d的应变信号如图6所示。可以看出，当安装了应变片的齿轮进行啮合接触时，应变信号会出现明显的周期性脉冲，频率为从动轮轴频4.16 Hz。同时从图6中应变值的对比可以看到，脉冲幅度大小随着裂纹深度的增大而减小。
通过测量应变来计算变啮合刚度的另一个关键是需要定义测量应变的啮合位置。从接触到脱离，测试齿的啮合时间为5 ms。测量应变的啮合区域如图7a所示，齿面上从接触到脱离的正常载荷变化如图7b所示，其中，节点A表示测试齿开始啮合，节点B表示测试齿开始进入单齿啮合，节点C表示测试齿开始接触第2个双齿接触，节点D表示测试齿脱离。由图7可以看出，节点A之前的应变信号受到前齿啮合的影响，在AB范围内，齿根部位受压应力和拉应力的影响，主应力表现为压应力，然后转变为拉应力。在B和C节点，当前齿开始脱离和后齿进入啮合时，应变波形出现明显的冲击现象。在CD范围内，测试齿开始退出啮合，主应力变为拉应力。
2.2 齿轮根部应力计算的有限元建模
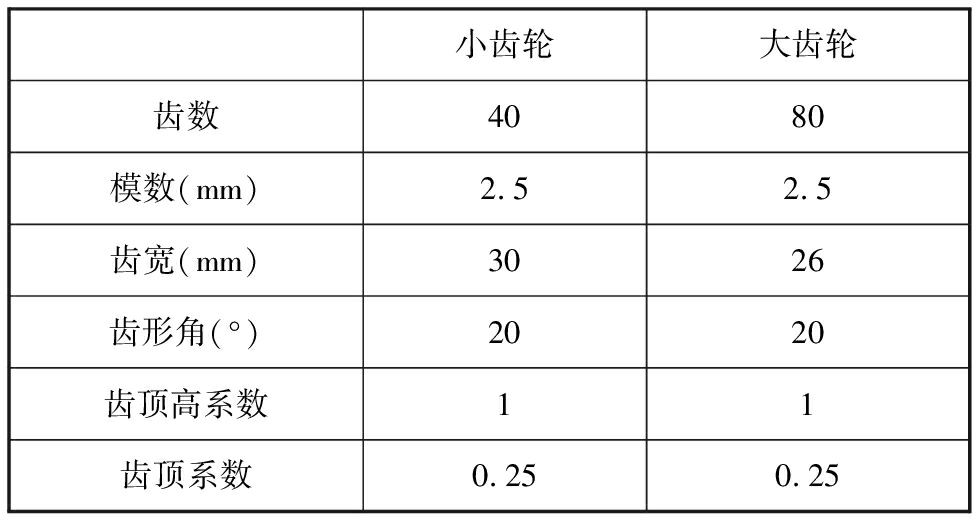
实验台齿轮参数见表1。
表1 实验台齿轮参数
Tab.1 The parameters of the gear pair
小齿轮大齿轮齿数4080模数(mm)2.52.5齿宽(mm)3026齿形角(°)2020齿顶高系数11齿顶系数0.250.25
(a) 正常齿
(b) d=0.5 mm
(c) d=1.0 mm
(d) d=1.5 mm
(e) d=2.0 mm
图6 不同裂纹齿轮的齿根应变信号
Fig.6 The tooth root strain signal of different gear crack
根据齿轮参数及实验运行工况构建有限元模型。为合理划分计算精度与成本，只取每个齿轮的五齿模型，轮缘长度取4m(m为模数)。将三
(a) 测量应变的啮合分布区域
(b) 待测齿从啮合到脱离的载荷变化
图7 测量应变的啮合分布区域及载荷变化
Fig.7 The meshing distribution area of
the measured strain and the load change
维实体几何模型导入ABAQUS软件进行计算，齿轮模型如图8所示。进一步，按实验要求设定边界条件，小齿轮作为主动轮转速500 r/min，大齿轮为从动轮负载据矩T=50 N·m，通过齿轮啮合接触分析，得到齿轮单双齿啮合过程的应力分布云图，见表2；提取实验装置上每个应变片覆盖的所有节点应力最大值，得到齿轮啮合周期内的齿根动态应力。
图8 齿轮啮合对的有限元模型
Fig.8 The FE model of the gear pair
表2 齿轮单双齿啮合过程的应力分布云图
Tab.2 The stress distribution of the gear double-tooth contact and single-tooth contact
d=0.5 mmd=1.0 mmd=1.5 mmd=2.0 mm第1次双齿接触单齿接触第2次双齿接触
2.3 齿轮时变啮合刚度反求
本文将遗传算法作为优化工具，对测得的齿轮实验台传动过程中啮合齿轮根部应力以及利用有限元仿真齿轮啮合过程得到的应力值进行迭代寻优。将测试齿的啮合旋转角数目离散为21，其中双齿接触点和单齿接触点的数目分别为8和5。优化参数二进制字符串长度定为28，变异和交叉概率分别为0.9和0.5。考虑到每个旋转角的结果都需要优化，为提高计算效率，遗传代数设为15，因此，测试齿从啮合到脱离经过3360次迭代后，可以得到最佳的结果。遗传算法的主要参数见表3。优化过程中，目标函数变化趋势如图9所示，说明对于4种不同的裂纹深度0.5 mm、1.0 mm、1.5 mm、2.0 mm，在15代之前可以完成优化迭代。
表3 优化算法参数
Tab.3 The parameters of the optimization method
旋转角计算次数21种群数量10二进制字符串28变异概率0.9交叉概率0.5迭代范围108～109遗传代数15
图9 目标函数变化趋势
Fig.9 The change trend of the objective function
根据解析法计算结果，设定迭代范围为108～109。根据上文，正常齿轮时变啮合刚度计算结果如图10所示。为了验证结果的准确性，将反求计算得到的结果与解析法[2]和有限元法进行比较，误差判据依照ISO6336-1—2006标准，结果见表4。根据图10，本文计算所得时变啮合刚度曲线与解析法计算结果相似；由表4可知，从对比结果来看，本文结果更接近ISO标准，解析结果误差较大，单齿啮合刚度误差达16.365%。
(a) 解析法
(b) 本文方法
图10 正常齿轮啮合刚度计算结果
Fig.10 The TVMS calculation result of healthy gear
表4 正常齿轮啮合刚度误差对比
Tab.4 The comparison of the healthy gear meshing stiffness
ISO标准解析法[2]有限元法本文方法单齿啮合刚度最大值(108N/mm)2.808 13.357 63.097 12.681 5与ISO标准的相对误差 (%)016.36510.2914.508时变啮合刚度平均值(108N/mm)4.278 14.762 64.471 54.184 2与ISO标准的相对误差(%)010.1734.522.193
(a) d=0.5 mm
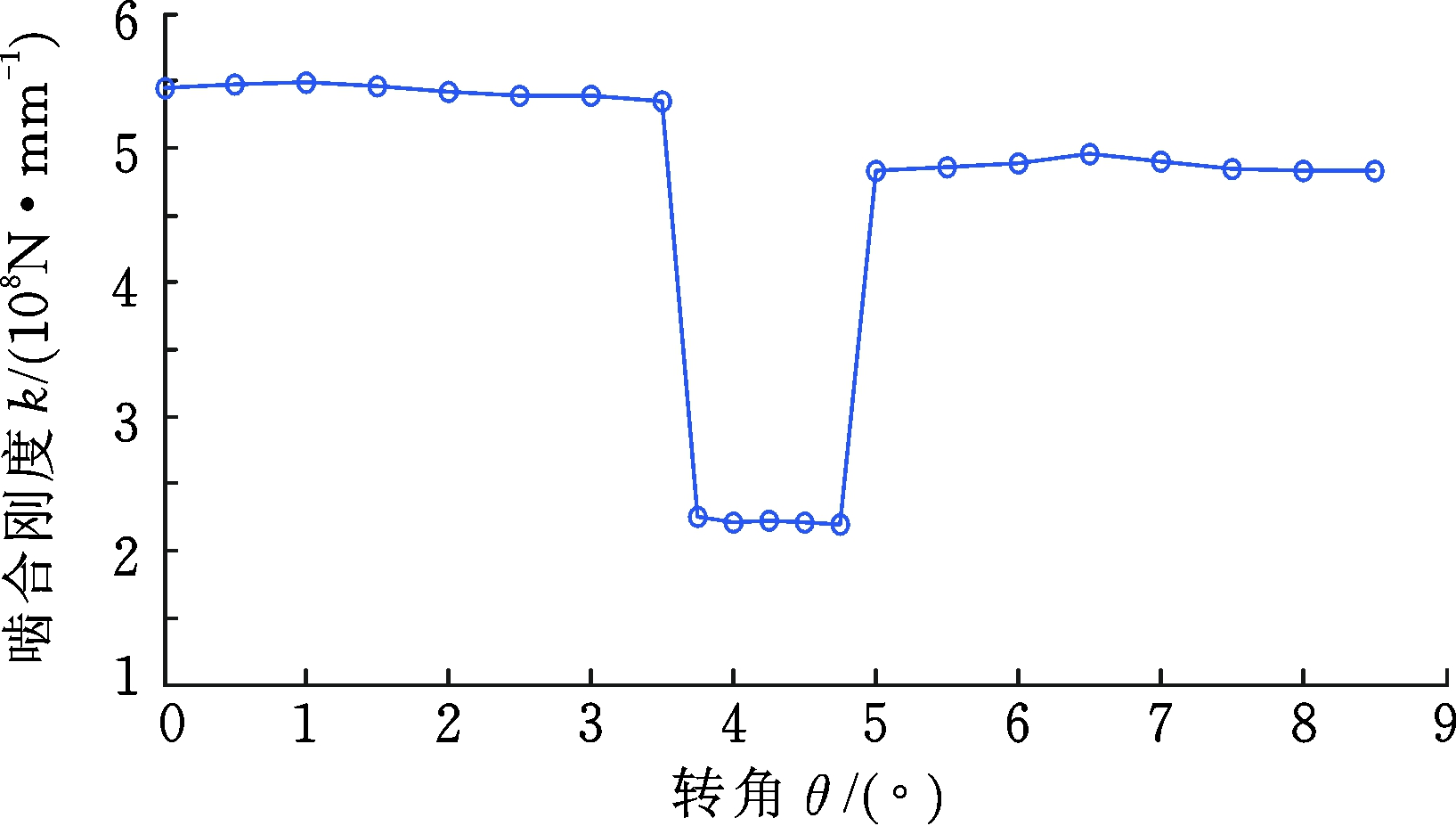
(b) d=1.0 mm
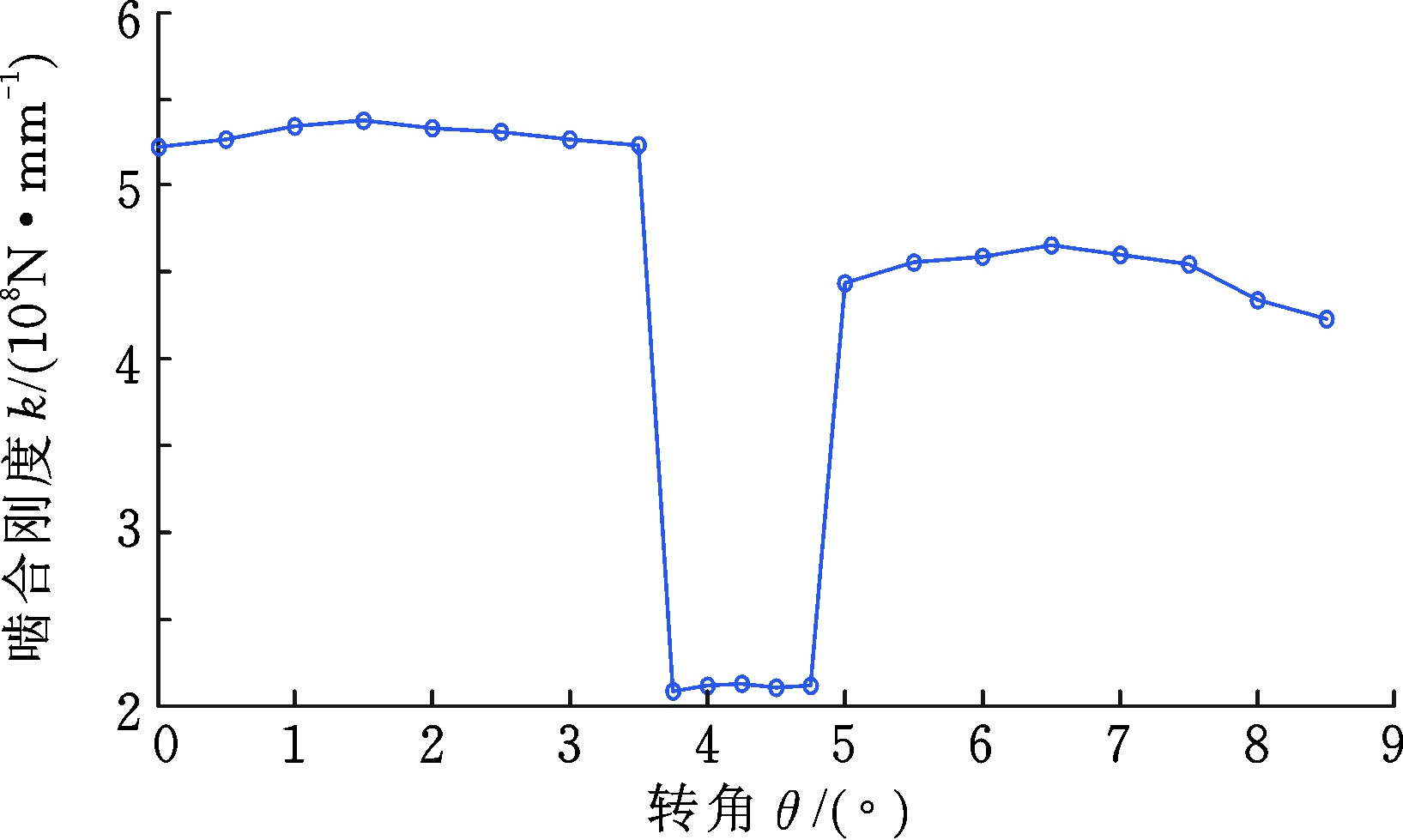
(c) d=1.5 mm
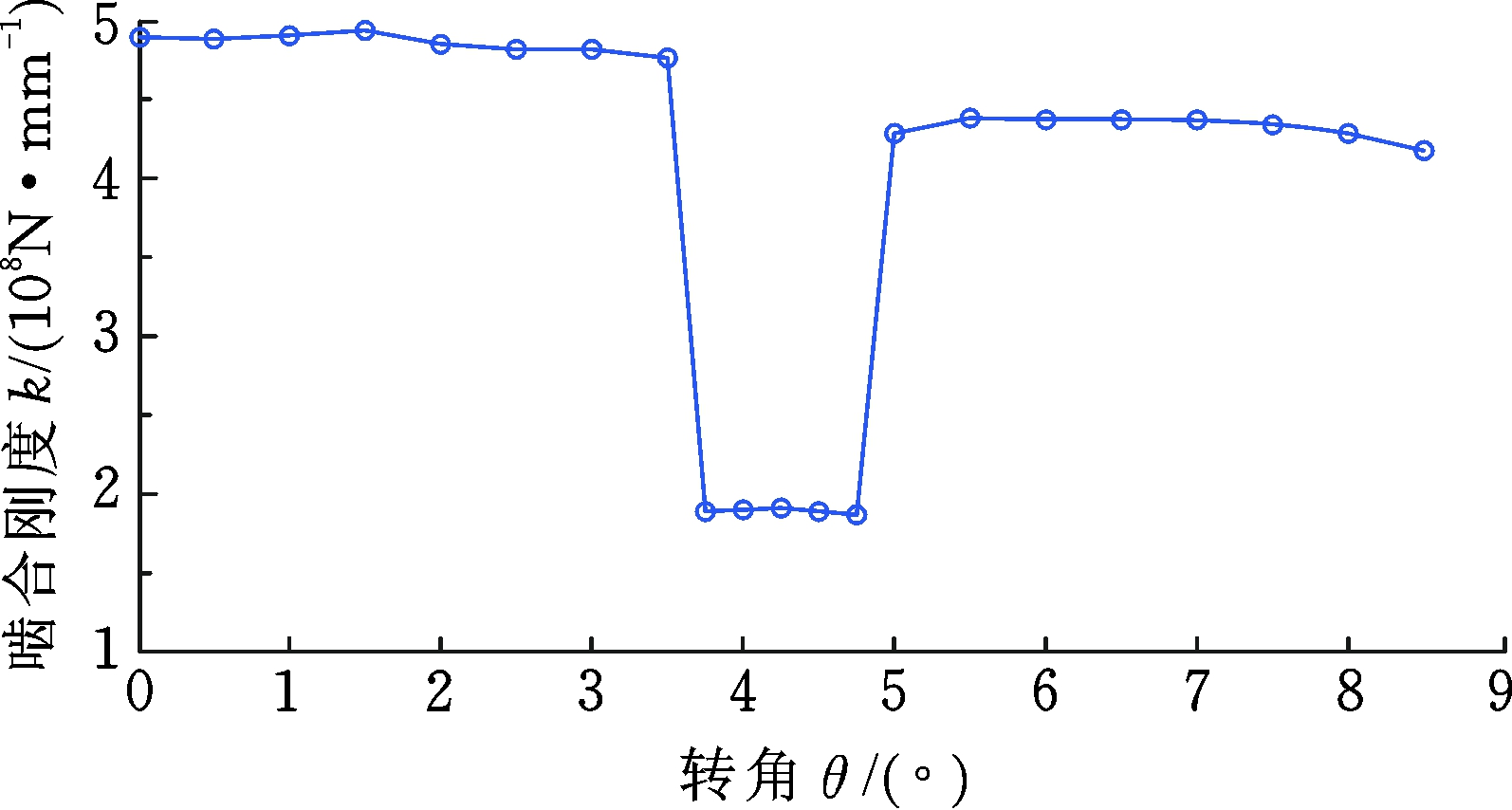
(d) d=2.0 mm
图11 不同裂纹深度下的时变啮合刚度
Fig.11 The TVMS of different crack levels
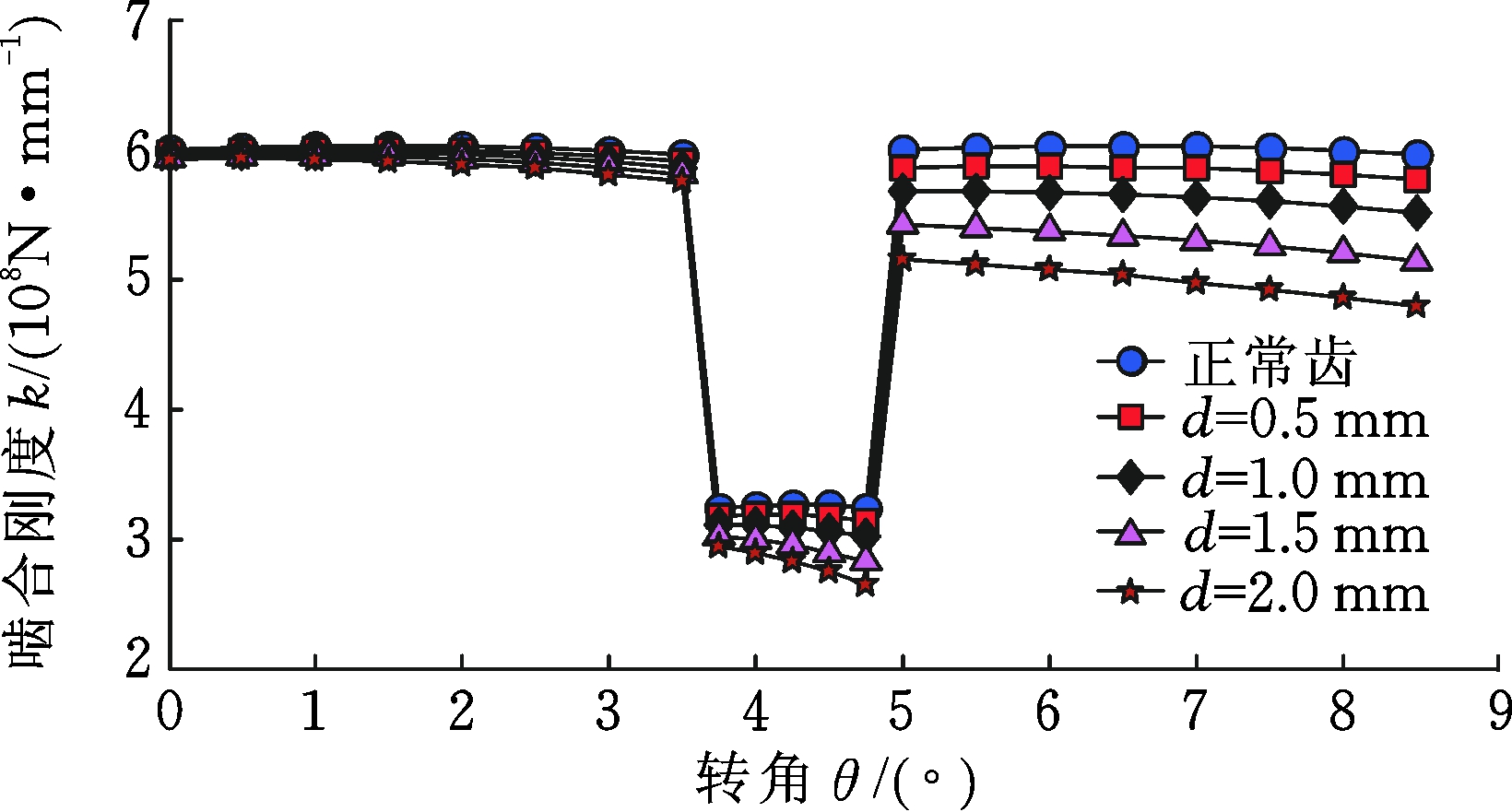
(a) 解析法
(b) 本文方法
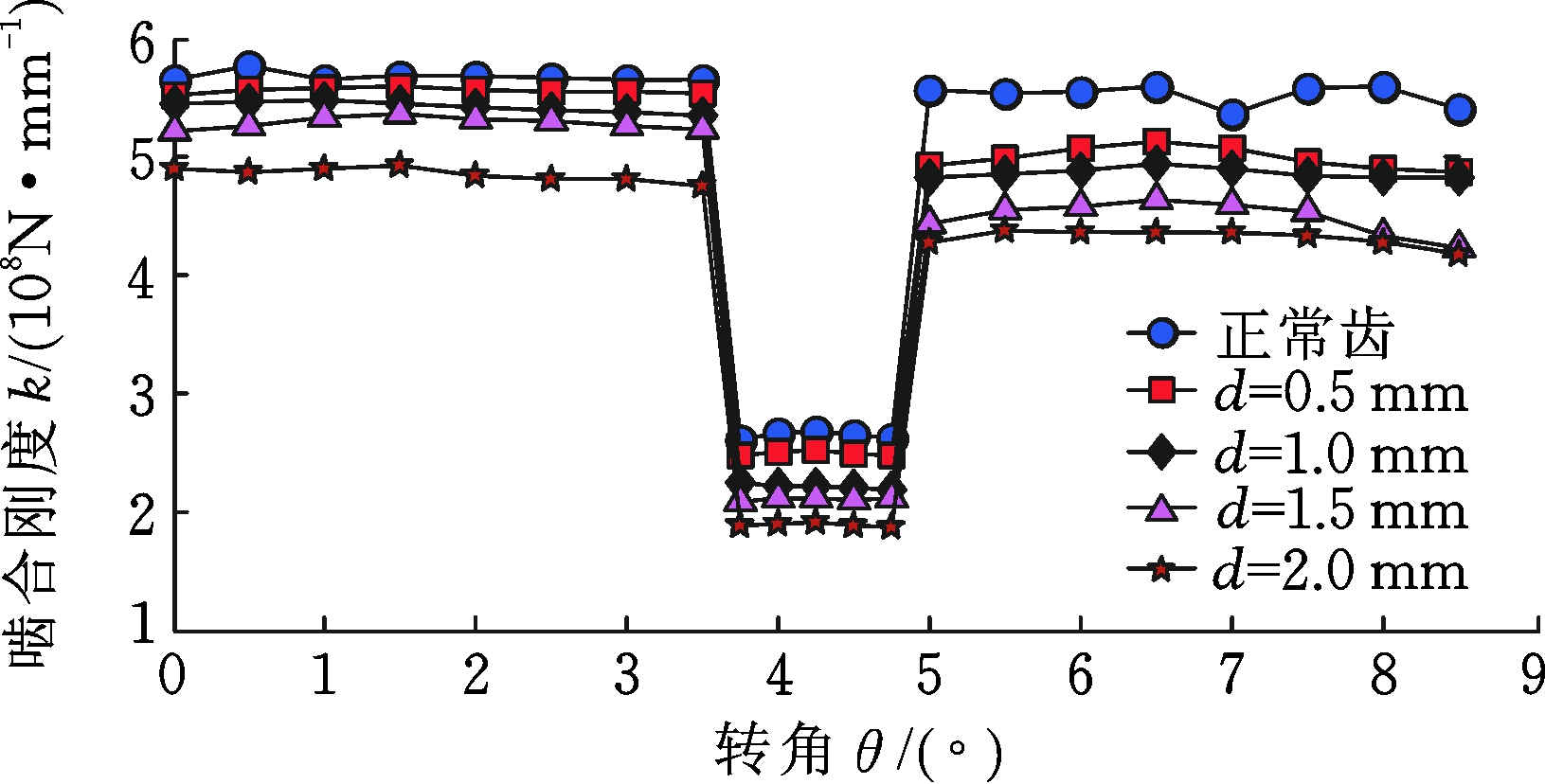
图12 两种方法的时变啮合刚度对比
Fig.12 The comparison of TVMS of two methods
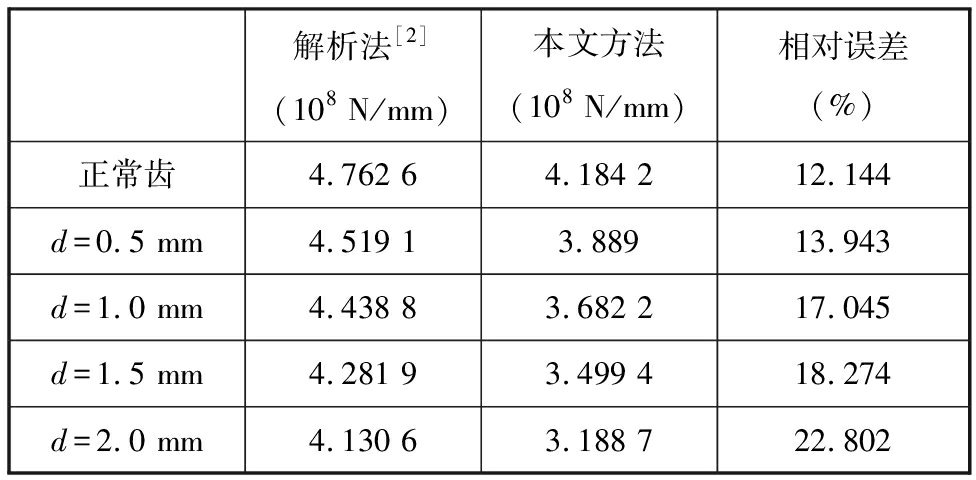
不同齿根裂纹故障下的时变啮合刚度计算结果如图11、图12所示。结果表明，4种裂纹深度(0.5 mm、1.0 mm、1.5 mm、2.0 mm)的啮合刚度随裂纹的增大而减小。鉴于ISO标准不存在故障刚度计算方法，故将本文计算结果与解析法计算得到的啮合刚度结果进行对比，4种裂纹深度的对比误差分别为13.943%、17.045%、18.274%、22.802%。由表5可知，本文方法求得的平均啮合刚度较小，当裂纹深度取0～0.5 mm及1.0～1.5 mm时，两种方法的相对误差的差值较小，分别为12.144%与13.943%、17.045%与18.274%，而裂纹深度取0.5 mm～1.0 mm及1.5～2.0 mm的相对误差差值较大，说明当齿根裂纹深度变化时，啮合刚度的变化存在两个增幅区域。
表5 两种方法的齿轮裂纹平均啮合刚度对比
Tab.5 The comparison of average TVMS
of gear crack in two methods
解析法[2](108 N/mm)本文方法(108 N/mm)相对误差(%)正常齿4.762 64.184 212.144d=0.5 mm4.519 13.889 13.943d=1.0 mm4.438 83.682 217.045d=1.5 mm4.281 93.499 418.274d=2.0 mm4.130 63.188 722.802
3 齿轮系统动力学建模
根据搭建的齿轮系统实验台(图3)，建立6自由度齿轮系统动力学模型，如图13所示。齿轮系统动力学设计参数见表6。
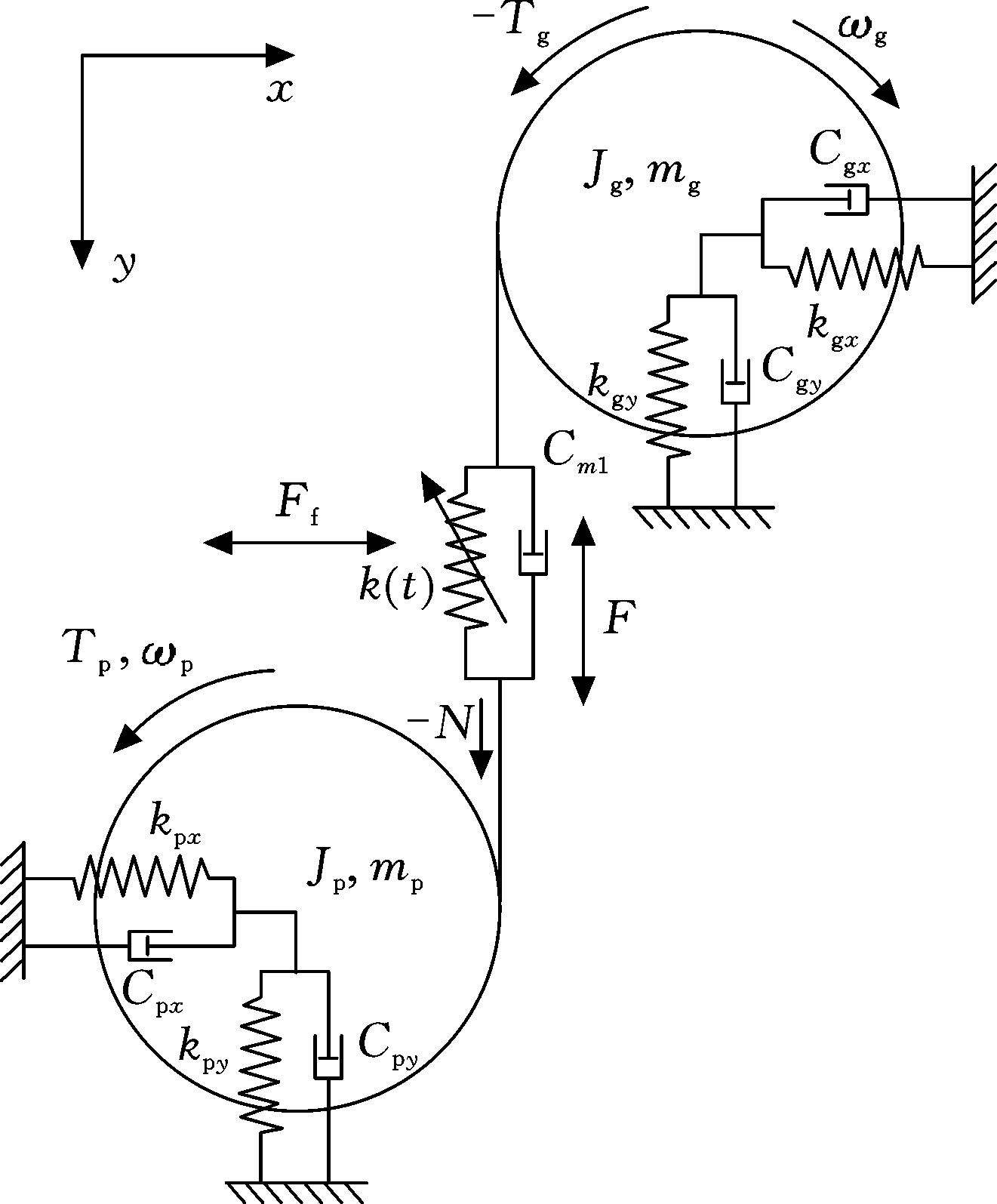
图13 齿轮系统6自由度模型
Fig.13 The 6-DOF model of gear system
该模型忽略啮合误差、润滑劣化情况，将齿轮系统简化成2个集中转动惯量和4个支撑刚度、其动力学方程为
(10)
式中，xp、xg、yp、yg分别为主动轮、被动轮的x方向和y方向平动位移；mp、mg分别为主动轮和被动轮的质量；jp、jg分别为主动轮和被动轮的转动惯量；Cpx、Cpy、Cgx、Cgy、kpx、kpy、kgx、kgy分别为齿轮系统的阻尼系数和支撑刚度系数；Tp、Tg分别为主被动轮转矩；F、Ff分别为时变啮合刚度力和摩擦力。
表6 齿轮动力学模型设计参数
Tab.6 The parameters of the gear dynamic model
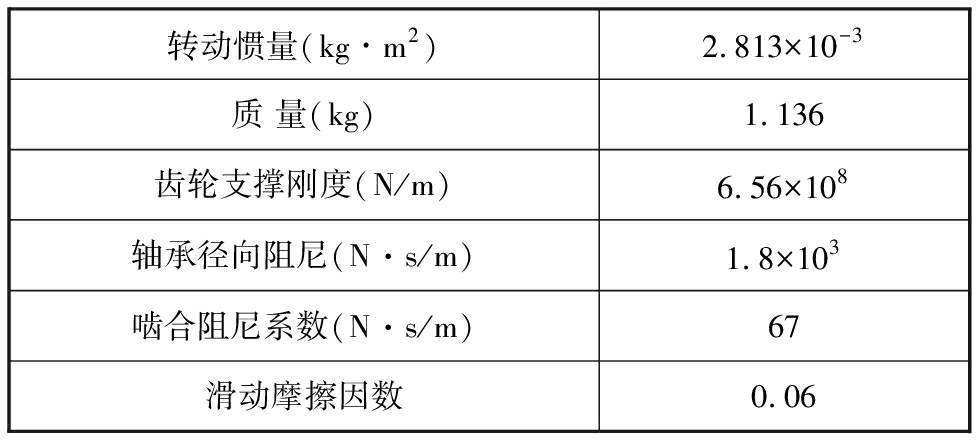
转动惯量(kg∙m2)2.813×10-3质 量(kg)1.136齿轮支撑刚度(N/m)6.56×108轴承径向阻尼(N·s/m)1.8×103啮合阻尼系数(N·s/m)67滑动摩擦因数0.06
4 齿根裂纹动力学仿真
将计算得到的时变啮合刚度代入式(10)，齿轮系统输入轴转速为500 r/min，裂纹故障特征频率为裂纹齿轴频4.17 Hz，对应周期0.24 s，啮合频率为333.33 Hz，采用Runge-Kutta法求解动力学方程，得到不同裂纹状态下的齿轮动力学响应，如图14所示。由图14可知，裂纹出现故障时，会出现周期性的冲击，故障频率为裂纹齿所在轴的转频4.17 Hz (0.24 s)。
(a) 健康齿轮
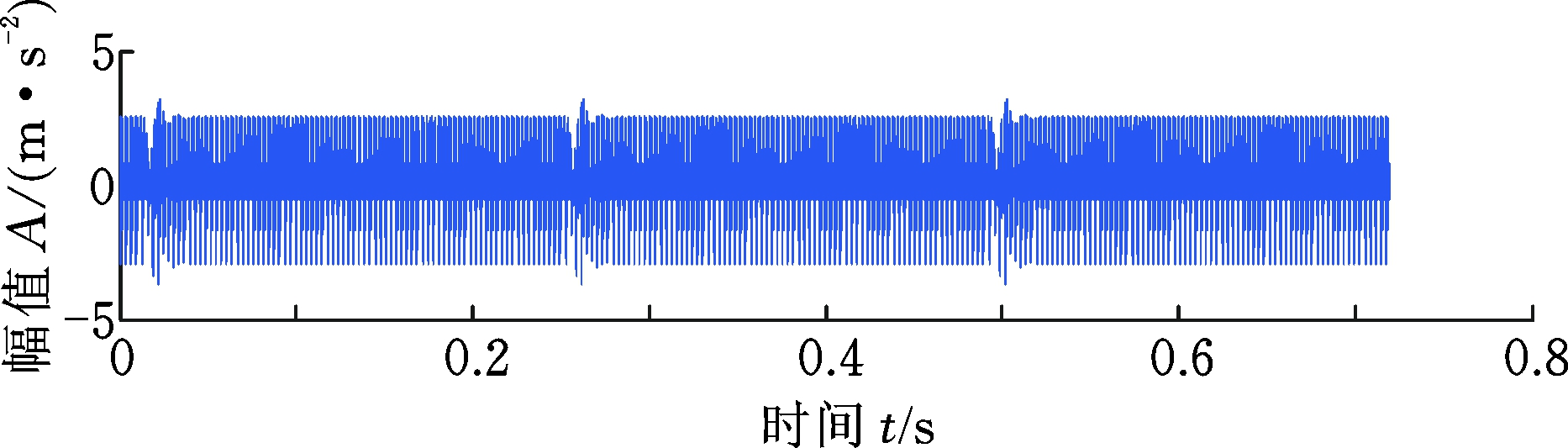
(b) d=0.5 mm
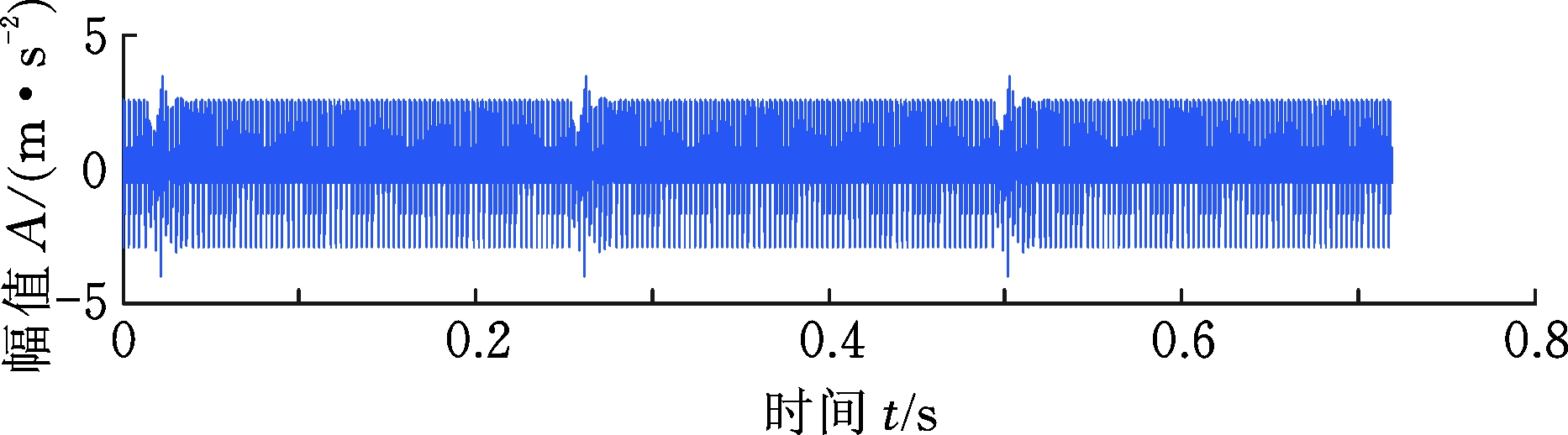
(c) d=1.0 mm
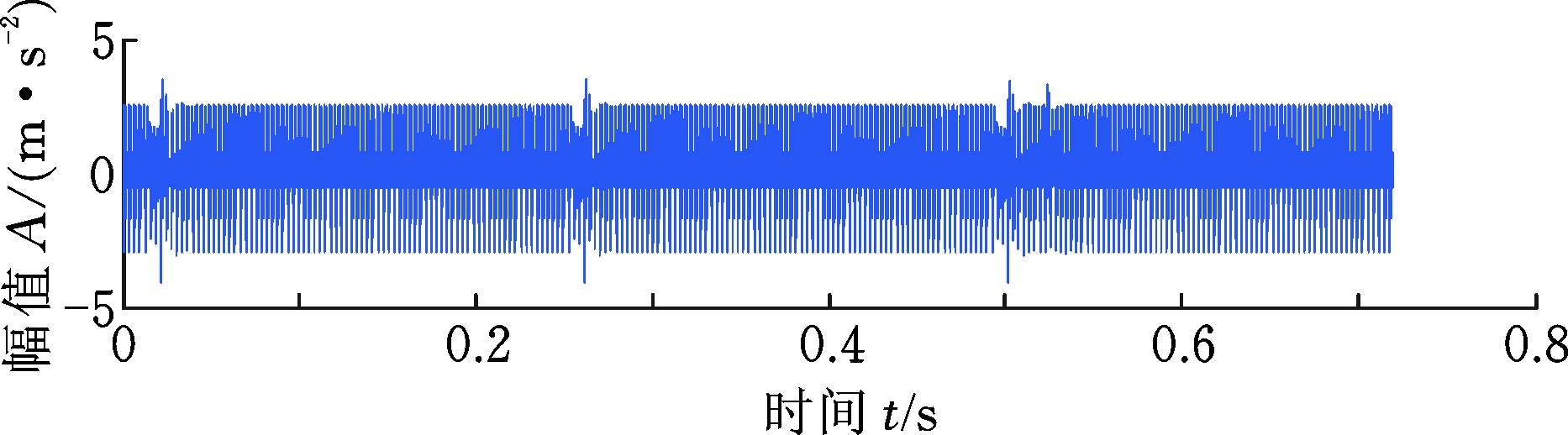
(d) d=1.5 mm
(e) d=2.0 mm
图14 齿轮仿真信号时域波形
Fig.14 The time domain waveform of gear dynamic signal
将不同裂纹程度的仿真时域波形进行整合观察，如图15所示，由于裂纹引起的啮合刚度减小，导致时域波形幅值发生变化，且幅值大小随着裂纹深度的增大而逐渐增大。进一步，齿轮裂纹动力学仿真信号频域波形如图16所示。由图16的频谱可以发现，正常齿轮信号在啮合频率333.33 Hz及其倍频处存在明显的冲击，然而当存在裂纹故障时，在啮合频率及其倍频附近会出现明显的边频带，其带宽为故障齿轮所在轴的转频4.17 Hz。
(a) 仿真响应时域波形
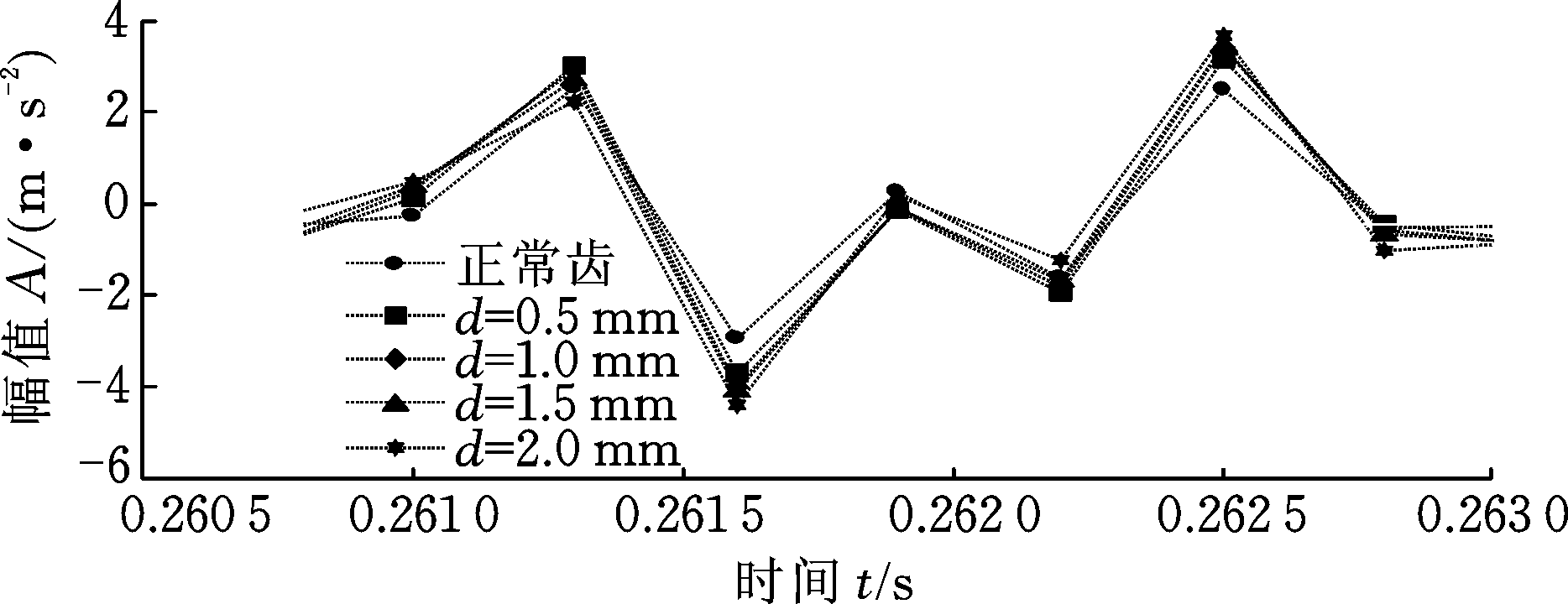
(b) 局部放大图
图15 齿轮裂纹仿真响应时域波形及局部放大图
Fig.15 The part enlargement of the gear
crack dynamic response
(a) 正常齿轮
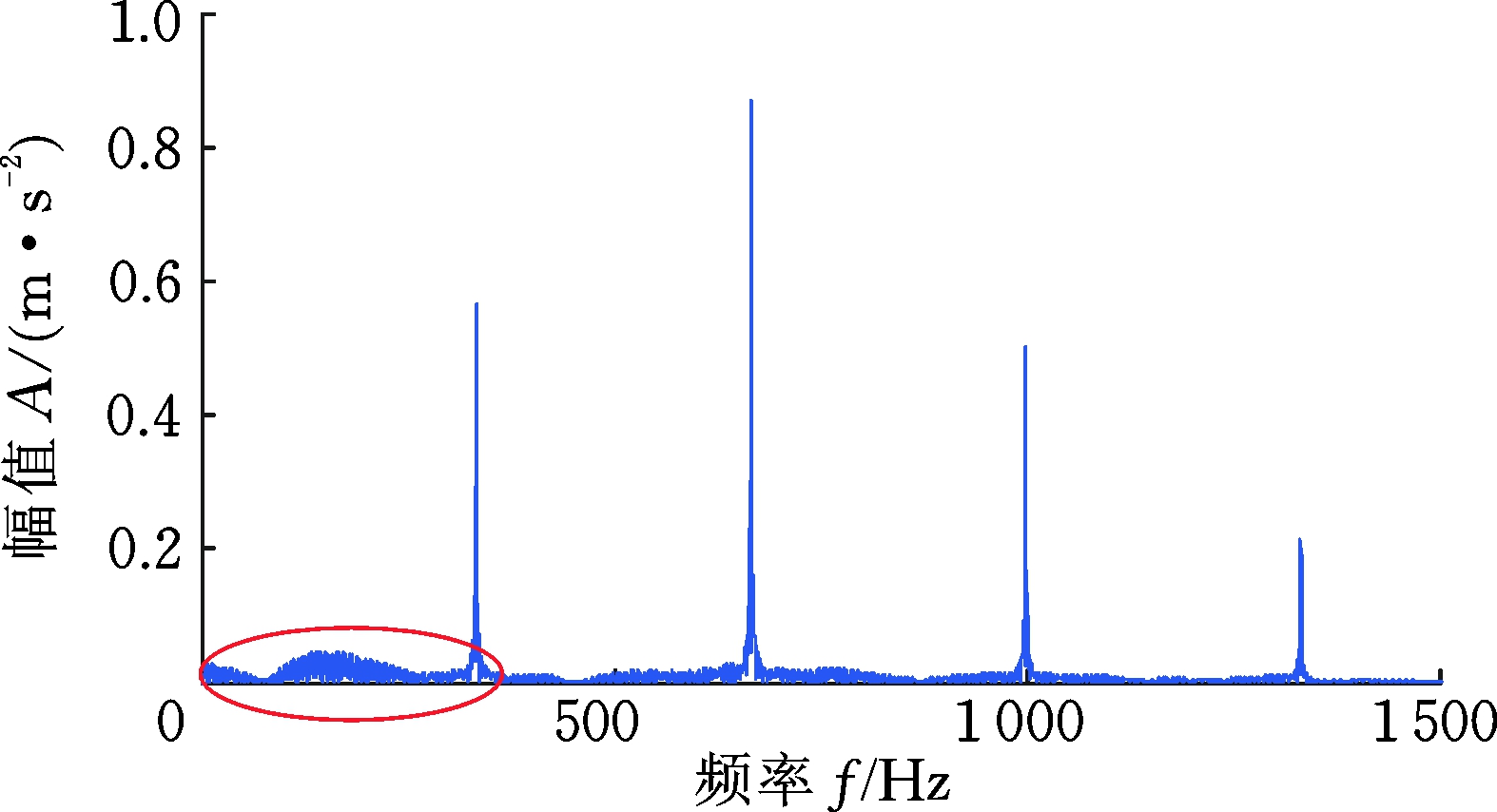
(b) d=2.0 mm
(c) 频谱0～300 Hz放大图(正常齿轮)
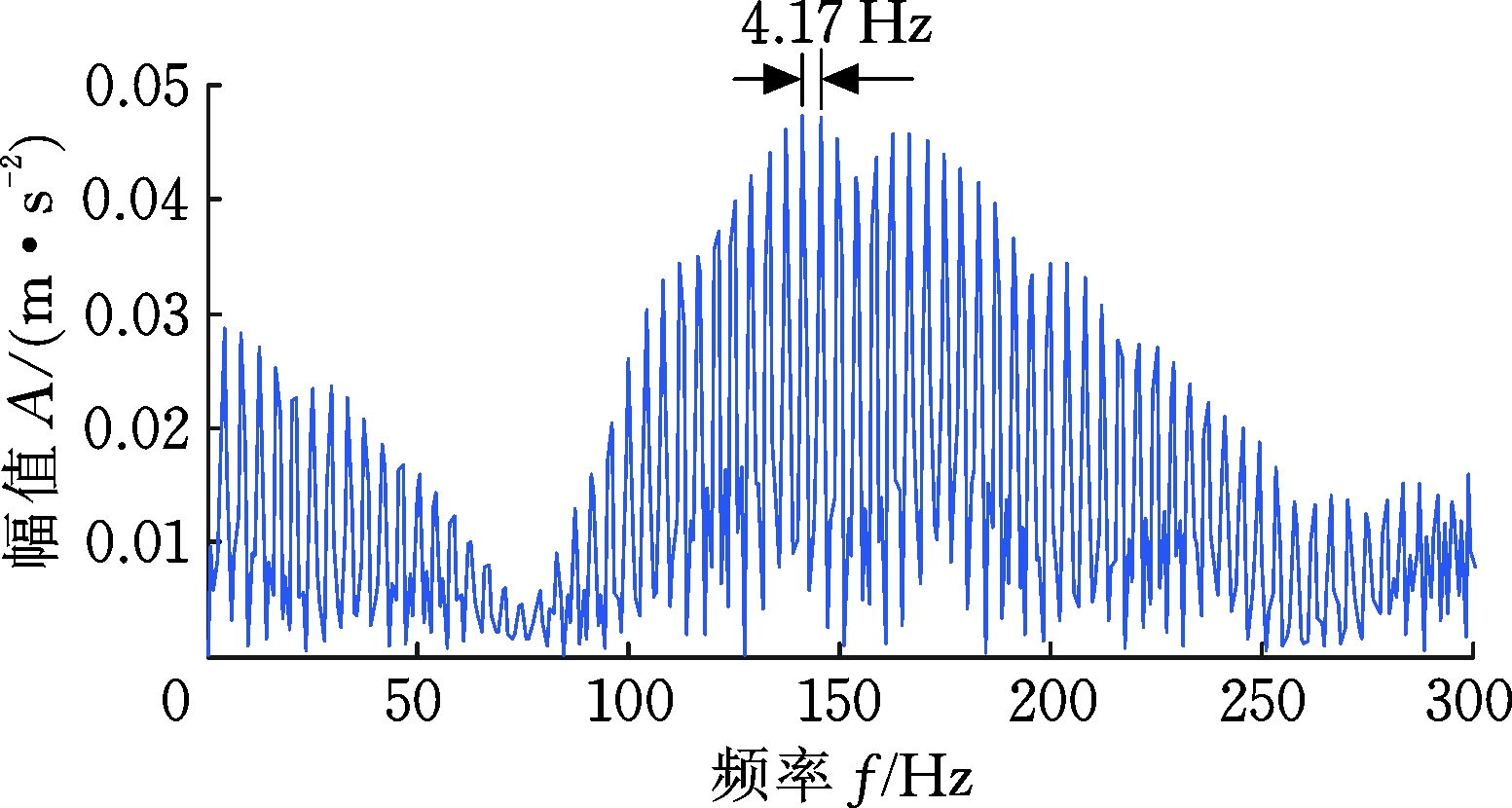
(d) 频谱0～300 Hz放大图(d=2.0 mm)
图16 齿轮裂纹仿真响应频谱
Fig.16 The frequency domain of gear crack dynamic response
5 结论
本文方法基于实际齿根裂纹的测量应力进行反求，更加接近真实的齿根裂纹故障时变啮合刚度，其计算结果具备验证手段和说服力。同时，根据实验仿真案例，相比其他方法，本文方法计算结果更加精确，并且在满足计算精度的前提下减小了计算量。通过构建齿轮系统多自由度动力学模型，分析裂纹状态下的动力学响应，本文方法不仅能为动力学建模提供准确的动力学参数，而且能有效地揭示裂纹故障状态下的齿轮系统振动机理，为齿轮裂纹故障诊断提供理论依据。
[1] ZHOU Xiaojun, SHAO Yimin, LEI Yaguo, et al. Time-varying Meshing Stiffness Calculation and Vibration Analysis for a 16DOF Dynamic Model with Linear Crack Growth in a Pinion[J]. Journal of Vibration and Acoustics, 2012, 134(1): 011011-011011-11.
[2] CHAARI F, FAKHFAKH T, HADDAR M. Analytical Modeling of Spur Gear Tooth Crack and Influence on Gear Mesh Stiffness[J]. European Journal of Mechanics A/Solids, 2009,28:461-468.
[3] 万志国,訾艳阳，曹宏瑞 ，等.时变啮合刚度算法修正与齿根裂纹动力学建模[J].机械工程学报,2013,49(11):153-160.
WAN Zhiguo, ZI Yanyang, CAO Hongrui,et al. Time-varying Mesh Stiffness Algorithm Correction and Tooth Crack Dynamic Modeling[J]. Journal of Mechanical Engineering,2013,49(11):153-160.
[4] RINCON A F D,VIADERO F,IGLESIAS M,et al. A Model for the Study of Meshing Stiffness in Spur Gear Transmissions[J]. Mechanism and Machine Theory, 2013,61:33-58.
[5] LIANG Xihui, ZUO Mingjian, PANDEY M. Analytically Evaluating the Influence of Crack on The Mesh Stiffness of a Planetary Gear Set[J]. Mechanism and Machine Theory, 2014,76:20-38.
[6] MOHAMMED O D, RANTATALO M, AIDANP
J O,et al. Vibration Signal Analysis for Gear Fault Diagnosis with Various Crack Progression Scenarios[J]. Mechanical Systems and Signal Processing, 2013,41(1/2):176-195.
[7] PANDYA Y, PAREY A. Failure Path Based Modified Gear Mesh Stiffness for Spur Gear Pair with Tooth Root Crack[J]. Engineering Failure Analysis, 2013,27:286-296.
[8] CHEN Zaigang, SHAO Yimin. Dynamic Simulation of Spur Gear with Tooth Root Crack Propagating Along Tooth Width and Crack Depth[J]. Engineering Failure Analysis, 2011,18(8):2149-2164.
[9] HE S, CHO S, SINGH R. Prediction of Dynamic Friction Forces in Spur Gears Using Alternate Sliding Friction Formulations[J]. Journal of Sound and Vibration, 2008,309(3/5):843-851.
[10] WU Jiateng, YANG Yu, YANG Xingkai,et al. Fault Feature Analysis of Cracked Gear Based on LOD and Analytical-FE Method[J]. Mechanical Systems and Signal Processing, 2018,98:951-967.
