0 引言
随着复杂曲面类零件需求量的增加和性能要求的不断提高[1],传统柔性工具配合游离磨粒的加工方式[2]效率过低,已难满足实际应用的加工效率需求,迫切需要提高复杂曲面零件的加工效率,同时保证工件表面质量。
软固结气压砂轮由密集磨粒群通过黏结剂固结在橡胶基体层构成空心半球,它可根据加工局部曲率的变化进行适应性的气压调控,可实现抛光区中抛光工具曲率与模具曲率的良好吻合,获得高精密的几何形态曲面和高品质的光整加工效果,从而实现复杂曲面的高效率、高精度的自动化抛光。但非绝对约束下的磨粒群易随机形成破坏性结构,导致材料去除效果不理想和表面划痕损伤,这种现象在自由曲面加工中尤为突出。
为了进一步提高加工效率,获得更理想的工件表面,国内外学者主要通过调整宏观作用参数来实现磨粒群整体宏观运动控制,从而提高加工效率和加工质量。伦敦光学试验室WALKER等[3]采用不断优化加工轨迹的方法;哈尔滨工业大学宋剑锋等[4]采用驻留时间控制算法和边缘精度控制方法;JAKOBSEN等[5]为了避免深划痕的产生,采用较为质软的磨粒进行加工;金明生等[6]对气囊抛光的行间距优化问题进行了仿真和试验。
这些方法虽然取得了一定的效果,但只考虑宏观参数的影响,忽略了磨粒群微观相互作用。磨粒群尽管宏观上近似受控,但微观上仍属于自由端群体,存在剪胀效应。颗粒物质剪胀效应是指密集颗粒群沿剪切面剪切过程中,表层颗粒随剪位移发生上抬,从而引起整体颗粒群的体胀或体缩现象[7],这种现象在磨粒群加工方法中显而易见。剪胀效应随机形成的破坏性结构一方面易使加工质量产生偏差,另一方面易对工件表面产生划痕损伤,其可控性是超精密加工研究的关键。
本文针对软固结气压砂轮的内部磨粒群剪胀效应对被加工件材料去除的影响规律展开了相关研究。
1 软固结磨粒群微观特性及材料去除原理
1.1 磨粒群加工的微观剪胀结构
由颗粒物质的剪胀研究可知[8],当气压砂轮对工件进行加工时,两者接触,产生力的作用的同时产生剪胀效应。微观上,软固结磨粒群在工件表面滑动过程中受到剪应力后导致磨粒群内部产生连锁反应形成挤压,在柔性介质环境下形成磨粒群微动,内部结构进行重新排列,从而产生剪胀效应,固结磨粒群体积应变发生膨胀和剪缩,孔隙比发生变化,影响内部力传递的大小及其稳定性。
以规则排列的颗粒为例,解释软固结磨粒群的单个孔隙胞元承受外载时发生的剪胀剪缩演化过程[8],如图1所示。

(a) 初始构型
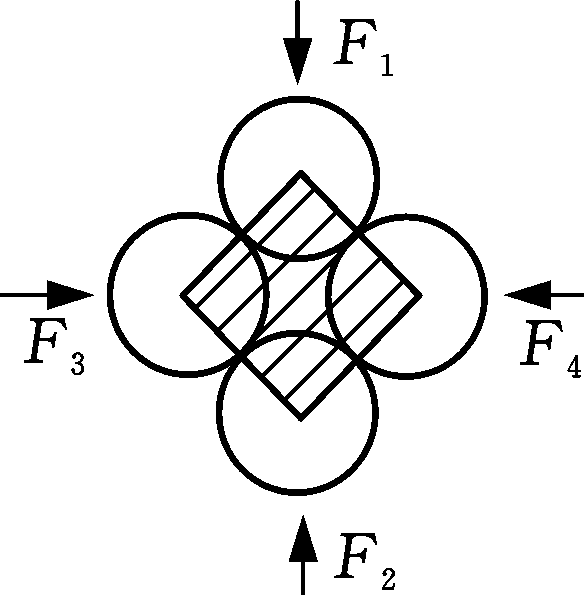
(b) 最大孔隙胞元状态
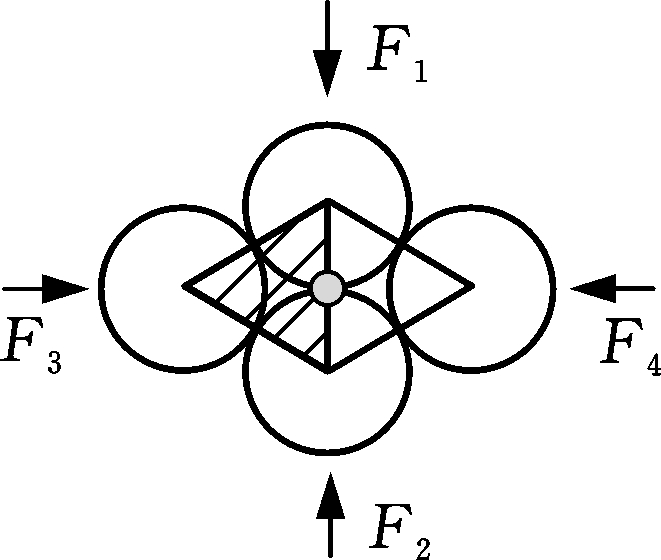
(c) 坍塌剪缩状态
图1 磨粒群微观剪胀剪缩演化模型简图
Fig.1 Evolution model of micro-dilatancy of abrasives
计算表明,图1a和图1c孔隙比较小,即颗粒处于排列最密实的状态(虽然两者排列状态不同)。图1a为孔隙胞元的初始构型,孔隙胞元的配位数Nm=3,在初始加载阶段,颗粒体系的内部结构非常稳定,内部接触不发生破坏,也没有新的接触生成。随着加载的进行,原点处的接触发生破裂,该处传递力的路径也消失,颗粒体内部发生剧烈变化,孔隙胞元的构型改变,从图1a排列状态转变为图1b的排列状态,Nm=4。通常,新形成的孔隙胞元的方向与大主应力方向一致。进一步加载时,当接触点处的摩擦因数超过极限时发生滑动。在这个阶段,既没有接触发生破裂也没有新接触生成,因此孔隙胞元的构型不变只是形状改变。孔隙胞元在外载的作用下进一步发展,直到不能承受外部应力,发生坍塌剪缩(图1c)。
1.2 颗粒剪胀效应下孔隙比与阻尼系数关系模型
在该软固结磨粒群气压砂轮中,磨粒间相互离散接触,剪胀性是其基本特性之一。
黏结颗粒系统的黏弹性可以用适当的数学模型来描述。经典Kelvin-Voigt模型将固体骨架部分近似为弹簧,孔隙液近似为黏壶来描述黏弹性本构模型[9]。以此为基础考虑软固结磨粒群结构性因素,孔隙对应变-时间关系曲线存在影响,受力变化过程中,随着颗粒孔隙受力变小,单元体内颗粒群结构将会发生变化,孔隙骨架所占体积增大,孔隙空间减小[10]。因此考虑骨架与孔隙液对总载荷的分担,引入孔隙度φ,则有
σ=E*ε(1-φ)+βε′φ
(1)
式中,E*为等效弹性模量;σ为拉压力产生的内部应力;E为磨粒层的弹性模量;e为孔隙比;ν为泊松比;ε为应变;ε′为应变速率;β为阻尼系数。
由式(1)可建立软固结磨粒群在加工试验时的孔隙比e与黏结磨粒群的阻尼系数β的数学模型:
(2)
由式(2)可知,孔隙比e与阻尼系数β成反比,阻尼系数的变化影响孔隙比。不同阻尼系数下的软固结磨粒群在加载作用下产生的剪胀效应不同,最终所达到的稳定态也不同。
1.3 颗粒孔隙受力下的材料去除压力函数
Preston方程[11]是在磨削加工中应用广泛的材料去除模型:
M=![]() kpvpdt
kpvpdt
(3)
式中,M为材料去除量;v为磨粒在加工处的相对运动速度;p为磨粒在t时刻的正接触压力;kp为Preston方程系数。
磨粒在t时刻的正接触压力可由接触面的压力平均值F和实际接触面积A确定,可以表示为
(4)
传统的Preston方程没有考虑微观磨粒的作用,因此软固结磨粒气压砂轮光整加工方法的应用存在一定的局限性,需要对其进行修正。
考虑采用数字图像技术对光弹试验结果进行处理,并用彩色梯度算法表征颗粒材料的平均受力情况,为粒子间力的分布和演化提供独特视角[12]。
当有效应力在边界处作用时,在接触点产生了正向接触力和切向力。但边界上的均匀应力并没有被颗粒均匀承担,而是由部分颗粒承担大部分的力。接触面的压力平均值F与有效应力p′的应用状态、孔隙比e、粒子直径d有关[13]:
(5)
根据传统的孔隙比与有效平均应力的e-p表达式关系[14],可得
(6)
(7)
式中,k、b为模型参数。
式(7)为磨粒群作用接触面应力方程,分析可知,孔隙比与该应力成反比,即接触压力会随着剪胀效应的变化而变化。
综上可知,软固结气压砂轮的材料去除模型为
(8)
材料去除量M与孔隙比e为反比关系,结合式(2)可知,孔隙比e受阻尼系数β的影响且与阻尼系数β成反比,据此可知材料去除量M与阻尼系数β成正比,随着阻尼系数的增大,孔隙比减小,剪胀效果增强,从而可提高材料去除量M;粒径d与材料去除量M为正比关系,粒径的增大也能提高材料去除量M。
2 软固结磨粒仿真结果及讨论
2.1 不同阻尼系数颗粒的接触力网
采用PFC3D建立了微型软固结磨粒群样例模型,参数设计如表1所示。由于主要研究软固结气压砂轮的动态特性,故在PFC3D中磨料的形状可以视为半球形。
表1 磨粒群样本参数
Tab.1 Abrasives sample parameters

样本半径(mm)磨粒直径(μm)磨粒数目N摩擦因数μ507510 0000.4
对磨粒层施加1 MPa载荷,通过改变阻尼系数,得到4组磨粒群内部结构参数,如表2所示。
表2 磨粒群仿真参数
Tab.2 Abrasives simulation parameters

分组法向弹簧刚度系数kn切向弹簧刚度系数kt法向阻尼系数βn切向阻尼系数βtA1×1081×1081.0×1051.0×105B1×1081×1084.0×1054.0×105C1×1081×1086.5×1056.5×105D1×1081×10800
当软固结磨粒群密集排布,磨粒自由活动空间小,受到外部加工载荷作用时,会形成诸多强度迥异的力链。图2显示了不同阻尼系数的软固结磨粒群接触力网。

(a) A组接触力网
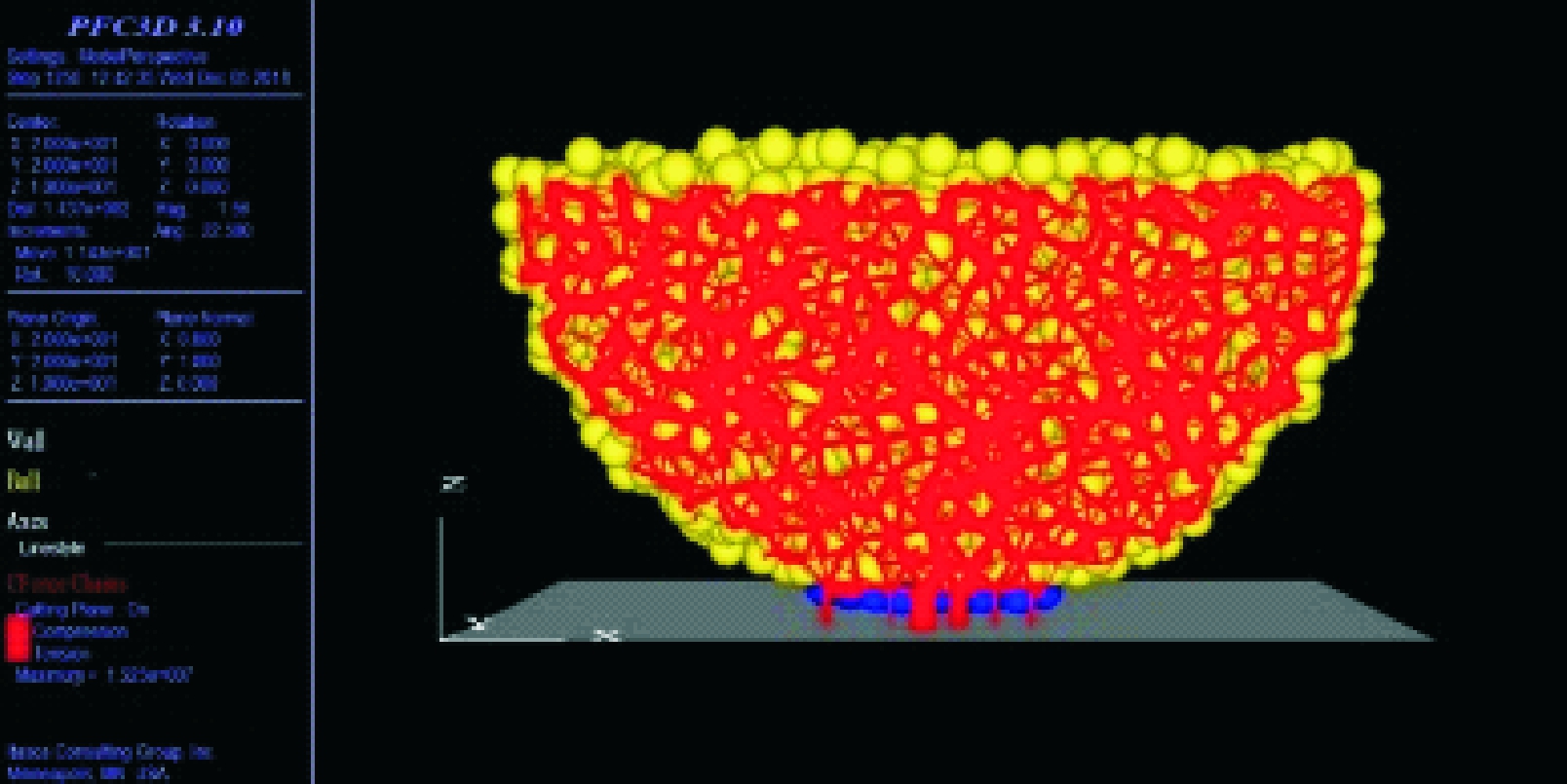
(b) C组接触力网
图2 软固结磨粒群接触力网
Fig.2 Contact force net of soft-consolidation abrasives
通过改变磨粒群的阻尼系数,形成了不同的接触力网以适应加工需求。在应力传递过程中,通常表现为阻尼系数增大,孔隙胞元的配位数减少,接触力网更加密集,磨粒群之间有更多的强力链,接触面磨粒群应力增大且集中,更适合高效加工。而游离形态下的磨粒群则在下压过程中就出现磨粒逃逸现象,应力不集中,无法形成系统的接触力网。
2.2 剪胀效应
不同阻尼系数的软固结磨粒群宏观上运动状态一致,但微观上黏结剂作用于磨粒群后,使磨粒群之间受拉或者受压,造成颗粒间位移产生微小变化,形成剪胀效应。不同阻尼系数下的磨粒群接触力网的强度差异与磨粒群的剪胀效应有关。
磨粒群的运动过程分为2个阶段:阶段1是磨粒群下压过程,磨粒群整体向下运动;阶段2是磨粒群以一定速度进行切削,并从原先的静态平衡状态步入动态平衡。为了更好地观察颗粒群的剪胀状态,分别对游离磨粒群和软固结磨粒群的位移状态进行观察比较,如图3所示。

(a) 下压过程磨粒速度图

(b) 切削阶段的游离形态磨粒速度图

(c) 切削阶段的软固结磨粒速度图
图3 动态速度变化图
Fig.3 Dynamic velocity change chart
图3a是阶段1的磨粒速度,两种磨粒群的速度状态一致。进入阶段2后,速度产生变化。图3b是切削阶段的游离形态磨粒速度,颗粒速度方向向外,出现逃逸现象,无法形成应力集中。图3c是切削阶段的软固结磨粒速度,磨粒群在切削过程中发生滑移,颗粒速度指向接触面,基本无逃逸现象,有利于形成应力集中。
进一步观察颗粒群的剪胀状态,软固结磨粒群在加工时的位移效果图见图4。
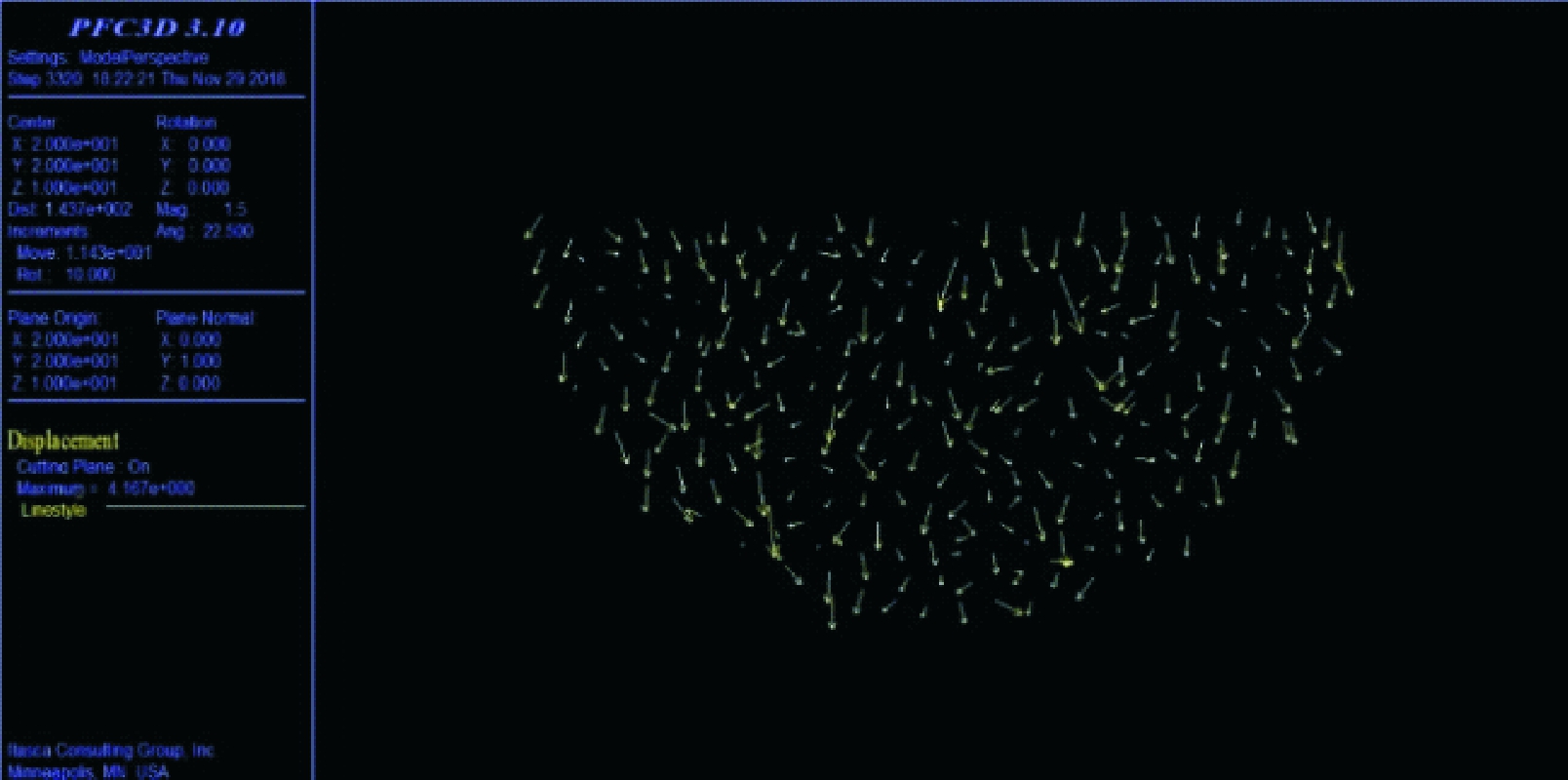
图4 位移效果图
Fig.4 Displacement effect diagram
被黏结的磨粒群并不能随着速度方向自由移动,软固结状态下的磨粒受到黏结剂各个方向的弹性支撑,避免了粒子逃逸,且颗粒间产生相互挤压,发生剪胀现象,产生自适应微动。剪胀效应发生后的磨粒群对表层接触磨粒产生更为有效的挤压,有益于复杂曲面工件表面的材料去除及表面划痕的减少。
2.3 不同程度剪胀效应下的表面应力仿真分析
根据式(2)和式(7)进行黏结剂阻尼系数对磨粒群接触应力影响的应力-时间仿真,对表2所示的前3组不同阻尼系数黏结剂参数进行仿真。仿真结果如图5所示。
仿真结果表明,磨料的运动可分为2个阶段:阶段1为初始加载阶段,研磨剂被压缩,颗粒体的孔隙比先下降,产生剪缩,切割力迅速增大,随着变形的增大,排列致密的颗粒体发生膨胀,切割力减小,剪胀现象一直伴随在随后的加载过程,直到出现静态平衡;在阶段2中,孔隙比变化率很小,气压砂轮磨粒群从静态平衡转变为一种新的动态平衡,达到稳定态,即临界状态。在上述模拟条件下,A组的工件表面的平均压力强度最终约为0.22 MPa(图5a),B组的工件表面的平均压力强度最终约为0.27 MPa(图5b),而C组最终约为0.3 MPa(图5c)。由此可得,阻尼系数对磨粒群孔隙比的改变可影响形成高效率加工的集中力,可以提高力链的强度。对磨粒群的应力分析验证了理论模型的可信度。对粒子微观运动和宏观运动的模拟研究确定加工过程中发生的磨粒群剪胀剪缩的规律。
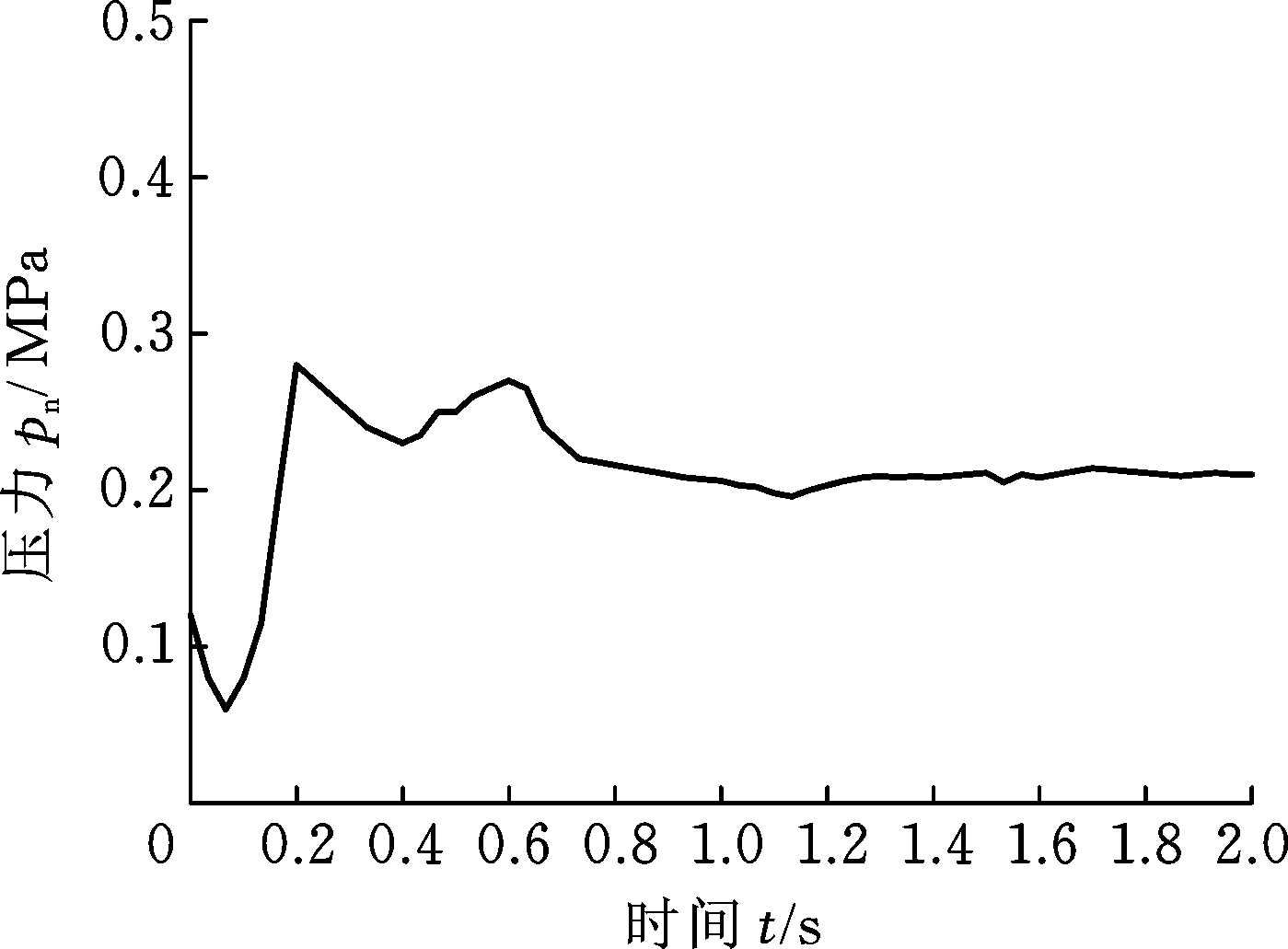
(a) β1=1.0×105(A组)
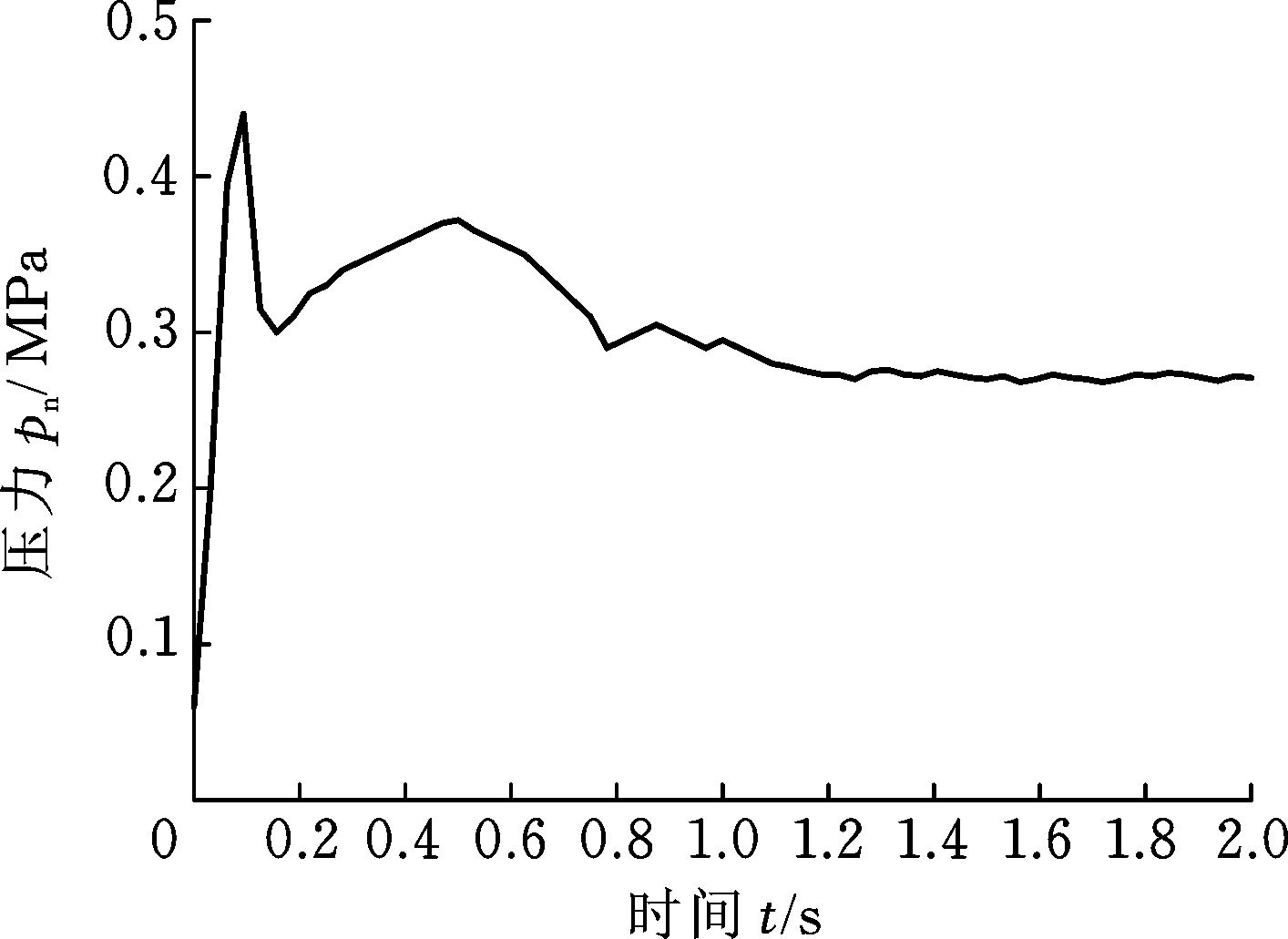
(b) β2=4.0×105(B组)

(c) β3=6.5×105(C组)
图5 不同阻尼系数下的表面应力曲线
Fig.5 Stress curve under different damping coefficients
3 试验和讨论
3.1 软固结磨粒群接触力的测量
为了验证不同阻尼系数黏结剂和不同粒径磨粒对接触应力的影响,首先对软固结磨粒气压砂轮在光整加工中的接触力进行测量。力传感器测力系统如图6所示。软固结气压砂轮如图7所示。
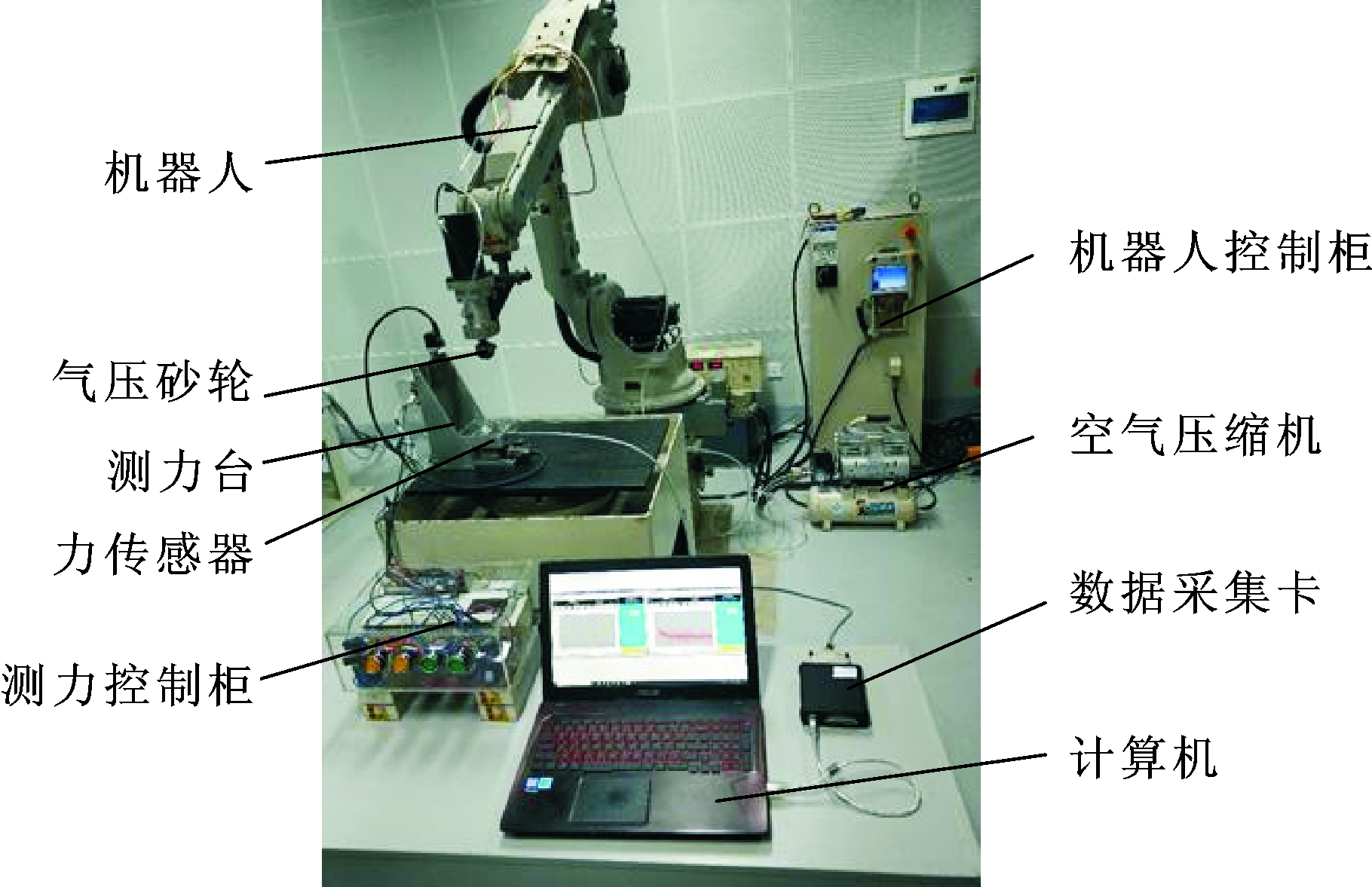
图6 力传感器测力系统
Fig.6 Force measuring system of force sensor

图7 软固结磨粒群气压砂轮
Fig.7 Soft-consolidation abrasives pneumatic wheel
制备砂轮头的黏结剂的选择直接关系到其阻尼系数对磨粒群剪胀效应的影响,选取环氧树脂AB胶、650聚氨酯、酸性硅酮密封胶这3种黏结剂进行试验。根据表3的参数,用不同黏结剂混合不同粒径的白刚玉磨粒制成3组软固结磨粒气压砂轮(每组18个进行试验,试验数据取平均值)。
表3 磨粒群试验参数
Tab.3 Abrasives test parameters
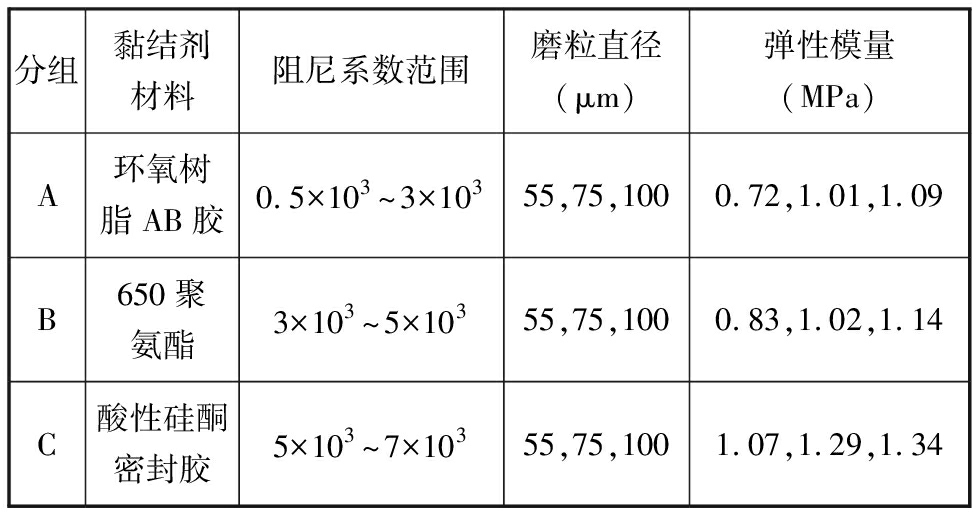
分组黏结剂材料阻尼系数范围磨粒直径(μm)弹性模量(MPa)A环氧树脂AB胶0.5×103~3×10355,75,1000.72,1.01,1.09B650聚氨酯3×103~5×10355,75,1000.83,1.02,1.14C酸性硅酮密封胶5×103~7×10355,75,1001.07,1.29,1.34
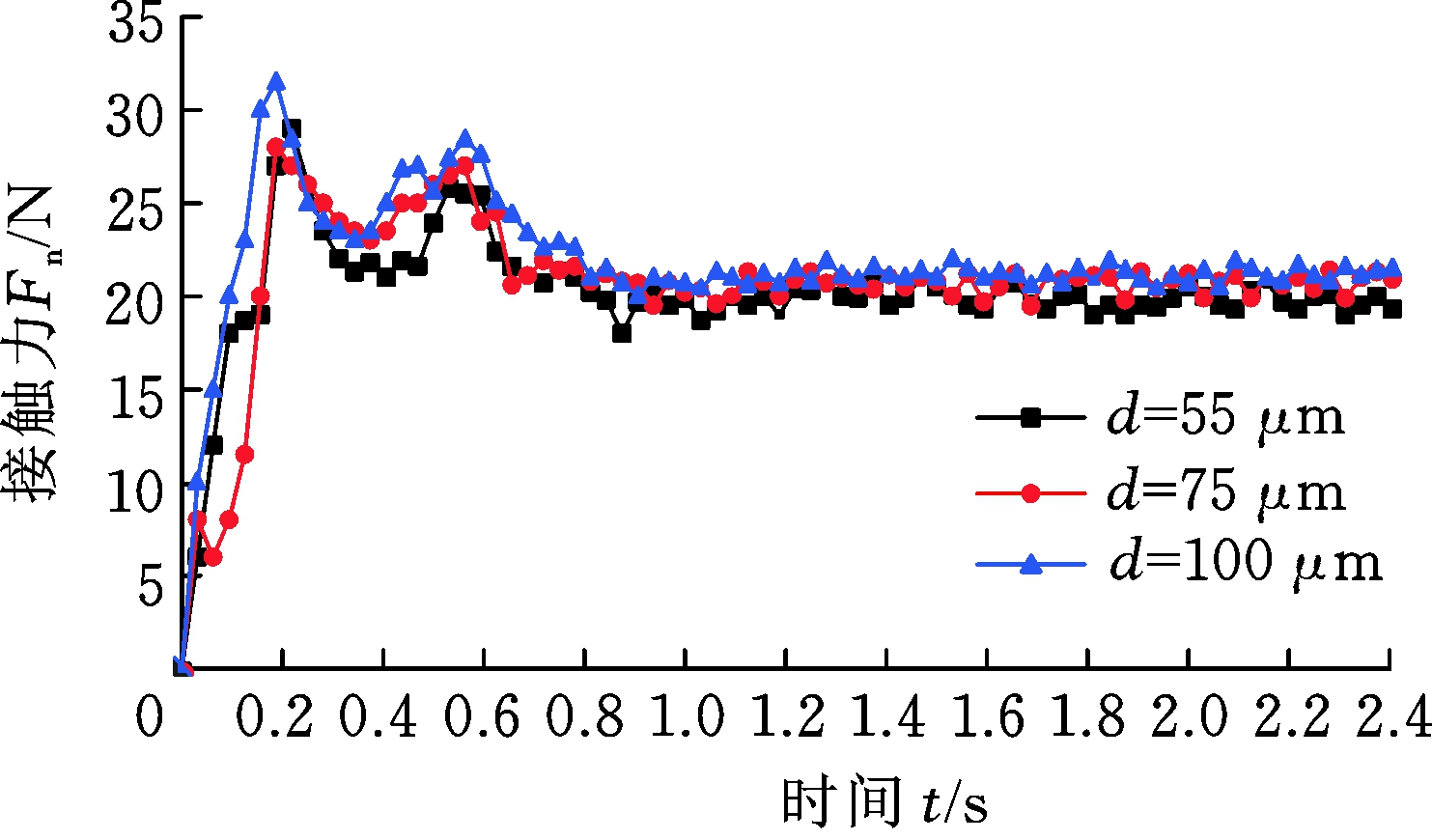
参数设置参考文献[15-16],以表4所示的工艺参数作为试验条件进行以下接触力的测量和材料去除试验。采用表3对应的3组不同阻尼系数砂轮头,记录工作过程中的接触力变化数据,如图8所示。
表4 加工参数设计
Tab.4 Design of machining parameters
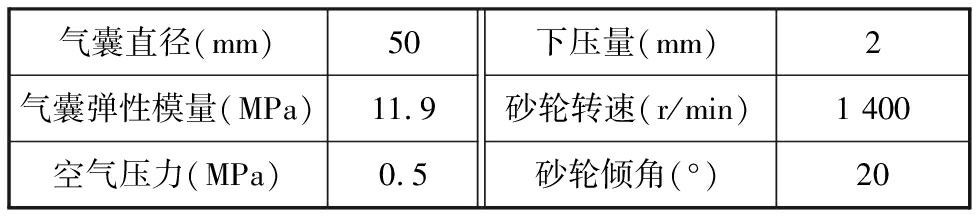
气囊直径(mm)50气囊弹性模量(MPa)11.9空气压力(MPa)0.5下压量(mm)2砂轮转速(r/min)1 400砂轮倾角(°)20
由试验结果可以发现,接触力的波动规律与不同阻尼系数颗粒的接触应力仿真结果基本相符。接触力在试验初期发生明显变化,最后都达到动态平衡状态,验证了磨粒群的剪胀效应。阻尼系数越大,最后剪胀效应下所达到的平衡状态下的接触力越大。不同粒径下的软固结磨粒群都存在剪胀效应,在同样的阻尼系数黏结剂条件下,随着颗粒直径的增大,所产生的平衡状态接触力也明显增大。
(a) A组

(b) B组

(c) C组
图8 力传感器测力曲线图
Fig.8 Force-measuring curve of force sensor
试验结果与2.3节的仿真分析相符,证实了阻尼系数对孔隙比的影响,阻尼系数越大,软固结磨粒稳定态的孔隙比越小,力链强度越大,加工接触力越集中,且这一规律存在于不同粒径下的软固结磨粒群中。
3.2 颗粒粒径对曲面加工的影响
根据理论部分的材料去除压力函数以及压力测试分析可知,磨粒粒径是影响材料去除的重要因素。将压力测力台撤出后放上硬度为434 HV、表面粗糙度Ra为400~500 nm的发动机叶片试样进行加工试验。加工试样如图9所示。
将粒径为55 μm、75 μm、100 μm的磨粒用酸性硅酮密封胶黏结制作3组砂轮,根据表4加

(a) 凸面加工

(b) 凹面加工
图9 加工工件图
Fig.9 Machined workpiece drawing
工参数进行了3 min的加工试验,利用高精度电子分析天平测量加工后工件的质量变化,取多组试验数据平均值后可得每组的材料去除量,加工后的表面粗糙度也测量并取平均值,结果如图10所示。
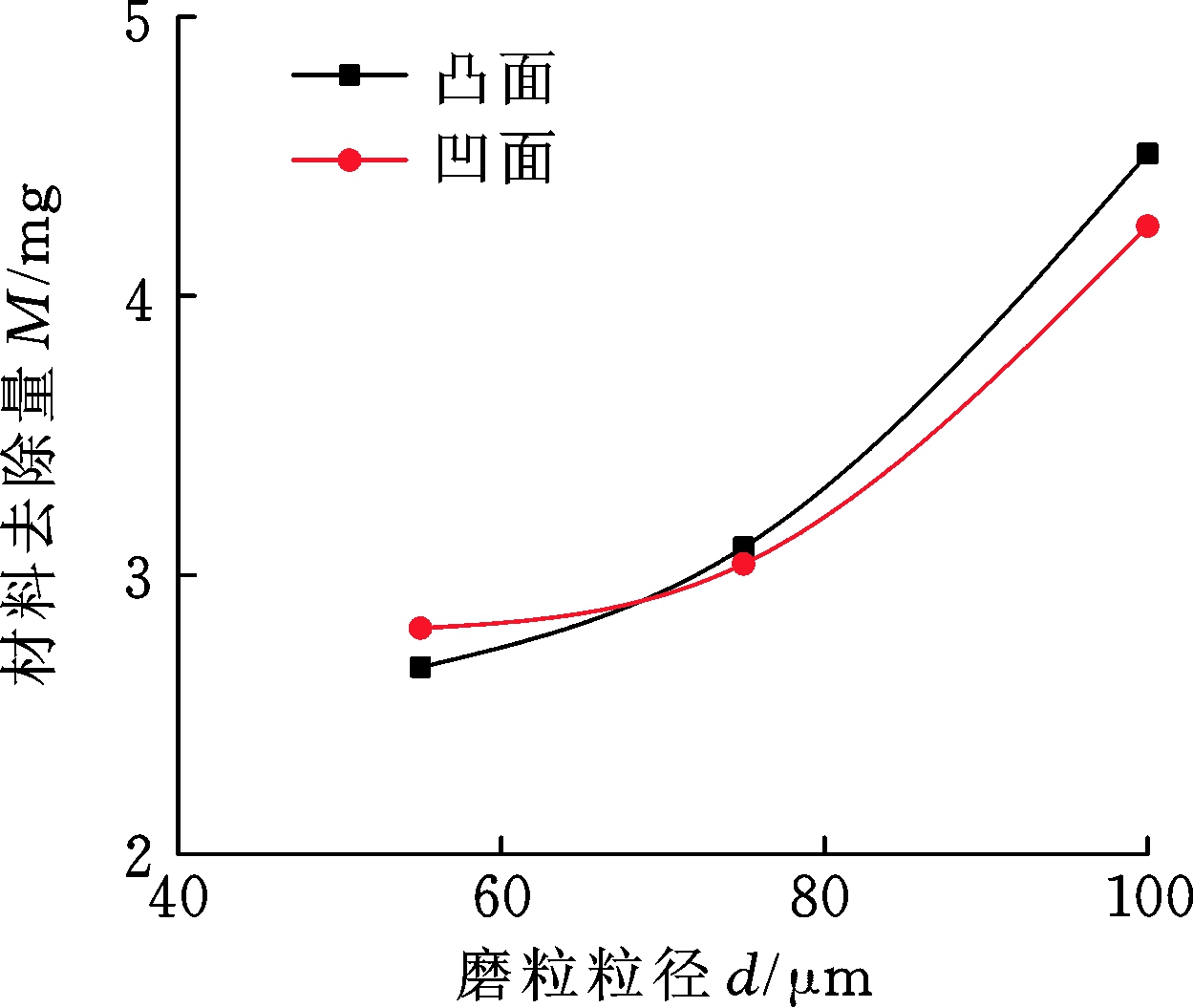
(a) 加工3 min工件材料去除量
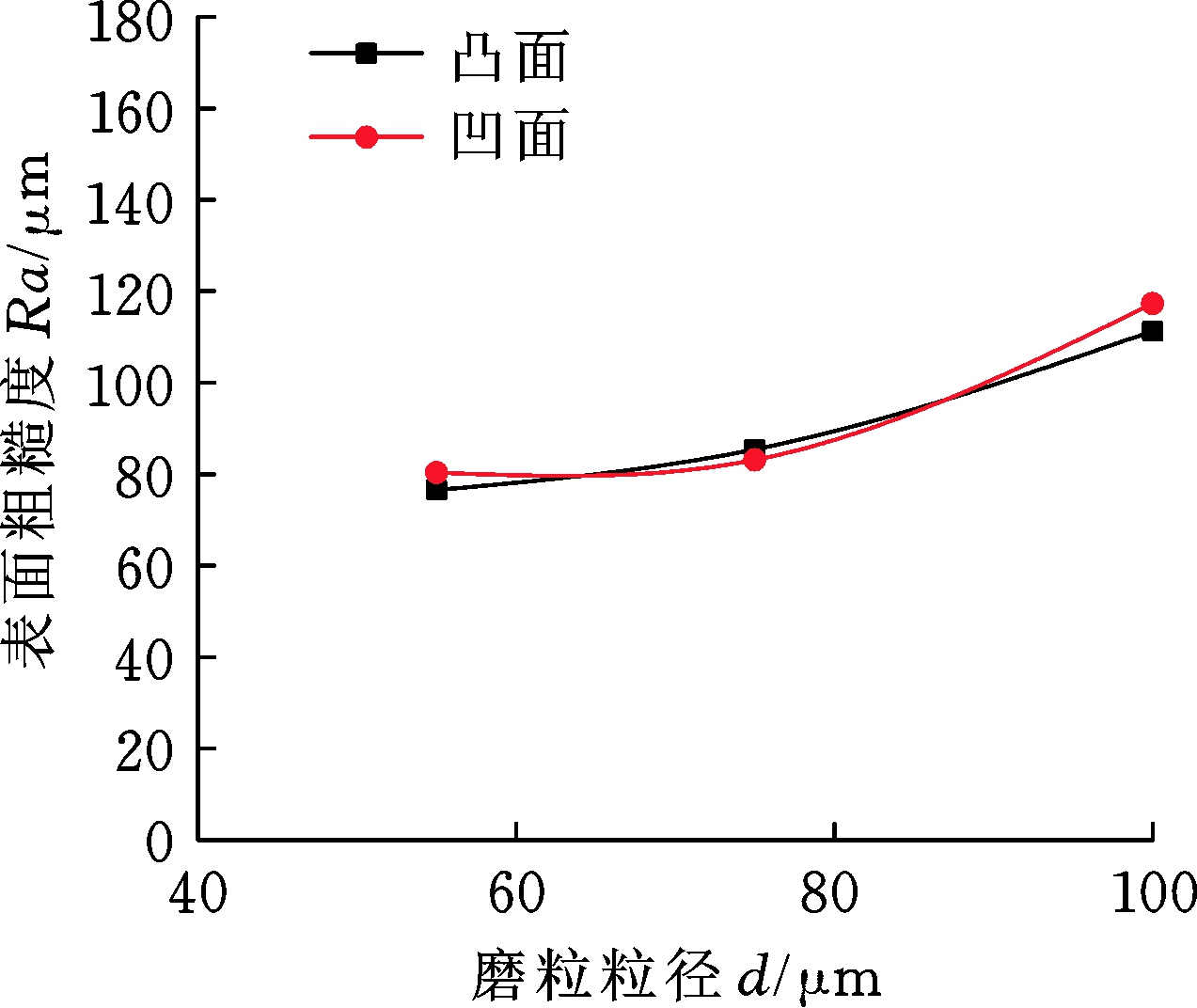
(b) 加工3 min后工件表面粗糙度
图10 不同粒径的软固结磨粒群对曲面的加工
Fig.10 The processing of curved surface by
soft-consolidation abrasives of different sizes
由图10a可知,随着颗粒粒径的增大,3 min加工的材料去除量提高。当磨粒粒径从55 μm提升到100 μm,3 min加工时间内,用酸性硅酮密封胶结剂的磨粒群对曲面模具材料去除量提高约1.64 mg。由图10b可知,工件表面粗糙度开始随磨粒粒径的增大的变化不明显,而后随着粒径的增大呈现上升趋势。粒径在75 μm左右时可在保证加工效率的同时控制表面质量,控制表面粗糙度。不同曲面的材料去除趋势基本一致。以下采用75 μm粒径的磨粒对凸面模具进行进一步试验。
3.3 不同阻尼系数的剪胀效应对曲面加工的影响
为了验证阻尼系数下的剪胀效应对曲面加工的加强作用,分别采用游离磨粒(气囊抛光)和酸性硅酮密封胶黏结的软固结砂轮头对凸面模具进行3 min加工,取多组试验数据平均值。与式(2)和式(8)修正材料去除模型进行对比,如图11所示。
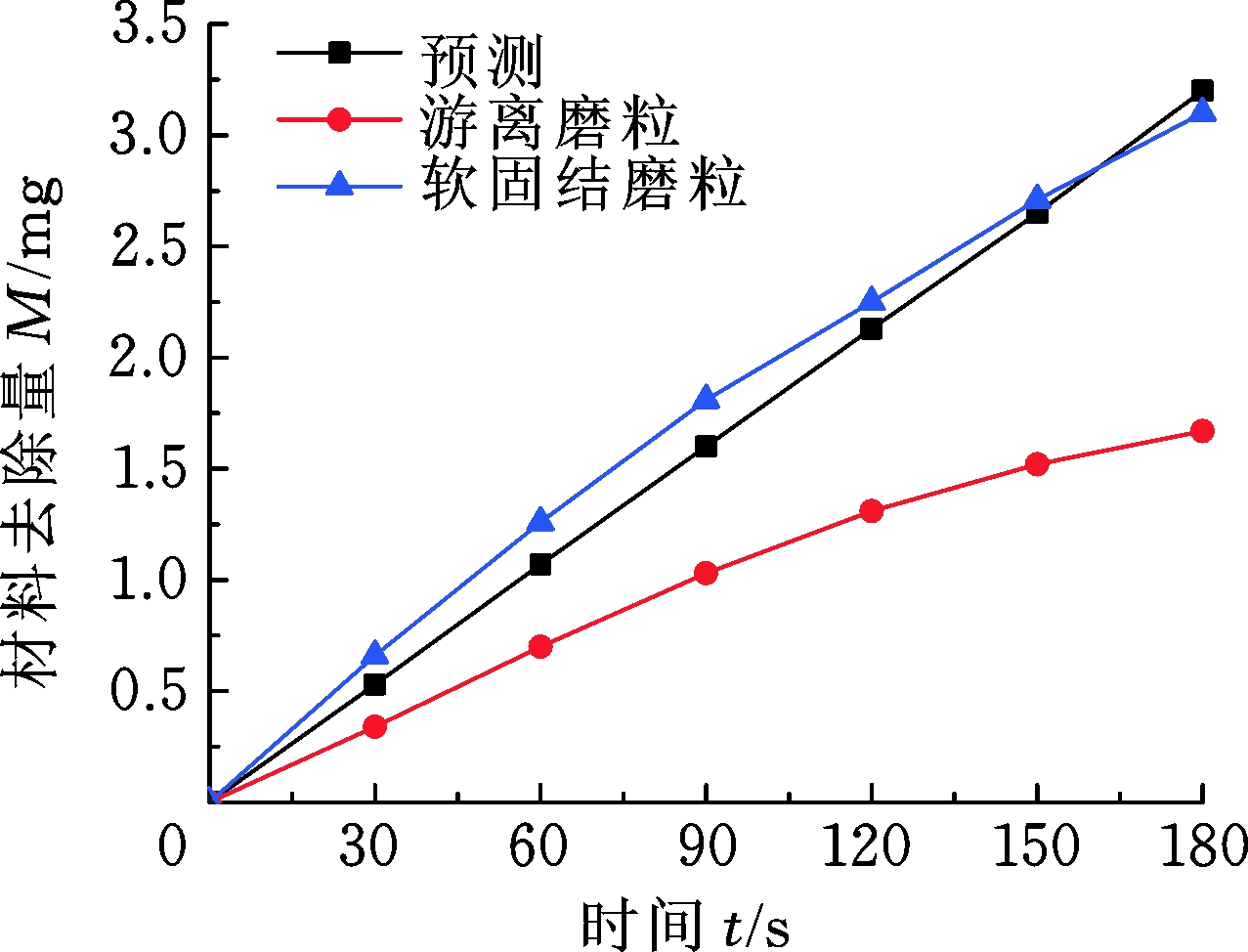
图11 两种状态下的材料去除量及预测曲线对比
Fig.11 The comparison of material removal and
prediction curves under two conditions
预测曲线即根据式(2)、式(8)的材料去除模型所得,对比图11的预测曲线和软固结磨粒群气压砂轮的加工曲线,阻尼系数黏结剂下的软固结磨粒群材料去除曲线与理论修正材料去除方程基本吻合。试验结果说明修正材料去除方程能够应用于软固结气压砂轮的材料去除定量分析。对比图11的软固结磨粒群气压砂轮和游离磨粒(气囊抛光)的材料去除曲线可以看出,软固结磨粒群材料去除量明显高于游离磨粒的材料去除量,3 min加工时间内提高了约1.43 mg的材料去除量。
对不同阻尼系数黏结剂配置下的软固结磨粒群砂轮进行试验,取多次试验数据平均值,得到3 min材料去除量,如表5所示。
表5 3min材料去除量
Tab.5 Material removal in 3min processing

分组黏结剂材料阻尼系数范围材料去除量(mg)A环氧树脂AB胶0.5×103~3×1033.10B650聚氨酯3×103~5×1032.67C酸性硅酮密封胶5×103~7×1032.35D01.67
对比表5加工试验组数据可知,在其他试验条件都相同的情况下,随着对黏结剂阻尼系数的提高,对大型曲面的模具的材料去除量提高。当阻尼系数从A组提高至C组,3 min的加工时间内,软固结磨粒群对曲面磨具材料去除量提高了约31.91%。这一规律与仿真结果以及接触力测量结果一致。随着阻尼系数的改变,气压砂轮的磨粒群产生不同规律的剪胀效应,孔隙率发生变化。阻尼系数越大,则越快达到稳定状态,且对应的孔隙率越小,应力传递更加有效集中稳定。
加工的同时,每0.5 min检测工件表面的粗糙度,发现各组的粗糙度改变存在差异,取多组试验数据平均值,得图12所示数据。

图12 不同阻尼系数黏结剂下加工曲面表面粗糙度
Fig.12 Surface roughnesses of machined surface
with different damping coefficient binders
图12显示了不同曲面的粗糙度在不同加工条件下的变化。加工工件经过C组黏结剂中的磨粒群气压砂轮的加工后,表面质量提高最明显,可实现凸面工件表面粗糙度Ra在3 min内从350.26 nm下降至85.44 nm。在其他条件相同的情况下,随着黏结剂阻尼系数的提高,表面质量的提高效果越好,阻尼系数从A组提升至B组,表面粗糙度下降近32.34%。
软固结磨粒群在不同阻尼系数黏结剂下对凸面加工后的工件微观形貌如图13所示。可以看出,加工前工件表面有明显划痕,经过软固结气压砂轮的加工,试验组加工所得到的工件表面质量都有明显提高,且阻尼系数C组加工后的表面质量明显优于A、B、D组,划痕明显减少。不同加工效果的主要原因是,不同阻尼系数的黏结剂制作的气压砂轮发生的剪胀效应有差异,剪胀效应的程度不同,稳态下的颗粒排列不同,孔隙比不同;阻尼系数越高,孔隙比越小,加工应力越集中,去除越均匀,加工质量越高。

(a) 原始表面

(b) 加工后表面(A组)

(c) 加工后表面(B组)

(d) 加工后表面(C组)

(e) 加工后表面(D组)
图13 加工表面形貌对比图
Fig.13 The comparison of the machined surface topography
4 结论
(1)本文采用微观分析的方法分析了磨粒在柔性支撑环境下的剪胀效应,以及不同阻尼系数黏结剂中磨粒群剪胀效效后的孔隙比变化对接触面的影响,解决了颗粒群在复杂曲面加工时非固定状态下的力学分析的难点。
(2)在软固结磨粒群黏弹性本构模型基础上,建立孔隙率与黏结磨粒系统阻尼系数的数学模型。根据磨粒群微观剪胀剪缩结构分析,以及结合孔隙比与平均应力的关系,得出磨粒群作用接触面的应力方程,并基于Preston方程建立了软固结磨粒群材料去除模型。
(3)基于PFC3D仿真,分析了不同阻尼系数黏结剂中的磨粒群的剪胀剪缩作用,以及内部孔隙比变化对应的应力规律,并通过力传感器测力设备验证了剪胀效应对接触力的影响,可通过阻尼系数的调整改变接触应力,通过仿真和试验分析揭示了软固结磨粒群剪胀态下的动态变化规律。
(4)进行了气压砂轮加工试验,通过材料去除试验,不同阻尼系数的黏结剂和磨粒粒径都影响材料的去除,对砂轮的接触过程与材料去除预测模型进行了拟合,验证该方程能够应用于软固结气压砂轮的材料去除定量分析。可根据剪胀效应的规律,提高黏结剂阻尼系数来提高曲面模具材料的去除量,在相同加工时间内,阻尼系数提高5.0×105左右,材料去除量累计提高近31.91%,曲面模具的粗糙度降低近32.34%,工件划痕明显减少。
[1] 周志雄, 周秦源, 任莹晖. 复杂曲面加工技术的研究现状与发展趋势[J].机械工程学报, 2010, 46(17):105-113.
ZHOU Zhixiong, ZHOU Qinyuan, REN Yinghui. Current Research and Development Trends of Complex Surface Machining Technology[J]. Journal of Mechanical Engineering, 2010, 46(17): 105-113.
[2] 张利, 李研彪, 金明生, 等. 用于模具自由曲面的新型气囊抛光中磨粒场的分析[J].中国机械工程, 2014,25(6):832-835.
ZHANG Li, LI Yanbiao, JIN Mingsheng, et al. Analysis of Abrasive Field in New Airbag Polishing for Mould Free Surface [J]. China Mechanical Engineering, 2014,25(6): 832-835.
[3] WALKER D D, BALDWIN A, EVANS R, et al. A Quantitative Comparison of Three Grolishing Techniques for the Precessions Process[C]∥Proceedings of SPIE. San Diego, 2007:66711H.
[4] 宋剑锋, 姚英学, 谢大纲, 等.气囊抛光工艺参数的正交试验分析[J]. 光学技术, 2009, 35(2):315-318.
SONG Jianfeng, YAO Yingxue, XIE Dagang, et al.Orthogonal Experimental Analysis of Process Parameters for Balloon Polishing[J]. Optical Technology, 2009, 35(2):315-318.
[5] JAKOBSEN P D, LANGMAACK L, DAHL F, et al. Development of the Soft Ground Abrasion Tester (SGAT) to Predict TBM Tool Wear, Torque and Thrust[J]. Tunnelling and Underground Space Technology,2013, 38: 398-408.
[6] 金明生, 计时鸣, 张利, 等. 连续进动气囊抛光行间距优化及试验研究[J]. 中国机械工程, 2013, 24(7): 862-865.
JIN Mingsheng, JI Shiming, ZHANG Li, et al.Optimizing Row Spacing of Continuous Precession Airbag Polishing and Experimental Study [J]. China Mechanical Engineering, 2013, 24(7): 862-865.
[7] REYNOLDS O. On the Dilatancy and Media Composed of Rigid Particles in Contact[J]. Philosophical Magazine, 1885, 5(20): 469-481.
[8] 迟明杰, 赵成刚, 李小军. 剪胀性砂土本构模型的研究[J].岩土力学, 2008,29(11):2939-2944.
CHI Mingjie, ZHAO Chenggang,LI Xiaojun. Study on Constitutive Model of Dilatant Sandy Soil[J]. Geotechnical Mechanics, 2008,29(11):2939-2944.
[9] 金爱兵, 王凯, 张秀凤, 等. 基于颗粒流程序的广义Kelvin模型及其应用[J].岩土力学, 2015,36(9):2695-2701.
JIN Aibing, WANG Kai, ZHANG Xiufeng, et al. Generalized Kelvin Model Based on Particle Flow Program and Application[J]. Geotechnical Mechanics, 2015,36(9):2695-2701.
[10] 徐献芝, 蔡键, 李传亮, 等. 考虑孔隙比变化的黏弹性土体本构模型[J].土木工程学报,2000(3):108-110.
XU Xianzhi, CAI Jian, LI Chuanliang,et al. Viscoelastic Soil Constitutive Model Considering Porosity Ratio Change[J]. Journal of Civil Engineering, 2000(3):108-110.
[11] PRESTON F W. Glass Technology[J]. Journal of the Society of Glass Technology, 1927, 11: 277-281.
[12] 杨荣伟, 程晓辉. 光弹颗粒材料的直剪试验研究[J].岩土力学,2009, 30(增刊):103-109.
YANG Rongwei, CHENG Xiaohui. Direct Shear Experimental Study of Photoelastic Granular Materials [J]. Geotechnical Mechanics,2009, 30(S): 103-109.
[13] SANTAMARINA J C. Soil Behavior at the Microscale: Particle Forces[J]. Geotechnical Special Publication, 2003(119):25-56.
[14] 周驰. 软土压缩e-p曲线模型及其工程应用[D].长沙: 湖南大学, 2012.
ZHOU Chi. A e-p Curve Model for Soil Compression Process and Its Engineering Applications[D]. Changsha: Hunan University,2012.
[15] ZENG X, JI S M, JIN M S, et al. Research on Dynamic Characteristic of Softness Consolidation Abrasives in Machining Process[J]. International Journal of Advanced Manufacturing Technology, 2016, 82(5/8): 1115-1125.
[16] CHEN G D, SUN Y Z, ZHANG F H, et al. Dynamic Accuracy Design Method of Ultra-precision Machine Tool[J].Chinese Journal of Mechanical Engineering, 2018, 31: 1-9.
