0 引言
现代工业产品结构日益复杂、工作环境日趋极端,这对产品性能提出了更高的要求。然而,在实际产品(如航空航海装备液压密封结构、高端精密机床高速重载轴承、旋转机械转子系统等)的设计、制造、运营及维护等方面,广泛存在着各种不确定性因素[1]。这些不确定性与产品的高性能要求之间存在不可调和的矛盾,其故障概率往往因不确定性的存在而增大,可靠性显著降低,甚至导致产品无法实现既定功能,因此,在设计阶段就应考虑不确定性的影响,平衡产品可靠性和性能指标。考虑不确定性有多种方式,本文仅涉及基于概率理论的随机不确定性下的相关优化方法[2-4]。
安全系数法是工程中最常用的设计方法,该方法针对确定性设计优化(DDO)结果设置安全系数,在牺牲一定性能的前提下提高产品的可靠性。但确定安全系数只能根据既有经验、质量控制手段等,没有充分的理论依据,并且往往为了保证可靠性而过度牺牲产品性能。随着现代产品各项指标日趋复杂,安全系数法很难契合实际设计需求。20世纪80年代以来,国内外学者逐渐认识到,发展完备的可靠性设计优化(reliability-based design optimization, RBDO)理论迫在眉睫[5-7],这对科学地提高产品的安全性、耐久性等服役性能,促使产品适应日益增长的实际需求,减少产品运营和维护成本具有重要意义[8]。RBDO通过构造概率约束来考虑影响产品性能的多方面不确定因素,例如材料属性、几何特性、装配环境、外在载荷等,通过计算失效概率(或可靠度)这一关键指标来衡量当前设计结果是否满足不确定性设计要求。近年来,尽管部分RBDO理论方法逐渐开始应用于航空航天、远洋深海、特种装备等领域,但未来RBDO还将面临越来越多的失效模式(即概率约束)、越来越耗时的数值分析过程、越来越复杂的不确定性信息和越来越严苛的可靠性设计要求,要想进一步推进RBDO理论的应用,亟需发展实用性更强、适用面更广的高效可靠性设计优化方法。
处理RBDO问题的常用解决方案一般从概率解析角度或代理模型角度出发。基于概率解析的RBDO方法[9-11],如双循环法、解耦法和单循环法等,均致力于构造等效概率约束。此类方法在当前设计解处进行可靠性分析,然后根据可靠性分析结果来构造等效概率约束,基于等效概率约束进行确定性优化,即可得到RBDO优化解。实现此过程的核心是可靠性分析的实施策略和等效概率约束的构造方式。尽管概率解析法适用于诸多RBDO问题,但对于需要借助某些耗时的数值分析软件或程序的问题(例如:福特汽车公司一次汽车碰撞实验大致花费36~160 h[12]),概率解析法效率偏低,甚至对于某些含复杂约束的问题,概率解析法求解精度不足。为此,基于代理模型的RBDO方法应运而生[13]。代理模型,即替代RBDO过程中复杂且耗时的数值分析软件或程序的数学模型,也称为响应面模型、近似模型或元模型。精准的代理模型可以大大提高可靠性分析和优化效率,因此,如何构建代理模型是此类方法的关键技术难题。
此外,在推动RBDO的实际应用时,还应考虑实际中大量存在的随时间变化的不确定信息[14](如材料的性能衰减和腐蚀退化、随机动态载荷等),时变不确定性下的结构可靠度通常随时间递减,常规RBDO结果往往不能保证全生命周期内安全可靠,因此,在RBDO的基础上还需要引入时间变量和随机过程,发展更为复杂的时变可靠性设计优化(time-dependent reliability-based design optimization, TRBDO)理论。如果将RBDO看作一个内环为可靠性分析、外环为确定性优化的双环嵌套结构,那么TRBDO则在该双环结构外层再嵌套一层时间尺度上的循环结构。这对本身就复杂耗时的RBDO来说,无疑是雪上加霜。
随机不确定性下的可靠性设计优化理论提出至今历经了几十年的蓬勃发展,本文根据RBDO的不同发展阶段从概率解析和代理模型两个方面系统介绍RBDO的研究现状和进展。
1 基于概率解析的可靠性设计优化
1.1 可靠性设计优化数学模型
RBDO的示意图见图1。由于不确定性的存在,确定性优化得到的最优解无法满足可靠性设计要求,需要进一步在迭代中考虑可靠性分析结果,从而得到RBDO最优解。理论上,RBDO最优解位于概率约束边界上,且在确定性约束上存在一个与之对应的最可能失效点,二者在标准正态空间内的距离即是设计结果的可靠度。

图1 可靠性设计优化示意图
Fig.1 Illustration of reliability-based design optimization
RBDO数学模型定义如下:

(1)
i=1,2,…,I;j=1,2,…,J
式中,d为确定性设计变量;μX为随机设计变量X的均值;![]() 和
和![]() 和
和![]() 分别为d和μX的上下界;μP为随机参数P的均值,随机参数的分布参数已知,它只参与可靠性分析;
分别为d和μX的上下界;μP为随机参数P的均值,随机参数的分布参数已知,它只参与可靠性分析;![]() 为最大允许失效概率;Prob(·)为失效概率算子;gc(d,X,P)为功能函数,也称为极限状态函数。
为最大允许失效概率;Prob(·)为失效概率算子;gc(d,X,P)为功能函数,也称为极限状态函数。
概率约束函数定义为失效概率小于或等于最大允许目标失效概率![]() 其中,失效概率由失效概率算子Prob(·)求得,Prob(·)将功能函数g(d,X,P)≤0定义为失效事件。显然,g(d,X,P)=0对应的极限状态边界将整个空间分为安全域Ωs={d,X,P|g(d,X,P)>0}和失效域Ωf={d,X,P|g(d,X,P)≤0}。由于随机变量X和随机参数P具有不确定性,在任意设计点处,功能函数输出响应也具有不确定性,故发生失效事件的概率可定义为
其中,失效概率由失效概率算子Prob(·)求得,Prob(·)将功能函数g(d,X,P)≤0定义为失效事件。显然,g(d,X,P)=0对应的极限状态边界将整个空间分为安全域Ωs={d,X,P|g(d,X,P)>0}和失效域Ωf={d,X,P|g(d,X,P)≤0}。由于随机变量X和随机参数P具有不确定性,在任意设计点处,功能函数输出响应也具有不确定性,故发生失效事件的概率可定义为
(2)
式中,fX,P(X,P)为随机变量和随机参数的联合概率密度函数。
式(2)的求解是一个不规则复杂空间上的多维积分问题,计算成本较高,求解难度较大。
根据式(1)可知,RBDO优化模型具有双层循环结构,如图2所示。内层循环进行可靠性分析,计算当前设计点的失效概率是否满足概率约束;外层循环根据可靠性分析结果,逐步寻找满足概率约束的最优解。基于这种双层循环结构,为避免式(2)所示的直接积分,人们提出了两种代表性的方法:可靠度指标法(reliability index approach, RIA)[5,15-16]和功能度量法(performance measure approach, PMA)[17-19]。

图2 可靠性设计优化的双层循环结构[20]
Fig.2 The double-loop structure of RBDO[20]
RIA将式(1)转化为如下模型:

(3)
式中,![]() 为第c个约束的目标可靠度。
为第c个约束的目标可靠度。
计算可靠度指标β(d,μX,μP)需要借助下面的可靠性分析:

(4)
由式(4)得到标准正态空间(U空间)中的最可能失效点(most probable point, MPP)UMPP,且有β(d,μX,μP)=‖UMPP‖。20世纪六七十年代以来,涌现了许多求解式(4)的经典可靠性分析方法[21-27]。
PMA将式(1)转化为如下模型:
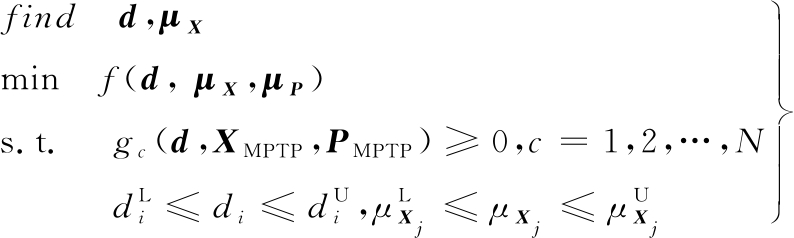
(5)
其中,最小性能目标点(minimum performance target point, MPTP)XMPTP和PMPTP需要通过下式的逆可靠性分析求得:
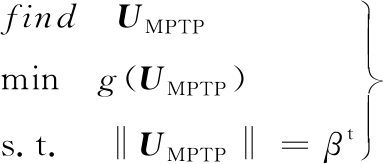
(6)
(7)
近年来,发展高效精确的逆可靠性分析方法也一直是可靠性设计优化领域中的热点研究问题之一[28-31]。
研究表明,与RIA方法相比,PMA方法收敛更稳定,不易受可靠度指标大小的影响,且PMA更适合处理含非活跃约束的问题[17-18]。但RIA和PMA方法都是双层循环优化结构,计算效率偏低。为此,人们根据确定性优化和可靠性分析在RBDO求解框架中的布局,分别研究了解耦策略和单循环策略。
1.2 基于解耦策略的可靠性设计优化
在解耦策略方面,1994年,LI等[32]借助线性规划来解决RBDO问题,他们根据上一步迭代的可靠性结果和灵敏度分析结果,对可靠度指标进行线性近似,从而构建近似概率约束,这是最早提出的解耦策略之一。类似地,人们还提出了其他近似策略[33-36]。程耿东等[37-39]对传统序列近似规划法进行改造,提出了针对RBDO问题的序列近似规划(sequential approximate programming, SAP)算法。MENG等[40]用二阶可靠度方法替换一阶可靠度方法,进一步提高了SAP的精度。ZOU等[41]提出了另外一种直接解耦法,该方法直接从可靠性分析出发,根据当前失效概率(或当前可靠度)和灵敏度信息,对概率约束进行一阶泰勒级数展开近似。总体来说,上述解耦方法从RIA模型出发,根据当前可靠性分析结果和灵敏度分析结果对式(3)中的可靠度指标进行近似,从而得到近似概率约束。近似可靠度指标可以表示为
(8)
另一类方法从PMA模型出发构造如式(5)所示的概率约束。事实上,该概率约束是将式(1)中的功能函数向可行域内以一定准则平移而得到的。例如,WU等[42-43]提出了安全因子法(SFA),在任意优化迭代步,通过可靠性分析计算安全因子,再基于安全因子构造等效概率约束。QU等[44]提出了类似的安全因子概念,通过基于响应面近似的蒙特卡罗模拟法计算概率充分因子(PSF)。2002年,DU等[45]在美国机械工程师学会举办的设计自动化会议上提出了著名的序列优化和可靠性评估(sequential optimization and reliability assessment, SORA)法。值得一提的是,YANG等[46]认为,虽然SFA法和SORA法的实现过程不同,但是二者在概念上是一致的。
已有研究测试了SORA的效果,与SAP等解耦策略相比,SORA法具有较强的稳定性,适用面较广,与双循环法相比,则能在一定程度上兼顾精度和效率[47]。为此,SORA法受到了人们的广泛关注和推崇,其优化模型如下:
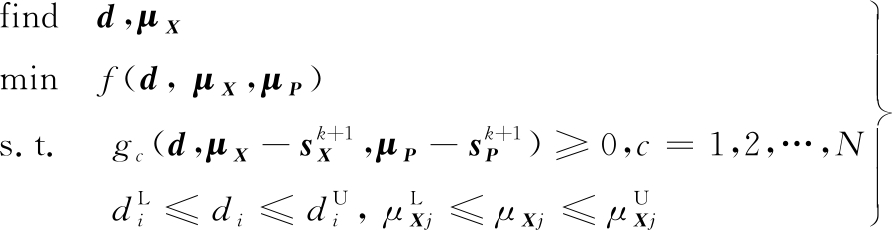
(9)
式中,![]() 分别为第k+1步优化迭代的随机设计变量X和随机参数P的偏移向量,根据该偏移向量,SORA法将确定性约束向安全域内平移得到等效概率约束。
分别为第k+1步优化迭代的随机设计变量X和随机参数P的偏移向量,根据该偏移向量,SORA法将确定性约束向安全域内平移得到等效概率约束。
虽然SORA方法的综合性能较好,但它每一步优化之后仍需要进行逆可靠性分析,且根据分析结果构建的偏移向量并不一定完全精确。为进一步提高SORA方法的高效性和实用性,国内外学者提出了一系列的改进方法。例如,一些学者在SORA的基础上发展了凸线性SORA(CL-SORA)法[48]、鞍点近似法[49]等。CHEN等[50]提出了自适应解耦法(ADA),通过更新角策略和可行性判断准则来提高求解效率。YI等[51]使用近似可靠性分析结果来替换真实可靠性分析结果。由于SORA方法的核心是构造偏移向量,故CHEN等[52]提出了最优偏移向量(OSV)。类似地,HUANG等[53]提出了增量偏移向量(ISV)。此外,除了处理随机不确定性下的RBDO问题,SORA方法也被推广应用于其他问题[54-59]。
除此之外,近年来在解耦策略方面也出现了一些新的研究工作。例如:TORII等[60]通过最小二乘近似来处理偏移向量;CHEN等[61]发展了多设计点方法;GOSWAMI等[62]提出移动约束阈值的解耦策略;HAO等[63]提出了基于等几何分析的RBDO框架。总体上,对解耦方法求解效率的不懈追求促使人们不断进行更深入的探索。
1.3 基于单循环策略的可靠性设计优化
在单循环策略方面,1992年,MADSEN等[64]首次使用Karush-Kuhn-Tucker(KKT)条件代替概率约束,从而令常规优化算法可直接用于求解RBDO问题。KUSCHEL等[65-66]进一步改进了该工作,并将其推广用于时变可靠性问题。AGARWAL等[67]同样采用了类似KKT条件,使用逆可靠性分析代替了可靠性分析,力图使算法更加稳定。但AOUES等[47]通过标准算例测试表明,此类方法稳定性仍然不足。
与上述策略不同,CHEN等[68]于1997年提出了单环单变量(SLSV)方法,但是该方法的效率和精度受到多方面的影响,例如,初始点的选取、约束的非线性程度等。在SLSV方法的基础上,LIANG等[69]发展了单循环法(SLA),并应用于系统可靠性设计优化[70]。与SLSV法不同,SLA法通过引入KKT条件来近似活跃约束的MPTP点,且近似MPTP点所需要的单位方向向量通过真实梯度计算求得,而不是近似求得。SLA法的优化模型如下:
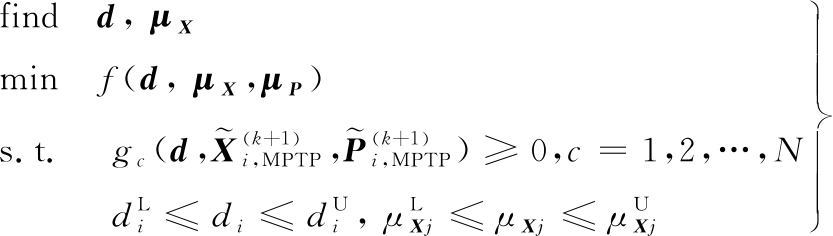
(10)
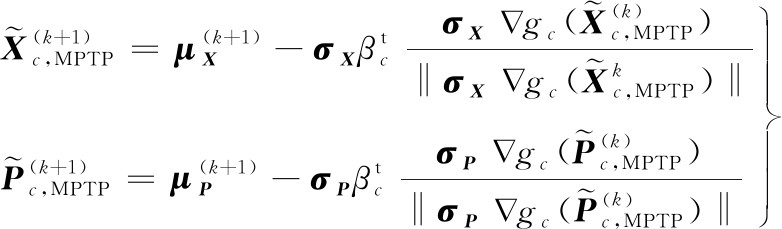
(11)
式中,![]() 和
和![]() 为近似MPTP点;σX和σP为随机变量和随机参数的标准差。
为近似MPTP点;σX和σP为随机变量和随机参数的标准差。
为构建等效概率约束,SLA法只需计算近似MPTP点和其梯度信息。尽管SLA法具有较高的求解效率,但对于某些较为复杂的强非线性问题,SLA法求解精度不足,有时甚至无法收敛。为了提高SLA法的综合性能[71],JEONG等[72]使用上一步MPTP点的共轭梯度来近似MPTP点;JIANG等[73]提出近似MPTP的有效性判断准则,自适应选择近似MPTP点或真实MPTP点以构建更加准确的等效概率约束;KESHTEGAR等[74]使用增强混沌控制策略[31]来加强SLA概率约束的精度;MENG等[75]从控制收敛的角度提高了SLA收敛的可能性。
还有一些学者将以SLA为代表的方法称为迭代单循环法,并提出了完全单循环法[20,76],其中最具代表性的方法即为SHAN等[20]提出的可靠度设计空间(RDS)法。RDS的优化模型如下:

(12)
与SLA方法对比可知,RDS方法直接计算当前设计点的梯度信息,并用来代替其MPTP点的梯度信息,所以,优化过程中搜索设计点和计算梯度信息同时进行,并且,经过RDS方法处理的约束构成了一个可靠度设计空间。但RDS方法存在两个缺陷:①RDS法假设梯度信息易于获取,当梯度信息不易获取时,其效率较低;②当约束函数较为复杂时,RDS法构建的近似关系不够准确。针对这两个缺陷,JIANG等[77]提出了迭代可靠度设计空间法,以提高RDS方法的综合性能。
对比式(8)、式(10)和式(12),可以发现上述SORA、SLA和RDS方法的共同点,即都是基于偏移向量将确定性约束向可行域内平移的方法。因此,它们具有如下统一模型:

(13)
区别在于,各方法利用不同的偏移向量![]() 来构造等效概率约束。进一步对比可见,SORA方法所用的偏移向量为
来构造等效概率约束。进一步对比可见,SORA方法所用的偏移向量为
![]()

![]() ‖σX
‖σX
![]()
SLA所用的偏移向量为
![]()

![]()

![]()
而RDS方法所用的偏移向量为
![]()

![]()
三种方法使用不同的梯度信息来计算偏移向量,理论上,真实MPTP点的梯度信息
![]() 精度较高,但计算成本较高;近似MPTP点的梯度信息
精度较高,但计算成本较高;近似MPTP点的梯度信息
![]() 和设计点的梯度信息
和设计点的梯度信息
![]() 精度偏低,但计算成本较低,且
精度偏低,但计算成本较低,且
![]() 和
和
![]() 各有优势。若能借助某些实时精度准则,自适应判断上述梯度信息的精度水平,并据此作出最能兼具精度和效率的选择,将大大提高此类方法的整体适应能力。
各有优势。若能借助某些实时精度准则,自适应判断上述梯度信息的精度水平,并据此作出最能兼具精度和效率的选择,将大大提高此类方法的整体适应能力。
2 基于代理模型的可靠性设计优化
2.1 RBDO中代理模型研究
在实际中,计算约束函数响应往往需要借助有限元分析、计算流体动力学等成本昂贵的数值分析工具,为了提高分析和优化效率,通常使用代理模型来代替这些计算复杂且耗时的数值分析模型。代理模型也称为近似模型、元模型、响应面模型[78]。常用的代理模型包括:多项式响应面(PRSM)[79]、径向基函数(RBF)、克里金(Kriging)模型[80]、人工神经网络(ANN)[81]、支持向量回归(SVR)[82]、混沌多项式展开(PCE)[83]等。因具备上述替代属性,故代理模型被广泛应用于各个领域,限于笔者水平,本文仅涉及面向可靠性设计优化的代理模型研究。此外,近十几年来,研究人员提出了各种面向可靠性分析的主动学习函数和加点策略[84-95],基于代理模型的可靠性分析逐渐发展为一个重要研究方向。因为RBDO在任意一个设计解处都需要对概率约束进行可靠度评估,所以理论上这些基于代理模型的可靠性分析方法经过一定程度的扩展和改进之后,大部分是可以应用于RBDO的。由于篇幅有限,本文主要总结直接面向RBDO问题的代理模型方法。
在RBDO中建立代理模型有三种方式[7]:①分别以设计点和对应的可靠性分析结果(失效概率或可靠度指标)为代理模型的输入和输出,建立二者之间的对应关系[96-98];②在当前设计解附近区域内构建功能函数的代理模型,基于该局部代理模型在当前设计解处进行可靠性分析[99-100];③对任意功能函数,直接整体构建一个代理模型,基于该模型进行分析和优化[101-102]。
第一种方式在每一个样本点(即设计点)处都需要进行一次可靠性分析,且该可靠性分析必须调用真实函数。可见这种方式占用的计算资源较多,尤其是对于样本点数量较多的情况。第二种方式需要在每一个优化迭代步都建立局部代理模型,不易重复利用既有的样本点,这导致算法不够高效。对比而言,第三种方式优势较为明显,因此得到人们的广泛认可。以下介绍第三种建模方式的发展现状。
2.2 整体构建功能函数代理模型研究
在整体构建功能函数的代理模型方面,代理模型最初引入RBDO领域仅是简单替代计算成本昂贵的数值分析模型,避免重复调用、浪费计算资源。但这种建模方式下,RBDO最优解的准确性严重依赖于代理模型的整体精度水平,这导致进行RBDO之前需要花费大量精力构建代理模型,效率较低。随着国内外相关研究的不断深入,代理模型不再仅是机械地与传统RBDO方法相结合,而是逐渐发展为一类以RBDO需求为驱动的、根据RBDO过程的历史信息逐步自适应添加新样本的方法,研究与RBDO过程高度耦合的加点策略是推动代理模型法发展的重要环节。
在构造加点准则方面,针对约束函数建模主要有两种策略:设计域全局建模策略和设计驱动的局部建模策略。设计域全局建模策略的目标是精确近似整个约束边界,当代理模型达到预定精度之后,再根据建好的模型搜索RBDO最优解。而设计驱动的局部建模策略则关注可能出现最优解的局部区域,因为该局部区域内的约束边界的精度真正决定了最优解的精度。局部建模策略依次进行建模和优化,在每个迭代步的当前优化解附近采样建模,然后根据更新后的模型搜索下一步优化解,如此循环往复,直至找到最优解。图3给出了这两种策略[101,105],它们都分为完全独立的三个部分。可靠性分析和优化结果对采样过程没有影响,在局部建模策略中,采样建模和优化迭代则耦合在一起,将优化迭代信息实时反馈给采样加点过程。
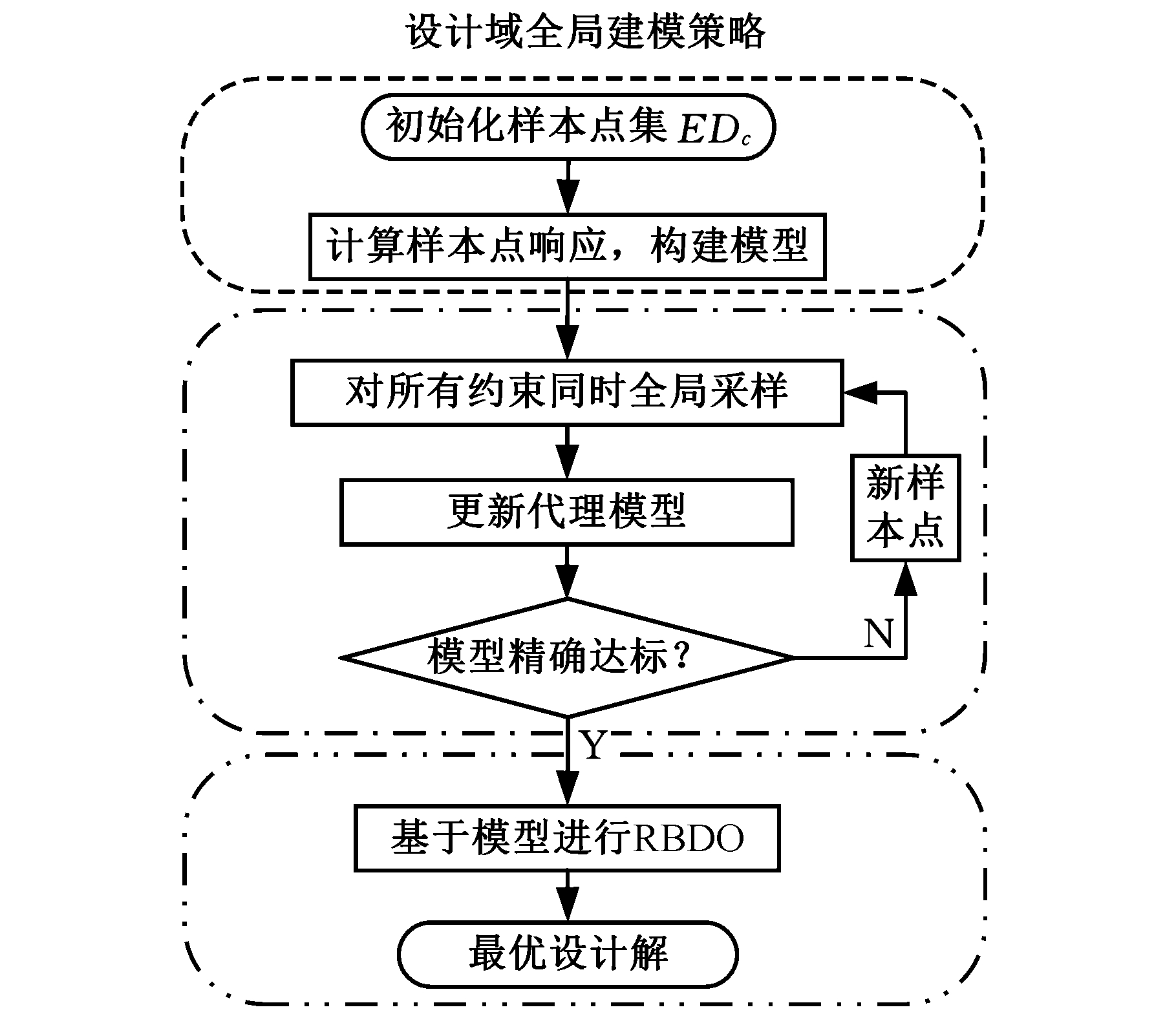
(a)设计域全局建模策略

(b)设计驱动的局部建模策略![]()
图3 全局和局部约束边界建模策略示意图
Fig.3 Illustration of global and local constraintboundary modeling strategies
2.2.1 约束边界全局建模
约束边界全局建模包括一次采样和序列采样,一次采样通过空间填充采样方法(如拉丁超立方采样[103]、最大熵采样[104]等)在设计空间内均匀布置一定量的样本点,基于大量样本点直接建立代理模型,从而精确拟合整个约束函数。这是最直观的做法,但也是效率偏低的建模方法。
为节省样本点资源,在序列采样方面,LEE等[105]提出了约束边界采样(constraint boundary sampling, CBS)方法,该方法的目标是近似整个约束边界,即可行域边界,并不关心代理模型在非边界位置的拟合精度。
如果集中精力将样本点布置在可行域边界附近、确保约束边界精度,即可在约束边界上精确搜索到最可能失效点,从而将精确的可靠性分析结果传递给优化层。为了实现这一思想,CBS方法借助Kriging模型可以同时提供预测均值和预测方差的特性,提出如下加点准则:

(14)
式中,![]() 分别为Kriging模型的预测均值和方差;D为点x与已有样本点之间的最小距离。
分别为Kriging模型的预测均值和方差;D为点x与已有样本点之间的最小距离。
通过![]() 可自主选择约束边界附近的样本点来更新Kriging模型,CBS值越大说明候选点越符合要求。BICHON等[106]将基于Kriging模型的高效全局优化(EGO)方法[107]和高效全局可靠性分析(EGRA)方法[84]相结合,分别用于处理优化环节和可靠性分析环节。
可自主选择约束边界附近的样本点来更新Kriging模型,CBS值越大说明候选点越符合要求。BICHON等[106]将基于Kriging模型的高效全局优化(EGO)方法[107]和高效全局可靠性分析(EGRA)方法[84]相结合,分别用于处理优化环节和可靠性分析环节。
此外,PAPADRAKAKIS等[108]将神经网络、进化策略及蒙特卡罗模拟法组合,通过训练神经网络代替约束函数、使用进化算法构造无需梯度的优化方式来处理RBDO问题。YOUN等[109]、KANG等[110]、SONG等[111]则将基于移动最小二乘的响应面法用于RBDO。
尽管此类约束边界全局建模策略能很好地拟合出可行域边界,为精确搜索RBDO最优解提供必要条件,但此类方法仍然不可避免地会浪费部分样本资源。这是因为RBDO过程中部分约束为非活跃约束,对最优解的搜索没有贡献;或者由于目标函数的关系,部分可行域在最优解搜索时会被直接忽略。为此,人们提出了理论上更为高效的约束边界局部建模策略。
2.2.2 约束边界局部建模
约束边界局部建模策略旨在过滤掉不影响最终优化结果的部分可行域,甚至筛选出非活跃约束,避免将样本点配置在上述区域或约束附近,进而将样本点集中配置在其他关键区域,以提高建模效率。
根据这一基本思想,LEE等[101]提出了类似图3b所示的基于动态Kriging的RBDO框架,并分别从超球体局域、加点准则、约束过滤、局域增强等方面诠释了该采样框架。基于类似框架,ZHUANG等[112]提出了序列期望提升采样(ERI)准则,选择最具精度提升可能性的点作为新增样本点;WANG等[113]提出了最大置信增强(MCE)准则和累计置信水平度量指标,选择具有最大置信水平的点作为新增样本点。由于每一迭代步的自适应采样区域对建模效果至关重要,CHEN等[114]提出了以当前设计点为采样中心的局部自适应采样(LAS)方法,且根据约束函数的非线性程度自适应调整局部采样区域的大小;LI等[115]则提出了以MPP为采样中心的局部自适应采样方法(LMPP),并根据MPP点筛选可行约束(活跃约束)和不可行约束(非活跃约束)。还有一些学者将信赖域引入RBDO[116-118],在信赖域内构建代理模型,且信赖域的大小和中心位置随着优化的进行不断更新。
此外,图3所示两种约束建模策略并未考虑目标函数对加点准则的影响,但在实际中,目标函数往往在一定程度上决定了重点搜索方向。为此,CHEN等[119]提出了重要边界采样(IBS)策略,根据目标函数来识别重要区域,并在重要区域精确拟合约束边界。同样,MENG等[120]提出了自适应边界采样(ADBS)方法,通过构造基于多目标优化的加点策略以同时考虑目标函数和约束边界的重要性,使新增样本点尽可能分布在目标函数的下降方向上。
上述方法均为Kriging模型在RBDO中的应用,在其他模型方面,BASUDHAR等[93,121-122]、BOROSON等[123]基于支持向量机(SVM)模型提出一系列面向可靠性分析和RBDO的加点准则。LIU等[124-125]将SVM用于确定局部采样范围。此外,在变标准差、高维问题、系统可靠性等方面,代理模型也有一定的应用[126-130]。
3 时变可靠性设计优化
3.1 时变可靠性设计优化数学模型
TRBDO在RBDO的基础上进一步考虑了包含随机过程和时间变量的情况,其数学模型如下:
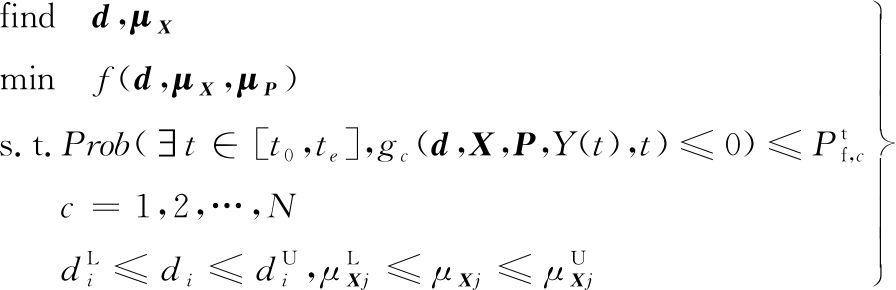
(15)
式中,t为时间变量;Y(t)为随机过程,即一簇随机变量的集合,在任意时刻它都是随机变量。
对比式(1)和式(15)可知,TRBDO模型比RBDO更复杂,在任意时刻它都可看作某个RBDO过程。
3.2 基于概率解析的时变可靠性设计优化
解析TRBDO方面的研究工作主要集中于时变可靠性分析(time-dependent reliability analysis, TRA)。1945年,RICE[131]定义了跨越事件并提出了跨越公式,奠定了跨越率方法的理论基础。为简化计算过程,在假设跨越事件相互独立的前提下,LUTES等[132]基于随机过程模型将时变失效概率的计算转化为跨越率积分,因此跨越率的计算方法成为了研究重点。随后,ANDRIEU-RENAUD等[133]利用FORM法在相邻时间点处得到的可靠性指标和灵敏度系数,推导了适用于一般时变问题跨越率计算的PHI2方法,大大提高了计算效率。在此基础上,SUDRET[134]提出了稳定性更强的改进PHI2方法,利用可靠性指标的增量对跨越率进行解析推导。尽管这些基于独立假设的方法大大简化了时变可靠性计算,但当跨越事件具有较强的相关性时,以上方法均不再适用。由此,HU等[135]提出了联合跨越率法,该方法可更加准确地评估时变失效概率。除以上跨越率法之外,人们还发展了复合极限状态法[136]、极值分布法[137-138]、Gamma过程法[139-140]、复合随机过程法[141]等。
在TRBDO方面,KUSCHEL等[66]首次尝试在TRBDO框架中使用基于FORM的跨越率法进行时变可靠性分析,LI等[142]基于TRA进行生命周期成本优化,但这些方法都将TRA嵌套在TRBDO中,需要大量重复调用功能函数。HU等[143]引入等效最可能失效点(equivalent most probable point, EMPP)的概念,通过极值分析和鞍点近似来计算逆MPP点,并将SORA法拓展应用于TRBDO,但该方法只能处理仅含稳态随机过程的问题。JIANG等[144-145]提出了另一种形式的EMPP,将TRBDO转换为基于PMA的RBDO,每一次迭代优化仅需要一次TRA、一次可靠性分析、一次逆可靠性分析和一次确定性优化。此外,HUANG等[146]还提出了TRBDO的单循环法。YU等[147]则提出了兼顾时变属性和空间属性的系统可靠性设计优化的解耦策略。整体上,TRBDO的多层嵌套形式带来了极大的解耦难度,且解析TRA方法对于复杂约束的处理仍有缺陷,这导致现有方法的求解精度或效率无法得到保证。
3.3 基于代理模型的时变可靠性设计优化
在基于代理模型的TRBDO方面,研究人员的注意力也大多集中在时变可靠性分析方面[148-150],WANG等[151]首先提出了双循环嵌套极值响应方法(NERS),内环通过EGO方法[107]搜索极值响应,外环建立极值响应的近似模型。进一步地,WANG等[152]提出了基于置信度的自适应极值响应面(AERS)法,将其拓展到了一般时变问题。在基于双环结构的极值法基础上,HU等[153]提出了混合高效全局优化(mix-EGO)方法,进一步提高了内环极值响应搜索及外环采样的效率。这些方法有效地解决了TRA问题,但其双循环结构仍需要承担较大的计算负担。为解决这个问题,WANG等[154]提出了基于等效随机过程转换(equivalent stochastic process transformation, eSPT)的方法,通过将随机过程等效转换为随机变量的方式,降低了计算成本,提高了采样效率,但eSPT法的停止准则因问题而异,无法提前确定。HU等[155]进一步提出了基于单环Kriging建模的单循环方法(SILK),SILK法能高效搜索跨越点,从而建立能够对随机点精确分类的全局响应模型,可更为有效地减少训练点数。JIANG等[156]提出了实时预测误差辅助的主动学习Kriging法(real-time estimation error-guided active learning Kriging, REAL),该方法通过推导出基于Kriging模型的时变误分概率和失效概率预测误差区间,进而根据时变误分概率和预测误差区间来构造加点策略和终止准则。此外,处理含非高斯随机过程[157]、小失效概率问题[158]、高维问题[159-160]、系统级问题[161]的TRA方法也得到了一定发展。
在TRBDO方面,近两年逐渐出现了少量报道[147, 162]。HAWCHAR等[163]提出了基于全局Kriging模型的TRBDO法,该方法为每个时变功能函数建立一个Kriging模型,且这些模型建立在一个人工增广的可靠性空间中。LI等[164]则提出了基于序列Kriging建模的TRBDO方法,该方法将随机过程和时间参数转化为随机变量。然后通过自适应采样来精确识别潜在的瞬时失效事件。序列Kriging建模是一种局部建模策略,它只关注RBDO最优解的周边区域。除了这些建模策略之外,WANG等[165]还提出了集成模型验证的TRBDO方法,通过物理实验数据来提高设计结果的置信度。同时,他们还提出了一个面向时变可靠稳健性设计优化的多目标框架[166]。
总的来说,无论是基于概率解析还是基于代理模型的TRBDO,都还处于初始发展阶段,仍有许多问题亟待探索。
4 可靠性设计优化未来发展趋势展望
综观上述研究进展,(时变)可靠性设计优化一直是近二十年来的热点研究方向,尽管国内外研究人员已取得若干重要成果,但在许多方面仍有待深入研究和探索,具体如下:
(1)权衡效率和精度的概率解析法最优框架。尽管已有部分研究者尝试在可靠性设计优化过程中混合使用解耦法和单循环法,从而兼顾求解效率和精度,但高精度的解耦法与高效率的单循环法的结合仍稍显僵硬[73, 167-168]。笔者在第1节中提炼出了三种概率解析法(SORA、SLA和RDS)的统一模型,三者的区别在于构造等效概率约束时所采用的偏移向量不同(计算效率和精度均不同)。在统一模型的框架下,可对不同概率约束进行差异化处理。通过偏移向量判断准则,自适应混合三种不同的偏移向量构建方式,从而可实现概率约束重要性筛选、高精度偏移向量和近似偏移向量的合理规划等目标。无论何时,以最低的计算成本得到满足精度要求的优化结果都是概率解析法的最终目标。
(2)基于代理模型的可靠性设计优化的全局优化算法。虽然基于代理模型的可靠性设计优化能处理含复杂耗时数值分析模型的问题,但鲜有算法同时考虑昂贵目标函数和约束函数,且确保搜索到全局最优解[7]。现有方法要么不考虑昂贵目标函数的情况,要么使用梯度优化算法求解优化解,这无法满足产品愈发复杂的实际情况。将代理模型全局优化算法或模型辅助的进化算法引入可靠性设计优化是一种潜在的解决方案,通过对目标函数和约束函数分别建立代理模型,构造目标函数指引的加点策略,进而构造能同时平衡目标下降要求和约束可行要求的寻优策略,从而实现高效搜索可靠性设计优化全局最优解的目标。
(3)兼顾全生命周期服役性能的时变可靠性设计优化。工程实际中存在大量固有性能衰退、外在动态载荷等情况,在设计阶段考虑这些动态属性是确保产品在全生命周期内实现预期功能的重要环节。然而时变可靠性设计优化的发展仍处于起步阶段,现有工作主要集中在时变可靠性分析方面,而时变可靠性设计优化过程较时变可靠性分析要复杂得多,且后者的相关方法并不能仅仅通过简单扩展即可用于前者。因此,在概率解析法方面,应继续探索将时变可靠性设计优化三层嵌套结构(时间环、优化环、可靠性分析环)充分解耦的高效算法,构造符合问题特征的等效时变概率约束。在代理模型法方面,应发展一套以随机设计变量、随机过程、时变变量等为输入的直接建模理论,以及面向时变问题的加点策略和寻优策略。无论是概率解析方面还是代理模型方面,都亟需进一步开展研究。
(4)不确定性信息不完备下的(时变)可靠性设计优化。本文仅总结了随机不确定性信息完备的可靠性设计优化的研究进展,但在实际中往往还存在由于经验信息不足而导致随机变量的分布类型、分布参数未知的情况。针对这种数据不充分的情形,研究人员提出了具有一定保守置信水平的设计策略[169-171]。此外,还可从不确定性模型参数校正出发,通过结合历史数据和合理配置新增样本点,校正随机变量的分布类型和分布参数[172],进而使用更新后的随机变量进行可靠性设计优化。
[1] 张义民. 机械可靠性设计的内涵与递进[J]. 机械工程学报, 2010, 46(14):167-188.
ZHANG Yimin. Connotation and Development of Mechanical Reliability-based Design[J]. Journal of Mechanical Engineering, 2010, 46(14):167-188.
[2] 王军, 邱志平. 结构的概率-非概率混合可靠性模型[J]. 航空学报, 2009, 30(8):1398-1404.
WANG Jun, QIU Zhiping. Probabilistic and Non-probabilistic Hybrid Reliability Model of Structures[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(8):1398-1404.
[3] 郑静, 姜潮, 倪冰雨,等. 随机-认知不确定性的相关性分析模型及可靠性计算方法[J]. 中国机械工程, 2016, 27(7):925-933.
ZHENG Jing, JIANG Chao, NI Bingyu, et al. An Aleatory and Epistemic Mixed Uncertainty Model Considering Parametric Correlation and Its Reliability Analysis[J]. China Mechanical Engineering, 2016, 27(7):925-933.
[4] 姜潮. 基于区间的不确定性优化理论与算法[D].长沙:湖南大学, 2008.
JIANG Chao. Theories and Algorithms of Uncertain Optimization Based on Interval[D]. Changsha:Hunan University, 2008.
[5] NIKOLAIDIS E, BURDISSO R. Reliability Based Optimization:a Safety Index Approach[J]. Computers &Structures, 1988, 28(6):781-788.
[6] VALDEBENITO M A, SCHU LLER G I. A Survey on Approaches for Reliability-based Optimization[J]. Structural and Multidisciplinary Optimization, 2010, 42(5):645-663.
LLER G I. A Survey on Approaches for Reliability-based Optimization[J]. Structural and Multidisciplinary Optimization, 2010, 42(5):645-663.
[7] MOUSTAPHA M, SUDRET B. Surrogate-assisted Reliability-based Design Optimization:a Survey and a Unified Modular Framework[J]. Structural and Multidisciplinary Optimization, 2019, 60(5):2157-2176.
[8] 郭书祥, 吕震宙, 李为吉, 等. 论基于概率模型的结构可靠性优化设计[J]. 空军工程大学学报(自然科学版), 2001, 2(2):67-70.
GUO Shuxiang, LYU Zhenzhou, LI Weiji, et al. Probabilistic Reliability-based on Optimization of Structures[J]. Journal of Air Force Engineering University(Natural Science Edition), 2001, 2(2):67-70.
[9] 杨迪雄, 易平. 概率约束评估的功能度量法的混沌控制[J]. 计算力学学报, 2008, 25(5):647-653.
YANG Dixiong, YI Ping. Chaos Control of Performance Measure Approach for Evaluationof Probabilistic Constraints[J]. Chinese Journal of Computational Mechanics,2008, 25(5):647-653.
[10] LI F, WU T, HU M, et al. An Accurate Penalty-based Approach for Reliability-based Designoptimization[J]. Research in Engineering Design, 2010, 21(2):87-98.
[11] 孟增. 结构可靠度优化设计的高效稳健算法研究[D].大连:大连理工大学, 2015.
MENG Zeng. Efficient and Robust Algorithms for Reliability-based Design Optimization of Structures[D]. Dalian: Dalian University of Technology, 2015.
[12] SIMPSON T W, BOOKER A J, GHOSH D, et al. Approximation Methods in Multidisciplinary Analysis and Optimization:a Panel Discussion[J]. Structural and Multidisciplinary Optimization, 2004, 27(5):302-313.
[13] 张崎. 基于Kriging方法的结构可靠性分析及优化设计[D].大连:大连理工大学, 2005.
ZHANG Qi. Structural Reliability Analysis and Optimization Based on Kriging Technique[D]. Dalian: Dalian University of Technology, 2005.
[14] 张义民. 机械动态与渐变可靠性理论与技术评述[J]. 机械工程学报, 2013, 49(20):101-114.
ZHANG Yimin. Review of Theory and Technology of Mechanical Reliability Fordynamic and Gradual Systems[J]. Journal of Mechanical Engineering, 2013, 49(20): 101-114.
[15] ENEVOLDSEN I, SØRENSEN J D. Reliability-based Optimization in Structural Engineering[J]. Structural Safety, 1994, 15(3):169-196.
[16] WU Y T. Computational Methods for Efficient Structural Reliability and Reliability Sensitivity Analysis[J]. AIAA Journal, 1994, 32(8):1717-1723.
[17] TU J, CHOI K K, PARK Y H. A New Study on Reliability-based Design Optimization[J]. Journal of Mechanical Design, 1999, 121(4):557-564.
[18] LEE J-O, YANG Y-S, RUY W-S. A Comparative Study on Reliability-index and Target-performance-based Probabilistic Structural Design Optimization[J]. Computers &Structures, 2002, 80(3/4):257-269.
[19] YOUN B D, CHOI K K, DU L. Enriched Performance Measure Approach for Reliability-Based Design Optimization[J]. AIAA Journal, 2005, 43(4):874-884.
[20] SHAN S, WANG G G. Reliable Design Space and Complete Single-loop Reliability-based Design Optimization[J]. Reliability Engineering & System Safety, 2008, 93(8):1218-1230.
[21] HASOFER A M, LIND N C. Exact and Invariant Second-moment Code Format[J]. Journal of Engineering Mechanics-ASCE, 1974, 100(1):111-121.
[22] RACKWITZ R, FLESSLER B. Structural Reliability under Combined Random Load Sequences[J]. Computers & Structures, 1978, 9(5):489-494.
[23] YANG D. Chaos Control for Numerical Instability of First Order Reliability Method[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(10):3131-3141.
[24] DU X, HU Z. First Order Reliability Method with Truncated Random Variables[J]. Journal of Mechanical Design, 2012, 134(9):091005.
[25] CHAKRABORTY S, CHOWDHURY R. A Semi-analytical Framework for Structural Reliability Analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 289:475-497.
[26] KESHTEGAR B. Chaotic Conjugate Stability Transformation Method for Structural Reliability Analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 310:866-885.
[27] MENG Z, LI G, YANG D, et al. A New Directional Stability Transformation Method of Chaos Control for First Order Reliability Analysis[J]. Structural and Multidisciplinary Optimization, 2016, 55(2):601-612.
[28] WU Y T, MILLWATER H, CRUSE T. Advanced Probabilistic Structural Analysis Method for Implicit Performance Functions[J]. AIAA Journal, 1990, 28(9):1663-1669.
[29] YANG D, YI P. Chaos Control of Performance Measure Approach for Evaluation of Probabilistic Constraints[J]. Structural and Multidisciplinary Optimization, 2009, 38(1):83-92.
[30] MENG Z, LI G, WANG B P, et al. A Hybrid Chaos Control Approach of the Performance Measure Functions for Reliability-based Design Optimization[J]. Computers & Structures, 2015, 146:32-43.
[31] HAO P, WANG Y, LIU C, et al. A Novel Non-probabilistic Reliability-based Design Optimization Algorithm Using Enhanced Chaos Control Method[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 318:572-593.
[32] LI Weiji, YANG Li. An Effective Optimization Procedure Based on Structural Reliability[J]. Computers & Structures, 1994, 52(5):1061-1067.
[33] CHANDU S V, GRANDHI R V. General Purpose Procedure for Reliability Based Structural Optimization under Parametric Uncertainties[J]. Advances in Engineering Software, 1995, 23(1):7-14.
[34] AGARWAL H, RENAUD J E. New Decoupled Framework for Reliability-based Design Optimization[J]. AIAA Journal, 2006, 44(7):1524-1531.
[35] M NGUEZ R, CASTILLO E. Reliability-based Optimization in Engineering Using Decomposition Techniques and FORMS[J]. Structural Safety, 2009, 31(3):214-223.
NGUEZ R, CASTILLO E. Reliability-based Optimization in Engineering Using Decomposition Techniques and FORMS[J]. Structural Safety, 2009, 31(3):214-223.
[36] CHAN K Y, SKERLOS S J, PAPALAMBROS P. An Adaptive Sequential Linear Programming Algorithm for Optimal Design Problems with Probabilistic Constraints[J]. Journal of Mechanical Design, 2007, 129(2):140-149.
[37] 程耿东, 许林. 基于可靠度的结构优化的序列近似规划算法[J]. 计算力学学报, 2006, 23(6):641-646.
CHENG Gengdong, XU Lin. Sequential Approximate Programming Approach to Reliability Based Structural Optimization[J].Chinese Journal of Computational Mechanics,2006, 23(6):641-646.
[38] CHENG G, XU L, JIANG L. A Sequential Approximate Programming Strategy for Reliability-based Structural Optimization[J]. Computers & Structures, 2006, 84(21):1353-1367.
[39] YI P, CHENG G, JIANG L. A Sequential Approximate Programming Strategy for Performance-measure-based Probabilistic Structural Design Optimization[J]. Structural Safety, 2008, 30(2):91-109.
[40] MENG Z, ZHOU H, HU H, et al. Enhanced Sequential Approximate Programming Using Second Order Reliability Method for Accurate and Efficient Structural Reliability-based Design Optimization[J]. Applied Mathematical Modelling, 2018, 62:562-579.
[41] ZOU T, MAHADEVAN S. A Direct Decoupling Approach for Efficient Reliability-based Design Optimization[J]. Structural and Multidisciplinary Optimization, 2006, 31(3):190-200.
[42] WU Y T. Efficient Probabilistic Design by Converting Reliability Constraints to Approximately Equivalent Deterministic Constraints[J]. Journal of Intergrated Design and Process Sciences, 1998, 2(4):13-21.
[43] WU Y T, SHIN Y, SUES R, et al. Safety-factor Based Approach for Probability-based Design Optimization[C]∥Proceedings of the 19th AIAA Applied Aerodynamics Conference. Seattle, 2001.
[44] QU X, HAFTKA R T. Reliability-based Design Optimization Using Probabilistic Sufficiency Factor[J]. Structural and Multidisciplinary Optimization, 2004, 27(5):314-325.
[45] DU X, CHEN W. Sequential Optimization and Reliability Assessment Method for Efficient Probabilistic Design[J]. Journal of Mechanical Design, 2004, 126(2):225-233.
[46] YANG R, GU L. Experience with Approximate Reliability-based Optimization Methods[J]. Structural and Multidisciplinary Optimization, 2004, 26(1/2):152-159.
[47] AOUES Y, CHATEAUNEUF A. Benchmark Study of Numerical Methods for Reliability-based Design Optimization[J]. Structural and Multidisciplinary Optimization, 2010, 41(2):277-294.
[48] CHO T M, LEE B C. Reliability-based Design Optimization Using Convex Linearization and Sequential Optimization and Reliability Assessment Method[J]. Structural Safety, 2011, 33(1):42-50.
[49] DU X. Saddlepoint Approximation for Sequential Optimization and Reliability Analysis[J]. Journal of Mechanical Design, 2008, 130(1):011011.
[50] CHEN Z, QIU H, GAO L, et al. An Adaptive Decoupling Approach for Reliability-based Design Optimization[J]. Computers & Structures, 2013, 117:58-66.
[51] YI P, ZHU Z, GONG J. An Approximate Sequential Optimization and Reliability Assessment Method for Reliability-based Design Optimization[J]. Structural and Multidisciplinary Optimization, 2016, 54(6):1367-1378.
[52] CHEN Z, QIU H, GAO L, et al. An Optimal Shifting Vector Approach for Efficient Probabilistic Design[J]. Structural and Multidisciplinary Optimization, 2013, 47(6):905-920.
[53] HUANG Z L, JIANG C, ZHOU Y S, et al. An Incremental Shifting Vector Approach for Reliability-based Design Optimization[J]. Structural and Multidisciplinary Optimization, 2015, 53(3):523-543.
[54] DU X, GUO J, BEERAM H. Sequential Optimization and Reliability Assessment for Multidisciplinary Systems Design[J]. Structural and Multidisciplinary Optimization, 2008, 35(2):117-130.
[55] ZHANG X, HUANG H Z. Sequential Optimization and Reliability Assessment for Multidisciplinary Design Optimization under Aleatory and Epistemic Uncertainties[J]. Structural and Multidisciplinary Optimization, 2009, 40(1):165-175.
[56] YIN X, CHEN W. Enhanced Sequential Optimization and Reliability Assessment Method for Probabilistic Optimization with Varying Design Variance[J]. Structures and Infrastructure Engineering, 2006, 2(3/4):261-275.
[57] LI Y, JIANG P, GAO L, et al. Sequential Optimisation and Reliability Assessment for Multidisciplinary Design Optimisation under Hybrid Uncertainty of Randomness and Fuzziness[J]. Journal of Engineering Design, 2013, 24(5):363-382.
[58] WANG L, XIONG C, HU J, et al. Sequential Multidisciplinary Design Optimization and Reliability Analysis under Interval Uncertainty[J]. Aerospace Science and Technology, 2018, 80:508-519.
[59] LI F, LIU J, WEN G, et al. Extending SORA Method for Reliability-based Design Optimization Using Probability and Convex Set Mixed Models[J]. Structural and Multidisciplinary Optimization, 2019, 59(4):1163-1179.
[60] TORII A J, LOPEZ R H, F. MIGUEL L F. A General RBDO Decoupling Approach for Different Reliability Analysis Methods[J]. Structural and Multidisciplinary Optimization, 2016, 54(2):317-332.
[61] CHEN Z, WU Z, LI X, et al. A Multiple-design-point Approach for Reliability-based Design Optimization[J]. Engineering Optimization, 2019, 51(5):875-895.
[62] GOSWAMI S, CHAKRABORTY S, CHOW-DHURY R, et al. Threshold Shift Method for Reliability-based Design Optimization[J]. Structural and Multidisciplinary Optimization, 2019, 60(5):2053-2072.
[63] HAO P, WANG Y, MA R, et al. A New Reliability-based Design Optimization Framework Using Isogeometric Analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 345:476-501.
[64] MADSEN H, HANSEN P F. A Comparison of Some Algorithms for Reliability Based Structural Optimization and Sensitivity Analysis[M]∥Reliability and Optimization of Structural Systems’ 91. Berlin:Springer, 1992:443-451.
[65] KUSCHEL N, RACKWITZ R. Two Basic Problems in Reliability-based Structural Optimization[J]. Mathematical Methods of Operations Research, 1997, 46(3):309-333.
[66] KUSCHEL N, RACKWITZ R. Optimal Design under Time-variant Reliability Constraints[J]. Structural Safety, 2000, 22(2):113-127.
[67] AGARWAL H, MOZUMDER C K, RENAUD J E, et al. An Inverse-measure-based Unilevel Architecture for Reliability-based Design Optimization[J]. Structural and Multidisciplinary Optimization, 2007, 33(3):217-227.
[68] CHEN X, HASSELMAN T, NEILL D, et al. Reliability Based Structural Design Optimization for Practical Applications[C]∥Proceedings of the 38th Structures, Structural Dynamics, and Materials Conference. Kissimmee, Florida, 1997:2724-2732.
[69] LIANG J, MOURELATOS Z P, TU J. A Single-Loop Method for Reliability-Based Design Optimization[C]∥ASME 2004 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Salt Lake City, Utah, 2004:419-430.
[70] LIANG J, MOURELATOS Z P, NIKOLAIDIS E. A Single-loop Approach for System Reliability-Based Design Optimization[J]. Journal of Mechanical Design, 2007, 129(12):1215-1224.
[71] MENG Z, KESHTEGAR B. Adaptive Conjugate Single-loop Method for Efficient Reliability-based Design and Topology Optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 344:95-119.
[72] JEONG S B, PARK G J. Single Loop Single Vector Approach Using the Conjugate Gradient in Reliability Based Design Optimization[J]. Structural and Multidisciplinary Optimization, 2016, 55(4):1329-1344.
[73] JIANG C, QIU H, GAO L, et al. An Adaptive Hybrid Single-loop Method for Reliability-based Design Optimization Using Iterative Control Strategy[J]. Structural and Multidisciplinary Optimization, 2017, 56(6):1271-1286.
[74] KESHTEGAR B, HAO P. Enhanced Single-loop Method for Efficient Reliability-based Design Optimization with Complex Constraints[J]. Structural and Multidisciplinary Optimization, 2018, 57(4):1731-1747.
[75] MENG Z, YANG D, ZHOU H, et al. Convergence Control of Single Loop Approach for Reliability-based Design Optimization[J]. Structural and Multidisciplinary Optimization, 2018, 57(3):1079-1091.
[76] LI F, WU T, BADIRU A, et al. A Single-loop Deterministic Method for Reliability-based Design Optimization[J]. Engineering Optimization, 2013, 45(4):435-458.
[77] JIANG C, QIU H, LI X, et al. Iterative Reliable Design Space Approach for Efficient Reliability-based Design Optimization[J]. Engineering with Computers, 2020, 36(1):151-169.
[78] 韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11):3197-3225.
HAN Zhonghua. Kriging Surrogate Model and Its Application to Design Optimization: a Review of Recent Progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11):3197-3225.
[79] EDWARDS J R. Alternatives to Difference Scores:Polynomial Regression and Response Surface Methodology[M]∥DRASGOW F, SCHMITT N eds. Measuring and Analyzing Behavior in Organizations:Advances in Measurement and Data Analysis.San Francisco:Jossey-Bass Inc., 2002:350-400.
[80] SACKS J, WELCH W J, MITCHELL T J, et al. Design and Analysis of Computer Experiments[J]. Statistical Science, 1989, 4(4):409-423.
[81] YAO X, LIU Y. A New Evolutionary System for Evolving Artificial Neural Networks[J]. IEEE Transactions on Neural Networks, 1997, 8(3):694-713.
[82] SMOLA A J, SCHÖLKOPF B. A Tutorial on Support Vector Regression[J]. Statistics and Computing, 2004, 14(3):199-222.
[83] XIU D, KARNIADAKIS G E. The Wiener-Askey Polynomial Chaos for Stochastic Differential Equations[J]. SIAM Journal on Scientific Computing, 2002, 24(2):619-644.
[84] BICHON B J, ELDRED M S, SWILER L P, et al. Efficient Global Reliability Analysis for Nonlinear Implicit Performance Functions[J]. AIAA Journal, 2008, 46(10):2459-2468.
[85] ECHARD B, GAYTON N, LEMAIRE M. AK-MCS:an Active Learning Reliability Method Combining Kriging and Monte Carlo Simulation[J]. Structural Safety, 2011, 33(2):145-154.
[86] DUBOURG V, SUDRET B, DEHEEGER F. Metamodel-based Importance Sampling for Structural Reliability Analysis[J]. Probabilistic Engineering Mechanics, 2013, 33:47-57.
[87] XIAO N C, ZUO M J, ZHOU C. A New Adaptive Sequential Sampling Method to Construct Surrogate Models for Efficient Reliability Analysis[J]. Reliability Engineering & System Safety, 2018, 169:330-338.
[88] ZHANG J, XIAO M, GAO L, et al. A Combined Projection-outline-based Active Learning Kriging and Adaptive Importance Sampling Method for Hybrid Reliability Analysis with Small Failure Probabilities[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 344:13-33.
[89] ZHANG J, XIAO M, GAO L, et al. A Novel Projection Outline Based Active Learning Method and Its Combination with Kriging Metamodel for Hybrid Reliability Analysis with Random and Interval Variables[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 341:32-52.
[90] XIAO N C, YUAN K, ZHOU C. Adaptive Kriging-based Efficient Reliability Method for Structural Systems with Multiple Failure Modes and Mixed Variables[J]. Computer Methods in Applied Mechanics and Engineering, 2020,359:112649.
[91] JIANG C, QIU H, YANG Z, et al. A General Failure-pursuing Sampling Framework for Surrogate-based Reliability Analysis[J]. Reliability Engineering & System Safety, 2019, 183:47-59.
[92] HURTADO J E. An Examination of Methods for Approximating Implicit Limit State Functions from the Viewpoint of Statistical Learning Theory[J]. Structural Safety, 2004, 26(3):271-293.
[93] BASUDHAR A, MISSOUM S, SANCHEZ A H. Limit State Function Identification Using Support Vector Machines for Discontinuous Responses and Disjoint Failure Domains[J]. Probabilistic Engineering Mechanics, 2008, 23(1):1-11.
[94] PAPADOPOULOS V, GIOVANIS D G, LAGAROS N D, et al. Accelerated Subset Simulation with Neural Networks for Reliability Analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 223/224:70-80.
[95] KAYMAZ I, MCMAHON C A. A Response Surface Method Based on Weighted Regression for Structural Reliability Analysis[J]. Probabilistic Engineering Mechanics, 2005, 20(1):11-17.
[96] FOSCHI R, LI H, ZHANG J. Reliability and Performance-based Design:a Computational Approach and Applications[J]. Structural Safety, 2002, 24(2/4):205-218.
[97] LEHK D, SLOWIK O, NOVáK D. Reliability-based Design:Artificial Neural Networks and Double-loop Reliability-based Optimization Approaches[J]. Advances in Engineering Software, 2018, 117:123-135.
D, SLOWIK O, NOVáK D. Reliability-based Design:Artificial Neural Networks and Double-loop Reliability-based Optimization Approaches[J]. Advances in Engineering Software, 2018, 117:123-135.
[98] KIM C, CHOI K K. Reliability-based Design Optimization Using Response Surface Method with Prediction Interval Estimation[J]. Journal of Mechanical Design, 2008, 130(12):121401.
[99] AGARWAL H, RENAUD J. Reliability Based Design Optimization Using Response Surfaces in Application to Multidisciplinary Systems[J]. Engineering Optimization, 2004, 36(3):291-311.
[100] PAPADRAKAKIS M, LAGAROS N D, PLEVRIS V. Design Optimization of Steel Structures Considering Uncertainties[J]. Engineering Structures, 2005, 27(9):1408-1418.
[101] LEE I, CHOI K K, ZHAO L. Sampling-based RBDO Using the Stochastic Sensitivity Analysis and Dynamic Kriging Method[J]. Structural and Multidisciplinary Optimization, 2011, 44(3):299-317.
[102] SHI L, LIN S-P. A New RBDO Method Using Adaptive Response Surface and First-order Score Function for Crashworthiness Design[J]. Reliability Engineering & System Safety, 2016, 156:125-133.
[103] MCKAY M D, BECKMAN R J, CONOVER W J. Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code[J]. Technometrics, 1979, 21(2):239-245.
[104] CURRIN C, MITCHELL T, MORRIS M, et al. Bayesian Prediction of Deterministic Functions, with Applications to the Design and Analysis of Computer Experiments[J]. Journal of the American Statistical Association, 1991, 86(416):953-963.
[105] LEE T H, JUNG J J. A Sampling Technique Enhancing Accuracy and Efficiency of Metamodel-based RBDO:Constraint Boundary Sampling[J]. Computers & Structures, 2008, 86(13/14):1463-1476.
[106] BICHON B J, ELDRED M S, MAHADEVAN S, et al. Efficient Global Surrogate Modeling for Reliability-Based Design Optimization[J]. Journal of Mechanical Design, 2013, 135(1):011009.
[107] JONES D R, SCHONLAU M, WELCH W J. Efficient Global Optimization of Expensive Black-box Functions[J]. Journal of Global Optimization, 1998, 13(4):455-492.
[108] PAPADRAKAKIS M, LAGAROS N D. Reliability-based Structural Optimization Using Neural Networks and Monte Carlo Simulation[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191(32):3491-3507.
[109] YOUN B D, CHOI K K. A New Response Surface Methodology for Reliability-based Design Optimization[J]. Computers & Structures, 2004, 82(2):241-256.
[110] KANG S-C, KOH H-M, CHOO J F. An Efficient Response Surface Method Using Moving Least Squares Approximation for Structural Reliability Analysis[J]. Probabilistic Engineering Mechanics, 2010, 25(4):365-371.
[111] SONG C Y, LEE J. Reliability-based Design Optimization of Knuckle Component Using Conservative Method of Moving Least Squares Meta-models[J]. Probabilistic Engineering Mechanics, 2011, 26(2):364-379.
[112] ZHUANG X, PAN R. A Sequential Sampling Strategy to Improve Reliability-based Design Optimization with Implicit Constraint Functions[J]. Journal of Mechanical Design, 2012, 134(2):021002.
[113] WANG Z, WANG P. A Maximum Confidence Enhancement Based Sequential Sampling Scheme for Simulation-based Design[J]. Journal of Mechanical Design, 2014, 136(2):021006.
[114] CHEN Z, QIU H, GAO L, et al. A Local Adaptive Sampling Method for Reliability-based Design Optimization Using Kriging Model[J]. Structural and Multidisciplinary Optimization, 2014, 49(3):401-416.
[115] LI X, QIU H, CHEN Z, et al. A Local Kriging Approximation Method Using MPP for Reliability-based Design Optimization[J]. Computers & Structures, 2016, 162:102-115.
[116] GAO T, LI J. A Derivative-free Trust-region Algorithm for Reliability-based Optimization[J]. Structural and Multidisciplinary Optimization, 2017, 55(4):1535-1539.
[117] GASPAR B, TEIXEIRA A, SOARES C G. Adaptive Surrogate Model with Active Refinement Combining Kriging and a Trust Region Method[J]. Reliability Engineering & System Safety, 2017, 165:277-291.
[118] ZHANG J, TAFLANIDIS A, MEDINA J. Sequential Approximate Optimization for Design under Uncertainty Problems Utilizing Kriging Metamodeling in Augmented Input Space[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 315:369-395.
[119] CHEN Z, PENG S, LI X, et al. An Important Boundary Sampling Method for Reliability-based Design Optimization Using Kriging Model[J]. Structural and Multidisciplinary Optimization, 2014, 52(1):55-70.
[120] MENG Z, ZHANG D, LIU Z, et al. An Adaptive Directional Boundary Sampling Method for Efficient Reliability-based Design Optimization[J]. Journal of Mechanical Design, 2018, 140(12):121406.
[121] BASUDHAR A, MISSOUM S. Adaptive Explicit Decision Functions for Probabilistic Design and Optimization Using Support Vector Machines[J]. Computers & Structures, 2008, 86(19/20):1904-1917.
[122] BASUDHAR A, MISSOUM S. An Improved Adaptive Sampling Scheme for the Construction of Explicit Boundaries[J]. Structural and Multidisciplinary Optimization, 2010, 42(4):517-529.
[123] BOROSON E, MISSOUM S. Stochastic Optimization of Nonlinear Energy Sinks[J]. Structural and Multidisciplinary Optimization, 2017, 55(2):633-646.
[124] LIU X, WU Y, WANG B, et al. An Adaptive Local Range Sampling Method for Reliability-based Design Optimization Using Support Vector Machine and Kriging Model[J]. Structural and Multidisciplinary Optimization, 2016, 55(6):2285-2304.
[125] LIU X, WU Y, WANG B, et al. An Efficient RBDO Process Using Adaptive Initial Point Updating Method Based on Sigmoid Function[J]. Structural and Multidisciplinary Optimization, 2018, 58(6):2583-2599.
[126] SONG H, CHOI K K, LEE I, et al. Adaptive Virtual Support Vector Machine for Reliability Analysis of High-dimensional Problems[J]. Structural and Multidisciplinary Optimization, 2012, 47(4):479-491.
[127] CHO H, BAE S, CHOI K K, et al. An Efficient Variable Screening Method for Effective Surrogate Models for Reliability-based Design Optimization[J]. Structural and Multidisciplinary Optimization, 2014, 50(5):717-738.
[128] CHO H, CHOI K K, LEE I, et al. Design Sensitivity Method for Sampling-based RBDO with Varying Standard Deviation[J]. Journal of Mechanical Design, 2015, 138(1):011405.
[129] LI M, SADOUGHI M, HU C, et al. High-dimensional Reliability-based Design Optimization Involving Highly Nonlinear Constraints and Computationally Expensive Simulations[J]. Journal of Mechanical Design, 2019, 141(5):051402.
[130] YANG X, LIU Y, MI C, et al. System Reliability Analysis through Active Learning Kriging Model with Truncated Candidate Region[J]. Reliability Engineering & System Safety, 2018, 169:235-241.
[131] RICE S O. Mathematical Analysis of Random Noise[J]. Bell System Technical Journal, 1945, 24(1):46-156.
[132] LUTES L D, SARKANI S. Random Vibrations:Analysis of Structural and Mechanical Systems[M]. Burlington:Elsevier Butterworth-Heinemann, 2004.
[133] ANDRIEU-RENAUD C, SUDRET B, LEMAIRE M. The PHI2 Method:a Way to Compute Time-variant Reliability[J]. Reliability Engineering & System Safety, 2004, 84(1):75-86.
[134] SUDRET B. Analytical Derivation of the Outcrossing Rate in Time-variant Reliability Problems[J]. Structure and Infrastructure Engineering, 2008, 4(5):353-362.
[135] HU Z, DU X. Time-dependent Reliability Analysis with Joint Upcrossing Rates[J]. Structural and Multidisciplinary Optimization, 2013, 48(5):893-907.
[136] SINGH A, MOURELATOS Z P, LI J. Design for Lifecycle Cost Using Time-dependent Reliability[J]. Journal of Mechanical Design, 2010, 132(9):091008.
[137] ANG A H-S, TANG W H. Probability Concepts in Engineering Planning and Design, Vol. 2:Decision, Risk, and Reliability[M]. New York:John Wiley & Sons, 1984.
[138] CHEN J B, LI J. The Extreme Value Distribution and Dynamic Reliability Analysis of Nonlinear Structures with Uncertain Parameters[J]. Structural Safety, 2007, 29(2):77-93.
[139] van NOORTWIJK J M, van der WEIDE J A, KALLEN M J, et al. Gamma Processes and Peaks-over-threshold Distributions for Time-dependent Reliability[J]. Reliability Engineering & System Safety, 2007, 92(12):1651-1658.
[140] PAN Z, BALAKRISHNAN N. Reliability Modeling of Degradation of Products with Multiple Performance Characteristics Based on Gamma Processes[J]. Reliability Engineering & System Safety, 2011, 96(8):949-957.
[141] GNEDENKO B V, BELYAYEV Y K, SOLOVYEV A D. Mathematical Methods of Reliability Theory[M]. New York:Academic Press, 2014.
[142] LI J, MOURELATOS Z, SINGH A. Optimal Preventive Maintenance Schedule Based on Lifecycle Cost and Time-dependent Reliability[J]. SAE International Journal of Materials and Manufacturing, 2012, 5(1):87-95.
[143] HU Z, DU X. Reliability-based Design Optimization under Stationary Stochastic Process Loads[J]. Engineering Optimization, 2016, 48(8):1296-1312.
[144] JIANG C, FANG T, WANG Z X, et al. A General Solution Framework for Time-variant Reliability Based Design Optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 323:330-352.
[145] FANG T, JIANG C, HUANG Z, et al. Time-Variant Reliability-based Design Optimization Using an Equivalent Most Probable Point[J]. IEEE Transactions on Reliability, 2019, 68(1):175-186.
[146] HUANG Z L, JIANG C, LI X M, et al. A Single-loop Approach for Time-variant Reliability-Based Design Optimization[J]. IEEE Transactions on Reliability, 2017, 66(3):651-661.
[147] YU S, WANG Z. A General Decoupling Approach for Time- and Space-variant System Reliability-based Design Optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 357:112608.
[148] ZHANG D, HAN X, JIANG C, et al. Time-dependent Reliability Analysis through Response Surface Method[J]. Journal of Mechanical Design, 2017, 139(4):041404.
[149] JIANG C, WANG D, QIU H, et al. An Active Failure-pursuing Kriging Modeling Method for Time-dependent Reliability Analysis[J]. Mechanical Systems and Signal Processing, 2019, 129:112-129.
[150] YU S, WANG Z, ZHANG K. Sequential Time-dependent Reliability Analysis for the Lower Extremity Exoskeleton under Uncertainty[J]. Reliability Engineering & System Safety, 2018, 170:45-52.
[151] WANG Z, WANG P. A Nested Extreme Response Surface Approach for Time-Dependent Reliability-based Design Optimization[J]. Journal of Mechanical Design, 2012, 134(12):121007.
[152] WANG Z, CHEN W. Confidence-based Adaptive Extreme Response Surface for Time-variant Reliability Analysis under Random Excitation[J]. Structural Safety, 2017, 64:76-86.
[153] HU Z, DU X. Mixed Efficient Global Optimization for Time-dependent Reliability Analysis[J]. Journal of Mechanical Design, 2015, 137(5):051401.
[154] WANG Z, CHEN W. Time-variant Reliability Assessment through Equivalent Stochastic Process Transformation[J]. Reliability Engineering & System Safety, 2016, 152:166-175.
[155] HU Z, MAHADEVAN S. A Single-loop Kriging Surrogate Modeling for Time-dependent Reliability Analysis[J]. Journal of Mechanical Design, 2016, 138(6):061406.
[156] JIANG C, QIU H, GAO L, et al. Real-time Estimation Error-guided Active Learning Kriging Method for Time-dependent Reliability Analysis[J]. Applied Mathematical Modelling, 2020, 77:82-98.
[157] HU Z, MAHADEVAN S. Time-dependent Reliability Analysis Using a Vine-ARMA Load Model[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part B:Mechanical Engineering, 2017, 3(1):011007.
[158] LING C, LU Z, ZHU X. Efficient Methods by Active Learning Kriging Coupled with Variance Reduction Based Sampling Methods for Time-dependent Failure Probability[J]. Reliability Engineering & System Safety, 2019, 188:23-35.
[159] CHENG K, LU Z. Time-variant Reliability Analysis Based on High Dimensional Model Representation[J]. Reliability Engineering & System Safety, 2019, 188:310-319.
[160] LI H S, WANG T, YUAN J Y, et al. A Sampling-based Method for High-dimensional Time-variant Reliability Analysis[J]. Mechanical Systems and Signal Processing, 2019, 126:505-520.
[161] HU Z, ZHU Z, DU X. Time-Dependent System Reliability Analysis for Bivariate Responses[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part B:Mechanical Engineering, 2017, 4(3):031002.
[162] LI J, CHEN J. Solving Time-variant Reliability-based Design Optimization by PSO-t-IRS:a Methodology Incorporating a Particle Swarm Optimization Algorithm and an Enhanced Instantaneous Response Surface[J]. Reliability Engineering & System Safety, 2019, 191:106580.
[163] HAWCHAR L, EL SOUEIDY C P, SCHOEFS F. Global Kriging Surrogate Modeling for General Time-variant Reliability-based Design Optimization Problems[J]. Structural and Multidisciplinary Optimization, 2018, 58(3):955-968.
[164] LI M, BAI G, WANG Z. Time-variant Reliability-based Design Optimization Using Sequential Kriging Modeling[J]. Structural and Multidisciplinary Optimization, 2018, 58(3):1051-1065.
[165] WANG Z, CHENG X, LIU J. Time-dependent Concurrent Reliability-based Design Optimization Integrating Experiment-based Model Validation[J]. Structural and Multidisciplinary Optimization, 2018, 57(4):1523-1531.
[166] YU S, WANG Z, WANG Z. Time-dependent Reliability-based Robust Design Optimization Using Evolutionary Algorithm[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part B:Mechanical Engineering, 2019, 5(2):020911.
[167] YOUN B D. Adaptive-loop Method for Non-deterministic Design Optimization[J]. Proceedings of the Institution of Mechanical Engineers, Part O:Journal of Risk and Reliability, 2007, 221(2):107-116.
[168] LIM J, LEE B. A Semi-single-loop Method Using Approximation of Most Probable Point for Reliability-based Design Optimization[J]. Structural and Multidisciplinary Optimization, 2016, 53(4):745-757.
[169] CHO H, CHOI K K, GAUL N J, et al. Conservative Reliability-based Design Optimization Method with Insufficient Input Data[J]. Structural and Multidisciplinary Optimization, 2016, 54(6):1609-1630.
[170] MOON M-Y, CHOI K, GAUL N, et al. Treating Epistemic Uncertainty Using Bootstrapping Selection of Input Distribution Model for Confidence-based Reliability Assessment[J]. Journal of Mechanical Design, 2019, 141(3):031402.
[171] MOON M-Y, CHO H, CHOI K, et al. Confidence-based Reliability Assessment Considering Limited Numbers of Both Input and Output Test Data[J]. Structural and Multidisciplinary Optimization, 2018, 57(5):2027-2043.
[172] XI Z. Model-Based Reliability Analysis with Both Model Uncertainty and Parameter Uncertainty[J]. Journal of Mechanical Design, 2019, 141(5):051404.
