0 引言
锂离子电池作为电动汽车的动力提供源，具有环保无污染、不消耗石油资源的优点，其中的磷酸铁锂电池具有能量密度大、自放电率低、无记忆效应、绿色无污染的优势，被越来越多地应用到汽车行业和电池组中[1]。锂电池失效会引起严重后果，如电池过充过放时可能导致电池过热而引起自燃，因此电池管理系统的发展越来越受到重视[2]。在电池管理系统中，电池荷电状态(state of charge，SOC)管理是主要的模块之一。SOC通常被定义为电池剩余可用容量与电池标称容量的比值[3]。SOC受锂电池内部化学反应和锂离子传输的影响，处于非线性动态过程，难以被准确计算，只能通过电池的一些外部参数来估计得出。SOC反映了电池的剩余电量，可以避免过充过放，减少锂离子的消耗，延长使用寿命。SOC估计值越准确，电池管理系统决策越高效，如减少电动汽车因电量不准导致的锂电池充电次数，在不同路况下提供合适的功率以减少不必要的能量消耗等[4]。
估计SOC值的方法很多，如安时法、开路电压(open circuit voltage，OCV)法、神经网络法、卡尔曼滤波算法、扩展卡尔曼滤波(extended Kalman filter，EKF)算法等[5-7]。安时法作为估计SOC值的标准方法，简单方便，但其初始值的不确定导致迭代误差过大。开路电压法需要电池长时间静置以消除迟滞效应，实用性不高。神经网络法不需要掌握电池的内部结构，但依赖训练数据的准确性和学习方法。卡尔曼滤波法在电池的电路模型基础上，把电池内部的变量转化为具体物理意义的实际参数来估计SOC值，在SOC初始值不准确的情况下也可以得到准确值，其缺点在于依赖电池模型的精确性，适用于线性系统。EKF法在非线性系统中的运用越来越广泛。ZHU等[8]建立了磷酸铁锂电池的2阶模型，结合EKF算法估计SOC值。LEE等[9]建立自调整的OCV-SOC函数，加上测量噪声，运用EKF法估计SOC值。LAI等[10]基于多模型辨识参数，结合安时法和EKF法来估计SOC值。
本文建立磷酸铁锂电池的等效电路模型，并分析模型参数与SOC的关系，提出估计SOC值的EKF方法，得出开路电压和模型参数与SOC的函数关系并验证模型的准确性，最后在北京公交车动态应力测试(Beijing bus dynamic stress test，BBDST)实际工况下仿真估计SOC值，并与标准的安时积分法得出的SOC结果进行比较。
1 等效电路模型与EKF原理
1.1 实验对象
本文选用的单体电池为天津力神电池股份有限公司生产的磷酸铁锂电池，型号为18650EC，主要参数如表1所示。
表1 锂电池型号参数
Tab.1 Parameters of Li-ion battery
直径×高度(mm×mm)额定容量(mA·h)充电截止电压(V)放电截止电压(V)标称电压(V)18×651 3003.62.83.2
1.2 建立电池模型
根据准确的电池模型，可以建立等效电路中可测参数(电流、电压等)与电池内部参数(SOC、电阻、电容)的关系。估计SOC值的模型有Thevenin模型、多阶阻容模型、通用非线性(general nonlinear，GNL)模型和新一代汽车合作伙伴关系(PNGV)模型等。其中，PNGV模型[11]具有确定的物理意义和表达过程，成为锂离子电池等效电路模型中使用较广泛的模型。PNGV模型如图1所示。其中，E、Cb分别为电池电压源、电池电容； Ub为由Cb产生的电压；UOCV为E和Ub构成的回路的开路电压；R0为欧姆内阻；RP、CP为电池的极化效应参数，分别表示电阻、电容；IL、UL分别为电流和端电压，规定电流充电方向为正，放电为负。
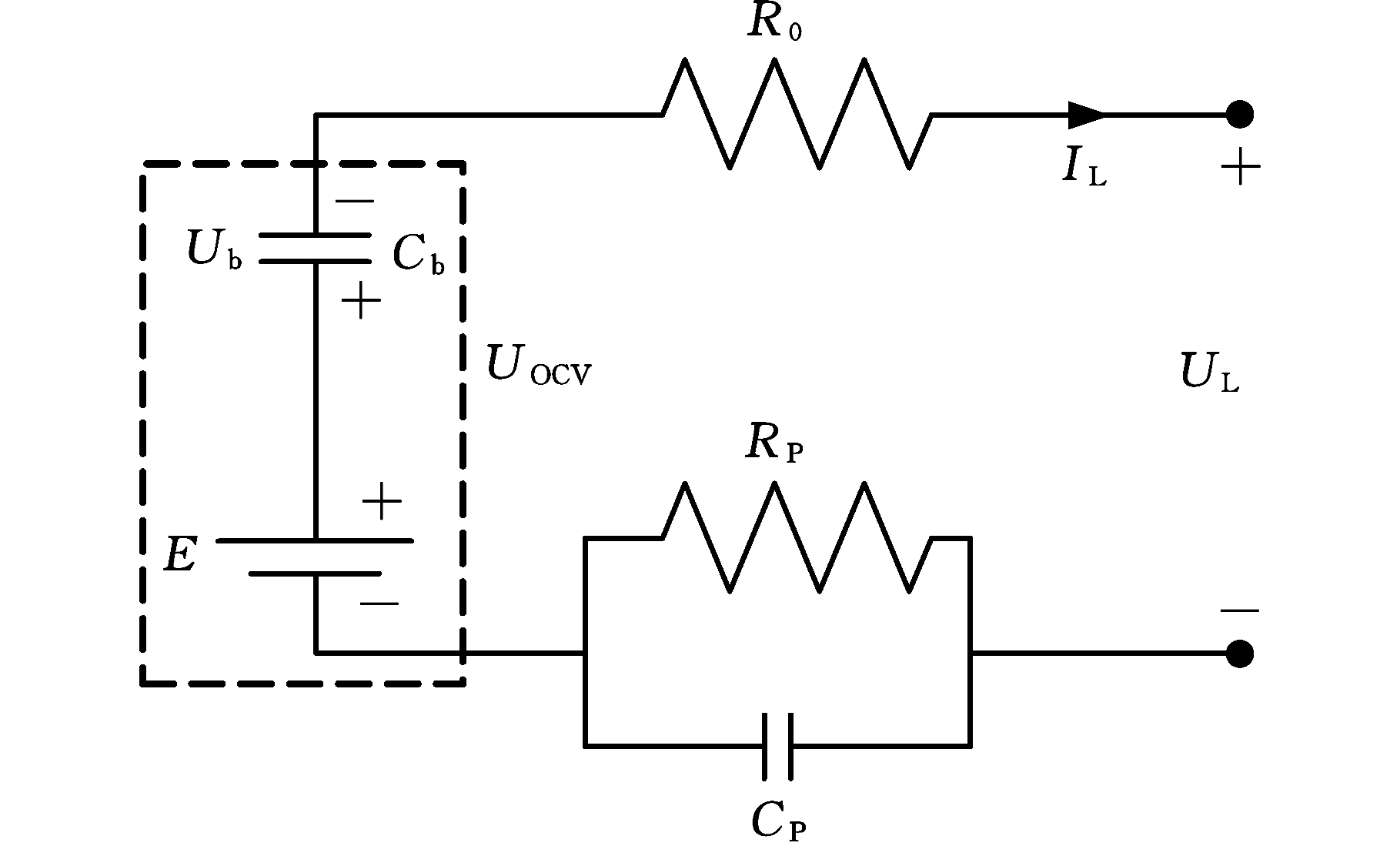
图1 PNGV模型[11]
Fig.1 PNGV model[11]
等效电路的数学方程式如下：
UL=UOCV-ILR0-UP
(1)
(2)
式中，UP为电池的极化效应参数，表示电压；τ为时间常数，τ=CPRP。
1.3 模型参数辨识
模型中电池内部的参数(UOCV、R0、RP、CP)均与SOC有着直接的函数关系。其中，OCV-SOC曲线由标准测试实验获取，极化效应的参数与SOC的关系可由混合脉冲功率特性测试(hybrid pulse power characterization，HPPC)辨识得出。
1.3.1 OCV-SOC曲线实验
在《Freedom Car 电池测试手册》中，详细说明了测试OCV的标准实验，包括电池的标准充放电和小电流充放电实验。其中充放电倍率(C)是指电流的大小，以本文为例，电池容量为1.3 A·h，1C就是容量除以1 h，即1C为1.3 A。
本文实验以0.02C电流充放电，采样时间为18 s，划分SOC区间为10 000份，记录电池的电流电压等数据。
OCV与SOC的曲线是估计SOC值的依据之一，其准确性直接影响SOC值的准确性。在处理离散的电池数据(SOC、电压)时，采用多项式插值、分段插值等方法，可以得到准确的函数表达式。WENG等[12]提出了统一的OCV模型来估计SOC，对OCV与SOC不同的函数关系进行误差分析。
1.3.2 HPPC测试
模型中的参数(R0、RP、CP)不能直接测量，故采用HPPC测试得出电流和电压的数据，依据电流和电压图形中的特征点，结合电路方程式，辨识出参数值。JIANG等[13]采用恒电流间歇滴定法(galvanostatic intermittent titration technique，GITT)和阻抗谱法分析磷酸铁锂电池，当电池SOC值处于0.1～0.9工作区间时，OCV-SOC曲线较为平缓，电池内部情况稳定；而在0～0.1和0.9～1区间时，OCV-SOC曲线较陡峭，OCV变化较大，电池性能差异较大。
本文实验在采用HPPC测试电池时，在边缘区间选取多个值，分别取SOC值为1、0.95、0.9、0.8、…、0.1。HPPC测试步骤如下：电池静置后以4 A电流脉冲放电，持续时间为15 s；静置120 s，电压出现回弹现象；采用脉冲充电，持续时间为15 s；静置120 s；记录电池电流电压的数据；在不同的SOC值处，循环重复测试步骤。
参数辨识的具体流程如下。
(1)脉冲放电时，欧姆内阻引起电压迅速下降：
R0=(U1-U2)/IL
(3)
(2)依据能量守恒定律，有
Cb=ΔQ/(U1-U5)
(4)
(3)脉冲放电结束后，电压U4缓慢上升至U5，对应RC电路的零输入响应。利用MATLAB中的curve fitting模块，结合实验数据，得出初始极化电压U0和τ参数值：
UP=U0exp(-t/τ)
(5)
(4)在15 s放电过程中，电压U2缓慢下降至U3，对应RC电路的零状态响应：
(6)
结合步骤(3)，得出CP。
式(3)～式(6)中，ΔQ为过程中放电电量；U1、U2、U3、U4、U5分别为电池脉冲测试前静置电压、放电瞬间电压、持续15 s后电压、放电结束后的电压和静置120 s后的电压。
1.4 EKF原理和状态空间方程
1.4.1 EKF原理
卡尔曼滤波器基于最小二乘法原理，在滤波器中引入状态空间方程，根据前一时刻的状态向量估计值和下一时刻的输出观测值，迭代出当前时刻的状态向量，同时更新误差协方差，并修正系数增益，逐渐修正状态向量，使结果趋近于真实值。扩展卡尔曼滤波(EKF)是在卡尔曼滤波的基础上，对非线性系统进行泰勒多项式展开，忽略高阶的误差，转化为线性的系统，进而运用卡尔曼滤波法进一步计算。
假设非线性离散状态空间模型如下：
(7)
式中，f(xk,uk)、h(xk,uk)分别为过程函数和观测函数，均为非线性函数；xk为状态向量；yk为观测向量；uk为输入向量；wk、vk分别为过程和测量高斯白噪声，两者互不相关，wk～(0,Qk),vk～(0,Rk);Qk、Rk分别为过程噪声和测量噪声的方差矩阵。
对非线性系统进行泰勒多项式展开，省去高阶部分，记
整理如下：
(8)
扩展卡尔曼滤波的步骤如下。
(1)设定状态向量和误差协方差的初始值：
(9)
(2)向前一步状态预测和误差协方差估计：
(10)
(3)卡尔曼滤波增益：
(11)
(4)更新下一时刻的状态向量和误差协方差矩阵：
(12)
式中，I为单位矩阵。
(5)重复循环步骤(1)～步骤(4)。
1.4.2 状态空间方程离散化
在PNGV模型中，建立的模型式(1)和式(2)是连续的，EKF原理处理的系统是离散的，因此需要对模型进行离散处理。整理式(1)和式(2)并代入到EKF系统中，展开数学表达式如下：
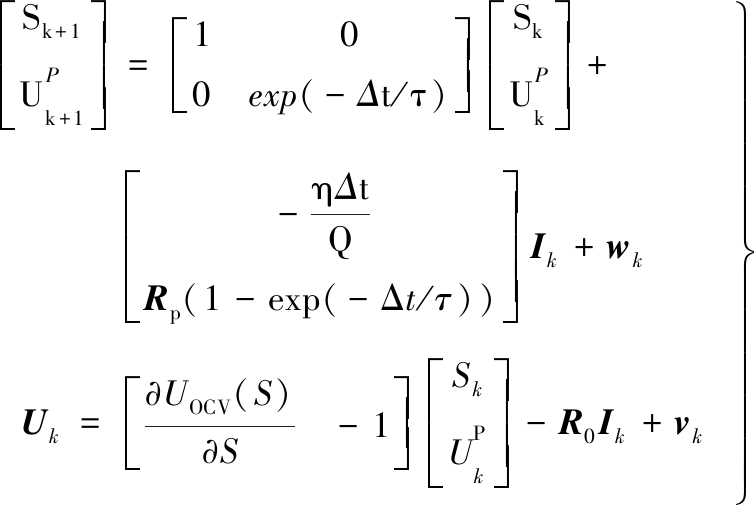
(13)
其中，状态向量
分别为k时刻的SOC值和极化电压；Ik为输入电流，即uk=Ik；观测向量为电池的端电压，即yk=Uk；Δt为采样时间，Δt=1 s；η为电池充放电库仑系数，η=1；Q为锂电池的额定容量。
2 模型验证与分析
2.1 OCV-SOC曲线关系
实验原始数据来自于课题组前期实验的充放电测试[14]。OCV-SOC曲线如图2所示，其中，平均电压为充电与放电过程中开路电压的平均值。
图2 OCV-SOC曲线
Fig.2 OCV-SOC curves
磷酸铁锂电池在充放电过程中存在滞回电压[15]的现象，充电和放电的平衡电势曲线并不完全重合。开路电压可以由充放电的平衡电压加权得到。在小电流充放电时，采集数据的间隔较小，欧姆内阻电压和极化效应较小且相反，充放电开路电压的系数为0.5，即
(14)
式中，
分别为充电平衡电压和放电平衡电压。
以SOC值为变量x，f(x)为开路电压与SOC函数，拟合方程为
f(x)=p1x6+p2x5+p3x4+p4x3+
p5x2+p6x+p7
(15)
拟合多项式系数取值如下：p1=-16.25,p2=63.3,p3=-94.94,p4=69.8,p5=-26.32,p6=4.908,p7=2.915。
2.2 HPPC测试
HPPC测试得到的图形包括电流和电压图，在不同SOC值处的图形趋势是一致的。以S=0.4为例，电流和电压如图3、图4所示。
图3 脉冲电流曲线
Fig.3 Pulse current curve
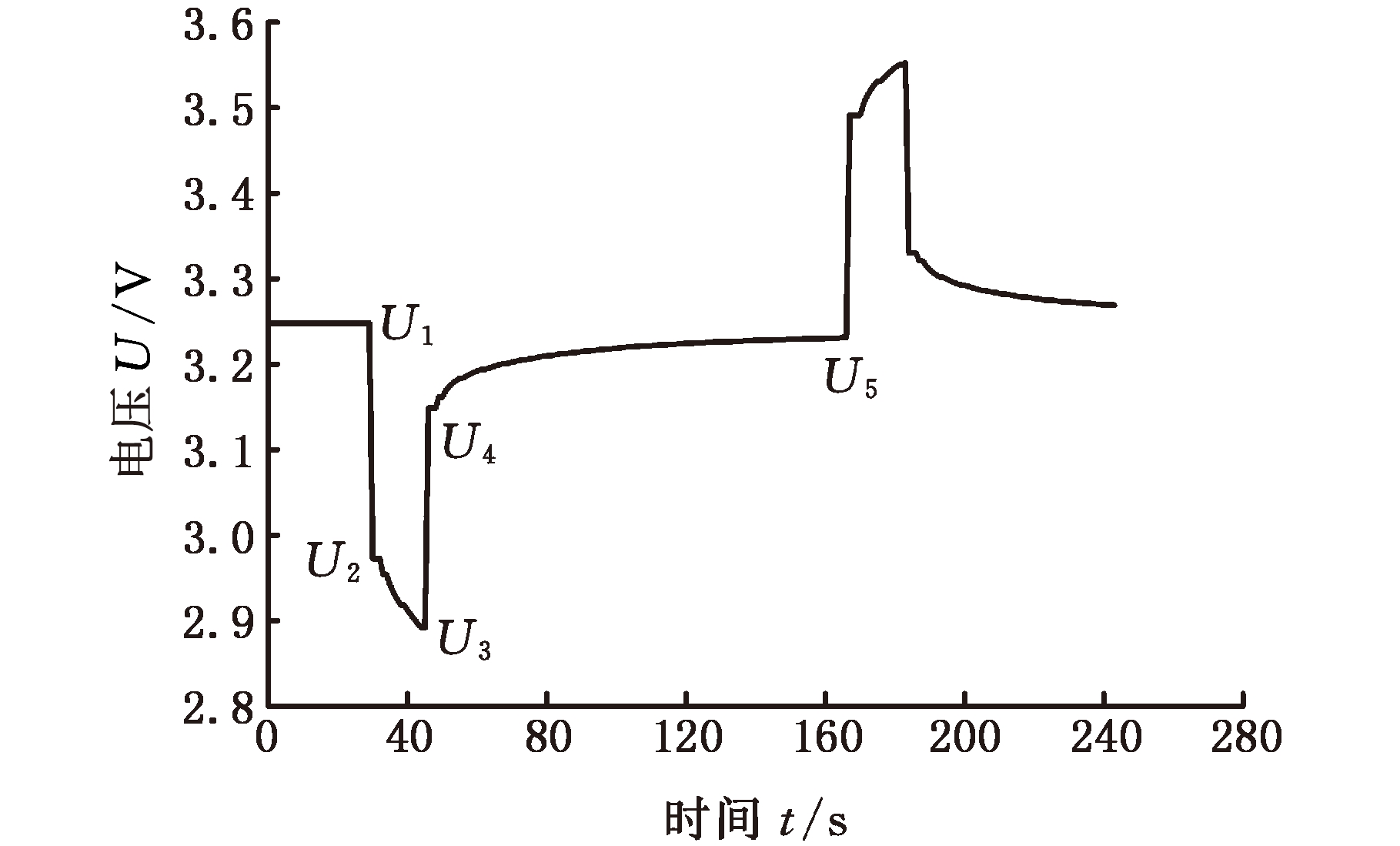
图4 脉冲电压曲线
Fig.4 Pulse voltage curve
根据图形的特性分析，在不同SOC值处结合辨识步骤，参数R0、RP、CP、τ取值如表2所示。
表2 PNGV模型辨识参数值
Tab.2 Identified parameters of PGNV model
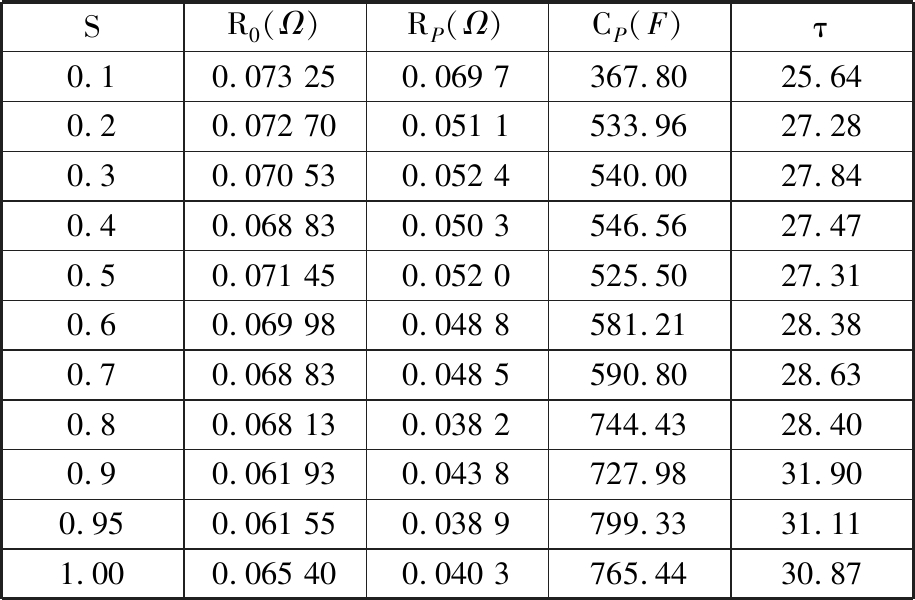
SR0(Ω)RP(Ω)CP(F)τ0.10.073 250.069 7367.8025.640.20.072 700.051 1533.9627.280.30.070 530.052 4540.0027.840.40.068 830.050 3546.5627.470.50.071 450.052 0525.5027.310.60.069 980.048 8581.2128.380.70.068 830.048 5590.8028.630.80.068 130.038 2744.4328.400.90.061 930.043 8727.9831.900.950.061 550.038 9799.3331.111.000.065 400.040 3765.4430.87
设SOC值为变量y，g(y)为参数与SOC值的拟合多项式函数。考虑到拟合曲线与离散数据的误差和相关性，设拟合方程为
g(y)=q1y6+q2y5+q3y4+q4y3+
q5y2+q6y+q7
(16)
拟合多项式的系数如表3所示。
表3 拟合多项式系数
Tab.3 Coefficients of fitted polynomials
R0RPCPq11.1560.308 5-3 728q2-3.893-2.4117 710q33.375.83-395 20q4-1.154-6.3145 330q50. 114 43.301-255 90q6-0.002 12-0.801 56 636q70.073 2440.122 4-80.43
2.3 模型验证
图5 S为0.1、0.2、0.3时电压对比
Fig.5 Voltage contrast over SOC from 0.1, 0.2 to 0.3
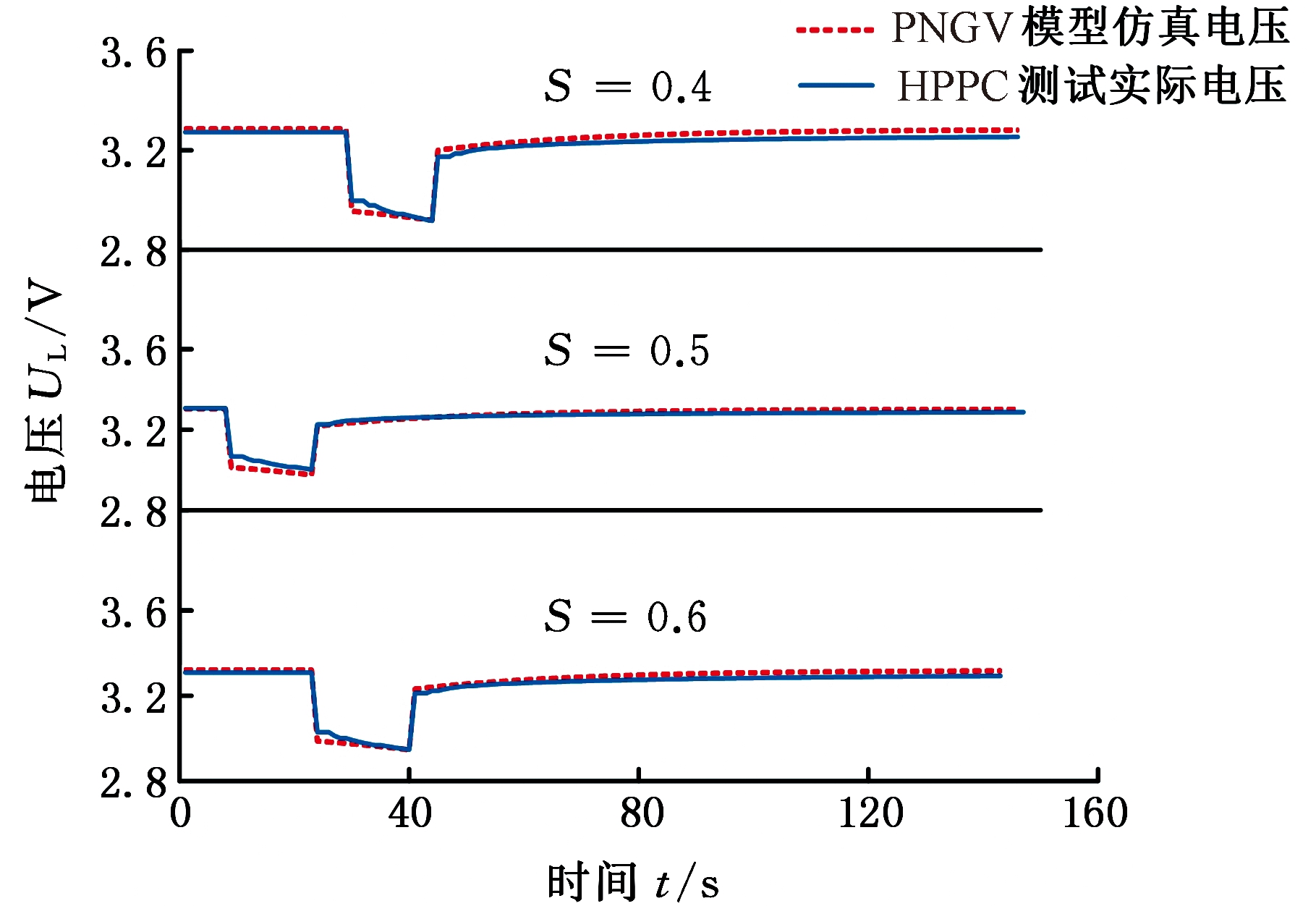
图6 S为0.4、0.5、0.6时电压对比
Fig.6 Voltage contrast over SOC from 0.4, 0.5 to 0.6
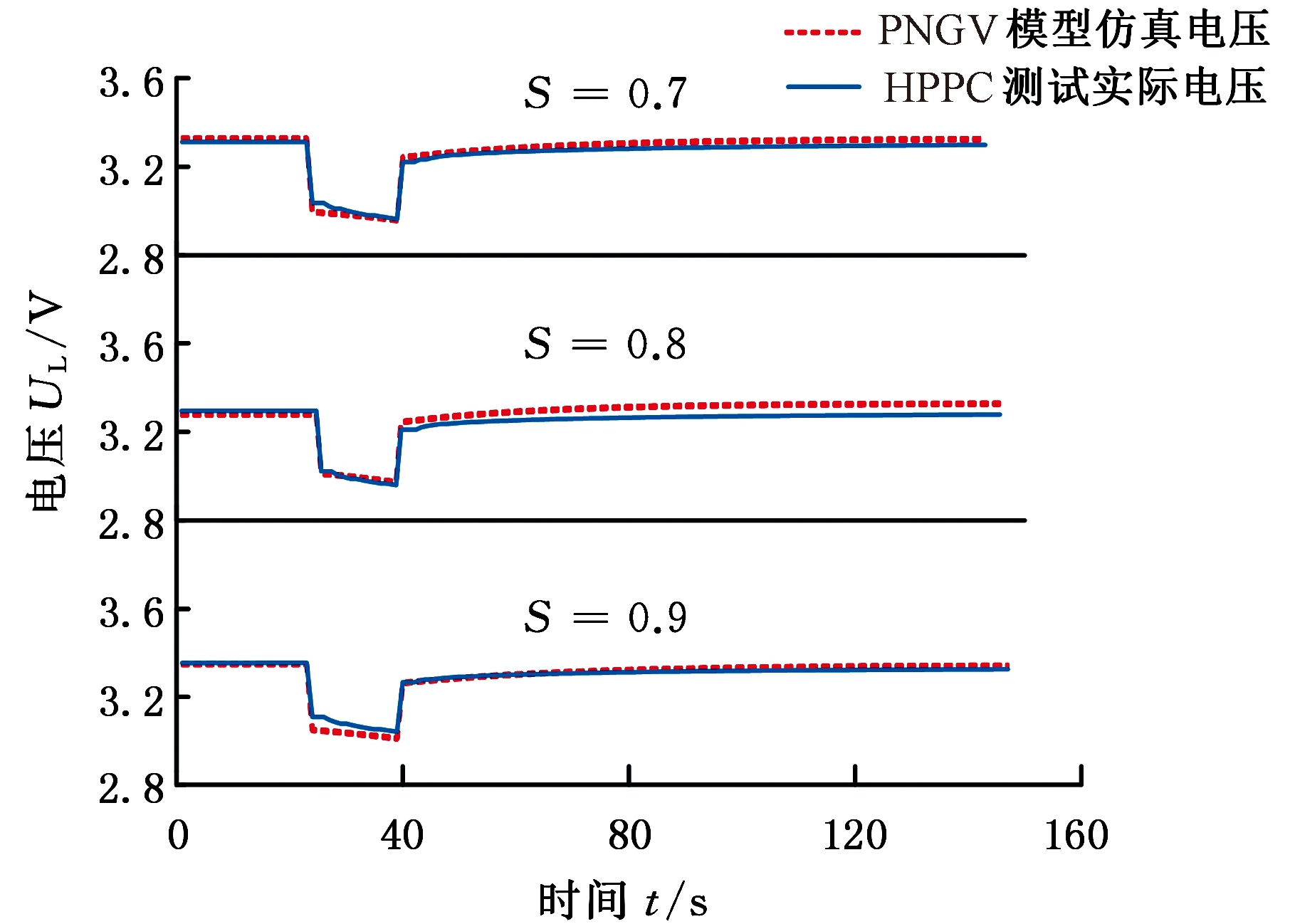
图7 S为0.7、0.8、0.9时电压对比
Fig.7 Voltage contrast over SOC from 0.7, 0.8 to 0.9
利用已建立的OCV-SOC函数关系和模型参数与SOC的函数关系，以及HPPC测试的实验数据，以电流I作为仿真系统的输入，端电压UL作为输出，将MATLAB得出的仿真电压与测试的实际电压进行比较。在SOC值为0.1～0.9时，模型仿真电压与实验实际电压如图5～图7所示。由图5～图7可以看出，在HPPC测试时，从初始时刻t=0至静置阶段，仿真电压和测试电压均保持恒定，但两者并不完全相同，存在曲线不重合的现象。测试电压是由电池静置一段时间(几小时或者几天)达到稳定值得到的，对磷酸铁锂电池而言，存在着迟滞效应，即出现回弹电压的现象，电压先缓慢地上升，直至达到稳定的状态，平衡电势就认为是开路电压，也就是测试电压值。开路电压[16]受静置时间的影响，本实验的静置不充分，导致测试电压值偏高。仿真电压是根据OCV-SOC函数关系得到的，采取多项式拟合方式本身也会有一定的误差。由此，测试电压和仿真电压之间会产生不重合的现象。
电池的瞬间放电即电压出现突降的现象，是由欧姆内阻造成的。在图5～图7中，仿真电压的最低值均比测试电压要小，这正是受到欧姆内阻效应的影响，因辨识得到的参数欧姆内阻较真实值偏大，导致电池电压降偏大引起仿真电压值小于测试值。
在放电15 s过程中,仿真电压与测试电压均缓慢下降，原因在于电池内部存在极化效应，锂离子的运动速率低于电子转移的速率。仿真电压小于测试电压也是受到极化电压初始值的影响，在电池放电的时候，极化电压初始值难以确定，本文设定的初始值相较于真实值偏大，导致仿真电压小于测试电压。
电池放电结束时，电压瞬间上升，仿真电压值比测试值要大，其原因与上述分析欧姆内阻的阻值偏大一致。
放电结束后，锂离子会受到电池电解液中溶液电导率的影响。溶液的电导率低，电池中的锂离子经过扩散和相位转变两个阶段，回到平衡状态，出现电压回弹特性的现象[15]。根据图5～图7，在不同的SOC值处，放电结束后一段时间，端电压的值均不相同且SOC值越大，电压越高，与OCV-SOC描述的曲线关系一致。
当SOC值分别取不同值时(0.9、0.8、…、0.1)，根据电池的仿真电压与测试电压，得出模型最大相对误差的绝对值，如图8所示。
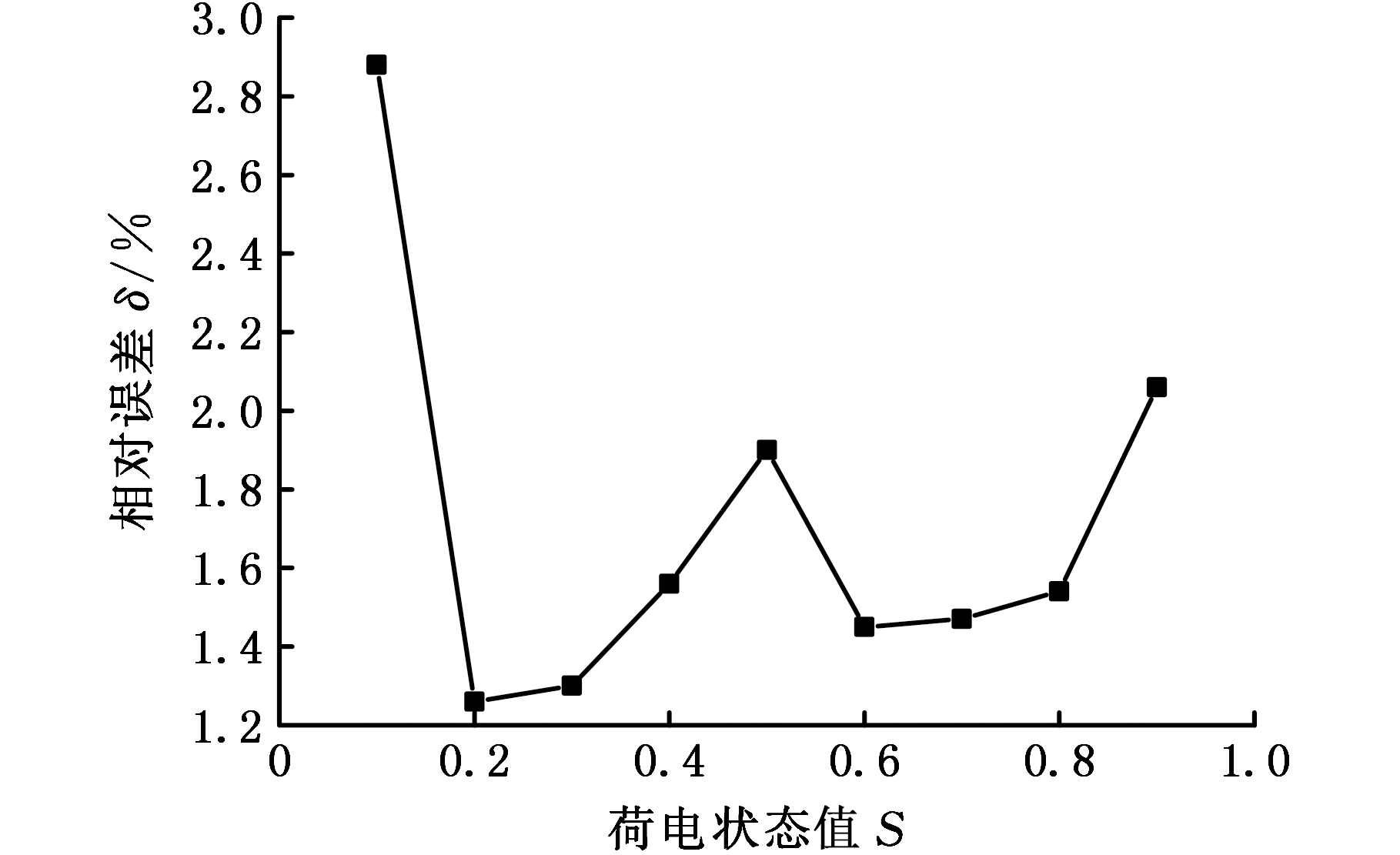
图8 不同SOC值时相对误差
Fig.8 Relative errors with different SOC
由图8可以看出，SOC值为0.1时模型最大相对误差达到了2.88%，而SOC值在其他值时最大误差均小于2%。由OCV-SOC图形(图2)可以看出，电池在SOC值为0～0.1区间时，电压曲线较为陡峭，小的波动会引起电压较大的变化；在0.1～0.9区间内，电压相对来说变化较为平稳，OCV-SOC曲线比较平坦，模型的误差波动也因此较小。
由图5～图7总体来看，用HPPC测试的数据进行仿真得到的电压与实际的电压近似程度较高，最大误差不超过3%。本文建立的PNGV模型准确性较高，可作为估计SOC值的等效电路模型。关于等效模型的误差，电池的极化电压初始值的不确定是影响误差的重要因素之一，可使用精确的方法，如电化学阻抗谱仪在频域上分析和确定模型中参数的方法，来确定极化电压的初始值[17]，这也是验证模型准确性的重要措施。
3 实际工况测试与对比分析
3.1 实验工况
本文采用北京公交车动态应力测试(BBDST )数据，结合PNGV模型和EKF，估计锂电池的SOC值。同时，将安时法作为估计SOC值的标准进行比较，验证工况下的相对误差。安时法公式如下：
(17)
式中，S0为初始SOC值；St为t时刻SOC值。
孙逢春等[18]建立BBDST数据，给出将电池组的测试工况转化到单体电池或电池模块测试工况上的数学表达式：
(18)
式中，Ua、Qa、Pa分别为被测试车辆A电池组的电压、容量和车辆的功率；Ub、Qb、Pb分别为被测试的电池单体或模块的电压、容量和电池的功率；λa为电池等效系数。
被测试车辆装载锂离子动力电池组384V@360A·h和100 kW交流异步电动机，本文测试的单体电池参数为3.2V@1.3A·h，则经计算，测试的单体电池的等效系数λa=3×10-5。锂电池动态应力测试如表4所示。
根据表4，在高精度电池检测系统中对电池的工况进行恒功率循环测试，单次循环时间为300 s，采用7次循环。实验原始数据来自课题组前期实验的充放电测试[14]，得出电池在不同脉冲功率下的电压和电流图形，如图9、图10所示。
3.2 SOC结果与分析
在BBDST动态工况测试的条件下，以测试电流作为系统的输入，测试电压作为输出，在MATLAB中仿真得出估计的SOC值；采用安时法计算出的SOC值作为真实值,两者进行比较，验证EKF的准确性。
运用EKF估计SOC值时，设定初始值如下：
表4 BBDST测试过程
Tab.4 BBDST testing process
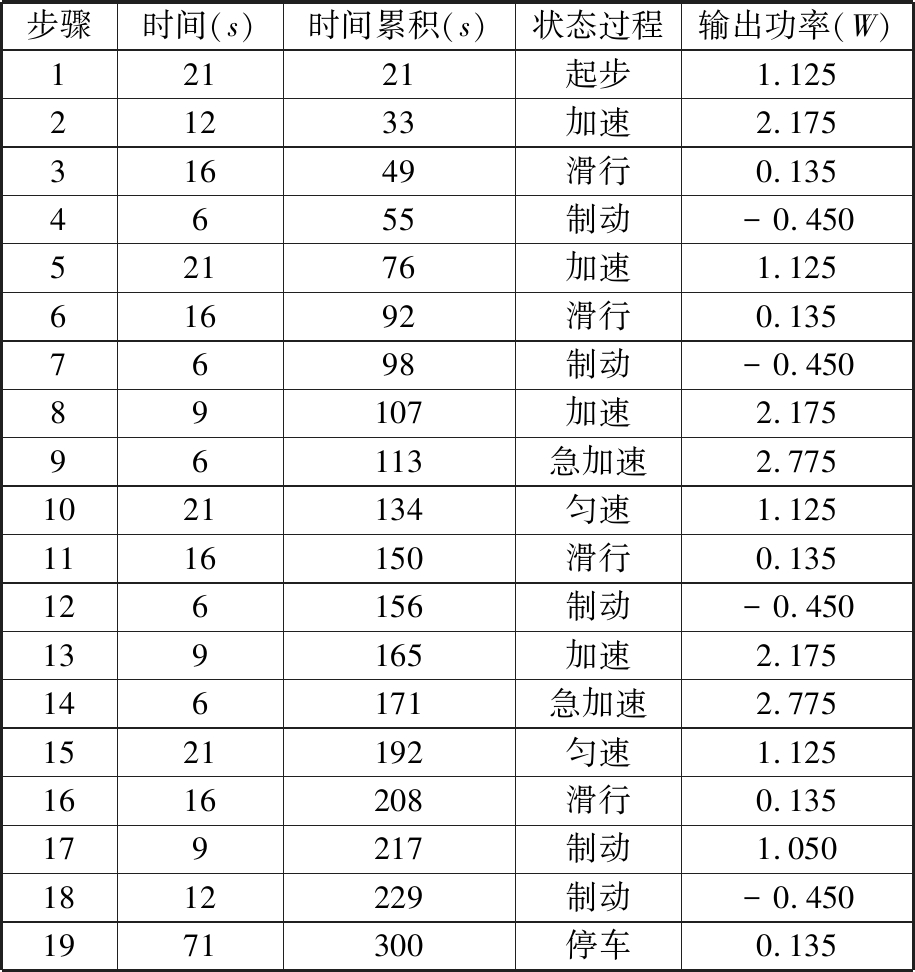
步骤时间(s)时间累积(s)状态过程输出功率(W)12121起步1.12521233加速2.17531649滑行0.1354655制动-0.45052176加速1.12561692滑行0.1357698制动-0.45089107加速2.17596113急加速2.7751021134匀速1.1251116150滑行0.135126156制动-0.450139165加速2.175146171急加速2.7751521192匀速1.1251616208滑行0.135179217制动1.0501812229制动-0.4501971300停车0.135
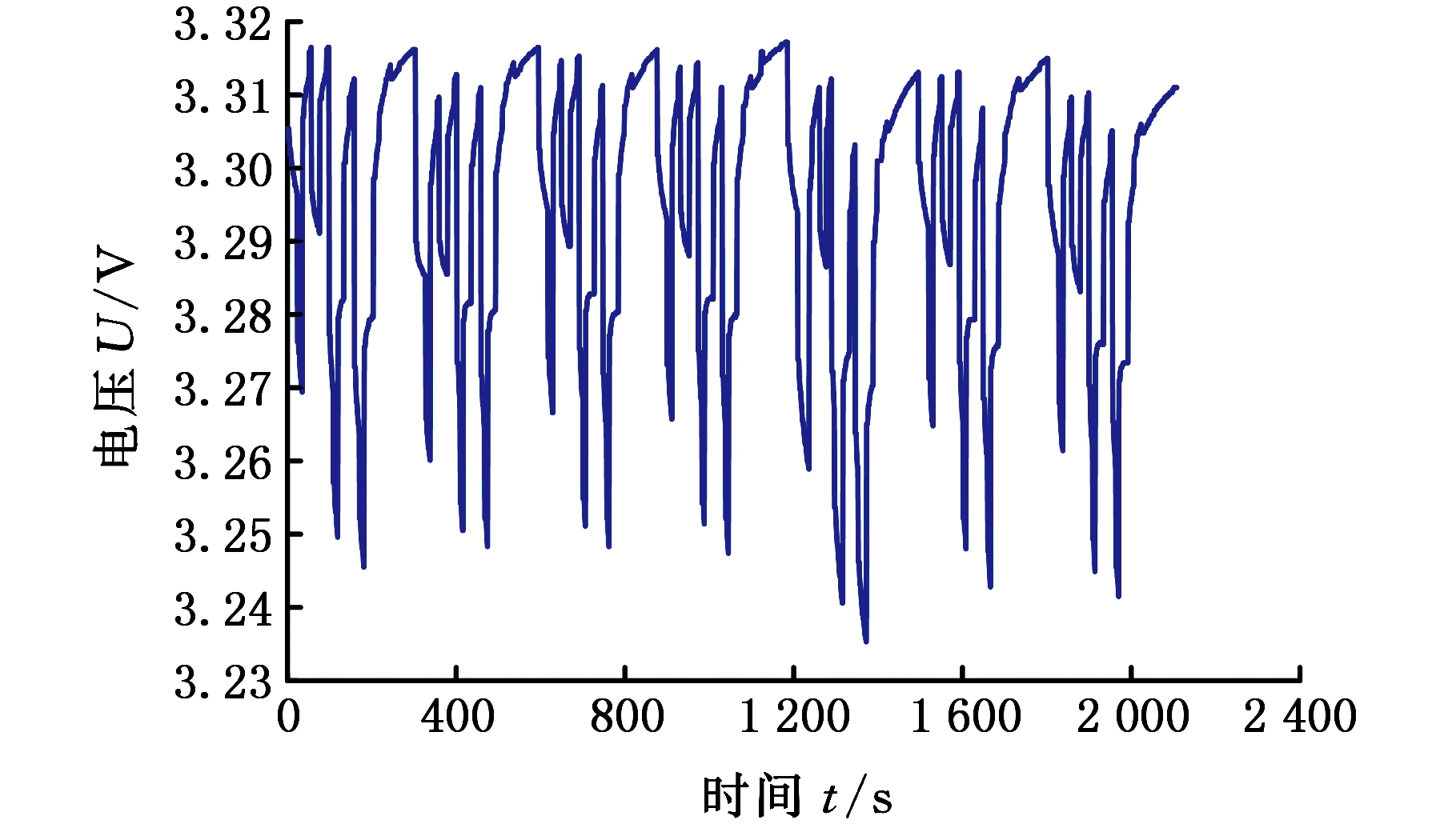
图9 BBDST电压
Fig.9 BBDST voltage
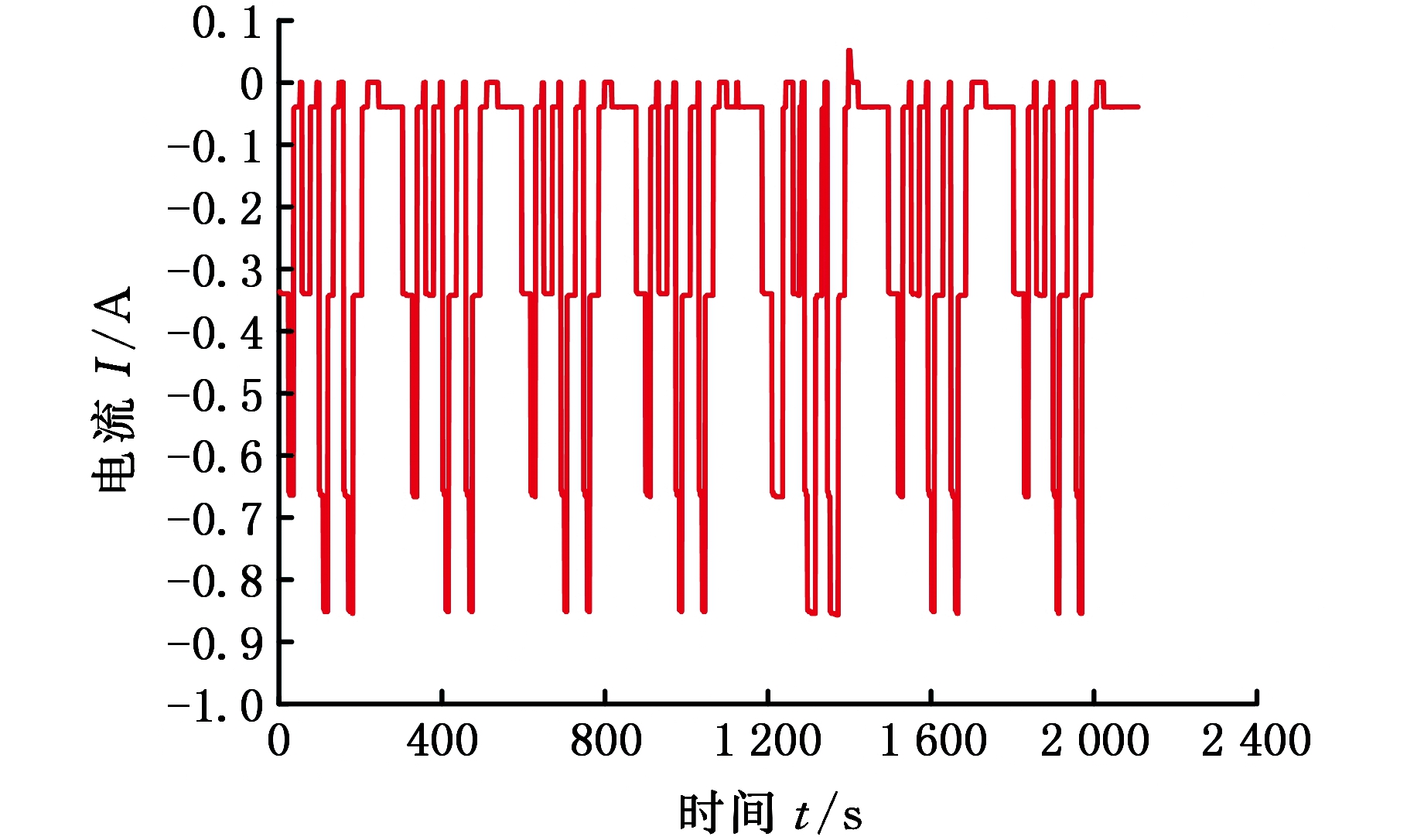
图10 BBDST电流
Fig.10 BBDST current
在BBDST工况测试下，EKF估计SOC的仿真值、安时法的真实值以及误差如图11、图12所示。
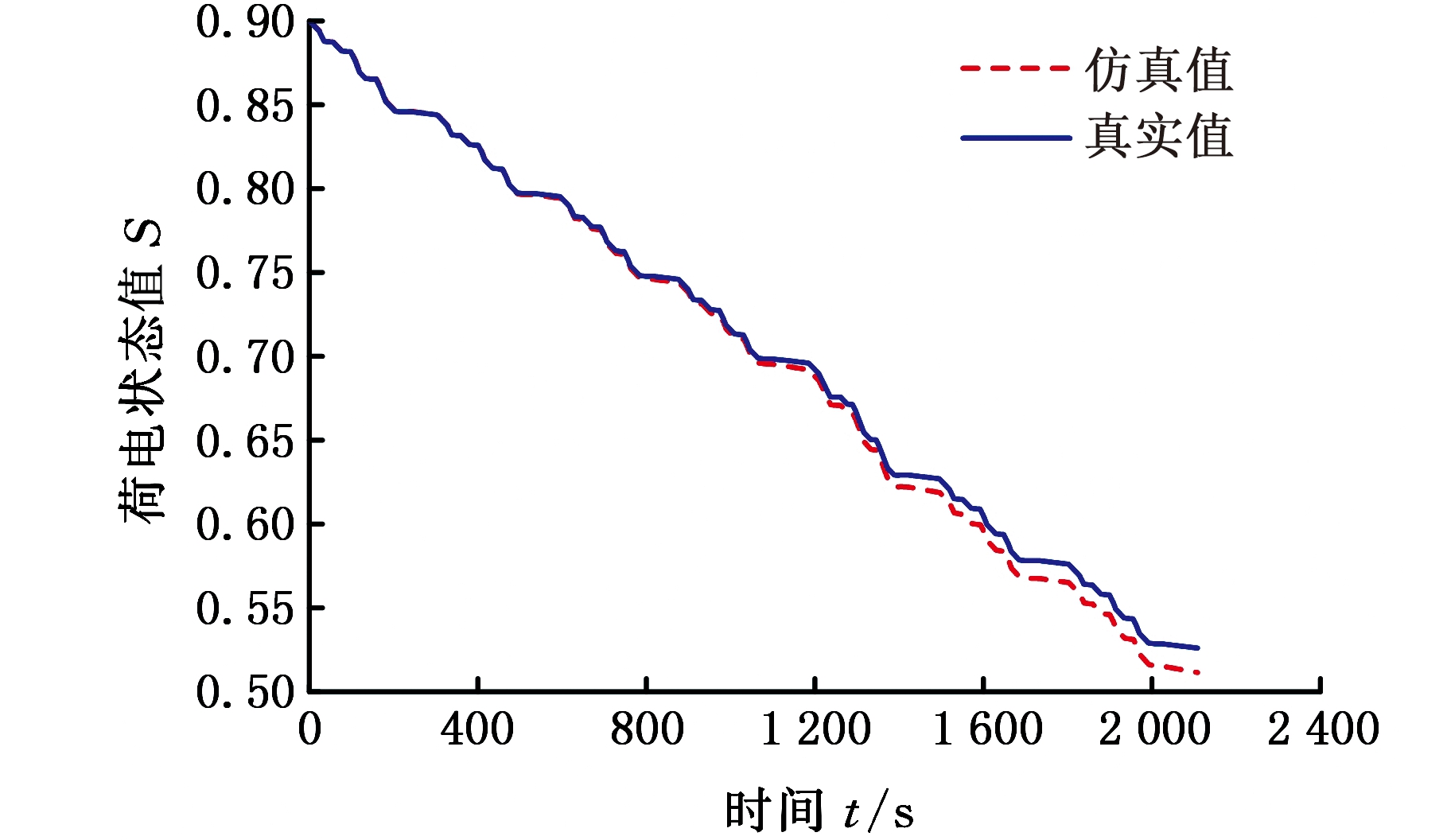
图11 SOC仿真值与真实值
Fig.11 Simulated and measured value of SOC
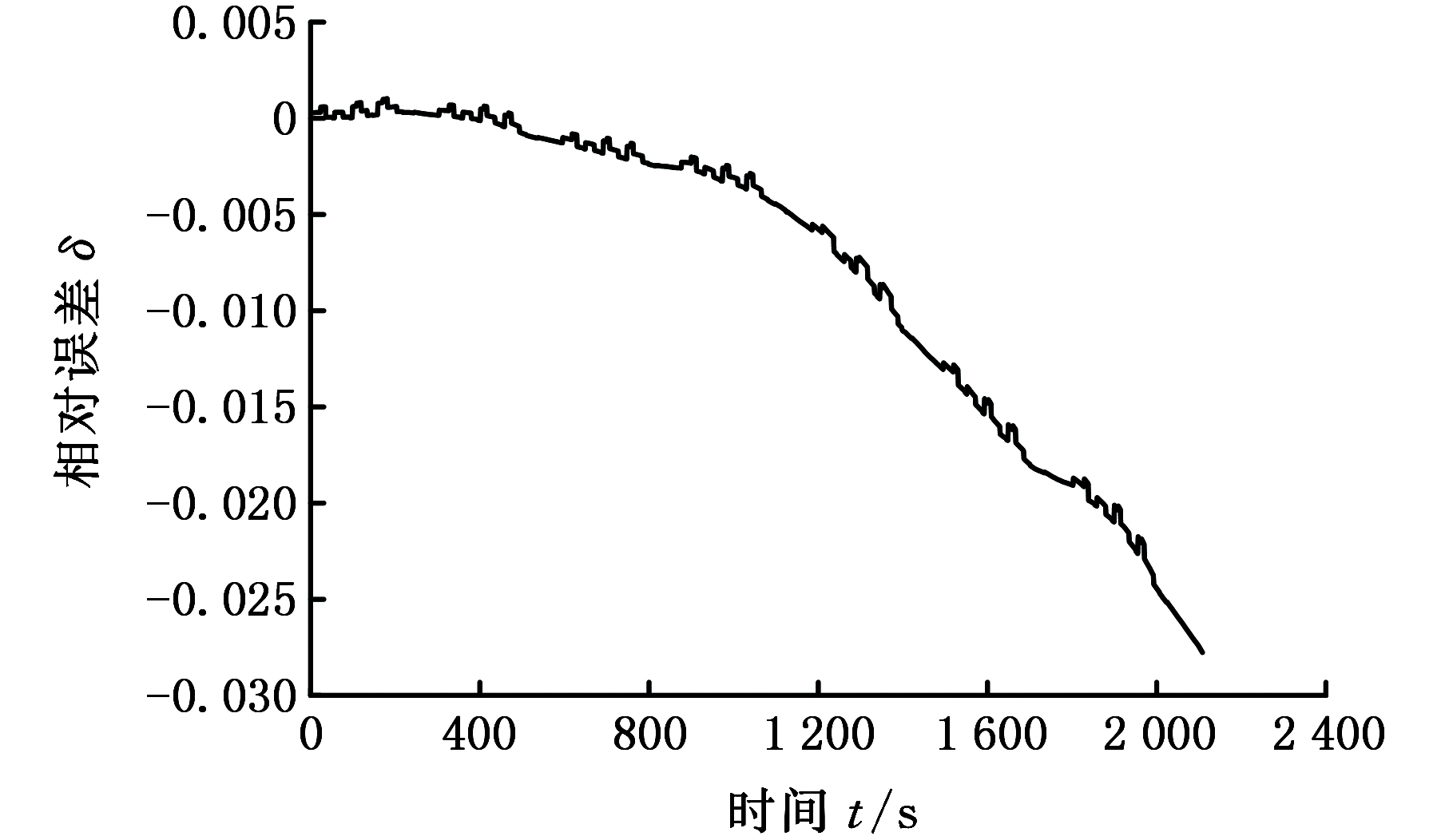
图12 SOC估计的相对误差
Fig.12 Relative error of estimated SOC
由图11可以看出，SOC初始值为0.9 ，在SOC从0.9下降到0.65过程中，仿真值与真实值的变化趋势相近；在0.65以后逐渐下降的过程中，两者之间的结果差异逐渐扩大。由图12看出，随着SOC值的减小，两者的相对误差逐渐变大，最大绝对值达到了2.78%。
4 结论
本文以磷酸铁锂电池为对象，建立了欧姆内阻、极化特性参数的PNGV模型，采用扩展卡尔曼滤波法来估计电池SOC值。模型参数受电池内部因素的影响，通过开路电压和参数辨识测试，建立了PNGV模型，同时在HPPC测试下，验证了模型的准确性，误差不超过3%，故该模型可以用来估计SOC值。在BBDST工况下，结合电流电压测试精度问题引起的噪声方差，运用扩展卡尔曼滤波法结合PNGV模型来估计SOC值，与标准SOC估计的安时法比较，误差最大为2.78%。测试结果表明，运用EKF方法估计SOC值的误差较小，准确性较高，可以作为SOC估计的实用方法。
运用扩展卡尔曼滤波法估计SOC值时，在BBDST测试的电流和电压工况下，需要添加高斯白噪声，表示测试电流电压传感器的精度误差。本文中，在设定参数的初始值时，对于过程噪声和测量噪声方差的初始值，尚未展开具体的实验来验证噪声的初始值对估计SOC值的影响，在今后的工作中，需要进一步改进和探究。
[1] YUAN C, DENG Y, LI T, et al. Manufacturing Energy Analysis of Lithium Ion Battery Pack for Electric Vehicles[J]. CIRP Annals—Manufacturing Technology,2017, 66(1)：53-56.
[2] CHEN Z, SUN H, DONG G, et al. Particle Filter-based State-of-charge Estimation and Remaining Dischargeable Time Prediction Method for Lithium-ion Batteries[J]. Journal of Power Sources, 2019, 414: 158-166.
[3] GUO J, LI Z, PECHT M. A Bayesian Approach for Li-ion Battery Capacity Fade Modeling and Cycles to Failure Prognostics[J]. Journal of Power Sources, 2015, 281: 173-184.
[4] MOURA S J, ARGOMEDO F B, KLEIN R, et al. Battery State Estimation for a Single Particle Model with Electrolyte Dynamics[J]. IEEE Transactions on Control Systems Technology，2017, 25(2): 453-468.
[5] MIN C, RINCON-MORA G A. Accurate Electrical Battery Model Capable of Predicting Runtime and I-V Performance[J]. IEEE Transactions on Energy Conversion，2006, 21(2): 504-511.
[6] SCHMID T ALEXANDER P, BITZER M, IMRE 
W, et al. Experiment-driven Electrochemical Modeling and Systematic Parameterization for a Lithium-ion Battery Cell[J]. Journal of Power Sources，2010, 195(15): 5071-5080.
[7] BUBNA P, BRUNNER D, ADVANI S G, et al. Prediction-based Optimal Power Management in a Fuel Cell/Battery Plug-in Hybrid Vehicle[J]. Journal of Power Sources，2010, 195(19): 6699-6708.
[8] ZHU Z, SUN J, DAN L. Online State of Charge EKF Estimation for LiFePO4 Battery Management Systems[C]∥International Symposium on Intelligent Signal Processing and Communication Systems. Taipei, 2012:609-614.
[9] LEE S, KIM J, LEE J, et al. State-of-charge and Capacity Estimation of Lithium-ion Battery Using a New Open-circuit Voltage Versus State-of-charge [J]. Journal of Power Sources，2008, 185(2): 1367-1373.
[10] LAI X, QIAO D, ZHENG Y, et al. A Fuzzy State-of-charge Estimation Algorithm Combining Ampere-Hour and an Extended Kalman Filter for Li-ion Batteries Based on Multi-model Global Identification[J].Applied Sciences-basel，2018, 8(11):2028.
[11] 张云清，赵景山. 美国“新一代汽车合作计划”(PNGV)及其涉及的关键高新技术[J]. 科技进步与对策，2001, 18(1): 173-175.
ZHANG Yunqing, ZHAO Jingshan. The New Generation Automobile Cooperation Plan(PNGV) and Its Key High-technology [J]. Science and Technology Progress and Policy，2001, 18(1): 173-175.
[12] WENG C, SUN J, PENG H. A Unified Open-circuit-voltage Model of Lithium-ion Batteries for State-of-charge Estimation and State-of-health Monitoring[J]. Journal of Power Sources，2014, 258: 228-237.
[13] JIANG J, SHI W, ZHENG J, et al. Optimized Operating Range for Large-format LiFePO4/Graphite Batteries[J]. Journal of the Electrochemical Society，2014,161(3):A336-A341.
[14] 李玥锌. 锂离子电池SOC估计和剩余寿命预测研究[D]. 大连:大连理工大学, 2017.
LI Yuexin. Research on SOC Estimation and Residual Life Prediction of Lithium-ion Batteries [D]. Dalian :Dalian University of Technology, 2017.
[15] 谭晓军. 电动汽车动力电池管理系统设计[M].广州：中山大学出版社, 2011.
TAN Xiaojun. Design of Power Battery Management System for Electric Vehicles [M]. Guangzhou: Sun Yat-sen University Press, 2011.
[16] HURIA T, CERAOLO M, GAZZARRI J, et al. Simplified Extended Kalman Filter Observer for SOC Estimation of Commercial Power-oriented LFP Lithium Battery Cells[J].SAE Technical Paper, 2013-01-1544.
[17] JIANG Y, ZHANG C, ZHANG W, et al. Modeling Charge Polarization Voltage for Large Lithium-ion Batteries in Electric Vehicles[J]. Journal of Industrial Engineering and Management, 2013, 6(2): 686-697.
[18] 孙逢春，孟祥峰，林程，等. 电动汽车动力电池动态测试工况研究[J]. 北京理工大学学报，2010, 30(3): 297-301.
SUN Fengchun, MENG Xiangfeng, LIN Cheng, et al. Research on Dynamic Test Conditions of Electric Vehicle Power Battery[J]. Journal of Beijing Institute of Technology，2010, 30(3): 297-301.
