0 引言
大型船舶动力部件不仅要承受弯曲力矩、扭转力矩以及交变载荷等作用力,还要面临载荷巨大、工作环境恶劣等诸多独特的工作状况,这就要求其不仅要有良好的内部组织,还要拥有很高的尺寸精度[1]。在原有的车间难以满足日益增长的生产需求,且车间物料搬运成本也无法得到缩减的情况下,大型船舶动力部件生产车间必须加快转型升级。
车间设备布局在设施规划问题中一直是一个重要的研究方向,车间的最终布局结果对系统的实际产能、生产效率等均有重大影响,直接影响到整个生产系统的总体性能[2]。
车间布局问题要同时满足几何条件约束和一些特定的定性与定量条件,属于NP难题。设备布局根据物流设备的不同,可以分为线性单行布局、线性多行布局、U形布局和环形布局。在传统研究中,关于设备布局的方法一般有图论法和数学统计方法。但对于NP难题,诸多学者开始转向运用启发式算法进行求解。TAYAL等[3]通过大数据手段对数据进行收集,得到多目标随机动态设施布局模型,之后用萤火虫算法(firefly algorithm,FA)和通用加扰算法(common scrambling algorithm,CSA)的混合算法对该问题进行了解析,但采集的数据是否准确以及对数据的处理是否合适对结果影响较大。LI等[4]提出了一种自适应学习粒子群算法,该算法通过4种不同的策略来处理不同类型的搜索空间,但收敛速度不高。龚全胜等[5]对遗传算法(genetic algorithm,GA)与模拟退火算法(simulated annealing algorithm,SAA)的基本原理、运算过程和优缺点进行了分析,提出了GA-SAA算法,该算法克服了GA局部寻优能力较差及SAA求解效率较低的问题,但仍没有考虑零件生产工艺的差异性。归纳起来,以上的解决方案都只是考虑物流成本最小这一个因素,忽略了其他目标如空间占用率等。
本文针对上述问题,应用一种新模式粒子群优化算法[6](简称DMPSO算法)对大型船舶动力部件生产车间进行优化。该算法的优点在于实时调整惯性权重和粒子飞行路线,从而有效减少粒子搜索的盲目性,有效避免陷入局部最优以及解决收敛精度低等问题,提高了粒子搜索到全局最优解的可能性。应用DMPSO算法求解车间布局问题不仅能够改善近似最优解的优化程度,并且计算效率高,实践应用性很强。此外,本文重点考虑了船舶动力部件装配与精加工工艺步骤的连贯性以及车间面积利用等因素,引入车间面积占有率和空间面积利用率两个概念,以增强车间的布局冗余能力和车间布局合理性。通过CATIA软件对DMPSO算法优化后的布局进行了三维可视化建模,从而给车间设备布局改造提供设计和改进依据。
1 车间布局问题描述及数学模型
1.1 问题描述
车间布局问题由车间的设备和设备所需要的摆放空间构成[7],本文将车间布局问题视为满足一定约束条件的多行设备布局问题。
首先,忽略车间设备的形状细节,假定其都为矩形块状结构,而且每台设备的长和宽已知,各设备分行排列,并与X轴平行。各设备间的横向(X向)和纵向(Y向)间距要求已知,各设备中心位置位于同一水平线上,布局空间和设备的拓扑模型如图1所示。
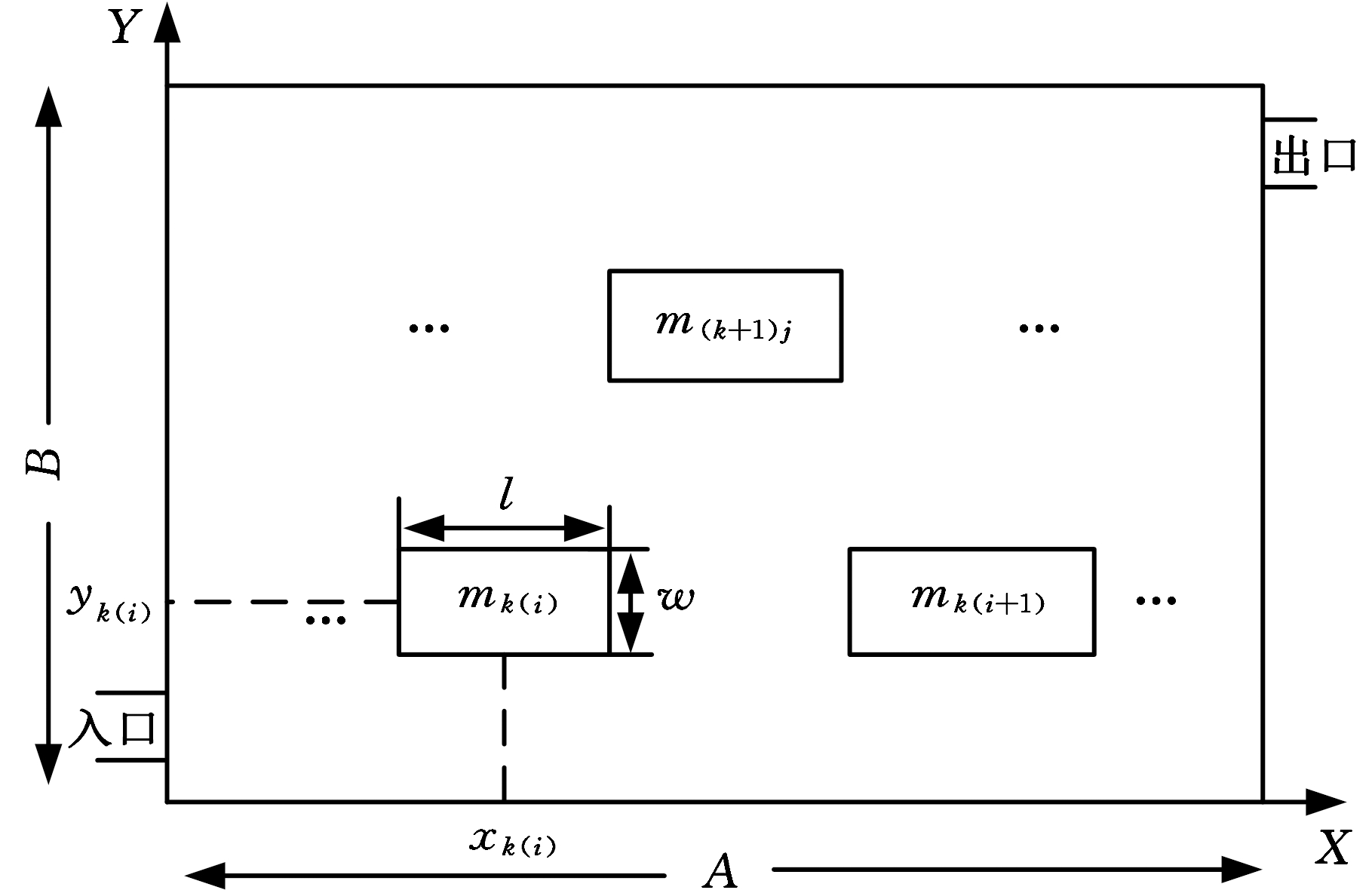
图1 车间和设备拓扑
Fig.1 Workshop and equipment topology
假设车间设备数为n,车间总长度为A,总宽度为B,l和w分别表示设备在X轴和Y轴上的长度,x与y分别表示设备中心点在X轴和Y轴上的位置,故xk(i)表示第k行第i台设备mk(i)中心点的X坐标,yk(i)表示设备mk(i)中心点的Y坐标。
假设设备编号为m1,m2,…,mn,引入一开关变量:
(1)
i=1,2,…,n k=1,2,…,r
式中,r为设备布置总行数。
设H(k)表示布置在第k行的设备总和,则
1.2 数学模型
考虑上述问题描述和相关假设,可以建立以减少物料搬运成本为目标的设备布局优化模型,从而确立较为合理的物料搬运路径。布局问题是一个经典问题,很多学者在数学模型的建立方面已经做了大量详细的研究[8-12]。实际生产过程中,多数车间的运输路径都是平行于车间的四壁,故假定设备间的物流路径都平行于X轴或Y轴。考虑到使物料搬运成本最少以及车间占有面积最小,建立目标函数表达式如下:
(2)
式中,C为物料搬运成本与车间面积占有率的加权和;Pij为设备i和设备j之间每单位距离的搬运费用;Qij为设备i和设备j之间物料搬运频率;Dij为设备i和设备j之间的直角距离;η为车间面积占有率;f1和f2为权重因子,且f1+f2=1,目的就是求得物料搬运成本的最小值。
对于多行布局问题,有
Dij=|xi-xj|+|yi-yj|
(3)
考虑生产车间实际情况,主要约束条件有以下几条。
(1)一台设备只能布置在某一行中,且只能出现一次,故有
(4)
(2)两相邻设备之间不出现交叉或重叠。行内约束条件为
(5)
式中,d为相邻两设备间必须保持的最小间距,d≥0,且为常数;lk(i)为第k行第i台设备在X轴上的长度。
若将设备两端墙壁视为设备mk(0)和mk(H(k)+1),则有
(6)
列内约束条件为
yk(1)=yk(2)=…=yk(H(k))=Yk
(7)
其中,Yk为第k行各设备中心的Y坐标,有
(8)
式中,h为相邻两行设备间必须保持的最小间距,已知h≥0,且为常数;wk(i)为第k行第i台设备在Y轴上的长度。
若将两端墙壁视为设备,则有
(9)
当k=0时,wk(i)=0;当k=r+1时,w(r+1)i=0。
若考虑到船舶动力部件加工工艺要求,如曲轴红套过程必须在单套过程之后,精加工必须在曲轴红套过程之后,则要求相关设备必须布置在同一行相邻位置或同一列相邻位置,故有
(10)
(11)
(3)设备在X方向和Y方向上的布置不应超过整个车间的总长度A和总宽度B。考虑到车间内的安全通道和车间工作人员的活动,各设备与车间四周的墙壁应保留一定的安全距离,设其在X方向上的最小间距为A0,在Y方向上的最小间距为B0,同理可得约束条件如下:
行方向
(12)
列方向
(13)
(4)空间面积利用率大于70%。为了避免车间空间资源浪费,空间面积利用率需保证在合理范围,则有
![]() >70%
>70%
(14)
其中,S0为所有设备占地面积之和;S为能容纳所有布局设备的最小面积,有
(15)
(16)
2 车间布局问题的DMPSO算法设计
DMPSO算法依据粒子的分布情况和算法所处的迭代阶段动态改变惯性因子大小,并依据粒子历史最优位置的更新情况不断对粒子的飞行起点进行调整。DMPSO算法流程如图2所示。
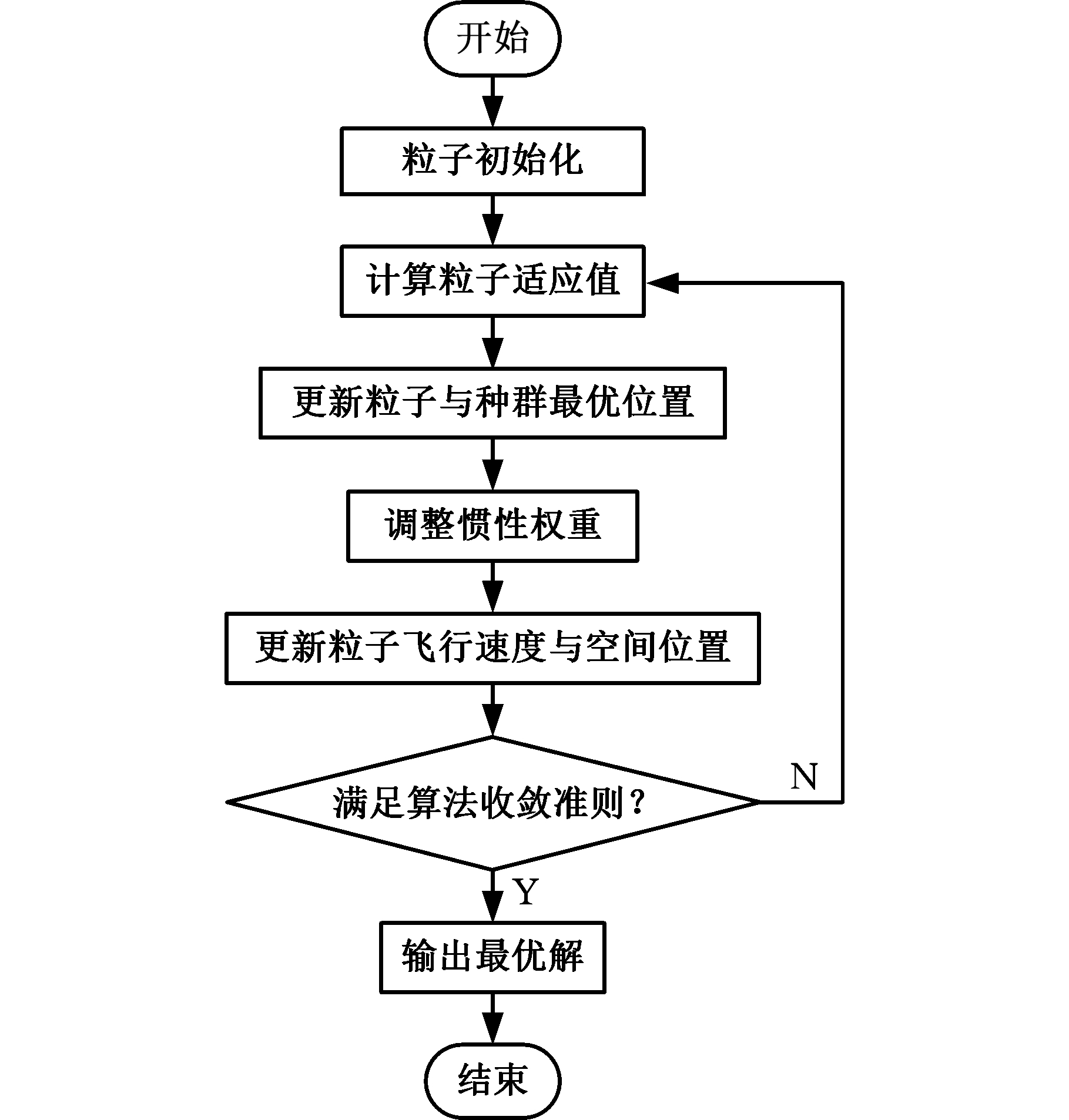
图2 DMPSO算法流程图
Fig.2 Flow chart of DMPSO algorithm
2.1 DMPSO编码设计
DMPSO算法设计原则与基本PSO算法[13]相同,假设车间内设备数为m,每个布局候选方案可表示为一个粒子,则对于每个粒子的编码都可以表示为一个2m维向量,每个设备的X坐标为前m维向量,每个设备的Y坐标为后m维向量,用数学式表示为
P=(x1,x2,…,xm,y1,y2,…,ym)
(17)
每个粒子的飞行方向和速度也为一个2m维向量,前m维向量表示设备在X方向上的移动速度,后m维向量表示设备在Y方向上的移动速度,即
V=(vx1,vx2,…,vxm,vy1,vy2,…,vym)
(18)
基本PSO算法中,粒子在t时刻的飞行速度和位置根据下式进行迭代更新:
(19)
(20)
vID∈[-vmax,vmax]
式中,ω为惯性因子;c1和c2为加速因子;r1和r2为(0,1)范围内的两个随机数;![]() 为粒子I在第K次迭代中飞行速度的第D维向量,
为粒子I在第K次迭代中飞行速度的第D维向量,![]() 为粒子I在第K次迭代中位置的第D维向量;pID为粒子I经历的历史最优位置pI的第D维向量;pGD为群体目前搜索到的最优位置pG的第D维向量;vmax为粒子每一维的最大飞行速度。
为粒子I在第K次迭代中位置的第D维向量;pID为粒子I经历的历史最优位置pI的第D维向量;pGD为群体目前搜索到的最优位置pG的第D维向量;vmax为粒子每一维的最大飞行速度。
取下式为车间布局问题的适应度函数:
(21)
在实际车间布局问题中,需考虑特定的约束条件,可以设定一个惩罚项为Pk,采用自动换行的方法能够保证设备在X方向上不会发生超出工作区域的情况,故只需对车间最后一行设备在Y方向上是否会超出车间区域进行判断,即
(22)
式中,T为正的大数惩罚值。
2.2 DMPSO算法参数设定
2.2.1 群体规模
一般情况下,设定种群规模M的大小在20~40之间就能充分对解空间进行搜索,对于十分复杂的问题,种群规模可以取到100~200。SHI等[14]的实验结果表明,增大M对改善算法收敛精度的效果并不明显,而算法的计算复杂度却随着M的增大而快速增加,反而达不到寻优效果。
2.2.2 惯性因子ω设定与粒子飞行模式调整
惯性因子的大小对粒子的全局与局部搜索能力之间的平衡有重大影响,ω值较大,全局寻优能力强,局部寻优能力弱,ω值较小,则利于局部搜索。对于惯性因子ω的研究,文献[14]提出线性递减策略,即
(23)
式中,ω1、ω2为惯性因子的最大值和最小值;N和L分别为算法的最大迭代次数和当前代数。
但该方法不能有效提升算法性能,对处理复杂、非线性问题能力十分有限,因为其对ω的调整只考虑了算法所处的当前迭代次数。
在DMPSO算法迭代过程中,着重考虑了粒子的分布情况,用粒子分布情况和迭代阶段来共同决定ω的大小,可以有效避免算法陷入局部最优。故引用一个惯性因子变异算子λ,其大小由粒子在解空间内的分布情况决定,如下式所示:
(24)
为了实时监测解空间内的粒子分布情况,DMPSO算法采用文献[15]提出的一种分布熵形式,如下式所示:
(25)
其中,解空间被均分为相等区域,Q表示相等区域的个数,Mq表示第L次迭代后每个区域内的粒子个数,q=1,2,…,Q。而惯性因子变异算子λ的具体调整方式如下式所示:
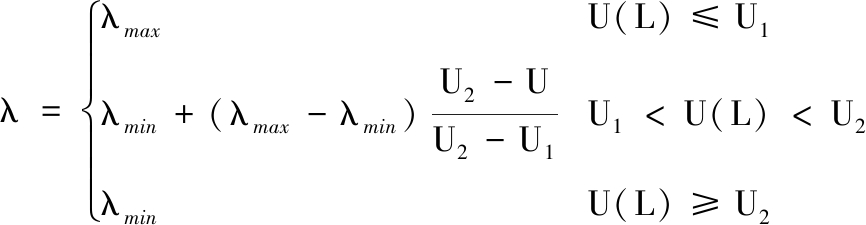
(26)
其中,U1、U2分别为粒子分布熵的上下限值(应满足U1>U2),超出门槛值范围时,对λ赋某一定值。
在经过多次迭代后,粒子不断向全局最优解附近聚集,此时增大λ来加强全局搜索必定会影响算法最终的收敛性。故以分布情况调整ω大小的方式仅适用于算法迭代前期和中期,即L<RN(R为粒子分布检测结束标志,满足0<R<1)时。当算法进入迭代后期,即l≥RN时,为ω赋一较小的定值λmin,以加强算法局部搜索能力,保证算法最终收敛。
为了更好地改善算法的性能,DMPSO算法还通过调整粒子飞行模式来提高粒子收敛精度,全局最优解最可能出现在每个粒子的历史最优位置,故使偏离历史最优位置的粒子重新回到其历史最优位置pi处能大大提高找到全局最优解的可能性,故在DMPSO算法中对式(20)进行修改,得到下式:
(27)
2.2.3 加速因子(c1,c2)的设定
加速因子c1和c2通过调整粒子自身经验与群体经验影响粒子的运动轨迹。如果c1=0,则粒子只有群体经验对粒子的运动产生作用,此时其收敛速度可能较快,但对于一些复杂问题可能导致局部收敛,如果c2=0,则只有自身经验作用于粒子的运动,群体中粒子不具备信息交互的能力,从而难以找到较好的解[16]。
一般来说,可以把c1和c2看成一个控制参数,即φ=c1+c2,φ的值应该在一定范围内。在DMPSO算法中,本文对比3组具有代表性的加速因子方案,从而保证其寻优速度和优化质量,并对最后结果进行对比分析,从中选择最优的加速因子方案。
3 计算实例
3.1 车间概述
本文给出的大型船舶动力部件生产车间为264 m×72 m的船用曲轴生产车间,其主要产品包括7G80ME-C曲轴、10S90ME-C型低速船用柴油机曲轴等。车间内主要包括数控曲拐专用立车、红套孔镗床、数控双柱立式车床以及数控曲轴精加工机床等10个加工机床,曲拐单套区域,曲轴红套坑以及一个原料堆放区,一个成品存放区。为方便描述,现用序号来描述各车间设备,如表1所示,其中编号为3、7、11、15为同一型号设备,车间各个设备的尺寸如表2所示,曲轴车间的初始布局如图3所示。
在曲轴生产车间中,各个设备之间的物料搬运单价和搬运量都是一定的,故设备间的搬运距离是影响物料搬运成本的唯一因素。考虑到车间中的实际情况,A0和B0分别为各设备在X轴和Y轴方向上与墙壁的安全距离,A0=6.8 m,B0=5.3 m。
表1 车间设备序号及名称
Tab.1 Serial number and name of workshop equipment

序号12345名称原料堆放双柱立式车床精加工车床(1)自由端加工曲拐立车序号678910名称成品存放精加工车床(2)曲拐单套红套孔镗床曲轴复套序号1112131415名称精加工车床(3)数控卧车数控镗铣床齐二镗铣床精加工车床(4)
表2 车间设备尺寸
Tab.2 Workshop equipment dimensions

设备12345尺寸(m×m)18.2×1113.8×7.830.9×11.813.8×512.6×7.3设备678910尺寸(m×m)55.5×11.230.9×11.837.1×912.7×3.535.3×10.5设备1112131415尺寸(m×m)30.9×11.821.4×5.59.8×8.711.7×8.630.9×11.8
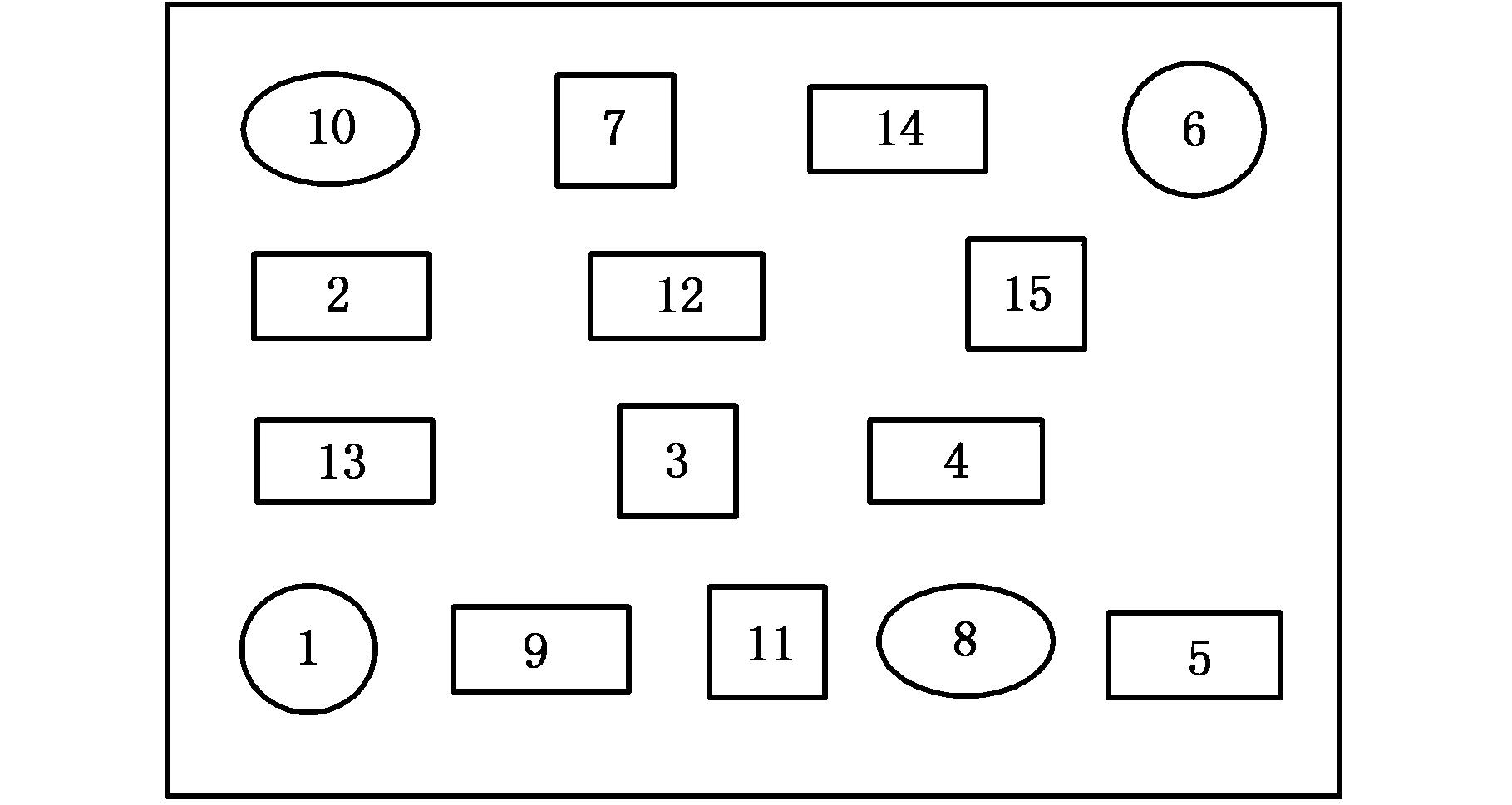
图3 车间初始布局图
Fig.3 Workshop initial layout
根据工艺生产流程,设备间物料搬运线路均为直线,故两设备间的距离用距心之间的直角距离来计算,物料搬运单价矩阵Pij和物料搬运频率矩阵Qij如下式所示:

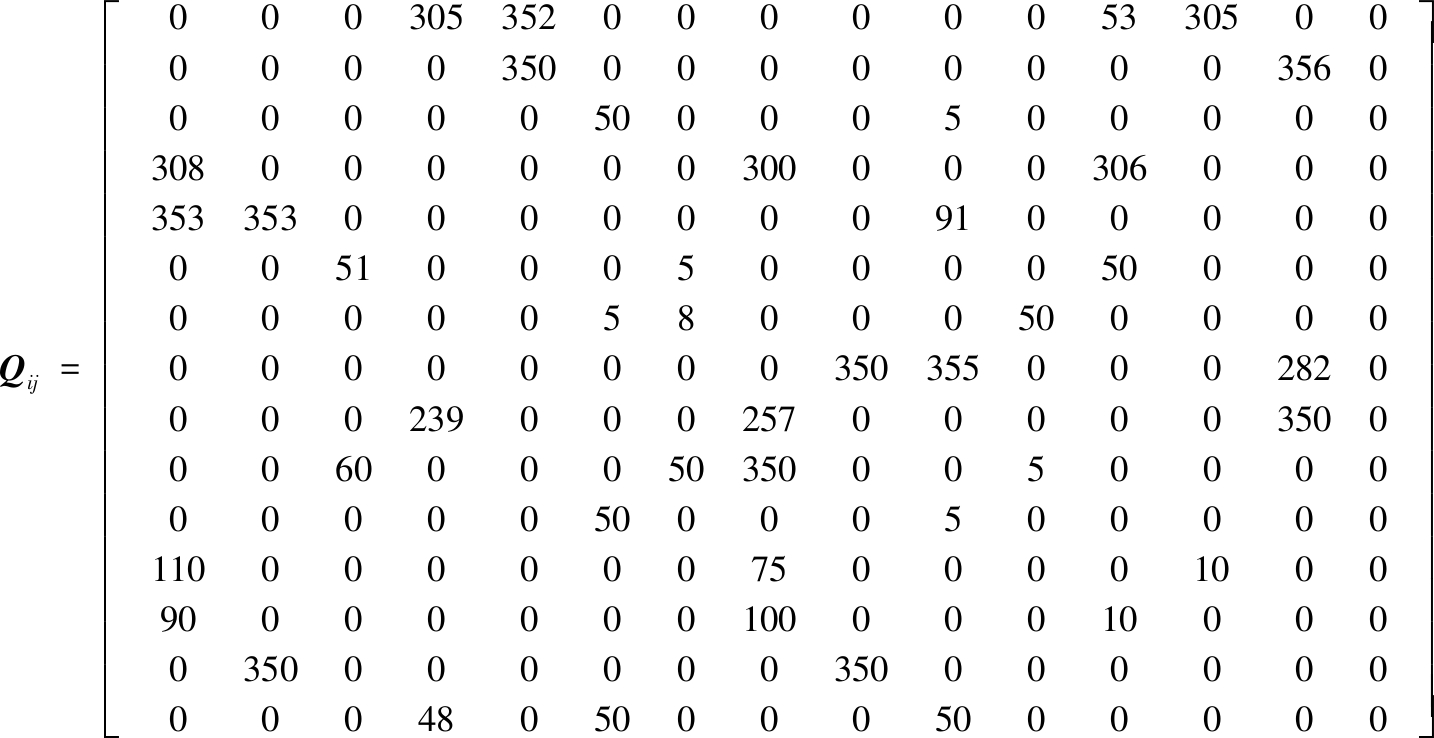
其中,物料搬运单价矩阵Pij中,a表示运输曲轴零件的天车,a=0.03元/(m·件),b表示地面遥控车,b=2×10-3元/(m·件),c表示运输曲轴的天车,c=0.5元/(m·件),Qij为生产车间搬运50根船用曲轴各设备间的搬运频率矩阵。
3.2 优化过程及相关参数设定
本文在用DMPSO算法对曲轴生产车间进行布局优化时,由于需保证船舶动力部件装配与精加工工艺步骤的连贯性,故序号为7、10的设备处于相邻位置,考虑空间面积利用率等因素,需将约束不等式(式(14)与式(15))作为边界条件加入DMPSO算法中,选取种群规模M=28,粒子维度(即设备数量)T=15,分布熵下限值U2=1.8 ,上限值U1=3.5,粒子分布检测结束标志R=0.85,f1=0.8,f2=0.2,惯性系数ω、迭代次数N、加速因子c1和c2等相关参数设定见表3。选取3组不同的加速因子参数,得到3组不同的数据,为保证DMPSO算法在优化过程中的优化质量和寻优速度,选取三组数据中最好的寻优结果作为最终的车间优化方案。
表3 DMPSO算法参数设定对比
Tab.3 Comparison of DMPSO algorithm parameter setting
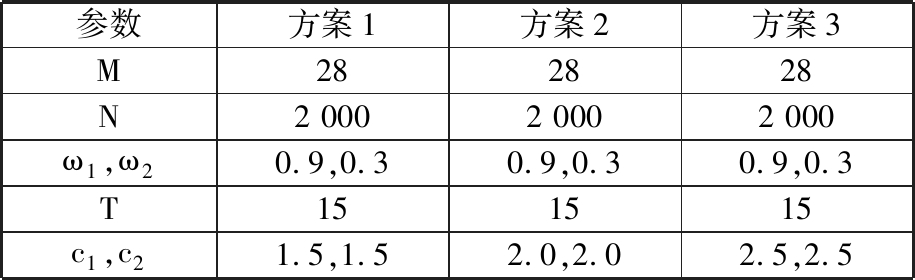
参数方案1方案2方案3M282828N2 0002 0002 000ω1,ω20.9,0.30.9,0.30.9,0.3T151515c1,c21.5,1.52.0,2.02.5,2.5
3.3 优化结果及分析
本文使用DMPSO算法在MATLAB仿真平台上对车间布局进行仿真,根据上述参数,为保证得到的结果更具可靠性,上述三个方案中,每个方案都运行30次,取其中相对较好的5次计算结果,再计算5次结果的平均值作为该方案的平均适应度值,对比数据如表4所示。
表4 三种方案对比分析
Tab.4 Comparative analysis of three schemes
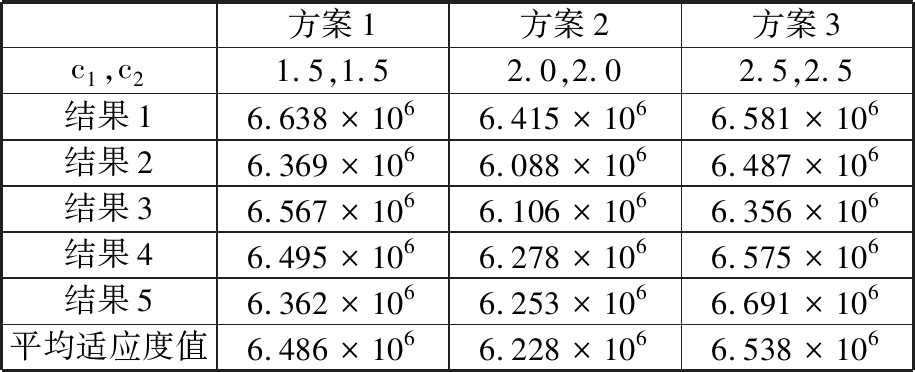
方案1方案2方案3c1,c21.5,1.52.0,2.02.5,2.5结果16.638×1066.415×1066.581×106结果26.369×1066.088×1066.487×106结果36.567×1066.106×1066.356×106结果46.495×1066.278×1066.575×106结果56.362×1066.253×1066.691×106平均适应度值6.486×1066.228×1066.538×106
对比3组数据可发现,当c1=c2=2.0时,平均适应度值为6.228×106,在3组数据中最小,此时优化效果最好,得到优化后布局方案物料搬运总成本约为7.785×106元,而曲轴公司提供的初始布局方案物料搬运成本约为8.951×106元。由此可见,通过DMPSO算法优化后的布局方案确实能有效减少车间物料搬运成本,通过计算能够得出其物料搬运成本下降率达到了13.03%,说明DMPSO算法在解决车间布局问题上是有效的。
在利用DMPSO算法对曲轴车间案例进行求解时,其优化过程如图4所示。
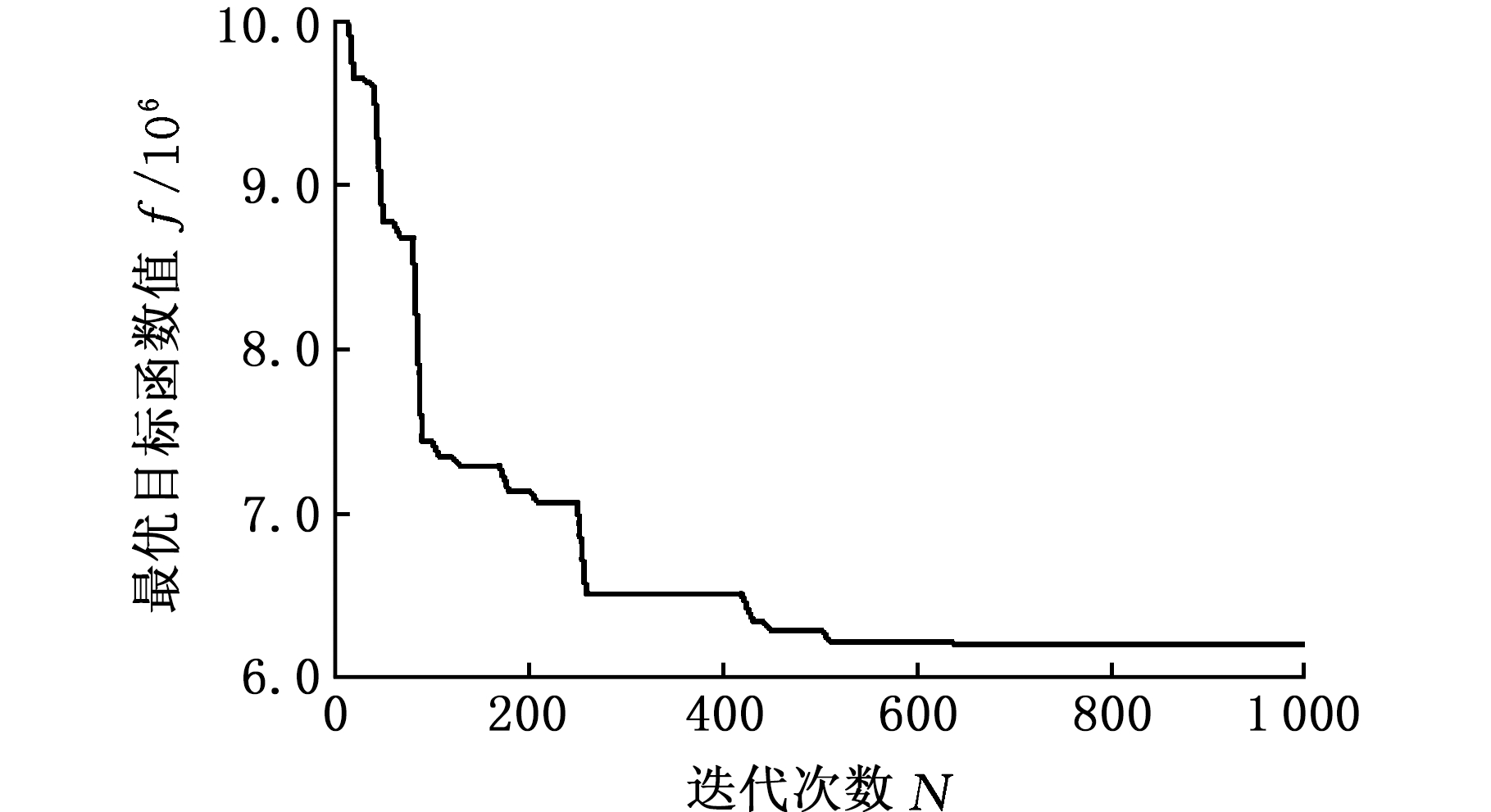
图4 DMPSO算法优化过程
Fig.4 Optimization process of DMPSO algorithm
从优化结果可以看出,大概在第630代左右,函数值基本停止波动,达到收敛,说明该算法具有较好的收敛能力。
3.4 车间优化结果
根据DMPSO算法对车间布局的优化结果,再结合曲轴生产的具体工艺流程,并考虑实际车间预留的人行通道,可以得到最终如图5所示的车间布局,其中每个设备的具体坐标如表5所示。
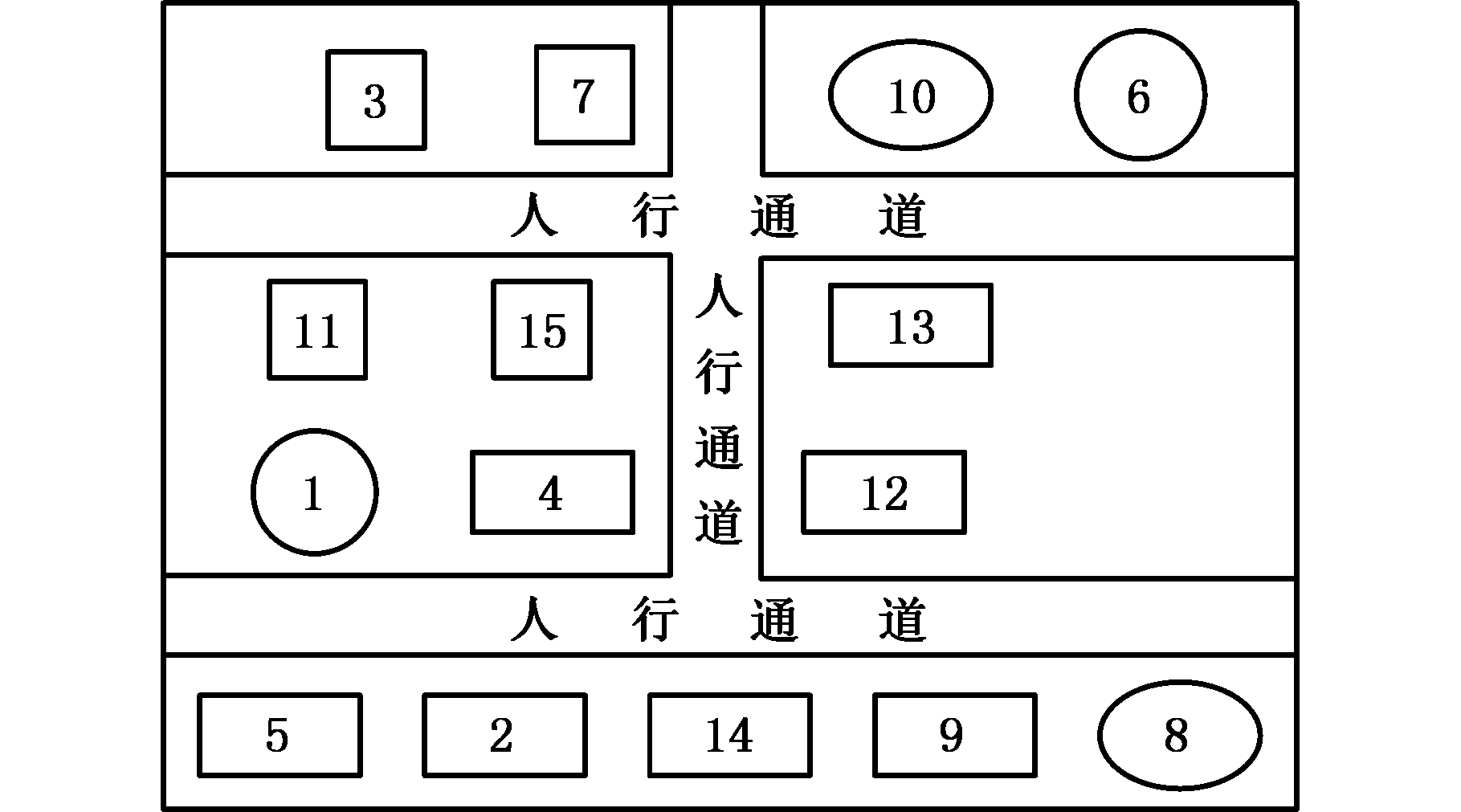
图5 车间最终布局
Fig.5 Final layout of workshop
4 建立车间布局三维模型
在经过DMPSO算法优化得到最终的车间布局方案后,本文利用CATIA软件对曲轴生产车间进行三维建模。根据优化后得到的车间布局方案,选取CATIA功能模块中的机械设计模块对车间设备进行比例为1∶1的三维可视化建模,再利用装配设计模块按照最终布局方案对各个设备进行排列。CATIA软件具备漫游功能,设计人员可以根据需要浏览车间内设备的布局情况,对布局方案进行调整和优化,大大提高了工作效率。图6所示为使用CATIA软件建立的曲轴车间设备布局模型。
表5 车间设备最终坐标
Tab.5 Final coordinates of workshop equipment
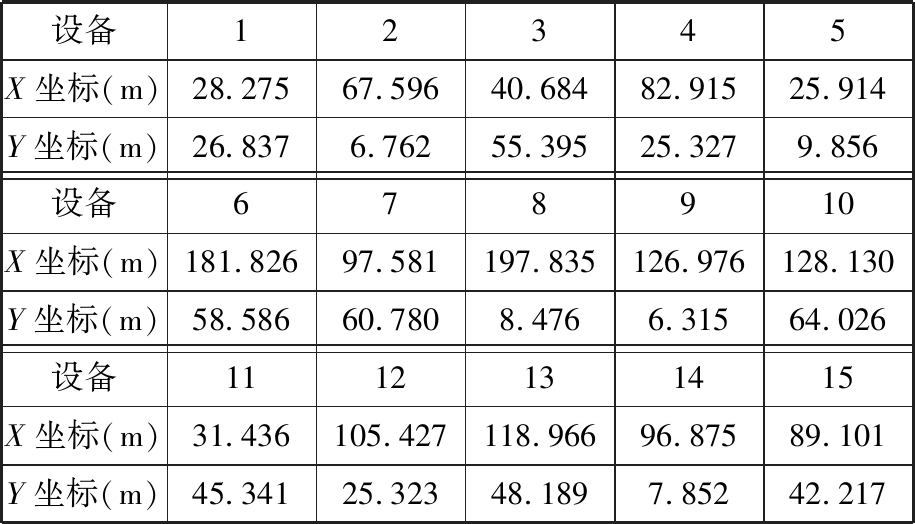
设备12345X坐标(m)28.27567.59640.68482.91525.914Y坐标(m)26.8376.76255.39525.3279.856设备678910X坐标(m)181.82697.581197.835126.976128.130Y坐标(m)58.58660.7808.4766.31564.026设备1112131415X坐标(m)31.436105.427118.96696.87589.101Y坐标(m)45.34125.32348.1897.85242.217

图6 曲轴车间布局三维模型
Fig.6 3D model of crankshaft workshop layout
5 结语
(1)本文应用一种新模式PSO算法(DMPSO算法)求解车间布局优化问题,为保证算法的局部与全局搜索能力,根据算法所处的迭代阶段和粒子的分布情况动态改变惯性权重的大小,并实时调整粒子的飞行路线,提高了粒子得到全局最优解的可能性。
(2)采用二维向量表征车间设备的空间位置,并建立相应的布局数学模型,同时考虑大型船舶动力部件装配与精加工工艺步骤的连贯性以及车间面积利用率等因素,引入车间面积占有率和空间面积利用率两个概念,确立了相关约束条件以保证优化后的车间布局符合实际需求。
(3)给出了船用曲轴生产车间设备布局案例,结果表明,经过DMPSO算法优化后得到的车间布局方案确实降低了物料搬运成本,下降率达到了13.03%,证明该算法有较强的寻优能力,在实际车间设备布局中切实可行。
[1] 张金国,刘春林,王刚伟,等.船舶动力装置模块化建造工艺设计及精度分配[J].中国舰船研究,2018,13(1):140-144.
ZHANG Jinguo, LIU Chunlin, WANG Gangwei, et al. Modularization Construction Process Design and Precision Distribution of Ship Power Plant[J]. Chinese Naval Ship Research 2018,13(1):140-144.
[2] 张青雷,郝文玲,段建国,等.考虑系统重用和加工任务重现的制造系统布局重组规划[J].机械工程学报,2015,51(3):170-181.
ZHANG Qinglei, HAO Wenling, DUAN Jianguo, et al. Layout Reorganization Planning of Manufacturing System Considering System Reuse and Processing Task Reproduction [J]. Journal of Mechanical Engineering 2015,51(3):170-181.
[3] TAYAL A,SINGH S P.Integrating Big Data Analytic and Hybrid Firefly-chaotic Simulated Annealing Approach for Facility Layout Problem[J]. Annals of Operations Research,2016: 1-26.
[4] LI C, YANG S,NGUYEN T T. A Self-Learning Particle Swarm Optimizer for Global Optimization Problems[J].IEEE Transactions on Systems, Man, and Cybernetics, Part B(Cybernetics), 2012,42(3):627-646.
[5] 龚全胜,李世其.基于遗传算法的制造系统设备布局设计[J].计算机工程与应用,2004(26):202-205.
GONG Quansheng, LI Shiqi. Equipment Layout Design of Manufacturing System Based on Genetic Algorithm [J]. Computer Engineering and Application, 2004 (26): 202-205.
[6] 杜江,袁中华,王景芹.动态改变惯性权重的新模式粒子群算法[J].安徽大学学报(自然科学版),2018,42(2):60-66.
DU Jiang, YUAN Zhonghua, WANG Jingqin. a New Pattern Particle Swarm Optimization for Dynamically Changing Inertial Weights[J]. Journal of Anhui University (Natural Science Edition),2018,42(2):60-66.
[7] 郭源源,王谦,梁峰.基于粒子群优化算法的车间布局设计[J].计算机集成制造系统,2012,18(11):2476-2484.
GUO Yuanyuan, WANG Qian, LIANG Feng. Shop Layout Design Based on Particle Swarm Optimization Algorithm [J]. Computer Integrated Manufacturing System, 2012, 18(11):2476-2484.
[8] 丁祥海,姚文鹏.基于粒子群算法的多目标可重构设施布局方法[J].中国机械工程,2017,28(7):852-861.
DING Xianghai, YAO Wenpeng. A Multi-objective Reconfigurable Facility Layout Method Based on Particle Swarm Optimization Algorithm [J]. China Mechanical Engineering 2007,28(7): 852-861.
[9] XIE Fang, JI Shouwen, TONG Lu, et al. Research of Working-areas Layout Study Method in Logistics Park Based on Genetic Algorithm[C]∥2008 IEEE International Conference on Service Operations, Logistics and Informatics. Beijing, 2008:1365-1370.
[10] 陈希,王宁生.基于遗传算法的车间设备虚拟布局优化技术研究[J].东南大学学报(自然科学版),2004,34(5):627-631.
CHEN Xi, WANG Ning. Research on Virtual Layout Optimization of Workshop Equipment Based on Genetic Algorithm [J]. Journal of Southeast University (Natural Science Edition) 2004, 34(5): 627-631.
[11] ZHANG Y, ZHANG H, XIA M M, et al. Research on Applying Unidirectional Loop Layout to Optimize Facility Layout in Workshop Based on Improved Genetic Algorithm[C]∥2009 IITA International Conference on Control, Automation and Systems Engineering. Zhangjiajie, 2009:144-147.
[12] 邓兵,林光春.改进SLP和遗传算法结合的车间设备布局优化[J].组合机床与自动化加工技术,2017(8):148-151.
DENG Bing, LIN Guangchun. Optimization of Workshop Equipment Layout with Improved SLP and Genetic Algorithm[J]. Combined Machine Tools and Automatic Machining Technology,2017(8): 148-151.
[13] 李建荣,廖达雄,陈冰,等.基于粒子群算法的车间布局优化应用研究[J].中国制造业信息化,2011,40(3):6-9.
LI Jianrong, LIAO Daxiong, CHEN Bing, et al. Application of Particle Swarm Optimization in Shop Layout Optimization[J]. China’s Manufacturing Industry Informatization, 2011, 40(3): 6-9.
[14] SHI Y, EBERHART R. A Modified Particle Swarm Optimizer[C]∥1998 IEEE International Conference on Evolutionary Computation Proceedings. Anchorage, 1998:69-73.
[15] 邵增珍,王洪国,刘弘.具有启发式探测及自学习特征的降维对称微粒群算法[J].计算机科学,2010,37(5):219-222.
SHAO Zengzhen, WANG Hongguo, LIU Hong. A Reduced Dimensional Symmetric Particle Swarm Optimization Algorithm with Heuristic Detection and Self Learning Characteristics[J]. Computer Science,2010,37(5):219-222.
[16] SHI Y, HOU L, ZHENG X. Solving Workshop Layout by Hybridizing Invasive Weed Optimization with Simulated Annealing[C]∥2015 IEEE 19th International Conference on Computer Supported Cooperative Work in Design. Calabria, 2015:484-488.
