0 引言
近年来,我国大力推进交通基础设施建设,在大型交通工程上不断取得突破和发展。随着各种交通工程的进行,传统的工法和工程机械无法满足各种新的工程需求,大量的新工法和新设备不断涌现。
刚性悬挂四轮车辆力学问题属于四点支撑的超静定问题。许多学者针对各种不同机械设备的具体工况展开了相关研究,如赵延治等[1]对钳夹车的双层并联过约束起升机构进行了力学研究;刘振国等[2]以超静定理论对起重机多支腿反力进行了求解;王月云等[3]基于ANSYS对高空作业车的支腿进行仿真分析;张希望[4]基于工程实践,总结了一套高安全系数的计算方法;张小广等[5]通过拓扑优化设计对起重机支腿进行研究。
本文以刚性悬挂四轮车辆为研究对象,进行悬挂分支的静力解算,定义了不均衡载荷系数,基于载运偏载和悬挂分支刚度分析了台车的均载特性。
1 刚性悬挂四轮车辆力学解算
1.1 车辆整体设计
台车满载后重心较高,考虑其特殊工况下的稳定性和安全性,采用全刚性悬挂设计,简化后的台车结构如图1所示。台车满载重力为G,轴距为L2,轮距为L1,悬挂与轮辋的连接点分别为A、B、C、D,设四点所受的支反力分别为FA、FB、FC、FD,以台车的形心为坐标原点,台车满载后的重心相对形心沿车长度方向上的偏移量为x,沿宽度方向上的偏移量为y。
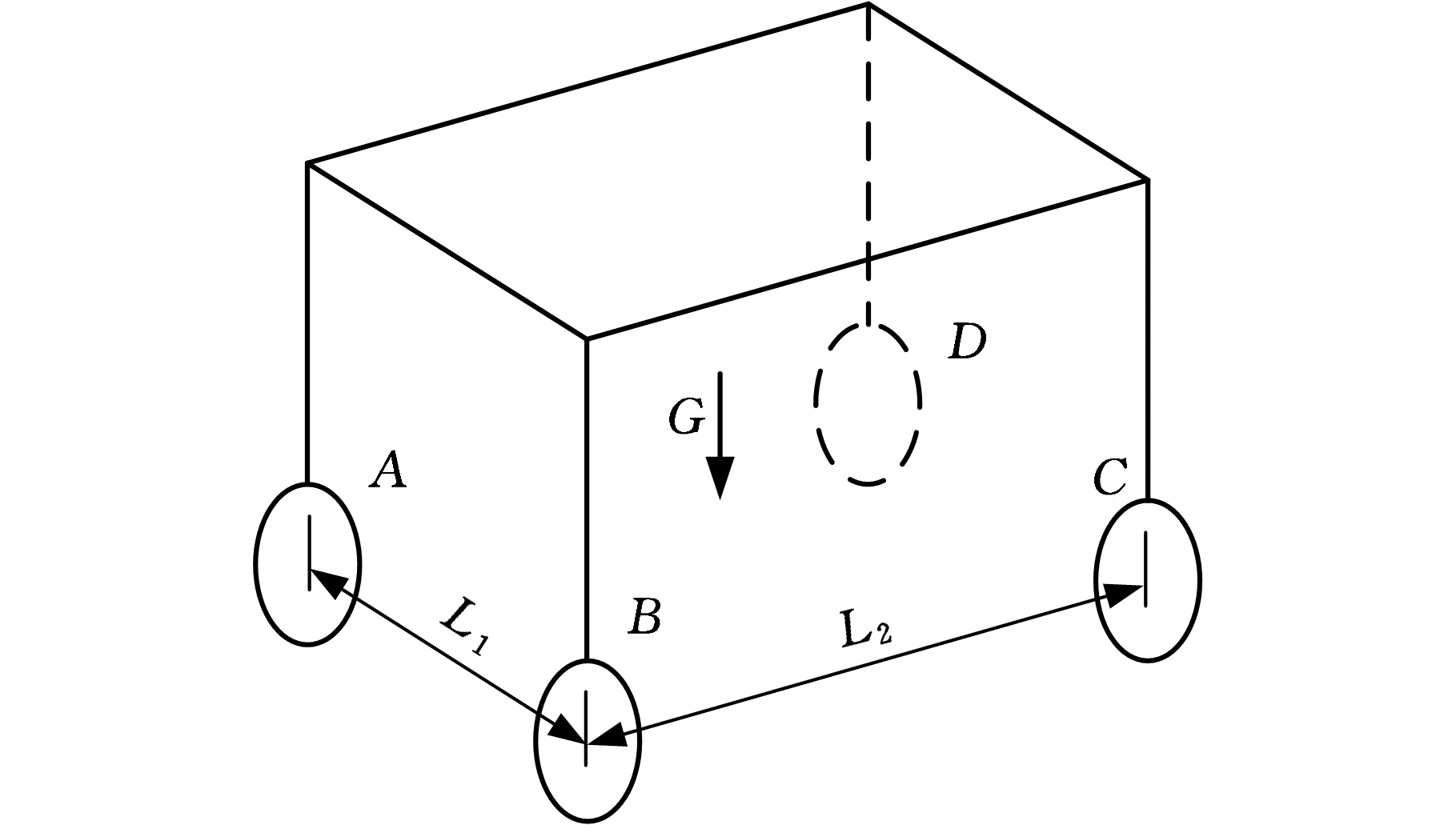
图1 台车结构示意图
Fig.1 Structural representation of vehicle
1.2 轮胎承载刚度
在标准气压下对台车所用轮胎进行承载实验,研究轮胎承载与下沉量的关系。实验中,轮胎负载分12次从1 kN逐渐加载至12 kN,通过拉线传感器采集下沉量数据,重复测量取平均值,结果显示轮胎的下沉量与负载成近似线性关系。如图2所示,将所得实验数据通过MATLAB进行拟合,可得标准气压下轮胎的承载刚度K。
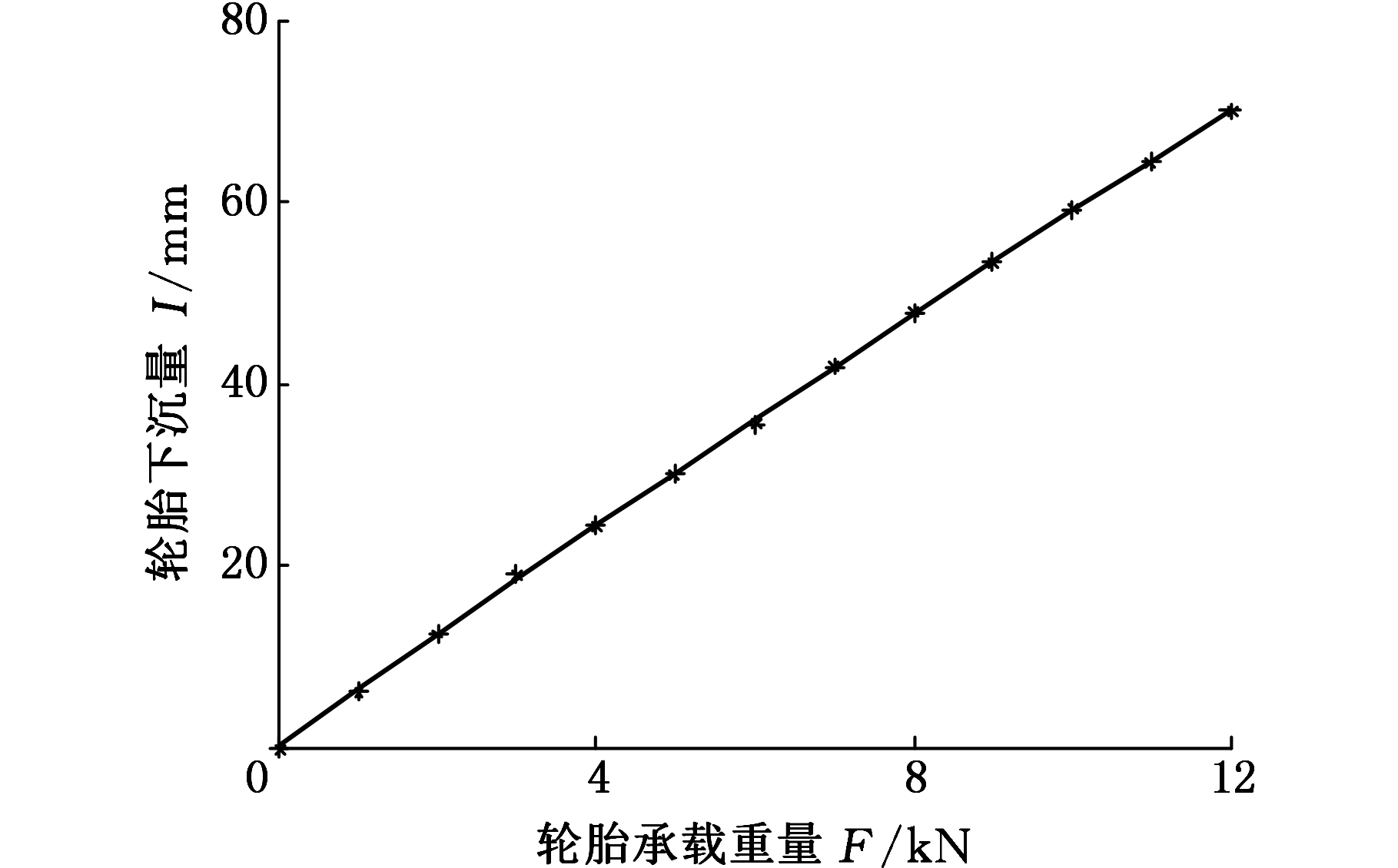
图2 轮胎承载实验数据
Fig.2 Experimental data of tire loading test
车辆实际使用过程中,气压对轮胎的承载刚度影响是巨大的,孙达[6]通过理论建模计算和实验验证的方法对气压与轮胎下沉量的关系进行了研究,本文将轮胎气压与轮胎下沉量的关系进一步简化表示为轮胎气压与轮胎承载刚度的关系:
K=f(p)
(1)
式中,p为轮胎实际气压。
车辆在实际使用过程中很难保精确证所有轮胎的气压相等,因而各轮胎的实际承载刚度很难保持一致,设A、B、C、D四个悬挂分支所对应的承载刚度分别为K1、K2、K3、K4。
1.3 车辆悬挂静力解算
图1所示车辆模型的静力平衡方程如下:
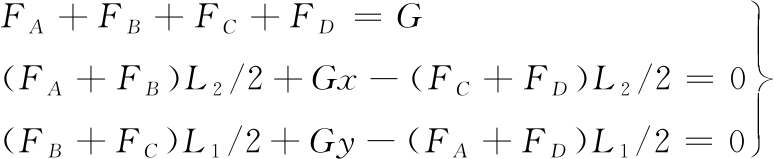
(2)
由于车架刚度远大于轮胎的刚度,因此根据轮胎的承载下沉量增加变形协调方程[7]。车架刚度大,当轮胎承载变形后,点A1、B1、C1、D1仍构成平面,设其为平面M,如图3所示。

图3 台车承载变形示意图
Fig.3 Diagram of vehicle deformation
设轮胎承载后,点A、B、C、D的位移分别为Δ1、Δ2、Δ3、Δ4,以B点为例,根据小变形原理,设轮胎变形后的点B1位于点B的正下方,在B点处建立笛卡儿坐标系,则平面M的方程为
(3)
D1点为台车承载变形后D点的对应点,将其坐标(L2,L1,Δ4)代入式(3),可得关于Δ1、Δ2、Δ3、Δ4的变形协调方程:
(4)
轮胎下沉量也可以用刚度方程来表示,简写为
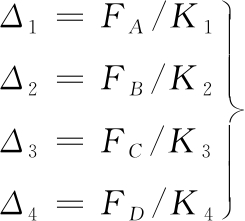
(5)
将式(5)代入式(4),可得附加力的平衡方程:
(6)
联立式(2)、式(6)可解得基于刚度的各分支支反力。
2 刚性悬挂四轮车辆均载性分析
2.1 台车不均衡载荷系数
为了有效衡量台车的均载特性,结合台车实际情况,参考统计学中均方差的概念,定义不均衡载荷系数λ来衡量台车的均载特性:
(7)
式中,![]() 为FA、FB、FC、FD的平均值。
为FA、FB、FC、FD的平均值。
式(7)的主体内容是4个分支支反力的均方差,反映了分支支反力的离散程度,由于台车满载重量与分支支反力为近似线性关系,所以用均方差除以G使系数适用于台车不同载重量的工况,将以上结果以e为底数进行指数运算是为了扩大系数的分辨率,使之具备更好的平滑性和阶段性。
反映到台车上,不均衡载荷系数是衡量台车均载性的系数,其理论取值范围是[1, ∞),当不均衡载荷系数的值为1时,各分支的支反力完全相等,台车处于完全均载状态,随着不均衡载荷系数的增大,各分支支反力的离散程度不断扩大,台车的均载性变差。
2.2 台车偏载对均载性的影响
首先分析偏载对台车均载性的影响,假设台车4个轮胎的承载刚度相等,则台车偏载量与各分支支反力的关系如图4所示。图4中,4个曲面仅有一个公共点,即当且仅当台车无偏载时,各分支支反力相同,台车可实现完全均载。用不均衡载荷系数来描述台车偏载对均载性的影响,结果如图5所示。
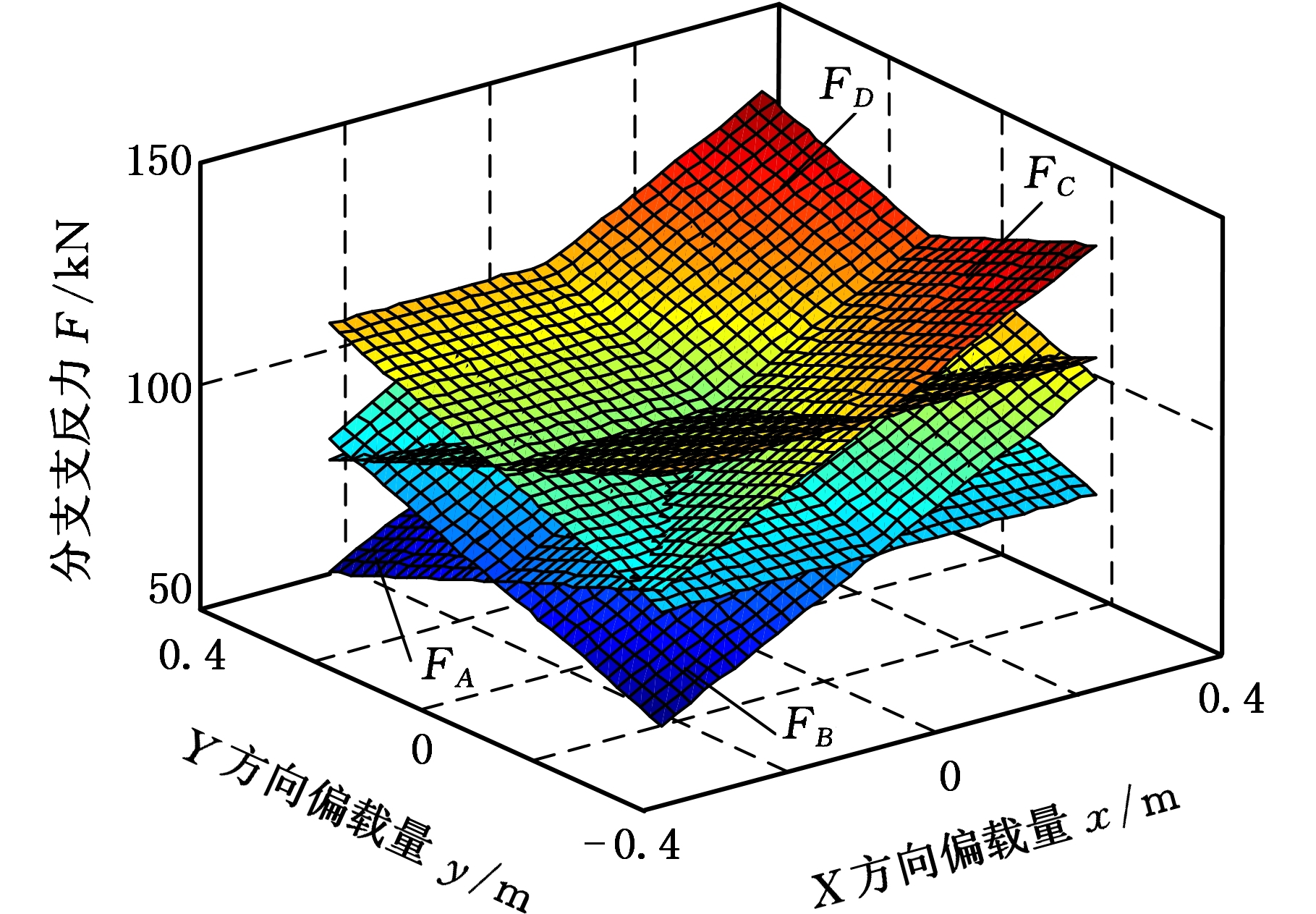
图4 偏载量与支反力的关系图
Fig.4 The relationship between bias load and supporting reaction
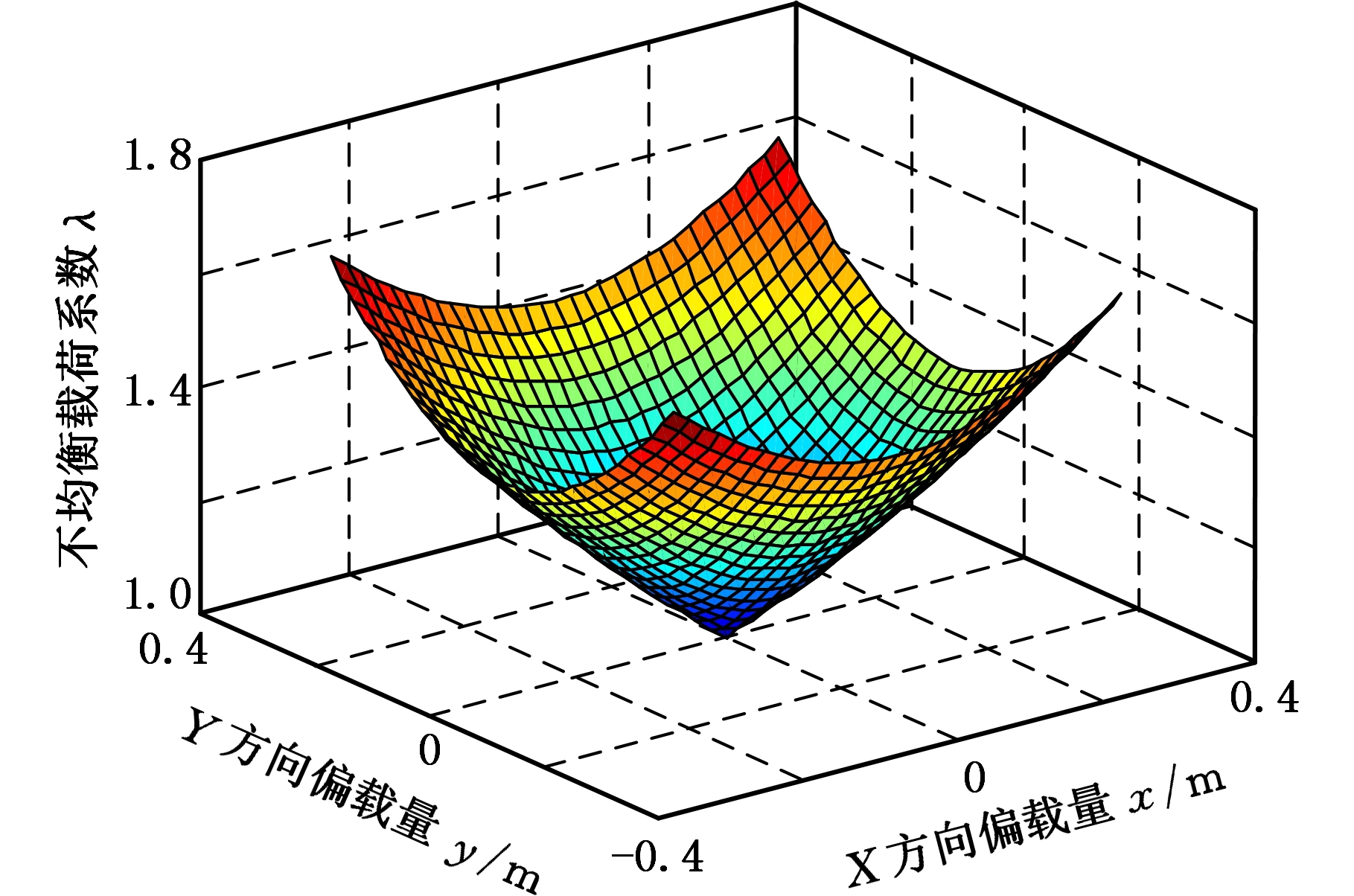
图5 偏载与不均衡载荷系数的关系
Fig.5 The relationship between bias load and unbalanced load coefficient
将图5用等高线形式表示,如图6所示,等高线呈椭圆形,不均衡载荷系数变化较为均匀,且Y方向上的偏载量对台车不均衡载荷系数的影响大于X方向的偏载量对台车不均衡载荷系数的影响。台车轴距大于轮距,不均衡载荷系数对横向的偏载更为敏感。
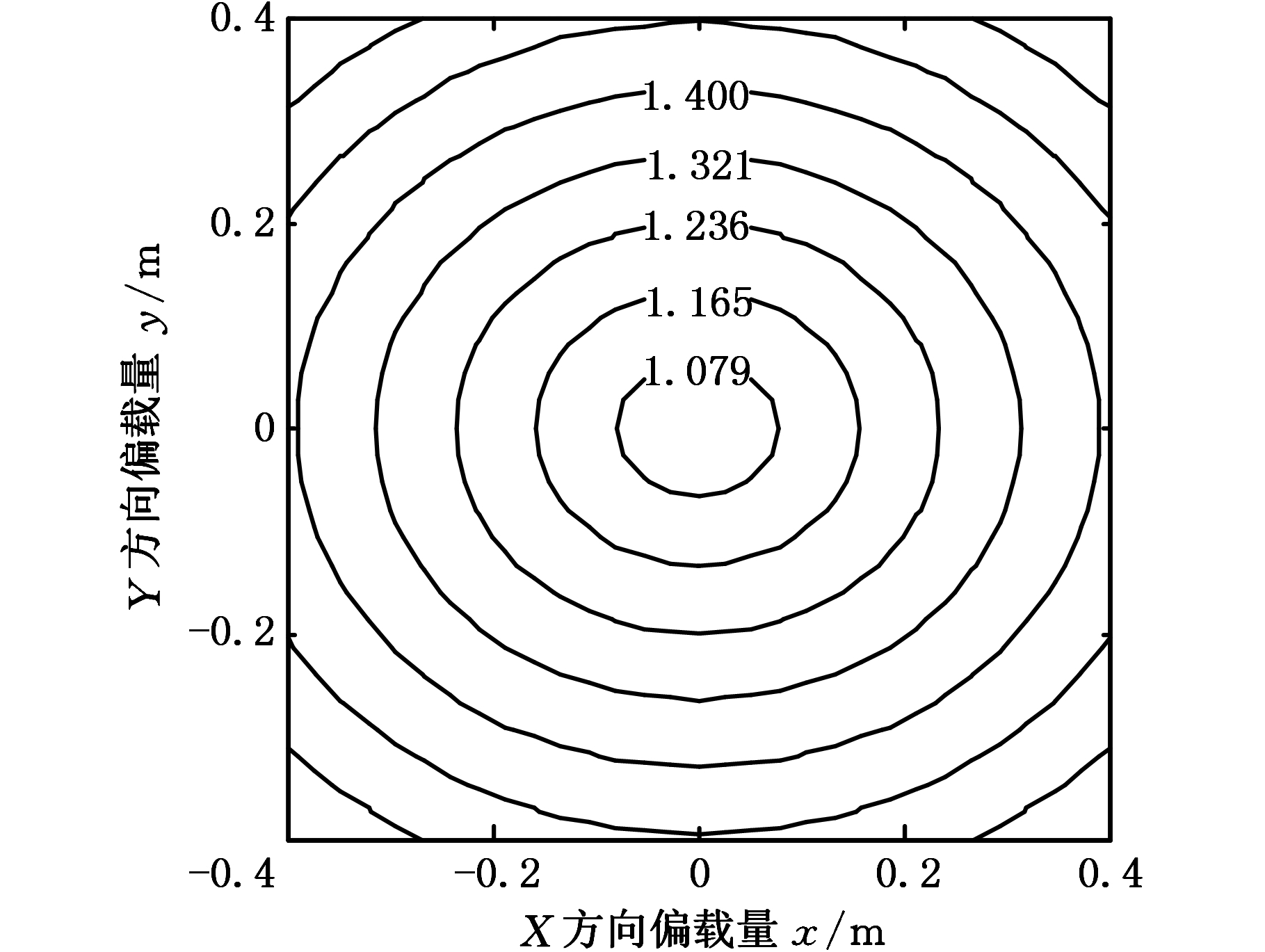
图6 偏载与不均衡载荷系数关系等高线图
Fig.6 Contour map of the relationship between bias load and unbalanced load coefficient
2.3 分支刚度对均载性的影响
为了全面而系统地研究分支刚度对车辆分支支反力的影响,采用空间性能图谱理论[8]对各分支刚度进行量纲一化处理,令i分支的量纲一承载刚度为
ki=Ki/T
(8)
T=K1+K2+K3+K4
由式(8)得k1+ k2+ k3+ k4=1。
令D分支轮胎的刚度为标准刚度,即k4=0.25,分析其他分支刚度变化对其支反力的影响。假设整车的重心与车架的形心重合,分支承载力与刚度之间的关系如图7所示,图中FA与FC的曲面重合,FB与FD的曲面重合,两曲面的交线表示4个分支的支反力大小相等,此时台车处于完全均载状态。两曲面的差值为支反力的差值,绘制出的等高线如图8所示。

图7 分支支反力与刚度的关系
Fig.7 The relationship between supporting reaction and stiffness
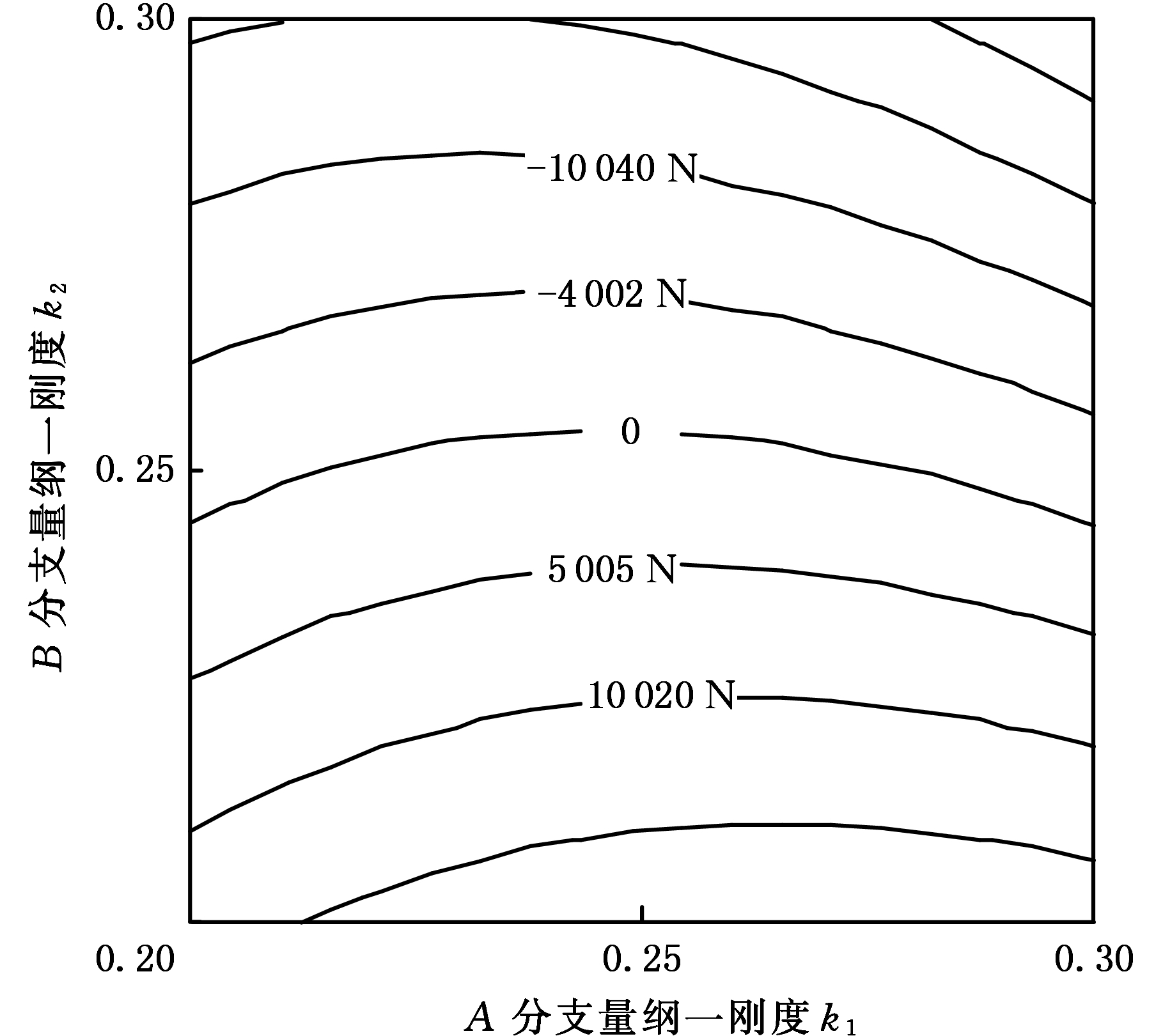
图8 分支支反力差值
Fig.8 The difference value of different supporting reaction
图8中,随着各分支刚度的变化,分支支反力差值相应变化,图中的“0”线表示台车各分支承载力相等,台车处于完全均载状态。例如,当4个分支刚度分别为0.25、 0.25、 0.25、 0.25时,各分支刚度相等,各分支支反力也相等,台车处于完全均载状态。分支A~D的刚度分别为0.28、0.25、0.22、0.25时,虽然各分支刚度存在偏差,但各分支支反力相等,台车仍处于完全均载状态。
用不均衡载荷系数来描述分支刚度对均载性的影响,如图9所示。图9中的“1”线表示台车的4个分支力相等,因此台车处于完全均载状态,等高线之间距离呈中间宽、两边窄的趋势分布,说明随着分支刚度偏差的增大,台车的不均衡载荷系数也变大,且不均衡载荷系数变化速度大于刚度偏差变化速度。
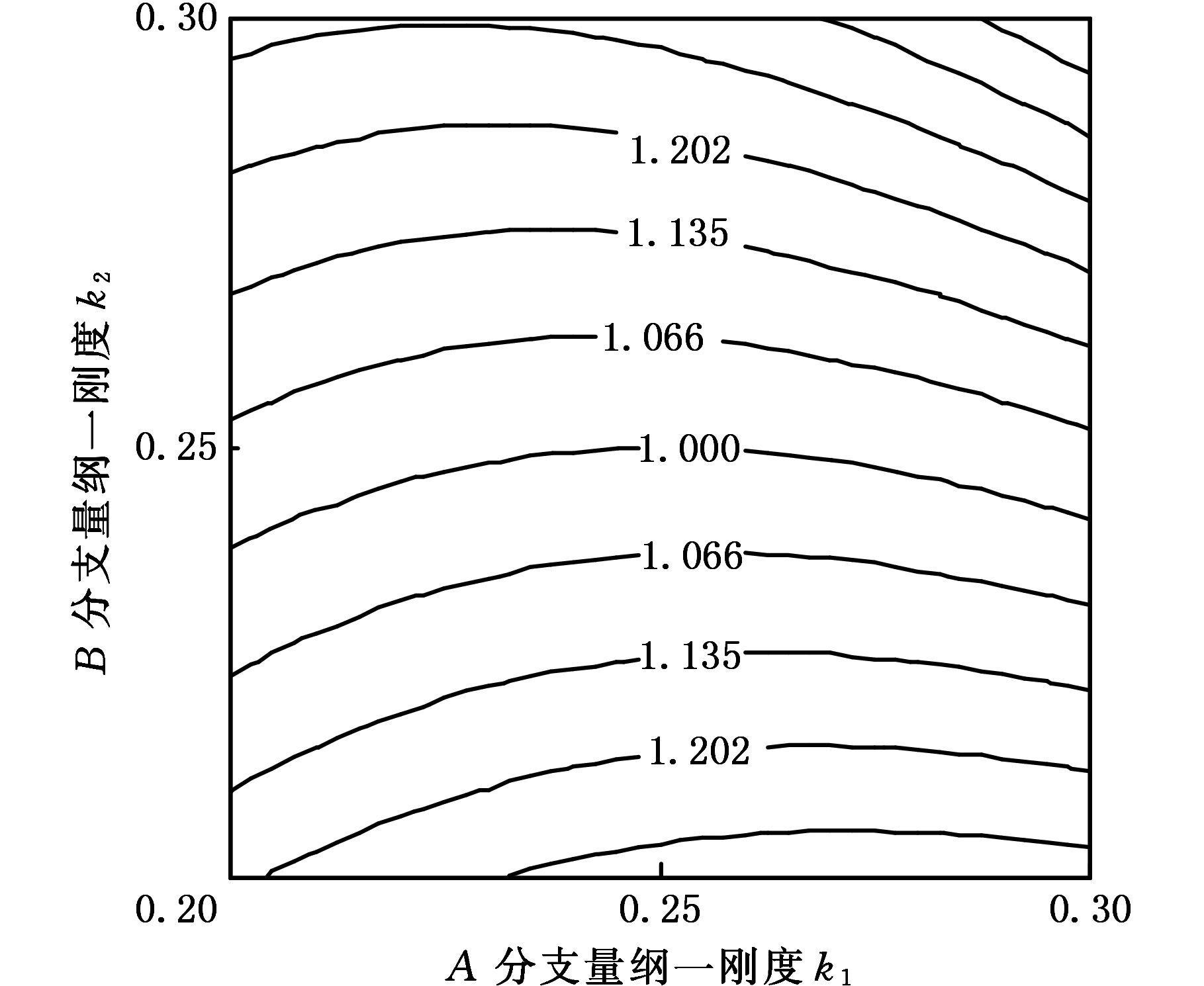
图9 分支刚度与不均衡载荷系数关系等高线图
Fig.9 Contour map of the relationship between stiffness and unbalanced load coefficient
图10所示为台车存在某偏载的情况下,分支刚度与承载力之间的关系,4个曲面无公共点即各分支的承载力无法完全相等,台车无法实现完全均载。

图10 某偏心距下各分支支反力与刚度关系
Fig.10 The relationship between supporting reaction and stiffness under a bias load
台车处于某偏载状态时,分支刚度与台车不均衡载荷系数的关系如图11所示。图11中不存在“1”线,即台车不存在完全均载的情况,这是由台车偏载决定的。等高线呈中间宽、两边窄的趋势分布,说明分支刚度偏差和台车不均衡载荷系数正相关,且不均衡载荷系数的变化速度大于刚度偏差变化的速度。
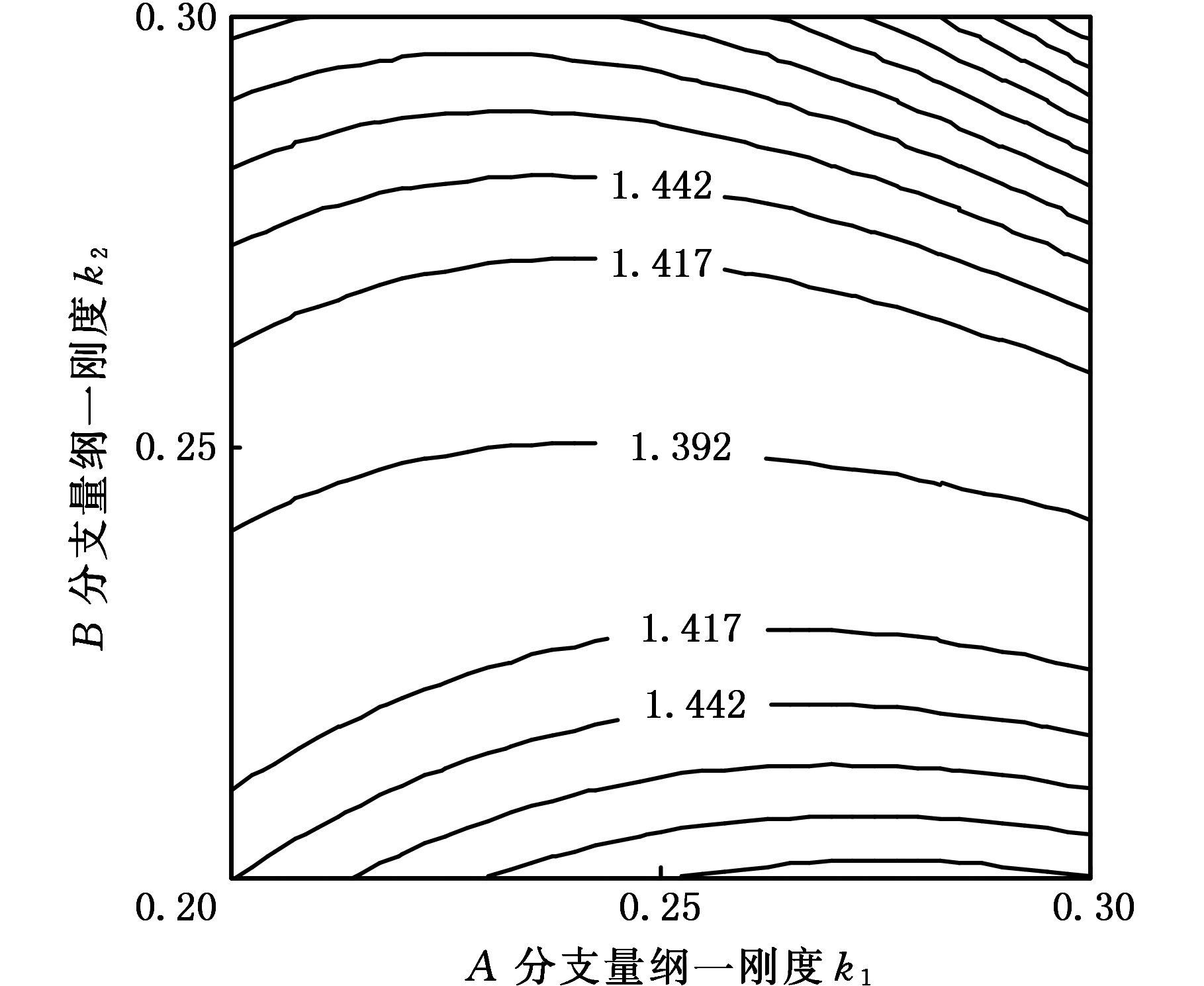
图11 某偏载下分支刚度与不均衡载荷系数 关系等高线图
Fig.11 Contour map of the relationship between stiffness and unbalanced load coefficient under a bias load
图9、图11中的每条等高线上的数据点(不均衡载荷系数)对B分支刚度的变化更为敏感,这是由预先令D分支的刚度为标准刚度所引起的,同时也说明了保持对角分支刚度的相近更利于提高台车的均载性。
3 轮胎承载实验及台车均载性实验
3.1 轮胎承载实验
轮胎承载实验主要研究气压、载荷对轮胎下沉量的影响。实验分为两部分,第一部分测量标准胎压下载荷与下沉量的关系,第二部分测量固定10 t载荷下不同胎压对轮胎下沉量的影响。主要实验设备见表1。
表1 主要设备和仪器
Tab.1 Main instruments andequipments
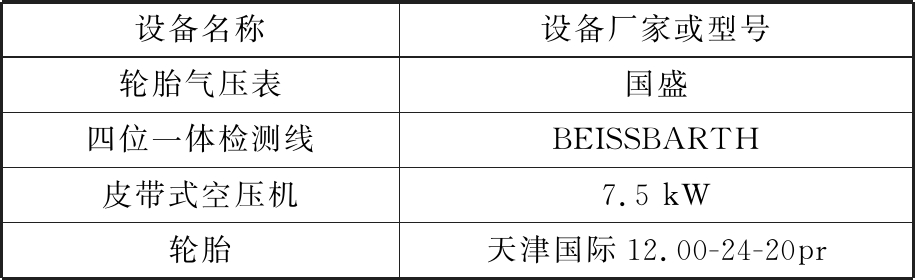
设备名称设备厂家或型号轮胎气压表国盛四位一体检测线BEISSBARTH皮带式空压机7.5 kW轮胎天津国际12.00-24-20pr
轮胎在10 kN载荷下,胎压分10次从1.15 MPa逐渐递减至0.70 MPa,通过拉线传感器采集下沉量数据,重复测量取平均值,将下沉量换算成刚度后,用MATLAB进行二次函数拟合,结果如图12所示。

图12 胎压与刚度关系
Fig.12 The relationship between type pressure and tire stiffness
3.2 台车均载性实验
台车满载后的重心可通过计算获得,实际支反力用轴重仪测得[9-10],选取4组数据进行实验(图13),结果如表2所示。

图13 均载性实验
Fig.13 Load-sharing experiment
将第一次实验所得的结果相加,作为台车满载质量进行计算,台车4个分支的计算支反力与实际支反力的对比如图14所示,不均衡载荷系数的对比如表3所示。图14中,实际测量值与理论计算值趋势基本保持一致,最大误差不超过6%,在误差允许范围内,验证了台车力学解算的正确性。表3中,4次实验的实验值略小于计算值。理论计算中,车架视为刚体。实际实验过程中,车架会有轻微的变形,车架的轻微变形对台车的均载有促进作用,整车的受力状态是向着均衡的方向发展的,因而会使台车的不均衡载荷系数出现一定幅度的向小偏移。在误差允许范围内,实验结果反映了台车的均载状态,证明了不均衡载荷系数的适用性。
表2 均载试验数据点
Tab.2 Data points of load-sharing experiment
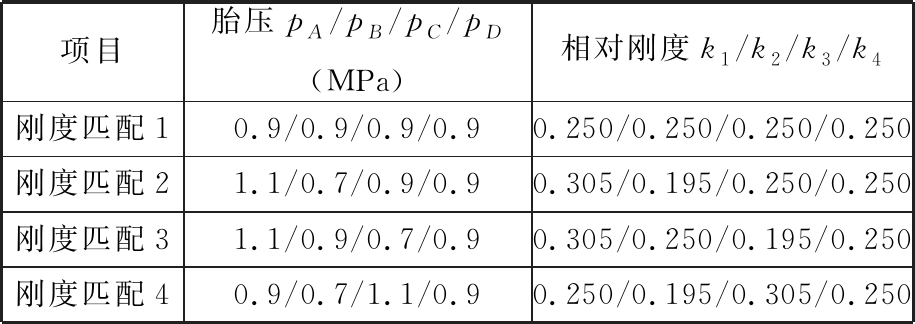
项目胎压pA/pB/pC/pD(MPa)相对刚度k1/k2/k3/k4刚度匹配10.9/0.9/0.9/0.90.250/0.250/0.250/0.250刚度匹配21.1/0.7/0.9/0.90.305/0.195/0.250/0.250刚度匹配31.1/0.9/0.7/0.90.305/0.250/0.195/0.250刚度匹配40.9/0.7/1.1/0.90.250/0.195/0.305/0.250

(a)刚度匹配1

(b)刚度匹配2

(c)刚度匹配3
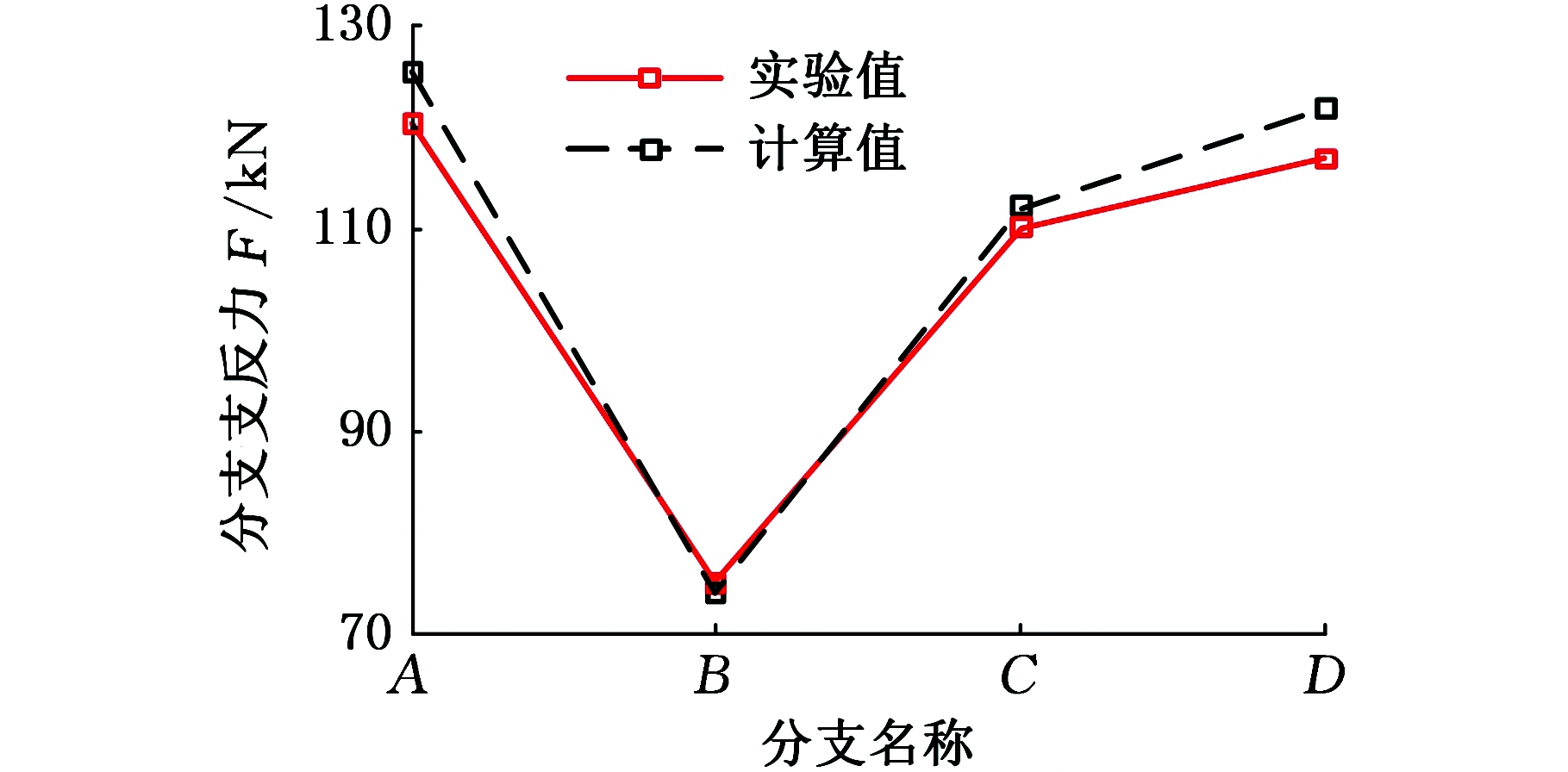
(d)刚度匹配4
图14 静力分析实验数值对比
Fig.14 Numerical comparison of static calculation and experiment
表3 不均衡载荷系数的计算与实验值
Tab.3 Numerical comparison of unbalanced load coefficient between static calculation and experiment

实验工况计算值实验值刚度匹配11.501.37刚度匹配21.611.60刚度匹配31.501.36刚度匹配41.601.53
4 结论
本文以刚性悬挂四轮车辆为研究对象进行了悬挂承载静力解算,得到了基于分支刚度的支反力解析解。通过定义台车的不均衡载荷系数,分析得到了载运偏载量和分支刚度对台车均载性的影响规律,通过实验,对计算和分析结果进行了验证。结果表明,胎压会引起轮胎刚度的变化,轮胎刚度的变化对各分支的支反力有明显的影响,通过定义不均衡载荷系数,可以有效地反映台车的均载状态。
[1] 赵延治, 焦雷浩, 王向南,等. 钳夹车双层并联过约束机构力学解算与均载性分析[J]. 中国机械工程, 2017, 28(5): 576-582.
ZHAO Yanzhi, JIAO Leihao, WANG Xiangnan,et al. Static Calculation and Load Sharing Characteristics Analysis of Double Parallel over Constrained Lifting Mechanisms of Schnabel Car[J]. China Mechanical Engineering, 2017, 28(5):576-582.
[2] 刘振国, 滕儒民, 吴海帆, 等. 一种八支腿起重机支腿反力研究[J]. 机械设计与制造, 2015(5):12-15.
LIU Zhenguo, TENG Rumin, WU Haifan,et al. Research on Outrigger Reaction Force of Eight-outrigger[J]. Machinery Design & Manufacture, 2015(5):12-15.
[3] 王月云, 耿林, 张小委. 基于ANSYS Workbench分析影响高空作业车支腿软腿因素[J]. 农业装备技术, 2017, 43(5): 50-52.
WANG Yueyun, GENG Lin, ZHANG Xiaowei. Analysis of the Factors Affecting the Leg Soft Leg of Aerial Vehicle Based on ANSYS Workbench[J]. Agricultural Equipment & Technology, 2017, 43(5):50-52.
[4] 张希望. 汽车起重机支腿压力实用型计算法[J]. 建筑机械化, 2018(3):31-34.
ZAHNG Xiwang. A Practical Method for Calculating the Outrigger Pressure of Truck Crane[J]. Construction Mechanization, 2018(3):31-34.
[5] 张小广, 颜涛, 贾晓杰,等. 起重机支腿结构拓扑优化设计[J]. 工程机械, 2014, 45(5):37-40.
ZHANG Xiaoguang, YAN Tao, JIA Xiaojie,et al. Topological Optimization Design of Crane Outrigger Structure[J]. Construction Machinery and Equipment, 2014, 45(5):37-40.
[6] 孙达. 汽车轮胎滚动半径试验研究[D]. 秦皇岛:燕山大学, 2005.
SUN Da. Test and Research of Automobile Tyre Rolling Radius[D]. Qinhuangdao: Yanshan University, 2005.
[7] 韩玮, 刘志军. 基于平面法求解刚性支承平面多点支承的反力[J]. 建筑机械, 2013(7):100-101.
HAN Wei,LIU Zhijun. The Solution of Point Supported Reaction in Rigid Plane Based on Planar Method[J]. Construction Machinery, 2013(7):100-101.
[8] 刘辛军, 汪劲松, 高峰. 并联六自由度微动机器人机构的设计方法[J]. 清华大学学报(自然科学版), 2001, 41(8): 16-20.
LIU Xinjun, WANG Jinsong, GAO Feng. Design of 6-DOF Parallel Microrobotics Mechanism [J]. Journal of Tsinghua University(Science and Technology), 2001, 41(8):16-20.
[9] 韦志康, 何水龙, 杨蓉, 等. 基于LabVIEW的汽车轴重测量系统[J]. 汽车实用技术, 2010(1):50-53.
WEI Zhikang,HE Shuilong, YANG Rong,et al. Axle Load Measurement System for Automobile Based on LabVIEW [J], Automobile Applied Technology, 2010(1):50-53.
[10] 中华人民共和国国家质量监督检验检疫总局. 机动车安全技术检验项目和方法[J]. 汽车与安全, 2015(2):58-85.
AQSIQ. Items and Methods of Power-driven Vehicles Safety Technology Inspection[J]. Automobile and Safety, 2015(2): 58-85.