0 引言
某型航空发动机自服役以来,在外场使用中,频繁出现附件机匣锥齿轮破裂的故障,表现为重载锥齿轮齿根处断裂,严重影响了发动机的运行安全性和使用寿命。因此,找到造成附件机匣锥齿轮破裂故障的主要因素,降低附件机匣锥齿轮破裂故障发生率已经迫在眉睫。
在影响齿轮破坏失效数值仿真和试验测试分析方面,国内外学者进行了较多的研究。DAWSON[1]认为润滑油膜厚度与粗糙度的比值对齿轮齿面破坏至关重要。HANDSCHUH等[2]开发了二维传热模型来模拟齿轮齿面摩擦温度,获得了齿面承受的载荷与接触面润滑剂量的关系。YOGESH等[3]提出的累积衰减指数方法能反映不同齿轮参数对总齿轮啮合刚度恶化程度的影响。崔伟成等[4]为了准确地诊断齿轮故障,根据齿轮故障振动信号的多分量调幅-调频特征,提出了一种局部均值解调法与局部特征尺度分解相结合的方法,并通过试验验证了该方法的有效性。李福益等[5]对某型涡扇发动机的下垂直锥齿轮辐板断裂排故进行试验研究,在试验器上进行故障再现试验及低周疲劳试验,确定了故障的主要原因是锥齿轮辐板加工厚度偏小且严重超差和表面粗糙度高。许愕俊等[6]对中央传动锥齿轮进行了行波共振破坏试验和数据分析,认为在弧齿锥齿轮设计之初就应对其进行动态响应计算和试验验证,调整齿轮行波共振动频。王大勇[7]计算了薄辐板结构齿轮的固有特性,绘制了行波共振图,采用模态叠加法计算了薄辐板齿轮在共振转速和工作转速下的稳态响应并绘制动应力曲线。李其汉等[8-9]对盘形锥齿轮振动特性进行深入研究,给出了该齿轮的行波共振条件及振动特性。郭兴辉等[10]研究了航空发动机锥齿轮的重合度和模态阻尼比对行波振动应力的影响,得出重合度对行波振动应力的响应较大、模态阻尼比对其影响较小的结论。韩二中等[11]对圆锥齿轮行波共振应力响应进行仿真计算,算出了圆锥齿轮的二、三节径行波共振应力响应。彭毓敏等[12]考虑啮合刚度、齿侧间隙和轴承支撑间隙等因素,运用集中质量法建立了三自由度直齿圆柱齿轮副弯扭耦合非线性振动模型,并据此研究了各参数对齿轮系统非线性振动特性的影响。在齿轮安装误差分析方面,刘光磊等[13-14]提出了低安装误差敏感性设计方法,定量分析了不同条件下安装误差对航空弧齿锥齿轮传动误差的影响,得出传动误差对小轮安装距误差更敏感的结论。尽管国内外学者对齿轮破裂分析问题开展了大量的研究工作,但关于装配参数对齿轮破裂故障影响的研究鲜有开展。
本文从宏观、微观角度对附件机匣传动锥齿轮的破裂形式进行了判断,并结合相关理论分析、有限元模态计算以及试验验证,探讨了附件机匣锥齿轮的齿轮间隙和主动锥齿轮垂直安装角度偏差对齿根应力的影响以及和破裂故障之间的联系。
1 理论方法
1.1 行波共振原理
锥齿轮与轮盘的形状非常相似,振动形式通常有节圆型、节径型和节圆节径复合型。实际工作中最易发生的节径型振动可以看成是由正反两方向的2个形状相同的余弦波(前行波和后行波)叠加而成的。前行波与顺齿轮转向相同,后行波与齿轮转向相反。前后行波的固有频率与激振频率相等时,齿轮就会引起行波共振[8]。
锥齿轮在旋转条件下产生节径型轴向振动时,主动锥齿轮前后行波共振频率与其动频、转速及节径数的关系可表示为
fF=fD+nm/60
(1)
fB=fD-nm/60
(2)
式中,fF为主动锥齿轮前行波振动频率,Hz;fB为主动锥齿轮后行波振动频率,Hz;fD为主动锥齿轮动频,Hz;n为主动锥齿轮转速,r/min;m为主动锥齿轮行波共振节径数。
主动锥齿轮行波共振转速与其动频、齿数及节径数的关系为
(3)
式中,前行波共振时取“-”;后行波共振时取“+”;z1为主动锥齿轮齿数。
1.2 模态分析理论
模态分析的经典定义:将线性定常系统振动微分方程组中的物理坐标转换为模态坐标,使方程组解耦,成为一组以模态坐标的模态参数描述的独立方程,以便求出系统的模态参数。坐标变换的变换矩阵为模态矩阵,其每列为模态振型[15]。对于本次研究的附件机匣锥齿轮,使用有限元素法可精确求解固有频率,建立有限元方程[16]:
(4)
式中,M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;![]() 分别为加速度矩阵、速度矩阵和位移矩阵;F(t)为载荷矩阵;t为时间。
分别为加速度矩阵、速度矩阵和位移矩阵;F(t)为载荷矩阵;t为时间。
因为齿轮的固有频率和振型与所受外力无关,小阻尼对固有频率和振型影响不大,因此,结构的自由振动方程可简化为
(5)
弹性体的自由振动可以分解为一系列的简谐振动的叠加。发生简谐振动时,位移的正弦函数表达式为
q(t)=Asinωt
(6)
式中,A为系统振动的振幅矩阵;ω为振动圆频率。
将式(6)代入式(5)得
(K-ω2M)q(t)=0
(7)
对于正定系统,式(7)有N个固有圆频率和N个非零向量(振型向量),则振型矩阵为
u=[q1(t) q1(t) … qN(t)]
(8)
由振型矩阵的正交性得
uTMu=diag(H1, H2,…,HN)
(9)
式中,Hi为系统第i阶主质量,i=1,2,…,N。
正则化振型矩阵为
(10)
由正则化振型矩阵的正交性得
(11)
式中,I为N阶单位矩阵。
2 数值仿真与试验研究
首先,计算附件机匣主动锥齿轮的固有频率和模态振型;然后,在齿轮啮合状态下,研究不同的啮合齿轮齿轮间隙和主动锥齿轮垂直安装角度对主动锥齿轮齿根应力的影响;最后,分析齿轮装配参数对齿轮破裂故障的影响。
2.1 求解模型
求解模型为一组啮合的附件机匣锥齿轮,包括主动和从动锥齿轮。主从动锥齿轮尺寸参数如表1所示,几何尺寸如图1所示。
表1 主从动锥齿轮主要尺寸参数
Tab.1 Geometric parameters of driving and driven bevel gears

基本参数主动锥齿轮 从动锥齿轮旋向左右齿数2530模数(mm)4.781压力角(°)20齿顶系数0.25螺旋角(°)15

图1 主从动锥齿轮几何尺寸
Fig.1 Geometries of driving and driven bevel gears
2.2 材料参数
锥齿轮材料为航空发动机用渗碳齿轮钢,该材料在20 ℃下的物理参数如下:密度7 841 kg/m3,弹性模量200 GPa,泊松比0.3。
2.3 有限元模型及边界条件
建立齿轮有限元模型时,对主动锥齿轮齿轮轴施加零位移约束条件,有限元计算模型采用二阶四面体网格划分形式,在齿根处进行网格细化,有限元计算模型如图2所示。研究齿轮啮合间隙变化对主动锥齿轮齿根应力的影响时,将齿轮啮合间隙分别调整为63.1 μm、145.2 μm、228.3 μm、298.1 μm、368.1 μm、445.1 μm、502.3 μm、615.2 μm和732.0 μm。研究主动锥齿轮垂直安装角度偏差对主动锥齿轮齿根应力的影响计算时,在445.1 μm齿轮啮合间隙工况下,选取角度偏差为2°、1°、-1°、-2°及无偏差共5种工况。

(a)主动锥齿轮

(b)啮合锥齿轮
图2 有限元计算模型
Fig.2 Finite element calculation model
2.4 模态试验
为了验证主动锥齿轮模态计算结果的准确性,校正模态计算模型,运用锤击法,采用单点激励多点响应的方式,针对主动锥齿轮进行模态试验。
试验装置包括计算机、Dong Hua Dynamic Acquisition System(DHDAS)动态信号采集分析系统、力锤、加速度传感器、锥齿轮等。根据模态计算结果在主动锥齿轮上粘贴8个加速度传感器进行试验,加速度传感器在主动锥齿轮齿背处、沿周向均匀布置,如图3所示,试验设备装置如图4所示。

图3 模态试验测点布置
Fig.3 Modal test point layout

图4 试验设备装置示意图
Fig.4 Test equipment installation schematic
2.5 仿真与试验结果对比分析
数值仿真和试验测试获得的主动锥齿轮的模态振型和固有频率结果如图5、图6和表2所示。
由图5、图6和表2分析发现:试验测试结果中,主动锥齿轮存在一节径和二节径两种振型,一节径振型的频率为8 416.4 Hz,二节径振型的频率为9 537.9 Hz。仿真计算得出主动锥齿轮存在3种振型:一节径振型、一节圆伞型振型、二节径振型,它们的静频分别为8 628 Hz、9 498.1 Hz 和9 650.5 Hz。一节径和二节径模态频率试验结果与仿真结果吻合度较好,误差分别为2.45%和1.17%,但试验并没有出现主动锥齿轮的一节圆伞型振型,可能是结构中的一节圆伞形振动不明显。

一节径 一节圆 二节径
图5 仿真计算振型图
Fig.5 Vibration modes of simulation calculation
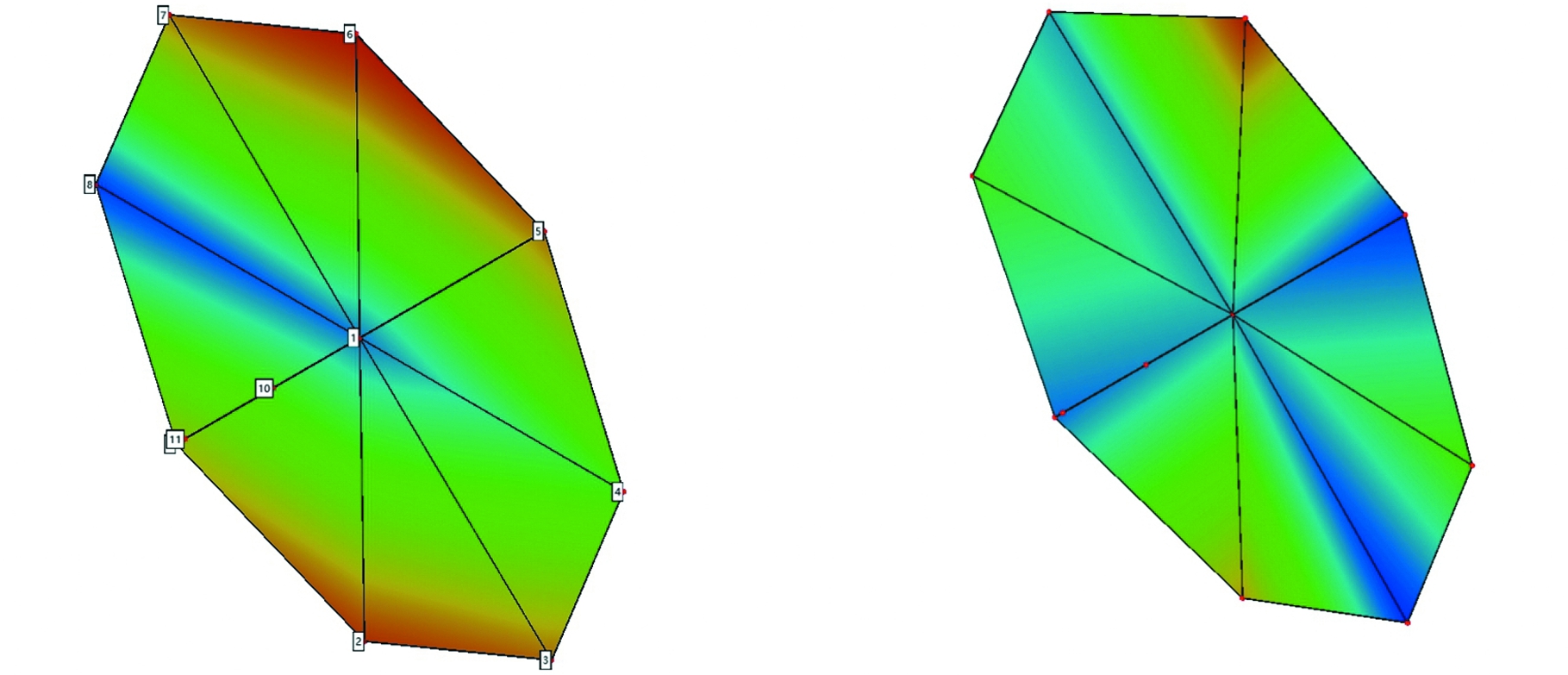
(a)一节径 (b)二节径
图6 试验测试振型图
Fig.6 Vibration modes of test
表2 仿真与试验的固有频率和振型
Tab.2 Comparison of natural frequencies and vibration modes simulation and test results

振型仿真频率(Hz)试验频率(Hz)误差(%)一节径8 628.08 416.42.45一节圆9 498.1二节径9 650.59 537.91.17
对误差原因进行判断和分析,产生误差的主要原因可能是有限元模型的简化和试验时加速度传感器质量对齿轮结构的影响。
3 装配参数对齿轮齿根应力的影响
3.1 啮合锥齿轮的齿轮间隙
工艺规定齿轮间隙控制在0.2~0.6 mm以内。为了研究工艺是否合理,计算不同齿轮间隙对齿根应力的影响,齿轮间隙732.0 μm的锥齿轮啮合状态如图7所示,主动锥齿轮齿根处的应力如图8所示,齿轮间隙对主动锥齿轮齿根应力的影响如图9所示。

图7 锥齿轮啮合(啮合间隙为732.0 μm)
Fig.7 Engagement of bevel gear
(working backlash is 732.0μm)

图8 主动锥齿轮齿根应力云图
(啮合间隙为732.0 μm)
Fig.8 Root stress nephogram of the driving bevel gear
(working backlash is 732.0 μm)

图9 齿轮间隙对主动锥齿轮齿根应力的影响
Fig.9 Effect of gear backlash on root stress of the driving bevel gear
由图9可以看出,齿轮间隙从63.1 μm逐渐增大到732.0 μm的过程中,齿根应力整体上变化不大,呈现先减后增的趋势,最大齿根应力从14.4 MPa先减小到13.6 MPa后增大到17.9 MPa,最大变化量仅为4.3 MPa。
综上所述,附件机匣锥齿轮的齿轮装配间隙对齿根应力影响较小,齿轮装配间隙控制在0.2~0.6 mm之间是合理的。齿轮装配间隙过小时,主动锥齿轮的齿根应力会增大,因为齿轮间隙过小会影响齿轮润滑,齿轮得不到充分润滑时,齿面摩擦会导致齿面温度急剧升高,增大发生破裂故障的几率;间隙过大时,附件机匣锥齿轮在传动过程中会受到比较大的冲击载荷,这种冲击载荷会增大齿根应力,增加发生齿轮破裂故障的几率,对齿轮的寿命产生影响。
3.2 主动锥齿轮垂直安装角度的偏差
分析主动锥齿轮垂直安装角度偏差对齿根应力的影响,安装角度偏差定义为主动轮的轴线向顺时针方向时为正,向逆时针方向为负。445.1 μm安装间隙工况下,角度偏差为1°时,锥齿轮啮合状态如图10所示,主动锥齿轮齿根应力分布如图11所示。主动锥齿轮安装角度偏差对齿根应力的影响如图12所示。

图10 锥齿轮啮合(安装角度偏差为1°)
Fig.10 Engagement of bevel gear
(installation angle deviation is 1°)

图11 主动锥齿轮齿根应力云图(安装角度偏差为1°)
Fig.11 Root stress nephogram of the driving bevel gear
(installation angle deviation is 1°)

图12 安装角度偏差对主动锥齿轮齿根应力的影响
Fig.12 Effect of installation angle deviation on root stress of the driving bevel gear
由图12可以看出,主动锥齿轮的垂直安装角度偏差从-2°增大到2°的过程中,齿根应力逐渐减小,最大齿根应力从29.3 MPa降低到13.6 MPa。主动锥齿轮的垂直安装角度偏差对主动锥齿轮的齿根应力影响较大,所以需要严格控制主动锥齿轮的垂直安装角度。齿轮装配时,需要严格检查附件机匣是否变形,因为附件机匣出现变形会影响主动锥齿轮的垂直安装角度,进而使附件机匣锥齿轮的破裂故障发生率增大,严重影响飞机的飞行安全。
4 主动锥齿轮破裂故障复现试验
在齿轮装配间隙为445.1 μm,主动锥齿轮的垂直安装角度偏差为0°和2°工况下,在齿轮试验器上进行齿轮行波共振疲劳试验。锥齿轮垂直安装角度偏差为0°时,二节径后行波共振状态下的疲劳循环次数超过108的齿轮完好、无裂纹。锥齿轮垂直安装角度为2°时,试验齿轮在二节径后行波共振状态下疲劳循环次数内发生了疲劳断裂。将产生破裂故障的主动锥齿轮放在金相显微镜下观察,发现断口具有节径型振动疲劳断裂特征,可以看到明显的疲劳源、裂纹扩展区和最后断裂区,断定主动锥齿轮掉块断裂属于疲劳断裂,疲劳起始于齿轮小端齿槽与凹面交界处的倒棱处。主动锥齿轮掉块断口宏观形貌如图13所示,金相显微镜下疲劳弧线如图14所示。

图13 主动锥齿轮掉块断口宏观形貌
Fig.13 Macroscopic fracture morphology of the driving bevel gear

图14 疲劳弧线
Fig.14 Fatigue arc
故障分析表明主动锥齿轮具有节径型振动疲劳断裂特征,计算结果表明主动锥齿轮存在节径型振动,验证了主动锥齿轮的节径型振动疲劳断裂。由坎贝尔图(图15)可以看出,主动锥齿轮的一节径前行波频率fF1、一节径后行波频率fB1、二节径后行波频率fB2与50E激振频率线在巡航转速和设计点转速之间有交点,说明该锥齿轮在工作转速范围内可能存在上述3个行波共振频率。因此,可以推断在齿轮发生行波共振时,齿轮安装角度偏差导致齿轮疲劳破坏。为了提高主动锥齿轮的运行可靠性,第一,精确控制齿轮安装角度;第二,调整主动锥齿轮的设计尺寸(例如增大齿轮辐板厚度)或改变齿轮材料,将行波共振转速调到设计转速外,防止发生行波共振,提高齿轮运行的可靠性。

图15 主动锥齿轮坎贝尔图
Fig.15 Campbell diagram of the driving bevel gear
5 结论
(1)仿真和试验结果表明,主动锥齿轮在设计点转速内存在一节径和二节径的振型;模态仿真得到的主动锥齿轮静频与试验测得静频基本一致,一节径静频误差控制在2.45%以内,二节径静频误差控制在1.17%以内,验证了仿真计算模型的正确性。
(2)齿轮装配间隙的变化对齿根应力的影响较小,附件机匣锥齿轮齿轮间隙参数为0.2~0.6 mm的工艺要求是合理的。
(3)主动锥齿轮安装角度偏差对齿轮齿根应力的影响影响较大,因此需要控制角度偏差。
(4)主动锥齿轮破裂故障复现试验可以得出:在齿轮安装角度存在偏差、齿轮恰好处于行波共振转速范围时,齿轮极易出现疲劳断裂故障。
[1] DAWSON P H. Effect of Metallic Contact on the Pitting of Lubricated Rolling Surfaces[J]. Journal of Mechanical Engineering Science, 1962, 4(1): 16-21.
[2] HANDSCHUH R F, POLLY J, MORALES W. Gear Mesh Loss-of-lubrication Experiments and Analytical Simulation[C]∥67th American Helicopter Society International Annual Forum. Virginia Beach, 2011: 2412-2421.
[3] YOGESH P, ANAND P. Simulation of Crack Propagation in Spur Gear Tooth for Different Gear Parameter and Its Influence on Mesh Stiffness[J]. Engineering Failure Analysis, 2013, 30(30):124-137.
[4] 崔伟成, 许爱强, 李伟, 等. 局部特征尺度分解结合局部均值解调的齿轮故障诊断[J]. 中国机械工程, 2016, 27(24): 3332-3337.
CUI Weicheng, XU Aiqiang, LI Wei, et al. Gear Fault Diagnosis Based on LCD and LME Demodulation Approach[J]. China Mechanical Engineering, 2016, 27(24): 3332-3337.
[5] 李福益, 廖学军, 蔡显新. 某型涡扇发动机中下垂直锥齿轮辐板断裂排故试验研究[J]. 航空发动机, 2003, 29(2): 16-20.
LI Fuyi, LIAO Xuejun, CAI Xianxin. Troublshooting for Cone Gear Spoke Fracture in Typical Turbofan[J]. Aeroengine, 2003, 29(2): 16-20.
[6] 许锷俊, 梁世昌, 常春江, 等. 中央传动锥齿轮共振破坏的实验研究[J]. 航空动力学报, 1988(3):193-198.
XU Ejun, LIANG Shichang, CHANG Chunjiang,et al. Bevel Gear Resonance Failures in Central Gearing System of an Aeroengine[J]. Journal of Aerospace Power, 1988(3):193-198.
[7] 王大勇. 航空薄辐板齿轮固有特性及稳态响应分析[J]. 机械传动, 2016, 40(5): 145-147.
WANG Dayong. Inherent Characteristic and Steady Response Analysis of Aviation Gear with Thin-spoke[J]. Journal of Mechanical Transmission, 2016, 40(5): 145-147.
[8] 李其汉, 晏砺堂, 赵福安. 盘形锥齿轮振动特性和故障分析[J]. 航空学报, 1987, 8(10): 482-487.
LI Qihan, YAN Litang, ZHAO Fuan. The Analysis for Lateral Vibration Characteristics and Faults of Bevel Gear[J]. Acta Aeronautica et Astronautica Sinica, 1987, 8(10): 482-487.
[9] 晏砺堂, 李其汉. 盘形锥齿轮的横向振动特性分析[J]. 航空动力学报, 1988, 3(3): 199-202.
YAN Litang, LI Qihan. Analysis of Lateral Vibration of a Bevel Gear[J]. Journal of Aerospace Power, 1988, 3(3): 199-202.
[10] 郭星辉, 鄂中凯, 陈良玉, 等. 弧齿锥齿轮波动应力分析[J]. 东北工学院学报, 1993, 14(5): 464-467.
GUO Xinghui,E Zhongkai, CHEN Liangyu, et al. Analysis of Spiral Bevel Gear Fluctuation Stress[J]. Journal of Northeastern Institute of Technology, 1993, 14(5): 464-467.
[11] 韩二中, 郭星辉, 颜世英, 等. 圆锥齿轮行波共振应力响应仿真计算[J]. 航空动力学报, 1988, 3(3): 207-210.
HAN Erzhong, GOU Xinhui, YAN Shiying,et al. Simulating Calculations for Stress Responses of Travelling Wave Resonance in Bevel Gear[J]. Journal of Aerospace Power, 1988, 3(3): 207-210.
[12] 彭毓敏, 马超, 栾忠权, 等. 多因素条件下单级齿轮系统的非线性特性[J]. 中国机械工程, 2018, 29(8): 937-942.
PENG Yumin, MA Chao, LUAN Zhongquan, et al. Nonlinear Characteristic of Single Stage Gear System under Condition of Multiple Factors[J]. China Mechanical Engineering, 2018, 29(8): 937-942.
[13] 刘光磊, 樊红卫, 谷霁红, 等. 航空弧齿锥齿轮低噪声和低安装误差敏感性设计[J]. 航空发动机, 2010, 36(2): 9-12.
LIU Guanglei, FAN Hongwei, GU Jihong, et al. Sensitivity Design of Low Noise and Installation Error for Aero Spiral Bevel Gear[J]. Aeroengine, 2010, 36(2): 9-12.
[14] 刘光磊, 张瑞庭, 赵宁, 等. 安装误差对航空弧齿锥齿轮传动误差曲线的影响分析[J]. 航空发动机, 2012, 38(2): 32-35.
LIU Guanglei, ZHANG Ruiting, ZHAO Ning, et al.Effect of Installation Error on Transmission Error Curve for Aero Spiral Bevel Gears[J]. Aeroengine, 2012, 38(2): 32-35.
[15] 刘笑天, 蒋超奇, 江丙云, 等. ANSYS Workbench 有限元分析工程实例详解[M]. 北京: 中国铁道出版社, 2017: 191-197.
LIU Xiaotian, JIANG Chaoqi, JIANG Bingyun, et al. The Engineering Example Details of ANSYS Workbench Finite Element Analysis[M]. Beijing: China Railway Publishing House, 2017:191-197.
[16] 刘天文. 某型航空发动机中心锥齿轮动力学特性研究[D]. 南京: 南京航空航天大学, 2015: 23-45.
LIU Tianwen. Dynamic Characteristics Research of the Central Bevel Gear in an Aero-engine[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2015: 23-45.
