0 引言
弧齿锥齿轮在机械动力传输领域被广泛应用,但其啮合理论和加工技术复杂,因此弧齿锥齿轮的高性能齿面设计一直是各国学者研究的重点。通过常规齿面接触分析(tooth contact analysis,TCA)[1]能得到齿轮副的传动误差、接触斑点,但不能对齿面的全部数字化信息进行提取,无法进行边缘接触分析,且常规TCA方法繁琐,坐标变换复杂,需要建立6个非线性方程、3个啮合方程,还需要求解每一接触点的主曲率、主方向,涉及参量众多。近几年发展起来的ease-off曲面分析方法可以替代传统的齿面接触分析,是弧齿锥齿轮的齿面设计、啮合性能分析的新方法。KOLIVAND等[2]提出了一种局部和全局ease-off准双曲面齿轮加载的齿面接触分析方法。聂少武等[3]为提高弧齿锥齿轮齿面修正的效率,提出了一种仅修正小轮齿面偏差的等效修正方法,通过比较实测齿面与设计齿面之间的失配值,计算出小轮齿面等效偏差。魏冰阳等[4]求解齿面对应点的离差,利用最小二乘法构建ease-off二阶密切曲面,获得了轮齿完备的啮合信息。DING等[5-6]基于ease-off曲面建立精确的模型和目标函数,利用局部分析算法,对其非线性问题进行了研究。SHIH等[7]基于五轴联动数控铣齿机床的展成加工,提出了ease-off齿面优化设计方案,利用ease-off曲面度量齿面误差,进行轮齿接触分析。以上研究均采用两曲面对应点的直线距离构建ease-off差曲面。笔者基于转角误差构建的ease-off差曲面更易于解析和提取传动误差等啮合信息。与现行的啮合仿真方法相比,本文方法更易于进行齿面数值化、数值接触仿真和承载接触分析。
齿面接触分析时,需要求出与实际加工大轮完全共轭的理论齿面方程[1,8-10],因此本文提出一种等切共轭的新方法来进行共轭齿面的计算。
1 等刀盘切触共轭
1.1 三面等切共轭原理
如图1所示,曲面Σ2、Σt、Σc在总体坐标系下分别以角速度ω2、ωt、ωc沿各自轴线做回转运动,固定点o2、ot、oc位于3根回转轴线上。运动曲面Σ2、Σt在点M切触传动,运动曲面Σt、Σc也在点M切触传动。设曲面Σ2上M点的径矢为r2,曲面Σt上M点的径矢为rt,曲面Σc上M点的径矢为rc。M点处的三个曲面两两相切,三个曲面的公共法矢记为n。
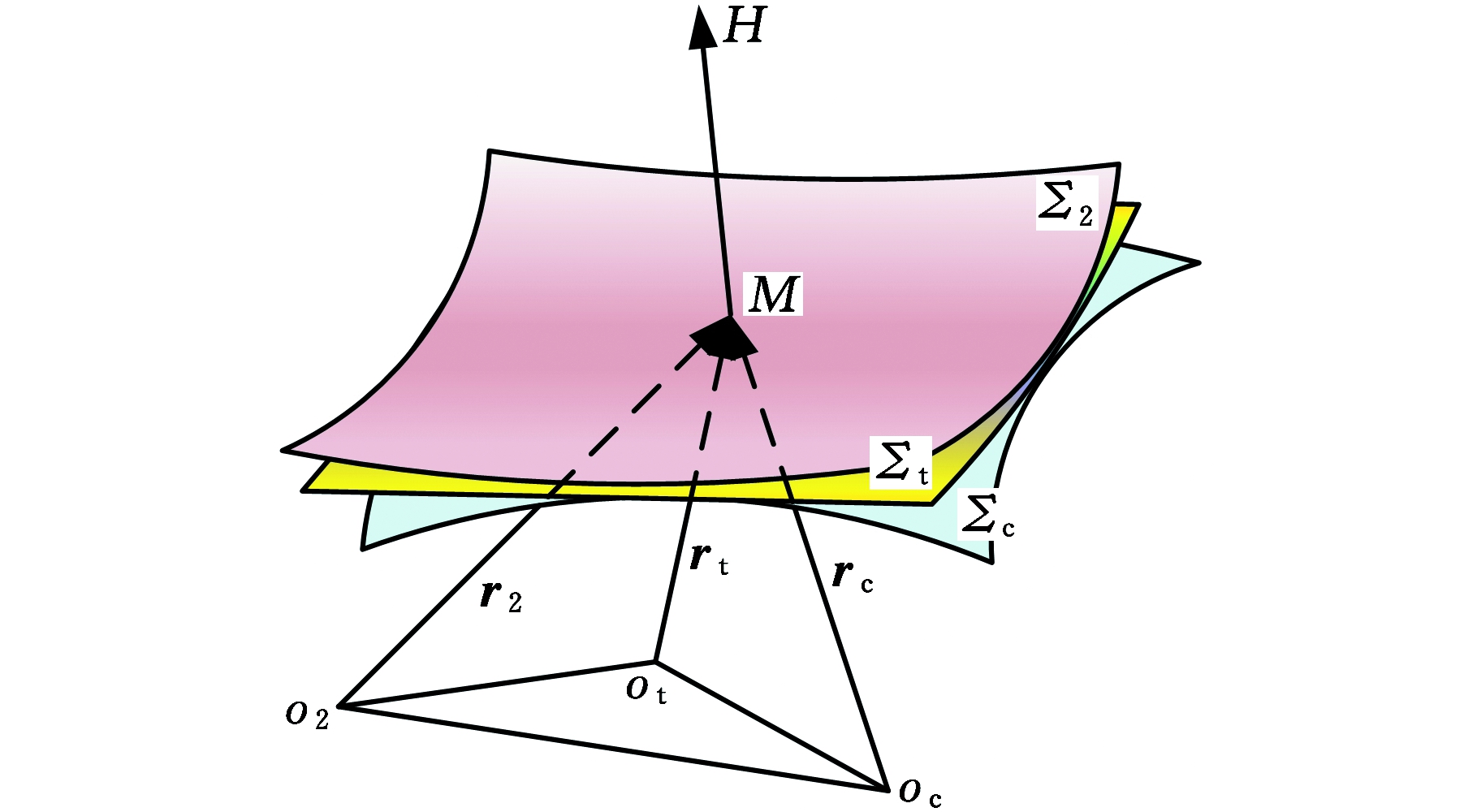
图1 相切三曲面
Fig.1 Three tangent surfaces
为了满足连续啮合条件,运动过程中运动曲面Σ2与Σt在接触位置应满足
(ω2×r2-ωt×rt)·n=0
(1)
同理,运动曲面Σ2与Σc在同一个接触位置满足
(ωt×rt-ωc×rc)·n=0
(2)
联立式(1)、式(2)可得(ω2×r2-ωc×rc)·n=0。
曲面Σ2与Σc在M点处相切且法线方向速度相等,即两曲面相切并能持续啮合,根据共轭判定条件可得Σ2与Σc共轭。如果Σt为刀具曲面,则与刀具曲面分别共轭的曲面Σ2和曲面Σc亦共轭,即“等切共轭”。这在齿轮加工上称为间接展成法。本文ease-off曲面的建立与解析方法出于这一思想。
1.2 弧齿锥齿轮等切共轭产成坐标系
如图2所示,Sm2(Om2xm2ym2zm2)为产成大轮时的切削机床坐标系,Smc(Omcxmcymczmc)为产成小轮时的切削机床坐标系,轴线zmc、zm2共线反向。盘刀为假想无厚度切削锥面(产成轮),刀尖平面位于Om2xm2ym2平面内,盘刀在产成齿面过程中绕zm2-zmc轴线回转,其中,z2为大轮回转轴线,zc为小轮回转轴线,回转轴线zc、z2位于Om2zm2xm2平面内并互相垂直,z2与xm2的夹角为机床根锥角λm2。
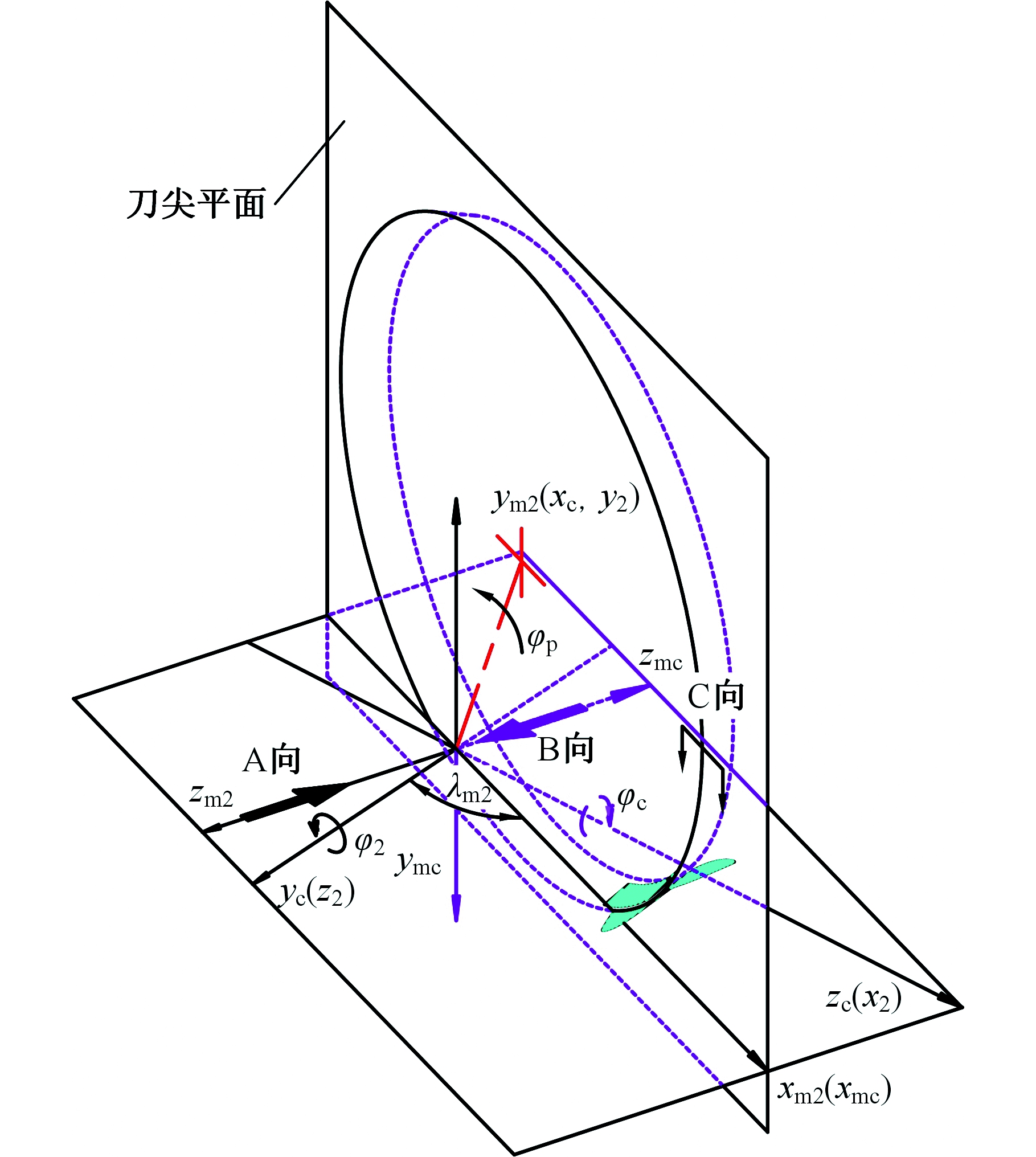
图2 等刀盘产成大小轮齿面的坐标系
Fig.2 Coordinate systems of gear and pinion generated by equal cutter cone
图3 大轮产成坐标系(A向视图)
Fig.3 Gear production coordinate system(A directional view)

图4 共轭小轮产成坐标系(B向视图)
Fig.4 Conjugate pinion generation coordinate system(B directional view)
大轮在产成过程中绕z2轴逆时针旋转,假想盘刀内锥面产成大轮凸面;小轮在产成过程中绕zc轴顺时针旋转,假想盘刀外锥面产成小轮凹面。如图3所示,产成轮绕zm2逆时针旋转φp角,大轮绕z2轴逆时针旋转φ2角,完成大轮产成。大轮和产成轮的滚比m2=φ2/φp,径向力位为Sr,角向刀位为q。将B向视图逆时针旋转180°,如图4所示,产成轮绕zmc顺时针旋转φg角,在相同参考坐标系下,小轮产成时的产成轮转动方向和转动角度与大轮产成时的相同,为了计算方便,将φg记为φp,小轮绕zc轴顺时针旋转φc角,完成小轮产成。小轮和产形轮的滚比mc=φc/φp。在大小轮产成过程中,被产成的大轮曲面和小轮曲面分别与同一个产成锥面共轭切触,因此大轮曲面与小轮曲面发生共轭传动,传动比mc2=φc/φ2。
1.3 小轮产成参数的确定
在大轮展成加工参数已知的前提下,根据以上的分析,可由对称关系得到共轭小轮产成参数。
(1)滚比。根据大小轮之间传动比Z2/Z1,可确定小轮与产成轮之间的滚比:
mc=m2Z2/Z1
式中,m2为大轮产成滚比。
本文选取大轮齿数Z2=41,小轮齿数Z1=11。
(2)机床根锥角。z2与zm2的夹角为产成大轮时的机床根锥角λm2,则产成小轮时的根锥角为
λmc=90°-λm2
(3)刀盘齿形角。大轮产成的锥面在刀尖平面上方,小轮产成的锥面在刀尖平面下方,如图5、图6所示。刀盘齿形角大小相同,向左侧倾斜的为21.5°,向右侧倾斜的为-21.5°。

图5 大轮产成坐标系下产形轮锥截面图
Fig.5 Section of generation cone in gear generation coordinate system
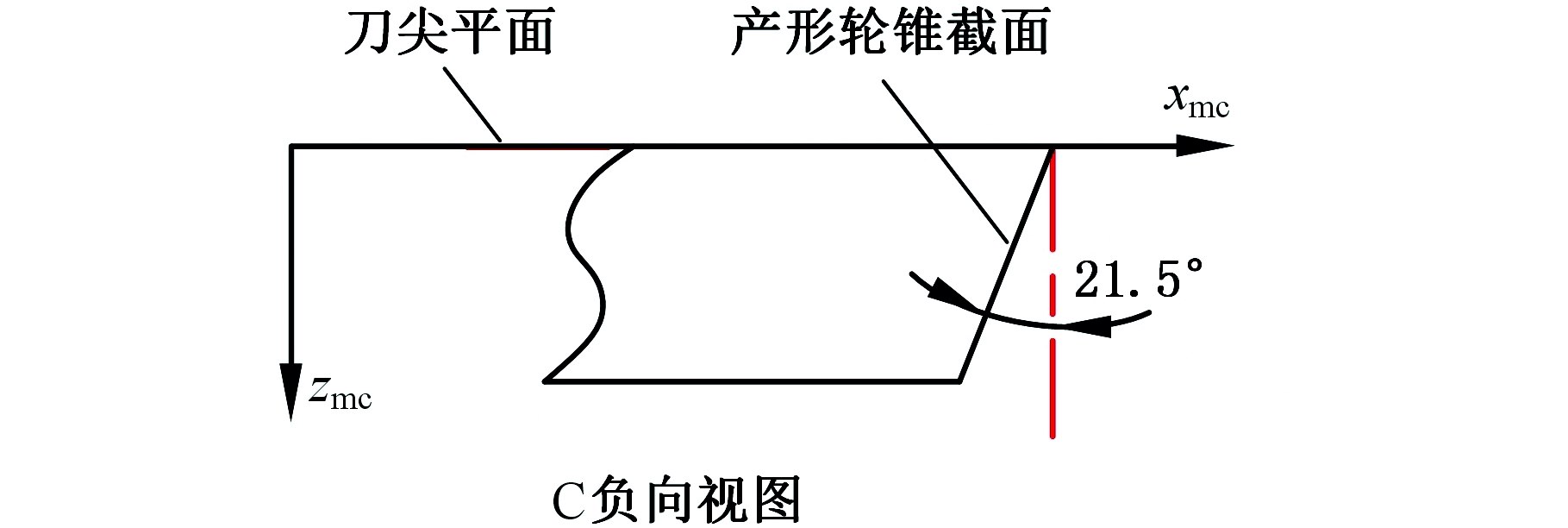
图6 小轮产成坐标系下产形轮锥截面图
Fig.6 Section of generation cone in pinion generation coordinate system
(4)刀位。小轮产成时,径向刀位、角向刀位的数值与大轮相同,但相位不同,角向刀位取负值。
大轮和共轭小轮产成参数如表1所示。
表1 产成参数
Tab.1 Generation parameters
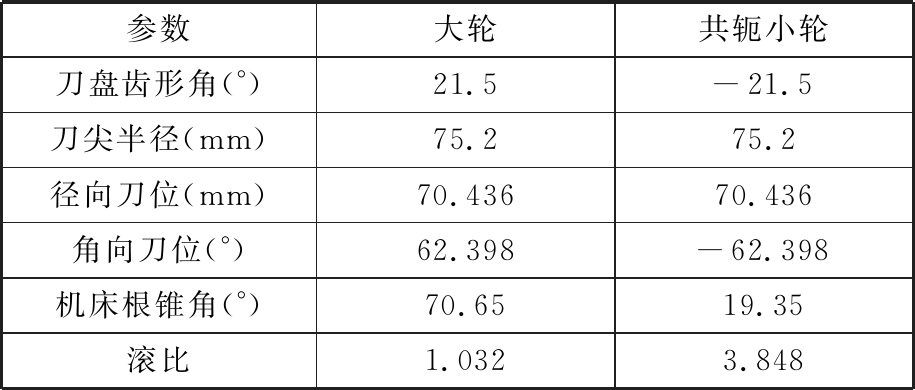
参数大轮共轭小轮刀盘齿形角(°)21.5-21.5刀尖半径(mm)75.275.2径向刀位(mm)70.43670.436角向刀位(°)62.398-62.398机床根锥角(°)70.6519.35滚比1.0323.848
2 齿面方程
产形轮上发生切触的共轭点在产成大轮的同时也产成小轮,则用于产成大轮的产形轮参数u2、θ2同样可以用于小轮。大轮与小轮的齿面方程推导过程相同。在摇台坐标系下,大轮的产形轮参数表达式为

np=(cosαcosθ2,cosαsinθ2,-sinα)
式中,u2、θ2为与刀盘有关的曲面参数;r为大轮的刀尖半径;α为大轮的刀盘齿形角;Sr为大轮的径向刀位[4]。
摇台坐标系Sg (Ogxgygzg)下,小轮的产形轮参数表达式为
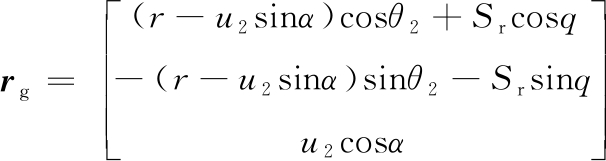
ng=(-cosαcosθ2,cosαsinθ2,-sinα)
共轭小轮齿面Σc的参数表达式为
式中,M、L为坐标变换矩阵。
假设初始转角为0,根据滚比关系可知φc=mcφg=mcφp,由啮合方程可得φp=φp(u2,θ2)(每个发生共轭的参数点都有一个摇台转角与之对应)。因此共轭小轮的齿面Σc的参数表达式为
实际小轮的加工参数如表2所示。
表2 实际小轮加工参数
Tab.2 Processing parameters of actual pinion

刀盘齿形角α1(°)-18.5垂直轮位Em1(mm)1.520刀尖半径r1(mm)73.784轴向轮位Xd1(mm)-0.945径向刀位Sr1(mm)69.942床位Xb1(mm)0.218角向刀位q1(°)-65.196滚比m13.849机床根锥角γm1(°)13.333
实际加工出的小轮齿面参数表达式为
3 共轭小轮和实际加工小轮对应点计算
小轮齿面表达式的分量形式为
r1=(xr1,yr1,zr1)
如图7所示,在小轮坐标系下,等刀盘共轭曲面Σc和实际加工曲面Σ1存在误差。等刀盘共轭小轮齿面为rc(u2,θ2),对参数(u2,θ2)进行遍历,取出一定数量的点Rc(i,j)=(xRc(i,j),yRc(i,j),zRc(i,j)),其中,i=0,1,2,…,l;j=0,1,…,n。

图7 共轭小轮和实际小轮转角差值
Fig.7 Angle difference between conjugate pinion and actual pinion
利用旋转投影法:
对于每一个参数(u2,θ2),都可以求出与之对应的(u1,θ1)。将(u1,θ1)代入r1(u1,θ1)求出一系列与Rc(i,j)对应的点R1(i,j)=(xR1(i,j),yR1(i,j),zR1(i,j))。Rc(i,j)与R1(i,j)之间的转角误差为Δφ1(i,j),根据旋转投影关系,有
yR1(i,j)cosΔφ1(i,j)+
xR1(i,j)sinΔφ1(i,j)=yRc(i,j)
(3)
由式(3)可求出Δφ1(i,j)。
齿轮传动机构中,理想的啮合齿面是完全共轭的,其传动比为恒定值。实际工程应用中,由于齿轮加工机理、制造误差、受力变形等因素的影响,实际传动比在理论值上下波动。
4 建立ease-off曲面
在共轭小轮齿面的旋转投影中,Am为中点锥距,δ1为小轮分锥角。在二维投影平面下,新建直角坐标系xoy,其坐标原点为分锥线和中点锥距交叉点。
在xoy坐标系下,齿面点在投影面中的坐标为
利用旋转投影的方法建立共轭小轮齿面点与其在投影面内坐标点的映射关系。每个(x,y)对应的误差为转角误差Δφ1(i,j),根据(x,y,Δφ1(i,j))可以拟合出一个三维4次曲面:
找到Δφ1(x,y)的极值点Δφ0,如图7所示,将实际齿面绕z1(zc)轴逆时针旋转Δφ0,则共轭齿面和实际齿面在极值点处贴合。由于旋转实际齿面时,全部齿面点都参与旋转,因此旋转后,拟合曲面系数aij不变,只是整体减少角度误差Δφ0,则两齿面的4次误差齿面拟合方程为
Δφ1(x,y)=Δφ1(x,y)-Δφ0=![]()
(4)
主动齿轮转动一角度后,从动轮的实际转角与理论转角之间的偏差为传动误差[11]。已知小轮的转角误差,根据传动误差的定义可以推导出在小轮匀速转动的情况下大轮的转角误差
Δφ2(x, y)=Z1Δφ1(x, y)/Z2
(5)
根据式(5)可以得到大轮的旋转误差曲面即转角ease-off曲面。ease-off曲面包含了转角误差信息,与旋转角度相关的评价信息(比如传动误差)可以很方便地由ease-off曲面得到。
设共轭小轮齿面rc=(xrc,yrc,zrc)。令
其中,δ(x,y)为弧长误差,近似为弧端点之间的距离,根据(x,y,δ(x,y))可以拟合出弧长误差ease-off差曲面,其对应的等值线图(图8)清晰表示了齿面失配梯度,即小轮相对大轮共轭的修形量。图8中点为旋转投影面内所选序列点的投影。
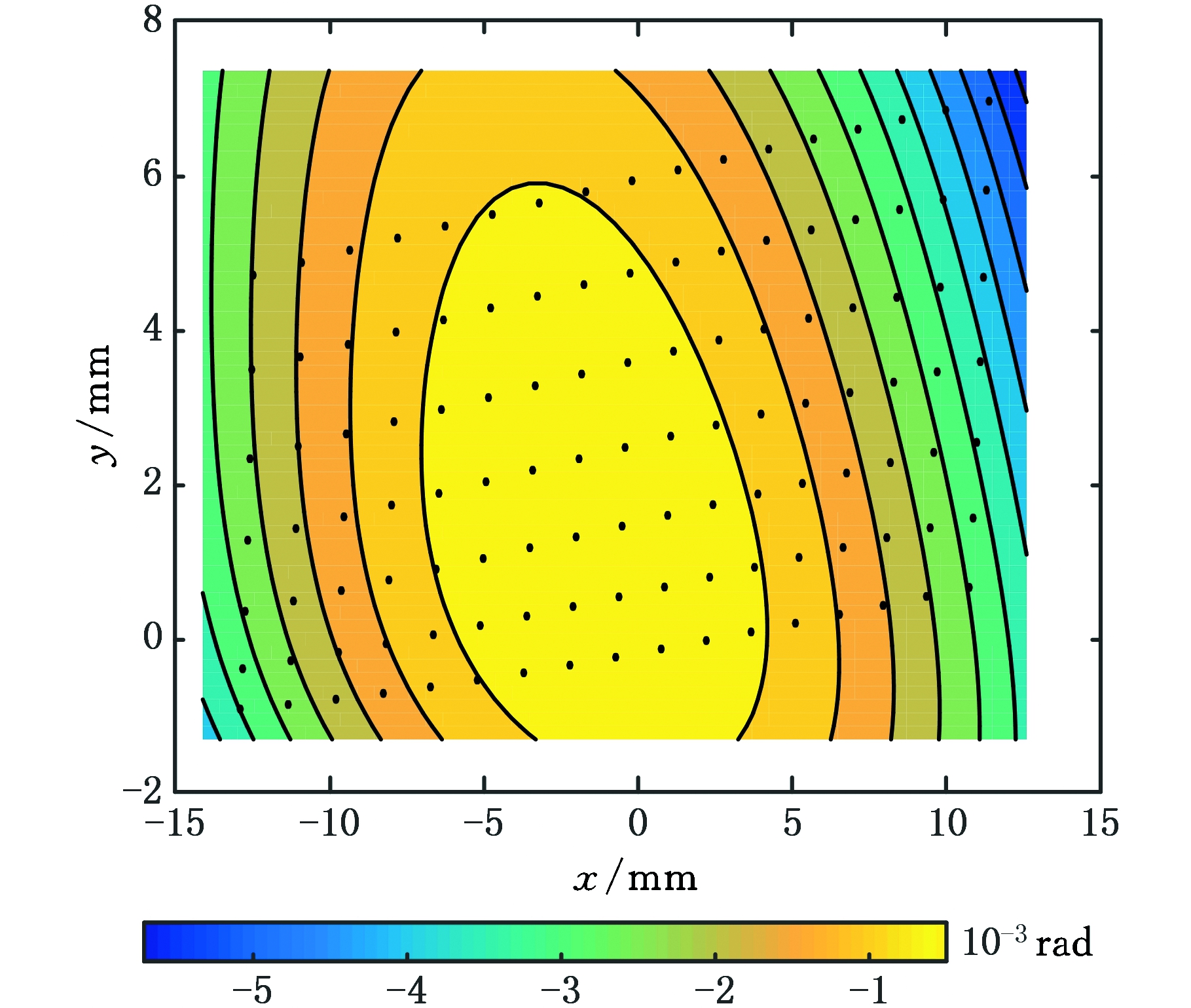
图8 Ease-off弧长误差等值线图
Fig.8 Ease-off arc length error contour
5 差曲线与传动误差解析
将由φc=mcφg=mcφp,φp=φp(u2,θ2)解得的u2(φc,θ2)代入共轭齿面rc=rc(u2,θ2),得到rc=rc(φc,θ2)。因为θ2为单变量,故φc遍历取值φc,i可得一族空间曲线,记为rc,i(θ2)。该曲线族即为共轭小轮转动时,共轭小轮与共轭大轮的多条接触线。共轭小轮的接触线在弧长ease-off曲面上的一系列映射曲线记为δi(x,y);接触线在转角ease-off曲面上的一系列映射曲线记为Δφ2,i(x,y)。ease-off曲面上曲线是瞬时接触线上实际齿面与共轭齿面对应点的离差值曲线即差曲线。差曲线的曲率为啮合齿面实际接触点诱导曲率的真实反映。
根据齿面的边界确定每条差曲线参数的取值范围,将ease-off曲面上的差曲线绘制到xoy坐标系内,图9为φc=φc,i时的差曲线投影图,图中,虚线为瞬时接触线,实线为修形后接触线上根据接触理论确定的实际接触段。
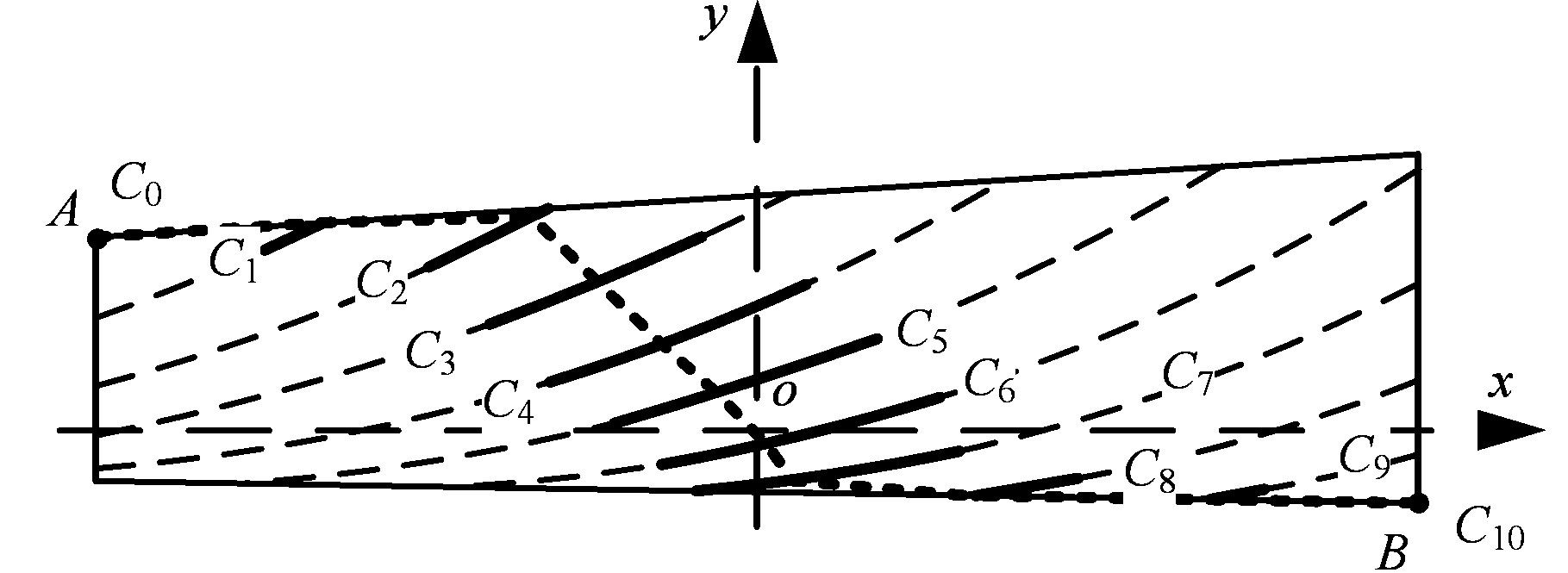
图9 差曲线投影及啮合迹线图
Fig.9 Difference curve projection and meshing trace
整个啮合过程中,齿轮从A点啮入(起始角为φc,0,对应的接触线记为C0,下同)、B点啮出(终止角为φc, 10)。在刚刚啮入(C0和C1线)和快要啮出(C8、C9和C10线)时,差曲线的极值点在边界,发生边缘接触。
将差曲线δi(x,y)的极值点记为δ0,i,使di(x,y)=δi(x,y)-δ0,i,使每个极值点处于零平面内,如图10所示。在投影平面内画出差曲线,连接每条差曲线的极值点(图10中空心圆)即可得到两轮齿的啮合迹线(图10中虚线)。按照常规涂色厚度0.006 35 mm,计算齿面干涉区域,由此可以获得齿面接触印痕。经过平移后,对于每条差曲线令di(x,y)=-0.006 35,求出每条差曲线与平面的交点(图10中的黑色圆点)。交点之间的差曲线即为接触印痕。将图10中信息影射至投影平面,如图9所示,图中粗实线即为接触印痕。
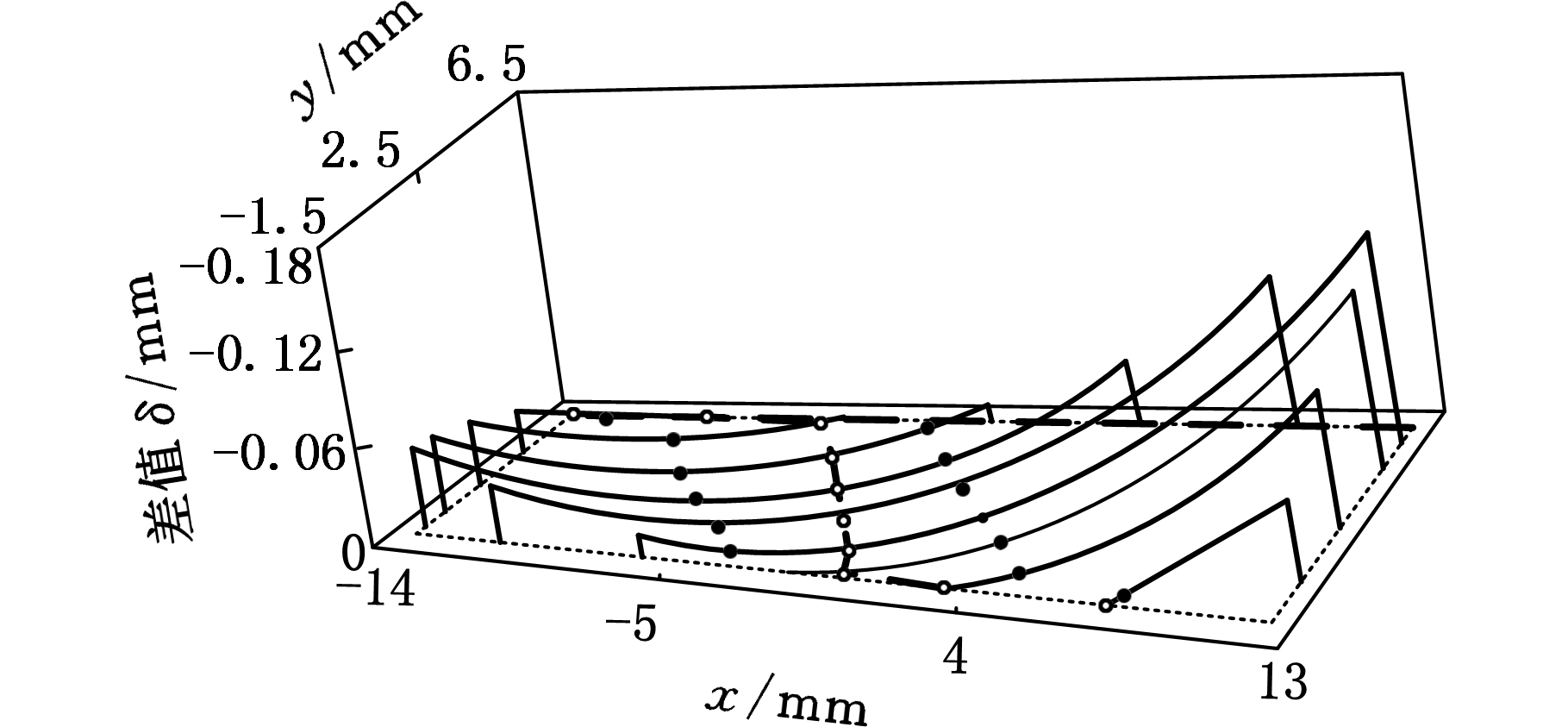
图10 全程差曲线
Fig.10 Difference curves in the whole process
两齿面完全共轭时,两齿面始终为线接触,而实际上小轮齿面和大轮为点接触。对于局部点接触的不完全共轭齿轮副来说,其传动比是变化的,存在传动误差。小轮匀速转动,转角从φc,0变化到φc,10的过程是一对轮齿完成啮合的整个过程。φc,i对应的差曲线Δφ2,i(x,y)的极值点记为Δφ20,i。以小轮转角φc为横坐标,Δφ20为纵坐标,将数对(φc,i,Δφ20,i)进行拟合即得到包括边缘接触的传动误差曲线,如图11所示,从误差传动曲线中可以提取以下啮合信息:①两齿转换交替点误差为-2.83×10-5 rad,三齿转换交替点误差为-1.96×10-4 rad;②传动误差曲线开口距离与一齿啮合周期的比值为总重合度,本文例子的总重合度为2.91;③根据极值点是否为端点可以判断出边缘接触点(图11中的黑点);④传动误差曲线上有效啮合区距离与啮合周期的比值为有效重合度,本文例子的有效重合度为1.75;⑤传动误差曲线斜率表示理论啮合相对角加速度的大小,误差曲线越陡峭,角加速度越大。

图11 传动误差曲线
Fig.11 Transmission error curves
6 结论
(1)提出了一种新的弧齿锥齿轮等切共轭的求解方法,由刀盘一次共轭即可得到理论齿面方程,克服了传统方法“刀具-大轮-小轮”两次共轭运算量大的缺陷。
(2)以实际齿面上点序列的转角误差为目标函数,构造了四次函数,建立了ease-off曲面,得到了ease-off曲面等值线图,避免了常规计算中对TCA的6个非线性方程组的求解,提高了计算效率。
(3)由ease-off曲面解析出的接触路径、差曲线、传动误差曲线可方便地进行边缘接触分析,克服了常规TCA方法的不足。
[1] LITVIN F L, FUENTES A. Gear Geometry and Applied Theory[M]. New York: Cambridge University Press, 2004.
[2] KOLIVAND M, KAHRAMAN A. An Ease-off Based Method for Loaded Tooth Contact Analysis of Hypoid Gears Having Local and Global Surface Deviations[J]. Journal of Mechanical Design, 2009,132(7):245-254.
[3] 聂少武, 邓静, 邓效忠, 等. 基于齿面Ease off拓扑的弧齿锥齿轮齿面偏差等效修正方法[J]. 中国机械工程, 2017,28(20):2434-2440.
NIE Shaowu, DENG Jing, DENG Xiaozhong, et al. Tooth Surface Error Equivalent Correction Method of Spiral Bevel Gears Based on Ease off Topology[J]. China Mechanical Engineering, 2017,28(20):2434-2440.
[4] 魏冰阳, 杨建军, 仝昂鑫, 等. 基于等距Ease-off曲面的轮齿啮合仿真分析[J]. 航空动力学报, 2017,32(5):1259-1265.
WEI Bingyang, YANG Jianjun, TONG Angxin, et al. Tooth Meshing Simulation and Analysis Based on Isometric Mapping Ease-off Surface[J]. Journal of Aerospace Power, 2017,32(5):1259-1265.
[5] DING H, TANG J, ZHOU Y, et al. A Multi-objective Correction of Machine Settings Considering Loaded Tooth Contact Performance in Spiral Bevel Gears by Nonlinear Interval Number Optimization[J]. Mechanism & Machine Theory, 2017,113:85-108.
[6] DING H, WAN G, ZHOU Y, et al. Nonlinearity Analysis Based Algorithm for Identifying Machine Settings in the Tooth Flank Topography Correction for Hypoid Gears[J]. Mechanism & Machine Theory, 2017,113:1-21.
[7] SHIH Y P, CHEN S D. Free-form Flank Correction in Helical Gear Grinding Using a Five-axis Computer Numerical Control Gear Profile Grinding Machine[J]. Journal of Manufacturing Science & Engineering, 2012,134(4):41006.
[8] 吴序堂. 齿轮啮合原理[M]. 西安: 西安交通大学出版社, 2009.
WU Xutang. Gear Meshing Principle[M]. Xi’an: Xi’an Jiaotong University Press, 2009.
[9] 曾韬. 螺旋锥齿轮设计与加工[M]. 哈尔滨: 哈尔滨工业大学出版社, 1989.
ZENG Tao. Design and Processing of Spiral Bevel Gear[M]. Harbin: Harbin Institute of Technology Press, 1989.
[10] 郑昌启. 弧齿锥齿轮和准双曲面齿轮[M]. 北京: 机械工业出版社, 1988.
ZHENG Changqi. Spiral Bevel Gear and Hypoid Gear[M]. Beijing: China Machine Press, 1988.
[11] 熊禾根. 机械传动系统Romax Designer建模、分析及应用[M]. 武汉:华中科技大学出版社, 2015.
XIONG Hegen. Modeling, Analysis and Application of Mechanical Transmission System Romax Designer[M]. Wuhan:Huazhong University of Science and Technology Press, 2015.
