0 引言
汽车的大量试验项目具有重复性强、持续时间长、操作要求精准等特点，使用驾驶机器人进行试验可降低试验人员劳动强度，提高试验准确性。目前，只有少数发达国家拥有此项技术，国内关于驾驶机器人的研究主要集中在东南大学、南京理工大学、中国汽车研究中心等几个单位[1-3]。
针对驾驶机器人运动学、动力学的分析主要集中在未施加负载的工况。汪俊等[4]对驾驶机器人换挡机械在空载工况下的驱动力进行优化，改善了驾驶机器人在空载情况下的性能，但未考虑驱动力受机械手末端负载变化的影响。卢伟等[5]对拖拉机驾驶机器人换挡机械手进行了动力学分析，考虑了机械手末端负载的变化，但未加入驱动器及控制部分。虞沈林等[6]建立了换挡机械手刚柔耦合模型并进行了运动学分析，但未考虑负载对换挡轨迹跟踪的影响。在实际的换挡运动过程中，换挡机械手所受负载通过机械手传递到电机轴处，干扰电机轨迹的跟踪效果，影响换挡机械手的换挡过程。
换挡机械手末端负载主要来自于换挡负载。PATEL等[7]对换挡负载的产生和影响换挡负载的参数进行了灵敏度分析。目前进行换挡负载模拟的方法主要是物理系统建模法和试验数据拟合方法。陈玉祥等[8]通过ADAMS建立换挡系统虚拟样机模型来模拟换挡负载的变化，精度高但过程复杂。ÖZPINAR 等[9]通过建立传动系统多体动力学模型来模拟换挡负载的变化。张志刚等[10]对同步器同步过程中不同阶段的摩擦理论进行研究，建立了同步器摩擦模型，该方法属于物理系统建模法，模拟精度高、理论性强，但在建模过程中需要对变速器实际工况参数进行辨识，过程复杂。YANG等[11]通过多项式拟合试验数据的方法建立了换挡过程中换挡负载的模型，但该方法的缺点是精度不足。
本文针对驾驶机器人换挡机械手在末端负载波动情况下的动力学特性进行分析，建立了驾驶机器人换挡机械手的运动学模型，求解了选挡及挂挡电机轴目标轨迹。搭建了换挡机械手的动力传递模型，在机械手末端负载波动模型中，以第三开链末端位置为驾驶机器人换挡机械手末端位置，通过物理模型和神经网络相结合的方法模拟机械手末端负载的变化。为准确模拟机械手末端负载的波动情况，本文在分析换挡负载特性的基础上，提出了一种结合物理系统建模和神经网络拟合的机械手末端负载波动模型。在换挡方向上，建立了阻尼系统换挡负载模型。在挂挡方向上，考虑挂挡方向负载时变及强非线性的特点，建立了神经网络挂挡负载模型。在机械手末端负载波动模型中，考虑了二次冲击及车辆颠簸负载。仿真与换挡机械手换挡性能试验验证了末端负载变化对换挡机械手轨迹跟踪有较大影响，为进一步优化提供了依据。
1 换挡机械手运动学建模
1.1 驾驶机器人换挡机械手整体结构
驾驶机器人换挡机械手结构模型如图1所示，图2为换挡机械手机构运动简图。换挡机械手换挡过程可以解耦为选挡和挂挡两个过程。选挡过程中，挂挡电机保持静止，选挡电机经连杆驱动选挡摇杆，使换挡手柄抓手完成横向选挡。挂挡过程中，选挡电机保持静止，挂挡电机经连杆驱动挂挡摇杆使换挡手柄抓手完成纵向挂挡。
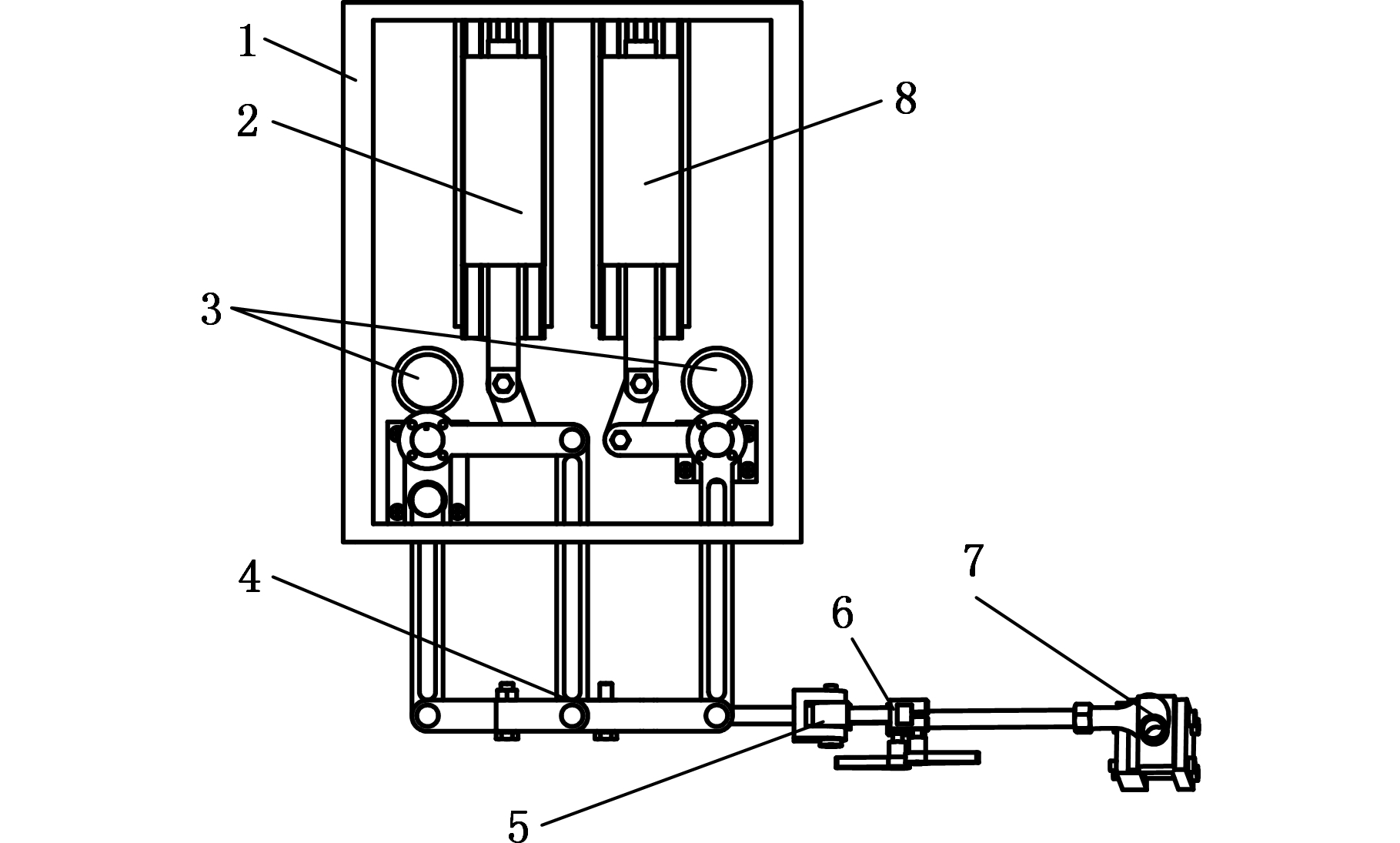
1.箱体 2.选挡电机 3.角度传感器 4.二自由度七连杆机构 5.角度调整机构 6.紧固手柄 7.换挡手柄抓手 8.挂挡电机
图1 换挡机械手结构模型
Fig.1 Shift manipulator structure model
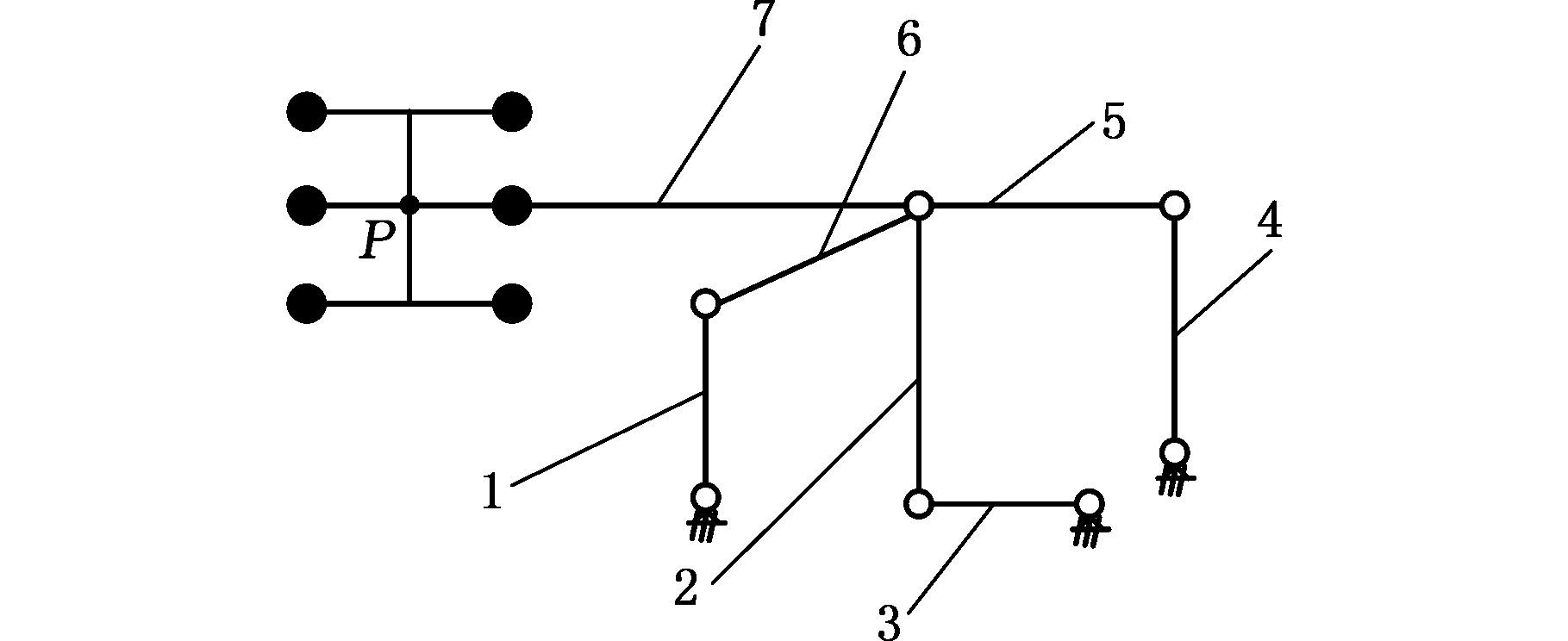
1.挂挡摇杆 2.第二连杆 3.选挡摇杆 4.调节杆 5.第三连杆 6.第一连杆 7.手杆
图2 换挡机械手机构运动简图
Fig.2 Movement diagram of shift manipulator
1.2 换挡机械手运动学模型
使用改进型D-H法描述换挡机械手各关节坐标系的运动，将换挡机械手分解为3个独立的开链：箱体、挂挡摇杆和第一连杆组成的第一开链；箱体、选挡摇杆和第二连杆组成的第二开链；箱体、调节杆和手杆组成的第三开链。换挡机械手3个开链坐标系如图3所示。图3中，(xnj, ynj)为第n(n=1, 2, 3)开链第j关节处坐标，lni为第n开链处第i连杆长度。换挡机械手各连杆参数如表1所示，关节角θj为坐标系j-1绕z轴转动到坐标系j的旋转角度；连杆偏移dj为坐标系j-1沿z移动到j坐标系的距离；连杆长度aj为连杆j-1的长度；连杆扭转角αj为坐标系j-1沿xj-1转动到坐标系j的旋转角度。
图3 换挡机械手三开链坐标系
Fig.3 Three open chain of shift manipulator coordinate system
表1 驾驶机器人换挡机械手连杆参数
Tab.1 Driving robot shift manipulator link parameters
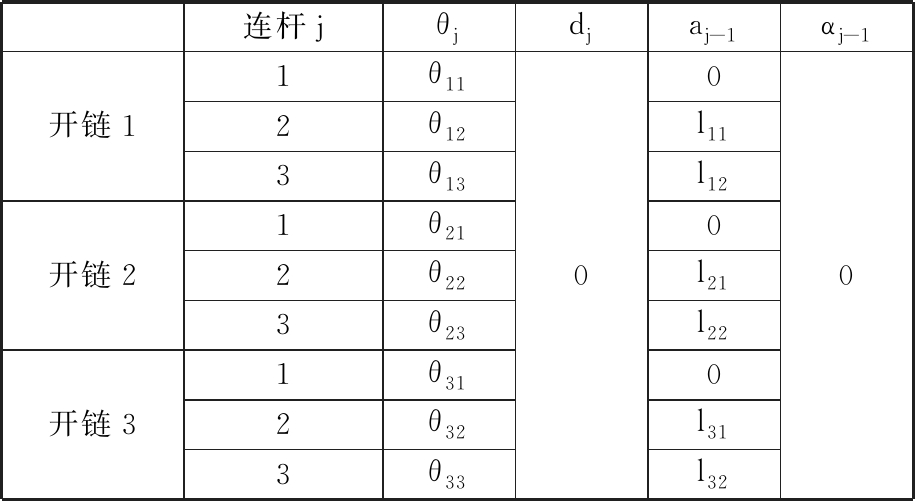
连杆jθjdjaj-1αj-1开链1开链2开链31θ112θ123θ131θ212θ223θ231θ312θ323θ3300l11l120l21l220l31l320
根据建立的换挡机械手3个开链坐标系，建立了换挡机械手运动学模型。将二自由度七连杆机构分解为3个独立的开链，每个开链的运动学模型只在模型参数上有区别，因此以第三开链为例，根据D-H表参数建立换挡机械手第三开链运动方程：
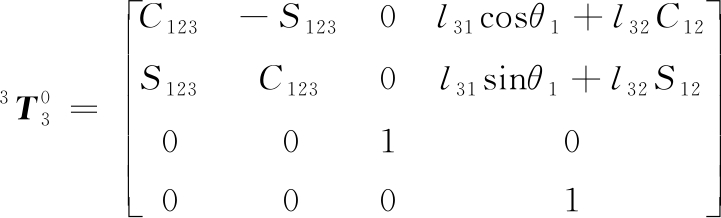
(1)
S123=sin(θ31+θ32+θ33)
C123=cos(θ31+θ32+θ33)
C12=cos(θ31+θ32) S12=sin(θ31+θ32)
将第三开链末端位置作为换挡机械手末端位置，则机械手末端位置可以表示为
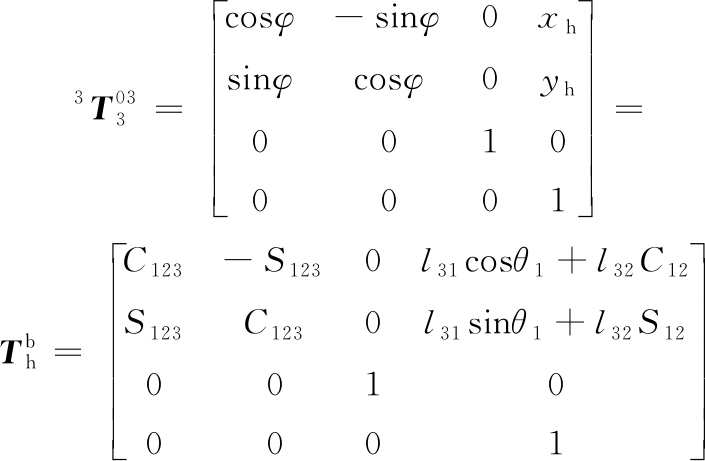
(2)
式中，
为机械手末端位置运动方程；φ为机械手末端相对于坐标系原点的关节角度；xh为机械手末端相对于坐标系原点沿x轴方向的位移；yh为机械手末端相对于坐标系原点沿y轴方向的位移。
利用代数解法对换挡机械手第三开链进行逆运动学求解，得出
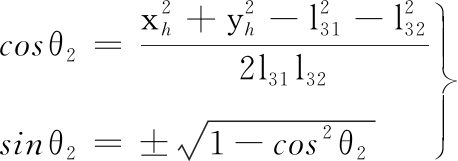
(3)
因为0≤θ2≤π，所以sinθ2取正，求出：
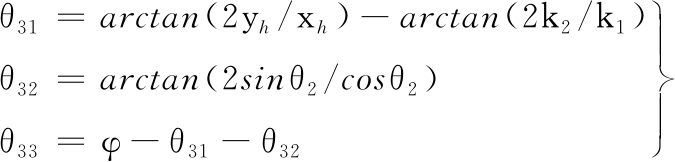
(4)
(5)
第一开链和第二开链的末端位置处于第三开链连杆3上，根据θ31、θ32、θ33和正运动学方法可以求出第一开链和第二开链末端位置的坐标，再通过逆运动学在第一、第二开链处求解出选挡摇杆和挂挡摇杆的转动角度。选挡电机和挂挡电机分别与摇杆组成曲柄滑块机构，通过曲柄滑块机构运动学方程可求解出选挡电机和挂挡电机的目标轨迹。
2 考虑负载波动的换挡机械手动力传递模型
为分析换挡机械手在机械手末端负载波动下的动力学特性，建立了换挡机械手动力传递过程模型。换挡机械手动力传递模型由换挡机械手虚拟样机模型、驱动电机模型及机械手末端负载波动模型组成。换挡机械手动力传递过程模型中，驱动电机模型包含选挡电机、挂挡电机的模型，以及选挡电机、挂挡电机的位置矢量控制器模型。机械手末端负载波动模型包含神经网络挂挡负载模型和阻尼系统选挡负载模型。机械手末端负载末端模型添加了二次冲击及行驶颠簸的负载模型。换挡机械手动力传递过程模型见图4。图4中，
为选挡电机目标轨迹；
为挂挡电机目标轨迹；e为位移误差；Iabc为控制电流；Fmx为选挡电机轴负载；vshift为挂挡方向速度；xx为选挡电机实际位移；xmx为选挡电机轴位移；xshift为挂挡方向位移；Fmg为挂挡电机轴负载；Fm为换挡负载；Fselect为选挡方向负载；xg为挂挡电机实际位移；xmg为挂挡电机轴位移；vselect：选挡方向速度；Fshift为挂挡方向负载；Fdbp为二次冲击负载；Fbum为行驶颠簸负载 。
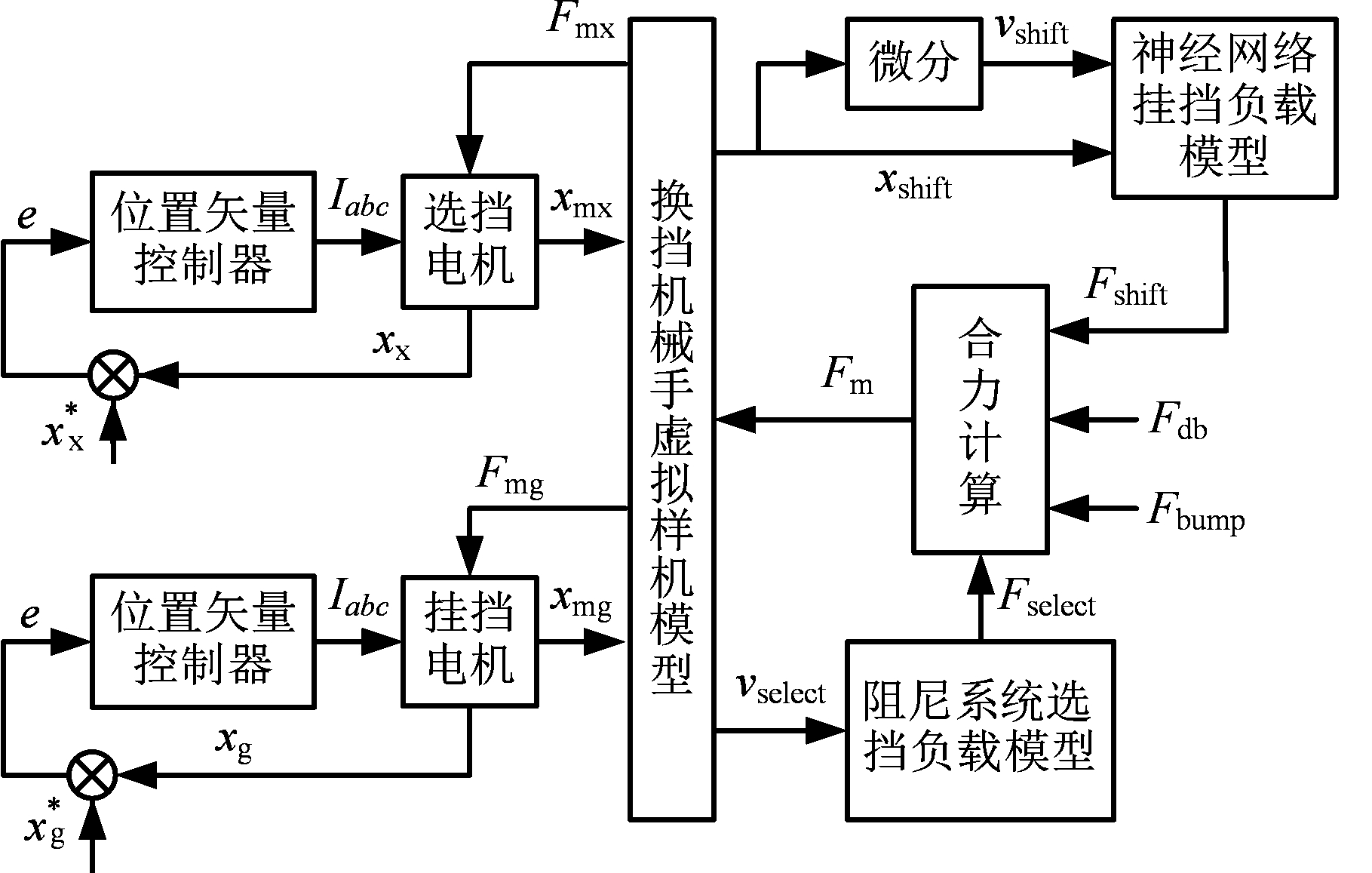
图4 考虑负载波动的换挡机械手动力传递模型
Fig.4 Shift manipulator power transfer model based on load fluctuations
在考虑负载波动的换挡机械手动力学传递模型中，选挡电机、挂挡电机的矢量控制器根据换挡机械手运动学求解出选挡电机、挂挡电机目标轨迹，完成电机轨迹的跟踪。选挡电机、挂挡电机驱动换挡机械手实现选挡动作、挂挡动作。机械手末端负载波动模型根据负载的不同，分为神经网络挂挡负载模型、阻尼系统选挡负载模型、二次冲击及行驶颠簸负载模型。机械手末端负载波动模型根据换挡机械手运动情况计算出各项负载，通过合力计算得到换挡负载。换挡负载经换挡机械手各连杆传递到选挡电机、挂挡电机轴处，形成电机轴负载。换挡机械手末端负载、克服机械手自身运动的惯性负载均影响电机轴负载。
2.1 换挡机械手虚拟样机模型
驾驶机器人换挡机械手动力学建模过程较为复杂，通过使用虚拟样机技术建立换挡机械手动力学模型，可以在机械手末端负载波动的情况下很好地模拟换挡机械手的动力学特性，建立的换挡机械手虚拟样机模型如图5所示。
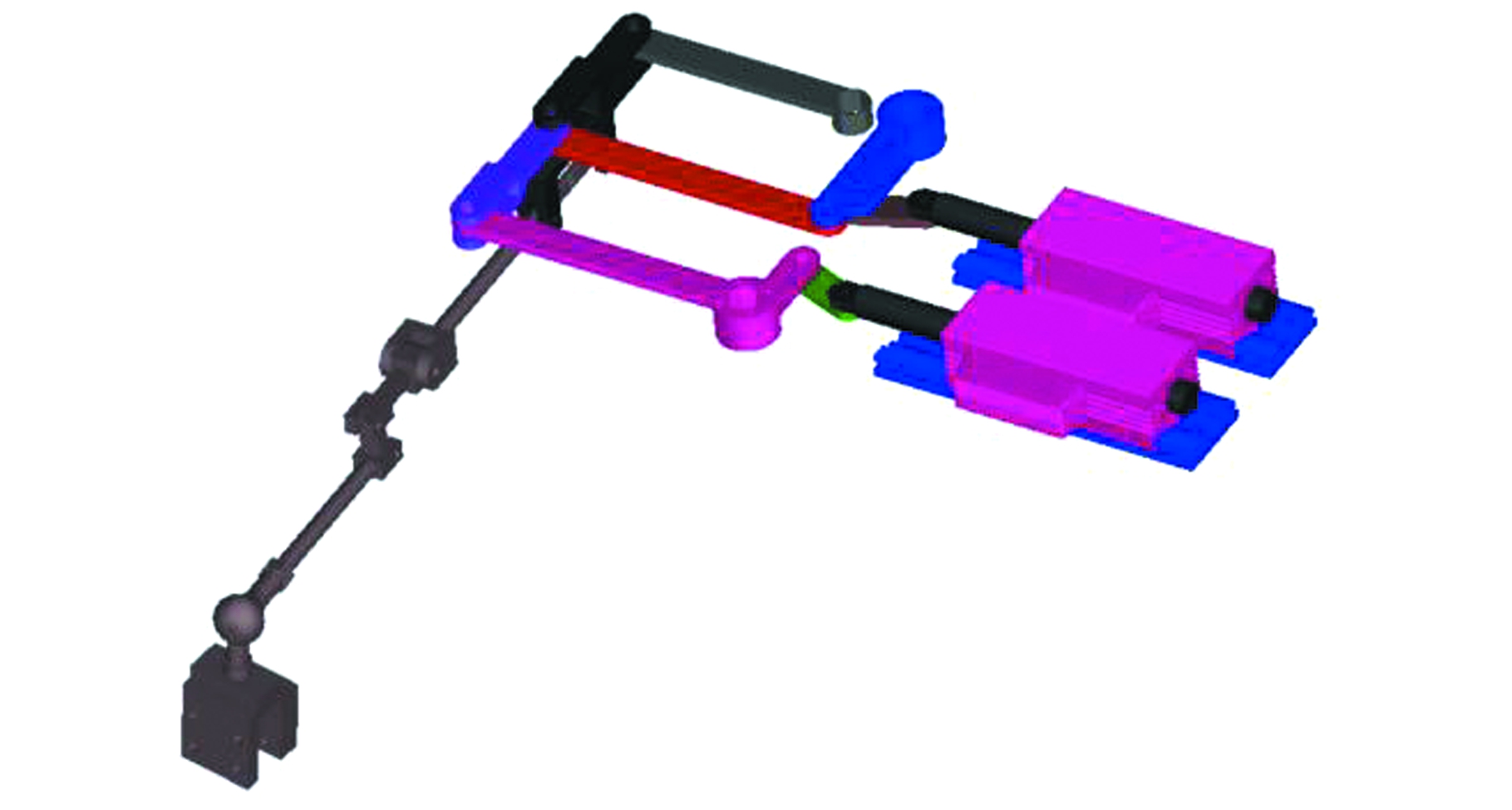
图5 换挡机械手虚拟样机模型
Fig.5 Shift manipulator virtual prototype model
将换挡机械手三维模型导入ADAMS中，建立驾驶机器人换挡机械手虚拟样机模型。忽略螺钉、螺母、垫片等对仿真影响不大的零件，忽略换挡机械手各个关节之间的间隙及阻尼，建立对应运动副、驱动及力来模拟直线电机驱动换挡机械手的选挡及挂挡。换挡机械手主要的运动副如表2所示，换挡机械手驱动及力如表3所示。
表2 换挡机械手主要的运动副
Tab.2 Main movement pairs of shift manipulator
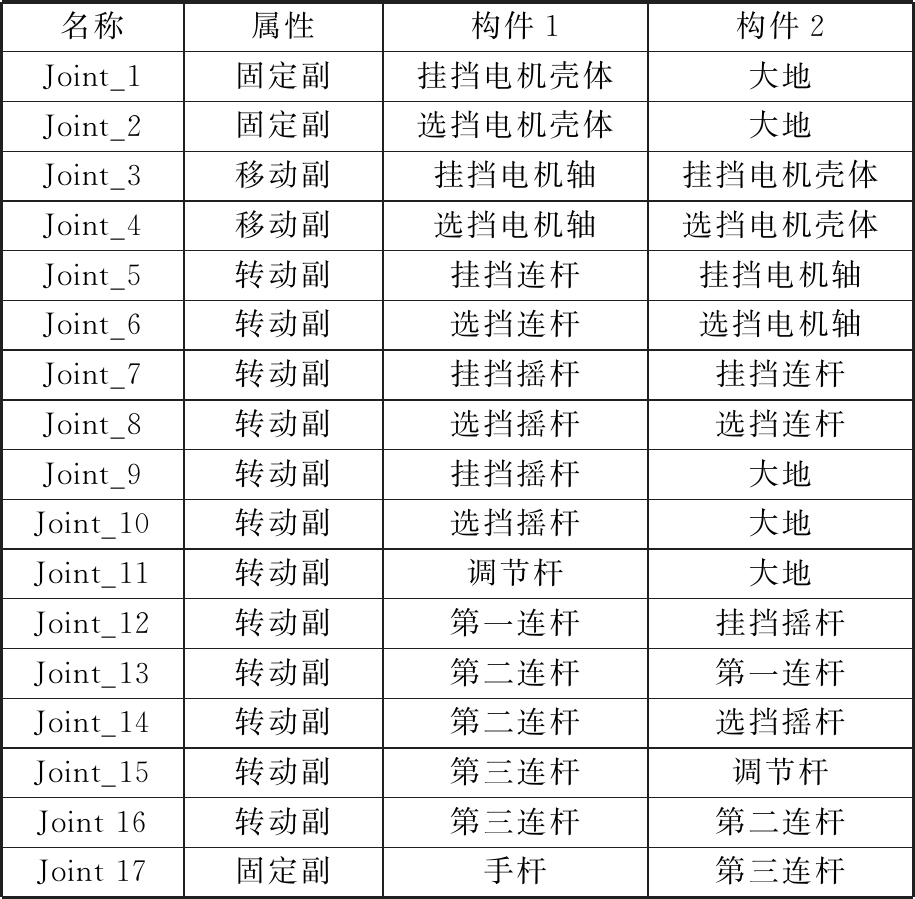
名称属性构件1构件2Joint_1固定副挂挡电机壳体大地Joint_2固定副选挡电机壳体大地Joint_3移动副挂挡电机轴挂挡电机壳体Joint_4移动副选挡电机轴选挡电机壳体Joint_5转动副挂挡连杆挂挡电机轴Joint_6转动副选挡连杆选挡电机轴Joint_7转动副挂挡摇杆挂挡连杆Joint_8转动副选挡摇杆选挡连杆Joint_9转动副挂挡摇杆大地Joint_10转动副选挡摇杆大地Joint_11转动副调节杆大地Joint_12转动副第一连杆挂挡摇杆Joint_13转动副第二连杆第一连杆Joint_14转动副第二连杆选挡摇杆Joint_15转动副第三连杆调节杆Joint 16转动副第三连杆第二连杆Joint 17固定副手杆第三连杆
表3 换挡机械手主要驱动和力
Tab.3 Main drive and force of shift manipulator
名称属性构件Motion_1位移驱动挂挡电机轴Motion_2位移驱动选挡电机轴Force_1力(挂挡方向)手杆Force_2力(选挡方向)手杆
2.2 换挡机械手驱动电机及控制器模型
换挡机械手的电磁直线执行器为无刷直流直线电机，其本体结构如图6所示。
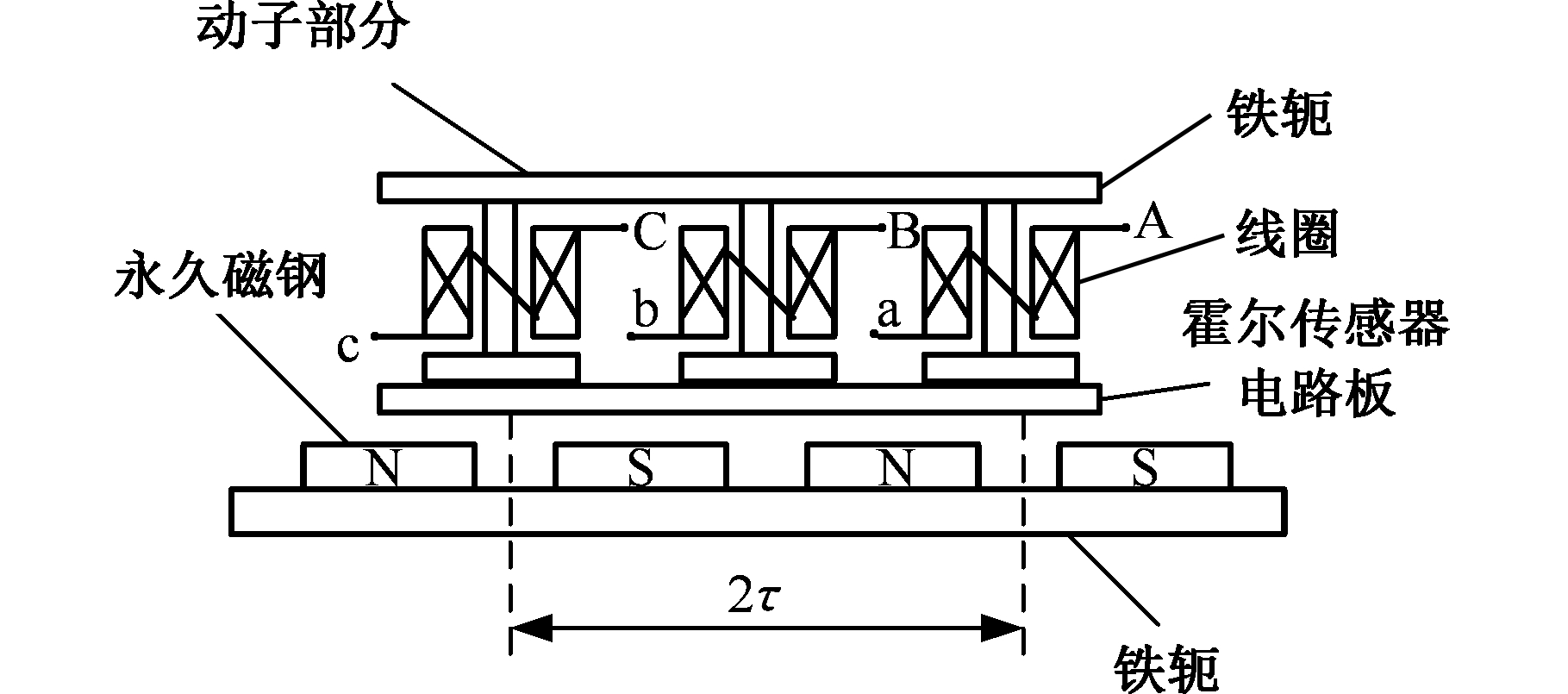
图6 电磁直线执行器本体结构图
Fig.6 Electromagnetic linear actuator structure diagram
换挡机械手电机矢量控制系统原理如图7所示。位置矢量控制器根据位移误差计算出定子两相指定电压Uα和Uβ。Uα和Uβ经电压空间矢量调制获得PWM波形。逆变器根据PWM波形控制相应IGBT的通断，输出控制电流Iabc。
图7 换挡机械手电机矢量控制结构图
Fig.7 Shift manipulator motor vector control block diagram
在d-q坐标系建立无刷直流直线电机运动模型，三相坐标系到d-q坐标系的变换公式为
(6)
直线电机d-q磁链方程为
(7)
式中，φd、φq分别为d轴、q轴的磁通量；Ld、Lq分别为d轴、q轴的电感；Id、Iq分别为d轴、q轴的电流；φf为永磁体在定子绕组中产生的磁通量。
直线电机d-q轴电压模型为
(8)
式中，ωe为直线电机对应角速度，ωe=πv/τ；v为直线电机的线速度；τ为电机的极距。
假设电机三相绕组完全对称，磁场沿气隙正弦分布时，直线电机d-q轴的电压方程为
(9)
电机产生的电磁推力为
(10)
式中，If为定子电流。
2.3 换挡机械手末端负载模拟
通过拉格朗日方程建立换挡机械手动力学模型：
(11)
式中，Mh为惯性力矩阵；C为科里奥利和离心力矩阵；
分别为各关节的角度、角速度和角加速度；τh为关节处所受的广义驱动力；τ0为关节处的阻力矩，与机械手末端所受阻力相关；H(θ)为约束矩阵；λ为拉格朗日乘子。
通过对换挡机械手动力学模型的分析可以看出，换挡机械手电机轴处的负载主要由两部分组成：惯性负载，换挡机械手在换挡过程中用来克服自身运动产生的惯性，可以通过虚拟样机模型计算得出；机械手末端负载，即经换挡机械手传递到挂挡电机轴、换挡电机轴处的负载。机械手末端负载可以分解为：选挡过程中，变速杆在空挡区域滑行受到的阻尼力；挂挡过程中，变速杆受到的结合套齿端与结合圈齿圈产生的相互作用力。选挡过程中，变速杆所受负载主要来自在空挡滑行过程中的摩擦力，因此可以将换挡方向负载简化为一个阻尼系统。换挡方向负载Fselect的大小只与选挡方向的速度有关：
Fselect=kvselect
(12)
式中，k为阻尼系数。
挂挡过程中变速杆所受负载主要包括：退挡时分离接合套齿端和接合圈齿圈产生的退挡力、进挡过程变速箱同步器同步时产生的同步力、接合套接合齿端与待接合圈接合齿端相碰撞产生的二次冲击力及换挡结束时的限位力。挂挡过程中，机械手末端受力复杂，具有强非线性，因此采用神经网络拟合的方法来模拟换挡机械手末端在挂挡过程中的受力。假设换挡机械手末端在挂挡过程中所受的力只与机械手末端挂挡速度与挂挡位移有关，建立神经网络挂挡负载模型：
Fshift=(xshift，vshift，w)
(13)
式中，w为经过训练后的神经网络参数，包括神经网络权重Wnm和偏秩bn。
神经网络结构是中间层激活函数为双曲正切函数的BP神经网络，采用梯度下降法进行反向传播完成对权值的更新。激活函数为
(14)
车辆在行驶过程中的颠簸和换挡过程中的二次冲击都会影响换挡机械手末端负载的变化，因此需要对车辆颠簸传递到机械手末端的负载及二次冲击进行建模，以更好地模拟驾驶机器人机械手末端的负载变化。行驶颠簸负载Fbump为车辆行驶中的颠簸通过底盘传递到机械手末端的负载，假设为高斯白噪声。二次冲击负载Fdb假设为高斯脉冲，脉冲最大值不超过最大同步力的70%[12-13]。二次冲击负载函数为
(15)
Kdb=0.7Fsynmax
(16)
式中，Kdb为最大同步力系数；Fsynmax为最大同步力；μ为最大二次冲击力出现时间与同步阶段结束时间之差；σ为高斯冲击标准差。
通过式(12)～式(16)分别求解出选挡负载、挂挡负载、颠簸负载和二次冲击负载，从而得出机械手末端负载
Fm=Fshift+Fselect+Fdb+Fbump
(17)
3 换挡机械手动力学特性仿真及结果分析
3.1 换挡机械手末端负载模型验证
为了验证所提出的换挡机械手末端负载模型的有效性，采集换挡过程中机械手末端的受力，建立机械手末端负载模型，然后对所该模型进行验证。神经网络训练参数如表4所示，部分训练数据如图8所示，训练过程中误差曲线见图9,图中曲线仅保留误差小于0.3的部分。
表4 神经网络训练参数
Tab.4 Neural network training parameters
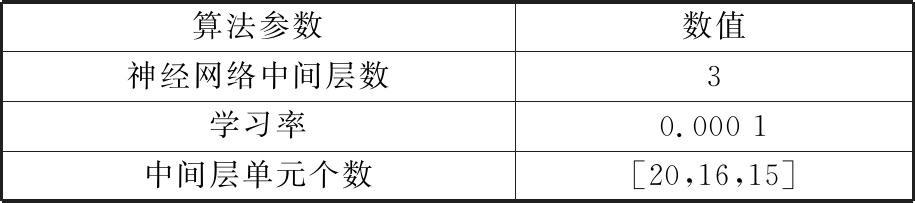
算法参数数值神经网络中间层数3学习率0.000 1中间层单元个数[20,16,15]
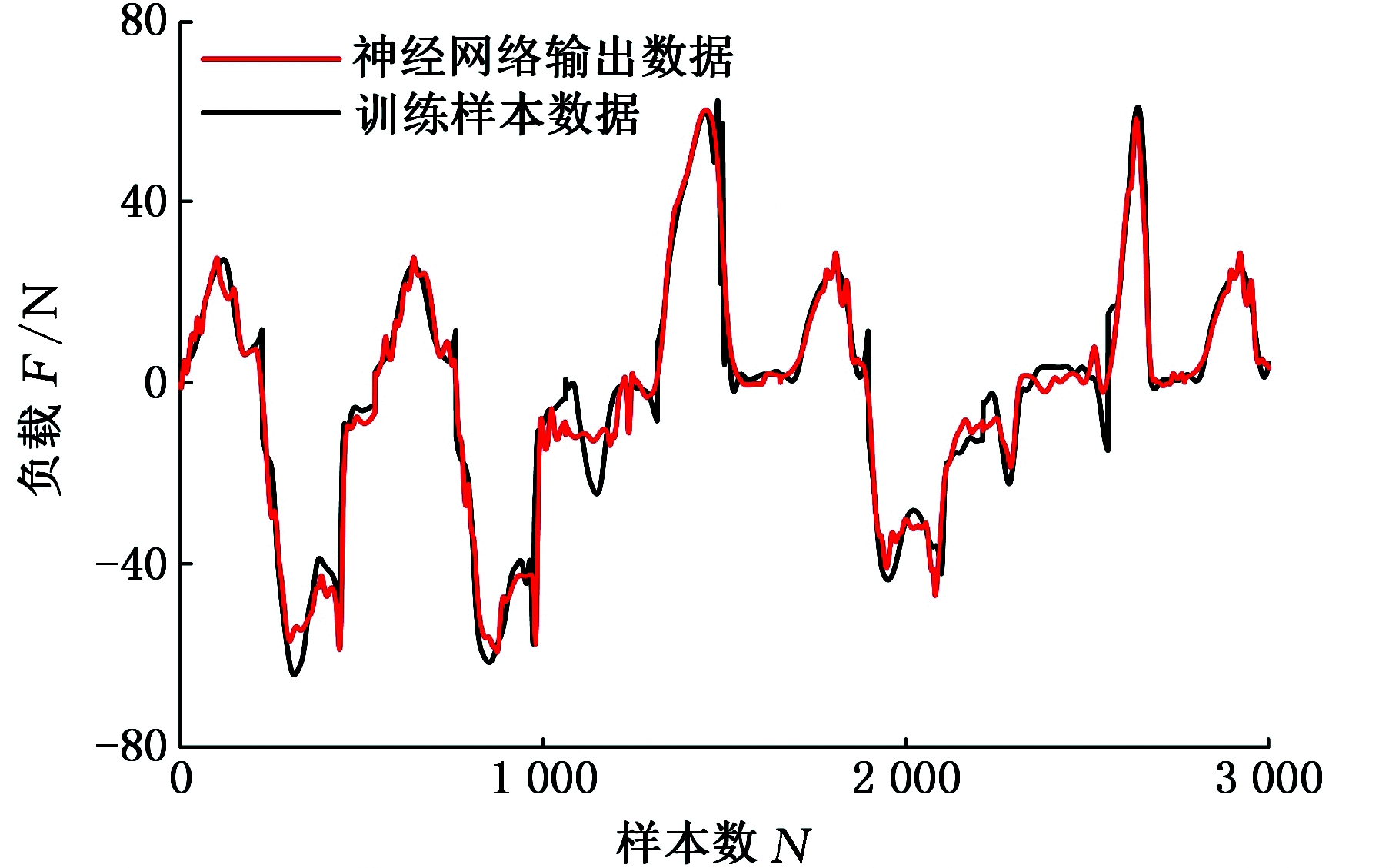
图8 部分训练样本对比数据
Fig.8 Comparison of partial training samples
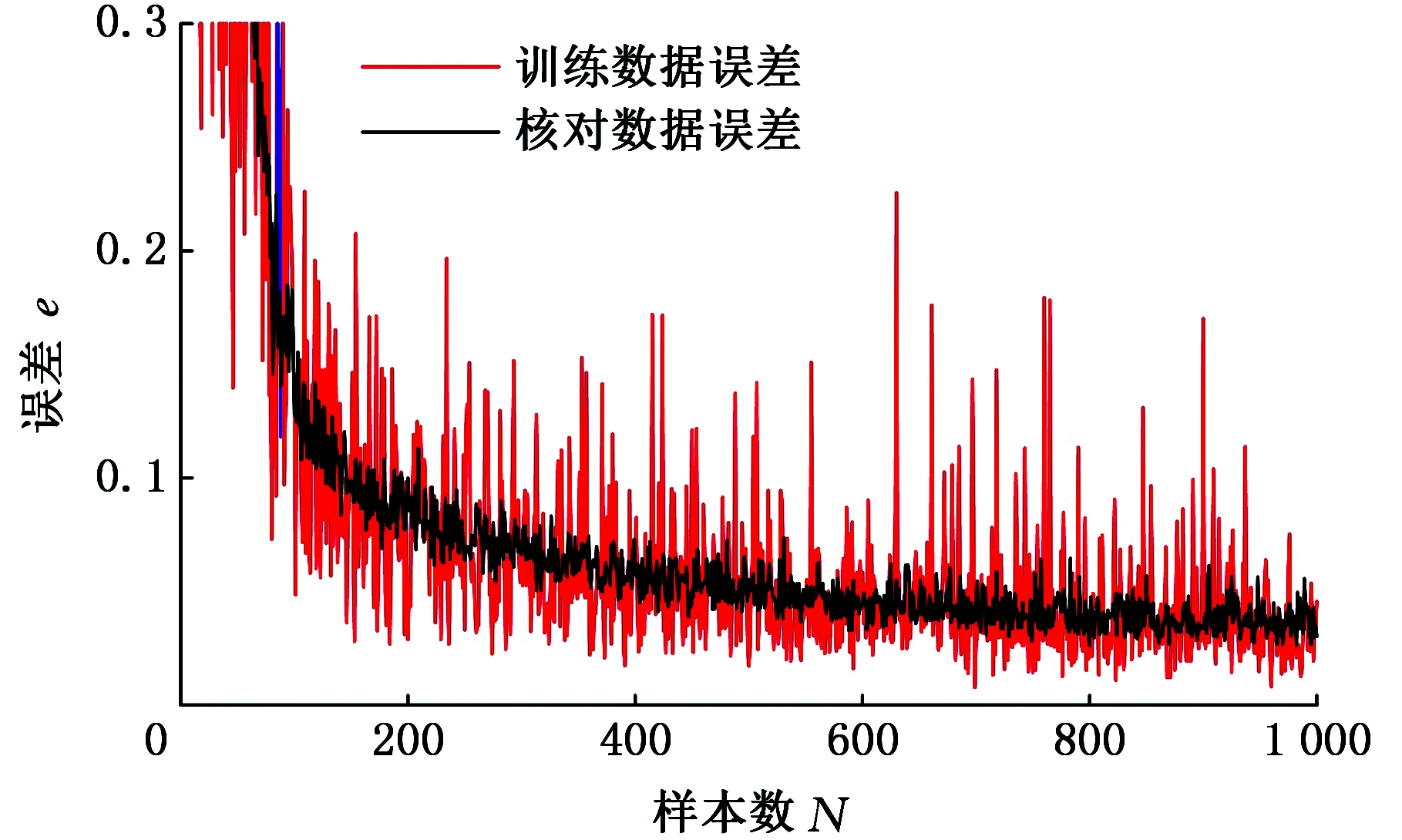
图9 训练过程中误差对比曲线
Fig.9 Error comparison during training
由图9可知神经网络训练误差收敛。在训练过程中，训练误差随着训练步数的增加不断减小，最终误差为0.03。挂挡负载大小与挂挡位移和挂挡速度有关，神经网络输出与样本数据对比如图10。
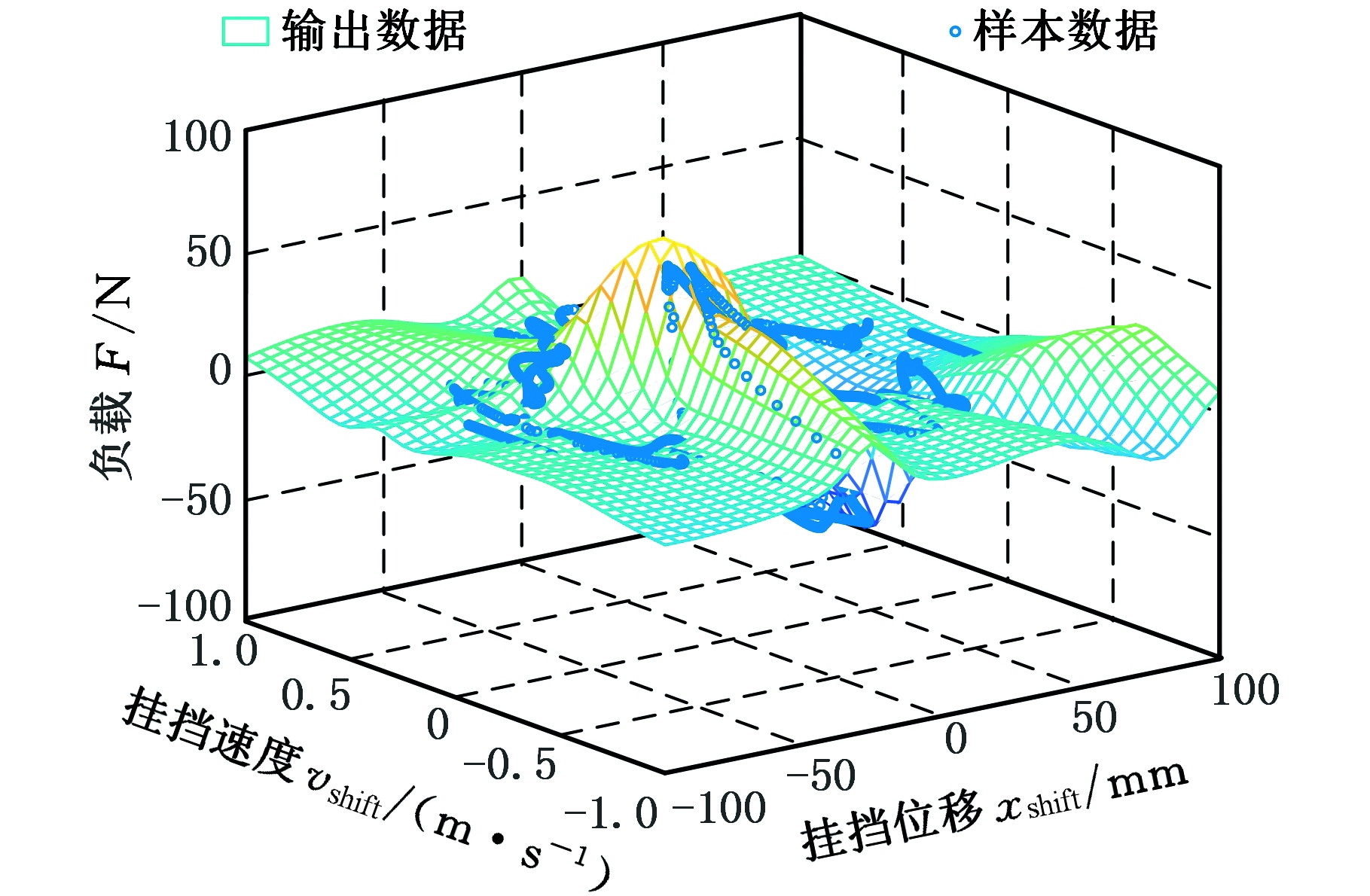
图10 神经网络挂挡负载拟合效果
Fig.10 Neural network gear load fitting effect
由图8和图10可得，机械手末端挂挡负载与试验输出基本一致，训练样本数据和神经网络输出数据之间误差的平均值为0.087 5 N，说明设计的神经网络挂挡负载模型完全能够达到机械手末端挂挡方向负载模拟的目的，验证了提出方法的有效性。
3.2 换挡机械手动力学特性仿真
换挡机械手设计要求是使换挡手柄在200 mm×200 mm的正方形区域内进行换挡运动。根据换挡机械手各连杆尺寸，结合式(1)～式(5)求解出选挡电机、挂挡电机的目标轨迹。
选挡电机、挂挡电机的位置矢量控制器控制电机对目标轨迹进行跟踪。由图11、图12可以看出，负载波动情况下，驾驶机器人换挡机械手可以很好地完成电机轴位移跟踪。
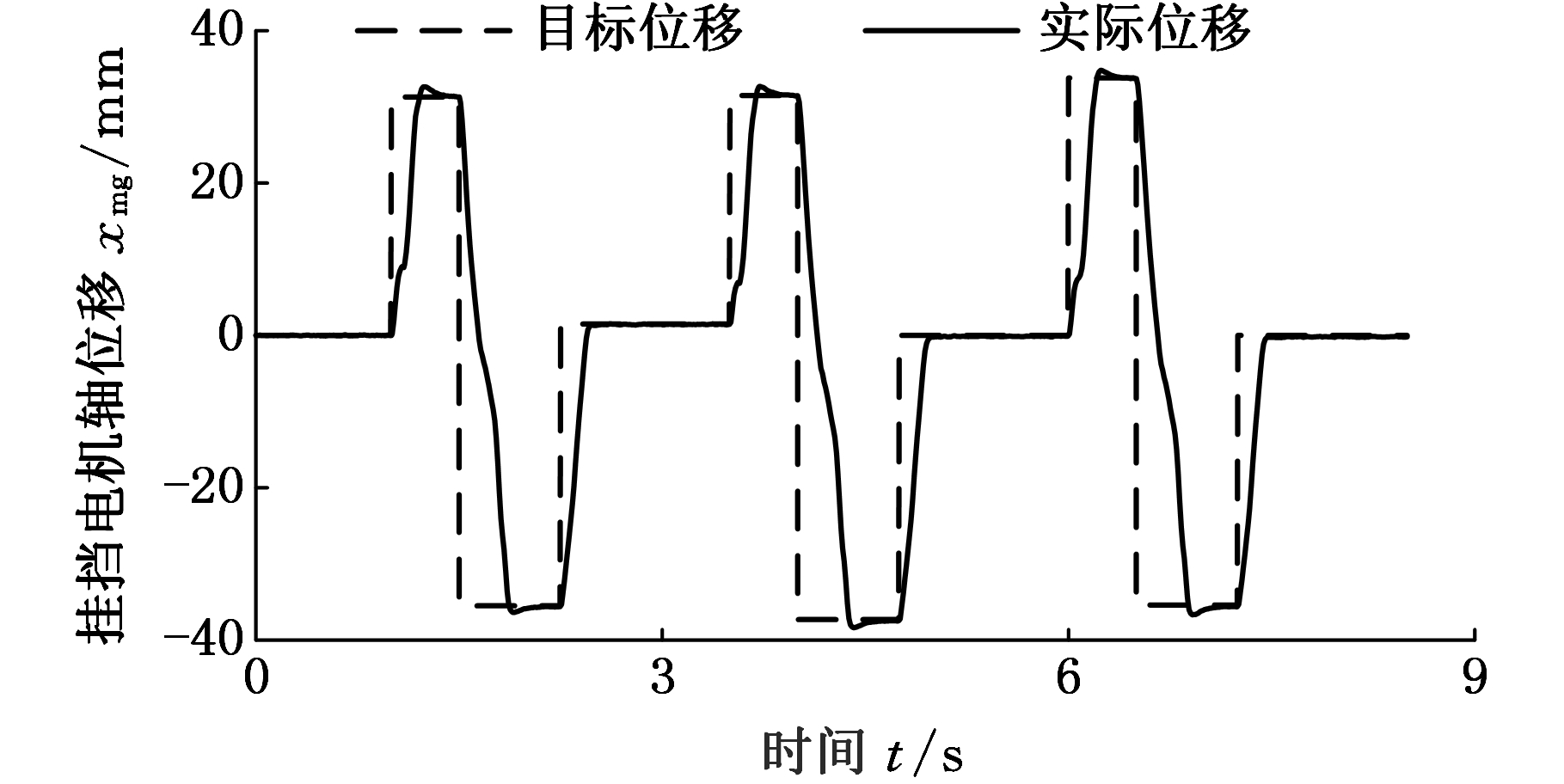
图11 挂挡电机轴位移跟踪曲线
Fig.11 Tracking curve of shift motor shaft displacement
图12 选挡电机轴位移跟踪曲线
Fig.12 Tracking curve of select motor shaft displacement
图13 换挡机械手运动轨迹对比
Fig.13 Comparison of the movement track of the shift manipulator
换挡机械手运动轨迹如图13所示，取选挡方向为x方向，挂挡方向为y方向。由图13可以看出，换挡机械手可以在“王”字形槽内实现换挡运动。换挡机械手在负载波动影响下的运动轨迹与未考虑负载波动的运动轨迹出现差异，尤其是在挂挡过程末端。虽然在实际换挡过程中，此时已进入“王”字形槽末端，不影响实际换挡，但在换挡机械手结构优化过程中，需要考虑负载波动情况下机械手运动轨迹的偏移，使机械手末端运动轨迹接近“王”字形槽。
由图14可以看出，考虑负载波动的挂挡方向最大速度为1 089 mm/s，未考虑负载波动的挂挡方向最大速度为676.2 mm/s，说明换挡机械手末端负载会影响机械手末端速度在挂挡方向的变化。由图15可以看出，考虑负载波动的选挡方向最大速度为353 mm/s，未考虑负载波动的选挡方向最大速度为151 mm/s，说明换挡机械手末端负载会影响机械手末端速度在选挡方向的变化，与挂挡方向速度变化结论类似。由图14、图15可以看出，换挡机械手末端速度在负载波动影响下会产生变化,因此在进行换挡机械手结构设计时，需要额外考虑机械手末端在负载波动影响下的速度变化。
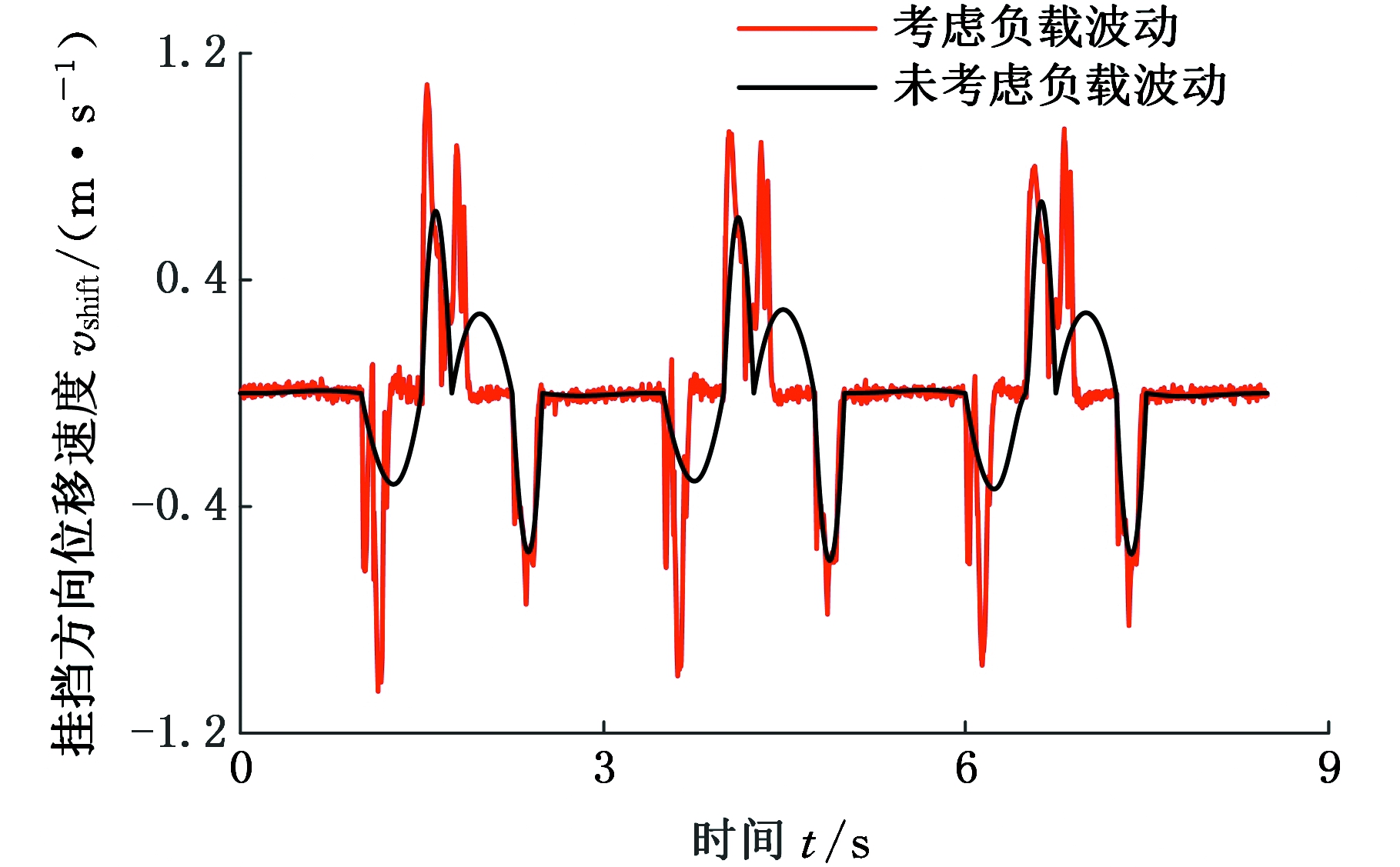
图14 换挡机械手末端挂挡方向速度
Fig.14 Gear speed of the shift manipulator
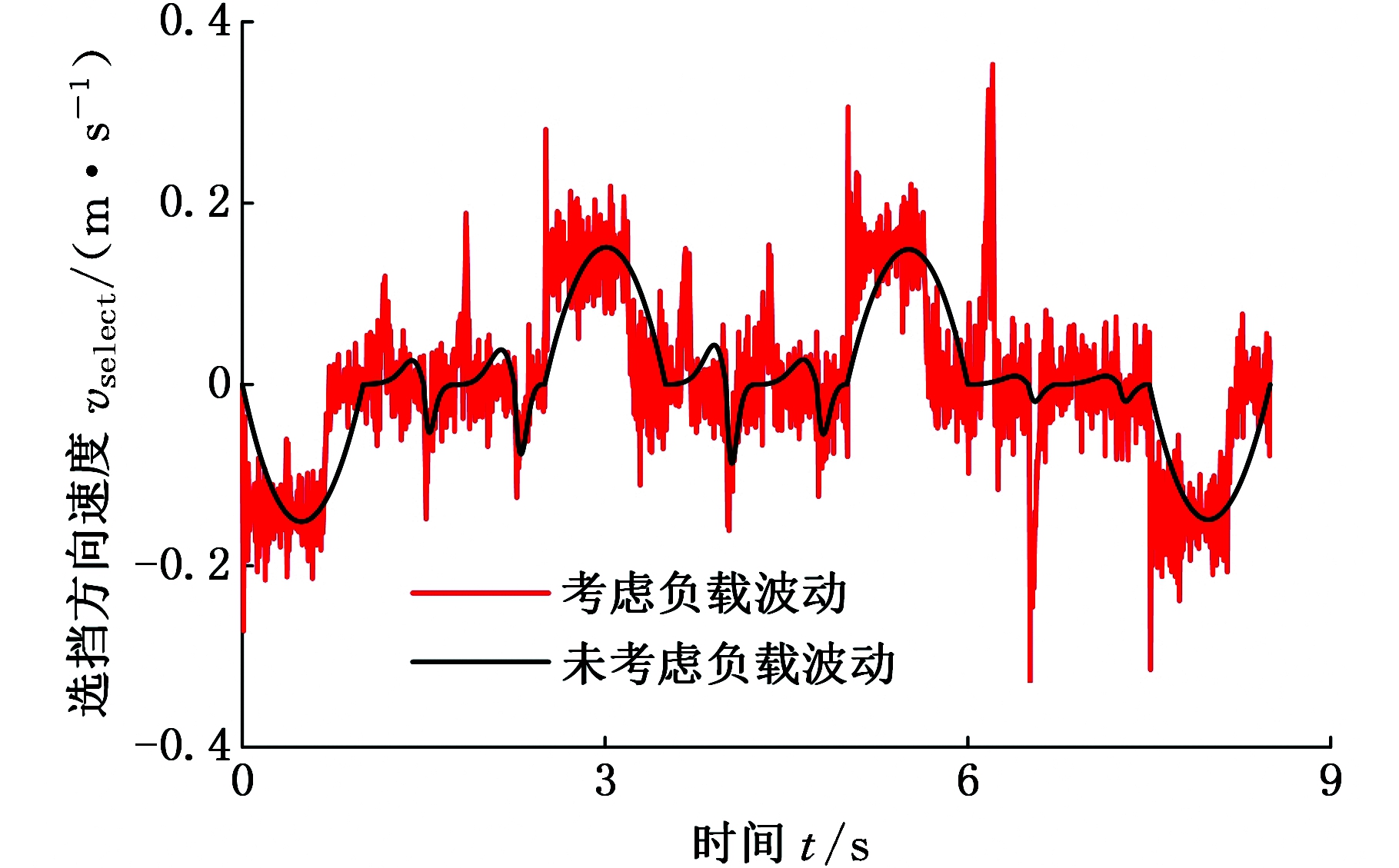
图15 换挡机械手末端选挡方向速度
Fig15 Selection speed of the shift manipulator
由图16可以看出，在未考虑负载波动情况下，换挡机械手挂挡电机轴处的最大负载为22.10 N，选挡电机轴处的最大负载为117.23 N，说明在未考虑负载波动情况下，选挡机械手所受负载更大。这点可从两电机轴处负载范围看出，挂挡电机轴处负载大部分处于-15 N～10 N之间，而选挡电机轴处负载则处在-50～10 N之间，这一现象是由机械手末端与电机的相对位置决定的。
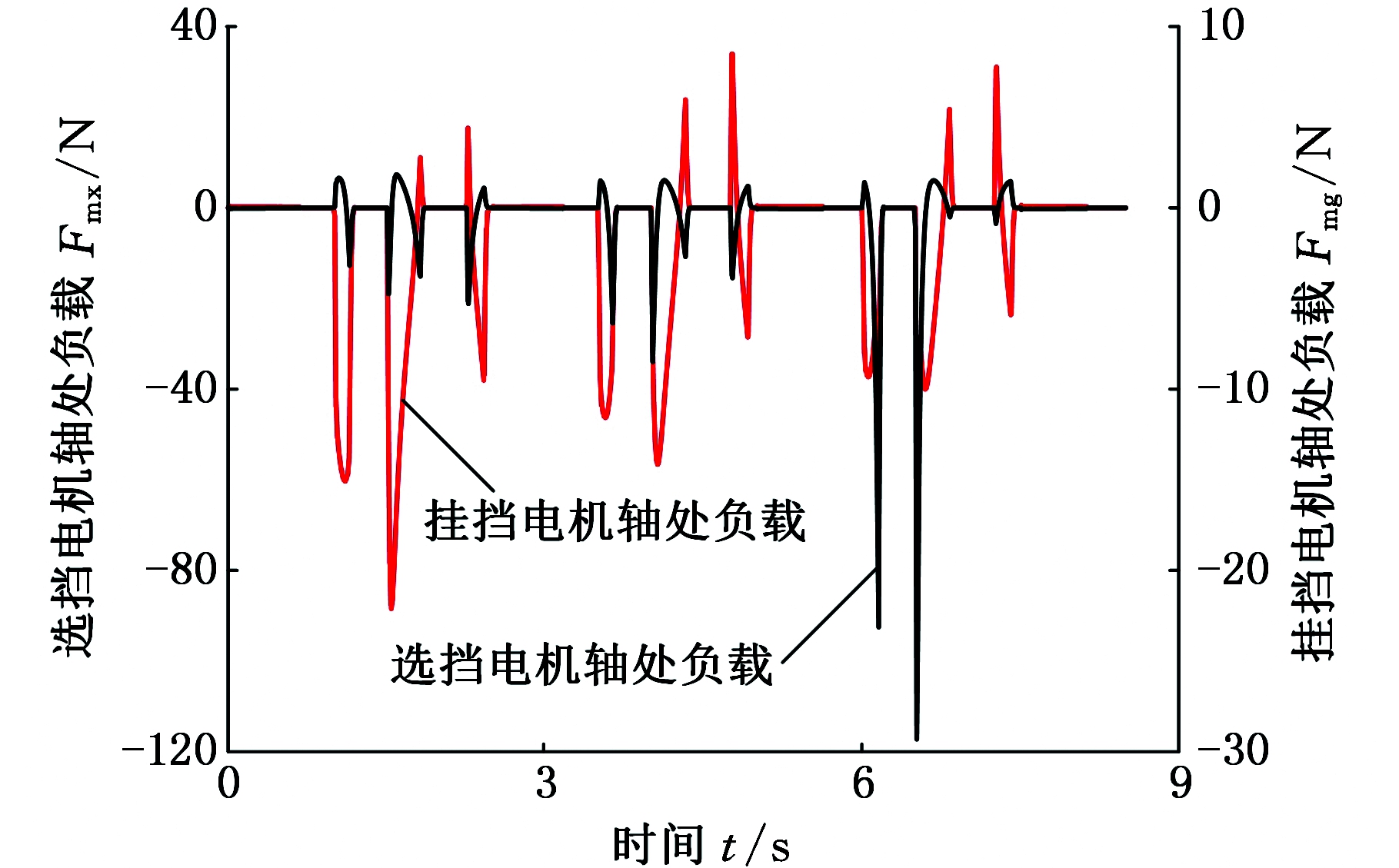
图16 未考虑负载波动的负载
Fig.16 Load without considering the load fluctuations
由图17a可以看出，换挡机械手末端挂挡方向的最大负载为67.99 N，平均负载为5.54 N；选挡方向的最大负载为7.62 N，平均负载为1.44 N。由图17b可以看出，所提出的换挡负载模拟方法可以很好地模拟出二次冲击负载。
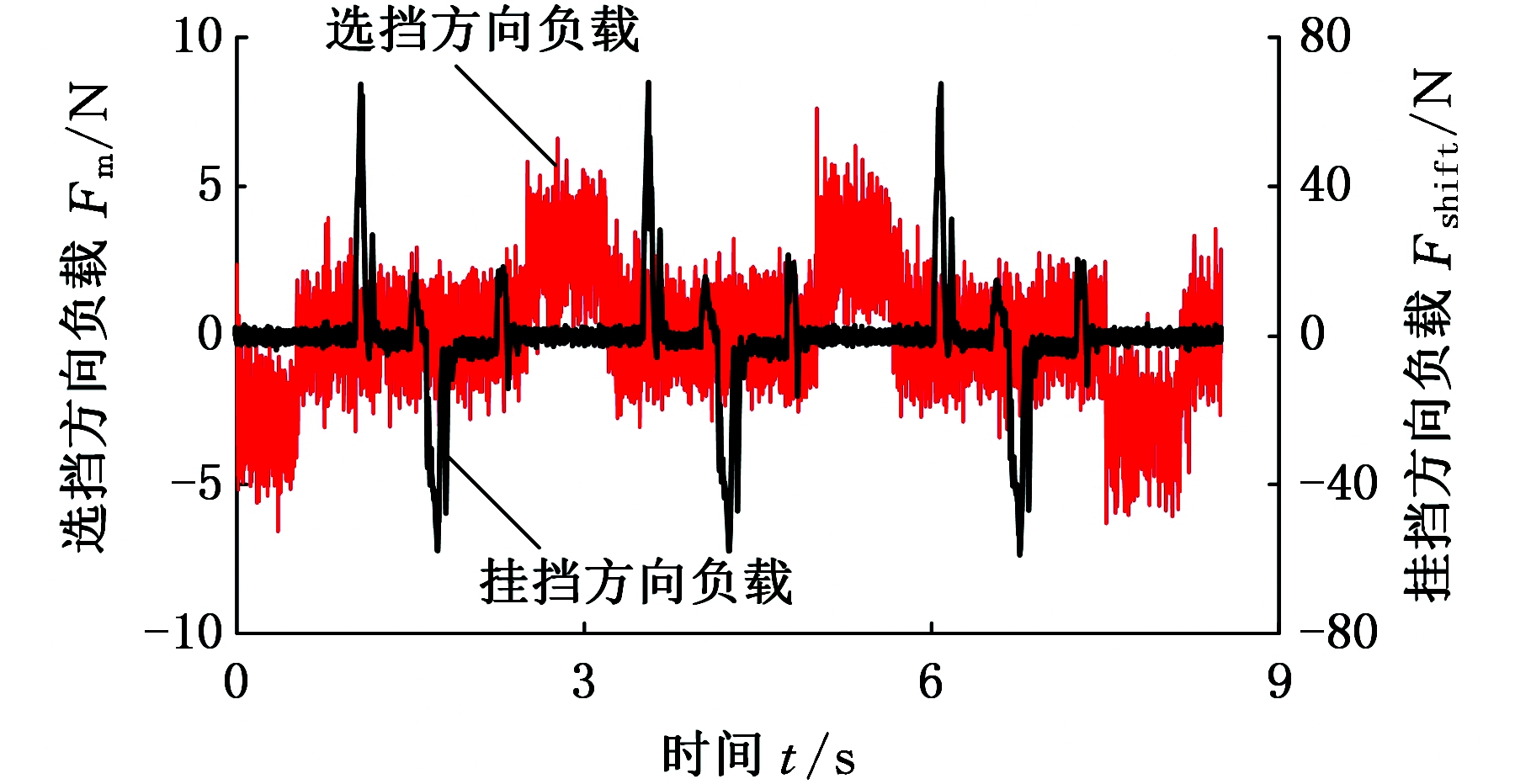
(a)换挡机械手末端负载
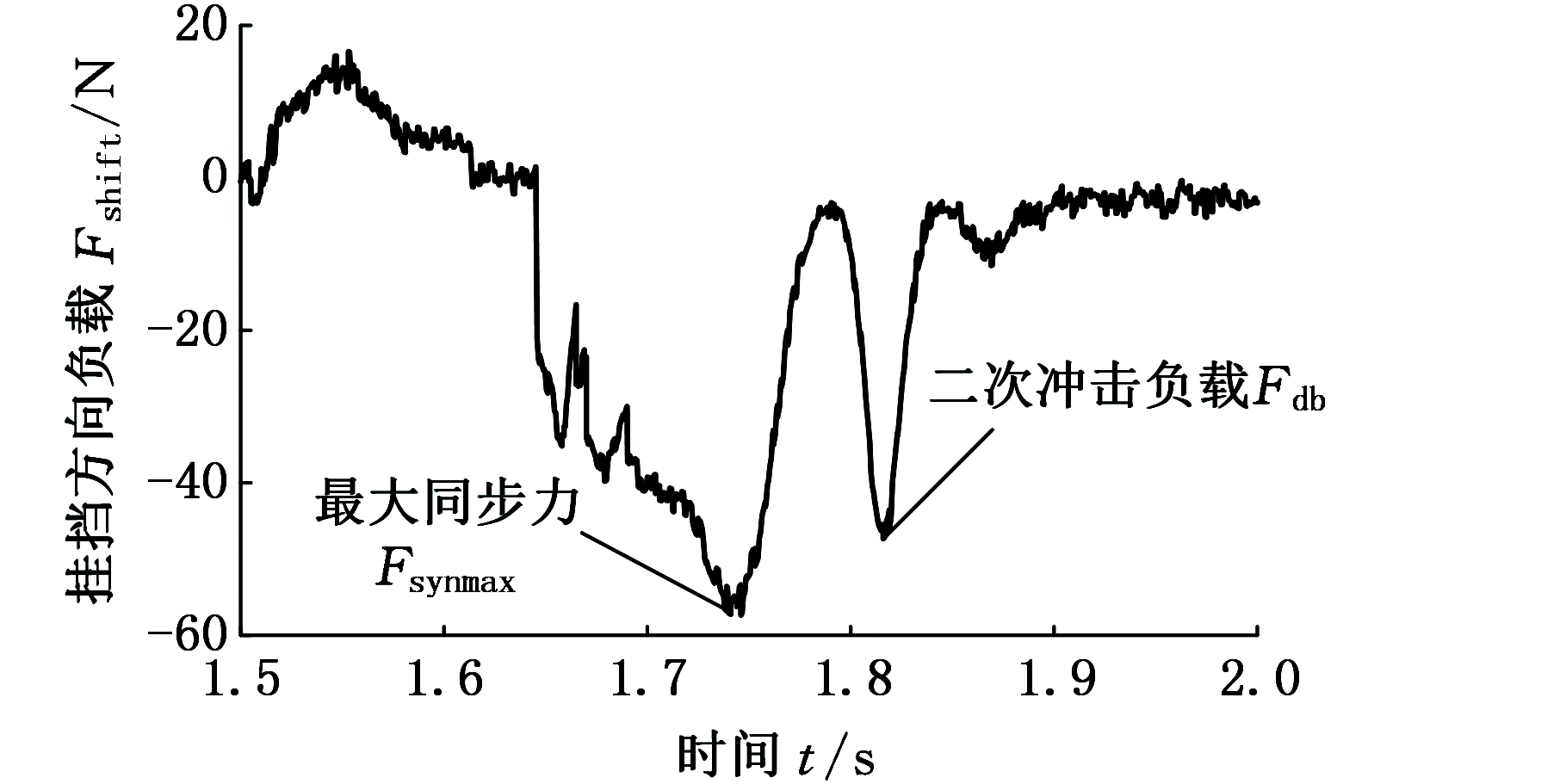
(b)挂三挡时二次冲击曲线
图17 换挡机械手负载
Fig.17 Shift manipulator load
由图18可以看出，挂挡电机轴处的最大负载为265.49 N，平均负载为17.97 N；选挡电机轴处的最大负载为125.25 N，平均负载为16.09 N。选挡电机轴、挂挡电机轴处负载大部分处于-200～200 N区间,在选用电机最大承受负载以内，不影响正常工作。
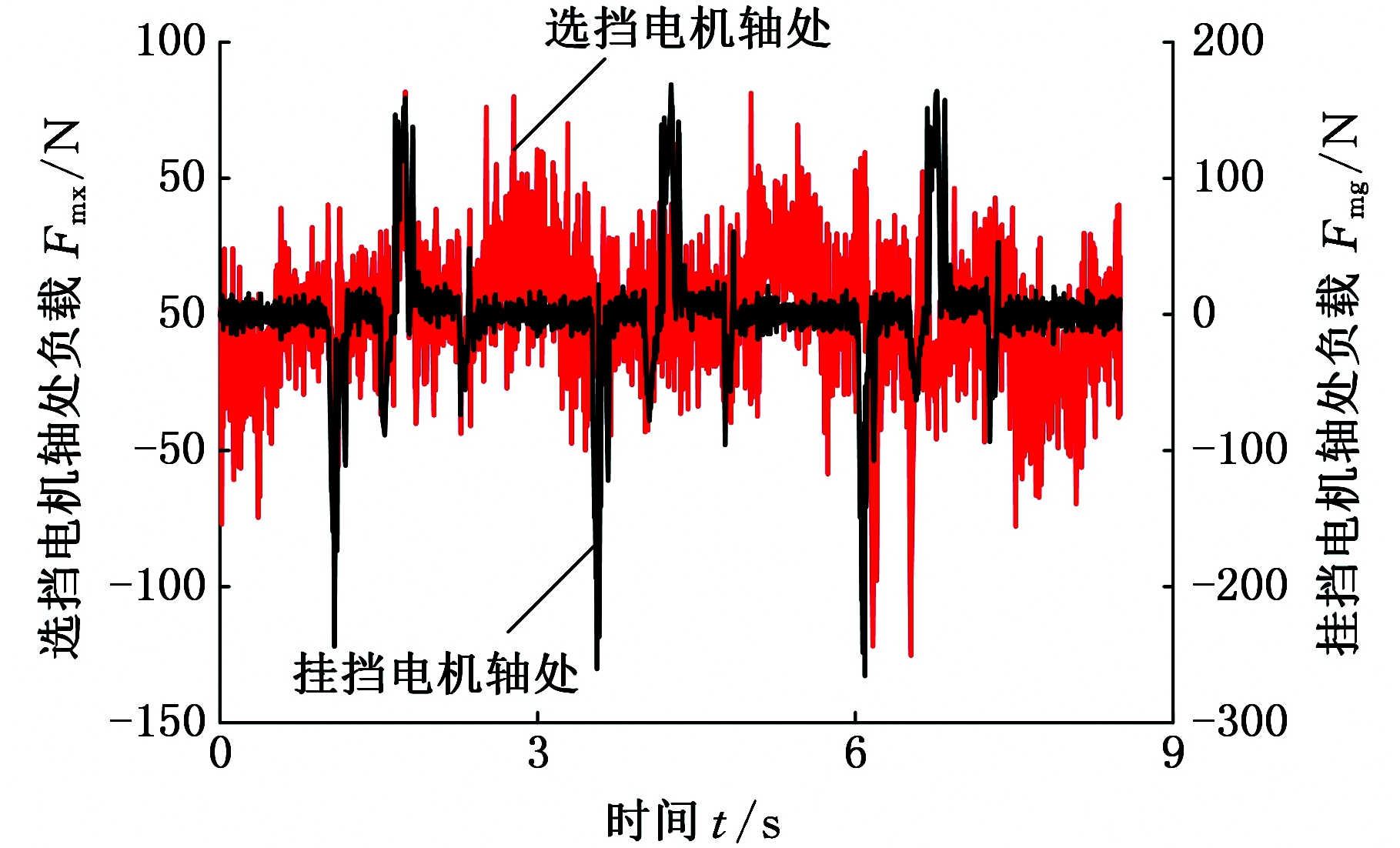
图18 考虑负载波动的选挡、挂挡电机轴处负载
Fig.18 Considering the load at the selected and geared motor shaft under load fluctuations
通过对比图16～图18可以看出，是否考虑负载波动时的电机轴处负载有较大变化。挂挡电机轴处的最大负载由未考虑负载波动的22.10 N上升为考虑负载波动的265.49 N，选挡电机轴处的负载由未考虑负载波动的117.23 N上升为考虑负载波动的125.15 N。挂挡电机轴处的负载变化更明显，这是由于在换挡机械手末端，挂挡方向负载比选挡方向负载变化更加频繁且变化幅值更大。因此在对驾驶机器人进行结构优化的过程中，需要考虑机械手末端负载波动对电机轴处负载的影响。
4 换挡机械手性能试验
为了验证考虑负载波动的换挡机械手的换挡性能，将驾驶机器人安装于试验车型上进行换挡机械手换挡性能试验，试验车型相关参数如表5所示，试验现场如图19所示。换挡过程中，实时采集换挡位移等试验数据，根据这些参数对驾驶机器人换挡机械手换挡性能进行评价。
表5 试验车型参数
Tab.5 Test vehicle parameters
车型长安悦翔变速箱传动比发动机排量1.5 L4缸4冲程水冷,多点电喷1挡3.582挡1.923挡1.28驱动方式前置前驱4挡0.955挡0.76
图19 试验现场图
Fig.19 Test site screen
试验结束后，将采集到的挂挡位移与所建立的换挡机械手仿真模型进行比较。图20为二挡挂三挡的位移曲线图。
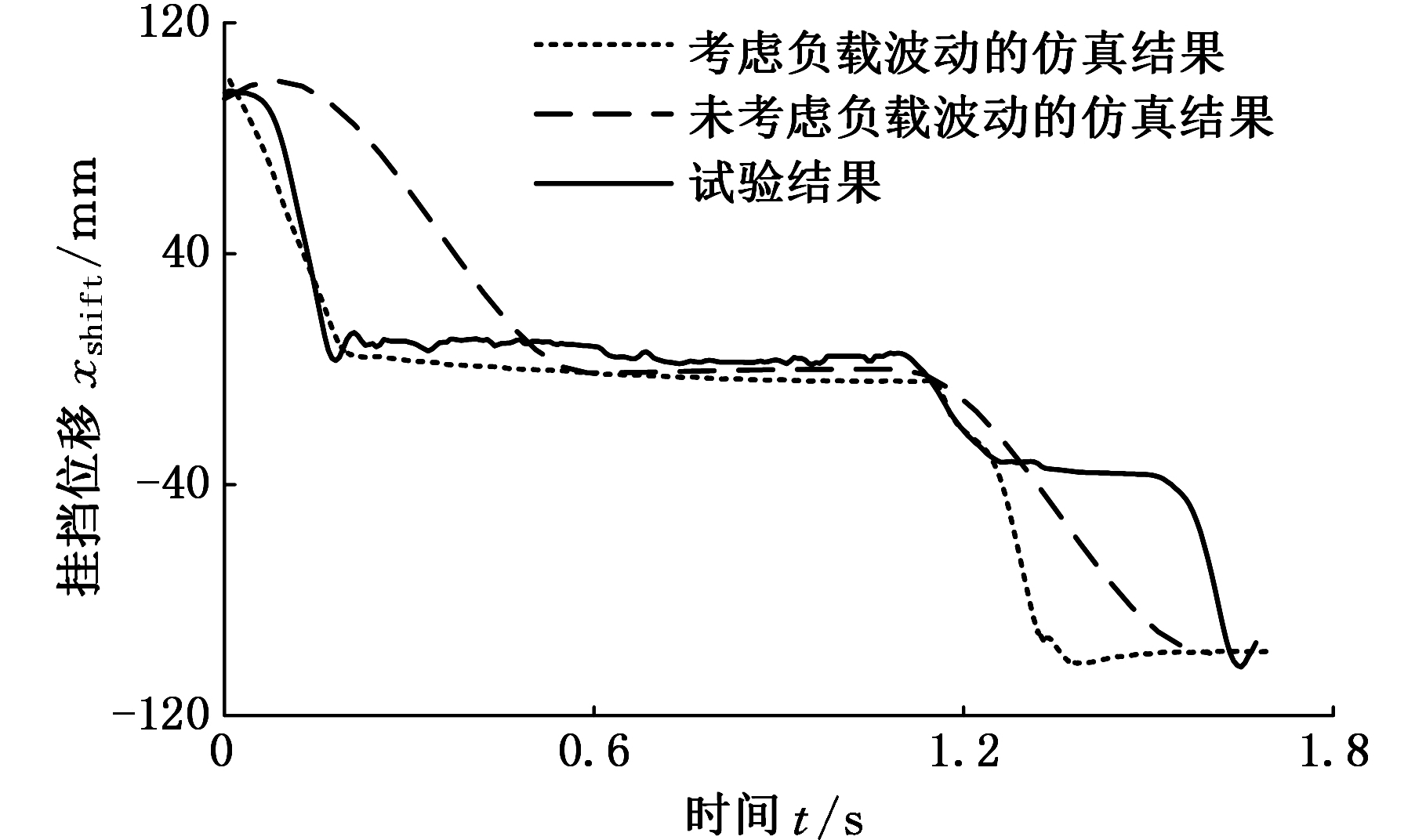
图20 二挡挂三挡的机械手位移
Fig.20 Displacement of the shift manipulator from 2nd to 3rd gear
换挡机械手的抓手操控变速器换挡杆完成从二挡脱离到挂入三挡的整个过程。换挡机械手首先操控变速器换挡杆从二挡脱离并运动到中间位置。退挡过程中，考虑负载波动的位移曲线更接近试验结果。选挡过程中，挂挡位移虽有波动但近似保持不变。选挡操作完成后，进行挂挡操作。进挡过程中，考虑负载波动的位移曲线更接近实际试验曲线，出现了由二次冲击导致的位移波动。图21、图22分别为二挡挂三挡的速度变化曲线和速度变化局部放大图。
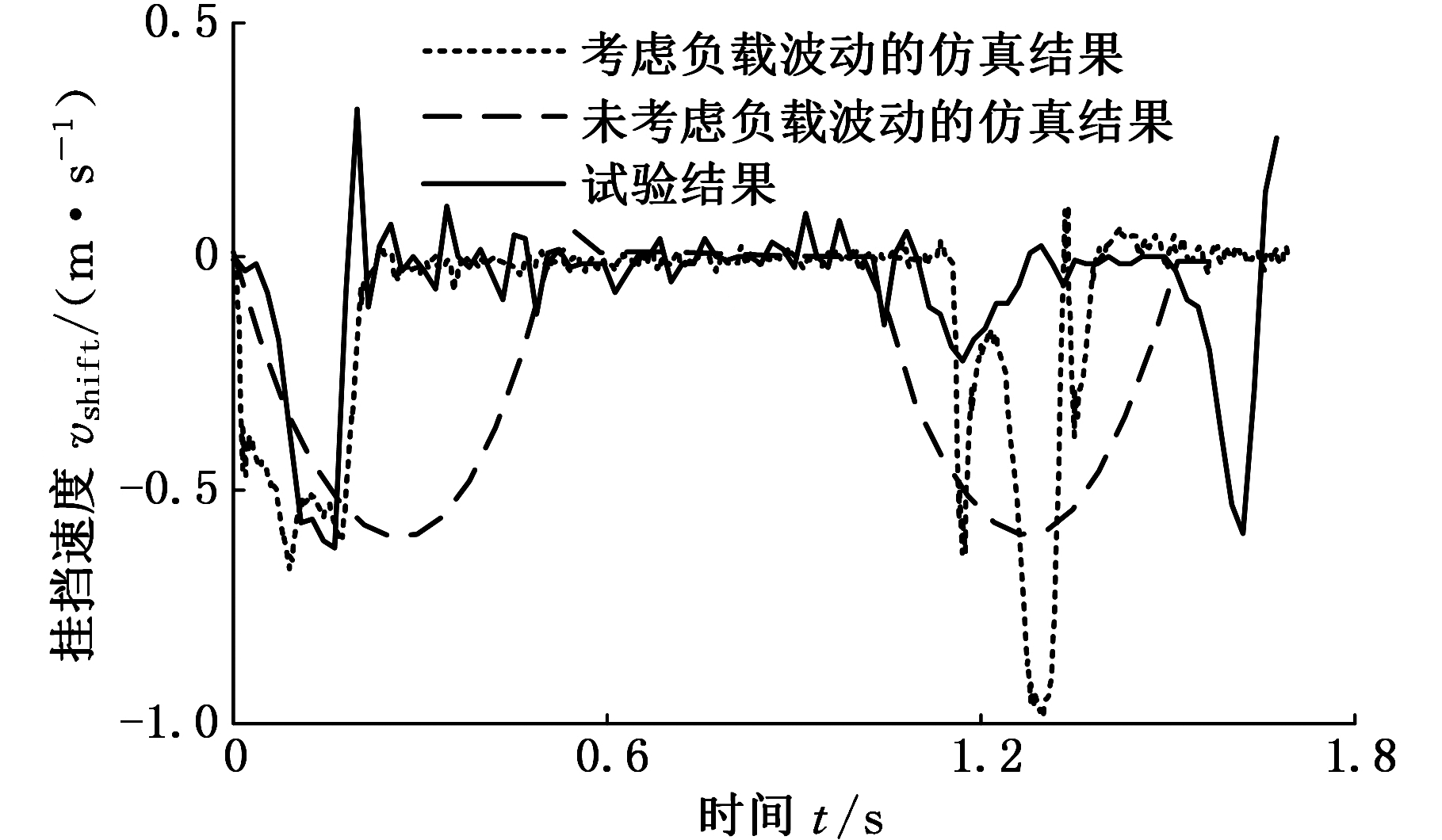
图21 二挡挂三挡的机械手末端速度
Fig.21 Speed of the shift manipulator from 2nd to 3rd gear
(a)退挡过程
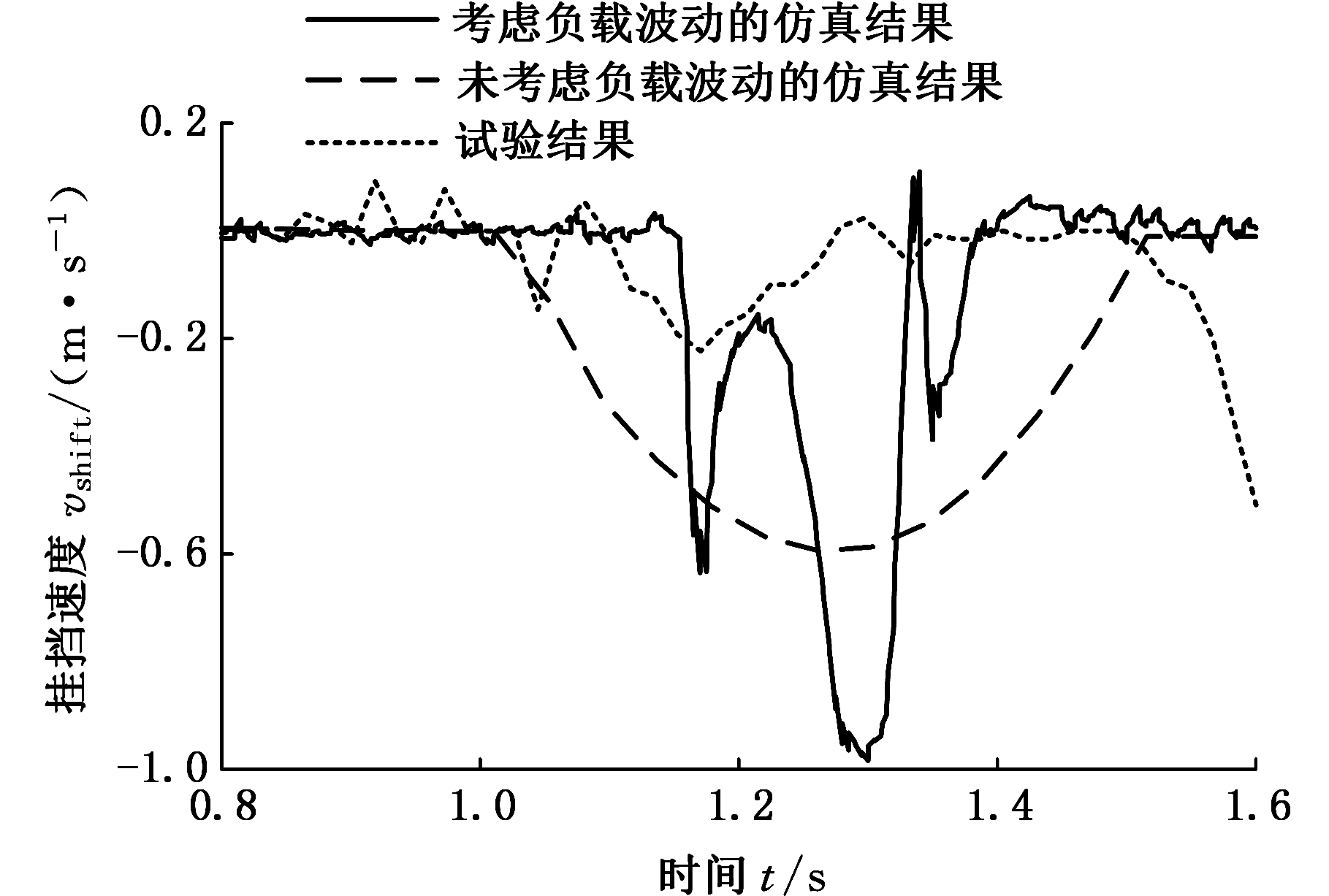
(b)进挡过程
图22 二挡挂三挡的机械手末端速度(局部)
Fig.22 Speed of the shift manipulator from 2nd to 3rd gear(partical)
由图21、图22可以看出，考虑负载波动的速度变化曲线与试验结果更加符合。由图22b的挂三挡时速度变化曲线可以看出，考虑负载波动的速度曲线和试验结果在速度变化趋势上更加接近，而未考虑负载波动的速度变化曲线更加平滑。
图23、图24所示分别为四挡挂五挡的位移及速度。四挡挂五挡的过程中，无论是在退挡阶段还是在进挡阶段，考虑负载波动的位移变化更符合试验结果。图25为四挡挂五挡的速度变化局部放大图。
通过对比试验曲线可以看出，考虑负载波动的虚拟样机仿真结果更接近试验结果，换挡位移和速度与整车试验结果趋于一致。
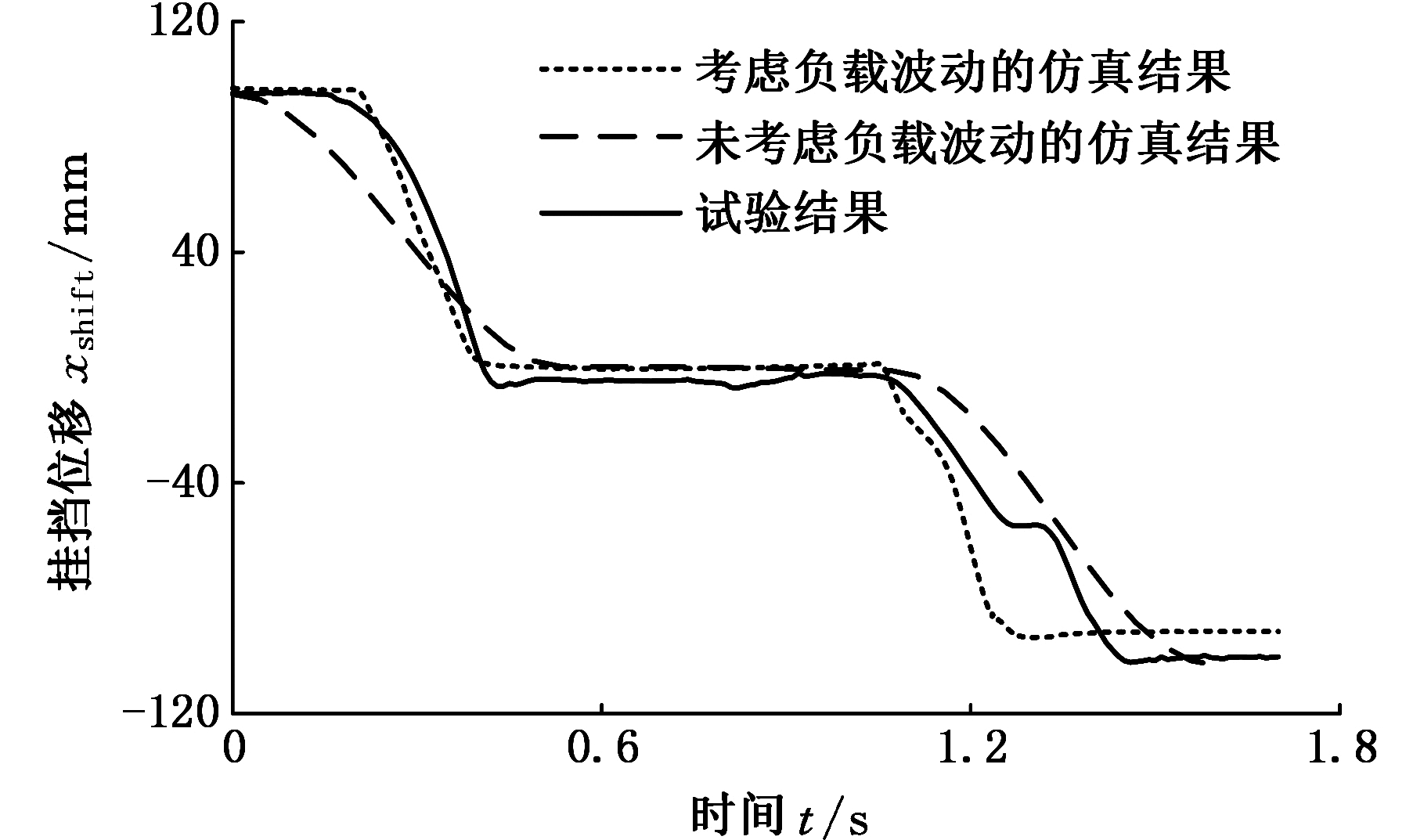
图23 四挡挂五挡的机械手末端位移
Fig.23 Displacement of the shift manipulator from 4th to 5th gear
图24 四挡挂五挡的机械手末端速度
Fig.25 Speed of the shift manipulator from 4th to 5th gear
(a)退挡过程
(b)进挡过程
图25 四挡挂五挡的机械手末端速度(局部)
Fig.25 Speed of the shift manipulator from 4th to 5th gear(partical)
5 结论
提出了一种换挡负载波动模拟方法，并针对负载波动下的驾驶机器人换挡机械手进行了动力学特性分析。
换挡机械手末端挂挡负载与试验输出基本一致，平均误差为0.087 5 N，验证了神经网络挂挡负载模型的有效性。
根据建立的换挡机械手动力传递模型，对换挡机械手在负载波动下的动力学特性进行了分析。负载波动对选挡方向、挂挡方向的速度及电机轴处负载有较大影响。考虑负载波动时，挂挡方向最大速度为1 089 mm/s，选挡方向最大速度为353 mm/s，挂挡电机轴处最大负载为265.49 N，选挡电机轴处负载为121.15 N。未考虑负载波动时，挂挡方向最大速度为676.2 mm/s，选挡方向最大速度为151 mm/s，挂挡电机轴处最大负载为22.10 N，选挡电机轴处负载为117.23 N。
仿真与换挡机械手换挡性能试验验证了末端负载变化对换挡机械手的换挡轨迹跟踪有较大影响。
研究还存在如下不足：换挡负载模型未考虑不同挡位换挡负载的差异性；模型忽略了换挡过程中变速杆与箱体之间的冲击。这些是未来工作中需要考虑的。
[1] CHEN G, ZHANG W G. Digital Prototyping Design of Electromagnetic Unmanned Robot Applied to Automotive Test[J]. Robotics and Computer-Integrated Manufacturing, 2015, 32:54-64.
[2] CHEN G, ZHANG W. Hierarchical Coordinated Control Method for Unmanned Robot Applied to Automotive Test [J]. IEEE Transactions on Industrial Electronics, 2015, 63(2):1039-1051.
[3] 陈刚, 张为公, 龚宗洋, 等. 用于汽车驾驶机器人的车辆性能自学习方法[J]. 中国机械工程, 2010, 21(4): 491-495.
CHEN Gang, ZHANG Weigong, GONG Zongyang, et al. A Vehicle Performance Self Learning Method Applied to Robot Driver[J]. China Mechanical Engineering, 2010, 21(4): 491-495.
[4] 汪俊, 陈刚, 王纪伟. 汽车驾驶机器人换挡机械手驱动力仿真优化[J]. 计算机仿真, 2017, 34(5): 347-352.
WANG Jun, CHEN Gang, WANG Jiwei. Driving Force Simulation and Optimization of Shift Manipulator for Vehicle Robot Driver[J]. Computer Simulation, 2017, 34(5): 347-352.
[5] 卢伟, 陈浩, 王玲,等. 拖拉机驾驶机器人换挡机械手运动分析[J]. 农业机械学报, 2016, 47(1): 37-44.
LU Wei, CHEN Hao, WANG Ling, et al. Motion Analysis of Tractor Robot Driver’s Gear Shift Mechanical Arm[J]. Transaction of the Chinese Society for Agricultural Machinery, 2016, 47(1):37-44.
[6] 虞沈林, 陈刚. 驾驶机器人换挡机械手刚柔耦合运动分析[J]. 汽车工程, 2018, 40(6): 733-748.
YU Shenlin, CHEN Gang. Kinematics Analysis of Rigid-flexible Coupling of Shift Manipulator for Robot Driver[J]. Automotive Engineering, 2018,40(6):733-748.
[7] PATEL H, TENDULKAR V, BAID H, et al. Gearshift Quality Sensitivity Analysis[J]. SAE International Journal of Advances and Current Practices in Mobility, 2019, 1(1): 137-142.
[8] 陈玉祥, 臧孟炎, 陈勇, 等. 基于虚拟样机技术的手动变速器换挡力分析[J]. 中国机械工程, 2012,23(8): 996-1000.
CHEN Yuxiang, ZANG Mengyan, CHEN Yong, et al. Shift Force Analysis of Manual Transmission Based on Virtual Prototyping Technology[J]. China Mechanical Engineering, 2012, 23(8): 996-1000.
[9] ÖZPINAR 
AKALIN O. Gearset Synchronization Modeling of a Heavy Commercial Vehicle Transmission and Correlation with Objective Measurements of Gear Shift Quality[J]. SAE Technical Paper: 2019-01-0031, 2019.
[10] 张志刚, 余晓霞, 郑燕杰, 等. 同步器摩擦特性建模仿真与试验[J]. 中国机械工程, 2019, 30(7): 825-831.
ZHANG Zhigang, YU Xiaoxia, ZHENG Yanjie, et al. Modeling Simulation and Tests of Friction Characteristics for Synchronizers[J]. China Mechanical Engineering, 2019, 30(7): 825-831.
[11] YANG C, HUA L, WANG Z, et al. Shift Performance Test and Analysis of Multipurpose Vehicle[J]. Advances in Mechanical Engineering, 2014, 6: 378176.
[12] 张志刚, 李尚, 苏洪, 等. 变速器换挡二次冲击强度频次分析[J]. 科学技术与工程, 2016, 16(20): 280-285.
ZHANG Zhigang, Li Shang, SU Hong, et al. Frequency Analysis on Double Bump Strength of Automobile Transmission[J]. Science Technology and Engineering, 2016, 16(20):280-285.
[13] 国家汽车标准化技术委员会. 汽车机械式变速器总成台架试验方法(第一部分：微型)：QC/T 568.1-2011[S]. 北京：中国计划出版社，2011.
National Automotive Standardization Technical Committee. Rig Testing Method for Auto Manual Transmission Assembly. Part 1: Mini-vehicle: QC/T 568.1-2011[S]. Beijing: China Planning Press, 2011
