0 引言
高速高效切削是机械加工技术发展的必然方向。刀具的光整工艺通过改变切削刃的轮廓、微观形状和刃区的微观结构,消除刃磨过程造成的微观缺陷,提高刀具的切削性能,提高刀具寿命和加工表面的质量[1-4]。因此,刀具切削刃的光整是实现高速高效切削的基础,研究刀具刃口钝化机制对改善现有刀具状况具有重要意义。
20世纪中叶,发达国家开始将高能超声波技术与机械零件表面处理领域相结合[5],例如超声波表面光整技术是近年来广泛使用的金属表面处理技术[6],该技术不仅继承了传统的滚压、喷丸等表面处理的优点,还弥补了滚压、喷丸等在加工过程中容易产生残余应力和表面划痕[7]的缺陷。目前超声波光整加工技术处于发展推广阶段,对各种材料展开的实验研究较少,缺少对设备使用具有指导意义的数据资料。
利用超声振动的原理,将超声振动与现有的钝化光整技术相结合[8-9],在达到普通钝化功能的前提下,运用超声振动辅助可不改变刀具基体成分,加快了钝化效率,大幅提高刀具性能,如有效改善表面形貌、延长刀具的疲劳寿命、增强刀具的耐腐蚀性、提高刀具的显微硬度、改善刀具的耐磨性,该技术在航空航天、轨道交通等零件表面质量要求高的场合具有广阔应用前景。
随着数值计算方法和接触力学的飞速发展,离散单元法(discrete element method, DEM)已经成为分析离散颗粒和几何体之间相互作用的重要手段[10-12]。目前将离散元分析软件EDEM(engineering discrete element method)运用在刀具刃口钝化的研究并不多。
本文采用EDEM软件对铣刀钝化过程进行仿真,主要研究钝化方式(有无超声振动)、钝化速度和钝化时间对刃口累积能量及刃口磨损量的影响;同时,利用钝化机进行铣刀钝化实验,研究钝化方式、钝化时间对铣刀的改善情况。
1 超声振动钝化光整设备的研制
1.1 超声振动研究
超声波振动辅助系统由超声波发生控制系统和铣刀弹簧夹头组成。超声波发生控制系统又由超声波变幅杆、超声波换能器和超声波电源三部分构成[13],是使机械振动平台产生超声振动的核心部分。超声波电源主要用于产生大功率的高频交流电流,驱动换能器的工作;换能器被驱动后,换能器将高频电能转化为机械能,从而产生机械振动;变幅杆和换能器配合改变超声振动振幅,是功率超声振幅的机械放大级[14];变幅杆与弹簧夹头连接,在安装铣刀后,使铣刀产生相应的振幅,从而在钝化中加入高频振动辅助。图1为超声波振动辅助设备示意图。

图1 超声振动设备示意图
Fig.1 Schematic diagram of ultrasonic vibration equipment
在设计的超声振动辅助设备中,其换能器及变幅杆如图2所示。
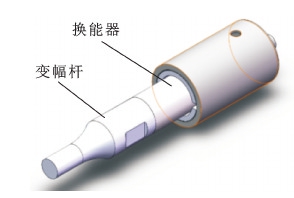
图2 换能器与变幅杆
Fig.2 Transducer and horn
在频率的选取中采用ANSYS的模态分析仿真,具体仿真结果如图3所示。各阶振型对应的固有频率如表1所示。
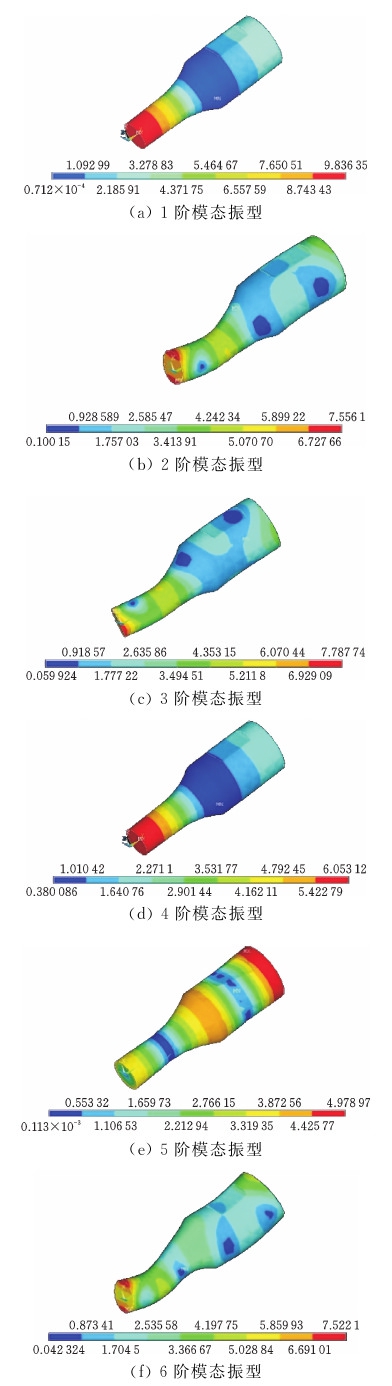
图3 各阶模态振型
Fig.3 Different order mode shapes
表1 各阶固有频率
Tab.1 Different order natural frequencies
阶数123456频率(Hz)19 43824 66025 02628 17832 49838 563
由图3可知,在固有频率28 178 Hz下,超声振动系统的振型为轴向的高频振动,且与弹簧夹头连接处振动最强烈。考虑到本文采用了简化的有限元模型,其中忽略了压电陶瓷晶片之间的薄金属电极的影响,简化了预应力螺栓的结构和超声变幅杆与弹簧夹头的连接,故仿真的结果不可避免地与理论结果有一定差距,但是误差在允许的范围内,选取合理的超声频率为28 000 Hz。
1.2 新型钝化装置介绍
根据现有成熟的拖拽式钝化机研制了一种简易超声振动辅助钝化机,利用带有超声振动的钝化机对刀具进行钝化实验,通过对刀具检测来证明超声振动带来的优越性。
该设备采用立式旋转超声钝化方法,刀具刃口钝化设备如图4所示。分散固态磨粒装在一个磨料桶中,磨料通常由棕刚玉和碳化硅按照一定比例混合配制而成。通过电机带动圆盘进行旋转,在圆盘上装有2个齿轮轴,而在齿轮轴上装有超声振动设备,与夹头形成一体。利用在大小旋转轴上安装的导电滑环,解决超声波发生器供电的导线缠绕问题。夹头可以夹持相应的刀具。通过一个固定的大齿轮,实现了刀具的公转、自转以及超声振动导致的纵向谐振。在超声钝化过程中,刀具刃口通过与分散固态磨粒不断的碰撞冲击,达到去除刃口微观缺陷的目的,实现高效均匀的刃口钝化。刀具沿着一定的轨迹运动,而分散的固体磨粒的运动是随机的,所以钝化过程是一个非常复杂的行为。
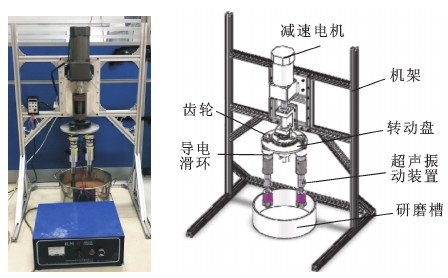
(a) 实物图 (b) 三维图
图4 刀具刃口钝化设备
Fig.4 Tool edge passivation equipment
1.3 刀具刃口钝化原理
刀具刃口钝化采用自制的立式旋转钝化方法。刀具安装在一根旋转的主轴上,主轴上同时装有超声振动辅助装置。在刀具钝化过程中,刀具的刃口不断与固态磨粒发生剧烈碰撞,达到去除刃口微观缺陷的目的,实现高效均匀的表面处理。
刀具可以在磨粒中实现公转和自转,在带有超声振动辅助的主轴上,刀具可以在纵向发生固定频率的谐振。
刀具的不同运动方式对刀具刃口的影响也不同。方式1是刀具做公转及自转的行星运动,其运动轨迹如图5a所示;方式2是刀具在方式1的基础上添加纵向的高频振动,其运动轨迹如图5b所示。

图5 不同运动方式下的刀具轨迹
Fig.5 Cutter track under different motion modes
2 EDEM离散元仿真
本文基于立式旋转钝化方法,通过离散元软件EDEM[15]建立两种不同的运动轨迹下的钝化模型,一种是普通的刀具行星运动方式,另一种是在此基础下带有超声振动辅助的运动方式。重点研究两种运动方式对磨粒状态、磨粒速度、刃口累积能量和磨损量等的影响规律。
2.1 材料接触参数及接触模型
通过EDEM软件中的GEGM数据库选择材料物性和接触参数,磨粒材料采用碳化硅,其接触参数如表2所示。
在接触模型的选择中,颗粒与颗粒之间选择Hertz-Mindlin(no ship)接触模型,颗粒与物体之间选择Hertz-Mindlin with Archard Wear磨损模型 [16]。
表2 接触参数
Tab.2 Contact parameters

磨粒铣刀泊松比0.140.3剪切模量(GPa)179.6234.6密度(kg/m3)3 20012 700静摩擦因数0.750.5滚动摩擦因数0.20.5恢复系数0.050.01磨损常数2×10-152×10-15
Hertz-Mindlin (no ship)接触模型是EDEM的默认模型,在力的计算方面准确且高效。在Hertz-Mindlin (no ship)接触模型中,法向力分量基于Hertz接触理论,切向力模型基于Middlin-Deresiewicz的理论。法向力和切向力都具有阻尼分量,阻尼数和恢复系数有关。切向摩擦力遵守库仑摩擦定律,滚动摩擦力通过接触独立定向恒转矩模型实现。
假设两颗球型颗粒发生碰撞,则法向力Fn是法向重叠量δn的函数,表达式如下:
(1)
(2)
(3)
式中,E*为当量弹性模量;R*为当量半径;υ、μ代表一颗球型颗粒;Eυ、υυ、Rυ和Eμ、υμ、Rμ分别为每颗球型颗粒的弹性模量、泊松比和球体的半径。
法向阻尼力的表达式为
(4)
(5)
(6)
(7)
式中,mi、mj为球型颗粒质量;m*为当量质量;![]() 为相对速度的法向分量;x为碰撞恢复系数;Sn为法向刚度。
为相对速度的法向分量;x为碰撞恢复系数;Sn为法向刚度。
切向力表达式为
Ft=-Stδt
(8)
(9)
式中,St为切向刚度;δt为切向重叠量;G*为当量剪切模量。
切向阻尼力表达式为
(10)
式中,![]() 为相对速度的切向分量。
为相对速度的切向分量。
切向力受库仑摩擦因数μs、法向力Fn限制,其中μs是静摩擦因数。仿真中,通过在接触表面施加一个力矩τi来考虑滚动摩擦:
τi=-μrFnRiωi
(11)
式中,μr为滚动摩擦因数;Ri为接触点到质心的距离;ωi为物体在接触点处的单位角速度。
Hertz-Mindlin with Archard Wear接触磨损模型基于材料的去除体积与颗粒对材料表面所做的摩擦功成正比的理论,相同半径的半球形峰元相接触时,其中一个峰元在塑性变形后的接触面积为δA,则有
(12)
式中,r为接触面积半径;FN为两对峰元所受法向载荷;H为材料弱的峰元硬度。
模型中假设一次滑动的结果产生一个磨损体积为δV的颗粒。经物理实验得出,磨损颗粒的形状是等轴的,则半球峰元的磨损体积为
(13)
当两峰元摩擦持续时,设最长滑动行程为δL:
δL=2r
(14)
则体积磨损率为
(15)
那么整个接触平面的体积磨损率为
(16)
式中,K1为修正因数;V为接触平面的磨损体积;N为平面所受法向载荷。
设K=1/(3 K1),则
(17)
式中,K为磨损系数;V为接触平面的磨损体积;L为滑动行程。
由此可以看出,磨损量与平面所受法向载荷、滑动行程成正比,与硬度成反比。
刀具钝化过程可以看作是磨粒对刀具刃口部分的微观磨损,因此只需要通过计算颗粒运动对设备表面参数的法向接触能量和切向接触能量来评估其磨损深度:
Q=WFndt
(18)
(19)
式中,Q为去除材料的体积;Fn为法向力;dt为磨程;W为磨损常数;Hp为被磨材料硬度。
EDEM软件中仅需输入W值,简化了参数输入过程。EDEM中Relative Wear模型模拟的是高冲击的区域,也就是为用户提供数据以证明磨损发生的区域。
采用三维软件SOLIDWORKS对实验所用的硬质合金铣刀进行建模,刀具直径为6 mm,刃长为10 mm,刀柄长为50 mm。由于只研究刃口的磨损,故为了提高软件的计算效率,对硬质合金铣刀采取一定的简化。简化后的刀具模型如图6所示。
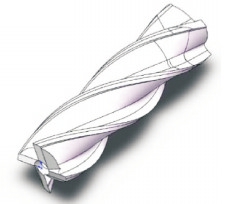
图6 铣刀三维模型
Fig.6 Milling cutter 3D model
采用ANSYS软件对铣刀三维模型进行网格划分,由于主要研究刃口部位的钝化,故对刀尖刃口部位网格细致划分。
将划分网格后的铣刀模型和磨料桶导入EDEM软件,添加磨粒工厂,采用Fill Section形式进行填充。选用EDEM软件中球状模型作为颗粒模型,设置颗粒半径为0.5 mm。
由于EDEM软件的理论基础是采用动态松弛法求解方程,每一步长都要基于前一步长计算颗粒和几何受力、速度、位置等特征参数,导致计算量巨大,因此,考虑到仿真效率等因素,将仿真时间设为5.08 s。刀具钝化仿真模型如图7所示。
图7 刀具钝化仿真模型
Fig.7 Tool passivation simulation model
2.2 仿真结果分析
参考实物装置对仿真软件进行设置。在方式1运动轨迹下,铣刀以0.1 m/s的速度匀速下降,0.08 s后停止降落,同时开启铣刀的公转和自转,设置自转速度是公转速度的3倍,公转速度np分别为30 r/min、40 r/min、50 r/min、60 r/min;在方式2运动轨迹下,在以上设置后加入谐振,其频率设置为28 kHz,振幅为20 μm。考虑到仿真效率等因素,总运动时间设为5.08 s。
2.2.1 刀具转速及超声振动对磨粒速度的影响
由图8可知,在两种不同的钝化方式下,磨粒的速度均随着刀具转速的增大而增大,即刀具转速越大,磨粒的运动越剧烈,磨粒与铣刀刃口接触的频率也更大,钝化的效率、效果也相应提高;当铣刀的公转速度达到60 r/min时,两种运动方式下的磨粒的平均速度并无太大差异,速度在15~20 mm/s上下波动。
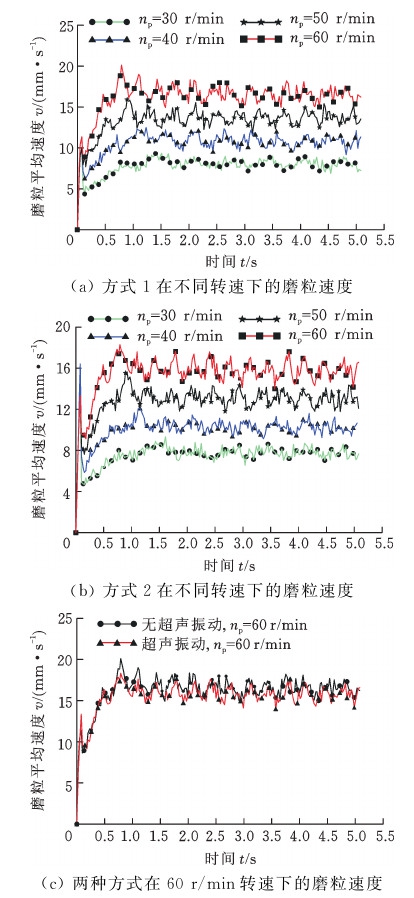
图8 不同方式不同转速的磨粒速度
Fig.8 Abrasive speeds under different modes and different rotating speeds
2.2.2 刀具转速及超声振动对铣刀刃口累积能量的影响
研究表明,累积能量损失与磨损量成正比[17]。未加超声振动辅助的钝化方式下,钝化速度对刃口法向累积能量和切向累积能量影响变化规律如图9a、图9b所示,铣刀刃口法向累积能量
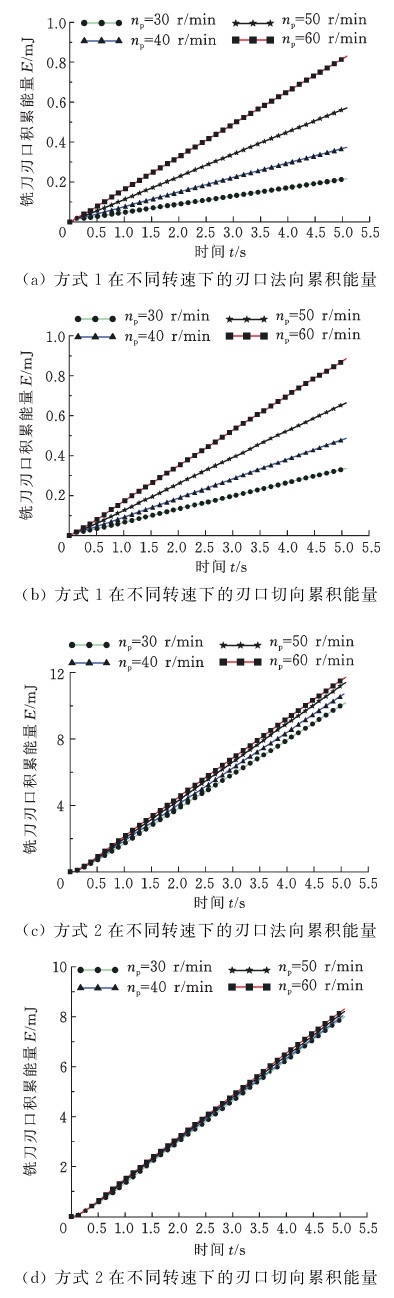
图9 不同转速的刃口累积能量
Fig.9 Accumulated energy under different rotating speeds
和切向累积能量均随钝化时间的增大而增大。不同刀具转速下,在公转速度为60 r/min时,5.08 s时法向累积能量为0.830 mJ, 切向累积能量为0.885 mJ,法向累积能量主要由冲蚀磨损产生,切向累积能量主要由磨粒磨损产生,因此铣刀的磨损主要由磨粒磨损造成,且随着公转速度的增大,法向及切向累积能量大大增加。在加入超声振动辅助的钝化方式下,钝化速度对刃口法向累积能量和切向累积能量影响变化规律如图9c、图9d所示,铣刀刃口法向累积能量和切向累积能量均随钝化时间的增大而增大。不同刀具转速下,在公转速度为60 r/min时,5.08 s时法向累积能量为11.7 mJ,切向累积能量为8.3 mJ,在此方式下,由于刀具的运动路径加入了上下谐振,导致冲蚀磨损占主导地位。如图10所示,加入超声振动辅助的钝化方式的累积能量(图10b)远远大于未加超声振动辅助的钝化方式的累积能量(图10a),尤其在法向累积能量方面差异更加明显。

图10 不同方向的刃口累积能量
Fig.10 Accumulated energy of different directions
2.2.3 刀具转速及有无超声振动对刃口磨损影响
铣刀刃口磨损量随钝化速度的变化规律如图11a、图11b所示,由图可知,在未加超声振动辅助和加入超声振动辅助的两种钝化过程中,随着公转速度的增大,铣刀磨损量也相应增大。其原因在于磨粒与铣刀的相对速度增大,相同时间内接触次数增多,因此磨损量增大。由图11c可知,在5.08 s时,公转速度为60 r/min时,未加超声振动辅助方式的刃口最大磨损量为4.16 nm,而加超声振动辅助方式的刃口最大磨损量为61.7 nm,后者的值远远大于前者,因为后者铣刀运动更加复杂,与磨粒碰撞更加剧烈,从而导致刃口磨损量增大。由此可知,带有超声振动的钝化方式在效率方面表现更加优越,这将大大缩短工作时间,提高工厂效益。

图11 不同方式不同转速的刃口磨损量
Fig.11 Blade wear under different modes and different rotating speeds
3 实验研究
3.1 实验方案
实验采用自行研制的超声振动钝化装置一台,超声波发生器一台,额定电压为220 V,功率600 W,输出频率为(28±1)kHz,超声光整工具系统工作频率为28 kHz。
钝化刀具选取直径6 mm的平头铣刀,钝化磨粒采用东莞市欧泰克抛光材料有限公司提供的钝化光整专用磨料。
本次实验采用正转1 min、反转1 min的循环模式,因为该模式下钝化效率更佳。钝化方式采用一般钝化实验以及带有超声振动辅助的钝化实验。钝化总时间分别采用10 min、20 min、30 min,钝化速度选择为公转速度60 r/min,自转速度180 r/min,通过显微镜拍出钝化前、钝化后的铣刀刃口与刃面进行实验对比;通过显微镜观测及计算,分别求出10 min、20 min、30 min时刻铣刀钝圆变径数值的变化,通过一系列对比实验,验证超声振动钝化的先进性。
3.2 试验结果与分析
采用两种钝化方式进行光整实验,对铣刀的刃口和刃面用扫描电镜观测,对比钝化前、无振动钝化、振动钝化的铣刀刃口和刃面形貌。如图12a、图12b所示,由钝化前铣刀的刃口和刃面可以看到,铣刀刃口有很多缺口,刃面的粗糙度也很大。由图12c~图12f可知,经过钝化后的铣刀的刃口和刃面的表面状态得到大大改善,表面的凹凸部位以及刃口的缺口明显得到改善,而带有超声振动钝化后的铣刀的表面形貌也优于不带超声振动辅助的铣刀,其刃面一致性也好于不带超声振动钝化后的铣刀。
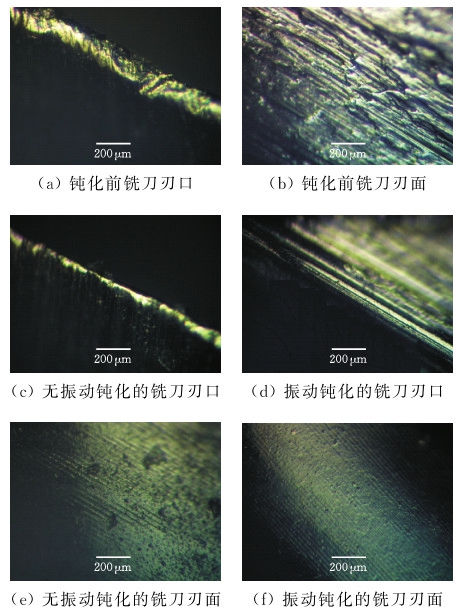
图12 不同振动钝化条件下的铣刀刃口和刃面
Fig.12 Milling tool edge and surface under different vibration passivation conditions
如表3所示,通过显微镜观测和三维软件计算,分别求出公转速度为60 r/min时不同实验时间下铣刀钝圆半径的数值。观察铣刀钝圆半径的变化可以发现,在带有超声振动辅助的钝化效率优于不带振动的钝化方式,将钝圆半径钝化到18 μm,带超声振动的方式大约能节约8 min左右时间,效率增进约26%。
表3 不同模式不同时刻的铣刀钝圆半径
Tab.3 Blunt circle radius of milling cutter under different modes and different time

10 min20 min30 min有振动的铣刀钝圆半径(μm)13.517.820无振动的铣刀钝圆半径(μm)10.215.618.1
4 结论
(1)本文通过离散元软件EDEM进行数值模拟与超声振动钝化光整实验研究,提出了一种新型钝化光整加工方法,即超声振动钝化光整加工方法,在普通的钝化设备中加入了一定高频的超声振动。带有超声振动辅助的钝化设备在钝化效率方面得到明显改善,大大缩短了钝化时间。
(2)在改变切削刃的轮廓、微观形状和刃区的微观结构方面,钝化效果得到了提升,尤其是减少了崩刃、凹坑,均匀性较好。
(3)表面形貌的大幅度改善提高了铣刀的寿命及其加工质量,为以后的刀具优化提供了依据。
[1] 桂育鹏.刀具刃口钝化技术的探讨[J].金属加工(冷加工),2004(6):43-44.
GUI Yupeng. Discussion on Tool Edge Passivation Technology[J].Metalworking(Metal Cutting), 2004(6): 43-44.
[2] UHLMANN E, OBERSCHMIDT D, KUCHE Y, et al. Cutting Edge Preparation of Micro Milling Tools[J].Procedia CIRP, 2014(14):349-354.
[3] 顾祖慰,张奇. 刀具钝化技术应用前景的展望[J].工具技术,2009(8):78-80.
GU Zuwei, ZHANG Qi. Prospect of Application of Tool Passivation Technology[J]. Tool Technology, 2009(8): 78-80.
[4] 夏雪. 刀具刃口钝化技术及方法的研究[J].装备制造技术,2014(10):204-205.
XIA Xue. Research on Tool Edge Passivation Technology and Method[J]. Equipment Manufacturing Technology, 2014(10):204-205.
[5] 甘雨林.AISI304不锈钢圆柱面的超声冲击表面强化及其组织性能的研究[D].大连:大连理工大学,2014.
GAN Yulin. Study on Strengthening and Effect of Properties of Cylindrical AISI304 Austenite Stainless Steel by Ultrasonic Impact Treatment[D]. Dalian:Dalian University of Technology,2014.
[6] 韩强.超声波表面光整新技术应用[J].纺织机械,2011,2:53-55.
HAN Qiang. Application of New Technology of Ultrasound Surface Finishing[J]. Textile Machinery,2011,2:53-55.
[7] 朱有利,王燕礼,边飞龙,等.金属材料超声表面强化技术的研究与应用进展[J].机械工程学报,2014,50(20):35-41.
ZHU Youli, WANG Yanli, BIAN Feilong, et al. Progresses on Research and Application of Metal Ultrasonic Surface Enhancement Technologies[J]. Journal of Mechanical Engineering, 2014,50(20):35-41.
[8] 许敏界.面向多线锯超声振动台研制及超声加工机理研究[D].杭州:浙江工业大学,2015.
XU Minjie. A Research and Development of Multi-wire Saw Technique with Ultrasonic Vibration and Its Machining Mechanism[D]. Hangzhou: Zhejiang University of Technology, 2015.
[9] 侯红亮,韩玉杰,牛涛,等.超声波技术在塑性成形方面的应用[J].航空制造技术,2015,17:48-57.
HOU Hongliang,HAN Yujie,NIU Tao, et al. Application of Ultrasound Technology in Plastic Forming[J]. Aviation Manufacturing Technology, 2015,17:48-57.
[10] MAKOKHA A B, MOYS M H, BWALYA M M, et al. A New Approach to Optimising the Life and Performance of Worn Liners in Ball Mills: Experimental Study and DEM Simulation[J]. International Journal of Mineral Processing, 2007,84(1/4):221-227.
[11] DJORDJEVIC N. Influence of Charge Size Distribution on Net-power Draw of Tumbling Mill Based on DEM Modelling[J]. Minerals Engineering, 2005,18(3):375-378.
[12] KWAN C C, MIO H, CHEN Y Q, et al. Analysis of the Milling Rate of Pharmaceutical Powders Using the Distinct Element Method (DEM)[J]. Chemical Engineering Science, 2005,60(5):1441-1448.
[13] 徐佳.振动辅助铝合金表面滚压纳米化研究[D].杭州:浙江工业大学,2017.
XU Jia. Study of Aluminum Nanocrystallization by Vibration-assisted Burnishing[D]. Hangzhou: Zhejiang University of Technology,2017.
[14] 谨亚辉.超声波变幅杆优化设计及加工机理试验研究[D].太原:太原理工大学,2010.
JIN Yahui. Optimum Design and Machining Mechanism Test of Ultrasound Amplifier[D]. Taiyuan: Taiyuan University of Technology, 2010.
[15] CLEARY P W. Dem Prediction of Industrial and Geophysical Particle Flows[J]. Particuology, 2010,8(2):106-118.
[16] AI J, CHEN J F, ROTTER J M, et al. Assessment of Rolling Resistance Models in Discrete Element Simulations[J]. Powder Technology, 2011, 206 (3): 269-282.
[17] 刘威.行星运动钝化对刀具刃口形貌的影响研究[D].贵阳: 贵州大学,2017.
LIU Wei. Study on the Effect of Planetary Motion Passivation on Tool Edge Morphology [D].Guiyang:Guizhou University ,2017.
