0 引言
剃齿加工具有生产率高、成本低等特点,但剃后工件齿轮会出现剃齿齿形中凹误差,严重影响齿轮的使用性能。目前针对剃齿齿形中凹误差的研究主要集中于重合度等剃齿参数内部激励与剃齿刀结构和修形方面[1-3],很少从切削机理[4]角度进行研究。
剃齿切削力(以下简称“剃削力”)是研究切削机理的重要因素。剃齿切削参数作为系统揭示剃齿齿形中凹误差形成机理的重要因素,研究人员较早就对其展开了研究。吕明等[5]通过剃齿试验得到了切削用量与剃齿径向力之间的经验公式。LITVIN[6]采用齿轮传动方法研究剃齿加工,对工件齿轮进行接触、传动分析。MORIWAKI等[7]在剃齿模型的基础上,利用经验公式计算切削量,并通过压痕试验建立了背吃刀量与齿面载荷分布的关系。上述文献大多基于经验公式进行研究,不利于分析切削参数与剃削力之间的内在联系。而在其他形式的加工中,张金等[8]针对铣齿加工的多切削刃、非自由切削等特点,采用间接测量试验法,并根据切削理论模型,计算铣齿加工理论切削力,分析研究了铣齿断续切削机理。HEIKKALA[9]研究了在已知切削条件下,基于简化切削力理论的铣削加工铣削力分量确定方法。ANTONIADIS等[10]基于一种模拟齿轮滚切的算法,建立了滚切直齿齿轮的切削力模型。
上述文献建立的切削模型虽主要研究铣削加工与滚切加工,但其对建立剃削力理论模型、分析切削参数与剃削力之间内部联系提供了研究思路。本文以金属切削理论为基础,建立了剃削力理论模型。基于单一变量原则,定量分析主轴转速、剃齿刀径向进给量以及工件齿轮轴向进给量等剃齿切削参数对剃削力的影响规律,并从切削参数的角度阐述剃齿齿形中凹误差形成机理。
1 建立剃削力模型
剃齿加工是一对空间相错轴螺旋齿轮无侧隙啮合过程,如图1所示。剃齿齿面间为点接触,在主轴转速、径向进给运动与轴向进给运动的作用下,两齿面产生相对滑移而形成切削运动,完成对工件齿轮的全齿宽剃削。图1中,Fr为剃齿径向力,Fnc(c=1,2,3,4)为剃齿法向作用力,Fc为剃削力。
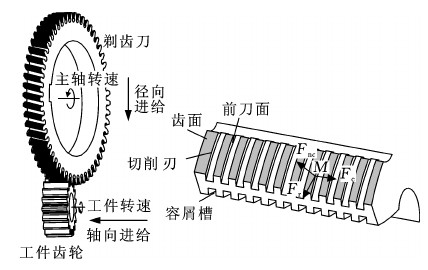
图1 剃齿加工及剃齿刀齿面示意图
Fig.1 Schematic diagram of gear shaving and tooth surface of shaving cutter
现以工件齿轮右齿面为研究对象,以剃齿加工中三点啮合状态为例,建立右齿面力学模型,如图2所示。图2中,K1、K2、K3、K4分别为有效啮合线的各啮合极限点;n1、n2分别为剃齿刀与工件齿轮转速。
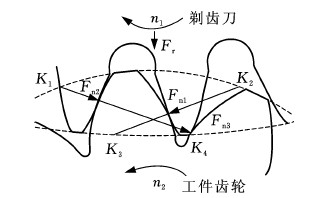
图2 剃齿三点啮合状态力学模型
Fig.2 Mechanical model with three point meshing state
根据金属切削原理可得切削力理论公式[11]:
F=τsacaw(1.4ξ+C)
(1)
式中,F为切削力;τs为材料剪切屈服点;ξ为材料变形系数;C值可由刀具前角γ0确定;acaw表示切削过程的切削面积。
在剃齿加工中,切削面积可表示为背吃刀量ap与轴向进给量f的乘积,则式(1)变为
F=τsapf(1.4ξ+C)
(2)
剃齿背吃刀量不能根据已加工表面与剃前未加工表面直接计算,剃齿背吃刀量又称为剃齿切削深度、压切量,由径向进给量决定。在推导背吃刀量之前,需先推导径向进给量和剃齿切削余量的关系,即一定的径向进给量会剃除工件齿轮齿面余量的大小。此时,可根据滚齿、铣齿加工按照公法线法来计算径向进给量fr,通过剃前、剃后工件齿轮的不同齿厚计算不同的公法线长度,计算出不同齿厚(即不同公法线)和径向进给量之间的位置关系,即
(3)
式中,α为剃齿法向压力角;Δ为剃齿切削余量。
在重合度大于1的剃齿加工中,一般有多对齿接触,其接触齿的对数以及接触力随着剃齿啮合状态变化而变化,它比两弹性体接触的情况更为复杂。考虑齿轮的局部接触变形,采用弹性力学公式,剃齿时不同啮合状态的压陷量[12] δc为
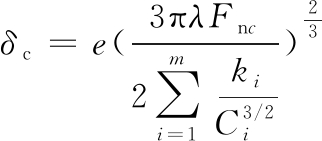
(4)
式中, e为剃齿刀容屑槽槽距与槽宽之比;μj、Ej(j=1,2)分别为剃齿刀与工件齿轮的泊松比和弹性模量;ki为接触点处的法曲率之差;A、B取决于两接触曲面主曲率大小及两主曲率方向之间的夹角,M、N是与A、B有关的系数。
剃齿时每次径向进给的背吃刀量
ap=Δfr+δc
(5)
式中,Δfr为剃齿刀每次径向进给量,当工件齿轮总切削余量已知时,该值由径向进给次数确定。
为便于计算,主轴转动与进给运动都以工件齿轮旋转一周为单元量来计算,同时每一次径向进给在工件齿轮齿面的全齿廓上为均匀剃削,将式(3)~式(5)代入式(2),则
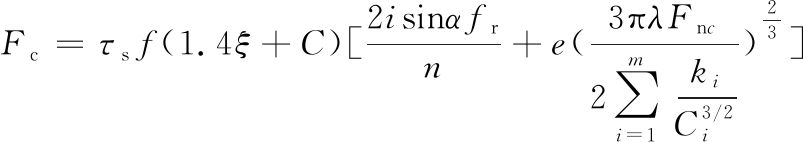
(6)
式中,n为主轴转速;i为传动比。
吕明等[5]通过自行研制的测力仪测得剃齿加工时工件齿轮轴上所承受的径向力,给出了剃齿径向力Fr的实验公式,即
Fr=Pe-Q/S
(7)
式中,P、Q均为与主轴转速n、剃齿刀径向进给量fr、工件齿轮轴向进给量f有关的参数;S为剃齿刀的径向进给序数。
当计算出剃齿径向力Fr后就可通过文献[13]求解出剃齿不同接触点的法向作用力Fnc,代入式(6),得到工件齿轮不同啮合状态的剃削力Fc。
2 剃齿切削参数对剃削力的影响
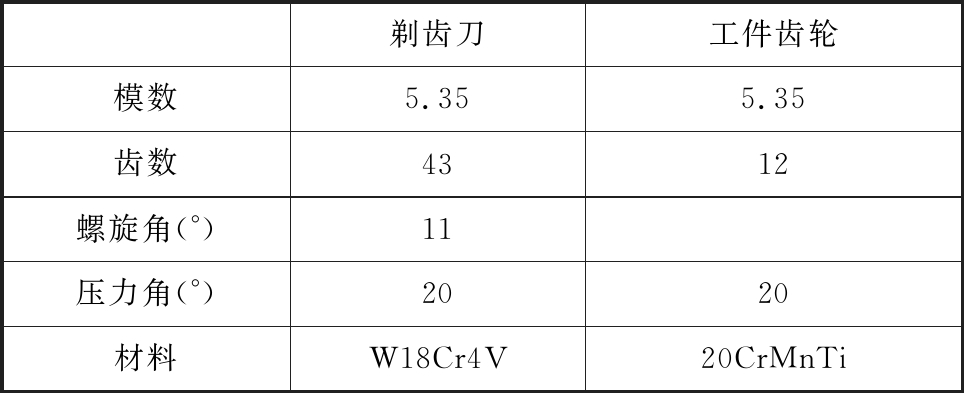
根据齿轮手册,选用的剃齿切削参数如下:主轴转速n分别为140 r/min、170 r/min、200 r/min、230 r/min;轴向进给量f分别为30 mm/min、36 mm/min、51 mm/min、60 mm/min;径向进给量fr分别为0.033 mm、0.039 mm、0.045 mm、0.058 mm。选取剃齿刀与工件齿轮参数如表1所示。
表1 剃齿刀与工件齿轮参数
Tab.1 Parameters of shaving cutter and work gear
剃齿刀工件齿轮模数5.355.35齿数4312螺旋角(°)11压力角(°)2020材料W18Cr4V20CrMnTi
2.1 主轴转速的影响
当f=60 mm/min、fr=0.045 mm时,基于单一变量原则,由式(6)确定工件齿轮右齿面上的剃削力Fc,得到不同主轴转速n下的剃削力Fc变化曲线,如图3所示。
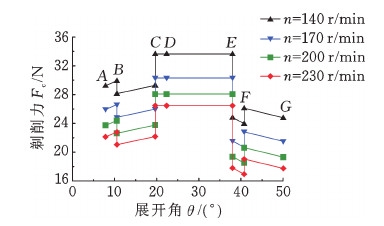
图3 不同主轴转速的剃削力曲线
Fig.3 Shaving cutting force with different spindle speeds
由图3可知,在工件齿轮右齿面上,剃齿刀与工件齿轮的接触点数从齿顶到齿根按照4点(FG段)—3点(EF段)—2点(DE段)—3点(CD段)—4点(BC段)—3点(AB段)的规律变化,这是由于剃齿法向作用力随啮合状态的变化而变化,导致剃削力的阶跃变化。在不同的主轴转速n条件下,工件齿轮齿面上的剃削力Fc变化规律基本一致。在工件齿轮齿廓节圆附近,即图3中的CD、DE段,剃削力Fc出现局部极大值,剃后工件齿轮齿面上该区域最易出现齿形误差。此外,工件齿轮根部所受剃削力Fc大于齿顶部所受剃削力Fc,也更易造成齿形中凹误差,这与工程实际相符。齿顶部的四点接触区域FG段所受的法向作用力Fnc大于三点接触区域EF段所受的法向作用力Fnc,这主要是因为在该三点接触区域BC段接触点所承受的法向作用力Fnc较小,大部分法向作用力Fnc由另外两接触点平衡[13]。而对于工件齿轮齿根处的四点接触区域BC段较之三点接触区域AB段所受的法向作用力Fnc较小,这主要是因为当工件齿轮齿廓上的接触点由四点接触向三点接触变化时,该三点接触区域法向作用力Fnc主要由AB段的接触点平衡。
齿轮节圆位置在CD段,而齿形中凹误差也易出现在CD段,其主要原因为:在重合度小于2的剃齿加工中,CD段的左右啮合线往往在单齿啮合区域,其受力不平衡。故应单独研究齿轮节圆处的剃削力。图4所示为工件齿轮节圆处(展开角为22.307°)应用式(6)确定的剃削力Fc的变化情况。
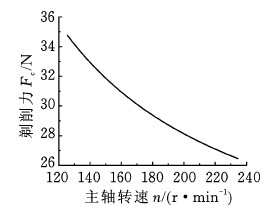
图4 不同主轴转速的节圆处剃削力曲线
Fig.4 Shaving cutting force with different spindle speeds at pitch circle
图4表明,随着主轴转速n的不断增大,工件齿轮节圆附近剃削力Fc不断减小,但剃削力的减小幅度会越来越小。这主要是因为在主轴转速实验范围内,主轴转速n的升高增大了剃齿过程中的切削速度,造成金属晶格流动速度大于晶格塑性变形速度,增大了剪切角;同时,切削速度的增大,导致切削温度升高,摩擦因数减小,从而使金属切削层的晶格变形程度降低,减小了剃削力[14]。这与在一定范围内增大切削速度可以提高工件加工精度的工程经验相符。但主轴转速过大时,会使得切削温度过高,导致工件齿轮齿面强度与硬度下降,齿轮啮合刚度减小,造成齿面成形质量下降。
2.2 轴向进给运动的影响
剃齿加工中径向进给量fr与轴向进给量f共同决定剃削体积的大小,因此轴向进给运动参数对剃削力有重要影响。当主轴转速n=170 r/min与径向进给量fr=0.045 mm不变时,改变轴向进给量f,应用式(6)确定剃削力Fc。图5为不同轴向进给量f对剃削力Fc的影响变化曲线。节圆处(展开角为22.307°)的剃削力变化如图6所示。
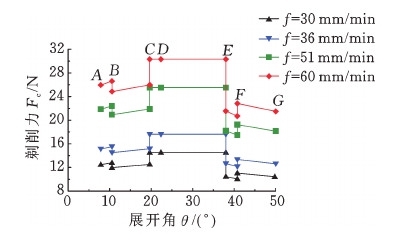
图5 不同轴向进给量的剃削力曲线
Fig.5 Shaving cutting force with different axial feedings
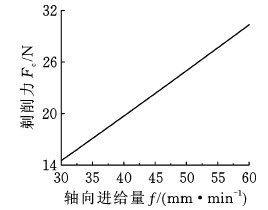
图6 不同轴向进给量的节圆处剃削力曲线
Fig.6 Shaving cutting force with different axial feedings at pitch circle
由图5可以看出,工件齿轮轴向进给量f的改变并未改变齿廓Fc的变化规律。这是因为剃齿时轴向进给运动是保证全齿宽剃削的必要条件,故对剃削力变化规律的影响并不明显。而增大轴向进给量f会导致Fc的增大,这主要是由于轴向进给量f增大后,剃齿时的剃削体积增大,所需剃削力也增大,造成金属晶格内晶面位移加剧,晶粒纤维化程度变高,齿面发生塑性变形的区域增大。同时,在不同轴向进给量f的两点接触区域DE段与三点接触区域CD段的剃削力都最大,也表明该处最先发生塑性变形,随着轴向进给量f的增大,塑性变形逐渐扩展至其余相邻区域。
由图6可知,齿轮节圆附近的剃削力Fc随工件齿轮轴向进给量f的增大而增大。对比图5,CD段与DE段正好在节圆附近,这也说明节圆位置处的剃削力最大,最易发生齿面余量过切现象。因此,剃齿齿形中凹误差最有可能在齿轮节圆附近开始累积,造成工件齿轮齿形中凹现象的出现。
2.3 径向进给运动的影响
当n=170 r/min与f=60 mm/min保持不变时,改变fr,应用式(6)确定剃削力Fc。图7为不同径向进给量fr的剃削力Fc变化曲线。应用式(6),固定齿轮展开角为22.307°,计算不同径向进给运动条件下的剃削力Fc,得到节圆处的剃削力变化曲线,如图8所示。
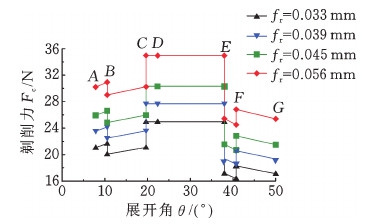
图7 不同径向进给量的剃削力曲线
Fig.7 Shaving cutting force with different radial feedings
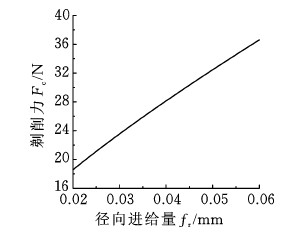
图8 不同径向进给量的节圆处剃削力曲线
Fig.8 Shaving cutting force with different radial feedings at pitch circle
图7表明,剃齿时径向进给量fr的改变并不显著影响工件齿轮齿廓的剃削力Fc的变化规律,而只影响剃削力Fc的大小。这是因为剃齿时不同径向进给量fr所对应的剃削深度不同,在一次加工过程中,剃削深度基本保持不变。图8中,增大剃齿时径向进给量fr会使Fc增大,这是由于径向进给量fr的增大导致单位时间剃削量增大,切屑与工件齿轮齿面内部材料的弹塑性变形抗力增大,塑性变形区域扩大。由于CD段与DE段在工件齿轮节圆附近,该处的剃削力Fc比齿廓其他区域的力更大,导致切削刃较深地压入工件齿轮齿面,造成过切,最终在齿廓上表现为节圆附近的齿形中凹误差。
2.4 剃齿切削参数与齿形中凹误差的关系
为提高工件齿轮的剃削效果,需研究不同剃齿切削参数对剃削力Fc的影响程度,得到不同剃齿切削参数对剃削力变化的影响主次顺序。一般情况下,对于函数g=f(x,y,z),可以通过因变量g对自变量x、y、z求偏导,得到不同自变量x、y、z对因变量g的影响程度。图4中,当主轴转速从125.581 r/min增大到234.419 r/min时,剃削力从34.764 N降低到26.460 N;图6中,轴向进给量从30 mm/min增大到60 mm/min时,剃削力从14.523 N增大到30.319 N;图8中,径向进给量从0.02 mm增大到0.06 mm时,剃削力从18.565 N增大到36.609 N。此外,当轴向进给量与径向进给量分别增大0.01 mm时,节圆附近剃削力分别增大为0.498 7 N与3.133 4 N,即增大相同大小的进给量,轴向进给量f映射的剃削力比径向进给量fr映射的剃削力增幅小。本文应用数值计算软件分别对主轴转速n、径向进给量fr以及轴向进给量f求偏导,得出主轴转速对剃削力Fc的偏导数约为-1.85、轴向进给量f对剃削力Fc的偏导数约为31.6、径向进给量fr对剃削力Fc的偏导数约为450.9。可见,径向进给量对剃削力的影响远大于主轴转速以及轴向进给量的影响。
根据文献[5,13]可知,剃齿切削力的大小在一定程度上可以反映齿形中凹误差。剃削力大时,在齿形上易形成误差。而剃齿切削参数中,径向进给运动对剃削力的影响最大,径向进给量过大易引起剃齿齿形中凹误差。因此,在剃齿加工中,当选定剃齿刀的几何参数后,首先根据工件齿轮齿面余量确定剃齿刀径向进给量,并通过齿轮手册选取轴向进给量与主轴转速范围。当剃齿切削参数范围确定后,就可得出剃齿过程剃削力的变化范围。在满足工件技术要求的前提下,尽量选取较小的剃削力,再根据工件齿轮节圆处的剃削力变化规律,优选出剃齿切削参数。
3 有限元仿真验证
CELIK[15]的研究表明仿真中采用五齿模型替代全齿模型可以满足工程需要。本文建立表1所示参数的剃齿刀与工件齿轮五齿加工模型,并在有限元软件中建模,部分设置如下:工件模型采用缩减积分单元C3D8R进行网格划分,材料断裂准则选用Johnson-Cook模型,分析步设置为显式动态分析,并选择几何非线性,对剃齿刀与工件齿轮施加耦合约束。根据实际剃齿加工运动,设置刀齿啮合边界条件,并分别施加表2所示的剃齿切削参数,其中第1组为对照组。
表2 剃齿切削参数
Tab.2 Shaving cutting parameters
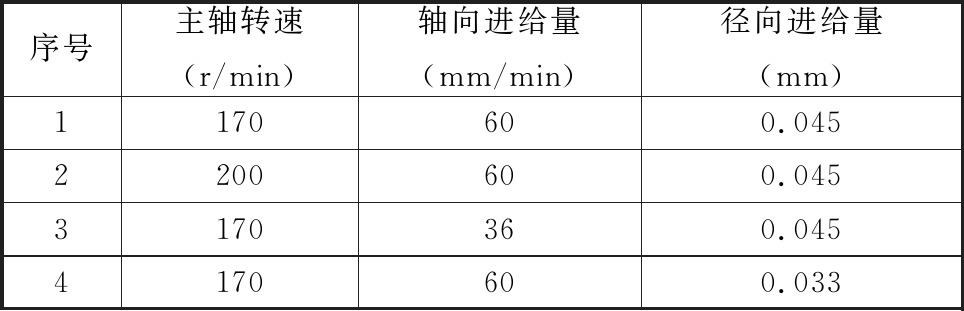
序号主轴转速(r/min)轴向进给量(mm/min)径向进给量(mm)1170600.0452200600.0453170360.0454170600.033
提取工件齿轮五齿模型中间齿的数据结果进行后处理分析。图9为不同变量条件下的理论剃削力与仿真剃削力对比图。
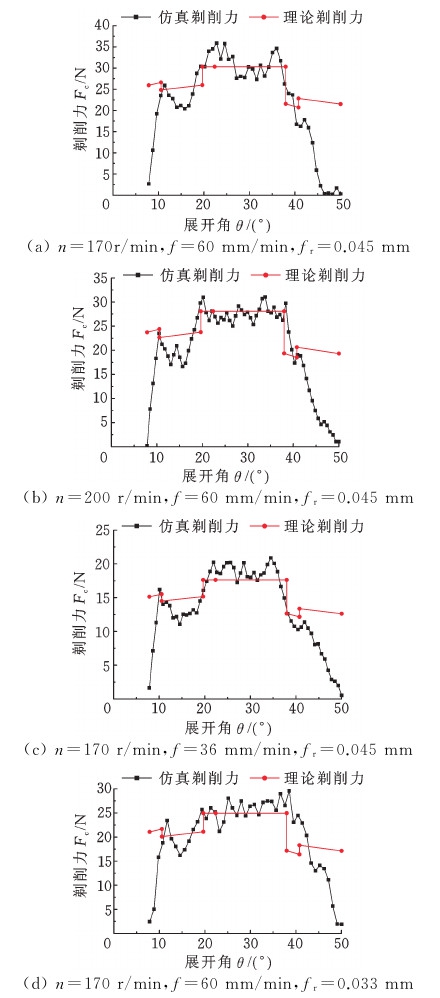
图9 理论剃削力与仿真剃削力对比图
Fig.9 Comparison of theoretical shaving cutting force and simulated shaving cutting force
图9表明,剃齿加工过程中的剃削力并不是很大,但由于剃齿刀与工件齿轮之间是点接触,导致接触点处的接触应力非常大,这个剃削力足以剃除齿面余量;不同啮合状态下的剃削力存在明显差异,仿真剃削力并不完全按照理论剃削力的状态突变而发生变化;在剃齿的初始阶段,仿真剃削力明显小于理论剃削力,这是由于仿真中当剃齿刀与工件齿轮啮合状态发生变化时,剃削力达到稳定状态会存在一个过渡区域,从而造成仿真剃削力小于理论剃削力。
同时,由图9对比可知,工件齿轮节圆附近的剃削力相对齿顶与齿根剃削力更大。表明剃齿刀会在工件齿轮节圆附近易过量剃除齿面余量,造成剃齿齿形中凹误差。以工件齿轮节圆附近仿真剃削力平均值为此处剃削力,其值分别为29.725 6 N、27.627 7 N、18.643 4 N、25.820 8 N。通过对比同一齿廓上剃削力理论值与仿真值,其变化规律大体一致,验证了理论模型的有效性。
4 剃齿试验验证
本试验在YX4230CNC5剃齿机上完成,采用LINKS CNC3906齿轮测量中心对剃后齿轮进行齿形检测。图10所示为剃齿加工试验与检测现场。

图10 剃齿加工试验与检测
Fig.10 Experiment and detection of gear shaving
试验所用剃齿刀与工件齿轮参数如表3所示;加工所用的切削参数及结果如表4所示,其中第2组为对照组。
表3 试验剃齿刀与工件齿轮参数
Tab.3 Parameters of shaving cutter and work gear
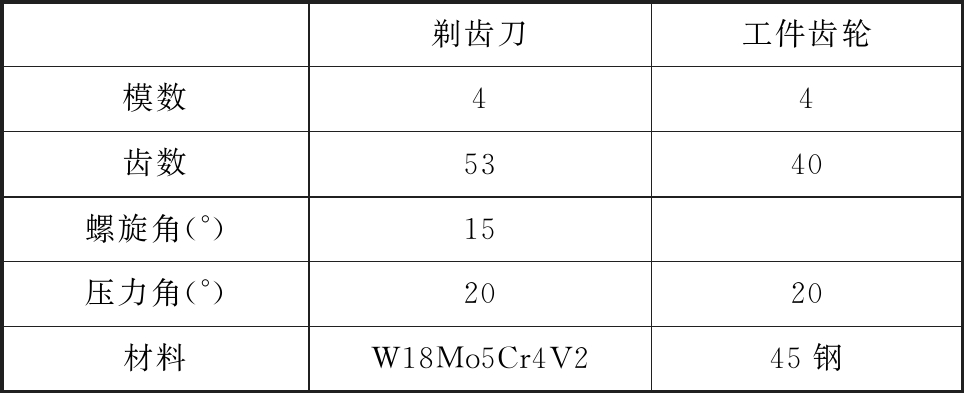
剃齿刀工件齿轮模数44齿数5340螺旋角(°)15压力角(°)2020材料W18Mo5Cr4V245钢
表4 剃齿切削参数及结果
Tab.4 Shaving cutting parameters and results
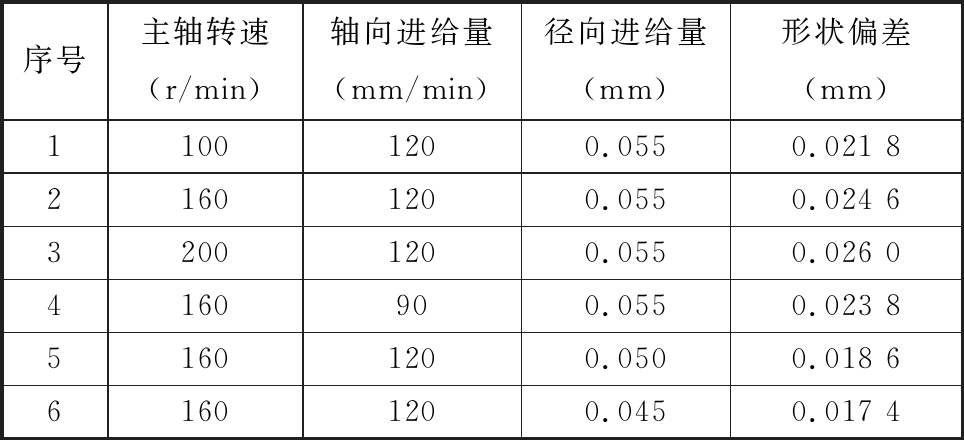
序号主轴转速(r/min)轴向进给量(mm/min)径向进给量(mm)形状偏差(mm)11001200.0550.021 821601200.0550.024 632001200.0550.026 04160900.0550.023 851601200.0500.018 661601200.0450.017 4
由表4可知,剃齿切削参数中主轴转速和工件齿轮轴向进给量对齿廓形状偏差的影响较小;而径向进给量对齿廓形状偏差的影响显著,且齿廓形状偏差随着径向进给量的减小而减小,由此验证了合理选择径向运动参数会减小或消除工件齿轮的齿形中凹误差。
5 结论
(1)不同切削参数条件下工件齿轮齿廓上的剃削力变化曲线表明:剃削力随着径向进给量与轴向进给量的增大而增大,而主轴转速的增大则会降低齿廓上的剃削力;剃削力的极大值出现在齿轮啮合的两点与三点接触区域,即齿轮的节圆附近,表明齿轮节圆附近更易产生齿形中凹误差。
(2)由不同切削参数对剃削力变化的影响规律分析表明:径向进给量对剃削力的影响要远大于轴向进给量和主轴转速对剃削力的影响,合理选取剃齿径向进给量对减小剃齿齿形中凹误差具有重要意义。
(3)利用有限元法分析了工件齿轮不同啮合状态下剃削力的影响规律,得出:节圆附近的剃削力比齿廓其他位置要大。通过对比理论与仿真结果可知,两者在一个齿廓上的变化规律大体一致。剃齿试验验证了上述理论模型和有限元法的正确性,表明该模型可以作为剃齿加工优化研究的理论依据。
[1] HSU R, FONG Z. Serration Design for a Gear Plunge Shaving Cutter[J]. Journal of Manufacturing Science and Engineering,2011, 133(2): 21004.
[2] LYU M, YANG X. Design and Manufacture of a Shaving Cutter with Unequal Depth Gashes[J]. Journal of Materials Processing Technology,2002, 129(1/3): 193-195.
[3] 刘磊, 蔡安江, 耿晨,等. 基于剃齿啮合传动特性的剃齿刀优化设计[J]. 航空动力学报, 2018, 33(5):1084-1092.
LIU Lei,CAI Anjiang, GENG Chen, et al. Optimal Design of Shaving Cutter Based on Gear Shaving Mesh Transmission Characteristic[J]. Journal of Aerospace Power, 2018, 33(5):1084-1092.
[4] MORIWAKI I, FUJITA M. Effect of Cutter Performance on Finished Tooth Form in Gear Shaving[J]. Journal of Mechanical Design, 1994, 116(3): 701-705.
[5] 吕明,冯肇锡,徐璞. 剃齿切削力的研究[J]. 太原工业大学学报, 1987(4): 61-73.
LYU Ming, FENG Zhaoxi, XU Pu. The Research on Shaving Force[J]. Journal of Taiyuan University of Technology, 1987(4): 61-73.
[6] LITVIN F. Computerized Generation and Simulation of Meshing of Modified Spur and Helical Gears Manufactured by Shaving[J]. Computer Methods in Applied Mechanics & Engineering, 2001, 190(39):5037-5055.
[7] MORIWAKI I, OKAMOTO T, FUJITA M, et al. Numerical Analysis of Tooth Forms of Shaved Gears[J]. JSME International Journal Series Ⅲ, 1990,33(4):608-613.
[8] 张金,黄筱调,彭琪,等. 铣齿断续切削机理的研究[J]. 机械工程学报, 2011, 47(13): 186-192.
ZHANG Jin, HUANG Xiaodiao, PENG Qi, et al. Mechanism of Intermittent Cutting in Gear Milling[J]. Chinese Journal of Mechanical Engineering, 2011, 47(13): 186-192.
[9] HEIKKALA J. Determining of Cutting-force Components in Face Milling[J]. Journal of Materials Processing Technology, 1995, 52(1): 1-8.
[10] ANTONIADIS A, VIDAKIS N, BILALIS N. A Simulation Model of Gear Skiving[J]. Journal of Materials Processing Technology, 2004, 146(2): 213-220.
[11] 武文革,辛志杰. 金属切削原理及刀具[M]. 北京: 国防工业出版社, 2009.
WU Wenge, XIN Zhijie. Metal Cutting Principle and Tool[M]. Beijing: National Defense Industry Press, 2009.
[12] 吕明,徐璞,蔺启恒. 剃齿时齿形中凹现象的形成机理[J]. 太原工业大学学报, 1987(4): 30-40.
LYU Ming, XU Pu, LIN Qiheng. The Forming Mechanism of Tooth-profile-concave Phenomena during Shaving [J]. Journal of Taiyuan University of Technology, 1987(4): 30-40.
[13] 蔡安江,刘磊,李玲,等. 剃齿啮合的接触特性分析及中凹误差形成机理研究[J]. 振动与冲击, 2018, 37(8): 68-86.
CAI Anjiang, LIU Lei, LI Ling, et al. Analysis on Contact Characteristic and Mechanism of Concave-errors Caused by Shaving[J]. Journal of Vibration and Shock, 2018, 37(8): 68-86.
[14] 刘战强,万熠,艾兴. 高速铣削中切削力的研究[J]. 中国机械工程, 2003, 14(9): 734-737.
LIU Zhanqiang, WAN Yi, AI Xing. Cutting Forces in High Speed Milling[J]. China Mechanical Engineering, 2003, 14(9): 734-737.
[15] CELIK M. Comparison of Three Teeth and Whole Models in Gear Analysis[J]. Mechanism and Machine Theory,1999, 34: 1227-1235.
