0 引言
无刷直流电机(brushless DC motor,BLDCM)具有结构简单、动态响应迅速、输出转矩大、可控性好、可靠性高等特点,在航空航天、工业自动化、医疗等领域得到越来越广泛的应用[1-3],但由于电磁转矩产生原理、电流换向以及齿槽效应等因素造成转矩波动[4],限制了其在某些高精度、高稳度系统中的应用。
为了抑制转矩波动、提高电磁转矩动态响应性能,直接转矩控制(direct torque control,DTC)方法被广泛应用到无刷直流电机上。直接转矩控制是对无刷直流电机输出转矩产生直接作用的一种高效的控制策略[5]。传统的直接转矩控制由转矩和磁链双环构成,电压矢量选择由转矩滞环和磁链滞环输出决定,并采用两个非零数字定义非零电压矢量、全零数字定义零电压矢量的控制策略,该策略必须经过一系列变换和计算来对磁链和转矩进行实时观测和控制。文献[6]采用此方式实现了对无刷直流电机直接转矩控制,但输出的电磁转矩仍存在较大幅度的波动。文献[7]在转矩和磁链双环控制的基础上,采用模糊控制调节电压矢量作用的时间,并采用全零数字的零电压矢量来使转矩下降,一定程度上减小了转矩脉动。文献[8]针对传统DTC中磁链观测和给定困难等问题,省去了磁链观测并根据转子位置与转矩滞环输出τ之间的关系来选择最优电压矢量,在需要减小电机转矩时并未采用全零矢量,而是采用非零电压矢量的反矢量,从而实现对电机转矩的直接控制。文献[9]提出了两相导通无刷直流电机空间电压矢量——正矢量、反矢量、零矢量定义方法,并通过对比实验得到这3种电压矢量对电磁转矩变化的影响,并据此提出了一种无刷直流电机直接转矩控制系统的实用设计方法。文献[10]在传统两相导通无刷直流电机直接转矩控制策略下提出了一种新型零矢量定义方法,对新型零矢量与传统零矢量进行了不同作用的理论分析,并通过仿真验证了新型零矢量的有效性。文献[11]在无磁链观测条件的基础上提出了一种基于占空比调节有效电压矢量和零矢量作用时间的直接转矩控制方法,采用一个非零数字来定义零矢量,该方法减小了相电流和转矩波动,但电磁转矩和占空比计算比较繁琐。
本文在前人无磁链观测直接转矩控制策略研究的基础上进行了一些新的探索,在转矩控制方面,采用相电流和霍尔信号相结合的方法观测转矩,利用转矩调节器和霍尔信号相结合的方法选择最优电压矢量,实现对转矩的实时控制;在零矢量选择方面,提出了一种两管导通零矢量,并对该两管导通零矢量和传统的全零数字定义零电压矢量进行了理论分析。基于以上控制策略,利用Simulink软件搭建相应的控制系统仿真模型,进行了转矩控制仿真,并利用DSP2812控制板搭建实验平台对该系统的控制效果进行了实验验证。
1 无磁链观测直接转矩控制策略
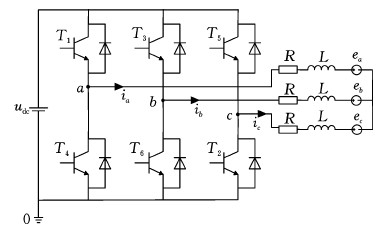
图1 无刷直流电机控制系统电路图
Fig.1 BLDCM control system circuit diagram
无刷直流电机定子常采用三相星形、无中线的整距集中绕组,其简化控制系统电路图见图1。根据以上控制系统可得到无刷直流电机电压平衡方程:

(1)
式中,ux为电机相电压;ix为电机相电流;ex为电机相反电动势;R、L分别为电机相电阻和相等效电感;x可为a、b、c。
针对传统直接转矩控制系统中电机磁链给定和估算困难、转矩获取复杂等缺点,本文提出了无磁链观测直接转矩控制策略,控制策略框图见图2,省略了磁链观测和调节模块,仅由转速外环和转矩内环构成。
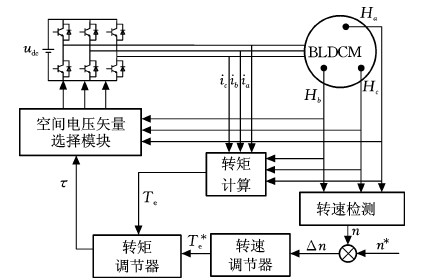
图2 无磁链观测直接转矩控制策略框图
Fig.2 Block diagram of direct torque control strategy without flux linkage observation
由于无刷直流电机梯形反电动势无法直接获取,故采用反电动势法来计算电磁转矩比较繁琐,本文根据电机电磁转矩产生原理,采用三相相电流来计算电机电磁转矩幅值,利用三路霍尔传感器信号来判断电磁转矩的方向;将相电流计算得到的电磁转矩和转速调节器输出的给定转矩值进行比较,再根据转矩调节器输出τ和霍尔信号来选择最优电压矢量,实现对电机电磁转矩的直接控制。
2 电磁转矩观测
在直接转矩控制系统中,电磁转矩观测十分重要,直接影响控制系统对电机转矩波动的控制效果。
2.1 两相静止坐标系下电磁转矩观测
无刷直流电机在两相静止坐标系下的电磁转矩计算公式为
Te=3p(ψsαisβ-ψsβisβ)/2
(2)
式中,p为电机极对数;ψsα、ψsβ分别为定子磁链在α、β轴上的分量;isα、isβ分别为定子电流在α、β轴上的分量。
采用式(2)对电机电磁转矩进行实时观测时需要将三相静止坐标系下电机定子磁链和电流通过坐标变换到两相静止坐标系上,这样就增加了电机控制系统的复杂程度;另一方面,由于电机在制造过程中很难保证气隙磁场的均匀分布,进而间接影响定子磁链的观测精度,从而造成电磁转矩的波动。
2.2 三相静止坐标系下电磁转矩观测
无刷直流电机在三相静止坐标系下电磁转矩计算公式[12]为
(3)
式中,Ω为转子机械角速度。
采用式(3)对电机电磁转矩进行实时观测时应注意对电机反电动势数值的估算精度,由于电机在实际设计和制造过程中很难实现平顶宽度为120°梯形波反电动势,故采用此方法将会造成电磁转矩波动。
2.3 基于霍尔信号和三相电流的电磁转矩观测

图3 霍尔传感器信号与电机反电动势形状函数、电流关系
Fig.3 Hall sensor signal and motor back-EMF shape function & current relationships
本文通过对电机反电动势的标幺化处理,得到三相电流与电磁转矩幅值之间的关系(图3),即一个电周期内霍尔传感器信号与电机反电动势形状函数、电流关系,经标幺化处理后,电机三相反电动势表示为

(4)
式中,ke为电机反电动势系数;n为电机转速;Ex(θ)是幅值为1的反电动势形状函数,x可为a、b、c。
结合式(3)、式(4)及kt=2ke,可得电磁转矩幅值:
Ts=kt(|ia|+|ib|+|ic|)/2
(5)
式中,Ts为电磁转矩幅值;kt为转矩常数。
根据图3所示的波形,分析各相反电动势形状函数和电流波形与霍尔传感器输出信号之间的关系,可以推导出电机正转时电磁转矩符号表达式[13],另由电机工作原理可知电机正转与反转时的电磁转矩互为相反数,综上,电机电磁转矩计算公式为
Te=Tz|Ts|=ktTz(|ia|+|ib|+|ic|)/2
(6)
其中,Tz为电磁转矩符号。式(7)所示电磁转矩计算公式无需获知电机反电动势数值和转子位置信息,只需获取霍尔传感器输出信号和三相电流值,就能实时观测电磁转矩幅值和方向,可进一步简化直接转矩控制系统。
根据以上3种电机电磁转矩计算公式所需的变量数量以及参数值的获取难度判断,第3种相比前两种可有效简化控制系统结构,本文采用的霍尔信号与相电流相结合的电磁转矩观测方法可避免电机结构上对电磁转矩波动的影响。
3 电压矢量选择

图4 空间电压矢量分布
Fig.4 Space voltage vector distribution
在无刷直流电机直接转矩控制技术中,电压矢量是极其重要的物理量,因为它是直接转矩控制系统的原始推动力[14-15],故在电机运行过程中如何选择最优空间电压矢量是首先需解决的问题。通常空间电压矢量采用6个数字表示法[8-9],如图4所示,分别用0、1表示功率管的导通、关断[16-18],每个功率管对应一种状态。无刷直流电机通常采用两相导通三相六状态全桥驱动方式,3个桥臂逆变器共组成8个状态,其中6个有效状态为V1(100001)、V2(001001)、V3(011000)、V4(010010)、V5(000110)、V6(100100)。由于逆变器每个时刻两导通相的开关状态都与电机内部形成的电压矢量一一对应,故逆变器有效状态也可用来表示电机空间电压矢量。根据图4,6个非零电压矢量将空间分成6个区域相等的扇区。
3.1 传统零矢量对电磁转矩作用的理论分析
传统无刷直流电机直接转矩控制系统中所采用的零矢量基本上都是全零数字零矢量,即V0 (000000)。假设某时刻两相导通无刷直流电机直接转矩控制系统的导通状态如图5所示,即a、c两相导通,b相关断,此时所选用的非零电压矢量为 V1(100001),电流流向从电源正极出发经a相流入c相最终到达电源负极。若此时采用V0来减小电机转矩,即将6个开关管全部关断,由于电机电感中的电流无法完成突变,为了使电机继续运行T2、T4续流二极管导通,电流流向变成图6所示。
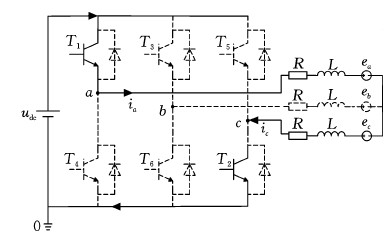
图5 V1作用时电流流向
Fig.5 Current flow when V1 acts
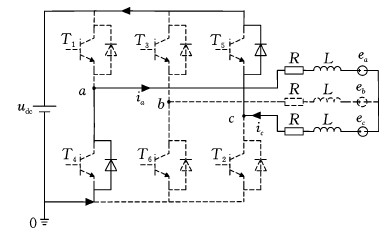
图6 V0作用时电流流向
Fig.6 Current flow when V0 acts
在图6所示的状态下,根据式(2),a、c两相电压方程可写为
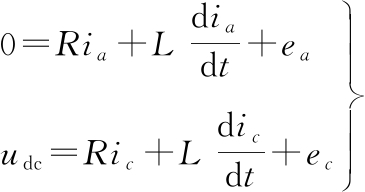
(7)
为便于分析,忽略定子电阻对电磁转矩的影响,此刻ea=-ec=E,ia=-ic,由式(3)可知,当电机转速恒定时,反电动势幅值E大小也是恒定的,故可得
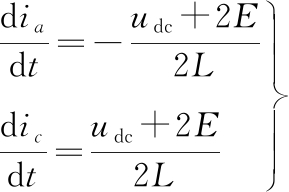
(8)
将上式代入式(7)可得
(9)
使用传统零矢量作用的无刷直流电机直接转矩控制最优空间电压矢量选择表见表1。
表1 传统零矢量空间电压矢量选择表
Tab.1 Traditional zero vector space voltage vector selection table

扇区霍尔信号τ10-1Ⅰ110V2V0V5Ⅱ010V3V0V6Ⅲ011V4V0V1Ⅳ001V5V0V2Ⅴ101V6V0V3Ⅵ100V1V0V4
3.2 两管导通零矢量对电磁转矩作用的理论分析
综上可知,采用传统零电压矢量V0在电机中所形成的是当前非零电压矢量的反矢量。现采用2个非零数字的6数字表示法来定义两管导通零电压矢量,由图4可看出,每个非零电压矢量都有2个与之垂直的两管导通零电压矢量。例如与非零电压矢量V1 (100001)垂直的2个两管导通零矢量为V20(010001)、V50 (100010)。仍以图5为当前导通状态,此时需要减小电机转矩,本文采用两管导通零矢量V50。施加V50后,电机在T1管和T5续流二极管的作用下继续运行,电流流向如图7所示。
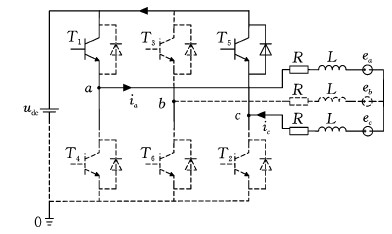
图7 V50作用时电流流向
Fig.7 Current flow when V50 acts
施加两管导通零矢量V50后,电机电压平衡方程可改写为

(10)
此时忽略定子电阻对电磁转矩的影响,由ea=-ec=E,ia=-ic,ib=0可得
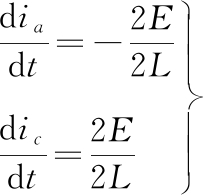
(11)
将上式代入式(7)可得
(12)
两管导通零矢量作用的无刷直流电机直接转矩控制最优空间电压矢量选择表见表2。
通过上述传统零电压矢量和两管导通零电压矢量对电机电磁转矩作用效果的理论分析,这两种零电压矢量都可减小电机电磁转矩,但由式(9)与式(12)可知,两管导通零矢量使电磁转矩减小速率要优于传统零矢量使电磁转矩减小速率。
表2 两管导通零矢量空间电压矢量选择表
Tab.2 Two-tube conduction zero vector space voltage vector selection table
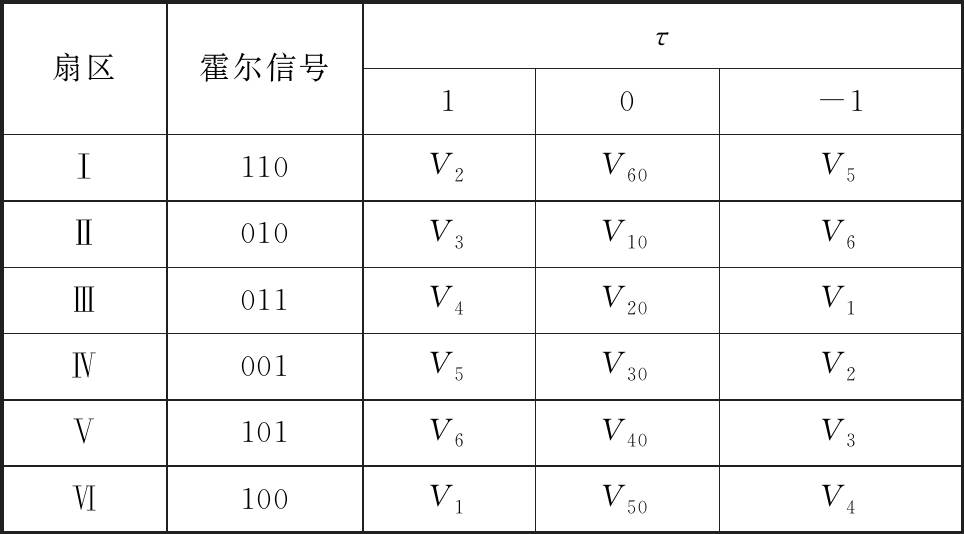
扇区霍尔信号τ10-1Ⅰ110V2V60V5Ⅱ010V3V10V6Ⅲ011V4V20V1Ⅳ001V5V30V2Ⅴ101V6V40V3Ⅵ100V1V50V4
4 仿真分析及实验验证
基于以上分析,在MATLAB/Simulink中搭建图8所示的控制系统仿真模型,电机参数为:额定电压48 V;额定转速1 200 r/min;额定转矩4 N·m;电枢电阻0.086 Ω;电枢电感0.787 m·h;转矩常数0.09 N·m/A。
4.1 传统零矢量仿真分析
经过上述传统零矢量对电磁转矩作用效果的理论分析,结合表1所示的传统零矢量空间电压矢量选择表,利用图8控制系统模型对传统零矢量进行仿真分析。
仿真工况1:电机在转速为500 r/min情况下,对电机施加大小为1 N·m的给定负载。电机输出实际转矩波形如图9a所示,电机在稳定运行情况下,实际转矩与给定负载差值波形如图9b所示。
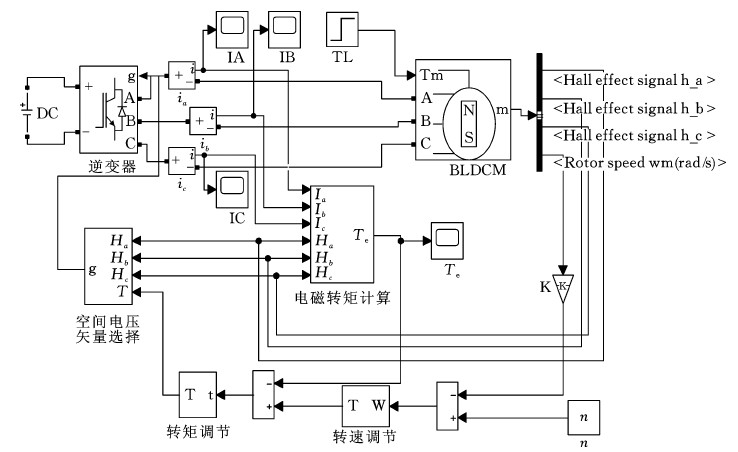
图8 控制系统仿真模型
Fig.8 Control system simulation model
仿真工况2:电机在转速为500 r/min情况下,对电机进行突加突减负载仿真,所施加负载大小为1.5 N·m,此时电机输出实际转矩波形如图10a所示,电机在稳定运行后突加突减负载时实际转矩与给定负载之间的差值如图10b所示。
从图9a、10a中可直观看出转矩波动幅度较大;从图9b中可得电机在传统零矢量恒定负载作用下,电机稳定运行后转矩波动最大正值为0.322 6 N·m,波动最大负值为-0.266 8 N·m,波动幅度为30.56%;从图10b中可得电机在传统零矢量突加突减负载作用下,转矩波动最大正值为0.334 5 N·m,波动最大负值-0.265 5 N·m,波动幅度为31.38%。

图9 传统零矢量恒定负载仿真波形
Fig.9 Traditional zero vector constant load simulation waveform

图10 传统零矢量突加突减负载仿真波形
Fig.10 Traditional zero vector sudden addition load simulation waveform
4.2 文献[10]新型零矢量仿真分析
采用图8控制系统仿真模型并结合文献[10]中的新型零矢量空间电压矢量选择表,对文献[10]中的新型零矢量作用效果进行仿真分析。
仿真工况1:采用与传统零矢量相同的仿真工况1,文献[10]的新型零矢量下电机输出实际转矩波形如图11a所示,电机实际转矩与给定负载之间差值波形如图11b所示。
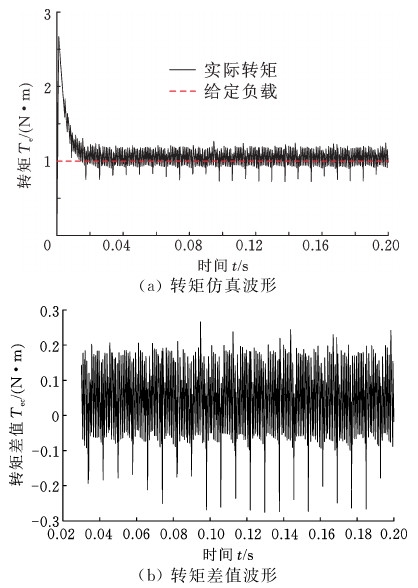
图11 新型零矢量恒定负载仿真波形
Fig.11 New zero vector constant load simulation waveform
仿真工况2:采用与传统零矢量相同的仿真工况2,文献[10]的新型零矢量下电机输出实际转矩波形如图12a所示,电机在稳定运行后突加突减负载实际转矩与给定负载之间的差值如图12b所示。
从图11a、12a中可直观看出电磁转矩有一定的波动;从图11b中可得电机在新型零矢量恒定负载作用下,电机稳定运行后转矩波动最大正值为0.266 27 N·m,波动最大负值为-0.275 63 N·m,波动幅度为25.65%;从图12b中可得文献[10]的新型零矢量突加突减负载作用下,转矩波动最大正值为0.251 8 N·m,波动最大负值为-0.280 5 N·m,波动幅度为27.43%。
4.3 两管导通零矢量仿真分析
经过上述两管导通零矢量对电磁转矩作用效果的理论分析,采用图8所示控制系统仿真模型并结合表2两管导通零矢量空间电压矢量选择表,对两管导通零矢量作用效果进行仿真分析。
仿真工况1:采用与传统零矢量相同的仿真工况1,两管导通零矢量下电机输出实际转矩波形如图13a所示,电机实际转矩与给定负载之间差值波形如图13b所示。
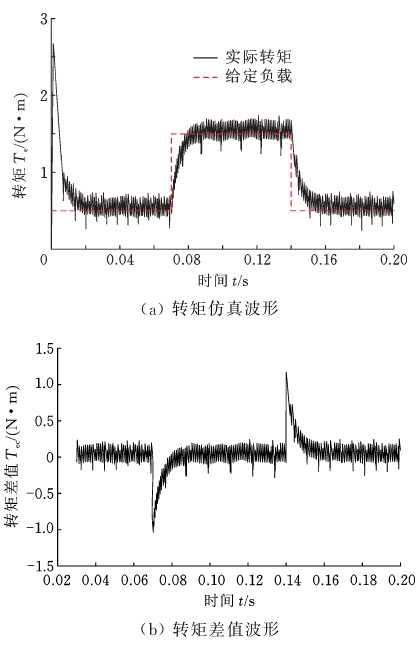
图12 新型零矢量突加突减负载仿真波形
Fig.12 New zero vector burst plus sudden load simulation waveform
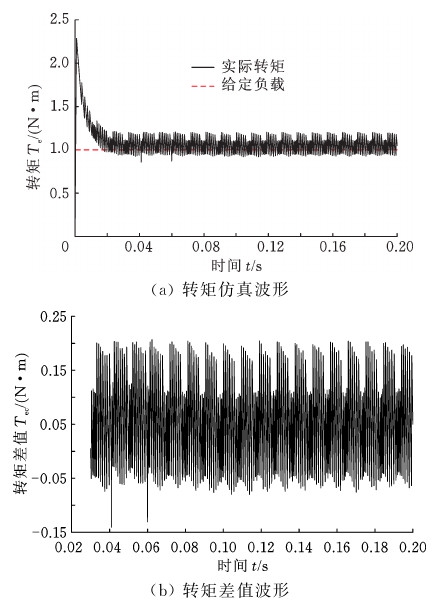
图13 两管导通零矢量恒定负载仿真波形
Fig.13 Two-tube conduction zero vector constant load simulation waveform
仿真工况2:采用与传统零矢量相同的仿真工况2,此时电机输出实际转矩波形如图14a所示,电机在稳定运行后突加突减负载实际转矩与给定负载之间的差值如图14b所示。

图14 两管导通零矢量突加突减负载仿真波形
Fig.14 Two-tube conduction zero vector sudden increase and decrease load simulation waveform
由图13a、14a可直观看出转矩波动幅度相对于图9a、10a、11a、12a均有明显减小,分别减小10.97%、9.03% 、6.06%、5.08%。由图13b可得电机在两管导通零矢量恒定负载作用下,电机稳定运行后转矩波动最大正值为0.207 N·m,相对于图9b减小了0.115 6 N·m,相对于图11b减小了0.059 27 N·m;波动最大负值为-0.141 N·m,相对于图9b减小了0.125 8 N·m,相对于图11b减小了0.134 63 N·m,波动幅度减小到19.59%。由图14b可得电机在两管导通零矢量突加突减负载作用下,转矩波动最大正值为0.285 N·m,相对于图10b减小了0.049 5 N·m,相对于图12b减小了-0.033 2 N·m;波动最大负值为-0.171 N·m,相对于图10b减小了0.094 5 N·m,相对于图12b减小了0.109 5 N·m,波动幅度减小到22.35%。
4.4 实验验证
搭建如图15所示的无刷直流电机直接转矩控制系统实验平台。在该实验平台上对电机在传统零矢量和两管导通零矢量条件下进行恒定负载、突加突减负载实验。实验波形如图16所示。比较图16a、16b与图16c、16d可知,电机在两管导

图15 控制系统实验平台
Fig.15 Control system experiment platform

图16 实验结果
Fig.16 Experimental result
通零矢量作用下比传统零矢量作用下输出转矩波动减小约10%,由32.46%减至21.58%。这再次证明了两管导通零矢量作用下电机运行更稳定,也证实了本文理论分析与仿真分析的正确性,以及所提出控制策略的有效性。
将图16与图9、图10、图13、图14对比,可见实验值与仿真尚有一定的偏差,偏差率约3.97%,这是由于电机实际参数和仿真参数无法达到理想的一致。
5 结论
在前人无刷直流电机两相导通无磁链观测直接转矩控制系统研究基础上,从简化系统结构、减小转矩波动入手,在转矩计算方面采用相电流与霍尔信号相结合的方法;在电压矢量选择方面,提出了一种两管导通零矢量及其最优电压矢量选择表。
通过理论分析得到两管导通零矢量对电机电磁转矩的控制效果要优于传统零矢量,采用仿真和实验两种手段,验证了转矩计算方法的可行性以及两管导通零矢量理论分析的正确性。本文研究成果对进一步研究无刷直流电机直接转矩控制具有一定的参考和实际应用价值。
[1] 王大方, 卜德明, 朱成, 等.一种减小无刷直流电机换相转矩脉动的调制方法[J].电工技术学报, 2014, 29(5): 160-166.
WANG Dafang, BU Degming, ZHU Cheng, et al. A Modulation Method to Decrease Commutation Torque Ripple of Brushless DC Motors[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 160-166.
[2] 李政, 胡广大, 崔家瑞, 等. 永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报, 2014, 34(3): 431-437.
LI Zheng, HU Guangda, CUI Jiarui, et al. Sliding-mode Variable Structure Control With Integral Action for Permanent Magnet Synchronous Motor[J]. Proceedings of the CSEE, 2014, 34(3): 431-437.
[3] AN Quntao, SUN Lizhi, LIU Chao, et al. Flux Linkage Self-control Based Direct Torque Control of Brushless DC Motor[J]. Proceedings of the CSEE, 2010, 30(12): 86-92.
[4] 姜卫东, 胡杨, 黄辉, 等. 采用坐标变换的无刷直流电机换相过程分析及减小换相转矩脉动的方法[J].中国电机工程学报, 2015, 35(24): 6527-6534.
JIANG Weidong, HU Yang, HUANG Hui, et al. The Commutation Process Analysis and the Method Reducing Commutation Torque Ripple of Brushless DC Motors Based on the Coordinate Transformation[J].Proceedings of the CSEE,2015,35(24): 6527-6534.
[5] MASMOUDI M, EI B B, MASMOUDI A. Direct Torque Control of Brushless DC Motor Directs with Improved Reliability[J].Institute of Electrical and Electronics Engineers Inc, 2014, 50(6): 3744-3753.
[6] 夏长亮,张茂华,王迎发,等. 永磁无刷直流电机直接转矩控制[J]. 中国电机工程学报,2008, 28(6): 104-109.
XIA Changliang, ZHANG Maohua, WANG Yingfa, et al. The Direct Torque Control for Permanent Magnet Brushless DC Motor[J]. Proceedings of the CSEE, 2008, 28(6): 104-109.
[7] 王晓远, 田亮, 冯华. 无刷直流电机直接转矩模糊控制研究[J].中国电机工程学报,2006,26(15): 134-138.
WANG Xiaoyuan, TIAN Liang, FENG Hua. Study of the Fuzzy Control on Direct Torque Control for BLDCM[J].Proceedings of the CSEE,2006,26(15): 134-138.
[8] 杨建飞,胡育文.无刷直流电机无磁链观测直接转矩控制[J]. 中国电机工程学报, 2011, 31(12): 90-95.
YANG Jianfei,HU Yuwen.Direct Torque Control of Brushless DC Motor without Flux Linkage Observation[J].Proceedings of the CSEE,2011,31(12): 90-95.
[9] 杨建飞, 胡育文, 刘建, 等. 两相导通BLDCM DTC电压空间矢量分析[J]. 电机与控制学报, 2018, 22(3): 95-104.
YANG Jianfei, HU Yuwen, LIU Jiang, et al. Analysis on Voltage Special Vector in Two-phase Conduction Direct Torque Control of Brushless DC Motor[J]. Electric Machines and Control, 2018, 22(3): 95-104.
[10] 姚绪梁,曾俊,张燕,等.无刷直流电机直接转矩控制的新型零矢量研究[J].电气传动,2017,47(3):3-7.
YAO Xuliang,ZENG Jun,ZHANG Yan,et al.Study on New Voltage Vector in Direct Torque Control of Brushless DC Motor[J].Electric Drive,2017,47(3): 3-7.
[11] 潘峰, 周运杰, 卢沁雄, 等. 基于占空比调节的无刷直流电机直接转矩控制[J]. 电机与控制应用, 2017, 44(11): 42-49.
PAN Feng, ZHOU Yunjie, LU Qinxiong, et al. Direct Torque Control with Duty Cycle Control Strategy for Brushless DC Motor[J].Electric Machines & Control Application, 2017, 44(11): 42-49.
[12] 朱俊杰, 粟梅, 王湘中, 等. 分段式滑模变结构无刷直流电机直接转矩控制[J]. 仪器仪表学报, 2013, 34(11): 2634-2640.
ZHU Junjie, SU Mei, WANG Xiangzhong, et al. Direct-torque-control of Brushless DC Motors Based on Segmented Sliding-mode-variable-structure[J]. Chinese Journal of Scientific Instrument,2013, 34(11): 2634-2640.
[13] 孙加伟. 无刷直流电机的直接转矩控制系统研究与设计[D]. 南京: 南京信息工程大学, 2017.
SUN Jiawei. Research and Design of Direct Torque Control System for Brushless DC Motor[D]. Nanjing: Nanjing University of Information Science & Technology, 2017.
[14] 张建伟,孙伟卿,金建中.无刷直流电机双模糊直接转矩控制系统的研究[J].机电工程,2017,34(7): 763-767.
ZHANG Jianwei, SUN Weiqing, JIN Jianzhong. Double Fuzzy Direct Torque Control System of BLDCM[J]. Journal of Mechanical & Electrical Engineering, 2017, 34(7): 763-767.
[15] 郑云广,陆可,谢建隆.无定子磁链观测的永磁同步电机直接转矩控制[J].微特电机,2017,45(12): 65-68.
ZHENG Yunguang, LU Ke, XIE Jianlong. A Direct Torque Control Strategy of PMSM without Flux Linkage Observation[J]. Small & Special Electrical Machines, 2017, 45(12): 65-68.
[16] 郭子钊, 佃松宜, 苏敏. 无刷直流电机直接转矩控制研究[J].计算机仿真, 2017, 34(1): 197-201.
GUO Zizhao, DIAN Songyi, SU Min. Study of Direct Torque Control of Brushless DC Motor[J]. Computer Simulation, 2017, 34(1): 197-201.
[17] 梅亮, 刘景林, 董亮辉, 等. 基于Simulink无刷直流电机直接转矩控制研究[J]. 微电机, 2013, 46(6): 62-66.
MEI Liang, LIU Jinglin, DONG Lianghui, et al. Study of Brushless DC Motor DTC Based on Simulink[J]. Micromotors, 2013, 46(6):62-66.
[18] 周渝, 佃松宜, 蒲明.新型无刷直流电机直接转矩控制优化研究[J].计算机仿真,2017,34(3):253-257.
ZHOU Yu,DIAN Songyi,PU Ming.Optimization Study for a Novel Brushless DC Motor Direct Torque Control[J].Computer Simulation,2017,34(3): 253-257.
