0 引言
为了满足汽车主机厂对零部件轻量化、高可靠性和长寿命的要求,汽车轮毂轴承从两个单列的轴承发展到第三代轮毂单元,其装配方式也由螺母锁紧发展到当前主流的轴铆接方法。轴铆接方法所需载荷远小于传统直压铆接,能实现结构轻量化,避免螺母松动导致轴承预紧力失效引起的不良后果[1]。但是轴铆工艺也存在预紧力过大或过小、内圈径向变形等缺点,影响轮毂轴承的寿命[2-3]。
国内外学者利用实验和仿真方法对轮毂轴承轴铆接装配进行了大量的研究[4-5]。TODA等[6]采用实验方法研究了内圈倒角尺寸、铆接角尺寸、铆接力和轮毂轴铆接区域的硬度对预紧力和内圈外径变化量的影响,研究发现内圈倒角尺寸和铆接力是影响预紧力的关键因素。程琼等[7]利用仿真方法将铆头以零度角加载,研究了铆接过程中进给速度对轮毂轴承预紧力的影响。MOON等[8]采用刚塑性有限元法模拟了铆接过程,比较了铆接力的实测结果与仿真结果,结果显示,在铆接中期差异小,在前期差异大,可能是因为没有考虑轮毂轴的弹性变形影响。牛荣军等[9]利用刚塑性方法将铆头设置为一定倾角的圆周轨迹,分析了轮毂轴端部大变形区域的等效应力和等效应变分布情况,通过对比总结出开裂性最大位置。杨军等[10]在仿真时将铆头设置为一定倾角的圆周轨迹,研究了铆头倾角和铆头停留时间对轮毂轴承预紧力的影响,发现铆头停留时间大于0.8s时预紧力达到相对稳定状态。梅怡[11]通过分析铆接机铆头的工作原理,对铆头的梅花状运动轨迹进行分析,推导出适用于该类径向运动要求的梅花状轨迹参数方程,对该类运动的设计分析提供了重要的参考。QU等[12]采用弹塑性有限元法模拟了轮毂轴承的铆接过程,利用试验测试的方法推导出符合实际的梅花运动轨迹,并研究了铆接力和摩擦因数对内圈预紧力的影响。
铆头以梅花轨迹运动时自转速度和进给速度对轮毂轴承最终性能影响的研究鲜见报道,因此,本文根据设备参数确定铆头梅花轨迹参数,利用有限元方法分析了以梅花轨迹加载时不同自转速度与进给速度条件下铆接成形过程中的相互作用力,研究铆头自转速度与进给速度对轮毂轴承预紧力及内圈径向变形等关键性能指标的影响规律。
1 轴铆仿真模型的建立与验证
1.1 轴铆过程分析
图1为本研究中轮毂轴承轴铆接过程的示意图。由铆接机驱动的铆头运动可视为由轴向平移运动和平面梅花状运动组成[11]。如图2所示,初始状态时点M和O1在x轴的正向,动圆O1(半径为R)绕着定圆O(半径为r)做纯滚动运动。当动圆的中心位置从O1移动到O′1时,动圆上点M的位置从M移动到M′。φ是动圆O1绕定圆中心O的公转角度,θ是动圆O1的自转角度。动圆O1和定圆O之间的关系满足等式

图1 轮毂轴承轴铆接过程示意图
Fig.1 Schematic diagram of the shaft riveting process of hub bearing

图2 铆头上点M的运动分析
Fig.2 Motion analysis of point M of punch
Rφ=rθ
(1)
初始状态时,图2中e1和e2满足等式
e1=e2
(2)
式中,e1为动圆中心O1与定圆中心O的距离;e2为动圆中心O1与M点距离。
e为动圆O1的半径R和定圆O的半径r之差,即
e=R-r
(3)
根据几何关系,点M的平面位移可以描述为[13]
(4)
如果平面运动轨迹具有完整的j瓣梅花的形状,则表示动圆绕定圆圆心O公转p圈,同时绕其自己的圆心O2自转j圈,从而保证点M可以返回到起始点。则
p=jr/R
(5)
在这个等式中, p=9,j=11[11]。
在本研究中,铆头的长度L为108.33 mm,最大倾角α为5°。 L和α满足等式
2e=Lsinα
(6)
铆头的公转角速度设为ω,t为运动时间,则
φ=ωt
(7)
点M的平面轨迹可写为
(8)
图3为对应的点M梅花运动轨迹。
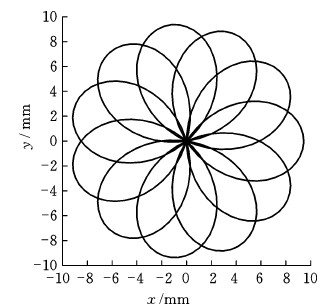
图3 铆头上点M的梅花运动轨迹
Fig.3 Plum blossom motion trajectory of point M of punch
图1标记的铆头中心点O与内圈的上表面之间的初始距离H为10.37 mm。基于内圈的上表面,铆头的轴向平移运动如图3所示,铆头的进给位移设为11.56 mm,图4中铆头进给速度为2.89 mm/s,把铆接过程分为4个阶段。在阶段1中,铆头下降但没有与轮毂轴接触。当铆头与轮毂轴接触时,阶段2开始。在阶段3,铆头的高度在2.89~5.89 s保持不变。在阶段4,铆头上升并与内圈分离。
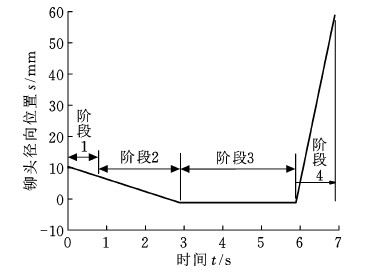
图4 铆头的轴向平移运动
Fig.4 Axial translational movement of punch
为了研究铆头自转速度和进给速度对摆辗成形结果的影响,选取不同的工艺参数进行仿真计算:①铆头进给速度vf选择4 mm/s时,选用7种不同的自转速度n(190,240,300,400,516,600,720 r/min)进行研究;②铆头自转速度n选择190 r/min时,选用7种不同的进给速度vf(2,2.5,2.89,4,5,5.78,8 mm/s)进行研究。
1.2 轮毂轴承材料性能
轮毂轴和内圈发生变形的过程中,其材料性能对最终变形结果有重要影响,故在仿真过程中需要首先确定材料的本构关系。按照GB/T 228.1—2010单轴拉伸标准的尺寸,将轮毂轴承材料加工成拉伸试样。使用SAE 1055合金作为轮毂轴材料,使用SAE 52100合金作为内圈材料。轮毂轴材料和内圈材料均按照产品生产工艺条件进行热处理。根据拉伸试验测试结果建立轮毂轴材料本构关系:
(9)
式中,σtrue为材料拉伸测试时的真实应力;εtrue为材料拉伸测试时的真实应变。
表1给出了轮毂轴材料的机械性能。
表1 轮毂轴材料SAE 1055的机械性能
Tab.1 Mechanical properties of hub shaft material SAE 1055

泊松比密度(kg/m3)弹性模量(GPa)屈服强度(MPa)抗拉强度(MPa)0.37 800214699.35907.67
内圈材料拉伸试验结果显示材料在拉伸过程中没有发生明显的塑性变形,在铆接仿真分析过程中应将其处理成弹性材料,表2给出了内圈材料性能。
表2 内圈材料SAE 52100的机械性能
Tab.2 Mechanical properties of inner ring material SAE 52100
泊松比密度(g/m3)弹性模量(MPa)0.37 8001.99×105
1.3 轴铆接过程仿真模型的建立和验证
选择通用有限元软件Abaqus的显式模块模拟铆接过程[14-15]。图5显示了轮毂轴承轴铆接仿真有限元模型。采用C3D8R单元类型[16-17],共有33 336个单元,如图5b所示,对轮毂轴大变形区域进行网格细化。铆头的刚度比轮毂轴端部的刚度高得多,因此将铆头处理成刚体,以减小计算负担。铆头与轮毂轴接触部分的形状非常复杂,其小误差也将对计算结果产生很大的影响。如果将铆头处理为离散刚体,则不仅影响计算精度,而且大大延长了计算机的运算时间。将铆头处理成解析刚性体则可以克服上述缺点。为了在铆接过

图5 轮毂轴承轴铆接有限元模型
Fig.5 Finite element model of the shaft riveting of hub bearing
程仿真过程中同时实现铆头的轴向平移运动和平面梅花轨迹运动,铆头分为两部分,如图5所示,将铆头的上部作为离散刚体处理,将下面的部分作为解析刚体处理,然后对这两个部分建立绑定关系。
轮毂轴的最终变形形状影响轮毂轴承的性能。铆接后的变形形状及尺寸仿真结果如图6所示,实验结果如图7所示。由分析可知,轮毂轴模拟最终变形形状与实验获得的形状一致,关键尺寸最大误差小于1.6%,表明预测结果是可以接受的。

图6 轴铆接仿真最终成形形状
Fig.6 Final deformed shape of shaft riveting simulation

图7 轴铆接实验最终成形形状
Fig.7 Final deformed shape of shaft riveting experiment
2 结果与讨论
2.1 轮毂轴承轴铆接过程变形状态
铆头自转速度190 r/min,进给速度2.89 mm/s,铆头轴向运动如图4所示,图8给出了4个阶段的变形特征。图8a显示有限元模型在阶段1时铆头和轮毂轴还未接触。当铆头与轮毂轴接触时,轮毂轴发生变形,如图8b所示。在阶段3,保持恒定高度的铆头旋转,使轮毂轴端部最终变形均匀。在阶段4,铆头上升并与内圈分离,内圈通过轮毂轴端部的塑性变形固定。

图8 轴铆接四个阶段的变形特征
Fig.8 Deformation characteristics of four stages in shaft riveting
2.2 铆头自转速度对轮毂轴承性能的影响
图9所示为铆接过程中铆接力(铆头对轮毂轴端部的压力)和内圈所受压力(轮毂轴端部对内圈的压力)的变化规律,铆接力在铆接阶段2结束(即2.89 s)处最大。如图10所示,铆头在不同自转速度下,铆接力最大值没有发生明显的趋势性变化。

图9 不同自转速度下轴铆成形内圈所受压力和铆接力
Fig.9 Force on the inner ring and clinching force in shaft riveting with different rotation speeds

图10 自转速度对铆接力最大值和预紧力的影响
Fig.10 Effect of rotation speed on maximum clinching force and clamping force
如图9所示,在铆接阶段4以前,铆头的自转速度决定铆接力和内圈所受压力的峰谷值变化周期。图9a中铆接力和内圈所受压力每0.2 s出现1次峰值,图9b中铆接力和内圈所受压力每0.15 s出现1次峰值,分别与铆头自转速度300 r/min和400 r/min相吻合。因为铆头在自转过程中以11瓣梅花轨迹摆铆,仅当轨迹点M转到最外端时,铆接力出现峰值。在5.89 s时进入铆接第四阶段,铆头上升,内圈所受压力降低并且稳定不变,这个压力即为轮毂轴承的预紧力。内圈所受压力的降低主要是铆头压力撤销后,内圈发生了回弹,然后在轮毂轴大变形区残余塑性变形的作用下预紧力稳定不变。图10给出了不同自转速度条件下预紧力的大小,可以看出随着铆头自转速度的增大,预紧力逐渐增大最后趋于稳定。
图11所示是铆接阶段2自转速度分别为300 r/min和600 r/min时铆接力的对比。从图中可以看出,自转速度为300 r/min时的铆接峰值压力比600 r/min时的铆接峰值压力大。自转速度为600 r/min时铆接力出现两次峰值,自转速度为300 r/min时铆接力出现一次峰值,增大自转速度可以降低铆接峰值压力,增加铆接次数,让铆接过程更平稳。
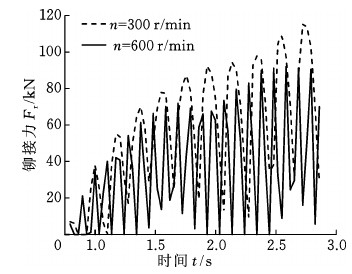
图11 轴铆接阶段2两自转速度铆接力对比
Fig.11 Comparison of clinching force at two rotational speeds in stage 2 of shaft riveting
如图12所示,内圈的外部直径最大Mises应力和最大径向变形随铆头自转速度的变化规律基本一致,自转速度在516 r/min时轮毂轴承内圈径向变形出现峰值79.2 μm。
在铆头自转速度为190 r/min、进给速度为2.89 mm/s的条件下,图13显示了轮毂轴端部两个位置A和B具有较大的塑性变形,其中A处的塑性变形容易形成褶皱,影响轮毂轴承的强度,故塑性变形不能太大[18-19]。图14所示是7种不同铆头自转速度下轮毂轴端部A处最大塑性应变(PEEQ)变化规律,塑性应变随着铆头自转速度的变化而波动,没有趋势性变化。
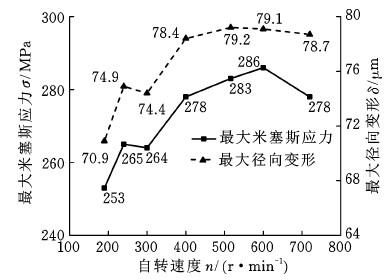
图12 自转速度对内圈Mises应力和径向变形的影响
Fig.12 Effect of rotation speed on von Mises stress and the radial variation of inner ring

图13 轮毂轴端部塑性应变分布
Fig.13 PEEQ distribution of hub shaft end
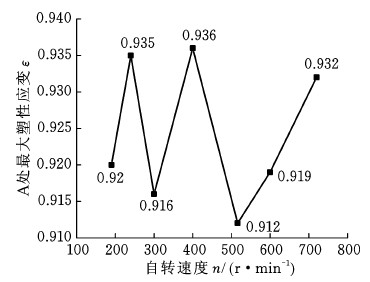
图14 自转速度对位置A处最大塑性应变的影响
Fig.14 Effect of rotation speed on maximum PEEQ at position A
2.3 铆头进给速度对轮毂轴承性能的影响
图15所示为进给速度对预紧力和铆接力最大值的影响规律。铆接力最大值与预紧力的规律基本一致,铆头进给速度为2.89 mm/s时,预紧力和铆接力最大值出现峰值,然后当进给速度增至8 mm/s时,预紧力和铆接力最大值快速增大。

图15 进给速度对铆接力最大值和预紧力的影响
Fig.15 Effect of feed speed on maximum clinching force and clamping force
图16所示为铆接阶段2进给速度与铆接力的关系。铆接峰值压力随着进给速度的增大而增大,降低进给速度可以降低铆接力峰值,增加铆接次数,让铆接过程更加平稳。
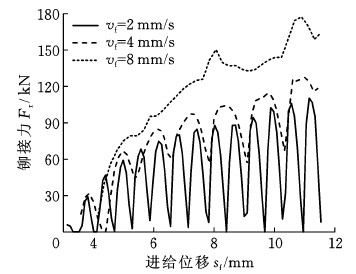
图16 轴铆接阶段2三进给速度下铆接力对比
Fig.16 Comparison of clinching force at three feed speeds in stage 2 of shaft riveting
图17所示是内圈最大径向变形量和内圈外部直径最大Mises应力随铆头进给速度的变化规律,内圈最大径向变形量和内圈外部直径最大Mises应力随进给速度的变化规律基本一致,当进给速度为2.89 mm/s时,内圈外部直径最大径向变形量和内圈外部直径最大Mises应力出现峰值,主要是由于在此进给速度下预紧力出现峰值(图15),大的内圈预紧力使其产生了大的周向变形。

图17 进给速度对内圈Mises应力和径向变形的影响
Fig.17 Effect of feed speed of on von Mises stress and the radial variation of inner ring
图18是轮毂轴端部A处最大塑性应变随铆头进给速度的变化规律,最大塑性应变在进给速度小于等于5.78 mm/s时出现波动,在进给速度为8 mm/s时急剧增大,主要是由于此时预紧力大幅增大(图15),轮毂轴端部发生大的塑性变形。
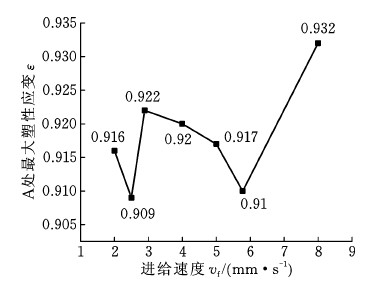
图18 进给速度对位置A处最大塑性应变的影响
Fig.18 Effect of feed speed on maximum PEEQ at position A
3 结论
(1)本文建立有限元模型模拟了轮毂轴承的铆接过程,将铆头分解为解析刚体和离散刚体实现其轴向平移和平面梅花状复合运动,从而提高了计算精度和计算效率,并通过实验验证了仿真模型。
(2)在进给速度为4 mm/s时,随着铆头自转速度的增大,轮毂轴承预紧力先增大然后趋于稳定,轮毂轴端部A处塑性变形没有趋势性变化。轮毂轴承内圈径向变形随自转速度升高而增大,到516 r/min时出现峰值。故为了保证轮毂轴承的性能,铆接过程应尽量选择低的自转速度。
(3)在铆头自转速度为190 r/min时,当进给速度为2.89 mm/s时,铆接力最大值、预紧力和内圈径向变形均出现峰值,继续增大铆头进给速度到8 mm/s时,对内圈径向变形影响不大,但预紧力、铆接力最大值和轮毂轴端部A处塑性变形均大幅增大,故为了提高生产效率并减小内圈径向变形,应选择4~5.78 mm/s的进给速度。
(4)通过比较铆头以梅花轨迹运动时不同自转速度和进给速度对轮毂轴整个塑形变形过程的铆接力,总结出提高铆头的自转速度或降低铆头的进给速度都能降低铆接过程阶段2的铆接力峰值,使铆接机振动减小,从而提高轮毂轴承产品质量。
[1] 曲杰, 张国杰, 徐小琴. 轮毂轴承单元轴铆合装配的铆头优化设计[J]. 华南理工大学学报 (自然科学版), 2016, 44(2): 60-66.
QU Jie, ZHANG Guojie, XU Xiaoqin. Optimization Design of Rivet Head for Shaft Riveting Assembly of Hub Bearing Unit[J]. Journal of South Chia University of Technology (Natural Science Edition), 2016, 44(2): 60-66.
[2] MORITA K. Trends of Production Engineering for Bearing and Unit Products[J]. KOYO Engineering Journal English Edition, 2001, 159: 31-36.
[3] HARRIS T A, KOTZALAS M N. Rolling Bearing Analysis Volume I: Essential Concepts of Bearing Technology[M]. Lonton: Taylor & Francis, 2006: 135-157.
[4] NAM C H, LEE M C, EOM J G, et al. Finite Element Analysis Model of Rotary Forging for Assembling Wheel Hub Bearing Assembly[J]. Procedia Engineering, 2014, 81: 2475-2480.
[5] CHO H, KIM N, ALTAN T. Simulation of Orbital Forming Process Using 3D FEM and Inverse Analysis for Determination of Reliable Flow Stress[J]. Revista de la Facultad de Ingenieria, 2009, 17(3): 299-308.
[6] TODA K, ISHII T, KASHIWAGI S, et al. Development of Hub Units with Shaft Clinching for Automotive Wheel Bearing[J]. KOYO Engineering Journal English Edition, 2001, 158: 26-30.
[7] 程琼, 赵文礼, 林辉, 等. 铆接过程中进给速度对轮毂轴承性能的影响[J]. 机械, 2014, 41(3): 56-59.
CHENG Qiong, ZHAO Wenli, LIN Hui, et al. The Effect of the Feed Speed in the Process of Riveting of the Performance of the Wheel Hub Bearing[J]. Machinery, 2014, 41(3): 56-59.
[8] MOON H K, LEE M C, JOUN M S. An Approximate Efficient Finite Element Approach to Simulating a Rotary Forming Process and Its Application to a Wheel-Bearing Assembly[J]. Finite Elements in Analysis & Design, 2007, 44(1/2): 17-23.
[9] 牛荣军, 李文洒, 康乃正, 等. 汽车轮毂轴承单元轴端铆合有限元分析[J]. 轴承, 2015(4):21-25.
NIU Rongjun, LI Wensa,KANG Naizheng, et al. Finite Element Analysis on Shaft End Riveting of Automobile Hub Bearing Units[J]. Bearing, 2015 (4):21-25.
[10] 杨军, 杨允松, 李伟, 等. 轿车轮毂轴承铆装工艺理论分析与试验研究[J]. 中国机械工程, 2017, 28(24): 2949-2956.
YANG Jun, YANG Yunsong, LI Wei, et al. Theoretical Analyses and Experimental Studies for Riveting and Assembly Processes of Automotive Hub Bearing Units[J]. China Mechanical Engineering, 2017, 28(24): 2949-2956.
[11] 梅怡. 梅花状径向铆接机的设计分析[J]. 制造技术与机床, 2012 (9): 60-63.
MEI Yi. Design Analysis on the Plum Blossom Type Radial Riveting Machine[J]. Manufacturing Technology & Machine Tool, 2012 (9): 60-63.
[12] QU J, ZHANG G. Numerical and Experimental Investigations of the Shaft-clinching Assembly Process of Automobile Wheel-hub-bearing Units[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2016, 230(13): 1-17.
[13] QU J, ZHANG G. Determination of Motion Equation of Rivet Head during Shaft Riveting Assembly Process for Wheel Hub Bearing Units[J]. Journal of Manufacturing Science & Engineering, 2016, 138(4): 041006.
[14] YUAN S J, CUI X L, WANG X S. Investigation into Wrinkling Behavior of Thin-walled 5A02 Aluminum Alloy Tubes under Internal and External Pressure[J]. International Journal of Mechanical Sciences, 2015, 92: 245-258.
[15] HU L, TENG B, YUAN S. Effect of Internal Pressure on Hydro Bending of Double-layered Tube[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2012, 226(10): 1717-1726.
[16] GOVINDASAMY G, JAIN M. Modeling and Experimental Assessment of Bending Characteristics of Laminated Bi-layer Sheet Materials[J]. Journal of Engineering Materials & Technology, 2016, 138(3): 031014.
[17] HAN X H, HUA L. 3D FE Modelling of Contact Pressure Response in Cold Rotary Forging[J]. Tribology International, 2013, 57(4): 115-123.
[18] LI H, YANG H, ZHAN M, et al. A New Method to Accurately Obtain Wrinkling Limit Diagram in NC Bending Process of Thin-walled Tube with Large Diameter under Different Loading Paths[J]. Journal of Materials Processing Technology, 2006, 177(1/3): 192-196.
[19] YANG H, LIN Y. Wrinkling Analysis for Forming Limit of Tube Bending Processes[J]. Journal of Materials Processing Technology, 2004, 152(3): 363-369.
