0 引言
并联操作手具有承载能力大、刚度高、动态响应好、无累积误差等特点,在工程领域获得了广泛应用。为保证各支链关节的正常运动,运动副间隙不可避免地存在。当多个运动副间隙共同作用于系统时,并联操作手运动学精确模型中的结构参数与代入运算的名义结构参数不相等,从而导致该操作手运动精度降低。
研究运动副间隙误差及其补偿方法对运动学精度的提高具有重要意义。国内外研究者做了大量研究工作,提出了不同的减小运动副间隙误差的方法。VENANZI等[1]利用虚功原理研究分析了运动副间隙误差;HUANG等[2]分析了2自由度并联机构含有运动副间隙时,其运动精度的变化规律;ABTAHI等[3]通过测量铰链的变量和位置变化量,实现了运动学标定;余跃庆等[4]完成了平面3自由度并联机构的误差建模,分析了间隙误差引起的杆长及输入角误差的变化特性,同时利用粒子群优化(PSO)算法有效补偿了间隙误差;丁建中等[5]提出了矩阵分块建模法,研究了铰链间隙对板式卫星天线的精度影响,同时采用PSO算法求解指向误差;郑恩来等[6]将运动副间隙考虑进一种柔性多连杆机构的动力学模型中,研究了机构输入转速和运动副间隙大小对机构的动态响应规律;陈修龙等[7]建立了球面副二状态模型,基于接触力、摩擦力模型分析了含不同球面副间隙的5自由度并联机构的动态性能。
本文以4自由度3T1R并联操作手2-RPaRSS[8]为研究对象,分别对转动副、球副进行建模分析,再建立单转动副作用的杆长误差模型和双球副共同作用的杆长误差模型,得出各杆件有效长度和名义长度的关系式;根据逆运动学方程,建立并联操作手位姿误差模型,同时引入驱动角补偿量。利用PSO算法[9]对补偿量寻优,同时提出一种自适应混合粒子群优化(AHPSO)算法,并给出了具体优化策略。
1 并联操作手2-RPaRSS的误差建模
并联操作手2-RPaRSS的拓扑结构如图1所示,由静平台0(正方形)、动平台1(等腰三角形)、子动平台2(等腰三角形)、一条具有三平移的混合支链和两条RSS型无约束支链组成。其中,混合支链由2条分别含有4个球副的平行四边形子混合支链组成,短边长均为n,点B3、B4为短边的中点。静坐标系oxyz以边长为a+b的静平台0的几何中心为原点,x轴垂直R3轴线,正方向指向R3,y轴垂直于R4轴线,正方向指向R4。

图1 并联操作手2-RPaRSS的机构简图
Fig.1 Parallel manipulator 2-RPaRSS mechanism diagram
静平台0上的4个驱动副R1、R2、R3、R4分别位于各边上,位置均向右偏离正方形中点(a-b)/2,且R1⊥R2,R3⊥R4。设定各驱动角α1、α2、α3、α4,用连杆lai(i=1,2,3,4)与x或y轴正方向夹角表示。转动副R5的轴线与动平台1的交点为动坐标系o′x′y′z′的原点,其x′轴、y′轴分别与静坐标系x轴、y轴反向且平行。设定|R5S11|在静平台上的投影与静坐标系ox轴负方向夹角表示动平台转动角度γ (见文献[8]),逆时针为正。
1.1 运动副的误差模型
在理想模型中,当两相连零件相对静止或发生相对运动时,其运动副的销和套的中心点重合。但在实际情况中,由于运动副间隙的存在使得销和套本应重合的中心点产生随机偏离,且偏离位置受运动副间隙大小的影响。在进行轨迹规划时,若忽略运动副间隙引起销和轴套的中心偏移,将杆的名义尺寸代入运算,将导致并联操作手实际路径与理想路径产生偏差。
1.1.1 转动副的误差模型
在转动副误差模型中,轴套中心为p点,半径为R,销轴的中心为q点,半径为r,两中心连线的距离为D。建立以轴套中心p为原点,op矢量方向为x轴方向的直角坐标系pxy,如图2所示。θ为两零件中心位置连线与x轴正方向逆时针夹角,定义为转动副误差角。令α为实际关节位移角,α′为名义关节位移角,Δα为关节位移角度偏差,杆的名义长度l=oq,有效长度l′=op。

图2 转动副误差模型
Fig.2 Error model of rotational pair
通过分析转动副的误差模型,可以得到杆的名义长度和名义关节位移角关系式分别为
(1)
(2)
根据误差模型,联立式(1)、式(2),可得杆长的变化量和转角的变化量分别为
(3)
(4)
考虑到转动副销轴位置的随机性,轴销和轴套中心距离和误差角均为随机变量,确定D、θ的取值范围为D∈[0,(R-r)],θ∈[0,2π]。
1.1.2 球副的误差模型
在球副误差模型中,球套中心为p点,半径为R,球销的中心为q点,半径为r。两中心的连线距离为D。如图3所示,以p点为原点,建立直角坐标系pxyz,θ为销与z轴正方向逆时针夹角,φ为pq连线在oxy平面投影与x轴正方向逆时针夹角。

图3 球副误差模型
Fig.3 Error model of ball hinge
考虑到球销位置的随机性,销轴中心q到球套中心p的距离D和其与z、x轴正方向夹角均为随机变量,位置偏移大小和角度的取值范围为
Δx=Dsinθsinφ
Δy=Dsinθcosφ
Δz=Dcosθ
θ∈[0,2π] φ∈[0,2π]
在并联操作手混合支链的平行四边形中,球套固定在短边杆上,球套中心点Si1、Si2(i=1,2,3,4)的坐标可通过各参数表示出来。由于杆Si1Si2两端的球销中心位置在各自球套内随机运动,从而产生杆长误差Δl。
令带有双球副的杆Si1Si2名义长度l=qq′,有效长度l′=pp′,如图4所示,带有双球副的杆长有效值和名义值分别为
(5)
(6)
式中,p点坐标为(px,py,pz);p′点坐标为(p′x,p′y,p′z)。
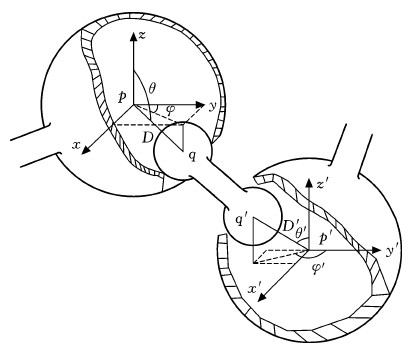
图4 带有双球副杆长的误差模型
Fig.4 Length error model of two ball hinges
联立式(5)、式(6),得到带有双球副的杆长变化量为
Δl=l′-l
(7)
1.1.3 建立含转动副R5的杆长误差模型
参考转动副误差模型的建立方法,得到含转动副R5的杆长误差模型,如图5所示。由于转动副R5的轴套在动平台1上,子动平台2和轴销为一整体零件,故将零件投影在子动平台2上,点R5与点R′5重合。

图5 含转动副R5的杆长误差模型
Fig.5 Length error model with rotational pair R5
轴套半径为R,轴销半径为r,动平台2为一等腰三角形,其底角为β,底角角度偏差分别为Δβ1、Δβ2。等腰三角形qB3B4的名义腰长分别为l3、l4,因受转动副间隙误差影响,令其有效长度分别为l′3和l′4,则l′3及底角角度变化量分别为
(8)
(9)
联立式(8)、式(9),并依据余弦定理可求得l′4和Δβ2。在理想模型中,φ为一固定角度值,但在实际求解机构逆运算时,因Δβ1、Δβ2的存在,使得φ的有效值随之发生改变,这将导致杆l3、l4投影在静坐标系x轴、y轴上的长度发生变化,从而产生额外的杆长计算误差(在求机构逆运算时需要投影长度)。由于角度φ发生变化,使得机构误差模型的建立复杂化,因此,将运动副间隙引起角度φ的误差转化成杆长变化量,通过比例关系得到杆l3、l4总变化量为
(10)
(11)
1.2 系统误差模型的建立和分析
根据系统的结构参数,可以确定在oxyz静坐标系中Ri点和动坐标原点o′的位置矢量,以及在o′x′y′z′动坐标系中Si1点的位置矢量。那么,oSi2(i=1,2,3,4)的坐标矢量分别为


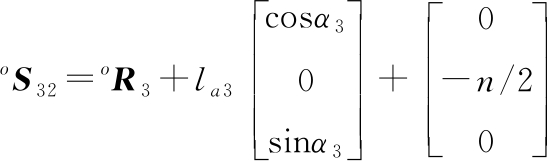
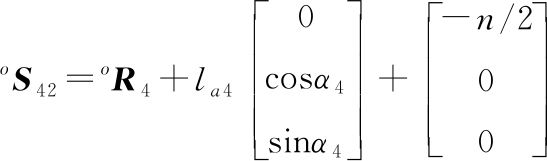
式中,αi(i=1,2,3,4)为各驱动角度;n为平行四边形从动臂的短边边长;lai(i=1,2,3,4)为各主动臂的长度。
o′Si1(i=1,2,3,4)的坐标矢量为
oSi1=Ro′Si1+oO′
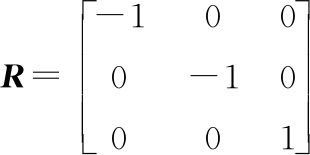
由杆长的相容方程|Si1Si2|=lbi(i=1,2,3,4),令并联操作手的4个运动学方程为

(12)
对式(12)进行全微分,得到关于输入、输出的误差关系式:
JPdα+JQdX+Jrdr=0
(13)



式中,JQ、JP分别为输出、输入雅可比矩阵;Jr为结构参数误差矩阵;dα、dX和dr分别为驱动角位移的微分、末端操作点位姿的微分和杆件尺寸的变化量;dx、dy、dz、dγ为操作手4个自由度上的输出误差 。
当det(JQ)≠0时,式(13)可改写为
(14)
对式(14)分析可知:
(1)引入驱动角补偿量η,令驱动角位移微分dαi=Δαi+ηi(i=1,2,3,4),通过确定η来调整dα,使得dX趋于零,完成对并联操作手运动副间隙误差的补偿。
(2)4自由度3T1R并联操作手2-RPaRSS输出的位姿误差、输入转角误差和杆件尺寸误差为强耦合的非线性函数,难以通过一般方法解出输入角度的补偿量。
2 一种自适应混合粒子群算法
由于PSO算法具有调整参数少、收敛速度快、算法易实现、能够记忆全局最优解等特点,在控制领域解决复杂优化问题上得到广泛应用,因此,采用PSO算法对4个输入角位移的补偿量进行寻优。
以操作手末端操作点的输出误差最小为补偿量的寻优目标,设定POS算法的适应度函数为
(15)
其中,系数ζi≥0(i=1,2,3,4)用来衡量并联操作手输出的4个自由度上的偏差对使用者的重要程度,文中取ζi=1。
在选取各系数时,设定ζ1=1,其他系数以ζ1为参考,根据各自的重要程度作相应的比例调整。若忽略某自由度上的偏差影响,则对应的系数可取0。文中将各自由度上的偏差作同等重要处理,取ζi=1。
种群由N个d维粒子组成,每个维度的搜索范围相同,且为并联操作手4个输入角补偿量的取值范围。粒子初始位置随机生成,经过粒子速度更新和位置更新,由适应度值来评价粒子,通过多次迭代搜索出最优位置。
标准PSO算法公式[10]为
(16)
(17)
式中,w为惯性权值;c1、c2分别为个体学习因子和种群学习因子;r1、r2是[0,1]之间随机数;vid、xid分别为第i个粒子在d维的速度和位移分量;k为迭代次数;pid为个体最优位置;pgd为种群最优位置。
基于MATLAB进行多次仿真测试,依据经验不断调整普通PSO算法各类参数至合适值,发现当迭代50次后,收敛精度仅达10-3数量级,当迭代100次后,收敛精度仅达10-5数量级,并且算法具有陷入局部最优的概率,此时收敛精度仅达到10-1数量级。总体而言,标准PSO算法应用于该机构运动副间隙误差补偿时收敛速度较慢,可靠性偏低,算法存在陷入局部最优的可能,间隙误差补偿效果不够理想。
为提高算法性能,满足实际需要,以50次迭代后收敛精度达到10-6数量级、100次迭代后收敛精度突破10-8数量级为算法改进目标,本文提出了一种自适应混合粒子群优化(AHPSO)算法。
2.1 权值自适应调整策略
权值随着迭代次数做出相应的变小调整,可以兼顾全局搜索与局部搜索,在一定程度上解决算法陷入局部最优的问题。引用权值调整策略[11],即
(18)
式中,kger、kiter分别为最大迭代次数和当前迭代次数;ws、we分别为初始迭代时的惯性权值和迭代至最大次数时的惯性权值。
权值自适应调整策略对算法的收敛精度提升有限,在迭代后期,算法仍有概率陷入局部最优,改进具有局限性。
2.2 学习因子自适应调节策略
学习因子反映了粒子与粒子之间、粒子与种群之间的信息传递程度和粒子运动的偏向程度。从学习因子入手,通过改变学习因子,使粒子在迭代初期有较强的个体学习能力,保持粒子多样性,提高算法收敛速度;同时使粒子在迭代后期具有较强的种群学习能力,保证粒子在局部范围内飞行,提高算法收敛精度。由于标准PSO算法在前期收敛速度较快,而后期收敛精度不高,遂采用指数递减方式调节c1和指数递增方式调节c2,使粒子提前具有较强的种群学习能力,并削弱个体学习能力,以进一步提高收敛精度。本文定义学习因子自适应调节率为
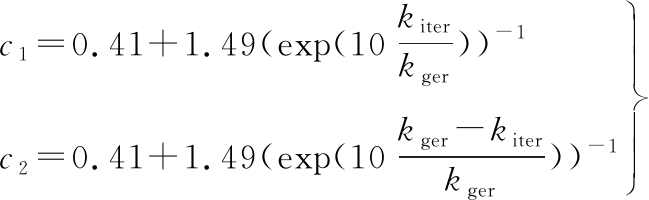
(19)
经多次随机取样测试,发现改进后的算法早熟问题得到了明显改善,收敛速度和收敛精度有明显提高,但部分测试次数获得的收敛精度还达不到理想的数量级要求。
2.3 混沌扰动范围自适应调节策略
混沌粒子群算法[12](CPSO)通过一种无规则的运动状态,在设定的扰动范围内对群体进行遍历性扰动。CPSO算法依据Logistic映射来描述非线性混沌系统的混沌状态,本文引用其映射关系[13]:
zid=4zi(1-zi)
式中,zi为[0,1]之间的随机数。
然后根据混沌函数生成一个扰动量Δx,即采用扰动公式[14]生成扰动量:
Δxid=-τ+2τzid
(20)
式中,Δxid为第i个粒子在d维的扰动量;zid为第i个粒子在d维的混沌函数;τ为混沌扰动范围。
最后,在每个粒子完成位置迭代更新后,由式(17)与式(20)相加,得到粒子的新位置:
(21)
通过比较同一个粒子在式(17)、式(21) 位置的适应度值,选择较优的位置进行再次更新。
CPSO算法在迭代初期,凭借较大的扰动范围,丰富了粒子多样性的同时,将惰性粒子抛出局部最优位置,从而加快收敛速度;在迭代后期,由于粒子的寻优范围较小,当有过大的扰动范围时,会使粒子越过最优解位置,局部搜索能力有限。可见,合适的混沌扰动范围对算法的性能提升至关重要。因此,本文提出混沌扰动范围自适应调节策略,即
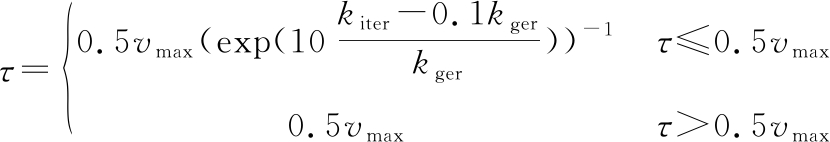
(22)
式中,vmax为粒子飞行最大速度限制。
通过混合权值自适应调整、学习因子自适应调节、混沌扰动范围自适应调节这3种策略,得到了一种AHPSO算法。
2.4 算法的流程
基于上述AHPSO算法,输入角补偿量的寻优过程描述如下。
(1)由误差模型生成机构的位姿误差。
(2)确定种群的粒子数量、每个粒子的维度,设置粒子的位置限制、速度限制及算法最大迭代步数。
(3)初始化算法中各类参数:粒子位置及速度、个体及种群最佳位置、个体及种群最佳适应度值。
(4)计算各粒子的适应度值(式(15))。
(5)比较适应度值大小得出并判断结果。若优于自身历史最优位置,进行个体最优位置更替;若种群中最好的粒子优于种群最优位置,进行种群最优位置更替。
(6)根据式(18)、式(19)更新惯性权值和学习因子,代入计算得粒子的速度和位置,同时将超速粒子做限制处理。
(7)根据式(22)更新混沌扰动范围,由式(20)生成扰动量并更新粒子位置,将新位置与未加扰动量位置进行位移限制处理。
(8)计算粒子新位置式(21)和未加扰动量位置式(17)适应度值进行比较,若前者优于后者,进行粒子个体位置更新和适应度值更新。
(9)判断是否完成迭代步数或达到算法收敛的数量级要求,若满足其中一个条件,则算法结束;若均不满足,则转至步骤(4)。
3 算法性能分析及仿真实验
为测试AHPSO算法的性能,对并联操作手原点坐标o(0,0,470,21°)进行间隙误差补偿仿真实验。将该算法代入误差模型中,分两次随机生成运动副间隙误差,对第一次随机生成的间隙误差进行50次算法迭代补偿,对第二次随机生成的间隙误差进行100次算法迭代补偿。实验得出,算法迭代50次的收敛过程及驱动角补偿量如图6、图7所示。算法迭代100次的收敛过程及驱动角补偿量如图8、图9所示。
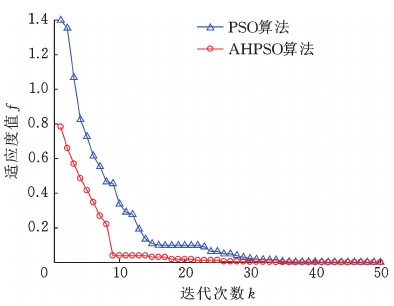
图6 位姿误差50次迭代的收敛过程
Fig.6 Posture error convergence process after 50 times iteration
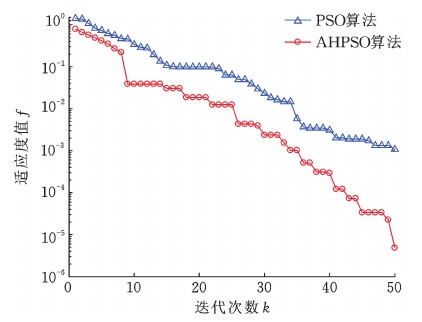
图7 位姿误差50次迭代的驱动角补偿量
Fig.7 Posture error compensation of drive angle after 50 times iteration
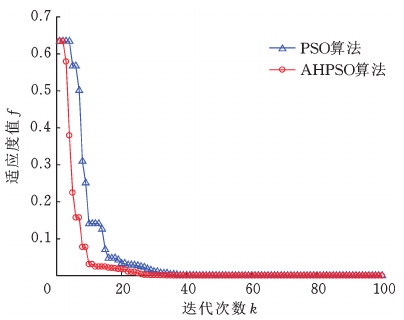
图8 位姿误差100次迭代的收敛过程
Fig.8 Posture error convergence process after 100 times iteration
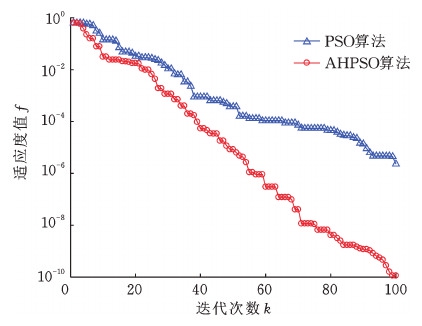
图9 位姿误差100次迭代的驱动角补偿量
Fig.9 Posture error compensation of drive angle after 100 times iteration
在上述两次算法仿真实验中,粒子的数量、初始位置、初始速度相同,种群的最佳位置和适应度值也相同。通过分析图6和图8可得,AHPSO算法通过惯性权值和学习因子自适应调节,收敛效果明显优于普通PSO算法。由图7和图9可知,AHPSO算法由于自始至终保持粒子多样性,混沌扰动范围自适应调节策略使得算法在后期局部搜索能力增强,收敛精度明显高于普通PSO算法。分析算法测试结果可知,当算法迭代至50次时,适应度值为4.966 7×10-6,当算法迭代至100次时,适应度值为1.980 3×10-10,达到了算法优化目标。
利用AHPSO算法寻优各位姿点驱动角补偿量,将角度补偿量与理想位姿点驱动角度共同作为输入,得到含有运动副间隙的并联操作手2-RPaRSS的三维空间和转角空间工作轨迹,如图10、图11所示,间隙误差补偿前后的精度如表1所示。

图10 并联操作手2-RPaRSS的三维空间工作轨迹
Fig.10 Three dimensional space work trajectory of 2-RPaRSS parallel manipulator
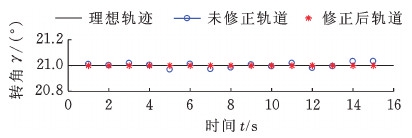
图11 并联操作手2-RPaRSS的转角空间工作轨迹
Fig.11 Corner space work trajectory of 2-RPaRSSparallel manipulator
表1 并联操作手误差补偿结果
Tab.1 Error compensation results of parallel manipulator

误差补偿前误差分量平均误差最大误差均方根误差|δx|(mm) 0.678 22.369 50.917 4|δy|(mm)0.864 22.662 01.085 2|δz|(mm)0.240 60.812 00.332 8|δγ| (10-2(°))1.667 33.280 01.948 3误差补偿后误差分量平均误差最大误差均方根误差|δx| (10-9mm)0.406 13.106 10.864 3|δy|(10-9mm)0.219 51.627 20.470 7|δz|(10-9mm)0.489 63.366 81.002 2|δγ| (10-11(°))0.574 22.765 81.066 7
观察图10、图11可知,间隙误差未补偿的末端轨迹与理想轨迹相比,高低起伏,偏差明显;而通过文中算法补偿后的末端轨迹与理论轨迹吻合较好。分析表1可得,补偿后的定位精度比补偿前的定位精度提高了9个数量级,各自由度上的误差分量在补偿后都比原来降低了99.9%以上。仿真实验表明,文中提出的AHPSO算法针对并联操作手2-RPaRSS的运动副间隙误差补偿效果显著,方法可行。
4 结论
本文依据运动副误差模型,对4自由度3T1R并联操作手2-RPaRSS进行误差建模,得到了关于输入、输出的误差关系式,同时引入驱动角补偿量。将误差补偿问题转化为求极值问题,提出了一种自适应混合粒子群优化(AHPSO)算法来寻优各驱动角补偿量,同时给出了算法的具体优化策略。基于MATLAB仿真实验可知,该优化算法的性能优良,能够在较少的迭代次数内完成高精度收敛,降低了计算机运行负担。在应对其他机构的运动副间隙误差补偿和运动学标定时,可依据算法调试经验,不断尝试调整迭代次数、种群数量和3种自适应调节策略中的相关参数,使算法达到预期的收敛精度。文中提出的误差补偿方法对含运动副间隙的4自由度3T1R并联操作手运动精度的提高具有实际价值和研究意义,并且该方法具有一定的通用性。
[1] VENANZI S, PARENTI-CASTELLI V. A New Technique for Clearance Influence Analysis in Spatial Mechanisms[J]. Journal of Mechanical Design, Transactions of the ASME, 2004, 126(4):581-592.
[2] HUANG T, CHETWYND D G, MEI J P, et al. Tolerance of a 2-dof Overconstrained Translational Parallel Fobot[J]. IEEE Transactions on Robotics, 2006, 2(1):167-172.
[3] ABTAHI M, PENDAR H, ALASTY A, et al. Experimental Kinematic Calibration of Parallel Manipulators Using a Relative Position Error Measurement System[J]. Robotics and Computer-Integrated Manufacturing, 2010, 26:799-804.
[4] 余跃庆,田浩. 运动副间隙引起的并联机器人误差及其补偿[J]. 光学精密工程, 2015, 23(5):1331-1339.
YU Yueqing, TIAN Hao. Error and Compensation of Parallel Robot Caused by Clearance between Kinematic Pairs[J]. Optics and Precision Engineering, 2015, 23(5):1331-1339.
[5] 丁建中,王春洁. 含铰链间隙板式卫星天线展开精度分析[J]. 北京航空航天大学学报, 2016, 42(12):2625-2631.
DING Jianzhong, WANG Chunjie. Deployment Accuracy Analysis of Plate Type Satellite Antenna with Hinge Clearance[J]. Journal of Beihang University, 2016, 42(12):2625-2631.
[6] 郑恩来,张航,朱跃,等. 含间隙超精密压力机柔性多连杆机构动力学建模与仿真[J]. 农业机械学报,2017, 48(1):375-385.
ZHENG Enlai, ZHANG Hang, ZHU Yue, et al. Dynamic Modeling and Simulation of Flexible Multi Link Mechanism with Clearance for Ultra Precision Press[J]. Journal of Agricultural Machinery, 2017, 48(1):375-385.
[7] 陈修龙,高文花,宋浩,等. 含球面副间隙的空间并联机构动力学特性分析[J]. 计算机集成制造系统,2018,24(3):660-670.
CHEN Xiulong, GAO Wenhua, SONG Hao, et al. Dynamic Characteristics Analysis of Spatial Parallel Mechanism with Clearance of Spherical Joints[J]. Computer Integrated Manufacturing Systems, 2018,24(3):660-670.
[8] 沈惠平,邵国为,邓嘉鸣,等. 一种新型低耦合度非全对称三平移一转动并联机械手及其运动学分析[J]. 中国机械工程,2017,28(19):2289-2299.
SHEN Huiping, SHAO Guowei, DENG Jiaming, et al. A Novel Not-fully Symmerical 3T1R PM with Low Coupling-degrees an Its Kinematics[J]. China Mechanical Engineering,2017,28(19): 2289-2299.
[9] EBERHAR R C, KENNEDY J. A New Optimizer Using Particle Swarm Theory[C]∥Proceedings of the 6th International Symposium on Micro Machine and Human Science. Nagoya, 1995: 39-43.
[10] 潘峰,陈杰,辛斌,等. 粒子群优化方法若干特性分析[J]. 自动化学报,2009,35(7):1010-1015.
PAN Feng,CHEN Jie,XIN Bin,et al. Several Analysis of Particle Swarm Optimizer[J]. Acta Automatica Sinica,2009,35(7):1010-1015.
[11] SHI Y, EBERHATR R C. Empirical Study of Particle Swarm Optimization[C]∥Proceedings of the 1999 Congress on Evolutionary Computation. Washington D C, 1999:1946-1950.
[12] LIU B, WANG L, JIN Y H, et al. Improved Particle Swarm Optimization Combined with Chaos[J]. Chaos Solitons&Fractals, 2005, 25(5): 1261-1271.
[13] 封京梅. 一种改进的粒子群优化算法[J]. 云南民族大学学报, 2017, 26(1):60-63.
FENG Jingmei. An Improved Particle Swarm Optimization Algorithm[J]. Journal of Yunnan University of Nationalities, 2017, 26(1): 60-63.
[14] 蔡燕敏. 一种新的混沌粒子群优化算法[J]. 智能计算机与应用, 2017, 7(2):63-65.
CAI Yanmin. A New Chaotic Particle Swarm Optimization Algorithm[J]. Intelligent Computers and Applications, 2017, 7(2): 63-65.
