0 引言
锂离子电池因其能量密度和功率密度高、无记忆效应、自放电率较低等诸多优点而被广泛应用在电动汽车及储能等领域[1]。但因其单体电压较低,有时不能达到实际应用场景对电压和容量的要求,因此需将电池串联成组[2]。由于制造工艺和运行环境不同,各单体电池的容量、内阻和开路电压存在差异,这些差异会导致诸多不利后果,如电池组实际使用中的“木桶效应”、单体过充、过放等[3]。
电池均衡技术[4-5]可有效缓解电池组容量衰减现象,延长电池组使用寿命,并在电池组运行过程中避免因各单体电池不一致性而造成的过充过放现象,从而保护电池单体和电池组整体安全。
现今均衡拓扑多采用分组[6-8]或分层式[9]结构,以缩短均衡时间。文献[10]将每两个物理相邻单体固定地分为一个子模组,但其分组缺乏目的性,影响不需均衡的电池,造成均衡时间较长。文献[11]通过将电池模组分到不同电池组中并引入顶层概念以实现高效电池均衡,但此方案存在分组过于复杂、层数冗杂、各单体电池能量大量耗散在不必要的组内均衡过程中等不足。文献[12]在文献[10]分组拓扑基础上增加了开关状态互补的桥臂,以增大均衡电流,实现单体一致性能量管理,但当物理不相邻各单体的荷电状态(SOC)或电压等参数动态变化时,不能将状态在某一阈值内的单体动态分组进行整体组间均衡操作,致使均衡效果不佳,不能有效降低电池间的不一致性。
上述传统分组均衡方法多采用将每k个物理相邻单体固定地分为一个子模组的分组方法进行均衡,分组缺乏目的性;当组内电池SOC或电压等参数动态变化时,子模组分组方式不能动态地随单体特性变化而动态变化,组内单体及单体数量固定,分组缺乏动态性和科学性。
为了克服上述分组均衡方法的局限性,进一步缩短均衡时间,降低各电池不一致性,提高电池组的整体能量利用率,优化均衡过程,本文提出了一种基于自适应拓扑的电池动态分组均衡方法。
1 分组均衡电路及工作原理
1.1 分组均衡电路简介
本文提出的基于Buck-Boost电路[13]的自适应动态分组均衡电路如图1所示,此电路适用于电池组充电状态或静置状态的均衡。当用于充电状态均衡时,应选用具有较宽电压输出范围的充电电源。
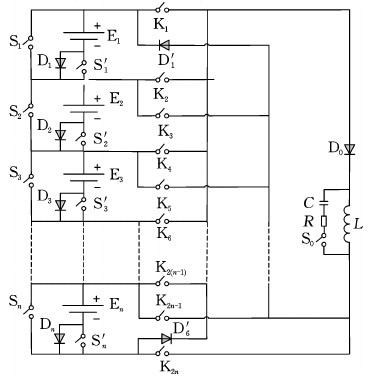
图1 基于Buck-Boost电路的新型分组均衡拓扑
Fig.1 New grouping equalization topology based on Boost-Buck circuit
如图1所示,电路包含:n个串联电池(E1、E2、E3、…、En)、 n+3个二极管(D0、D1、D2、…、Dn、D′1、D′6)、2n+1个普通开关(S0、S1、S3、…、Sn及S′1、S′2、S′3、…、S′n)、2n个MOS管(K1、K2、K3…、K2n)、储能电感L、电阻R、及电容C。电路中二极管的主要作用为避免电池正负极直接相连产生短路;Si开关与S'i开关为一对互斥开关;n的取值具有一般性,为简叙述简便,取n=6。在一次分组均衡过程中,进行基于密度的模糊C均值(DBFCM)聚类运算,假设聚类运算结果即动态分组结果为能量较高子组EH(E1、E3、E5)及能量较低子组EL(E2、E4、E6),将此结果导入均衡器中。
电路的具体工作过程详述如下。
(1)能量较高子组EH给储能电感充电。如图1所示,首先将开关S2、S4、S6闭合,其次控制MOS管K1、K12导通,将能量较高子组EH的能量转移给电感L,电路的电流经过能量较高子组EH的正极、K1、二极管D0、电感L、K12,最后回到EH负极。
(2)储能电感向能量较低子组EL放电。断开步骤(1)中闭合的开关,然后将开关S1、S3、S5闭合,此时E2、E4、E6串联成能量较低子组EL,并形成了电路的电流,经过电感L正极(等效为电源正极)、EL正极、EL负极、D′6、D0,最后回到电感L负极(等效为电源负极)。
由上可知,此电路可对各子组电池间均衡能量进行灵活高效转移,均衡效率提升明显。电阻R、电容C、开关S0在开关组(如S2、S4、S6)断开而开关组(如S1、S3、S5)未闭合期间给电感L提供续流回路,防止尖峰电压及浪涌电流损坏器件。此均衡电路仅用到MOS管正向导通特性。
1.2 均衡次数分析
图2为电感充放电过程中电流随时间变化曲线。其中tc时刻的电流值ILPK为电感充电过程峰值电流,电感平均电值为ILAVE。为了减小均衡能量在转移过程中的损耗,设定电感工作模式为电流断续模式(DCM)。
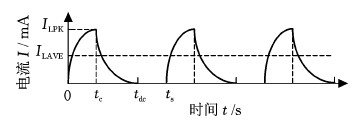
图2 电感电流曲线
Fig.2 Inductor current curve
电感充电阶段(0~tc):如图3a所示,由1.1节,并结合一阶电路全响应公式,可知电感充电期间t时刻流过电感的电流iL(t)为
iL(t)=iL(∞)+[iL(0+)-iL(∞)]e-t/τ=
(1)
式中,VM为充能回路MOS管等效正向导通压降;Re为充能回路等效电阻;VH为能量较高子组的电压;τ为时间常数,τ=L/Re。
电感放电阶段(tc~tdc):如图3b所示,结合1.1节,并依据一阶电路全响应公式,可得出电感放电阶段电感随时间变化的电流值为
(2)

图3 电感充电及放电示意图
Fig.3 Diagram of inductive charging and discharging
进一步简化整理得
(3)
式中,R′e为电感放电回路的等效电阻;Ke为简化等效常数。
因电感充放电过程非常迅速,时间较短,故分别将电感充放电阶段对应的电感电流值进行线性化处理,处理后的电感充放电电流曲线见图4。图4中实线直线即为线性化后的电感电流,虚线曲线为原始电感电流。
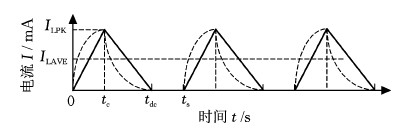
图4 线性化电感电流曲线
Fig.4 Linearized inductor current curve
充电阶段线性化处理后电感电流值
(4)
放电阶段线性化处理后电感电流值
(5)
可以得到电感充电阶段内电感充得能量为
(6)
电感一次能量传递能量效率公式为
(7)
由式(7)结合式(1)和式(2)可推得需要参与均衡的电池子组Ei的均衡次数为
(8)
式中,CN为电池子组内各单体电池额定容量之和;Si为第i个单体电池的SOC值;Save为电池子组平均SOC值。
均衡次数得出后,作为下文均衡过程步骤(5)的重要组成部分,实现电池组充电及静置均衡。
2 电池分组均衡算法
2.1 模糊C均值聚类算法
模糊C均值(FCM)聚类算法[14-16]是一种基于目标函数的模糊聚类算法,用于对象的聚类分析。
FCM算法基于以下最小化目标函数:
(9)
目标函数约束条件为
(10)
U=[uij] dij=‖xj-ci‖
式中,xj为下标为j的样本;ci为第i类的聚类中心;U为n×c隶属度矩阵;uij为每个样本j第i类的隶属度;dij为第j个样本与第i个聚类中心之间的欧氏距离;m为一个模糊性指标。
隶属度uij和聚类中心ci基于拉格朗日乘子法求得:
(11)

(12)
通过对上述目标函数的迭代优化实现聚类,迭代截止条件为目标函数Jm小于等于单体SOC阈值ε1且趋于稳定不变,当目标函数Jm满足迭代截止条件时迭代结束,完成聚类过程,得出电池单体聚类分组结果。
但FCM算法要求预先给出聚类个数c和初始隶属度矩阵,且算法精度对这两个参数高度敏感,使得FCM算法聚类结果不稳定、不理想,影响电池分组结果的精度。
2.2 基于密度的模糊C均值聚类算法
各单体电池状态矩阵X=[x1 x2 … xn],xi=(xi1,xi2,…,xid),i=1,2,…,n,d∈N+,X为n个单体电池样本数据,d为样本维度,在本文中,xj=(Sj1,VTEVj2),j=1,2,…,n,VTEV是单体端电压。将X划分为c个聚类,即G={g1,g2,…,gc},对应的c个聚类中心为C={c1,c2,…,cc}。
本文提出的基于密度的模糊C均值(DBFCM)聚类算法在上述FCM算法基础上,引入样本密度的概念,提出初始聚类中心及初始隶属度矩阵的生成方法,以解决FCM算法聚类精度和稳定性问题,提升电池单体聚类分组精度和稳定性。定义衡量每个样本xj的重要性的密度ρj为
(13)
(14)
djk=‖xj-xk‖
式中,djk为第j个样本与第k个样本的欧氏距离;χ(·)为定义的权重函数;dc为截止距离。
依据密度值ρj对所有样本xj进行降序排列,排列后样本Xa=(x′1,x′2,…,x′n),对应的密度为ρa=(ρ′1,ρ′2,…,ρ′n),截止密度为
(15)
其中,ξ为密度比率。潜在初始聚类中心集如下:
每两个潜在聚类中心之间距离应大于阈值距离,即
(16)
式中,d′ij为x′i和x′j间的距离;γ为距离比率。
设得到c个初始聚类中心点(c≤l),选取样本密度最高的x′1为初始聚类中心点x′1-ini,剩余c-1个初始聚类中心点从上述cl中(除x′1)选取,顺序是从对应密度值ρ′j由大到小的样本点x′i依次检验选取。选取标准如下:
dij=‖x′i-x′j-ini‖≥ε 1≤j≤i≤l
(17)
使用获得的初始聚类中心和样本的密度构造初始隶属度矩阵:

(18)

(19)
i=1,2,…,n k=1,2,…,c
式中,u′ij为降序排列样本集Xa中x′i对应的隶属度;ρck为聚类中心ck的密度。
至此初始聚类中心及初始隶属度矩阵已求出。后续步骤与传统FCM算法相同,不再赘述。最终经过算法流程,得出聚类结果为各个电池子组Ei及其包含的单体。
3 均衡过程
设置均衡采样时间域T,每个时间域T内,利用DBFCM算法实现电池聚类分组,基于动态的分组均衡电路进行分组均衡操作,完成均衡过程。本均衡电路采用以单体SOC及单体端电压作为综合判据。均衡流程图见图5。具体均衡流程为如下:

图5 均衡控制流程图
Fig.5 Balancing control flow chart
(1)在T时间开始时,测量电池组中各单体端电压,采用扩展Kalman滤波(extended Kalman filtering,EKF)法对SOC进行精确估算,计算所有单体电池SOC平均值Save。
(2)设定SOC阈值ε1和单体端电压阈值ε2。
(3)筛选出在阈值外待聚类分组均衡的电池,具体筛选过程如图5所示。
(4)利用式(17)从得到的潜在初始聚类中心集Cl中选取用于单体聚类分组算法DBFCM的初始聚类中心集C;依据式(18),使用获得的初始聚类中心和样本的密度构造初始隶属度矩阵U;进行DBFCM算法电池单体迭代聚类运算,最后得出电池聚类分组集G,即电池子组及其所含单体。
(5)将聚类结果中各电池子组视为新“单体”,依托提出的动态分组均衡拓扑进行各“单体”间均衡操作,均衡电流由式(1)、式(2)得出,且值可由PWM信号占空比进行调节,其中均衡次数Mi由式(8)得出,均衡电路具体操作1.1节中已阐述,均衡结束后进入下一次循环,周而复始。
4 实验与结果分析
4.1 实验设计
本文提出的用于电池分组的聚类算法与自适应均衡电路拓扑相互配套,联系密切,两者构成完整的电池均衡方法。将分组均衡拓扑及聚类算法相关策略作为整体,利用课题组研制的电池测试平台台架进行对比实验。
均衡电路中L=100 μH。实验所用20节A123 18650磷酸铁锂电池样本均从200多个串联电池总体中随机选取,总体充放电循环为600次,其中循环寿命为2 000次以上。单体电池具体参数如下:额定容量10 A·h,额定电压3.2 V,充电截止电压3.6 V,放电截止电压2.0 V。PWM开关频率为5 000 Hz;实验温度为25 ℃。
随机选取的20节电池分为A、 B两组,A组10个电池进行充电实验,B组则进行静置实验。对于A组充电实验和B组静置实验分别在充电状态和静置状态下对比验证本文均衡方法(动态分组实验)与文献[17]中任意单体间均衡方法(任意单体实验)以及文献[12]的基于固定分组均衡拓扑分组均衡方法(固定分组实验)均衡效果。充电实验(A1,A2,…,A10)、静置实验(B1,B2,…,B10)单体电池初始SOC值相同,分别为:55.10%,52.60%,55.60%,50.00%,56.00%,59.50%,51.60%,54.60%,58.00%,60.00%。
为定量判定均衡效果,首先定义均衡度D为:经过利用特定均衡方法进行均衡操作,均衡结束后电池组内各个单体SOC分布的离散程度,即
(20)
式中,Sj为均衡结束时标号为j的电池单体的SOC值;Save为均衡结束后电池组平均SOC值。
D值衡量均衡操作后电池组各单体SOC分布离散程度,并直接体现均衡效果。
考虑到EKF法对单体SOC的估算存在误差,而电池组多节单体电池串联,每节单体电池SOC值的估算误差传递到后续均衡过程最终会影响均衡效果,因此进行SOC误差传递分析。
误差传递分析主要有两种方式,分别是理论分析和实验分析。理论分析公式推导较为复杂,且分析结果与实际真实值相差较大,工程上常采用实验进行分析。本文采用实验法分析EKF法估算的SOC值的实际估算误差。
本文从A、B组电池中任意选取一节单体电池,采用EKF法进行了单节电池SOC估算实验,充电电流为0.5 C(以电池额定容量电流充放电2 h),实验温度25 ℃,得到充电磷酸铁锂单体电池SOC的真实值与估算值,其中真实值为对单体电池进行安时积分得到的SOC值,估算值为利用EKF法对SOC进行估算所得,如图6所示。由图可知,SOC值在平台期的估算误差在3%以内,因此可以利用该算法对SOC值进行估算。
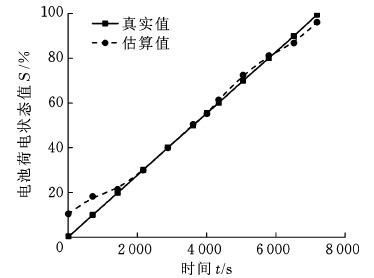
图6 EKF法估算误差图
Fig.6 Chart of estimation error by EKF
4.2 充电实验
充电实验开始前,对A组电池独立进行标准放空。将此10节电池串联成组进行充电,充电电流为5 A,只要有任意一节电池SOC值到达60%,充电均衡开启。固定分组实验、动态分组实验、任意单体实验按照此实验步骤依次进行。图7为动态分组充电实验0~800 s内每个单体电池SOC值变化曲线。图8为任意单体充电实验的实验过程图。当检测到任意单体电压达到充电截止电压3.6 V时,电池组充电过程停止,利用EKF法精确估算此时各单体电池的SOC值,充电结束后实验结果见表1。
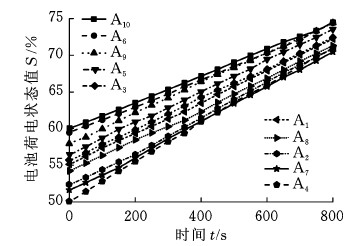
图7 动态分组充电均衡实验0~800 s图
Fig.7 Dynamic grouping charge equalization experiment during 0~800 s period

图8 任意单体充电均衡实验0~800 s图
Fig.8 Arbitrary cell charge equalization experiment during 0~800 s period
表1 充电均衡实验结果
Tab.1 Charging equaization experimental results
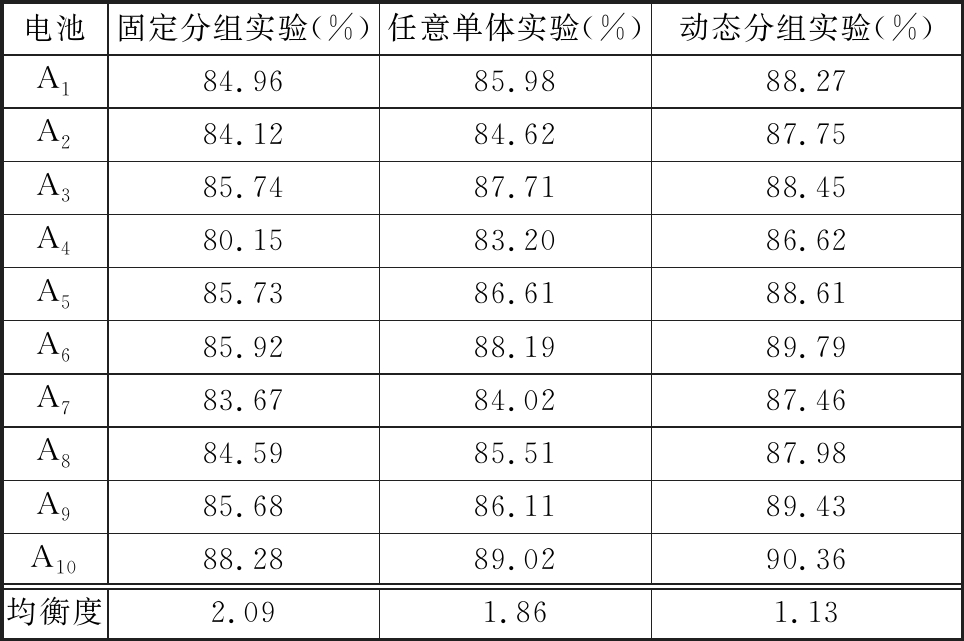
电池固定分组实验(%)任意单体实验(%)动态分组实验(%)A184.9685.9888.27A284.1284.6287.75A385.7487.7188.45A480.1583.2086.62A585.7386.6188.61A685.9288.1989.79A783.6784.0287.46A884.5985.5187.98A985.6886.1189.43A1088.2889.0290.36均衡度2.091.861.13
4.3 静置实验
静置实验开始前,对B组10节电池独立进行充电,直至各单体电池SOC值达到初始SOC值后充电停止,然后将此10节电池串联,进行静置实验。固定分组实验、动态分组实验、任意单体实验按照此实验步骤依次进行。图9、图10分别为动态分组静置实验、任意单体静置实验0~800 s过程图。电池组均衡过程停止条件为电池组中所有单体电池SOC值极差小于等于4%。利用E-Kalman滤波法精确估算此时各单体电池SOC值,实验结果见表2。

图9 动态分组静置均衡实验0~800 s图
Fig.9 Dynamic grouping resting equalization experiment during 0~800 s period
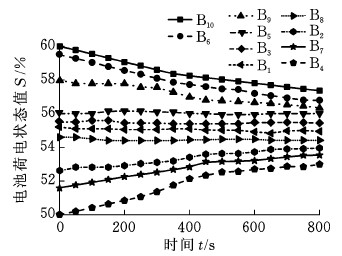
图10 任意单体静置均衡实验0~800 s图
Fig.10 Arbitrary cell resting equalization experiment during 0~800 s period
表2 静置均衡实验结果
Tab.2 The resting equalization experimental results

电池固定分组实验(%)任意单体实验(%)动态分组实验(%)B148.9248.9549.78B248.2348.2649.37B349.4649.1050.01B446.2147.3848.95B549.8049.5750.17B650.1850.0351.05B747.7647.6649.10B848.5448.7249.56B949.8349.7550.35B1050.5450.7151.47均衡度1.311.050.66
4.4 实验结果分析
4.4.1 充电实验结果
充电实验结束时每节电池的SOC值见表1。依据式(20),固定分组实验、任意单体实验、动态分组实验电池组的充入总容量占电池组额定容量的84.88%、86.09%、88.47%。
(1)均衡度D。依据式(20),可计算出固定分组实验、任意单体实验、动态分组实验的均衡度D依次为2.09、1.86、1.13,动态分组实验值与任意单体、固定分组实验值相比,分别减小0.73、0.96,因此在充电实验过程中,从均衡效果分析,本文提出的动态分组方法最好,任意单体均衡方法次之,而固定分组均衡法最差。
(2)均衡总用时。动态分组均衡方法、任意单体均衡方法、固定分组均衡方法总用时分别为1 185 s 、1 500 s、1 319 s,显然,动态分组均衡方法均衡耗时较短,较另二者分别减少约20%、10.15%。
(3)电池组充入总容量。对于电池组充入总容量,动态分组均衡方法与任意单体实验及固定分组实验相比,分别增加了2.38%、3.59%,本文提出的动态分组均衡方法均衡能量损耗比其他两种方法更少。
图7反映了电池组动态分组充电实验的均衡过程,在均衡开始时,依据DBFCM算法,电池E6、E9、E10被分为子组EH,E2、E4、E7被分为子组EL,子组EH向EL整体转移能量,电池E6、E9、E10的SOC值增长率降低,电池E2、E4、E7的SOC值增长率升高,随着电池能量变化,各电池子组组成依据DBFCM算法动态变化,进行组间能量转移,使得各单体电池的SOC值逐渐趋于一致。
4.4.2 静置实验结果
静置实验结束时每节电池的SOC值见表2。固定分组实验、任意单体实验、动态分组实验均衡度D分别为1.31、1.05、0.66,电池组剩余的总容量分别是其额定容量的48.94%、49.01%、49.98%。
(1)均衡度D。固定分组实验、任意单体实验、动态分组实验均衡度D依次为1.31、1.05、0.66,动态分组均衡法与任意单体、固定分组方法实验相比,分别减小了0.39、0.65,说明在静置实验中,从均衡效果分析,本文提出动态分组方法最好,任意单体均衡方法次之,而固定分组均衡法依然最差。
(2)均衡总用时。固定分组实验、任意单体实验、动态分组实验均衡总用时分别约为1 413 s、1 329 s、1 130 s,动态分组方法均衡总用时与任意单体、固定分组方法均衡用时相比,分别减少约15%、20%。
(3)电池组剩余总容量。固定分组方法、任意单体方法以及动态分组方法实验结束后,电池组剩余总容量分别为其额定容量的48.94%、49.01%、49.98%,动态分组方法电池组剩余的总容量相比任意单体方法、固定分组方法分别增加了0.96%、1.03%,三者实验值较为接近。
图9反映了电池组动态分组静置实验的均衡过程,均衡开始时,依据DBFCM算法,电池单体E6、E9、E10被分为子组EH,单体E4单独分为一组EL,EH向EL整体转移能量,当t=100 s时,E4、E7被分为一组EL,随着电池能量变化,各电池子组组成依据DBFCM算法动态变化,进行组间能量转移,使得各单体电池的SOC值逐渐趋于一致。
从均衡度D、均衡总用时及电池组充入总容量3个指标进行分析,在进行充电实验及静置实验时,动态分组均衡方法相比固定分组法实验结果更好,这可有效验证本文提出的自适应拓扑的可行性;动态分组实验与任意单体实验相比性能更优,验证了本文提出的基于自适应拓扑的电池动态分组均衡方法的优越性。
综上所述,本文提出的电池分组均衡方案能缩短均衡时间,减小单体电池间的不一致性,优化均衡过程。
5 结论
(1)针对传统均衡方案中电池分组方式存在的均衡能量利用率不高、均衡时间较长、均衡度不佳等问题,本文提出动态分组均衡方案,此方案在结合开关组与Buck-Boost电路特点基础上设计了用于电池分组均衡的自适应电路拓扑,提出了用于电池分组的基于密度的模糊C均值聚类算法。
(2)充电、静置均衡实验结果表明,提出的均衡方案能缩短均衡时间,提高电池组能量利用率,减小各单体电池间的不一致性。
后续的研究工作将研究进一步寻求并优化适用于本文电路的均衡控制算法及均衡能量具体转移路径规划,以进一步提高均衡效率,优化均衡过程。
[1] WANG L Y, POLIS M P, YIN G G, et al.Battery Cell Identification and SOC Estimation Using String Terminal Voltage Measurements[J]. IEEE Transactions on Vehicular Technology, 2012, 61(7):2925-2935.
[2] 刘红锐,张昭怀.锂离子电池组充放电均衡器及均衡策略[J].电工技术学报,2015,30(08):186-192.
LIU Hongrui, ZHANG Zhaohuai. The Equalizer of Charging and Discharging and the Balancing Strategies for Lithium-ion Battery Pack[J].Transactions of China Electrotechnical Society,2015,30(8):186-192.
[3] 赵奕凡,杜常清,颜伏伍.动力电池组能量均衡管理控制策略[J].电机与控制学报,2013,17(10):109-114.
ZHAO Yifan, DU Changqing,YAN Fuwu. The Energy Balance Management Control Strategy of Power Battery Pack[J]. Journal of Electric Machines and Control,2013,17(10):109-114.
[4] KUAN C C, CHI H L, YEH S F. Cycle Life Analysis of Series Connected Lithium-ion Batteries with Temperature Difference[J]. Journal of Power Sources, 2014,263:75-84.
[5] 刘征宇,马亚东,孙庆,等.基于动态模糊阈值的电池组均衡策略优化[J].中国机械工程,2017,28(5):624-629.
LIU Zhengyu, MA Yadong, SUN Qing, et al.Optimization of Battery Pack Equalization Strategy Based on Dynamic Fuzzy Threshold[J]. China Mechanical Engineering, 2017, 28(5):624-629.
[6] LEE S W, LEE K M, CHOI Y G, et al. Modularized Design of Active Charge Equalizer for Li-ion Battery Pack[J]. IEEE Transactions on Industrial Electronics, 2018,65(11):8697-8706.
[7] YE Y, CHENG K W E, YEUNG Y P B. Zero-current Switching Switched-capacitor Zero-voltage-gap Automatic Equalization System for Series Battery String[J]. IEEE Transactions on Power Electronics, 2012, 27(7):3234-3242.
[8] MONTEIRO V, ALVES P, MELENDEZ A A N, et al. A Novel Modular Voltage Balancing Topology for Active Battery Management System[C]//IEEE International Symposium on Industrial Electronics.Santa Clara,2016:793-798.
[9] 李泉,周云山,王建德,等.基于双层准谐振开关电容的锂电池组均衡方法[J].电工技术学报,2017,32(21):9-15.
LI Quan, ZHOU Yunshan, WANG Jiande, et al. Lithium Battery Pack Equalization Method Based on Two-layer Quasi-resonant Switched Capacitors[J]. Transactions of China Electrotechnical Society,2017,32(21):9-15.
[10] 董博,李永东.基于剩余容量估算的快速蓄电池均衡[J].清华大学学报(自然科学版),2012,52(3):374-379.
DONG Bo, LI Yongdong. Fast Battery Equalization Based on Residual Capacity Estimation[J]. Journal of Tsinghua University(Science and Technology), 2012,52(3):374-379.
[11] ZHANG Z, GUI H, GU D J, et al. A Hierarchical Active Balancing Architecture for Lithium-ion Batteries[J]. IEEE Transactions on Power Electronics, 2017, 32(4):2757-2768.
[12] 吕航,刘承志,尹栋,等.深海动力磷酸铁锂电池组均衡方案设计优化[J].电工技术学报,2016,31(19):233-238.
LYU Hang, LIU Chengzhi, YIN Dong. The Design and Optimize of Equalization Schemes for Underwater Power LiFePO4 Battery Stack[J]. Transactions of China Electrotechnical Society, 2016,31(19):233-238.
[13] WU T H, CHANG C S, MOO C S. A Charging Scenario for Parallel Buck-Boost Battery Power Modules with Full Power Utilization and Charge Equalization[C]//IEEE International Conference on Industrial Technology. Sevilla, 2015:860-865.
[14] LIANG B, CHENG X Q, LIANG J Y, et al. Fast Density Clustering Strategies Based on the K-means Algorithm[J]. Pattern Recognition, 2017,71:375-386.
[15] GAO T C, LI A H, MENG F, Research on Data Stream Clustering Based on FCM Algorithm[J].Procedia Computer Science, 2017,122:595-602.
[16] LIU L, SUN S Z, YU H, et al. A Modified Fuzzy C-Means(FCM) Clustering Algorithm and Its Application on Carbonate Fluid Identification[J]. Journal of Applied Geophysics, 2016,129:28-35.
[17] WANG Y J, ZHANG C B, CHEN Z H, et al. A Novel Active Equalization Method for Lithium-ion Batteries in Electric Vehicles[J]. Applied Energy, 2015,145:36-42.
