0 引言
近年来,自动引导车(AGV)已在智能物流系统中大量使用,它与设备、产线之间如何协同调度显得越来越重要,但这方面的研究比较欠缺,且绝大部分协同调度研究集中于解决前工序的生产调度及工序间物料配送的问题,忽略了后工序的加工特性。MAGGU等[1]在具有无限配送车辆情况下,解决了的生产线上下游协同调度的问题。ARMENTANO等[2]通过禁忌搜索算法解决了具有有限配送周期和有限容积车辆的生产与库存成本的最小化问题。方伯芃等[3]针对具有随机性、并发性、模糊性的不确定环境下的供应链系统,通过启发式寻优得到产业链生产与配送协同调度的最优方案。李凯等[4]在研究单机多车情况下的生产与配送问题时,将配送车辆容量进行了限制,在模型中考虑了制造商信誉惩罚成本和配送成本,建立了以总成本最低为目标的协同调度模型,并构造了模拟退火算法进行求解。关静等[5]针对钢铁企业中工件的生产与生产前运输的协同调度问题,考虑具有温降属性的工件在等待加工时会使处理时间延长等因素,建立了以最小化最大完工时间为目标的单机多车流水生产的调度模型,并证明了该问题属于强NP难问题。马文琼等[6]分析了多段装配流水车间工件加工和成品配送的协同调度特征,将产品的加工次序和配送批次作为决策变量,建立了以产品交付时间和运输费用整体最优为目标的调度模型,并提出了一种基于遗传算法和反向变邻域搜索的混合智能优化算法进行求解。刘玲[7]针对单机多车且未给定订单生产完成时间的协同调度问题,建立了以最小化最晚订单交付时间为目标的生产与配送协同调度模型,提出了一种混合禁忌搜索算法进行求解。卓雪雪[8]研究了并行批处理机环境下的协同调度问题,将该问题模型划分为组成批次阶段与各批次调度阶段,大型实例仿真表明在解决该类问题时,融合了下界算法的改进型最大最小蚁群算法(min max ant system,MMAS)的整体性能优于混合蚁群优化(hybrid ant colony optimization,HACO)算法。
当前,国内外学者对协同调度问题的研究更多地是将前工序的生产调度与物料配送相结合,单纯把后工序当作配送需求点而不考虑其加工特性,忽视了前工序、物料配送、后工序三者之间的关联调度。按需生产的拉式生产系统中,各订单的生产需求指令是由后工序发送到前工序的,后工序如何与前工序以及中间配送环节进行协同调度显得十分重要。本文研究了一种同时考虑配送车辆容量和数量限制且存在在制品缓存区的跨工序协同调度问题,假定前工序为单机批加工,后工序为多产线逐订单加工,各订单不可拆分且与后工序产线的对应关系已知。当前加工工序的一个订单加工批量小于批加工工序产能时,将多订单组合为一个批次进行加工。订单在前加工工序加工完成后,AGV就位装车,然后根据所设计的配送顺序配送到多个位置的后工序产线,订单在后工序各产线依照先进先出原则排队逐个进行加工。生产周期和产线前的缓冲队列等待时间对生产系统效率的影响很大,为此将调度目标定为整体最小化最大订单完工时间及各订单在产线队列缓冲时间。该类问题属于NP难问题,为此设计了一种融合模拟退火算法及解串算法的混合离散蝙蝠算法。
1 问题描述与模型建立
以往研究所建立的模型更多地是将后工序看作单纯的配送点,忽略了后工序的生产可能影响前工序的调度及工序间物料配送,造成实际应用中的在制品大量堆积,显著延长了产品的生产周期。本文研究的跨工序生产与配送协同调度问题的最主要特征是考虑了后工序的加工特性。如图1所示,跨工序协同调度模型可分为单机批加工工序(前加工工序)、工序间物料配送、多产线逐订单加工工序(后加工工序)3个阶段。

图1 跨工序协同调度模型
Fig.1 Cross process collaborative scheduling model
首先,后工序各产线发出多个订单需求至前工序,并确定加工批次与加工顺序。同批次内的订单同时开始加工,加工时间取决于该批次内加工时间最长的订单。一批订单在前工序加工完成后,若AGV已就位则可依次装车,否则需要等待。AGV的数量和容量有限,当AGV装载的在制品达到其最大容量时开始配送,并根据算法设计的顺序配送到后工序所需产线。当该运输批次所有配送任务完成后,返回到前工序等待下一次配送。后工序各产线依照订单需求进行加工,且加工时间为固定值。当在制品到达后工序时,若该产线处于忙碌状态,则需排队等待加工,加工完毕后,该订单整个加工流程结束。
本模型调度的目标是同时最小化最大订单完工时间与各订单在产线队列的缓冲时间。
假定:初始状态下,前工序、AGV以及各产线皆为闲置。 A条产线发出的n(A>n)个订单需求分别为J1、J2、…、Jn,订单与产线所属关系已知,各订单容量分别为W1、W2、…、Wn。前工序的单批次加工时间Rx为该批次加工时间最长的订单时间,x为批次号,前工序最大加工批量为Q。零件经过前工序后,可能的装车等待运输时间分别为D1、D2、…、Dn,而后经m辆AGV采用循环方式运输至后工序指定的产线进行加工。后工序产线前可能存在的队列缓冲时间为E1、E2、…、En,对应的产线加工时间分别为T1、T2、…、TA。每台AGV装载容量均为Z。设产线a到产线p的运输时间为tap(a,p∈[0, A]),往返时间相同即tap=tpa,taa=tpp=0,前工序至产线a的运输时间为t0a。订单在加工和运输过程中不可中断。队列缓存策略为先进先出(FIFO)。最后一个订单加工完成的时间记为Cmax,目标是最小化Cmax以及各订单在产线前的队列等待时间之和![]() 跨工序的协同调度模型如下。
跨工序的协同调度模型如下。
目标函数即最小化的最大完工时间及各订单在产线前队列等待时间之和为
(1)
式中,w1、w2分别为目标函数中最小化最大完工时间Cmax及各订单在产线前等待时间之和![]() 的权重;Cj为订单j的完工时间。
的权重;Cj为订单j的完工时间。
模型的约束如下:
(1)在批加工工序生产一批产品的时间取决于该批次加工时间最长的订单,即
(2)
式中,pj为订单j在批加工工序的加工时间;ejx为0-1变量,当订单j分配到第x加工批次进行加工时为1,其余为0。
(2)某订单的运输装载装车时间等于它的批加工工序结束时间与等待AGV到达时间之和,即
(3)
式中,qj为订单j的AGV装车时间,j=1,2,…,n;L为订单j所分到的加工订单批次;RL为订单j的批加工时间。
(3)各订单只能分配给一个批加工批次,即
(4)
(4)批加工工序的加工能力限制为
(5)
(5)批加工工序包含的订单数量之和等于总订单数,即
(6)
(6)批加工工序的加工开始时间等于上一批加工完工时间,即
hx=hx-1+Rx-1
(7)
式中,hx为前工序第x批次订单加工开始时间,h0=0。
(7)每个订单只能分配给一个运输批次,即
(8)
式中,rjk为0-1变量,当订单j分配到运输批次k进行运输时为1,其余为0。
(8)所有运输批次包含的订单数量之和等于订单总数,即
(9)
(9)运输批次k的开始时间为所属该运输批次订单的最晚装车时间与所属该运输批次AGV到达初始位置时间的较大值,即
(10)
式中,ak为运输第k批订单的开始时间,k=1,2,…,K;K为最大运输批次;δml为第m辆AGV输送次序为l的运输批次;zkm为0-1变量,当第k运输批次由第m(m=1,2,…,M)辆AGV运输时为1,其余为0;M为AGV数量;bk为第k运输批次运输完毕后返回到批加工车间准备下一轮运输的时间;lkm为第k批次在第m辆AGV上的输送次序。
(10)每个运输批次只能分配给1辆AGV,即
(11)
(11)所有AGV运输的批次之和为
(12)
(12)运输批次应满足其AGV装载容量限制,即
(13)
(13)各并行产线以订单为生产单元,即
(14)
(15)
式中,uaj为0-1变量,当订单j是由产线a提出需求时为1,否则为![]() 为0-1变量,当产线a上订单i先于订单j加工为1,否则为0; PN为极大数。
为0-1变量,当产线a上订单i先于订单j加工为1,否则为0; PN为极大数。
(14)每个订单到达该订单所属产线的时间为
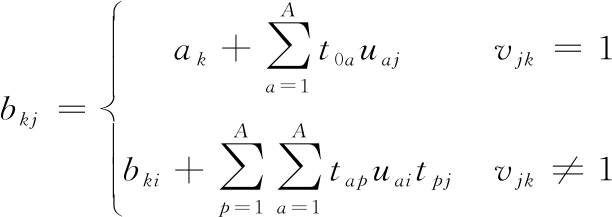
(16)
式中,bkj为第k运输批次中订单j的达到指定产线的时间;vjk为在第k运输批次中,订单j的运输序号,vik=vjk-1。
(15)某一订单的最终加工完成时间为
(17)
(16)某一运输批次完成运输返回到批加工工序的时间为
(18)
式中,gk,ap为0-1变量,当任意运输批次k经过产线a至产线p之间时为1,否则为0。
2 算法设计
蝙蝠算法作为一种新型的启发式算法,在继承和声算法、粒子群算法优点的同时,利用回声定位原理能同时搜索待优化解空间中的多个区域,通过频率调谐原理实现动态控制全局搜索与局部搜索的动态转换,从而获得比其他算法更好的收敛性。但蝙蝠算法只能解决连续域寻优问题[9],而本文所研究的协同调度问题属于离散排列组合问题,因此需要在传统蝙蝠算法的基础上进行离散化。此外,为了避免蝙蝠算法后期收敛速度慢、易陷入局部最优等缺点,该算法融合了变温度的模拟退火算法来提高其全局搜索能力和后期收敛效率。解串算法在解决路径规划问题时具有结构简单、计算效率高、便于实现等特点,所以本文将解串算法嵌套在蝙蝠算法来解决跨工序协同调度问题。
2.1 编码方式
混合离散蝙蝠算法求解跨工序协同调度问题时,首先要考虑编码问题,由于研究的问题包括生产调度和物料配送,因此采用单层整数编码方式。编码长度为n,各订单的编码位代表该订单在批加工工序的生产顺序,编码形式表示为
A=(m1,m2,…,mn)
(19)
式中,mi(i=1,2,…,n)为批加工工序生产排序为i的订单。
加工批次及运输批次划分需在满足批加工批量和运输批量要求的基础上进行划分。如图2所示,9个订单的订单容量分别为2、3、4、3、1、3、2、3、1,批加工工序加工批量为6,AGV的运输批量为4,假定一个工序编码A=(2,5,3,7,4,6,8,1,9)。按照生产序列以及加工批量限制,将J2、J5分配到加工批次1,J3、J7分配到加工批次2,J4、J6分配到加工批次3,J1、J8、J9分配到加工批次4。根据AGV运输批量限制,将J2、J5分配到运输批次1,J3分配到运输批次2,J7分配到运输批次3,J4分配到运输批次4,J6分配到运输批次5,J8分配到运输批次6,J1、J9分配到运输批次7。

图2 编码方式
Fig.2 Coding mode
2.2 混合离散蝙蝠算法设计
针对标准的蝙蝠算法易陷入局部最优,后期收敛速度慢等缺点,本文设计了一种混合离散蝙蝠算法(hybrid discrete bat algorithm,HDBA)来解决跨工序协同调度问题。
标准蝙蝠算法中,每只虚拟蝙蝠在n维(研究问题的维数)搜索空间主要通过位置矢量和速度矢量进行表达。搜索过程中,蝙蝠个体在迭代过程中经过位置矢量和速度矢量的更新后会逐渐逼近最优解。第t代蝙蝠个体i的速度矢量和位置矢量表达式为
vi,t=vi,t-1+(Xi,t-X*)
(20)
Xi,t=Xi,t-1+vi,t
(21)
fi=fmin+β(fmax-fmin)
(22)
式中,fi表示频率属性,蝙蝠个体的频率在[fmin, fmax]随机选择;fmax、fmin分别为脉冲频率的上下限;β为0~1之间的随机变量;X*为当前全局最佳位置。
假定协同调度问题的解决方案有n维,那么第i个蝙蝠的n维位置矢量Xi=(Xi1,Xi2,…,Xin)。矢量vi,t=(v1,t, v2,t, …, vk,t)可以看作k维方向矢量,全局最优解![]() 标准位置矢量和速度矢量公式可更新为
标准位置矢量和速度矢量公式可更新为
vi,t=φ(Xi,t-1,X*,fi,Mi,t)
(23)
Xi,t=ω(Xi,t-1, vi,t)
(24)
fi是一个大小位于fmin与fmax之间的随机整数,它代表了子代从父代X*和Xi,t-1复制单位的大小,将式(22)更新为
fi=μ(fmax, fmin)
(25)
变量Mi,t是介于1与Xi,t-1和X*的汉明距离的随机整数,Mi,0=0。向上圆整函数RUP(Mi,t/fi)为返回一系列排列vi,t的个数k。

图3 速度矢量更新
Fig.3 Speed vector update
式(23)包含参数 Xi,t-1、X*、fi、Mi,t,速度矢量如图3所示,首先左至右扫描父代的染色体,如果某一位基因在所有父代中的基因位相同,则将该基因复制到子代的同一位置。然后,未被安排的基因以fi为编组单元大小,从任意父代基因位进行交叉操作,将改组基因拷贝到子代相应基因位上(如果父代出现重复基因,则从任意父代未出现的基因上随机选择一个基因并将该基因复制到子代相同基因位上)。最后,子代染色体vi,t从左至右依照编组单元大小进行划分(vi,t存在最后一部分基因分组数量小于频率fi情况),根据Mi,t得到vi,t。图2示例的最终输出结果vi,t=(3,4,5,7,9,2,1,8)。
式(24)包含2个参数,蝙蝠i新的位置矢量为Xi,t,父代Xi,t根据式(23)所得的一系列组合vi,t进行对应基因位的交叉,具体流程如图4所示。fi≥3时,按照vi,t的编组大小,对Xi,t进行组内基因位随机交换。多次交换后,得到蝙蝠i在迭代t次后的位置矢量Xi,t。

图4 位置矢量更新
Fig.4 Position vector update
蝙蝠算法在进行个体局部搜索时,它的新解决方案会在当前最优解的随机游走过程中就近产生:
Xnew=Xold+εAt
(26)
式中,ε是-1~1之间的随机变异因子;At为所有蝙蝠在t代的平均响度,At=<Ai,t>;Ai,t为蝙蝠i在第t次迭代时的脉冲响度;Xold为局部搜索前的当前最优解;Xnew为局部搜索后产生的解。
如式(26)所示,传统蝙蝠算法邻域搜索中,ε和At作为一维连续变量并不适用于解决离散问题,为了解决离散问题同时提高局部搜索能力,则可更新局部搜索产生的解Xmid为
(27)
式中,Xe为当前最优解;RUP(·)表示向上圆整函数;RDOWN(·)表示向下圆整函数。
εAt≥0时,InsertionFun(Xe,|RUP(εAt)|)表示对Xe进行|RUP(εAt)|次随机基因插入操作。若Xe=(10, 5, 3, 7, 1, 9, 4, 2, 8, 6),|RUP(εAt)|=2,则对Xe进行2次随机基因插入操作。2次随机插入操作后更新的解为
Xe,Ⅰ=(10,5,7,1,9,3,4,2,8,6)
Xmid=Xe,Ⅱ=(10,5,7,1,3,4,2,8,9,6)
εAt<0时,ExchangeFun(Xe,|RUP(εAt)|)表示对Xe进行|RDOWN(εAt)|次随机基因交换操作。若Xe=(10,5,3,7,1,9,4,2,8,6),|RDOWN(εAt)|=2,则对Xe进行2次随机基因交换操作。2次随机交换操作后更新的解为
Xe,Ⅰ=(10,5,7,2,9,3,4,1,8,6)
Xmid=Xe,Ⅱ=(10,2,7,5,9,3,4,1,8,6)
经过局部搜索得到Xmid后,为提高精英群体的质量,采用变温度的模拟退火算法对Xmid进行退火操作。若Xmid优于Xe则保留新解,否则以概率exp(-Δθ′/θ)接受新解,其中,θ为当前退火温度,Δθ′为Xe与Xmid适应度函数的差值。本算法通过初始温度θ0、终止温度θend、退温系数λ来控制算法进程。该局部搜索方法提高了局部搜索能力,但也增加了时间计算成本,因此采用变温度的模拟退火算法以缩短计算时间,当前温度为
θ=RDOWN(θ0(1-t/(T+1)))
(28)
采用变温度的模拟退火算法,前期可提高算法的全局搜索能力,后期可加快算法的收敛,从而在总体上提高该算法的计算效率。
混合离散蝙蝠算法中,响度Ai,t和脉冲率ri,t同传统蝙蝠算法一样也要随着迭代过程进行更新:
Ai,t=αAi,t-1
(29)
ri,t=ri,0(1-e-γt)
(30)
其中,γ为脉冲频度的增加系数;α为一个恒量,对于任何0<α<1都有
(31)
ri,t直接影响个体执行局部搜索的概率,Ai,t决定局部搜索中解的偏移程度,初始时刻个体的响度较大,脉冲率较小;随着迭代的不断推进,响度不断减小,脉冲率不断增大,从而使算法结果逐渐最优化。
HDBA算法的伪代码如下:
Begin
1.初始化。设置迭代次数t=1;初始化蝙蝠种群的位置Xi、速度vi、频率fi、响度A、α、γ、初始温度θ0、终止温度θend、退温系数λ;
2.计算初始解fitness(X)=1/f(X)
3.while t 排列蝙蝠并找到最佳X*; for i=1:N(所有节点数) fi=μ(fmax, fmin); vi,t=φ(Xi,t-1,X*,fi,Mi,t); Xi,t=ω(Xi,t-1, vi,t); if(rand>r) then if(fitness(Xmid)>fitness(Xe)||rand< exp(-Δθ′/θ)) then Xe=Xmid; End if End if if(rand<A&&fitness(Xmid) then X*=Xe; fitness(Xmid)=f(Xe); Ai,t=αAi,t-1; ri,t=ri,0(1-e-γt); End if t=t+1; End for End while 可视化结果 End 协同调度问题中,每个运输批次内的配送顺序问题都可以看作是一个是车辆路径规划问题,可采用LI等[10]针对库存-路径问题所修改的MUS算法求解,具体的伪代码如下: Begin 初始化。设置迭代次数t=1,配送路径中目标点的数目为M,Li为配送路径中的任意一个需求点; While(t≤最大迭代次数) do i=0; While(i< M) do Li+1为运输路径中需求点Li的下一个物料需求点,找出Li+1周边u个相邻点,并从中随机选择一个目标点作为Lj; Li-1是运输路径中需求点Li的上一个物料需求点,找出Li-1周边u个相邻点,并从中随机选择一个目标点作为Lk; 如图5所示,从当前的配送路线中删除物料需求点Li;删除Li后,在重新生成的路径中找出距离目标点Li最近的2个点Lp和Lq; 点Lp+1表示运输路径中需求点Lp的下一个物料需求点,找出Lp+1周边m个相邻点,并从中随机选择一个目标点作为Lz; 如图6所示,将点Li重新插入到当前路径中; i=i+1 计算AGV到达各产线上料点时间bkj; End while t=t+1 End while 图5 点的移除操作 图6 点的插入操作 图7为基于HDBA+MUS算法的实现流程图。 图7 基于HDBA+MUS算法流程图 拟采用仿真实验来验证混合离散蝙蝠算法的有效性。实验对象选取某锅具生产企业自动化生产车间。该车间生产加工主要由两部分组成:辊淋涂批加工工序主要用于对原材料铝片表面上色;多条拉伸成形产线主要用于将铝片拉伸成锅。原材料在经过辊淋涂工序后由AGV送到各成形段需求产线进行加工。本仿真所研究的目的是求得其最优协同调度方案,从而使该生产系统具有较高的生产效率。仿真平台为MATLAB7.11.0。各项基本数据如下:产线A~F的订单数量分别为4、4、5、5、4、5;各订单大小在1、2、3中随机出现,在辊淋涂段加工时间在[0.1 h,0.6 h]区间内随机出现;辊淋涂段加工最大批量为10;产线A~F的加工时间分别为0.15 h、0.2 h、0.1 h、0.15 h、0.05 h、0.1 h;AGV数量为3;每台AGV最大运输批量为7。AGV在各产线间行驶时间如表1所示。 表1 AGV各产线行驶时间 Tab.1 AGV running time of each production line h 辊淋涂段产线A产线B产线C产线D产线E产线F辊淋涂段00.100.130.180.180.210.17产线A0.1000.050.070.080.120.10产线B0.130.0500.050.090.100.10产线C0.180.070.0500.020.100.10产线D0.180.080.090.0200.050.05产线E0.210.120.100.100.0500.07产线F0.170.100.100.100.050.070 为证明HDBA+MUS算法的有效性,选取解决协同调度问题中具有代表性的离散粒子群算法(MBPSO)算法[11]与Ullrich-GA算法[12]进行比较,迭代次数均为200,种群规模均为50。为了简化计算,通过蝙蝠算法求解调度问题时,多将fmax、fmin设置在0~3之间[13],为了增加种群多样性,避免过早收敛设置fmax=3,fmin=0,α=γ=0.9[14-15];采用求解车间内部调度问题的模拟退火操作中的参数值θ0=10,θend=0.1,λ=0.9。由于缩短订单的生产周期对协同调度问题来说至关重要,因此文献[16]均将其作为目标函数。针对后工序具有加工特性的协同调度模型的首要目标是尽量缩短后工序队列等待时间[17],考虑到最小化最大完工时间及各订单在产线前的队列等待时间对本文所研究的问题均十分重要,且具有相同量纲,设置目标函数权重w1=w2=1。 编码初始化采用随机全排列。为了对HDBA+MUS算法的收敛性进行分析,在经过200次迭代后得到HDBA+MUS、MBPSO、Ullrich-GA的仿真收敛曲线,见图8。 图8 仿真收敛曲线 从收敛曲线可以看出,HDBA+MUS的收敛能力要强于MBPSO与Ullrich-GA。这是因为MBPSO只选择适应度前20%的粒子进行随机两两交叉,同时其基于适应度变化的变异操作对平均适应度要求较高,一旦平均适应度偏差较大就会造成一部分较好的值跳不出局部最优。Ullrich-GA在解决跨工序协同调度问题时,只单纯地对生产调度与车辆路径规划进行随机编码而没有考虑两者之间的联系,可能导致每辆AGV配送开始时间较晚,进而延迟了订单的完工。HDBA+MUS在继承蝙蝠算法优秀的局部搜索能力的同时,通过与模拟退火操作相结合极大地提高了全局搜索能力,它在对染色体进行编码与解码时协同考虑了生产调度与车辆路径规划的关系,提高了可行解的适应度。 表2给出了混合离散蝙蝠算法所生成的具体最优生产配送调度方案。T、T′分别为此次配送的开始时间与返回到批加工工序的时间,V为所用AGV编号,C1为各个订单在批加工工序完工时间,C2为各个订单的到达各产线时间,C3为各个订单的成形段加工完工时间,可由整体配送顺序方案得到批加工工序生产顺序,Ωβ,γ表示产线Ω生产的第β个订单位于批加工工序批次γ中,Ω=A,B,…,F。C1[F1,1]表示产线F所安排生产的第1个订单在批加工工序所处批次1的完工时间,箭头连接表示这个配送批次里各订单的配送顺序,如F1,1→D1,1→E1,1→C1,1所示,C2[F1,1]表示该订单配送到产线F的时间,C3[F1,1]表示该订单在产线F加工完成的时间。 表2 最优生产配送调度方案 Tab.2 Optimal production and distribution scheduling scheme 批次1T=0.1;T'=0.65;V=1F1,1→D1,1→E1,1→C1,1C1[F1,1]=C1[D1,1]=C1[E1,1]=C1[C1,1]=0.1;C2[F1,1]=0.27;C2[D1,1]=0.32;C2[E1,1]=0.37;C2[C1,1]=C3[F1,1]=0.47;C3[D1,1]=0.62;C3[E1,1]=0.42;C3[C1,1]=0.67批次2T=0.3;T'=0.83;V=2F2,1→A1,1→D2,2C1[F2,1]=C1[A1,1]=0.1;C1[D2,2]=0.3;C2[F2,1]=0.47;C2[A1,1]=C3[F2,1]=0.57;C2[D2,2]=0.65;C3[A1,1]=0.87;C3[D2,2]=1.1批次3T=0.3;T'=0.7;V=3B1,2→F3,2C1[B1,2]=C1[F3,2]=0.3;C2[B1,2]=0.43;C2[F2,3]=0.53;C3[B1,2]=1.03;C3[F2,3]=0.87批次4T=0.7;T'=1.35;V=1C2,3→E2,3→B2,3→D3,3C1[C2,3]=C1[E2,3]=C1[B2,3]=C1[D3,3]=0.7;C2[C2,3]=0.88;C2[E2,3]=0.98;C2[B2,3]=C3[C2,3]=C3[E2,3]=1.08;C2[D3,3]=1.17;C3[B2,3]=1.18;C3[D3,3]=1.47批次5T=1.2;T'=1.81;V=2F4,3→C3,3→D4,3→B3,4→C4,4C1[F4,3]=C1[C3,3]=C1[D4,3]=0.7;C1[B3,4]=C1[C4,4]=1.2;C2[F4,3]=1.37;C2[C3,3]=C3[F4,3]=1.47;C2[D4,3]=1.49;C2[B3,4]=1.58;C2[C4,4]=1.63;C3[C3,3]=1.57;C3[D4,3]=1.64;C3[B3,4]=2.18;C3[C4,4]=1.73批次6T=1.2;T'=1.69;V=3A4,2→E4,3→F5,4→A3,4C1[A4,2]=C1[E4,3]=C1[F5,4]=C1[A3,4]=1.2;C2[A4,2]=1.3;C2[E4,3]=1.42;C2[F5,4]=1.49;C2[A3,4]=1.59;C3[A4,2]=1.6;C3[E4,3]=1.47;C3[F5,4]=1.69;C3[A3,4]=1.75批次7T=1.8;T'=2.44;V=1C5,5→D5,5→A4,5→B4,5→E4,5C1[C5,5]=C1[D5,5]=C1[A4,5]=C1[B4,5]=C1[E4,5]=1.8;C2[C5,5]=1.98;C2[D5,5]=2;C2[A4,5]=2.08;C2[E4,5]=2.23;C3[C5,5]=2.18;C3[D5,5]=2.15;C3[A4,5]=2.23;C3[E4,5]=2.38;C3[E4,5]=2.33目标函数min(maxCjj∈[1,n])=2.38;min∑ni=1Ei=0.1;w1min(maxCjj∈[1,n])+w2min∑ni=1Ei=2.48 (1)建立了考虑后工序加工特性的跨工序生产与配送协同调度模型。该模型以最小化最大完工时间和产线前等待时间为目标,假设前工序采用批加工,后工序多产线并行加工,两工序之间通过有限运输能力的AGV配送,且产线前存在队列缓冲时间。 (2)设计了混合离散蝙蝠算法。该算法在继承标准蝙蝠算法的基础上针对离散问题进行了改进,并与模拟退火算法相融合,提高了全局寻优能力和收敛效率,并嵌套MUS算法以解决车辆路径规划问题。与MBPSO算法及Ullrich-GA算法相比,本文算法极大缩短了产品的生产周期和生产系统中的队列等待时间。 在下一阶段,可以进一步考虑车间实际情况将产线负荷平整化,以及各工序扰动性等因素进行分析研究。 [1] MAGGU P L, DAS G. On 2×n Sequencing Problem with Transportation Times of Jobs[J]. Pure and Applied Mathematica, Science, 1980,129(12):1-6. [2] ARMENTANO V A, SHIGUEMOTO A L, LØKKETANGEN A. Tabu Search with Path Relinking for an Integrated Production-distribution Problem[J]. Computers & Operations Research, 2011,38(1):320-327. [3] 方伯芃, 孙林夫. 不确定环境下产业链生产与配送协同调度优化[J]. 计算机集成制造系统, 2018, 24(1):224-244. FANG Bopeng, SUN Linfu. Coordinated Scheduling Optimization of Production and Distribution of Industrial Chain under Uncertain Environment[J]. Computer Integrated Manufacturing System, 2018, 24(1): 224-244. [4] 李凯, 王明星. 单机多车情形生产与配送协同调度算法[J]. 计算机集成制造系统, 2014, 20(12):3011-3019. LI Kai, WANG Mingxing. Coordinated Scheduling Algorithm of Production and Distribution in the Case of Single Machine and Multi-vehicle[J]. Computer Integrated Manufacturing System, 2014, 20(12):3011-3019. [5] 关静, 唐立新. 工件带有温降的生产与前运输协调调度问题[J]. 系统工程学报, 2007, 22(6):639-643. GUAN Jing, TANG Lixin. Inbound Transportation and Production Coordinated Scheduling Problem with Temperature Reduction Jobs[J]. Journal of Systems & Management, 2007, 22(6):639-643. [6] 马文琼, 王凯. 两阶段装配流水车间加工与配送协同调度研究[J]. 工业工程与管理, 2016, 21(6):103-117. MA Wenqiong, WANG Kai. Coordinated Scheduling Problem for Two-stage Assembly Flowshop Production and Distribution[J]. Industrial Engineering and Management, 2016, 21(6):103-117. [7] 刘玲. 单机器生产与车辆路径协同调度问题建模与算法研究[D]. 武汉:华中科技大学, 2016. LIU Ling. Model and Algorithms for the Integrated Single Machine Scheduling and Vehicle Routing Problem[D]. Wuhan: Huazhong University of Science and Technology, 2016. [8] 卓雪雪. 批处理机环境下两阶段集成调度算法研究[D]. 合肥:安徽大学,2018. ZHUO Xuexue. Research on Batch Scheduling Processing on Parallel Machines with Two-stage Integrated Scheduling[D]. Hefei: Anhui University, 2018. [9] YANG X S. A New Metaheuristic Bat-inspired Algorithm[M]//Nature Inspired Cooperative Strategies for Optimization (NICSO2010). Berlin:Springer, 2010:65-74. [10] LI K, CHEN B, SIVAKUMAR A I, et al. An Inventory-routing Problem with the Objective of Travel Time Minimization[J]. European Journal of Operational Research, 2014, 236(3):936-945. [11] 薛梅, 周志平. 批处理机环境下生产与两阶段运输协同调度问题研究[J]. 中国管理科学, 2016, 24:22-28. XUE Mei, Zhou Zhiping. Coordinated Scheduling Problem of Production and Two-stage Transportation with a Batch-processing Machine[J]. Chinese Journal of Management Science, 2016, 24:22-28. [12] ULLRICH C A. Integrated Machine Scheduling and Vehicle Routing with Time Windows[J]. European Journal of Operational Research, 2013, 227(1): 152-165. [13] 尹建津, 张贝克. 改进蝙蝠算法解决FFSP问题及其应用研究[J]. 计算机工程应用, 2019, 55(9):243-247. YIN Jianjin, ZHANG Beike. Improved Bat Algorithm for Solving Flexible Flow Shop Scheduling Problem and Its Application[J]. Computer Engineering and Applications, 2019, 55(9):243-247. [14] 徐华, 张庭. 混合离散蝙蝠算法求解多目标柔性作业车间调度[J]. 机械工程学报, 2016,52(18):201-212. XU Hua, ZHANG Ting. Hybrid Discrete Bat Algorithm for Solving the Multi-objective Flexible JobShop Scheduling Problem[J]. Journal of Mechanical Engineering, 2016,52(18):201-212. [15] 韩忠华, 朱伯秋. 基于改进蝙蝠算法的柔性流水车间排产优化问题研究[J]. 计算机应用研究, 2017, 34(7): 1935-1938. HAN Zhonghua, ZHU Boqiu. Study for Flexible Flow Shop Scheduling Problem Based on Advanced Bat Algorithm[J]. Application Research of Computer, 2017, 34(7): 1935-1938. [16] 刘玲, 李昆鹏. 生产和运输协同调度问题的模型和算法[J]. 工业工程与管理, 2016,21(2):86-91. LIU Ling, Li Kunpeng. Model and Algorithms for the Integrated Production and Transportation Scheduling[J]. Industrial Engineering and Managemen, 2016, 21(2): 86-91. [17] 李修琳, 鲁建厦. 基于混合遗传算法的混流混合车间协同调度问题[J]. 中国机械工程, 2012, 23(8):935-940. LI Xiulin, LU Jiansha. Hybrid Genetic Algorithm for Mixed-model Hybrid-shop Scheduling Problem[J]. China Mechanical Engineering, 2012, 23(8):935-940.![]()
2.3 MUS算法

Fig.5 Point remove operation
Fig.6 Point insertion operation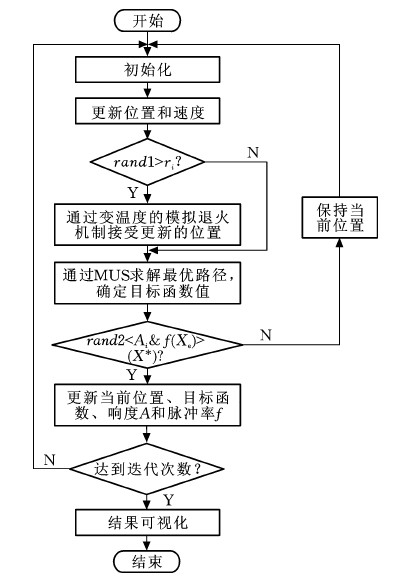
Fig.7 Flow chart of algorithm based on HDBA+MUS3 仿真研究
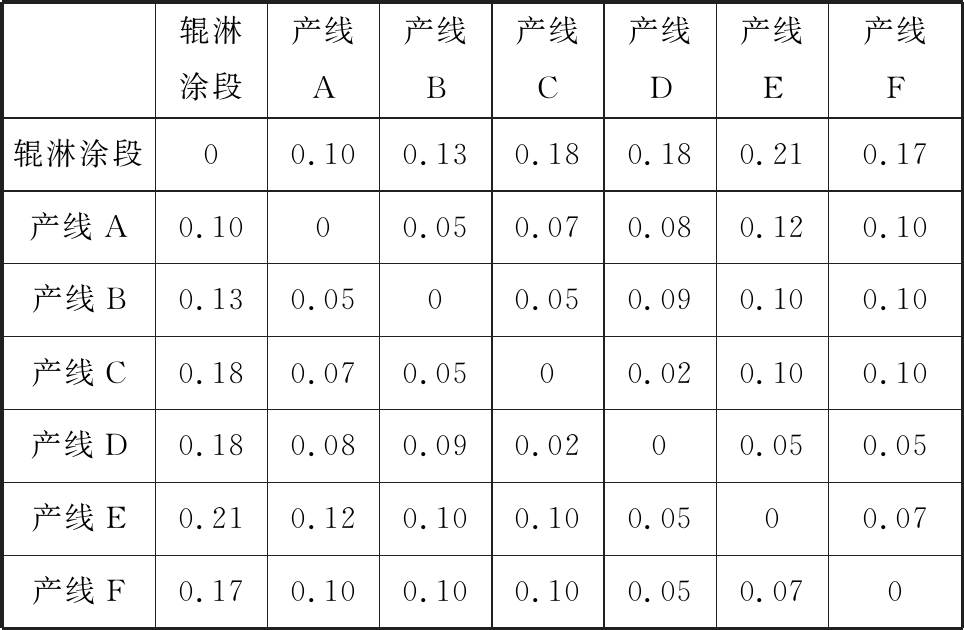

Fig.8 Simulation convergence curve
4 结论
