0 引言
2018年中国新车质量研究报告[1]显示,自主品牌新车质量问题数是120个PP100(每100台车辆的问题点数)。汽车质量问题仍是阻碍我国汽车行业发展的重要因素,点焊缺陷就是严重的质量问题之一。车身金属板之间的主要连接形式是点焊,普通小汽车一般具有3 000~5 000个焊点,车身结构的可靠性和乘员的安全性很大程度上依赖于可靠的焊接质量。然而,商业背景下的最优焊接参数和工业化生产下的最佳质量焊接参数并非一致,因此,设计焊点缺陷的疲劳寿命容限对寻求焊接成本与焊接质量之间的平衡点具有重要意义。
近年来,国内外学者针对焊点质量和缺陷对疲劳寿命的影响进行了大量研究,并取得了较好的成果。KHATIB等[2]通过建模计算焊接缺陷对焊缝疲劳强度的影响,提出基于容积法来预测疲劳寿命;CHAPETTI等[3]提出了一种基于应力强度因子的方法来估算焊缝疲劳寿命及评估缺陷严重性。以上研究主要针对焊接缺陷对焊缝疲劳寿命的影响,而对焊点缺陷的研究较少。KEPKA等[4]通过获取空-满载下的关键横截面的应力-时间关系,使用疲劳寿命分布函数作为参数基础,在设计阶段预测客车关键焊接结构的使用寿命。LEINENBACH等[5]通过试验分析与理论调查对比了钎焊有无缺陷的疲劳寿命评估,结果表明随着缺陷的增大疲劳强度降低,但缺乏不同缺陷S-N曲线的直接比较。
本文提出了一种基于超声回波的车身焊点缺陷的疲劳寿命预测评价方法。
1 超声检测技术
1.1 超声波检测原理
超声波检测为焊点质量在线检测和缺陷类型识别提供了可能。采用一定的方式使超声波进入点焊试件,超声波在点焊试件中传播并与试件材料以及其中的缺陷相互作用,导致其传播方向、声波大小或特征被改变;改变后的超声波通过检测设备被接收,并对其进行处理和分析;最后根据接收的超声波特征,评估试件本身及内部是否存在缺陷及缺陷类别。
超声波在介质中传播时会导致能量衰减,通过测量出的传播时间、信号幅值及其衰减程度就可评定工件中缺陷的严重程度,其工作原理如图1所示。

1.焊核区 2.上母材 3.下母材 4.耦合剂
5.软性薄膜 6.水柱 7.压电晶片
图1 超声波检测原理图
Fig.1 Ultrasonic testing schematic
1.2 判定焊点缺陷质量类别
近年来汽车企业多采用超声波无损检测来确保点焊质量,通过声波反射信号所提取的特征值来判别焊点缺陷类型及严重程度。为了获得不同缺陷类型,通过人为改变焊接参数来制造焊点缺陷,并且利用GE超声波检测设备对这些点焊接头进行检测,获得不同缺陷的回波波形,进而对相应特征值进行分析。其中,超声波检测仪评判点焊缺陷的相关性能参数见表1。
表1 超声波检测仪相关性能参数
Tab.1 Related performance parameters of ultrasonic detector

评判阈值探头数据底面回波(%)10型号G20MN4.5X缺陷回波(%)15数量编号67884-7480气孔阈值(%)15直径 (mm)4.5气孔回波宽度(%)0频率(MHz)20
焊点缺陷类型有漏焊、烧穿、焊核过小、气孔、裂纹、熔深过薄和粘焊等[6]。漏焊会降低接头的疲劳寿命,必须补焊;当气孔截面减小10%时,疲劳强度下降50%;出现在焊点圆周的裂纹不可接受,出现在焊点表面的较小裂纹可接受;熔深过薄和粘焊在生产中出现机会较少,烧穿和焊核过小是焊接中最常出现的缺陷,所以本文主要考虑烧穿和焊核过小的焊点缺陷,图2为焊点缺陷及对应波形。
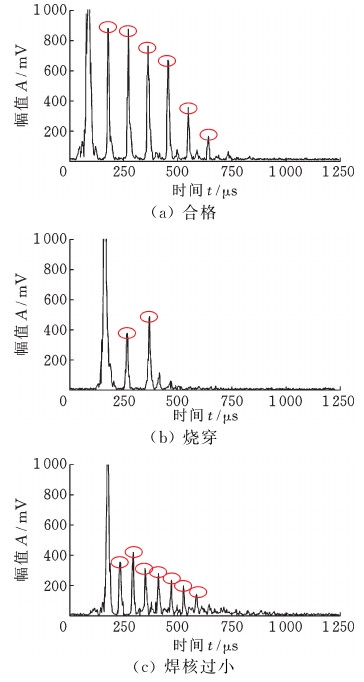
图2 主要焊点缺陷与波形
Fig.2 Spot welding defects and waveforms
在焊点质量检测中,由于焊点缺陷种类繁多,导致焊点质量识别比较困难,文献[7]建立了一种基于超声信号参数化和判别熵模型的汽车焊点质量智能识别方法。表2所示为焊点质量超声评价数据,根据焊点质量判定规则,提取超声回波的6个特征值来确定焊点的质量。6个特征分别是指底面回波波峰间隔S、回波幅值衰减率λ、底面回波个数N1、中间回波个数N2、回波序列中心频率f和回波序列总能量E。
表2 1.4 mm-1.4 mm两层板焊点特征值范围
Tab.2 Characteristic value range of spot welding for 1.4 mm-1.4 mm two-layer plate
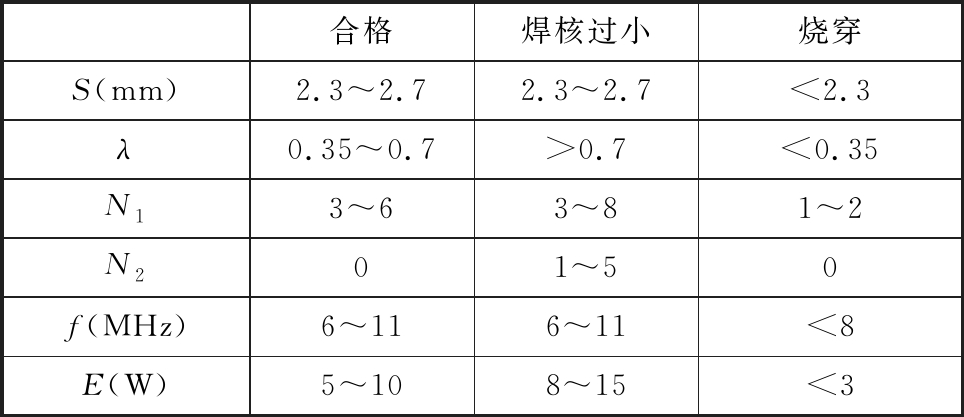
合格焊核过小烧穿S(mm)2.3~2.72.3~2.7<2.3λ0.35~0.7>0.7<0.35N13~63~81~2N201~50f(MHz)6~116~11<8E(W)5~108~15<3
1.3 损伤系数的推导
初始缺陷的点焊接头在裂纹萌生位置的应力特征可综合成为一个与底面回波波峰间隔S、回波幅值衰减率λ、底面回波个数N1、中间回波个数N2、回波序列中心频率f和回波序列总能量E等相关的损伤参数ζ,ζ可作为损伤修正系数。
由1.2节所述,通过超声无损检测求得回波的各个特征值,确立评定焊点质量类别的特征值集U:
U={S,λ,N1,N2,f,E}
(1)
然后建立各个特征值集U的权重影响因子ai的向量A:
A=(a1,a2,a3,a4,a5,a6)
(2)
各特征的影响权重可由频数统计法确定。同时根据表2建立相应特征值的评判范围矩阵R:

(3)
其次经模糊变换[8]得到影响焊点疲劳寿命的综合评价集B:
B=AR
(4)
最后将质量类别的评价集B与合格焊点的评价集B进行对比,计算不同缺陷的损伤系数ζ。
2 平均应力强度因子的修正
本文提出的基于超声回波的焊点缺陷对焊接疲劳寿命的影响研究流程见图3,图中K为应力强度因子,![]() 为修正平均等效应力强度因子。
为修正平均等效应力强度因子。
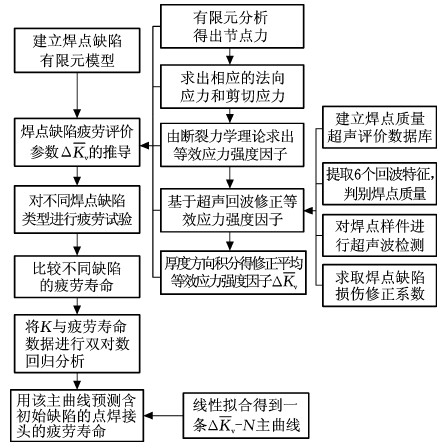
图3 焊点缺陷疲劳寿命预测方法流程图
Fig.3 Flow chart of fatigue life prediction for spot welding defect
2.1 焊点缺陷有限元模型
为准确模拟焊点位置、缺陷位置和提高计算准确率,本文在采用模块化焊点建模[9]的基础上,考虑焊点缺陷的存在,建立了包含初始缺陷的焊点疲劳仿真分析的模块化焊点模型,见图4。

图4 包含初始缺陷的模块化焊点有限元模型
Fig.4 Modular spot welding finite element model with initial defect
2.2 修正平均等效应力强度因子推导
基于线弹性断裂力学原理,对含初始缺陷的焊接接头进行应力分析,计算裂纹尖端的应力强度因子,可进而确定接头的疲劳寿命。
焊点周围各节点在整体坐标系(x,y,z)下可通过Abaqus软件直接计算输出,然后利用坐标转换成各个节点在局部坐标系(x′,y′,z′)下的节点力和力矩;最后根据做功相等原理求出各节点的线性力和力矩:
(5)
式中,f(x)、l(x)为l1上的线性力、位移分布;f(s)、l(s)为ln-1上的线性力、位移分布。
节点线性力矩也可由节点力矩通过相同的转换矩阵得到:
![]()

(6)
式中,F1,F2,…,Fn-1为节点的节点力;f1,f2,…,fn-1为节点的线性力;l1,l2,…,ln-1为焊点周围各节点间距。
基本的断裂模式有Ⅰ型、Ⅱ型和Ⅲ型,Ⅰ型断裂也叫张开型断裂,与法向应力有关;Ⅱ型和Ⅲ型断裂分别又叫滑移型断裂和撕裂型断裂,与剪切应力有关;Ⅰ型和Ⅱ型属于面内断裂,焊点疲劳是考虑法向力和剪切力的面内复合型断裂模式,因此,由上式所求的焊点周围各节点的线性力和力矩可以得到相应节点处的法向结构应力和剪切结构应力:
σm=fy′/t σb=6mx′/t2
(7)
τs=fx′/t+6my′/t2
(8)
式中,σm为膜应力成分;σb为弯应力成分;τs为剪切应力成分;t为母板厚度;fx′、fy′分别为局部坐标系下x′、y′的线性力;mx′、my′分别为局部坐标系下x′、y′的力矩。
根据BROEK[10]的研究,同时考虑法向应力和剪切应力的等效应力强度因子可由下式计算得到:
(9)
(10)
(11)
其中,β为与材料延展性相关的系数,对于低碳钢β可取2,高碳钢β可取3;ΔKⅠ为Ⅰ型应力强度因子,ΔKⅡ为Ⅱ型应力强度因子;ΔKm为膜应力强度因子;ΔKb为弯应力强度因子;d为某一时刻的裂纹长度,tr为疲劳断裂临界裂纹长度。fm(d/tr)为应力强度因子相对于膜应力的几何修正系数,fb(d/tr)为应力强度因子相对于弯应力的几何修正系数,fs(d/tr)为应力强度因子相对于剪切应力的几何修正系数,它们的具体表达式[11]如下:
(12)
(13)
(14)
A0=1.121 4 A1=-1.634 9 A2=7.316 8
A3=-18.774 6 A4=31.802 8 A5=-33.229 5
A6=19.128 6 A7=-4.609 B0=1.121 52
B1=-3.040 57 B2=10.491 84 B3=-36.667 8
B4=110.099 B5=-255.681 84 B6=421.971 67
B7=-440.508 66 B8=199.373 26 B9=123.930 56
B10=-237.971 64 B11=136.170 68
B12=-28.910 05 C0=0.166 4 C1=5.039 9
C2=-10.994 1 C3=9.252 4
一般情况下,汽车车身焊点直径远大于板厚,焊点的主要断裂方式是贯穿板厚度方向的断裂,因此假定裂纹扩展长度tr近似等于板厚t(即tr≈t),则可取整个裂纹扩展的平均等效应力强度因子为
(15)
式(15)是指不含初始缺陷的点焊接头的裂纹尖端的平均等效应力强度因子,而在计算实际焊点尖端的应力强度因子时,需考虑不同缺陷引起的损伤差异而采取必要的修正,因此,根据1.3节所求得的损伤系数ζ提出了一种基于超声回波特征的平均等效应力强度因子的修正法。将求得的修正平均等效应力强度因子![]() 作为带初始缺陷的焊点疲劳寿命的评价参量:
作为带初始缺陷的焊点疲劳寿命的评价参量:
ζ=f(S,λ,N1,N2,f,E)
(16)
(17)
(18)
3 疲劳试验及分析
3.1 材料、样品制备及超声波检测
本研究的焊接试样材料为双相钢材料DP600GI,点焊试样厚度为1.4 mm-1.4 mm,DP600GI材料的屈服强度为432 MPa,抗拉强度为671 MPa,伸长率为22%。为保证点焊接头的一致性,所有试样的几何尺寸需一致,焊点直径满足![]() 所以焊核直径统一为7 mm。
所以焊核直径统一为7 mm。
依据控制焊接参数和焊接条件,采用手工焊来制备含烧穿和焊核过小两种焊接缺陷及合格焊点的焊点试件(图5),用于疲劳试验的拉剪试件的几何尺寸见图6。

图5 焊点试件
Fig.5 Spot welding testpiece

图6 焊点试件几何尺寸
Fig.6 Piece geometryspot welding test
为调查焊接缺陷尺寸大小的影响,选取不同缺陷大小的烧穿试件,以 a为缺陷长度,c为缺陷宽度,直线型缺陷取a分别为0.5 mm、1 mm、2 mm,椭圆型缺陷在长宽比a/c=2/3的基础上,取a分别为0.75 mm、1.5 mm、3 mm。
利用超声无损检测设备采集这些焊点试件的超声波信号,提取每个焊点样件的超声信号S、λ、N1、N2、f、E这6个特征值,并求出损伤修正参数ζ,当焊点合格时,损伤修正系数ζ=1。
3.2 剪切拉伸试验
为确定试样的准静态力学性能,在电液伺服疲劳试验机上进行剪切疲劳试验,试验过程中采用正弦加载、恒定振幅,加载载荷比R=0.1,加载频率为10 Hz,考虑试件不能承受压载荷,因此对焊点试件施加循环拉载荷。试验时为保证外力通过焊点中心,消除初始弯矩,试件两端同时使用与母材厚度相等的垫片。
3.3 试验结果

图7 含缺陷的双相钢焊点疲劳寿命比较
Fig.7 Fatigue life comparison of welding spot defects
图7所示为DP600GI点焊接头在不同初始缺陷下的疲劳试验结果。可以看出,相同载荷下,合格焊点的疲劳寿命最大,焊核过小的焊点疲劳寿命次之,烧穿焊点疲劳寿命最小。说明焊接初始缺陷对焊点疲劳寿命有影响,且不同缺陷影响不同。图8所示是不同尺寸的直线型和椭圆型烧穿缺陷的疲劳寿命。由图可知,初始缺陷尺寸越大,疲劳寿命越低;相同烧穿缺陷大小下,直线型缺陷对焊接疲劳寿命的影响大于椭圆型缺陷。
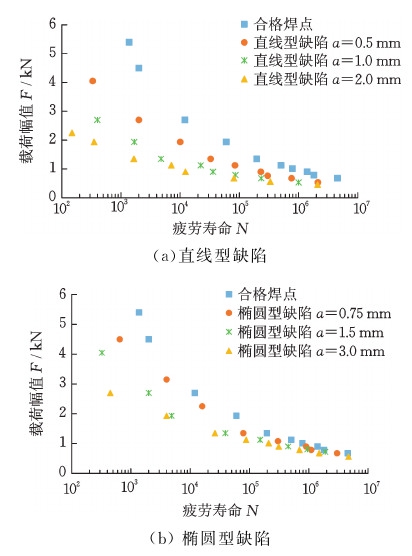
图8 烧穿缺陷下双相钢焊点的疲劳寿命比较
Fig.8 Fatigue life comparison of over burning spot welding
由以上分析尽管能发现焊接缺陷对焊点疲劳寿命的影响,但各点疲劳寿命分布比较分散,如果仅仅依靠文中试件的载荷寿命曲线,无法对其他未试验的焊点进行疲劳寿命评价和预测。
3.4 含初始缺陷的焊点疲劳寿命分析
目前,焊点疲劳寿命研究方法主要有基本载荷-寿命分析法、结构应力法和应力强度法。上述方法在应用时会面临许多问题,比如基本载荷-寿命分析法需拥有各种结构点焊的几何和材料等试验数据;结构应力法需凭经验判据来确定损伤模式;应力强度方法强调线性解法,受材料弹性和小变形影响,且没有考虑残余应力、焊接缺陷等相关因素。

图9 修正平均等效应力强度因子-疲劳寿命的
双对数分布图(R2=0.93)
Fig.9 Double logarithmic distribution of correction of the average equivalent stress intensity factor-fatigue life(R2=0.93)
对含初始缺陷的焊点疲劳寿命预测,基于超声回波特征对裂纹尖端的应力强度因子进行修正。图9所示为使用2.2节推导的修正平均等效应力强度因子对图7、图8中的合格焊点、小焊核焊点和烧穿焊点的疲劳寿命分布进行重新拟合得到的修正平均等效应力强度因子和疲劳寿命的对应关系。从图中可以看出,在![]() 曲线中,所有不同缺陷试件的焊点疲劳寿命分别分布在拟合直线附近,相关系数R2=0.93,证明了修正平均等效应力强度因子能够准确关联含焊接缺陷的焊点疲劳寿命,得出如下
曲线中,所有不同缺陷试件的焊点疲劳寿命分别分布在拟合直线附近,相关系数R2=0.93,证明了修正平均等效应力强度因子能够准确关联含焊接缺陷的焊点疲劳寿命,得出如下![]() 曲线:
曲线:
(19)
4 结论
(1)焊接初始缺陷对焊点疲劳寿命有影响,且影响程度与缺陷类型和大小有关。同一载荷下,合格焊点的疲劳寿命最长,焊核过小的焊点疲劳寿命次之,烧穿焊点疲劳寿命最短;初始缺陷尺寸越大,疲劳寿命越短;直线型缺陷对焊接疲劳寿命的影响大于椭圆型缺陷。
(2)利用断裂力学对焊点疲劳进行分析,将法应力和剪应力相耦合,再基于超声回波的6个特征,采用模糊数学理论得到了缺陷损伤系数,进而得到了修正平均等效应力强度因子作为含焊接缺陷的焊点疲劳寿命的评价参量。
(3)通过对疲劳试验数据进行双对数回归分析,得到了一条主曲线,能有效预测含初始缺陷的点焊接头的疲劳寿命,证明该预测方法有助于合理设计电阻焊点的缺陷容限。
[1] 君迪. 2018中国新车质量研究(IQS)[EB/OL][2019-01-04]. https://china.jdpower.com/zh-hans/press-releases/2018-iqs-cn.
J D POWER. 2018 China Initial Quality Study(IQS)[EB/OL].[2019-01-04]. https://china.jdpower.com/zh-hans/press-releases/2018-iqs-cn.
[2] KHATIB H, MANSOURI K, SALHI B, et al. BS7910 Numerical Modeling of the Welding Defect Influence on Fatigue Life of the Weld Bead with Analyzing Residual Stress Effects[J]. International Jo-
urnal of Engineering and Science, 2014, 10(4):11-18.
[3] CHAPETTI M, STEIMBREGER C. A Simple Fracture Mechanics Estimation of the Fatigue Endurance of Welded Joints[J]. International Journal of Fatigue,2019,125:23-24.
[4] KEPKA M, KEPKA M J. Deterministic and Probabilistic Fatigue Life Calculations of a Damaged Welded Joint in the Construction of the Trolleybus Rear Axle[J]. Engineering Failure Analysis, 2018,93:257-267.
[5] LEINENBACH C, KOSTER M, SCHINDLER H. Fatigue Assessment of Defect-free and Defect-containing Brazed Steel Joints[J]. Journal of Materials Engineering and Performance,2012,21:739-747.
[6] British Standards Institution. Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures[S]. London: BSI Standards Publication,2013.
[7] 宋凯,曾琼,何智成,等.基于超声参数化和熵模型的汽车焊点质量识别[J].机械工程学报,2016, 52(16):86-92.
SONG Kai, ZENG Qiong,HE Zhicheng, et al. Recognition of Vehicle Welding Spot Quality Based on Ultrasonic Parameterized and Entropy Model[J].Journal of Mechanical Engineering,2016,52(16):86-92.
[8] 李向伟,兆文忠,郑成德.基于质量模糊评判模型的焊缝疲劳寿命评估[J]. 焊接学报,2010, 31(8):49-52.
LI Xiangwei, ZHAO Wenzhong, ZHENG Chengde. Evaluation of Weld Fatigue Life Based on Quality Fuzzy Judgement Model[J].Transactions of the China Welding Institution,2010,31(8):49-52.
[9] LEE H,KIM N. Fatigue Life Prediction of Multi Spot Welded Panel Structures Using an Equivalent Stress Intensity Factor[J]. International Journal of Fatigue,2004,26:403-412.
[10] BROEK D. Elementary Engineering Fracture Mechanics[M]. 4th ed. Leiden: Martinus Nijhoff Publishers, 1987:8-23.
[11] TADA H,PARIS P,IRWIN G. The Stress Analysis of Cracks Handbook[M]. New York:ASME,2000:48-80.
