0 引言
据统计,产品的质量问题中有75%是在产品开发设计阶段产生的,而大部分质量问题的修改工作是在制造、试验、使用及维护等后续阶段完成的。在设计阶段,方案越完善,所产生的连带问题就越少。从决策的角度看,设计问题均可视为设计决策问题,基于设计规范、经验、案例、运行维护、用户反馈等数据进行分析、建模、求解而得到设计方案的过程,就是按照某种最优性准则获得决策方案的过程。随着设计流程的推进,不断有新的数据参与到设计决策过程中来,而每一次求解得到的最优设计决策也随着数据的累积而不断调整,直到设计方案在一定最优准则下达成目标。
目前在复杂产品的设计中,由于缺乏有效的工具与方法学的支持,设计方案的合理性很大程度上依赖于设计人员的经验和现场运行验证,即使面对同一个设计任务,不同设计人员的设计方案,其细节往往差别很大。因此,迫切需要基于设计规范及经验等相关数据对设计方案进行综合评估[1],使产品在使用过程中可能出现的问题在设计阶段就被发现并加以解决,从而降低产品成本,缩短研制周期,提高产品竞争力。为此,国内外学者开展了相关研究工作。王发麟等[2]提出了一种基于属性加权相似度的线缆敷设质量评估变精度粗糙集决策方法,相比传统的质量评估方法,该方法能提供更加符合实际的决策结果。张洁等[3]研究了基于大数据的车间运行分析与决策方法体系,提出了“关联+预测+调控”的车间运行分析与决策新模式以及车间运行分析与决策技术体系。张红旗等[4]提出了基于部分可观察马尔可夫决策过程理论的动态可靠性评价方法,通过不完全观测到的设备运行信息,对可靠性状态进行估计。李艳姣等[5]针对原有基于经验的料面形状决策模型的缺陷,提出了基于数据驱动的高炉料面形状优化决策模型,所构建的高炉料面优化决策模型能够及时根据生产情况的变化给出合理的料面形状,使高炉高效稳定运行。AFRIN等[6]提出了集成产品差异化和迁移学习方法的数据驱动框架,用于新产品需求预测。DU等[7]开发了数据驱动的方法用于设计具有高维设计变量的机械系统,使设计问题得到简化。SADATI等[8]对制造过程中基于数据驱动的建模和优化方法进行了研究并应用于轮胎制造企业。ALESSANDRO等[9]对产品创新过程中数据驱动的设计建模的作用和面临的挑战进行了总结和讨论。RUVALD等[10]考察了产品全生命周期各个阶段的不同数据,如设计数据、加工数据、过程数据、用户反馈数据等,根据这些数据的不同特点,在各阶段进行周期性的数据挖掘,为设计决策提供支持。GHOSAL等[11]基于已有的实验数据,开发了描述传感器响应幅度、响应时间和恢复时间三大主要特性的人工神经网络模型,并使用多目标优化技术以预先确定传感器参数集,提高了甲烷检测传感器的性能。NOVARA等[12]提出了一种数据驱动的两自由度非线性控制器的设计方法,该方法基于一个非线性控制器和线性控制器并行运行的两自由度架构,使用了凸优化工具,并通过仿真实例验证了该方法的有效性。CHIU等[13]开发了基于实例推理的客户在线评论分析方法,通过文本数据挖掘和感性工程的集成,提取客户偏好,实现了数据驱动的概念设计自动化,并应用于公路自行车的设计。
复杂产品设计方案的评估需要综合考虑设计、制造、试验、使用、维修等全生命周期各环节的要求,其方案属性即评价准则有多个,评估人员来自不同部门,其质量评估必然属于群决策问题。
本文建立了数据驱动的产品设计方案优化决策的理论框架,构建了单一评估人员的决策规则和指标权重的确定方法,在单人决策的基础上,给出了群体决策的集结方法,并以油田聚合物注入成套装置为对象进行应用。
1 数据驱动的产品设计方案决策框架
本文提出的数据驱动的产品设计方案优化决策框架如图1所示,它适用于产品设计过程的各个阶段。
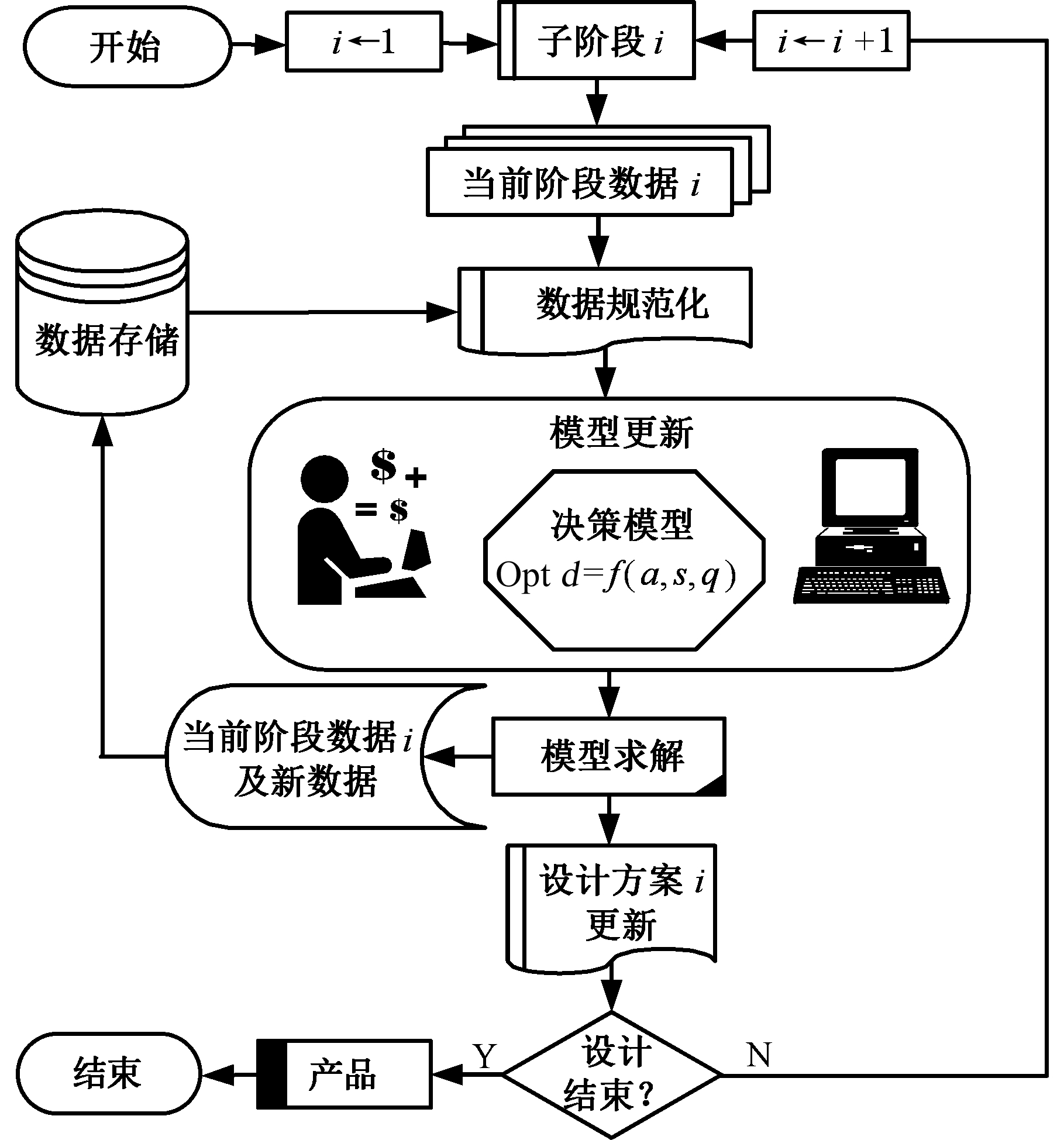
图1 数据驱动的产品决策框架
Fig.1 Data-driven product decision framework
在该设计框架里,设计方案的决策模型是其核心,从设计决策的角度来考察每一个设计子问题,数据影响设计过程的每一个阶段。数据存储单元用以存储从设计开始到设计结束过程中产生的所有相关数据,其中的数据在设计的每一个子阶段中都可以被调用,设计过程中的后续各个阶段可以调用之前阶段产生的数据,而且前面各阶段也可以调用后面各个阶段产生的数据进行设计迭代。各个设计子阶段产生的数据都对求解发挥作用,之后存入数据存储单元以供其他子阶段调用,数据存储单元用于整个设计过程的数据存储,其数据总量不断增大,设计迭代在数据的驱动下最终完成给定的任务。
2 决策模型
在复杂产品的设计中,整合设计历史、工艺、用户偏好等数据到研发中,能够为产品决策提供依据,通过数据分析,企业能够挖掘大量的顾客行为,有利于缩短产品开发时间,提高产品质量。但原始数据很多难以被直接应用,在产品决策过程中,常出现数据的量纲不同或数值差别较大的情况,为使结果客观准确,需要对数据做规范化处理。对于非结构化数据,最为常见的是在客户参与评价时,常常使用语言变量,对于这类数据,可以采用基于三角模糊数的转换方法[14]进行处理。
对决策准则重要性的认识常常存在较大的差异,需要通过一定的方法确定各准则的重要性,即权重。产品方案优化决策的主体包括与产品相关的各类人群,如产品设计、制造、销售、用户人群和企业管理部门人员等,其决策过程是一个群决策的过程,群决策是本文所提出的决策模型的关键因素,其流程如图2所示。

图2 决策模型的运行流程
Fig.2 Data-driven product decision-making process
2.1 单一决策人的决策方法
对于每一类成员单独做出的多属性决策,有多种方法可以使用,如加权和法、层次分析法(analytic hierarchy process,AHP)、消去与选择转换法(ELECTRE)等。本文使用逼近理想解排序法(technique for order preference by similarity to ideal solution,TOPSIS)进行决策,这种方法用相对贴近度值衡量评测对象的水平,对信息的利用充分,步骤清晰[15]。该算法步骤如下。
(1)建立规范化决策矩阵。对于m个方案n个属性的多属性决策问题,原始决策矩阵
X=[Xij]m×n ∀i,j
(1)
式中,Xij为方案i针对属性j的评价值。
对矩阵各元素进行规范化处理:
(2)
(2)构建加权规范化决策矩阵:
V=(vij)m×n=(ωjrij)m×n ∀i,j
(3)
式中,ωj为属性j的权重;rij为规范化之后的元素值。
(3)确定正理想解和负理想解。令v+为正理想解,v-为负理想解,即
v+={(maxvij|j∈J),(minvij|j∈J0),![]()
(4)
v-={(minvij|j∈J),(maxvij|j∈J0),![]()
(5)
式中,J0为成本型准则集;J为效益型准则集。
(4)计算各方案与理想解及负理想解的距离。方案i到理想解的距离
(6)
方案i到负理想解的距离
(7)
(5)各方案的相对贴近度(综合评价指数)
(8)
(6)按Gi大小排列方案的优劣次序。
2.2 决策指标的权重
产品方案决策问题需要解决各目标属性值的不可公度性问题,这一问题通过属性矩阵的规范化可以得到部分解决,但规范化方法不能反映目标的重要性,因此,引入权的概念。权是目标重要性的数量化表示,是衡量目标重要性的手段,本文使用熵法确定决策指标的权重。熵在信息理论中作为信息量的度量,定义为
(9)
其中,k是一个正常数,Pj是一个离散的概率分布。式(9)称为概率分布Pj的熵,当Pj = 1/n时,∀i,S(P1,P2,…,Pn)达到最大值。
产品决策矩阵是信息的载体,故熵可作为评价属性相对重要程度的工具。属性指标间的差异越大,说明提供的信息越多,该属性就越重要。在m个方案和n个属性(指标)的决策矩阵中,属性j的几何射影pij定义为
(10)
其熵Ej为
(11)
其中,k = 1/ln(m),以使0≤Ej≤1。权与熵是互反关系,用1-Ej来代替Ej,并使之归一化以保证下式成立:
0≤ωj≤1
ω1+ω2+…+ωn=1
则权值为
(12)
2.3 决策的集结
对备选方案集进行的评价需要集结群中各成员的意见以形成最终决策结果,本文采用Borda法将单人决策集结为群的决策。Borda函数由法国数学家Borda提出[16],使用Borda法进行决策集结的算法步骤如下。
设U={u1,u2,…, un},对U中的元素进行排序,评审专家m人发表m种意见:
V={v1,v2,…,vm}
其中,vi是第i种意见序列,即U中元素的某一个排序。令u∈U,Bi(u)表示第i种意见序列vi中排在u之后的元素个数,即
若u在vi中排在第1位,则Bi(u)= n-1;
若u在vi中排在第2位,则Bi(u)= n-2;
⋮
若u在vi中排在第k位,则Bi(u)= n-k。
定义u的Borda函数为
U中所有元素按Borda函数值的大小排序,此排序就是集结意见之后的群体决策结果。
当参与决策的人员较多且重要性差距较大时,专家经验更为重要,可赋予决策人不同权值,以突出专家的影响,并采用求加权和的方法求取每个方案的总Borda分。
3 实例研究
为了补充地层能量,实现注水驱油,提高采收率,需要将一定量的水注入地层。当油田开采进入高含水期后,产液量增加,出油含水率增大,需增加配套的脱水装置,导致成本增大,效益降低。为了降低采出液含水率,降低采油成本,采用向油田注入聚合物溶液的方法,可实现对地层残存小量原油的驱赶。聚合物驱油技术比水驱提高采收率20%以上,这是提高采收率、保证油田可持续发展的重要技术措施,目前,大庆油田、胜利油田、辽河油田等均广泛使用了这一技术,大庆油田是世界上聚合物驱油规模最大的油田。
聚合物注入成套装置是实施驱油技术的核心设备,其设计涉及流体、机械、材料、控制、多相流等多领域专业知识,设备投入大,试验周期长。评审专家拟将该成套装置的成本、流量精度、机械效率、密封性能、操作性能、制造工艺性6项作为评价指标,其中成本和流量精度数值越小越好,为成本型指标,其余4项为效益型指标;评审专家由设计、工艺和生产管理三组人员组成,从不同视角进行考察;为简化过程,本文只在产品设计的最终阶段,对5种设计方案(分别记为A、B、C、D、E)进行评价优选。
成套装置中的往复式高压注聚泵是最为关键的子系统,是对聚合物母液进行升压的动力装置,其整体布局采用经典的三柱塞卧式结构,具有结构紧凑、体积小、性能可靠的特点。动力端采用曲轴连杆传动机构,飞溅润滑,主结构参数选择上采用长行程、低往复次数、大柱塞直径,以提高容积效率。A、B、D三种方案采用齿轮减速器,方案A使用刚性凸缘联轴器,方案B使用十字滑块联轴器,方案D采用弹性套柱销联轴器,方案C使用窄V带减速机构,方案E采用普通三角带减速机构;在液力端,方案A、B、C采用直通式结构,上导向锥形阀,方案D和E采用阶梯型结构,下导向锥形阀,各阀均设计有阀簧以减小泵阀滞后角。过流通道采用圆滑过渡,变径处加工成倒角结构,以降低对聚合物溶液的机械降解,为降低流速及黏损率,入口流道直径设计取值比出口略大。
评价择优时,首先由设计组进行评价,其中成本、流量精度、机械效率直接采用原始数据,成本单位为万元,其余指标按5分制评价,评价值构成原始决策矩阵,见表1。首先计算指标权重,由式(10)得几何射影,见表2。由式(11)、式(12)计算熵和权值,共有5个方案,因此k=1/ln5=0.621 3,计算结果列于表3。由式(2)得规范化决策矩阵,见表4。由式(3)及前文得到的指标权重,得加权规范化决策矩阵,见表5。
表1 原始决策矩阵
Tab.1 Original decision matrix

指标1指标2指标3指标4指标5指标6A25±1.1%0.984.54.34.3B24±1.3%0.964.24.24.0C23±1.1%0.974.74.34.4D24.5±1.3%0.954.64.14.2E23.5±1.2%0.964.44.24.1
表2 几何射影pij
Tab.2 Geometric projection pij
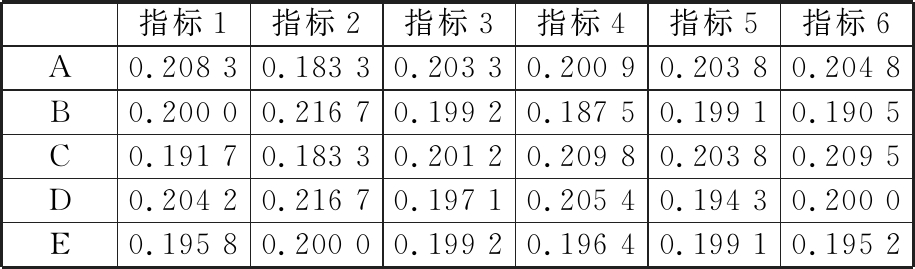
指标1指标2指标3指标4指标5指标6A0.208 30.183 30.203 30.200 90.203 80.204 8B0.200 00.216 70.199 20.187 50.199 10.190 5C0.191 70.183 30.201 20.209 80.203 80.209 5D0.204 20.216 70.197 10.205 40.194 30.200 0E0.195 80.200 00.199 20.196 40.199 10.195 2
表3 熵和权值
Tab.3 Entropy and weight

指标1指标2指标3指标4指标5指标6Ej0.999 70.998 20.999 90.999 50.999 90.999 61-Ej0.000 30.001 80.000 10.000 50.000 10.000 4ωj0.093 70.562 50.031 30.156 20.031 30.125 0
表4 规范化决策矩阵
Tab.4 Normalized decision matrix

指标1指标2指标3指标4指标5指标6A0.465 60.408 80.454 60.448 80.455 60.457 6B0.447 00.483 10.445 30.418 90.445 00.425 6C0.428 30.408 80.449 90.468 80.455 60.468 2D0.456 30.483 10.440 60.458 80.434 40.446 9E0.437 70.445 90.445 30.438 90.445 00.436 3
表5 加权规范化决策矩阵
Tab.5 Weighted normalized decision matrix
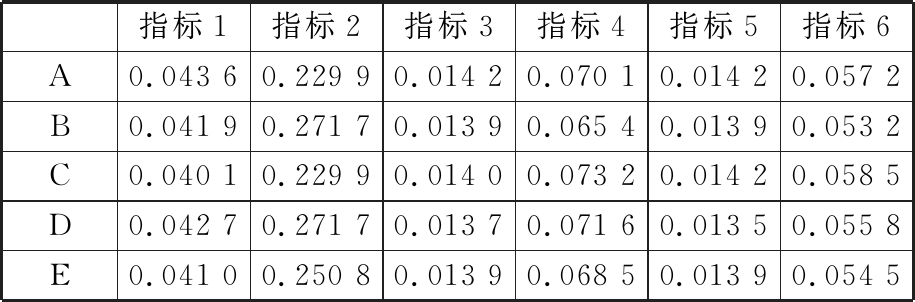
指标1指标2指标3指标4指标5指标6A0.043 60.229 90.014 20.070 10.014 20.057 2B0.041 90.271 70.013 90.065 40.013 90.053 2C0.040 10.229 90.014 00.073 20.014 20.058 5D0.042 70.271 70.013 70.071 60.013 50.055 8E0.041 00.250 80.013 90.068 50.013 90.054 5
由式(4)、式(5)可得理想解及负理想解,理想解为{0.040 1,0.229 9,0.014 2,0.073 2,0.014 2,0.058 5},负理想解为{0.043 6,0.271 7,0.013 7,0.065 4,0.013 5,0.053 2}。由式(6)、式(7)分别计算各方案与理想解及负理想解的距离,由式(8)计算各方案的相对贴近度,结果见表6。
表6 相对贴近度
Tab.6 Relative closeness
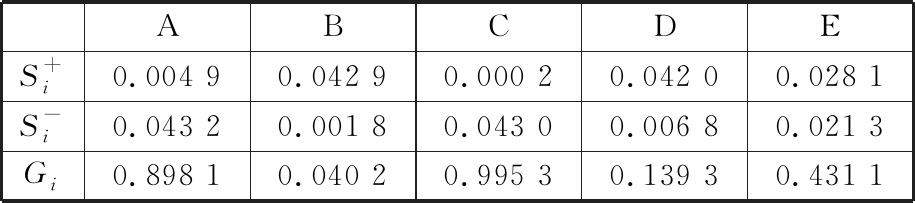
ABCDES+i0.004 90.042 90.000 20.042 00.028 1S-i0.043 20.001 80.043 00.006 80.021 3Gi0.898 10.040 20.995 30.139 30.431 1
根据相对贴近度大小,方案排序为C≻A≻E≻D≻B。工艺和生产管理人员的方案优选结果用同样的方法获得,本文直接给出排序结果,工艺人员排序结果为C≻E≻A≻B≻D,管理人员排序结果为A≻C≻E≻B≻D。
根据Borda函数的定义,方案数为5,即n=5,排在第一位的方案的Borda分为4,排在第二位的方案的Borda分为3,以此类推,可得各设计方案相应的Borda分值,然后计算其总分。本例中决策人员均为专业人员,从不同专业角度对方案进行评估,对他们的重要性视为相同。结果见表7。由总Borda分的大小,可知设计方案C为群决策得到的最优方案。
表7 Borda分值及总分
Tab.7 Borda score and total score

ABCDE设计人员30412工艺人员21403管理人员41302总分921117
4 结论
本文提出的数据驱动的设计方案优化决策方法适用于产品设计的各个阶段,通过信息熵获得方案属性的权重,通过TOPSIS法进行单一评审者的决策,通过Borda函数进行决策的集结,实现了设计方案的多属性群决策优化,尽可能避免了判断的主观性,为方案择优提供了更好的依据。
在创新性设计的前期阶段,设计约束较少,数据可能不够完善,知识发挥着重要作用,此时数据驱动还不能完全代替知识的作用,今后应进行数据与知识融合驱动的深入研究,以提高设计自动化水平。
工程优化方法的价值体现在应用上,除了理论体系的发展与完善外,开发运行可靠、使用方便的决策分析软件系统,将推进这些方法在工程实践中的推广和应用。
[1] 杨楠,叶迪,林杰,等.基于数据驱动具有自我学习能力的机组组合智能决策方法研究[J].中国电机工程学报,2019,39(10):2934-2945.
YANG Nan, YE Di, LIN Jie,et al.Research on Data-driven Intelligent Security-constrained Unit Commitment Dispatching Method with Self-learning Ability[J].Proceedings of the Chinese Society for Electrical Engineering,2019,39(10):2934-2945.
[2] 王发麟,廖文和,郭宇,等.复杂机电产品中线缆敷设质量评估的变精度粗糙集决策方法[J]. 中国机械工程,2015,26(15): 2062-2068.
WANG Falin, LIAO Wenhe, GUO Yu,et al. Variable Precision Rough Set Decision-making Method for Quality Assessment of Cable Harness Wiring in Complex Mechatronic Product[J].China Mechanical Engineering,2015,26(15):2062-2068.
[3] 张洁,高亮,秦威,等.大数据驱动的智能车间运行分析与决策方法体系[J]. 计算机集成制造系统,2016,22(5):1020-1028.
ZHANG Jie,GAO Liang,QIN Wei,et al. Big-data-driven Operation Alanalysis and Decision-making Methodology in Intelligent Workshop[J].Computer Integrated Manufacturing Systems,2016,22(5):1020-1028.
[4] 张红旗,邵晓东,胡祥涛. 基于部分可观察马尔可夫决策过程的机电装备动态可靠性评价方法[J]. 中国机械工程,2016,27(18): 2482-2487.
ZHANG Hongqi, SHAO Xiaodong,HU Xiangtao. Dynamic Reliability Assessment Method Based on POMDP for Electromechanical Equipment[J]. China Mechanical Engineering,2016,27(18):2482-2487.
[5] 李艳姣, 张森, 尹怡欣.基于数据驱动的高炉料面优化决策模型研究[J]. 控制理论与应用,2018,35(3):324-334.
LI Yanjiao, ZHANG Sen, YIN Yixin. Research on Optimization Model of Blast Furnace Burden Surface Based on Data Driven[J]. Control Theory & Applications,2018,35(3):324-334.
[6] AFRIN K, NEPAL B, MONPLAISIR L. A Data-driven Framework to New Product Demand Prediction: Integrating Product Differentiation and Transfer Learning Approach[J]. Expert Systems with Applications, 2018,18: 246-257.
[7] DU Xianping, ZHU Feng. A New Data-driven Design Methodology for Mechanical Systems with Highdimensional Design Variables[J]. Advances in Engineering Software, 2018,117: 18-28.
[8] SADATI N, CHINNAM R B, NEZHAD M Z. Observational Data-driven Modeling and Optimization of Manufacturing Processes[J]. Expert Systems with Applications, 2018,93: 456-464.
[9] ALESSANDRO B. Role and Challenges of Data-driven Design in the Product Innovation Process[J].IFAC PapersOnLine, 2018, 51/11:1107-1112.
[10] RUVALD R, FRANK M, JOHANSSON C. Data Mining through Early Experience Prototyping-a step towards Data Driven Product Service System Design[J]. IFAC PapersOnLine, 2018, 51/11:1095-1100.
[11] GHOSAL S, DEY S, BHATTACHARYYA P,et al. Data-driven Design of Ternary Alloy Catalysts for Enhanced Oxide-based Gassensors’ Performance[J]. Computational Materials Science, 2019,161: 255-260.
[12] NOVARA C, FORMENTIN S, SAVARESI S M,et al. Data-driven Design of Two Degree-of-freedom Nonlinear Controllers:the D2-IBC Approach[J]. Automatica, 2016,72: 19-27.
[13] CHIU M C, LIN K Z.Utilizing Text Mining and Kansei Engineering to Support Data-driven Design Automation at Conceptual Design Stage[J]. Advanced Engineering Informatics, 2018,38: 826-839.
[14] 陈宇,王娜,王晋东.利用三角模糊数的语言变量项集减项算法[J]. 清华大学学报(自然科学版),2017,57(8): 892-896.
CHEN Yu, WANG Na, WANG Jindong. An N-fold Reduction of Linguistic Variables Based on the Triangular Fuzzy Numbers[J]. Journal of Tsinghua University(Science&Technology),2017,57(8):892-896.
[15] 岳超源.决策理论与方法[M].北京:科学出版社, 2018:212-213.
YU Chaoyuan.Decision Theory and Method[M]. Beijing: Science Press, 2018:212-213.
[16] 谢季坚,刘承平.模糊数学方法及其应用[M]. 武汉:华中科技大学出版社,2013:128-129.
XIE Jijian, LIU Chengping.Fuzzy Mathematics Method and Its Application[M]. Wuhan: Huazhong University of Science and Technology Press, 2013:128-129.
